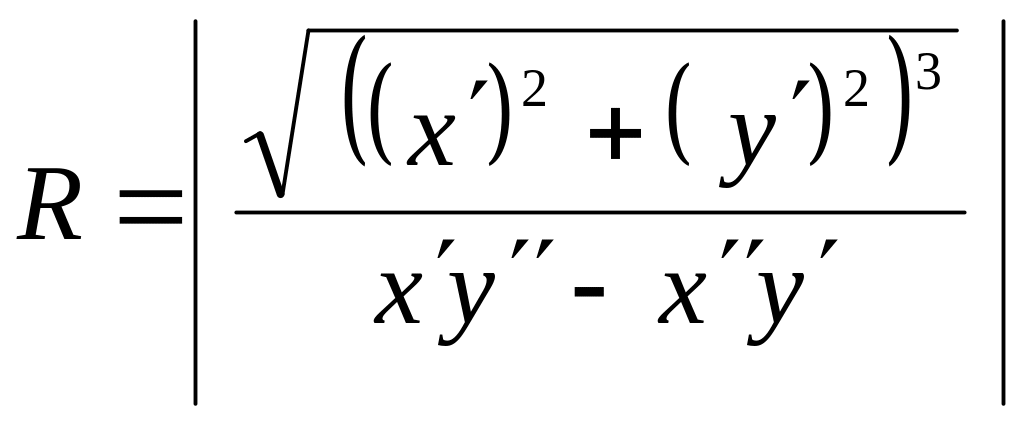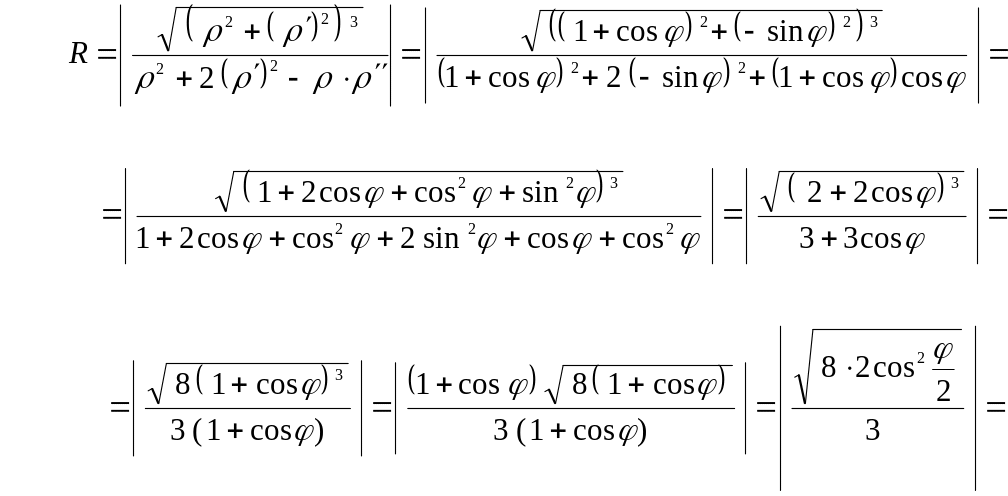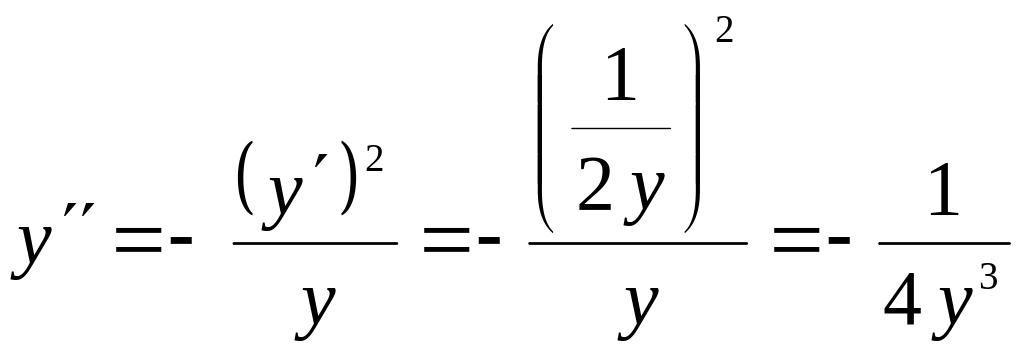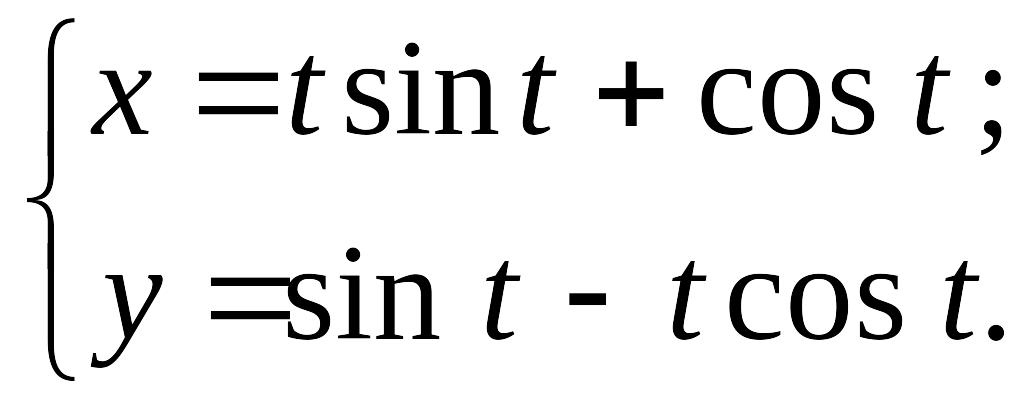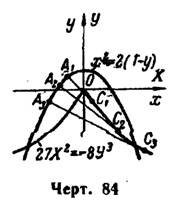Как найти координаты центра кривизны - Исправление недочетов и поиск решений вместе с Examum.ru

Радиус, центр и круг кривизны. Эволюта и эвольвента

Радиусом
кривизны называется величина, обратная
кривизне, т. е.

.

Если
плоская кривая отнесена к прямоугольной
системе координат и задана уравнением

,
то радиус кривизны

выражается формулой

Eсли
плоская кривая отнесена к прямоугольной
системе координат и задана параметрически
системой уравнений

, то радиус кривизны

выражается формулой

где

,

,

Если
плоская кривая отнесена к полярной
системе координат и задана уравнением

,
то радиус кривизны

выражается формулой

где

Окружностью
кривизны данной линии её точке А
называется
предельное положение окружности,
проходящей через три точки A,
B,
C
кривой, когда

и

.

Радиус
окружности кривизны равен радиусу
кривизны. Центр окружности кривизны
называется центром кривизны и находится
на нормали к линии, проведенной в точке
А
в сторону вогнутости этой линии.

Координаты

и

центра кривизны линии

вычисляются по формулам:

Эволютой
линии называется множество её центров
кривизны, а сама линия относительно
своей эволюты называется эвольвентой.

Формулы
для координат центра кривизны можно
рассматривать как параметрические
уравнения эволюты, где параметром
является абсцисса х
исходной линии.

Данная
линия может иметь лишь одну эволюту, но
у данной эволюты существует бесконечное
множество эвольвент.

Пример.
Найти
радиус кривизны линии

в
точке с абсциссой

Решение.
Найдем значения производных первого и
второго порядков функции

в точке с абсциссой

Подставим
найденные значения

в
формулу

Следовательно,
радиус кривизны
линии

в
точке с абсциссой

Пример.
Найти
радиус кривизны линии

в
точке

.

Решение.
Дифференцируя по t,
получим

Вычислим
значения производных в
точке

Подставляя
найденные значения

в
формулу

имеем

Следовательно,
радиус кривизны
линии

в
точке с абсциссой

Пример.
Найти
радиус кривизны кардиоиды

в
любой её точке.

Решение.
Найдем

Подставим
найденные выражения в формулу

Следовательно,
радиус кривизны
кардиоиды

в
любой её точке

Пример.
Найти
координаты

центра кривизны линии

в
точке

.

Решение.
Найдем значения производных первого
и второго порядков функции

в точке с абсциссой

Подставим
значения

и найденные
значения

в
формулы

Следовательно,
координаты
центра кривизны линии

в
точке

Пример.
Составить
уравнение эволюты кривой

.

Решение.
Продифференцируем дважды уравнение
параболы:

;

Так
как

,
то

Найдем
координаты

центра кривизны линии ,
предварительно выразив х
из уравнения

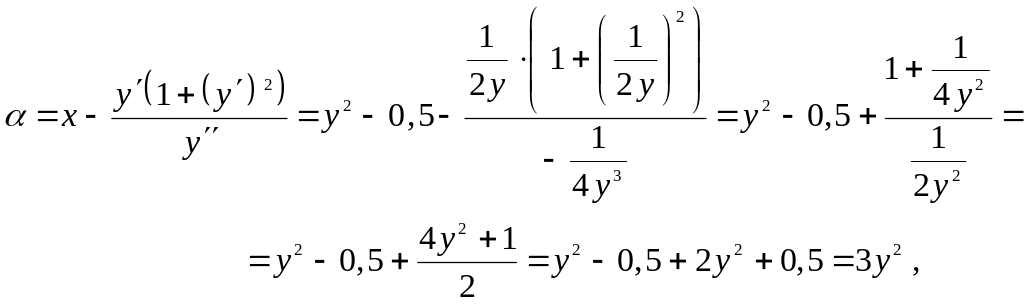
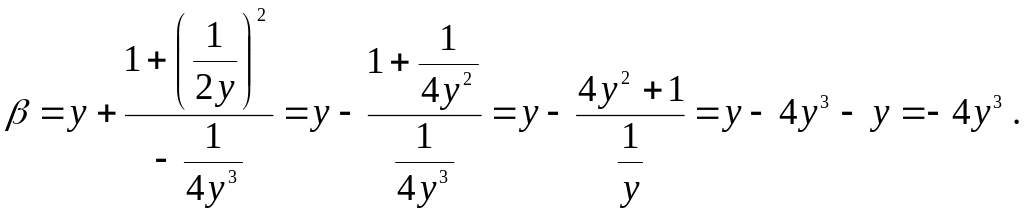
Имеем

—
уравнение эволюты в параметрической
форме. Выразим параметр у
из

и

;

Окончательно
получаем,

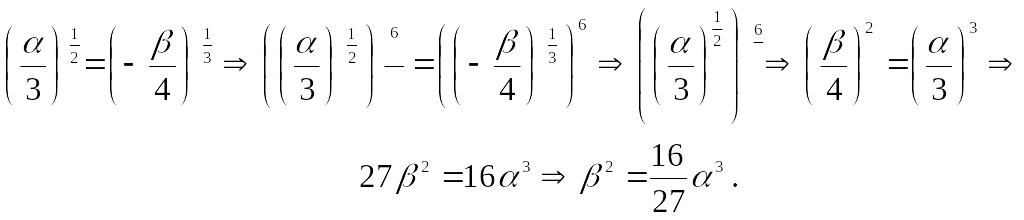
Следовательно,
уравнение
эволюты кривой

имеет вид

(уравнение
полукубической параболы).

Упражнения

1.
Найти радиус кривизны линии

в
точке A:

а)

,
A
(
2; 2 ), б)

,
A
(
0; 1 ) .

2.
Найти радиус кривизны трехлепестковой
розы

, при

.

3.
Найти координаты

центра кривизны линии

в
точке A:

а)

,
A
(
1; 1 ), б)

,
A
(
1; 0 ) .

4.
Составить уравнение эволюты кривой

а)

,
б)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Смысл понятий радиуса, круга и центра кривизны

В технических приложениях часто оказывается удобным использовать окружности для приближенной замены кривой в окрестностях рассматриваемых точек. Это существенно упрощает решение целого ряда задач за счет применения более удобных выражений.

Наиболее употребительными характеристиками любой кривой являются касательная и нормаль. Касательная — предельное положение секущей $MN$ при неограниченном приближении точки $N$ к точке $M$ вдоль кривой. Нормаль — прямая, проходящая через точку касания перпендикулярно касательной.

Уравнение касательной в точке $Mleft(x_{0} ,y_{0} right)$ к кривой $y=fleft(xright)$ имет вид $y-y_{0} =y’left(x_{0} right)cdot left(x-x_{0} right)$, уравнение нормали $y-y_{0} =-frac{1}{y’left(x_{0} right)} cdot left(x-x_{0} right)$.

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

Задача 1

Записать уравнения касательной и нормали к кривой $y=3cdot x^{2} -x+2$ в заданной точке $x_{0} =1$.

Значение функции в заданной точке: $y_{0} =yleft(x_{0} right)=yleft(1right)=3cdot 1^{2} -1+2=4$.

Значение производной в заданной точке:

[y’=left(3cdot x^{2} -x+2right)^{{‘} } =6cdot x-1; y’left(x_{0} right)=y’left(1right)=6cdot 1-1=5.]

Уравнение касательной: $y-4=5cdot left(x-1right)$ или $5cdot x-y-1=0$.

Уравнение нормали: $y-4=-frac{1}{5} cdot left(x-1right)$ или $x+5cdot y-21=0$.

Определение

Радиус кривизны — это параметр кривой, значение которого обратно значению кривизны $R=frac{1}{K} $. Следовательно, это такая же переменная величина, как и кривизна.

Если в данной точке $M$ построить нормаль к кривой и отложить на ней в сторону вогнутости кривой отрезок, равный по длине радиусу кривизны кривой в этой точке, то получим точку — центр кривизны. Окружность с центром в полученной точке и радиусом, равным радиусу кривизны — это круг кривизны. Так как данная кривая и её круг кривизны касаются в данной точке, то они имеют в данной точке общую касательную. Кроме того, значения кривизны кривой и круга кривизны в данной точке совпадают.

Важным свойством круга кривизны является то, что он является соприкасающимся кругом, то есть предельным положением круга, проходящего через три точки кривой, стремящимся к совпадению в данной.

Если некоторая точка перемещается вдоль кривой, то и соответствующий ей центр кривизны также описывает некоторую кривую. Геометрическое место центров кривизны данной кривой называется её эволютой. При этом данная кривая по отношению к своей эволюте называется её эвольвентой.

Вычисление радиуса и определение центра круга кривизны

Формулы для радиуса кривизны получить легко, если известны формулы для вычисления кривизны кривой.

При произвольном параметрическом задании кривой $x=xleft(tright)$ и $y=yleft(tright)$ имеем $R=frac{sqrt{left(left(x’_{t} right)^{2} +left(y’_{t} right)^{2} right)^{3} } }{y»_{tt} cdot x’_{t} -x»_{tt} cdot y’_{t} } $.

Если кривая задана в явном виде $y=fleft(xright)$, то $R=frac{sqrt{left(1+left(y’right)^{2} right)^{3} } }{y»} $.

Если кривая задана в полярных координатах $rho =rho left(phi right)$, то $R=frac{sqrt{left(rho ^{2} +left(rho ‘_{phi } right)^{2} right)^{3} } }{rho ^{2} +2cdot left(rho ‘_{phi } right)^{2} -rho cdot rho »_{phi phi } } $.

«Радиус, круг и центр кривизны» 👇

Задача 2

Найти радиус кривизны экспоненты $y=e^{x} $ при $x=0$.

Находим производные: $y’=e^{x} $; $y»=e^{x} $.

По формуле для радиуса кривизны получаем:

[R=frac{sqrt{left(1+left(y’right)^{2} right)^{3} } }{y»} =frac{sqrt{left(1+left(e^{x} right)^{2} right)^{3} } }{e^{x} } =frac{sqrt{left(1+e^{2cdot x} right)^{3} } }{e^{x} } .]

Вычисляем радиус кривизны экспоненты при $x=0$:

[Rleft(0right)=frac{sqrt{left(1+e^{2cdot 0} right)^{3} } }{e^{0} } =2cdot sqrt{2} . ]

Задача 3

Найти радиус кривизны кардиоиды $rho =1+cos phi $.

Находим производные: $rho ‘=-sin phi $; $rho »=-cos phi $.

Вычисляем:

[rho ^{2} +rho ‘^{2} =left(1+cos phi right)^{2} +left(-sin phi right)^{2} =2cdot left(1+cos phi right);]

[rho ^{2} +2cdot rho ‘^{2} -rho cdot rho »=left(1+cos phi right)^{2} +2cdot left(-sin phi right)^{2} -left(1+cos phi right)cdot left(-cos phi right)=]

[=3cdot left(1+cos phi right).]

По формуле для радиуса кривизны получаем:

[R=frac{sqrt{left(rho ^{2} +left(rho ‘_{phi } right)^{2} right)^{3} } }{rho ^{2} +2cdot left(rho ‘_{phi } right)^{2} -rho cdot rho »_{phi phi } } =frac{sqrt{left(2cdot left(1+cos phi right)right)^{3} } }{3cdot left(1+cos phi right)} =frac{2}{3} cdot sqrt{2cdot left(1+cos phi right)} =frac{4}{3} cdot cos frac{phi }{2} .]

Найдем координаты центра кривизны $Pleft(x_{C} ;y_{C} right)$ кривой $y=fleft(xright)$.

Координаты центра кривизны для точки $Mleft(x;yright)$ удовлетворяют уравнению нормали $y_{C} -y=-frac{1}{y’left(xright)} cdot left(x_{C} -xright)$.

Уравнение круга кривизны: $left(x-x_{C} right)^{2} +left(y-y_{C} right)^{2} =R^{2} $.

Решив систему $left{begin{array}{c} {y_{C} -y=-frac{1}{y’left(xright)} cdot left(x_{C} -xright)} \ {left(x-x_{C} right)^{2} +left(y-y_{C} right)^{2} =R^{2} } end{array}right. $, получим искомые координаты центра кривизны: $left{begin{array}{c} {x_{C} =x-frac{y’cdot left(1+y’^{2} right)}{y»} } \ {y_{C} =y+frac{1+y’^{2} }{y»} } end{array}right. $.

Координаты центра кривизны по существу являются параметрическими уравнения эволюты.

Задача 4

Найти эволюту параболы $y=x^{2} $. Результаты представить графически.

Находим производные: $y’=2cdot x$; $y»=2$.

По формулам $left{begin{array}{c} {x_{C} =x-frac{y’cdot left(1+y’^{2} right)}{y»} } \ {y_{C} =y+frac{1+y’^{2} }{y»} } end{array}right. $ находим координаты центра кривизны для произвольной точки $Mleft(x;yright)$.

Получаем:

[x_{C} =x-frac{2cdot xcdot left(1+left(2cdot xright)^{2} right)}{2} =-4cdot x^{3} ;]

[y_{C} =y+frac{1+left(2cdot xright)^{2} }{2} =3cdot x^{2} +frac{1}{2} .]

Полученные выражения фактически представляют собой параметрические уравнения эволюты, в которых $x$ является параметром. Если исключить параметр $x$ из этих уравнений, то может быть получено уравнение вида $Fleft(x_{C} ;y_{C} right)=0$, которое непосредственно связывает координаты эволюты.

Совмещенный график эвольвенты $y=x^{2} $ и её эволюты:

На графике синей линией изображена парабола $y=x^{2} $, а красной линией — её эволюта. Эволюта представляет собой полукубическую параболу.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

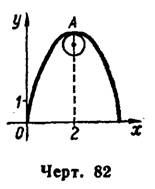
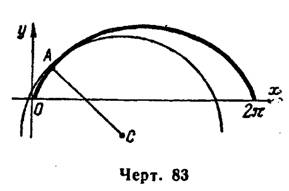
Пример 3. Найти координаты центра кривизны и построить кривую и круг кривизны кривой:
1) $y=4x-x^{2}$ в ее вершине;
2) x=t-sin t,: y=1-cos t в точке, где $displaystyle t=frac{pi }{2}$ .
Решение. 1) Данное уравнение определяет параболу, ось которой параллельна оси . Найдем ее вершину как точку, где касательная параллельна оси , т. е. где y'=0 :

y'=4-2x;: y'=0 при x=2;: y(2)=4.

Далее по формулам

$displaystyle X=x-frac{dot{x}^{2}+dot{y}^{2}}{dot{x}ddot{y}-dot{y}ddot{x}}dot{y}=x-frac{1+(y')^{2}}{y''}y',$

$displaystyle Y=y+frac{dot{x}^{2}+dot{y}^{2}}{dot{x}ddot{y}-dot{y}ddot{x}}dot{x}=y+frac{1+(y')^{2}}{y''}.; ; (2)$

находим координаты центра кривизны данной параболы в ее вершине (2; 4)

$displaystyle X=x-frac{1+(y')^{2}}{y''}y'=2;: Y=y+frac{1+(y')^{2}}{y''}=frac{7}{2}$

и строим параболу и круг кривизны в ее вершине (рис. 82).
2) Находим производные dot{x}=1-cos t,: ddot{x}=sin t,: dot{y}=sin t,: ddot{y}=cos t , их значения при $displaystyle t=frac{pi }{2}$ :

$displaystyle dot{x}left ( frac{pi }{2} right )=1,: ddot{x}left ( frac{pi }{2} right )=1,: dot{y}left ( frac{pi }{2} right )=1,: ddot{y}left ( frac{pi }{2} right )=0,$

и по формулам (2) координаты центра кривизны

$displaystyle X=x-frac{dot{x}^{2}+dot{y}^{2}}{dot{x}ddot{y}-dot{y}ddot{x}}dot{y}=frac{pi }{2}+1;: Y=y+frac{dot{x}^{2}+dot{y}^{2}}{dot{x}ddot{y}-dot{y}ddot{x}}dot{x}=-1.$

Затем строим данную циклоиду, ее точку $displaystyle Aleft ( frac{pi }{2}-1;1 right )$ , где
$displaystyle t=frac{pi }{2}$ , найденный центр кривизны $displaystyle Cleft ( frac{pi }{2}+1;-1 right )$ и круг кривизны (рис. 83).

Пример 4. В каких точках параболы $displaystyle y=sqrt{2}x^{2}$ радиус кривизны равен единице?
Решение. Находим производные displaystyle y'=2sqrt{2}x,: y''=2sqrt{2} и по формуле (1)

$displaystyle K=frac{left | y'' right |}{left [ 1+(y')^{2}right ]^{frac{3}{2}}}=frac{left | dot{x}ddot{y}-dot{y}ddot{x} right |}{(dot{x}^{2}+dot{y}^{2})^{frac{3}{2}}}, ; ; ; ; (1)$

радиус кривизны параболы в любой ее точке с абсциссой :

$displaystyle R(x)=frac{(1+8x^{2})^{frac{3}{2}}}{2sqrt{2}}.$

Полагая R(x)=1 , получим абсциссы искомых точек

$displaystyle 2sqrt{2}=(1+8x^{2})^{frac{3}{2}};: (2sqrt{2})^{frac{2}{3}}=1+8x^{2};: 8x^{2}=1;: x=pm frac{1}{2sqrt{2}}.$

$
Пример 5. В какой точке кривая $displaystyle y=e^{x}$ имеет наибольшую кривизну?
Решение. Находим производные $displaystyle y'=y''=e^{x}$ и кривизну данной кривой в любой точке:

$displaystyle K(x)=frac{e^{x}}{(1+e^{2x})^{frac{3}{2}}}.$

Далее ищем наибольшее значение функции K(x) , которая определена и непрерывна на всей числовой оси:

$displaystyle K'(x)=frac{e^{x}(1-2e^{2x})}{(1+e^{2x})^{frac{5}{2}}};: K'(x)=0$ при $displaystyle 1-2e^{2x}=0,$

т.е. в единственной точке $displaystyle x_{0}=-frac{ln 2}{2}$ . Определяя знаки K'(x) слева и справа от этой критической точки:

$displaystyle left{begin{matrix} X=x-frac{1+(y')^{2}}{y''}=x-frac{1+x^{2}}{-1}(-x);\ Y=y+frac{1+(y')^{2}}{y''}=1-frac{x^{2}}{2}+frac{1+x^{2}}{-1}; end{matrix}right.$

$displaystyle left{begin{matrix} X=-x^{3};\ Y=-frac{3}{2}x^{2}. end{matrix}right.$

Это параметрические уравнения эволюты. Исключая из них параметр , получим $displaystyle 27X^{2}=-8Y^{3}$ — уравнение полукубической параболы. Данная парабола и найденная ее эволюта изображены на рис. 84.

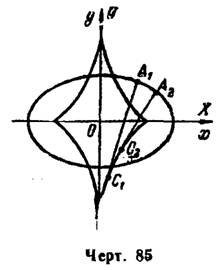
2) Из уравнений эллипса найдем производные dot{x}=-asin t,: ddot{x}=-acos t,: dot{y}=bcos t,: ddot{y}=-bsin t и по формулам (2) получим, после упрощений, параметрические уравнения эволюты эллипса

$displaystyle X=frac{c^{2}}{a}cos ^{3}t,: Y=-frac{c^{2}}{b}sin ^{3}t,$ где $displaystyle c^{2}=a^{2}-b^{2}$

Эллипс и его эволюта построены на рис. 85.

Источник

Пусть кривая (Gamma) задана натуральным уравнением. Будем предполагать, что в точке (MinGamma), где (overrightarrow{OM}=textbf{r}(s)), существует кривизна (k=k(s)neq 0). Тогда радиус кривизны кривой (Gamma) в точке (M) равен
$$
R=R(s)=frac{1}{k(s)}.label{ref42}
$$

Отложим на главной нормали кривой (Gamma) (рис. 22.9) в направлении главной нормали (nu=nu(s)) отрезок (MN) длиной (R=R(s)) и назовем точку (N) центром кривизны кривой (Gamma) в точке (M). Пусть (overrightarrow{ON}=rho).

Так как (overrightarrow{MN}=R(s)nu(s)), то получаем:
$$
boldsymbol{rho}=textbf{r}(s)+R(s)boldsymbol{nu}(s).label{ref43}
$$

Рис. 22.9

Используя формулу eqref{ref42} и равенство
$$
frac{d^{2}textbf{r}}{ds^{2}}=frac{dtau}{ds}=k(s)boldsymbolnu(s),nonumber
$$
запишем уравнение eqref{ref43} в следующем виде:
$$
boldsymbolrho=textbf{r}(s)+frac{1}{(k(s))^2}frac{d^2textbf{r}}{ds^2}.label{ref44}
$$

Предполагая, что во всех точках кривой (Gamma) кривизна отлична от нуля, построим для каждой точки кривой центр кривизны и назовем множество всех центров кривизны кривой (Gamma) эволютой этой кривой.

Если кривая (Gamma_1) — эволюта кривой (Gamma), то кривую (Gamma) называют эвольвентой кривой (Gamma_1). Уравнение эволюты кривой (Gamma), заданной натуральным уравнением, имеет вид eqref{ref44}.

Если кривая (Gamma) задана уравнением кривой в векторной форме, то уравнение эволюты этой кривой можно получить, заменив в равенстве eqref{ref44} (k) и (displaystylefrac{d^{2}textbf{r}}{ds^{2}}) их выражениями по формулам отсюда и отсюда.

В случае, когда плоская кривая (Gamma) задана уравнением (Gamma={x=x(t),;y=y(t),;alphaleq tleqbeta}), ее кривизна выражается формулой отсюда, а (displaystyle frac{d^2textbf{r}}{ds^2}) — формулой из этого утверждения, где
$$
textbf{r}’=(x’,y’),quad r″=(x″,y″),quad s’=sqrt{(x’)^{2}+(y’)^{2}},quad s″=frac{x’x″+y’y″}{s},nonumber
$$
и поэтому
$$
frac{d^{2}textbf{r}}{ds^{2}}=left(frac{x″}{(s’)^{2}}-frac{x'(x’x″+y’y″)}{(s’)^{4}},;frac{y″}{(s)^{2}}-frac{y'(x’x″+y’y″)}{(s’)^{4}}right)=\=left(displaystyle y’frac{x″y’-x’y″}{((x’)^{2}+(y’)^{2})^{2}},; x’frac{y″x’-y’x″}{((x’)^{2}+(y’)^{2})^{2}}right).nonumber
$$
Если (boldsymbolrho=(xi,eta)), то уравнение eqref{ref44} в координатной форме примет вид
$$
xi=x-y’frac{(x’)^{2}+(y’)^{2}}{x’y″-y’x″},quad eta=y+x’frac{(x’)^{2}+(y’)^{2}}{x’y″-y’x″}.label{ref45}
$$

Равенства eqref{ref45} задают эволюту кривой (Gamma) в координатной форме.

Замечание 1.

Приведем без доказательства физическое истолкование эволюты и эвольвенты. Пусть на эволюту натянута гибкая нерастяжимая нить. Если эту нить развертывать, оставляя все время натянутой, то конец нити опишет эвольвенту. Этим можно объяснить термины эволюта («развертка») и эвольвента («развертывающаяся»).

Пример 1.

Найти эволюту эллипса (x=acos t, y=bsin t).

Решение.

(triangle) В этом случае (x’=-asin t,;y’=bcos t,;x″=acos t,;y″= -bsin t),и формулы eqref{ref45} принимают вид
$$
xi=frac{a^{2}-b^{2}}{a}cos^3 t,quad eta=frac{b^{2}-a^{2}}{b}sin^{3}t.nonumber
$$
Следовательно, эволютой эллипса является астроида. (blacktriangle)

Рис. 22.10

Если плоская кривая задана уравнением (y=f(x)), то уравнения eqref{ref45} записываются в виде
$$
xi=x-frac{1+(f'(x))^{2}}{f″(x)}f'(x),qquad eta=f(x)+frac{1+(f'(x))^{2}}{f″(x)}.label{ref46}
$$

Пример 2.

Найти эволюту параболы (y=ax^{2}).

Решение.

Рис. 22.11

(triangle) Используя формулы eqref{ref46}, где (f(x)=ax^{2}), получаем
$$
xi=x-frac{1+4a^{2}x^{2}}{2a}2ax=-4a^{2}x^{3},qquad eta=ax^{2}+frac{1+4a^{2}x^{2}}{2a}=frac{1}{2a}+3ax^{2}.nonumber
$$
Исключая (x), получаем
$$
xi^{2}=frac{16a}{27}left(eta-frac{1}{2a}right)^{3}.nonumber
$$

Следовательно, эволютой параболы является полукубическая парабола. (blacktriangle)

Источник

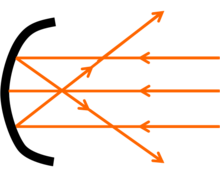
From Wikipedia, the free encyclopedia

A concave mirror with light rays

In geometry, the center of curvature of a curve is found at a point that is at a distance from the curve equal to the radius of curvature lying on the normal vector. It is the point at infinity if the curvature is zero. The osculating circle to the curve is centered at the centre of curvature. Cauchy defined the center of curvature C as the intersection point of two infinitely close normal lines to the curve.^[1] The locus of centers of curvature for each point on the curve comprise the evolute of the curve. This term is generally used in physics regarding the study of lenses and mirrors (see radius of curvature (optics)).

It can also be defined as the spherical distance between the point at which all the rays falling on a lens or mirror either seems to converge to (in the case of convex lenses and concave mirrors) or diverge from (in the case of concave lenses or convex mirrors) and the lens/mirror itself.^[2]

References[edit]

^ *Borovik, Alexandre; Katz, Mikhail G. (2011), «Who gave you the Cauchy—Weierstrass tale? The dual history of rigorous calculus», Foundations of Science, 17 (3): 245–276, arXiv:1108.2885, doi:10.1007/s10699-011-9235-x, S2CID 119320059
^ Trinklein, Frederick E. (1992). Modern physics (7th ed.). Austin: Holt, Rinehart and Winston. ISBN 0-03-074317-6. OCLC 25702491.{{cite book}}: CS1 maint: date and year (link)

Bibliography[edit]

Hilbert, David; Cohn-Vossen, Stephan (1952), Geometry and the Imagination (2nd ed.), New York: Chelsea, ISBN 978-0-8284-0087-9

Источник

Радиус, центр и круг кривизны. Эволюта и эвольвента

Смысл понятий радиуса, круга и центра кривизны

Вычисление радиуса и определение центра круга кривизны

See also[edit]

References[edit]

Bibliography[edit]