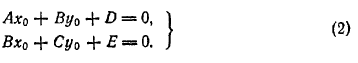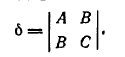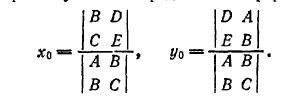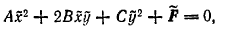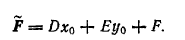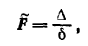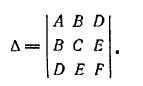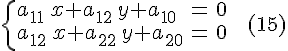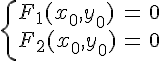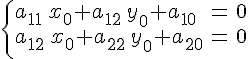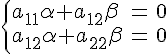Линия, которая в некоторой
декартовой системе координат определяется
уравнением второй степени, называется линией
второго порядка. Общее уравнение второй степени
(с двумя переменными) принято записывать в виде:
(1)
Центром некоторой линии называется
такая точка плоскости, по отношению к которой
точки этой линии расположены симметрично парами.
Линии второго порядка, обладающие единственным
центром, называются центральными.
Точка S(,
) является центром линии,
определяемой уравнением (1), в том и только в том
случае, когда ее кординаты удовлетворяют
уравнениям:
,
(2)
Обозначим через
определитель
этой системы:
.
Величина
составляется из
коэффициентов при старших членах уравнения (1) и
называется дискриминантом старших членов этого
уравнения.
Если
, то система (2) является
совместной и определенной, то есть имеет решение
и притом единственное. В этом случае координаты
центра могут быть определены по формулам
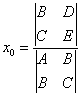
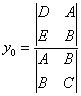
Неравенство
служит признаком
центральной линии второго порядка.
Если S(,
) — центр линии второго порядка,
то в результате преобразования координат по
формулам
,
(что соответствует переносу начала
координат в центр линии) ее уравнение примет вид
где A, B, C те же, что в
данном уравнении (1), а
определяется
формулой
.
В случае
имеет место
также следующая формула:
,
где
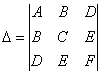
Определитель
называется
дискриминантом левой части общего уравнения
второй степени.
Линия, которая в некоторой декартовой системе координат определяется уравнением второй степени, называется линией второго порядка. Общее уравнение второй степени (с двумя переменными) принято записывать в виде:
Ах2 + 2Вху + Су2 + 2Dx + 2Ey + F = 0. (1)
Центром некоторой линии называется такая точка плоскости, по отношению к которой точки этой линии расположены симметрично парами. Линии второго порядка, обладающие единственным центром, называются центральными.
Точка S(x0; у0) является центром линии, определяемой уравнением (1), в том и только в том случае, когда ее координаты удовлетворяют уравнениям:
Обозначим через δ определитель этой системы:
Величина δ составляется из коэффициентов при старших членах уравнения (1) и называется дискриминантом старших членов этого уравнения.
Если δ ≠ 0, то система (2) является совместной и определенной, т. е. имеет решение и притом единственное. В этом случае координаты центра могут быть определены по формулам:
Неравенство δ ≠ 0 служит признаком центральной линии второго порядка
Если S(x0; у0) — центр линии второго порядка, то в результате преобразования координат по формулам
(что соответствует переносу начала координат в центр линии) ее уравнение примет вид
где А, В, С — те же, что в данном уравнении (1), a 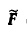
В случае δ ≠ 0 имеет место также следующая формула:
где
Определитель Δ называется дискриминантом левой части общего уравнения второй степени.
665. Установить, какие из следующих линий являются центральными (т. е. имеют единственный центр), какие не имеют центра, какие имеют бесконечно много центров:
1) 3x2 — 4ху -2у2 + Зх — 12у — 7 — 0;
2) 4x2 + 5ху + 3у2 — х + 9у — 12 = 0;
3) 4x2 — 4ху + у2 — 6x + 8y + 13 = 0;
4) 4x2 — 4ху + у2 — 12x + 6у — 11=0;
5) х2 — 2ху + 4у2 + 5х — 7у + 12 = 0;
6) x2 — 2ху + у2 — 6x + 6y — 3 = 0;
7) 4х2 — 20ху -4- 25у2 — 14x + 2у — 15 = 0;

666. Установить, что следующие линии явпяются центральными, и для каждой из них найти координаты центра:
1) 3x2 + 5ху + у2 — 8x — 11у — 7 = 0;
2) 5x2 + 4ху + 2у2 + 20x + 20у — 18 = 0;
3) 9x2 — 4xy — 7у2 — 12 = 0;
4) 2x2 — 6ху + 5у2 + 22x — 36у + 11 = 0.
667. Установить, что каждая из следующих линий имеет бесконечно много центров; для каждой их них
составить уравнение геометрического места центров:
1) х2 -6ху + 9у2 — 12x + 36y + 20 = 0;
2) 4x2 + 4ху + у2 — 8х — 4y — 21 = 0;
3) 25x2 — 10xy + y2 + 40x — 8y + 7 = 0.
668. Установить, что следующие уравнения определяют центральные линии; преобразовать каждое из них путем переноса начала координат в центр;
1) 3x2 — 6ху + 2у2 — 4x + 2y + 1 = 0;
2) 6х2 + 4ху + у2 + 4x — 2y + 2 — 0;
3) 4x2 + 6xy + y2 — 10x — 10 = 0;
4) 4x2 + 2xy + 6y2 + 6x — 10y + 9 = 0.
669. При каких значениях m и n уравнение
mx2 + 12ху + 9y2 + 4х + nу — 13 = 0
определяет:
1) центральную линию;
2) линию без центра;
3) линию, имеющую бесконечно много центров.
670. Дано уравнение линии 4x2 — 4xy + у2 + 6x + 1 = 0. Определить, при каких значениях углового коэффициента k прямая у = kx: 1) пересекает эту линию в одной точке; 2) касается этой линии; 3) пересекает эту линию в двух точках; 4) не имеет общих точек с этой линией.
671. Составить уравнение линии второго порядка, которая, имея центр в начале координат, проходит через точку M(6;-2) и касается прямой x — 2 = 0 в точке N(2; 0).
672. Точка Р (1; -2) является центром линии второго порядка, которая проходит через точку Q(0;-3) и касается оси Ох в начале координат. Составить уравнение этой линии.
Определение
9.1. Центром
линии второго порядка называется центр
симметрии этой линии.
ТЕОРЕМА
9.1. Пусть
относительно аффинной системы координат
задана линия второго порядка общим
уравнением
Для
того чтобы начало координат являлось
ее центром, необходимо и достаточно,
чтобы в уравнении
отсутствовали
члены с
и
в
первой степени, т.е. чтобы
,
иначе, чтобы уравнение линии имело
вид
Доказательство
достаточности. Если
,
то уравнение линии имеет вид
,
и если ему удовлетворяют
координаты
и
точки
,
то ему удовлетворяют и координаты
и
точки
,
симметричной точке
относительно
начала координат.
Доказательство
необходимости. Пусть
начало координат является центром
линии
.
Возьмем на линии произвольную точку
.
Ее координаты удовлетворяют уравнению
,
а так как начало координат
является
центром симметрии линии, то этому
уравнению удовлетворят и координаты
точки
,
симметричной точке
относительно
начала координат, т.е.
.
Вычитая
из
соотношение
,
находим, что координаты всех точек линии
удовлетворяют уравнению
.
Следовательно, уравнение линии приводится
к виду
,
то есть не
содержит членов с
и
в
первой степени.
ТЕОРЕМА
9.2. Если
относительно аффинной системы координат
задана линия второго порядка общим
уравнением
то
координаты
ее
центра определяются из системы
уравнений
причем
в случае несовместности этой системы
линия не имеет центра (т.е. является
параболой).
Доказательство. Произведем
перенос данной системы координат так,
чтобы новым началом стала точка
.
В новой системе координат уравнение
линии
будет
иметь вид (согласно формулам
).
По
предыдущей теореме точка
является
центром данной линии тогда и только
тогда, когда
или
подробнее
Определение
9.2. Любая
кривая второго порядка, имеющая
единственный центр называется
центральной.
Следовательно, кривая
является центральной, если
Замечание
9.1. При
приведении центральных кривых к
каноническому виду целесообразно
пользоваться следующим планом:
1. Найти
центр кривой.
2. Выполнить
параллельный перенос в центр и записать
уравнение кривой в перенесенной системе
координат
3. Повернуть
перенесенную систему координат на
угол
и
получить каноническую систему координат.
10 Пересечение кривой второго порядка с прямой. Асимптотические направления относительно кривой второго порядка
Пусть
задана кривая второго порядка общим
уравнением
и
прямая
параметрическими
уравнениями
.
Найдем
точки пересечения этой прямой с кривой
второго порядка.
Для этого подставим
значения переменных
и
из
уравнений
в
уравнение
.
Получаем уравнение с одним неизвестным
Преобразуем
его к виду
Введем
обозначения:
В
этих обозначениях, полученное уравнение,
запишется более просто, а именно
Находя
корни уравнения
,
и подставляя их в уравнения
,
мы получим координаты точек пересечения
кривой второго порядка и прямой
.
При этом возможны следующие случаи:
1.
.
Следовательно,
—
квадратное уравнение, а поэтому оно
имеет два корня (вещественных или
комплексных),значит, прямая пересекает
КВП в двух точках(вещественных или
комплексно-сопряженных).
2.
.
Тогда уравнение
примет
вид
.
a). Если
,
то прямая пересекает кривую в единственной
действительной точке.
b). Если
,
то прямая не имеет с кривой ни одной
общей точки(ни действительной, ни
мнимой).
c). Если
,
тогда любое значение
является
решением уравнения
,
а потому
лежит
на кривой второго порядка.
Определение
10.1. Множество
всех прямых, из которых любые две
параллельны, называется направлением.
Отметим,
что направление можно определить любым
направляющим вектором каждой из этих
прямых. Заметим, что коэффициент в
уравнении
зависит
только от направления прямой
и
не зависит от координат точки
,
лежащей на прямой.
Определение
10.2. Направление,
определяемое ненулевым вектором
,
называется асимптотическим направлением
относительно кривой второго порядка,
если любая прямая, параллельная
вектору
,
либо имеет с кривой не более одной общей
точки, либо содержится в кривой.
Из
предыдущего следует: направление,
определяемое ненулевым вектором
,
является асимптотическим направлением
относительно кривой второго порядка
,
тогда и только тогда, когда
Пользуясь
этой формулой, легко найти асимптотические
направления относительно кривой второго
порядка.
Если
,
то из
следует,
что
(
так как
—
ненулевой вектор), поэтому из
,
обозначая через
получаем
Отсюда
находим
Если
же
,
то уравнение
примет
вид
.
Этому уравнению удовлетворяют координаты
векторов
Выясним
теперь, сколько существует различных
асимптотических направлений относительно
кривой второго порядка.
Рассмотрим
три случая.
1.
и,
значит,
.
Из формулы
мы
заключаем, что относительно кривой
второго порядка не существует
асимптотических направлений.
2.
.
В этом случае существует два различных
асимптотических направления.
В самом
деле, если
,
то этот вывод следует из формулы
,
а если
,
то из
.
(Заметим, что в последнем случае
,
поэтому векторы из
не
коллинеарны.)
3.
.
Очевидно, что в этом случае имеем
единственное асимптотическое направление,
определяемое вектором
.
Действительно, если
,
то это вытекает из
,
а если
,
то из
.
(Заметим, что в последнем случае
,
поэтому векторы из
коллинеарны.)
Ранее
было показано, что
не
зависит от выбора системы координат. В
соответствии с таблицей значений
инвариантов и количеством асимптотических
направлений принято разделять кривые
второго порядка на три
класса:
эллиптические
, гиперболические
и параболические
.
Определение
10.3. Асимптотой
кривой второго порядка называется
прямая асимптотического направления,
которая либо лежит на кривой, либо не
имеет с ней общих точек.
ТЕОРЕМА
10.1. Асимптота
к кривой гиперболического типа задается
уравнением
где
удовлетворяют
.
Доказательство. Запишем
уравнение
в
виде
или
в эквивалентной форме
Отметим
сначала, что это уравнение является
уравнением первой степени. Действительно,
предположим, что
Откуда
следует, что
,
так как
.
А это противоречит тому, что вектор,
удовлетворяющий
,
ненулевой. Теперь необходимо проверить,
что прямая
имеет
асимптотическое направление, т.е. надо
убедится
в том, что вектор
имеет
асимптотическое направление. Действительно,
так как
—
вектор асимптотического направления,
то он удовлетворяют равенству
,
которое
равносильно
Таким
образом, вектор
коллинеарен
вектору асимптотического направления,
а значит, имеет асимптотическое
направление. Итак, прямая, заданная
уравнением
имеет
асимптотическое направление.
Кроме
того, если точка лежит на этой прямой,
то ее координаты
удовлетворяют
уравнению
:
.
Рассмотрим
выражение
Что
и требовалось доказать.
Замечание
10.1. Если
в общем уравнении кривой второго порядка
гиперболического типа
,
то уравнения
асимптот можно искать
в виде
где
определяются
по формуле
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
План урока:
Уравнение линии в координатах
Уравнение окружности
Уравнение прямой
Задачи на пересечение двух фигур
Уравнение линии в координатах
Если какое-то уравнение содержит две переменные – х и у, то какие-то пары значений этих чисел будут являться его решением, а какие-то нет. Однако каждой такой паре чисел можно сопоставить точку на координатной плоскости. Все вместе такие точки могут образовать линию, которую можно обозначить буквой L. В таком случае исходное уравнение называют уравнением линии L.
Мы уже рассматривали некоторые уравнения линий на плоскости, когда изучали графики функций. Если некоторую функцию у = у(х) рассматривать как уравнение, то тогда график функции у(х) будет той самой линией, которая задается уравнением. Например, парабола может быть задана уравнением у = х2.
Однако уравнение линии не обязательно выглядит как функция. Наиболее простой задачей является определение факта, принадлежит ли та или иная точка той линии, которая задана уравнением.
Задание. Какие из точек А (2;1), В (3; 2), С (– 2; 5) и D(0; 0) принадлежат линии, заданной уравнением:
Решение. Надо просто подставить координаты точек в уравнение и посмотреть, превратится ли оно при этом в верное равенство. Сначала подставляем точку А (2; 1):
Получилось верное равенство, значит, А принадлежит заданной линии. Теперь подставляем координаты В (3; 2):
Равенство неверное, следовательно, В на заданной линии не лежит. Проверяем третью точку С (– 2; 5):
Получили, что и С не является частью линии. Проверяем последнюю точку D (0; 0):
Справедливость равенства означает, что D принадлежит линии.
Ответ: А и D.
Использование координат и уравнений линии порождает две обратные друг другу задачи:
1) по заранее заданному уравнению определить геометрический вид линии;
2) для заданной геометрической фигуры, построенной на координатной плоскости, найти уравнение линии.
Геометрия занимается в первую очередь решением второй задачи. Первая же задача рассматривается по большей части в курсе алгебры при изучении графиков функций.
Уравнение окружности
Попытаемся составить уравнение окружности, про которую нам известен ее радиус (обозначим его буквой r) и координаты центра окруж-ти(х0; у0). Пусть некоторая точка М с координатами (х; у) лежит на окруж-ти. Тогда, по определению окруж-ти, расстояние между С и М равно радиусу r:
Но расстояние между точками М и С может быть вычислено по формуле
Если же точка М НЕ лежит на окруж-ти, то длина отрезка МС не будет равна r, и потому координаты М не будут удовлетворять уравнению (1). Получается, что (1) как раз и является уравнением окруж-ти.
Задание. Составьте уравнение окружности, имеющей радиус 5, если ее центр находится в точке (6; 7), и проверьте, лежат на ней точки H(2; 10)и Р(3; 8).
Решение. Сначала запишем уравнение окруж-ти в общем виде
Это и есть уравнение окруж-ти. При желании можно раскрыть скобки в правой части, но делать это необязательно. Теперь будем подставлять в полученное уравнение координаты точек Н и Р:
Проверка показала, что Н находится на окруж-ти, а Р – нет.
Задание. Начертите окружность, заданную уравнением
Именно эти значения и являются параметрами окруж-ти, которые нужны нам для ее построения. Ее центр находится в точке (х0; у0), то есть в (1; – 2), радиус равен r, то есть 2. В итоге выглядеть она будет так:
Особый случай представляет окруж-ть, центр которой находится в начале координат, то есть в точке (0; 0). В этом случае параметры x0 и y0 окруж-ти равны нулю, и уравнение
Например, окруж-ть с радиусом 4, если ее центр совпадает с началом координат, описывается уравнением:
Если при подстановке координат точки в уравнение получилось неверное равенство, то возможны два случая: либо точка находится внутри окруж-ти, либо она находится вне нее. Заметим, что в уравнении окруж-ти
левая часть представляет собой квадрат расстояния между точкой (х; у) и центром окруж-ти (х0; у0). Если оно больше квадрата радиуса, то точка находится вне окруж-ти, а если меньше – то внутри нее.
Задание. Определите для точек M(3; 4), N(2; 3), F(4; 4), лежат ли они на окруж-ти
x2 + y2 = 25
внутри нее или за пределами окруж-ти.
Решение.Снова подставляем координаты точек в уравнение окруж-ти:
Это ошибочное равенство, ведь в реальности левая часть больше:
32 > 25
Это значит, что F(4; 4) лежит вне окруж-ти. Убедиться в правильности сделанных выводов можно, построив заданную окруж-ть и отметив точки M, N и F:
Рассмотрим несколько более сложных задач по данной теме.
Задание.Запишите уравнение окружности с центром С(– 4; 2), и окруж-ть проходит через точку А(0; 5).
Решение. В данном случае радиус окруж-ти явно не указан, и его надо найти. Подставим в уравнение окруж-ти известные нам данные:
Задание. Даны точки К (– 2; 6) и М (2; 0). Запишите уравнение окруж-ти, в которой КМ будет являться диаметром.
Решение. Для составления уравнения нужно знать радиус окруж-ти и координаты ее центра. Обозначим центр буквой С. Ясно, что центр окруж-ти делит любой ее диаметр пополам, на два одинаковых радиуса, то есть является серединой диаметра. То есть С – середина КМ, а потому для поиска координат С используем формулы:
Итак, координаты центра теперь известны, это (0; 3). Чтобы найти радиус, поступим также, как и в предыдущей задаче – подставим координаты точек С и, например, К, в уравнение окруж-ти
Обратите внимание, что нам необязательно вычислять радиус, ведь для уравнении окруж-ти нужна его величина, возведенная в квадрат, и мы ее нашли. Теперь можем записать уравнение окончательно
Задание. Дано уравнение окружности
(x — 2)2 + (y — 4)2 = 9
Найдите точки этой окруж-ти, абсцисса которых равна 2.
Решение. Напомним, что абсцисса – это координат х точки. Она нам уже известна, х = 2. Остается только найти ординату, то есть координату у. Для этого подставим известное нам значение абсциссы в уравнение и решим его:
Обратите внимание, что у квадратного уравнения нашлось сразу 2 корня, они соответствуют двум точкам, (2; 1) и (2; 7).
Ответ: (2; 1) и (2; 7).
Задание. Составьте уравнение окружности, проходящей через точки D(3; 8), L(6; 7) и K(7; 0).
Решение. Эта задача сложнее предыдущих и потребует громоздких вычислений. Нам надо найти радиус окруж-ти r и ее центр (х0; у0). Запишем для точки D(3; 
Далее раскроем скобки в левой части, используя формулу квадрата разности (это необходимо для упрощения дальнейших расчетов):
В итоге нам удалось составить три уравнения, которые содержат три переменные: r, х0 и у0.Вместе они образуют систему уравнений, которую можно попробовать решить:
Далее можно, например, вычесть из (2) уравнение (3):
Нам удалось найти одно из интересующих нас чисел, у0. С помощью (5) легко найдем и х0:
x0 = 7y0 — 18 = 7*3 — 18 = 21 — 18 = 3
Итак, центр окруж-ти находится в точке (3; 3). Осталось найти радиус окруж-ти. Для этого подставим в уравнение окруж-ти вычисленные нами координаты центра, а также координаты одной из точек из условия, например, K(7; 0):
Радиус окруж-ти равен 5. Теперь мы можем окончательно записать уравнение окруж-ти
Чтобы убедиться в правильности найденного решения, можно подставить в полученное уравнение координаты трех точек из условия и посмотреть, обращают ли они его в верное равенство. Вместо этого мы для наглядности просто построим в координатной плоскости получившуюся окруж-ть и отметим на ней точки из условия:
Ответ: (х – 3)2 + (у – 3)2 = 25
Уравнение прямой
Пусть на координатной плоскости построена произвольная прямая m. Для составления его уравнения отметим две точки А(х1; у1) и В(х2; у2) так, чтобы прямая m оказалась серединным перпендикуляром для отрезка АВ:
Тогда, согласно свойству серединного перпендикуляра,про любую точку М(х; у), лежащую на m, можно сказать, что она равноудалена от А и В, и наоборот, любая точка, НЕ лежащая на m, НЕ равноудалена от А и В. Это означает, что для точки M, если она лежит на m, должно выполняться равенство:
Квадратные корни равны, если одинаковы их подкоренные выражения, поэтому
Заметим, что так как точки А и В – различные, то хотя бы одна из разностей (2х2 – 2х1) и (2у2 – 2у1) будет не равна нулю, поэтому в (2) хотя бы один их коэффициентов а и b точно ненулевой. Это означает, что уравнение (2) является уравнением первой степени. Заметим, что (2) называют общим уравнением прямой, так как оно описывает любую прямую на плоскости. При более глубоком изучении геометрии вы познакомитесь с множеством других видов уравнений прямой (нормальным, каноническим, тангенциальным, параметрическим и т. п.).
В последнем примере коэффициент с равен нулю, поэтому его просто не записали.
Заметим важный аспект – одна и та же прямая может описываться различными уравнениями вида (2). Например, пусть уравнение прямой выглядит так:
Это уравнение равносильно предыдущему, хотя у них и различны коэффициенты а, b и c. Это значит, что однозначно определить эти коэффициенты при решении задач в большинстве случаев невозможно. Поэтому удобней рассмотреть два отдельных случая.
1) Если коэффициент b в уравнении прямой (2) не равен нулю, то его можно привести к виду:
получим линейную функцию:
y = kx + d (3)
Из курса алгебры мы помним, что ее графиком как раз является прямая. В большинстве случаев уравнение прямой удобно записывать именно в таком виде. Напомним, что число k называется угловым коэффициентом прямой.Поэтому (3) так и называют – уравнением прямой с угловым коэффициентом. В качестве примера подобных уравнений можно привести:
Каждое из них описывает вертикальную прямую, параллельную оси Оу.
Задание. Прямая задана уравнением
4x + 2y + 6 = 0
Постройте ее на координатной плоскости
Решение. Для построения прямой надо всего лишь найти две различные точки, лежащие на ней, и соединить их. Мы будем брать произвольные значения координаты х, подставлять их в уравнение и находить соответствующее им значение координаты у. Подставим х = 1:
Получили другую точку (– 1; – 1). Осталось отметить эти две точки на и соединить их:
Задание. Составьте уравнение прямой, проходящей через точки D(1; 10) и Е(– 1; – 4).
Решение. Задачу можно решить разными способами.
Способ 1 – универсальный и более сложный.
В общем виде уравнение прямой выглядит так:
ax + by + c = 0
Нам надо найти коэффициенты а, b и c. Для этого просто подставляем координаты известных точек в уравнение. Начнем с координат D:
Нам удалось выразить коэффициента двумя различными выражениями (1) и (2). Так как в них одинаковы левые части, то можно приравнять и правые части:
Мы можем взять любое значение коэффициента с (кроме нуля), и при этом получатся различные, но равносильные друг другу уравнения. Удобно взять с = 3, тогда в уравнении исчезнут дроби:
Это и есть ответ задания.
Далее рассмотрим более простой способ, который, однако, может потребовать анализа различных вариантов.
Способ 2
Уравнение прямой может иметь либо вид
y = kx + d
если прямая является графиком линейной функции, либо вид
x = C
если прямая параллельна оси Оу. Во втором случае у всех точек прямой абсцисса должна быть одинакова, однако у точек D(1; 10) и Е(– 1; – 4) она различна, поэтому ее точно можно описать уравнением
y = kx + d
Надо найти коэффициенты k и d. Подставим в уравнение координаты D(1; 10):
Итак, уравнение можно записать так:
Задание. Запишите уравнение прямой, если ей принадлежат точки:
Подставим сюда уже известное нам значение d:
В (1) и (2) мы выразили d с помощью разных выражений, которые теперь можно приравнять:
То, что коэффициент k оказался нулевым, означает, что прямая параллельна оси Ох.
в) Попытаемся сделать те же действия, что и в двух предыдущих примерах, подставляя точки в уравнение у = kx + d:
На этот раз мы не смогли найти коэффициент k, а вместо этого получили ошибочное равенство. То есть уравнение просто не имеет решений. Что же это значит? Из этого факта следует, что в этом примере уравнение прямой НЕ может иметь вид
y = kx + b
Значит, оно имеет другой вид:
x = C
Действительно, у обеих точек (2; 7) и (2; 
x = 2
Ответ а) у = 1,5х + 3; б) у = 8; в) х = 2.
Задание. Найдите площадь треугольника MON, изображенного на рисунке, если известно, что M и N лежат на прямой, задаваемой уравнением:
Решение. ∆MON – прямоугольный, и для вычисления его площади нужно найти длины OM и ON. По рисунку видно, что М лежит на оси Ох, то есть у неё ордината нулевая:
yM = 0
Зная это, легко найдем и абсциссу М, ведь координаты М при их подстановке в уравнение прямой должны давать верное равенство:
Далее рассмотрим точку N. Она уже лежит на Оу, а потому у нее нулевой оказывается абсцисса:
Напомним, что площадь прямоугольного треугольника может быть вычислена по формуле:
Задачи на пересечение двух фигур
Метод координат помогает находить точки, в которых пересекаются те или иные геометрические фигуры. В большинстве случаев надо просто составить систему из уравнений, задающих эти фигуры, и найти их общее решение. В курсе алгебры мы уже рассматривали как решение простых, в основном линейных систем, так и решение более сложных, нелинейных систем. Рассмотрим несколько задач на эту тему.
Задание. Две прямые заданы уравнениями:
Определите, в какой точке они пересекаются.
Решение. Если точка пересечения прямых существует, то ее координаты являются решением каждого из двух уравнений. Таким, образом, нам надо просто решить систему:
Мы нашли единственное решение системы – это пара чисел (3; – 2). Эта же пара определяет координаты искомой нами точки.
Ответ: (3; – 2).
Задание. Найдите точки пересечения окруж-ти и прямой, если они задаются уравнениями
Решаем квадратное уравнение, используя дискриминант:
Мы нашли два различных значения у. Это значит, что прямая пересекается с окруж-тью в двух различных точках, а найденные нами числа – их ординаты. Отметим, что возможны случаи, когда корень только один (и тогда у окруж-ти с прямой одна общая точка, то есть они касаются), и когда корней вовсе нет (тогда окруж-ть и прямая не пересекаются). В нашем же примере осталось найти абсциссы точек. Для этого используем уравнение (3):
Получили в итоге пары точек (3; 
Ответ: (3; 
Задание. Две окруж-ти заданы уравнениями:
Для ее решения сначала раскроем скобки в обоих уравнениях и приведем подобные слагаемые:
Нам удалось выразить у через х. Теперь снова запишем одно из исходных уравнений окруж-ти, но заменим в нем у с помощью только что найденного выражения:
Мы нашли абсциссы точек пересечения окруж-тей, теперь можно вернуться к (1), чтобы найти и ординаты:
Получили точки (5; 2) и (4; 3).
Ответ:(5; 2) и (4; 3).
В конце решим одну задачу чуть более высокого уровня сложности.
Задание. К окруж-ти радиусом 5, чей центр совпадает с началом координат, построена касательная в точке (3; 4). Составьте уравнение этой касательной.
Решение. Сначала составим уравнение окруж-ти. Так как ее центр находится в начале координат, а радиус имеет длину 5, то оно примет вид:
Нам надо найти коэффициенты k и d, а для этого надо составить какие-нибудь уравнения с этими переменными. Нам известно, что касательная проходит через точку (3; 4), а потому эти координаты можно подставить в (2):
Обратите внимание, что мы получили квадратное уравнение относительно переменной х. Если бы нам были известны k и d, то мы смогли бы его решить, и тогда мы определили бы точки пересечения прямой и окруж-ти. В этой задаче k и d нам неизвестны, но мы знаем, что окруж-ть и прямая касаются, то есть имеют ровно одну общую точку. Но тогда и квадратное уравнение (4) должно иметь только одно решение! Это означает, что его дискриминант равен нулю. Сначала выпишем коэффициенты квадратного уравнения, используемые при вычислении дискриминанта:
Теперь у нас есть два уравнения, (3) и (5), которые содержат только переменные k и d. Осталось лишь совместно решить их. Для этого подставим (3) в (5):
В рамках урока мы выяснили, как выглядят уравнения окруж-ти и прямой, а также научились решать несколько типовых заданий, в которых эти уравнения необходимо использовать. Хотя формулы, используемые при этом, могут показаться слишком сложными, главное – просто набить руку в их применении, решая как можно больше задач.
-
Пересечение линии второго порядка и прямой.
Начать изучение
-
Тип линии.
Начать изучение
-
Диаметр линии второго порядка.
Начать изучение
-
Центр линии второго порядка.
Начать изучение
-
Сопряженные направления.
Начать изучение
-
Главные направления.
Начать изучение
-
Касательная к линии второго порядка.
Начать изучение
-
Особые точки.
Начать изучение
Пересечение линии второго порядка и прямой.
Рассмотрим линию второго порядка, заданную общим уравнением
$$
Ax^{2}+2Bxy+Cy^{2}+2Dx+2Ey+F=0label{ref1}
$$
в декартовой системе координат, и исследуем пересечение этой линии с произвольной прямой
$$
x=x_{0}+alpha t, y=y_{0}+beta t.label{ref2}
$$
Значения параметра (t), соответствующие точкам пересечения, должны удовлетворять уравнению, получаемому подстановкой eqref{ref2} в eqref{ref1}:
$$
A(x_{0}+alpha t)^{2}+2B(x_{0}+alpha t)(y_{0}+beta t)+C(y_{0}+beta t)^{2} +\+ 2D(x_{0}+alpha t)+2E(y_{0}+beta t)+F=0.label{ref3}
$$
Раскрывая скобки и приводя подобные члены, мы получим уравнение
$$
Pt^{2}+2Qt+R=0,label{ref4}
$$
в котором
$$
P=Aalpha^{2}+2Balphabeta+Cbeta^{2},label{ref5}
$$
$$
Q=(Ax_{0}+By_{0}+D)alpha+(Bx_{0}+Cy_{0}+E)beta,label{ref6}
$$
или, при другой группировке слагаемых,
$$
Q=(Aalpha+Bbeta)x_{0}+(Balpha+Cbeta)y_{0}+Dalpha+Ebeta.label{ref7}
$$
Свободный член — это значение многочлена при (t=0), то есть
$$
R=Ax_{0}^{2}+2Bx_{0}y_{0}+Cy_{0}^{2}+2Dx_{0}+2Ey_{0}+F=0.label{ref8}
$$
Вообще говоря, уравнение eqref{ref4} квадратное, имеет не больше двух корней, и прямая пересекает линию или в двух точках, или в одной точке (кратные корни), или не пересекает ее (комплексные корни). Но возможны “исключительные” прямые, для которых (P=0), то есть
$$
Aalpha^{2}+2Balphabeta+Cbeta^{2}=0,label{ref9}
$$
и, следовательно, уравнение eqref{ref4} является линейным. В этом случае оно имеет один корень при (Q neq 0), а при (Q=0) либо выполнено тождественно (если и (R=0)), либо не имеет решений. Следовательно, “исключительные” прямые или пересекают линию в единственной точке, или лежат на ней целиком, или не имеют с ней общих точек.
В равенство eqref{ref9} не входят координаты начальной точки прямой. Кроме того, оно остается справедливым, если умножить (alpha) и (beta) на общий ненулевой множитель.
Определение.
Направление, определяемое вектором, компоненты которого удовлетворяют уравнению eqref{ref9}, называется асимптотическим направлением линии второго порядка.
Тип линии.
Выясним, сколько асимптотических направлений может иметь линия второго порядка. Обозначив
$$
delta=begin{vmatrix}
A& B\
B& C
end{vmatrix},nonumber
$$
сформулируем следующее утверждение.
Утверждение 1.
Линия второго порядка имеет два асимптотических направления, если (delta < 0), одно, если (delta=0), и ни одного, если (delta > 0).
Доказательство.
Рассмотрим несколько случаев.
- Пусть (A=C=0). Тогда (B neq 0) и (delta=-B^{2} < 0). Уравнение eqref{ref9} имеет вид (2Balphabeta=0), и ему удовлетворяют векторы (1,0) и (0,1).
- Пусть (C neq 0). Тогда вектор (0,1) не является решением этого уравнения, и каждое решение можно задать угловым коэффициентом (k=beta/alpha), удовлетворяющим уравнению (Ck^{2}+2Bk+A=0). Дискриминант этого уравнения равен (B^{2}-AC=-delta). Следовательно, оно имеет два вещественных корня при (delta < 0), один корень при (delta=0) и не имеет вещественных корней при (delta > 0).
- Случай (A neq 0) исследуется аналогично случаю 2, только нужно рассматривать не угловой коэффициент, а отношение (alpha/beta).
Поскольку разобранные выше случаи исчерпывают все возможности, предложение доказано.
От противного нетрудно проверить, что и обратно число асимптотических направлений определяет знак (delta).
Мы определили асимптотические направления при помощи аналитического условия eqref{ref9}. Поэтому в принципе при изменении системы координат асимптотическое направление могло бы перестать быть асимптотическим, или, наоборот, обыкновенное направление стать асимптотическим. Из геометрического смысла асимптотических направлений видно, что в действительности асимптотические направления не зависят от выбора системы координат.
Используя канонические уравнения, легко проверить, что эллипс не имеет асимптотических направлений, парабола имеет одно, а гипербола — два асимптотических направления (рис. 9.1). Поэтому линии второго порядка называются линиями гиперболического, параболического или эллиптического типа, смотря по тому, имеют они два, одно или не имеют ни одного асимптотического направления.
Для линий гиперболического типа (delta < 0), для параболического типа (delta=0), а для эллиптического (delta > 0).
Диаметр линии второго порядка.
Назовем хордой любой отрезок, концы которого лежат на линии, а остальные точки на ней не лежат. Таким образом, хорда не может иметь асимптотического направления.
Предположим, что рассматриваемая линия второго порядка имеет по крайней мере одну хорду. Этому условию удовлетворяют эллипсы, гиперболы, пары пересекающихся прямых, параболы и пары параллельных прямых.
Фиксируем какое-нибудь неасимптотическое направление и исследуем множество середин хорд, имеющих это направление. Если начальная точка (M_{0}(x_{0}, y_{0})) секущей eqref{ref2} находится в середине хорды, то корни уравнения eqref{ref4} равны по абсолютной величине и отличаются знаком (рис. 9.2). Это будет так в том и только том случае, когда (Q=0). Используя eqref{ref7}, мы получаем, что середины хорд направления ((alpha, beta)^{2}) лежат на прямой
$$
(Aalpha+Bbeta)x+(Balpha+Cbeta)y+Dalpha+Ebeta=0.label{ref10}
$$
Определение.
Прямая eqref{ref10} называется диаметром линии второго порядка, сопряженным направлению ((alpha, beta)).
Стоит обратить внимание на то, что диаметром называется вся прямая. Это не означает, что середины хорд заполняют ее целиком. Так может быть, но возможно также, что множество середин хорд есть, например, отрезок или луч.
Конечно, остается сомнение, действительно ли уравнение eqref{ref10} определяет прямую: не окажутся ли в нем коэффициенты при переменных оба равными нулю? Допустим, что это так, то есть
$$
Aalpha+Bbeta=0, Balpha+Cbeta=0.nonumber
$$
Умножим первое из этих равенств на (alpha), второе — на (beta) и сложим. Мы получим равенство eqref{ref9}, которое по предположению не имеет места. Следовательно, уравнение eqref{ref10} определяет прямую.
Центр линии второго порядка.
Обозначим левую часть уравнения eqref{ref1} через (boldsymbol{Phi}(x, y)) и введем еще одно понятие.
Определение.
Точка (O(x_{0}, y_{0})) называется центром линии второго порядка (boldsymbol{Phi}(x, y)=0), если для любого вектора (boldsymbol{a}(alpha, beta)) выполнено равенство
$$
boldsymbol{Phi}(x_{0}+alpha, y_{0}+beta)=boldsymbol{Phi}(x_{0}-alpha, y_{0}-beta).label{ref11}
$$
По-видимому, это определение зависит от выбора системы координат, так как в нем участвует не линия, а многочлен, стоящий в левой части ее уравнения. Допустим, что координаты (x_{0}, y_{0}) точки (O) в некоторой системе координат удовлетворяют уравнению eqref{ref11}. Будут ли ее координаты ((tilde{x}_{0}, tilde{y}_{0})) в другой системе координат удовлетворять равенству того же вида для многочлена (tilde{boldsymbol{Phi}}(tilde{x}, tilde{y})), задающего ту же линию в новой системе координат? Легко видеть, что это так, потому что многочлен (tilde{boldsymbol{Phi}}) так и выбирается, чтобы для координат любой точки выполнялось равенство (tilde{boldsymbol{Phi}}(tilde{x}, tilde{y})=boldsymbol{Phi}(x, y)). Нам остается только выписать это равенство для точек, получаемых из (O) сдвигом на векторы (boldsymbol{a}) и (-boldsymbol{a}).
Ниже мы докажем, что в том случае, когда линия содержит хоть одну точку, центры линии и только они являются ее центрами симметрии. Однако понятие центра несколько более общее: линии, являющиеся пустыми множествами, имеют вполне определенные центры, хотя говорить об их центрах симметрии смысла нет. Например, каждая точка прямой (y=0) является центром линии с уравнением (y^{2}+1=0).
Получим систему уравнений для координат центра. С этой целью напишем подробнее равенство eqref{ref11}. Его левая часть равна
$$
A(x_{0}+alpha)^{2}+2B(x_{0}+alpha)(y_{0}+beta) +\+ C(y_{0}+beta)^{2}+2D(x_{0}+alpha)+2E(y_{0}+beta)+F.nonumber
$$
Правая часть отличается от левой только знаками у (alpha) и (beta). Поэтому при вычитании (boldsymbol{Phi}(x_{0}-alpha, y_{0}-beta)) из (boldsymbol{Phi}(x_{0}+alpha, y_{0}+beta)) уничтожаются все члены, кроме тех, в которые (alpha) и (beta) входят в первой степени, а члены с первыми степенями удвоятся. После упрощений мы получаем
$$
(Ax_{0}+By_{0}+D)alpha+(Bx_{0}+Cy_{0}+E)beta=0.label{ref12}
$$
Но равенство eqref{ref11}, а вместе с ним и равносильное равенство eqref{ref12} имеет место при любых (alpha) и (beta), в частности, при (alpha=1), (beta=0) и при (alpha=0), (beta=1). Отсюда следует, что координаты ((x_{0}, y_{0})) центра должны удовлетворять системе уравнений
$$
left{begin{array}{l}
Ax_{0}+By_{0}+D=0,\
Bx_{0}+Cy_{0}+E=0.
end{array}right.label{ref13}
$$
Легко видеть, что и обратно, если справедливы равенства eqref{ref13}, то, умножая их на произвольные числа (alpha) и (beta) и складывая, мы получим eqref{ref12}, а тем самым и eqref{ref11}.
Исследуем, обязательно ли существуют центры у линии второго порядка, а если они существуют, то сколько их и как они расположены. Система уравнений eqref{ref13} имеет единственное решение тогда и только тогда, когда
$$
delta=begin{vmatrix}
A& B\
B& C
end{vmatrix} neq 0.label{ref14}
$$
Таким образом, условие (delta neq 0) необходимо и достаточно для того, чтобы линия второго порядка имела единственный центр.
Линии второго порядка, имеющие единственный центр, называются центральными.
Полученное условие показывает, что центральными являются линии эллиптического и гиперболического типов.
Условие (delta=0) характеризует нецентральные линии. Это — линии параболического типа. При условии (delta=0) система eqref{ref13} либо не имеет решения, либо равносильна одному из составляющих ее уравнений (ранее мы уже доказывали этот факт). Это значит, что нецентральная линия либо не имеет центра (парабола), либо ее центры заполняют прямую линию (пары параллельных прямых, вещественных и мнимых, и пары совпавших прямых).
Утверждение 2.
Если линия второго порядка не является пустым множеством и имеет центр (O(x_{0}, y_{0})), то он — ее центр симметрии.
Доказательство.
В самом деле, рассмотрим произвольную точку линии (M(x, y)) и докажем, что симметричная ей относительно (O) точка (M_{1}(x_{1}, y_{1})) также лежит на линии. Точка (M_{1}) определяется равенством (overrightarrow{OM_{1}}=-overrightarrow{OM}). Если ((alpha, beta)) — координаты вектора (overrightarrow{OM}), то (x=x_{0}+alpha), (y=y_{0}+beta), а (x_{1}=x_{0}-alpha), (y_{1}=y_{0}-beta). Теперь ясно, что в силу eqref{ref11} из (boldsymbol{Phi}(x, y)=0) следует (boldsymbol{Phi}(x_{1}, y_{1})=0). Утверждение доказано.
Утверждение 3.
Если линия содержит хотя бы одну точку и имеет центр симметрии (O(x_{0}, y_{0})), то (O) является центром.
Доказательство.
Рассмотрим пересечение линии с прямой, проходящей через (O), приняв эту точку за начальную точку прямой. Имеются две возможности:
- Точка (O) лежит на линии. Пусть прямая имеет неасимптотическое направление. Тогда (O) — единственная точка пересечения, так как иначе с учетом симметрии точек пересечения было бы не меньше трех. Следовательно, уравнение eqref{ref4} имеет кратный корень (t=0), откуда вытекает (Q=0). Итак, координаты точки (O) удовлетворяют равенству (12) при любых (alpha) и (beta), соответствующих неасимптотическим направлениям. Выберем два различных неасимптотических направления ((alpha, beta)) и ((alpha’, beta’)) и рассмотрим равенства
$$
begin{array}{cc}
& (Ax_{0}+By_{0}+D)alpha+(Bx_{0}+Cy_{0}+E)beta=0,\
& (Ax_{0}+By_{0}+D)alpha’+(Bx_{0}+Cy_{0}+E)beta’=0.
end{array}nonumber
$$
как систему уравнений с коэффициентами (alpha), (beta), (alpha’), (beta’), причем ((alphabeta’-alpha’beta neq 0)). Мы получаем равенства eqref{ref13}, как и требовалось. - Точка (O) не лежит на линии. Если прямая пересекает линию в точке (M), которой соответствует значение параметра (t_{1} neq 0), то существует симметричная точка пересечения со значением параметра (-t_{1}). Тогда (Pt_{1}^{2}+2Qt_{1}+R=0) и (Pt_{1}^{2}-2Qt_{1}+R=0), откуда следует (Q=0).
Таким образом, если линия имеет точки пересечения с двумя различными прямыми, проходящими через (O), то, как и выше, мы можем получить равенства eqref{ref13} для координат (O). Докажем, что такие прямые обязательно найдутся. Действительно, в противном случае все точки линии лежат на одной прямой. Согласно теореме о существующих типах линий второго порядка линии только двух классов обладают этим свойством: пары совпавших прямых и пары мнимых пересекающихся прямых. Но и для того, и для другого класса все центры симметрии принадлежат линии, что противоречит сделанному предположению. Утверждение доказано.
Сопряженные направления.
Направление ((alpha’, beta’)), определяемое диаметром, сопряженным направлению ((alpha, beta)), называется сопряженным направлению ((alpha, beta)). Компоненты ((alpha’, beta’)), направляющего вектора диаметра eqref{ref10} согласно доказанному ранее утверждению 6 удовлетворяют условию
$$
(Aalpha+Bbeta)alpha’+(Balpha+Cbeta)beta’=0label{ref15}
$$
или
$$
Aalphaalpha’+B(alpha’beta+alphabeta’)+Cbetabeta’=0label{ref16}
$$
В последнее выражение пары чисел ((alpha, beta)) и ((alpha’, beta’)) входят симметричным образом. Поэтому имеет место следующее утверждение.
Утверждение 4.
Если направление ((alpha’, beta’)), сопряженное с ((alpha, beta)), не является асимптотическим, то сопряженным для ((alpha’, beta’)) будет направление ((alpha, beta)) (рис. 9.3).
Возникает вопрос, при каких условиях направление, сопряженное какому-нибудь направлению ((alpha, beta)) может оказаться асимптотическим. Это легко выяснить. Из равенства eqref{ref15} следует, что в качестве (alpha’) и (beta’) можно выбрать соответственно — (-(Balpha+Cbeta)) и ((Aalpha+Bbeta)). Подставим это в уравнение eqref{ref9} для асимптотических направлений:
$$
A(Balpha+Cbeta)^{2}-2B(Balpha+Cbeta)(Aalpha+Bbeta)+C(Aalpha+Bbeta)^{2}=0.nonumber
$$
После преобразований получаем ((AC-B^{2}) times (Aalpha^{2}+2Balphabeta+Cbeta^{2})=0). Поскольку исходное направление не асимптотическое, это произведение может обратиться в нуль только за счет первого сомножителя. Мы получаем новое утверждение.
Утверждение 5.
Если линия не центральная ((delta=0)), то для любого направления ((alpha, beta)) сопряженное направление — асимптотическое (рис. 9.4). Если линия центральная ((delta neq 0)), то направление, сопряженное любому направлению, не асимптотическое.
Главные направления.
Если диаметр перпендикулярен хордам, которым он сопряжен, то он является осью симметрии рассматриваемой линии.
Определение.
Направление ((alpha, beta)) и направление ((alpha’, beta’)) сопряженного ему диаметра называются главными направлениями, если они перпендикулярны.
Если система координат декартова прямоугольная, то для главного направления компоненты ((alpha, beta)) должны быть пропорциональны коэффициентам уравнения eqref{ref10}, то есть должно существовать такое число (lambda), что
$$
Aalpha+Bbeta=lambdaalpha, Balpha+Cbeta=lambdabeta.label{ref17}
$$
Исключая (lambda), мы получаем уравнение для (alpha) и (beta):
$$
(A-C)alphabeta+B(beta^{2}-alpha^{2})=0.label{ref18}
$$
Если положить (alpha=cos varphi), (beta=sin varphi), то уравнение eqref{ref18} превратится в уравнение (2B cos 2varphi = (A-C)sin 2varphi), которое, как мы видели, обязательно имеет решение относительно (varphi). Поэтому имеет место следующее утверждение.
Утверждение 6.
Каждая линия второго порядка имеет хотя бы одну пару главных направлений.
Более подробное исследование уравнения eqref{ref18} показывает, что либо эта пара единственная, либо каждая пара перпендикулярных направлений является главной. Последний случай имеет место, когда (A=C), (B=0). При этом уравнение линии приводится к одному из канонических видов: (x^{2}+y^{2}=a^{2}), (x^{2}+y^{2}=-a^{2}) или (x^{2}+y^{2}=0). В двух последних случаях линия не имеет хорд, и результат лишен геометрического смысла.
Касательная к линии второго порядка.
Как известно, касательной к какой-либо линии называется предельное положение секущей, когда хорда стягивается в точку. Выведем уравнение касательной к линии второго порядка, заданной уравнением eqref{ref1}. Дадим предварительно следующее определение.
Определение.
Особой точкой линии второго порядка называется ее центр, который лежит на линии.
Особыми точками являются: точка пересечения пары пересекающихся прямых, единственная точка пары мнимых пересекающихся прямых и каждая точка пары совпавших прямых. В особой точке касательная не определена. Если точка лежит на прямой, входящей в состав линии, то касательная в этой точке совпадает с прямой. Исключив эти случаи, мы фактически ограничиваемся рассмотрением касательных к эллипсам, гиперболам и параболам.
Рассмотрим точку (M_{0}(x_{0, y_{0}})), лежащую на линии (L), и прямую с начальной точкой (M_{0}), заданную уравнением eqref{ref2}. С нашей точки зрения, приведенное выше определение касательной означает, что уравнение eqref{ref4}, определяющее точки пересечения (L) и прямой, имеет два совпадающих корня.
Так как начальная точка принадлежит (L), в уравнении eqref{ref4} (R=0), и один из его корней равен нулю. Корни совпадают, если и второй корень равен нулю, для чего необходимо, чтобы (Q=0). Если при этом окажется, что и (P=0), то прямая принадлежит линии второго порядка. Этот случай мы исключили, и потому уравнение имеет кратный корень (t=0) в том и только том случае, когда (Q=0). Мы рассматриваем равенство (Q=0) как условие, определяющее направляющий вектор касательной:
$$
(Ax_{0}+By_{0}+D)alpha+(Bx_{0}+Cy_{0}+E)beta=0.label{ref19}
$$
Так как (M_{0}) не особая точка, обе скобки здесь одновременно в нуль не обращаются, и условие eqref{ref19} определяет (alpha) и (beta) с точностью до общего множителя. Точка (M(x, y)) лежит на касательной тогда и только тогда, когда вектор (overrightarrow{M_{0}M}) коллинеарен (boldsymbol{a}(alpha, beta)), то есть его координаты (x-x_{0}) и (y-y_{0}) удовлетворяют тому же условию, что и ((alpha, beta)):
$$
(Ax_{0}+By_{0}+D)(x-x_{0})+(Bx_{0}+Cy_{0}+E)(y-y_{0})=0.label{ref20}
$$
Это и есть уравнение касательной к линии (L) в точке (M_{0}), лежащей на линии. Уравнение eqref{ref20} можно записать и иначе, если заметить, что координаты (M_{0}) удовлетворяют уравнению eqref{ref1} и, следовательно,
$$
(Ax_{0}+By_{0}+D)x_{0}+(Bx_{0}+Cy_{0}+E)y_{0}+Dx_{0}+Ey_{0}+F=0.nonumber
$$
Прибавляя это равенство к eqref{ref20} и группируя слагаемые, получим окончательное уравнение
$$
Axx_{0}+B(xy_{0}+x_{0}y)+Cyy_{0}+D(x+x_{0})+E(y+y_{0})+F=0.label{ref21}
$$
Особые точки.
Напомним, что особая точка линии второго порядка — это ее центр, лежащий на линии. Исследуем, при каких условиях линия второго порядка имеет особую точку. Для координат ((x_{0}, y_{0})) особой точки должны быть справедливы равенства
$$
begin{array}{cc}
& Ax_{0}+By_{0}+D=0, Bx_{0}+Cy_{0}+E=0,\
& Ax_{0}^{2}+2Bx_{0}y_{0}+Cy_{0}^{2}+2Dx_{0}+2Ey_{0}+F=0.
end{array}nonumber
$$
Умножим первое из них на (x_{0}), второе на (y_{0}) и вычтем из третьего. Мы получим эквивалентную систему уравнений
$$
left{begin{array}{l}
Ax_{0}+By_{0}+D=0,\
Bx_{0}+Cy_{0}+E=0,\
Dx_{0}+Ey_{0}+F=0.
end{array}right.label{ref22}
$$
Выберем какой-нибудь базис в пространстве и рассмотрим вспомогательные векторы (boldsymbol{p}(A, B, D)), (boldsymbol{q}(B, C, E)) и (boldsymbol{r}(D, E, F)). Равенства eqref{ref22} представляют собой координатную запись векторного равенства
$$
x_{0}boldsymbol{p}+y_{0}boldsymbol{q}=-boldsymbol{r}.label{ref23}
$$
Отсюда следует, что при наличии особой точки векторы (boldsymbol{p}), (boldsymbol{q}) и (boldsymbol{r}) компланарны, и потому
$$
triangle=begin{vmatrix}
A& B& D\
B& C& E\
D& E& F
end{vmatrix}=0.label{ref24}
$$
Если линия центральная, то векторы (boldsymbol{p}) и (boldsymbol{q}) не коллинеарны, и условие компланарности eqref{ref24} равносильно существованию разложения eqref{ref23}, то есть существованию решения системы eqref{ref22}. Мы получили ещё одно утверждение.
Утверждение 7.
Центральная линия имеет особую точку тогда и только тогда, когда (triangle=0).
Итак, сочетание (delta < 0), (triangle=0) характеризует пары пересекающихся прямых, а (delta > 0), (triangle=0) — пары мнимых пересекающихся прямых.
Рассмотрим нецентральные линии. Для них существует центр, хотя бы не являющийся особой точкой, тогда и только тогда, когда (triangle=0). В этом (и только этом) случае векторы (boldsymbol{p}) и (boldsymbol{q}) коллинеарны. Действительно, так как (delta=0), по предложению 9 § 2 гл. II, если система уравнений eqref{ref13} имеет решение, она равносильна одному из составляющих ее уравнений: либо коэффициенты и свободный член одного из уравнений равны нулю, либо коэффициенты и свободные члены обоих уравнений пропорциональны. Тогда (triangle=0) независимо от (boldsymbol{r}).
Обратно, пусть для нецентральной линии (triangle=0). Докажем, что (boldsymbol{p}) и (boldsymbol{q}) коллинеарны, что равносильно совместности уравнений центра. Действительно, в противном случае (boldsymbol{r}) по ним раскладывается, и согласно eqref{ref23} существует особая точка. Она — центр, (boldsymbol{p}) и (boldsymbol{q}) коллинеарны, и мы получаем противоречие.
Утверждение 8.
Для нецентральных линий условие (triangle=0) равносильно существованию центра.
Итак, сочетание (delta=triangle=0) характеризует пары параллельных прямых (вещественных, мнимых или совпавших).
Из последних двух утверждений следует, что равенство (triangle=0) является инвариантным: оно не может измениться при переходе к другой системе координат.