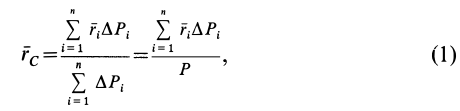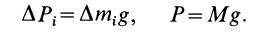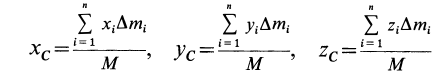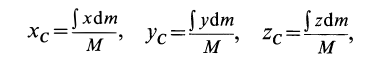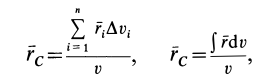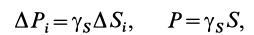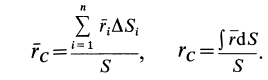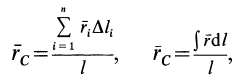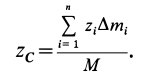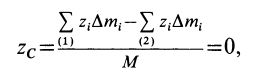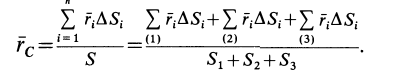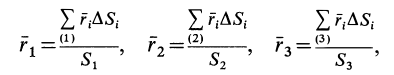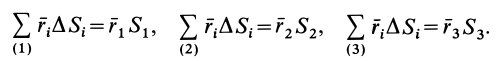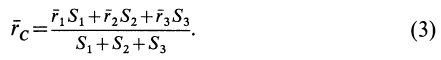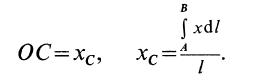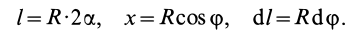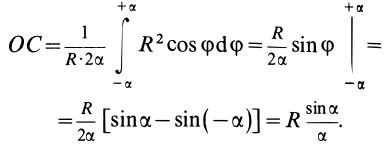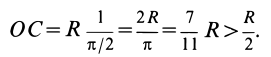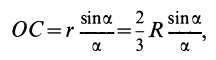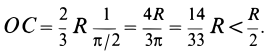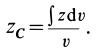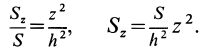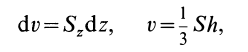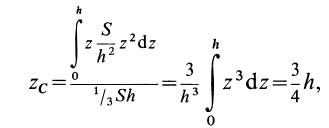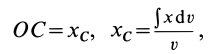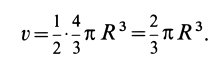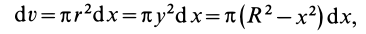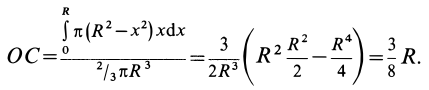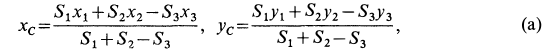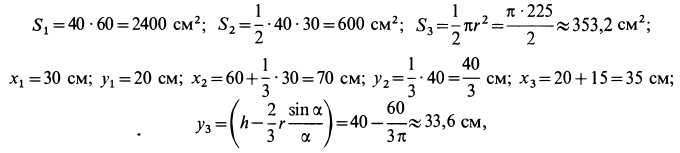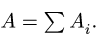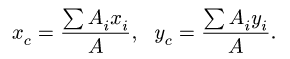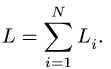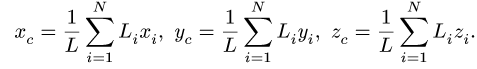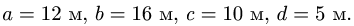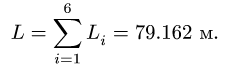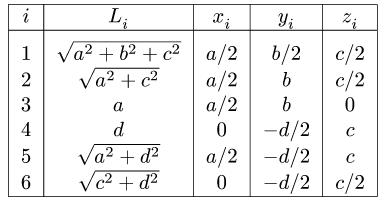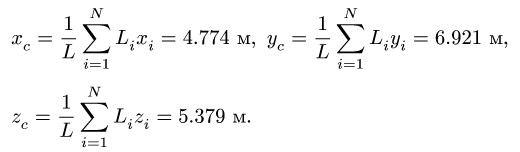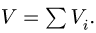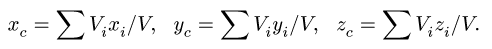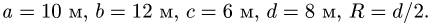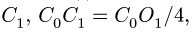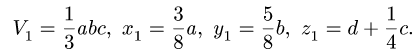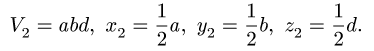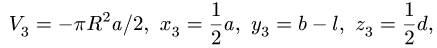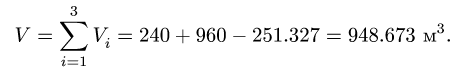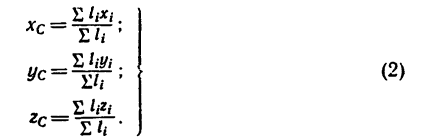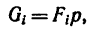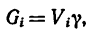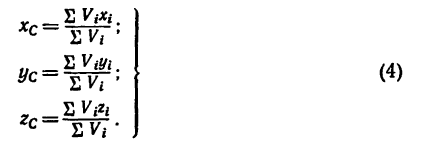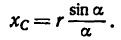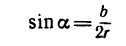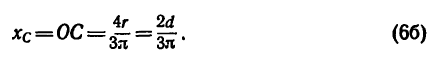1
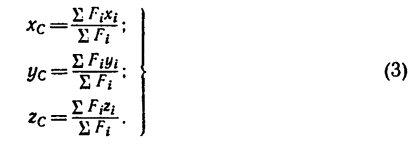
Центр тяжести площади треугольника.
Разобьем площадь треугольника АВD
(рисунок 118) прямыми, параллельными
стороне АD,
на большое число узких полосок, которые
можно рассматривать как отрезки
материальной прямой линии. Центр тяжести
каждой такой полоски лежит в ее середине,
т. е. на медиане FВ
треугольника АВD.
Следовательно, и центр тяжести площади
треугольника АВD
лежит на этой медиане.
Разбив площадь
треугольника АВD
прямыми, параллельными какой-нибудь
другой стороне, например ВD,
и рассуждая аналогичным образом, придем
к тому, что центр тяжести площади
треугольника должен лежать на медиане
ЕА.
Отсюда заключаем, что центр
тяжести площади треугольника лежит в
точке пересечения его медиан.
При этом, как
известно из геометрии,
. (1)
2. Центр тяжести
дуги окружности.
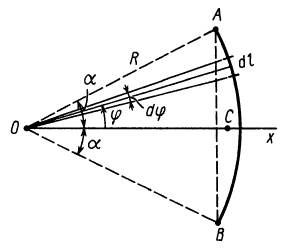
Пусть дана дуга АВ
окружности радиуса R
с центральным углом
(рисунок 119). Начало координат возьмем
к центре окружности и осьOx
направим перпендикуляр к хорде АВ.
Очевидно, ось Ox
будет осью симметрии для дуги АВ,
и, следовательно, центр тяжести дуги
окружности АВ
лежит на этой оси. Найдем координату
способом интегрирования. Для этого
выделим на дугеАВ
элемент
,
положение которого определяется углом.
Координатах
этого элемента будет
.
Подставляя эти значения в первую из
формул (4, §49), находим, чтоцентр
тяжести дуги окружности лежит на ее оси
симметрии на расстоянии от центра

угол
измеряется в радианах.
В частности, для
дуги полуокружности ()
имеем
.
3. Центр тяжести
площади кругового сектора.
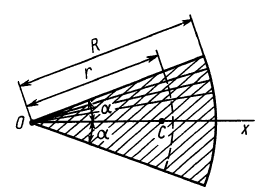
Рассмотрим круговой сектор ОАВ
радиуса R
с центральным углом
(рисунок 120). Разобьем мысленно площадь
сектораАОВ
радиусами, проведенными из центра О,
на элементарные секторы с центральным
углом
.
Эти элементарные секторы можно
рассматривать как плоские треугольники,
центры тяжести которых лежат на дугерадиуса
.
Следовательно, центр тяжести сектора
ОАВ
будет совпадать с центром тяжести дуги
,
положение которого найдется по формуле
(2).
Окончательно
получим, что центр
тяжести площади кругового сектора лежит
на его оси симметрии на расстоянии от
центра.
, (3)где
угол
измеряется в радианах.
В частности, для
сектора в виде полукруга ()
получим
. (4)
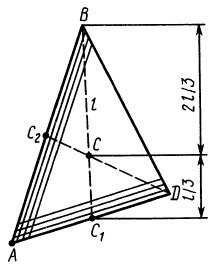
4. Центр тяжести
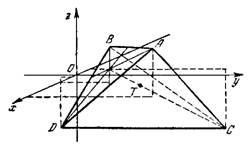
объема пирамиды.
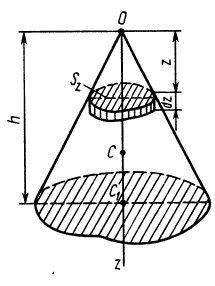
Для нахождения центра тяжести пирамиды
АВDЕ
(рисунок 121) разобьем ее высоту на n
равных частей и через точки деления
проведем плоскости, параллельные
основанию.
Е
неограниченно увеличивать, то каждый
из полученных слоев можно рассматривать
как треугольник. Центры тяжести площадей
этих треугольников лежат на прямой
,
соединяющей вершину пирамидыЕ
с центром тяжести
,
ее основания. Следовательно, на прямойбудет лежать и центр тяжести всей
пирамиды.
Точно так же найдем,
что центр тяжести данной пирамиды должен
лежать на прямой
,
соединяющей вершину пирамидыВ
с центром тяжести
ее граниАDЕ.
Поэтому искомый центр тяжести пирамиды
лежит в точке С,
где пересекаются прямые
и
.
Определим положение
точки С.
По свойству медиан треугольников имеем
и
;
из этих двух
равенств следует, что прямые
иВЕ
параллельны и
.
Но так как прямые
иВЕ
параллельны, то треугольники
иECB
подобны.
Из подобия
треугольников
иЕСВ
следует, что
.
Следовательно,
и
,
откуда находим
. (5)
Этот результат
будет также справедлив для любой
однородной многоугольной пирамиды, а
в пределе и для однородного круглого
конуса.
Таким образом,
центр тяжести объема однородной
треугольной пирамиды лежит на отрезке,
соединяющем вершину пирамиды с центром
тяжести ее основания, на расстоянии
одной четверти длины этого отрезка от
центра тяжести основания пирамиды.
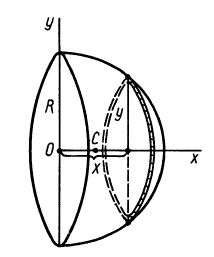
5. Центр тяжести
объема полушара.
Примем ось симметрии данного однородного
полушара радиуса R
за ось z,
а начало декартовых координат (Охуz)
– в геометрическом центре О
этого полушара (рисунок 122). Искомый
центр тяжести С
рассматриваемого полушара лежит на оси
симметрии z,
поэтому достаточно найти только
расстояние
.
При этом для вычисления искомой координатыприменим третью из формул (2,§49):

где
теперь интегрирование следует
распространить по объемуV
всего полушара. Объем полушара равен
.
Для вычисления
этого тройного интеграла воспользуемся
сферическими координатами, тогда
;
;
,где
r,
и 0
– сферические координаты (см. рисунок
122).
Отсюда элемент
объема
.
При этом вычисление тройного интеграла
сводится к последовательному вычислению
трех простых интегралов:


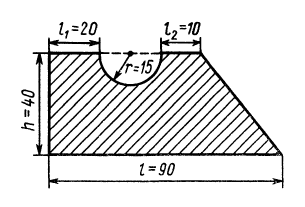
Задача 20.
Определить положение центра тяжести
площади поперечного сечения неравнобокого
угольника, полки которого имеют ширину
,
и толщину
(рисунок 123).
Решение.
Разобьем данную площадь на два
прямоугольника. Центры тяжести каждого
из прямоугольников лежат на пересечении
его диагоналей. Координаты этих центров
тяжести, так же как и площади прямоугольников,
легко определяются из рисунка 123.
Площади первого
и второго прямоугольников
;
.
Координаты центра
тяжести первого и второго прямоугольников
,
;
,
.
Координаты
и
центра тяжести площади поперечного
сечения данного неравнобокого угольника
определим по формулам:
Задача 21.Определить
положение центра тяжести площади круглой
пластины радиуса R,
с вырезом в виде прямоугольника со
сторонами a
и b
(рисунок 124).
Решение.
Так как пластина с вырезом имеет ось
симметрии, то ее центр тяжести лежит на
этой оси. Выбираем начало координат в
точке О
(рисунок 124) и направляем ось Ох
по оси симметрии. Для нахождения
координаты
центра
тяжести площади пластины с вырезом
дополняем площадь этой пластины до
полного круга.
П
полного круга;
центр тяжести этого крута совпадает с
началом координатО,
следовательно, абсцисса этого центра
.
Площадь вырезанного
прямоугольника
;
абсцисса центра тяжести площади этого
прямоугольника.
Применяя первую
из формул (1, §49), найдем абсциссу центра
тяжести площади данной круглой пластины
с вырезом:

Задача 22.
Определить положение центра тяжести
площади кругового сегмента АDВ
радиуса R,
если угол
(рисунок 125).
Решение.
Так как круговой сегмент имеет ось
симметрии, то его центр тяжести лежит
на этой оси. Примем эту ось за ось х.
Начало координат
возьмем в точке О
(рисунок 125). Для нахождения координаты
центра тяжести площади кругового
сегмента АDВ
дополним эту площадь до площади кругового
сектора ОАDВ.
Площадь треугольника
АОВ
определим по формуле
;
абсцисса
ее центра тяжести х1
= (2/3) ОЕ =
(2/3) Rcosα
.
Площадь кругового
сектора ОАDВ
определим по формуле
;
абсцисса ее центра тяжести.
Применяя первую
из формул (1, §49), найдем абсциссу центра
тяжести площади данного кругового
сегмента АDВ:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Задача №1. Вычислить координаты точки М, если луч ОМ наклонен к оси Ох под углом в 60°, а к оси Оу — под углом в 45° и что длина его равна 12.
Решение. Согласно условию α =60°, β =45°.
Воспользовавшись соотношением между квадратами направляющих косинусов, найдем угол α:
Координаты точки М определим по формулам:
Задача №2. Начало отрезка находится в точке А (3; 2; 7). Найти его конец, зная, что длина отрезка АВ равна 15, а углы между этим отрезком и осями координат удовлетворяют соотношению
sin α : sin β : sin γ = 3 : 4 : 5.
Решения этих задач подробно изложено в следующем видео
Задача №3. Вершины треугольника находятся в точках А (5; 3; -10), В (0; 1; 4), С (-1; 3; 2). Найти направляющие косинусы биссектрисы угла В.
Задача №4. Найти угол между лучом, лежащим в плоскости yOz и образующим с осью Oz угол 60° и лучом, лежащим в плоскости xOz и образующим с осью Oz угол 30°.
Решения этих задач подробно изложено в следующем видео
Задача №5. Найти центр тяжести пирамиды, вершины которой находятся в точках: А (8; 10; 4), В (3; 4; 3), С(-2; 11; -5), D (1; -1; -4).
Решение. Центр тяжести пирамиды находим как среднее арифметическое координат вершин пирамиды.
Рис.1
Ответ: Т (2,5; 6; -0,5).
Задача №6. Найти отношение, в котором делится отрезок, соединяющий точки М (2; 2; 5) и N (2; —3; —5), центром тяжести пирамиды с вершинами в точках А (3; —2; 7), В (3; 3; 2), С (-7; 5; -3), D (9; -6; -2).
Решения этих задач подробно изложено в следующем видео
Содержание:
Центр тяжести:
При рассмотрении движения тел, особенно таких, как самолеты, ракеты, космические корабли, важное значение имеет понятие центра тяжести.
Определения и формулы для вычисления центров тяжести
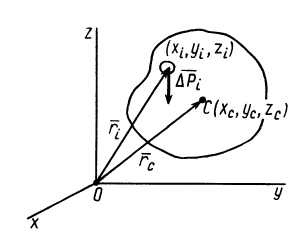
Для введения понятия центра тяжести разобьем мысленно рассматриваемое тело на достаточно большое число малых по сравнению с телом или элементарных его частей произвольной формы. Силу тяжести элементарной частицы тела с индексом
Радиус-вектор центра тяжести тела 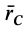
где 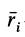

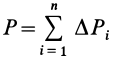

Рис. 88
Если в (1) перейти к пределу, увеличивая число элементарных частей 

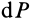
где 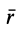
где 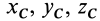
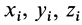
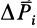
Используя понятие центра тяжести тела, введем понятие его центра масс. Силы тяжести элементарных частей тела и всего тела можно выразить через их массы 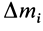
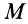

Подставляя эти значения сил тяжести в (1) и (1′) после сокращения на 
и соответственно
По формулам (2) и (2′) определяют радиус-вектор центра масс тела. Центр масс обычно определяют независимо от центра тяжести как геометрическую точку, радиус-вектор, которой вычисляется по формулам (2) или (2′). В проекциях на оси координат из (2) и (2′) получаем:
и
где 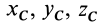
Для однородного тела силу тяжести элементарной частицы тела и ее массу можно вычислить по формулам
где 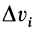


где 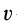


по которым определяют центр тяжести объема тела.
Если тело имеет форму поверхности, т. е. один из размеров мал по сравнению с двумя другими, как, например, у тонкого листа железа, то имеем
где 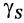
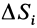
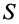
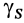
Для однородных тел типа проволоки, у которых два размера малы по сравнению с третьим, можно определить радиус-вектор центра тяжести длины линии по формулам
где 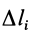
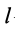
Методы определения центров тяжести (Центров масс)
Метод симметрии
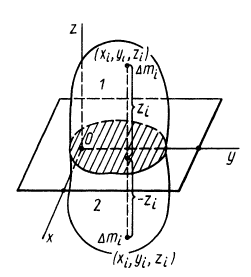
При определении центров тяжести широко используется симметрия тел. Докажем, что для однородного тела, имеющего плоскость симметрии, центр тяжести находится в плоскости симметрии. Для доказательства выберем начало координат в плоскости симметрии тела и одну из осей координат, ось 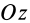
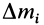
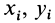
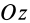
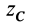
Разбивая сумму в числителе на две по симметричным частям тела, получаем, что
так как симметричные части тела 1 и 2 одинаковы.
Таким образом, центр масс расположен в плоскости симметрии и для его определения достаточно вычислить только две его координаты 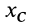
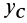
Аналогично доказывается, что для однородного тела, имеющего ось или центр симметрии, центр масс находится соответственно на оси симметрии или в центре симметрии.
Рис. 89
Метод разбиения на части (метод группировки)
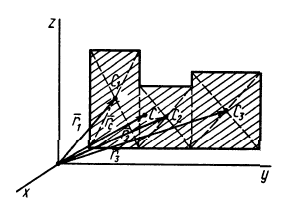
Некоторые тела сложной формы можно разбить на части, центры тяжести которых известны или предварительно могут быть определены. В таких случаях центры тяжести сложных тел вычисляются по общим формулам, определяющим центр тяжести, только вместо элементарных частиц тела берутся его конечные части, на которые оно разбито. Покажем это на частном примере плоской фигуры, изображенной на рис. 90. Плоскую фигуру можно разбить на три части, центры тяжести которых 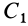
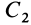
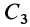
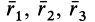
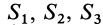
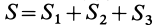
Используя определение центра тяжести и производя группировку слагаемых под знаком суммы по частям фигуры, на которые она разбита, получим
Радиусы-векторы центров тяжести частей тела выразятся в такой форме:
или
Используя эти формулы для радиуса-вектора всей фигуры, имеем
Полученная формула имеет ту же структуру, что и формула, определяющая радиус-вектор центра тяжести тела при разбиении его на элементарные частицы, только в нее входят величины для конечных частей тела.
Рис. 90
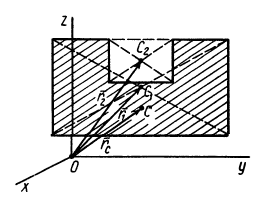
Метод отрицательных масс
Видоизменением метода разбиения на части является метод отрицательных масс. Проиллюстрируем его тоже на примере плоской фигуры (рис. 91). Для определения центра тяжести этой фигуры ее можно разбить на три части. Можно поступить по-другому. Для этого дополним нашу фигуру до прямоугольника и примем, что этот прямоугольник с площадью 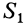
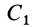
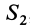
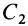
В отличие от обычного метода разбиения на части в формуле (4) массы и, следовательно, площади входят со знаком минус.
Метод отрицательных масс особенно удобен при вычислении положения центров тяжести тел, имеющих отверстия.
Рис. 91
Центры тяжести простейших тел
Для определения центров тяжести тел сложной формы методом разбиения на части или методом отрицательных масс необходимо уметь вычислять центры тяжести простейших тел, на которые разбивается тело сложной формы. Рассмотрим некоторые из тел, для определения центров тяжести которых известны простые способы их нахождения или вычисления по формулам.
Прямолинейный отрезок
Центр тяжести прямолинейного однородного отрезка располагается на его середине, а неоднородного— на самом отрезке и не может находиться вне отрезка.
Площадь треугольника
Для определения центра тяжести площади треугольника разобьем его прямыми линиями, параллельными одной из его сторон 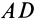

Затем разобьем треугольник на полоски прямыми линиями, параллельными другой стороне 
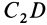

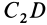
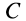

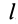
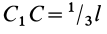
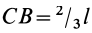
Рис. 92
Дуга окружности
Дуга окружности 
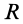
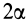
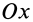

Рис. 93
В рассматриваемом случае
Подставляя эти значения в формулу для 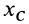
Таким образом,
Для полуокружности 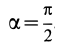
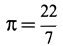
Площадь кругового сектора
Центр тяжести площади кругового сектора с радиусом 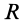
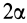
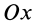
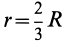
Рис. 94
Используя формулу для центра тяжести дуги окружности, получим
или
Для площади полукруга 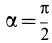
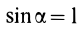
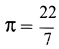
Объем пирамиды и конуса
Определим положение центра тяжести объема конуса (рис. 95). Для простоты рассмотрим прямой конус, у которого высота является осью симметрии. Высотой конуса является отрезок, соединяющий его вершину 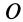
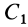
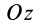
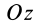
Разобьем конус плоскостями, перпендикулярными оси 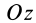
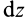
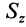
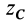
Отношения линейных размеров сечений к соответствующим размерам основания конуса пропорциональны их расстояниям до вершины конуса. Отношения площадей пропорциональны квадратам расстояний. Приняв 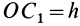
Учитывая, что
имеем
или
Таким образом, центр тяжести прямого конуса находится на расстоянии 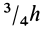
Рис. 95
Это справедливо для объема любого конуса и любой пирамиды, как прямых, так и наклонных, т. е. центр тяжести объема пирамиды или конуса находится на расстоянии 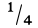
Объем полушара
Полушар имеет ось симметрии, которую примем за координатную ось 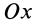
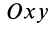
где 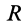
где 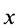
Объем элементарного диска
так как радиус диска 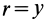
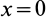
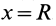
Таким образом, центр тяжести объема полушара находится от его центра на расстоянии
Это расстояние меньше половины радиуса полушара.
Рис. 96
Задача №1
Определить координаты центра тяжести площади плоской фигуры, имеющей размеры, указанные на рис. 97.
Рис.97
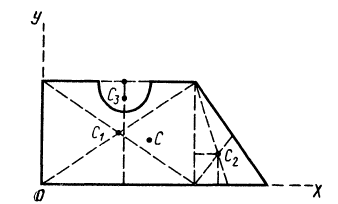
Рис. 98
Решение. Присоединим к заданной фигуре дополнительно полукруг 3 и разобьем полученную фигуру на прямоугольник 1 и треугольник 2. Получили три фигуры, две из которых имеют положительные площади (прямоугольник 1 и треугольник 2) и одна — отрицательную (полукруг 3). В выбранной системе координат для координат центра тяжести заданной фигуры имеем
где 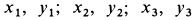
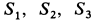
Вычислим площади и координаты центров тяжести отдельных фигур, учитывая рис. 98 Имеем:
так как 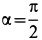
Подставляя полученные значения в (а), получим:
Центр тяжести плоской фигуры
постановка задачи. Найти площадь и координаты центра тяжести плоской фигуры.
План решения:
1. Разбиваем фигуру на простые отдельные части, положение центров тяжести которых известны.
2. Выбираем систему координат. Вычисляем площади и координаты 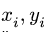
3. Находим общую площадь фигуры по формуле
4. Определяем координаты центра тяжести фигуры:
Задача №2
Найти площадь и координаты центра тяжести плоской фигуры. Криволинейный участок контура является половиной окружности с центром на оси Ох (рис. 74). Размеры на рисунке даны
Решение
1. Разбиваем фигуру на простые отдельные части, положение центров тяжести которых известны.
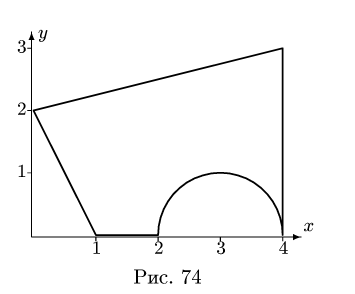
Центр тяжести прямоугольника находится в его геометрическом центре, положение центра тяжести других фигур, встречающихся в задачах, изображено на рис. 75
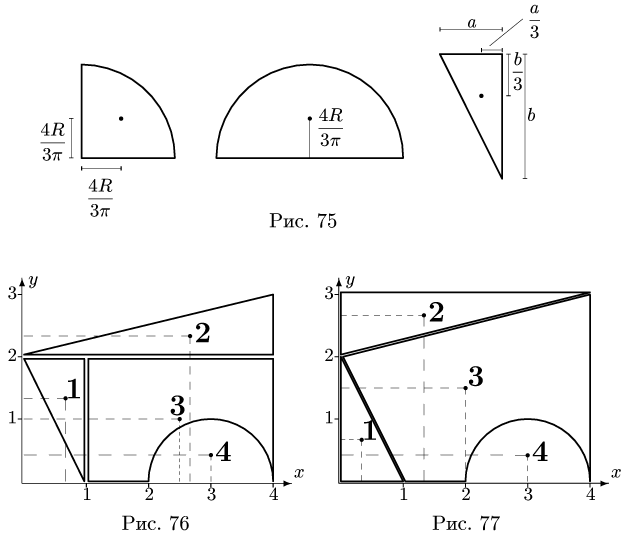
Представляем фигуру в виде двух треугольников 1,2, прямоугольника 3 и выреза 4 в виде полукруга (рис. 76).
2. Вычисляем площадь (в 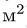
Площадь выреза берем со знаком минус.
3.Площадь фигуры
4. Находим координаты центра тяжести всей фигуры:
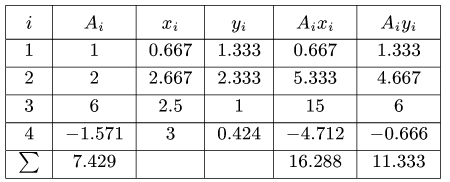
Вычисления удобно свести в таблицу:
Сначала заполняем столбцы 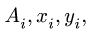
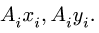
Замечание 1. Большинство задач на определение центра тяжести допускает несколько способов разбиения фигуры. Это можно использовать для проверки решения. Второй вариант разбиения фигуры в данном примере состоит из прямоугольника 3 с размерами 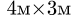
Замечание 2. Решение задачи в системе Maple V методом контурного интегрирования.
- Заказать решение задач по теоретической механике
Пространственная стержневая система
Постановка Задачи. Найти координаты центра тяжести пространственной фигуры, состоящей из N однородных стержней.
План решения:
1. Разбиваем фигуру на отдельные стержни.
2. Выбираем систему координат. Вычисляем длины и координаты 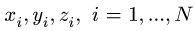
3. Находим суммарную длину стержней системы
4. Определяем координаты центра тяжести тела по формулам
Задача №3
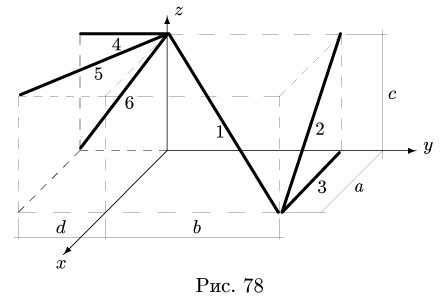
Найти координаты центра тяжести пространственной фигуры, состоящей из шести однородных стержней (рис. 78). Даны размеры:
Решение
1. Разбиваем фигуру на шесть стержней.
2. Выбираем систему координат (рис. 78). Вычисляем длины и координаты 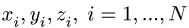
3. Находим суммарную длину стержней системы:
Промежуточные результаты удобно занести в таблицу:
4. Определяем координаты центра тяжести тела по формулам
Постановка задачи. Найти координаты центра тяжести однородного объемного тела.
План решения:
1. Разбиваем тело на простые части, положение центров тяжести которых известно.
2. Выбираем систему координат. Вычисляем объемы 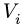
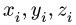
3. Находим общий объем тела по формуле
4. Определяем координаты центра тяжести тела:
Задача №4
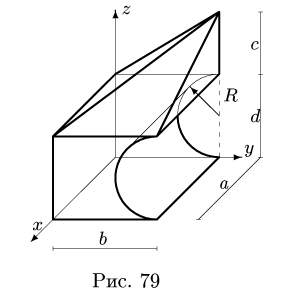
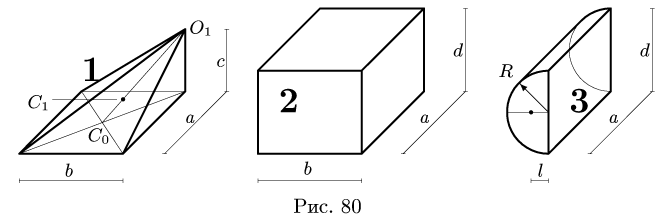
Найти координаты центра тяжести однородного объемного тела (рис.79);
Решение
1. Разбиваем тело на пирамиду 1, параллелепипед 2 и половину цилиндра 3 (рис. 80).
2. Выбираем систему координат. Вычисляем объемы 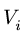
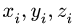
Центр тяжести параллелепипеда 2 совпадает с его геометрическим центром:
Объем половины цилиндра 3 берем со знаком минус:
где 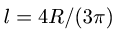
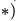
3. Находим общий объем тела:
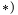
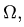
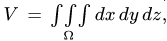
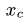
4. Определяем координаты центра тяжести тела:
Центр тяжести
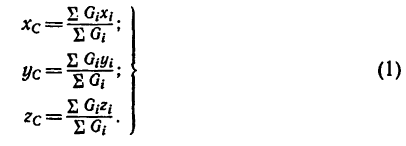
Центр тяжести — точка, через которую проходит линия действия равнодействующей элементарных сил тяжести. Он обладает свойством центра параллельных сил. Поэтому формулы для определения положения центра тяжести различных тел имеют вид:
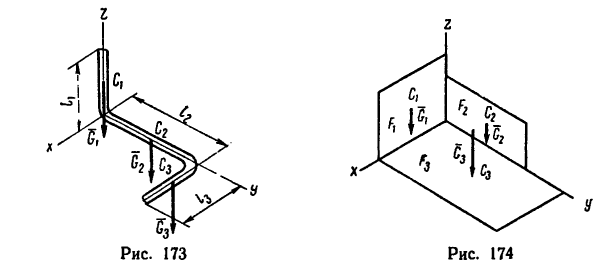
Если тело, центр тяжести которого нужно определить, можно отождествить с фигурой, составленной из линий (например, замкнутый или незамкнутый контур, изготовленный из проволоки, как на рис. 173), то вес 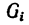
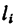
где d — постоянный для всей фигуры вес единицы длины материала.
После подстановки в формулы (1) вместо 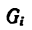
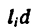
Если тело имеет вид фигуры, составленной из расположенных различным образом плоскостей или кривых поверхностей (рис. 174),
то вес каждой плоскости (поверхности) можно представить так:
где 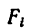
После подстановки этого значения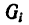
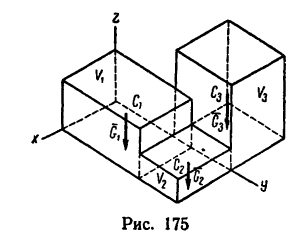
Если же однородное тело можно разделить на простые части определенной геометрической формы (рис. 175), то вес каждой части
где 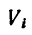
После подстановки значений 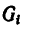
При решении некоторых задач на определение положения центра тяжести тел иногда необходимо знать, где расположен центр тяжести дуги окружности, кругового сектора или треугольника.
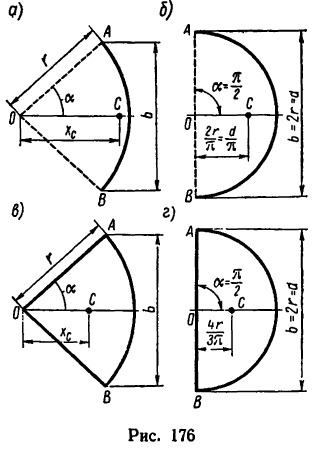
Если известен радиус дуги г и центральный угол 2а, стягиваемый дугой и выраженный в радианах, то положение центра тяжести С (рис. 176, а) относительно центра дуги О определится формулой
Если же задана хорда 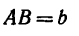
и тогда
В частном случае для полуокружности обе формулы примут вид (рис. 176, б)
Положение центра тяжести кругового сектора, если задан его радиус r (рис. 176, в), определяется при помощи формулы
Если же задана хорда сектора, то
В частном случае для полукруга обе последние формулы примут вид (рис. 176, г)
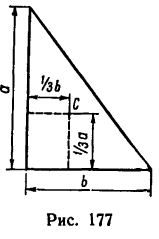
Центр тяжести площади любого треугольника расположен от любой стороны на расстоянии, равном одной трети соответствующей высоты.
У прямоугольного треугольника центр тяжести находится на пересечении перпендикуляров, восставленных к катетам из точек, расположенных на расстоянии одной трети длины катетов, считая от вершины прямого угла (рис. 177).
При решении задач на определение положения центра тяжести любого однородного тела, й составленного либо из тонких стержней (линий), либо из пластинок (площадей), либо из объемов, целесообразно придерживаться следующего порядка:
- выполнить рисунок тела, положение центра тяжести которого нужно определить. Так как все размеры тела обычно известны, при этом следует соблюдать масштаб;
- разбить тело на составные части (отрезки линий или площади, или объемы), положение центров тяжести которых определяется исходя из размеров тела;
- определить или длины, или площади, или объемы составных частей;
- выбрать расположение осей координат;
- определить координаты центров тяжести составных частей;
- найденные значения длин или площадей, или объемов отдельных частей, а также координат их центров тяжести подставить в соответствующие формулы и вычислить координаты центра тяжести всего тела;
- по найденным координатам указать на рисунке положение центра тяжести тела.
- Кинематика точки
- Плоское движение твердого тела
- Мгновенный центр скоростей
- Мгновенный центр ускорений
- Условия равновесия системы сил
- Плоская система сил
- Трение
- Пространственная система сил
Боковую поверхность этой антипризмы, состоящую из десяти правильных треугольников, можно назвать боковой поверхностью рассматриваемого икосаэдра. Основания пирамид (антипризмы) являются пятиугольниками, центры которых лежат на общей высоте, и поэтому один многоугольник повернут относительно другого на 36В икосаэдр можно вписать додекаэдр, имеющий двенадцать пятиугольных граней. Додекаэдр и икосаэдр являются взаимно соответствующими многогранниками. [c.108]
Пирамиду называют правильной, если основанием служит правильный многоугольник и высота пирамиды проходит через центр этого многоугольника (см. рис.95 и рис.96, а). [c.89]
Центр тяжести объема пирамиды (или конуса). Этот центр С лежит на прямой iE (рис. 112), где — вершина, а i — центр тяжести площади основания пирамиды при этом [c.94]
МИДЫ с центром тяжести К, ее основания. Очевидно, что центр тяжести объема пирамиды должен лежать на этой же прямой. Аналогично, центр тяжести объема пирамиды должен лежать и на прямой AL, соединяющей вершину А пирамиды с центром тяжести L грани BED. [c.146]
Следовательно, центр тяжести объема пирамиды находится в точке С пересечения прямых ЕК и AL. [c.146]
Так как конус представляет собой предел многогранной пирамиды, то расстояние от центра тяжести его объема до основания составляет одну четверть его высоты (рис. 196). [c.147]
Сущность этого метода состоит в следующем к данному телу / присоединяют второе тело // так, чтобы получилось новое тело III простой геометрической формы, центр тяжести которого легко можно определить. Например, продолжив две противоположные стороны данного четырехугольника до их пересечения, можно дополнить его до треугольника усеченный тетраэдр можно дополнить до четырехгранной пирамиды. Если при этом положение центра тяжести присоединенного тела // также легко можно определить, то к телу III применяем метод разбиения на простейшие части это тело можно рассматривать состоящим из двух частей данного тела I и добавленного тела II, и, следовательно, можно воспользоваться формулами (43). [c.134]
Центр тяжести пирамиды (рис. 1.93, а) или конуса (рис. 1.93, б) лежит на отрезке, соединяющем вершину пирамиды (конуса) с центром тяжести основания, на расстоянии /4 высоты пирамиды (конуса) . [c.75]
Решение. Примем за центр приведения начало координат О. При равновесии пирамиды главный вектор V и главный момент /Мд системы сил, приложенных к пирамиде, равны нулю У=0, mQ = 0. Так как по модулю [c.191]
Итак, центр тяжести пирамиды находится в точке а -g-й [c.124]
Этот же результат имеет место для любой пирамиды, т. е. центр тяжести пирамиды находится на расстоянии, равном высоты пирамиды от соответствующего основания. … [c.124]
Деля затем пирамиду на бесконечно большое число элементарных пластинок плоскостями, параллельными грани SAB, мы найдем, что центры тяжести этих площадок расположатся по прямой КС, где К — центр тяжести площади треугольника ASB, причем EK = ES. [c.221]
Положение центра тяжести объема пирамиды определяется равенством (21). Поэтому центры тяжести элементарных пирамид располо- [c.222]
Определить расстояние от центра тяжести однородной пирамиды до ее основания, если высота пирамиды 0,8 м. (0,2) [c.96]
Центры тяжести объема пирамиды и конус а. В основании пирамиды (рис. 104) лежит треугольник BDE с центром тяжести в точке Q. Если пирамиду рассечь на ряд треугольных пластинок сечениями, параллельными основанию, то центры тяжести этих пластинок образуют линию A i, на которой должен лежать центр тяжести объема пирамиды. Центр тяжести грани ADE находится в точке С2, а центры тяжести всех треугольных пластинок, образующихся при сечении пирамиды параллельно грани ADE, будут лежать на прямой j- Центр тяжести пирамиды должен лежать и на прямой oi следовательно, он находится в точке С пересечения линий АС и ВС , которая отстоит от основания на расстоянии [c.81]
Многоугольную пирамиду можно разделить диагональными плоскостями на ряд треугольных пирамид, и в результате аналогичных рассуждений получим, что центр тяжести ее находится подобным же образом. [c.81]
Итак, центр тяжести объема пирамиды лежит на прямой, сое- [c.81]
Центры тяжести объема пирамиды и кону с а. В основании пирамиды (рис. 1.106) лежит треугольник BDE с центром тяжести в точке С . Если пирамиду рассечь на ряд треугольных пластинок сечениями, параллельными основанию, то центры тяжести этих пластинок образуют линию ЛС,, на которой должен лежать центр тяжести объема пирамиды. Центр тяжести грани ADE находится в точке С. , а центры тяжести всех треуголь- [c.74]
Итак, центр тяжести объема пирамиды лежит на прямой, соединяющей центр тяжести основания с вершиной, на расстоянии И4 длины этой линии, считая от основания. [c.75]
Сначала строят развертку неусеченной пирамиды, все грани которой, имеющие форму треугольника, одинаковы. На плоскости намечают точку S, (вершину пирамиды и из нее, как из центра, проводят дугу окружности радиусом, равным действите.пьной длине ребра пирамиды., Действительную длину ребра можно определить по профильной проекции пирамиды (рис. 175, а). Например, длина s»e» или s»h» равна величине R, так как эти ребра параллельны плоскос и W и изображаются на ней действительной длиной. Далее по дуге окружности от любой точки, например А, огкладывают тесть оди- [c.98]
Правильный восьмиграиник октаэдр) . Он состоит из восьми равносторонних и равных между собой треугольников, соединенных по четыре у каждой вершины. Каждая из диагональных плоскостей делит октаэдр на две пирамиды с основаниями, имеющими вид квадрата. В октаэдр, опираясь вершинами в центры его граней, вписывается многогранник — куб. Поэтому куб и октаэдр можно назвать взаимно соответствующими (дуальными) многогранниками. [c.107]
Построить сферу, касательную к граням AB и SAB пирамиды SAB (рис. 223), взяв ее центр на ребре S . 241. Провести через прямую АВ плоскость, касательную к данной сфере (рис. 224, а). [c.173]
Сечение пирамиды или призмы (черт. Ill) может быть построено и с помощью теоремы Дезарга ( 2), если предварительно определена точка пересечения одного из ребер с заданной плоскостью 0L, например точка 1=ЗАг а и прямая т = аГ р (Р — плоскость основания многогранника). В перспективно-коллинеарном соответствии двух плоскостей а и линия т их пересечения является осью коллинеации, а вершина S пирамиды — центром. [c.51]
Центр тяжести объема четырехгранной пирамиды. Разобьем пирамиду плоскостями, лараллельными основапию ylfiD, на бесчисленное множество тонких треугольных пластинок (рис. 194). Центры тяжести этих пластинок лежат на прямой ЕК, соединяющей вершину Е пира- [c.146]
Таким образом, центр тяжести объема четырехгранной пирамиды леотт на отрезке, соединяющем вершину пирамиды с центром тяжести основания, на расстоянии 1/4 длины этого отрезка от центра тяжести основания. [c.146]
Если из центра тяжести объема пирамиды опустить перпендикуляр на осиованне, то длина его составит 1/4 высоты пирамиды. [c.146]
Найтн длину ребра AS = h пирамиды и положение центра тяжести всего тела, если известно, что он лежит на верхней грани куба. [c.123]
Определим координаты центра тяжести пирамиды. Для этого рассмотрим 1лементарный объем, полученный сечением пирамиды плоскостями, параллельными плоскости xSy, на расстояниях г и z- -dz от вершины. Имеем [c.123]
Центр тяжести объема пирамиды. Возьмем треугольную пирамиду (тетраэдр) SAB (рис. 221) и разделим ее на элементарные пластинки плоскостями, параллельными основанию AB . Центры тяжести этих элементарных пластинок лежат на прямой SF, соединяющей вершину пирамиды 5 с центром тяжести площади основания, который лежит на пересечении медиан треугольника AB , т. е. [c.221]
Центр тяжести объема сферического сектора. Пусть дан сферический сектор ОАСВ (рис. 222), вырезанный из сферы радиуса R. Определим центр тяжести его объема. Разобьем сектор на элементарные пирамиды с равновеликими площадями оснований, вершины которых будут в центре сферы. Поверхность всего сегмента [c.221]
Для активных жидкостей наличие активности двух знаков должно обусловливаться дисимметричным строением молекулы. Представление об асимметричных молекулах нашло себе широкое применение в органической химии и было положено в основу стереохимии, т. е. учения о пространственном распределении атомов в молекулах. Асимметрия органических молекул связывается со свойством атома углерода вступать в соединения с четырьмя атомами или атомными группами (радикалами), причем в получившейся молекуле эти группы расположены в вершинах четырехгранной пирамиды, в центре которой расположен атом углерода. Для простейших [c.617]
c.126
]
Курс теоретической механики Часть1 Изд3 (1965) — [
c.350
]