Как найти координаты центра тяжести сопромат - Исправление недочетов и поиск решений вместе с Examum.ru

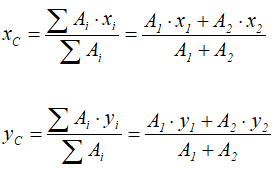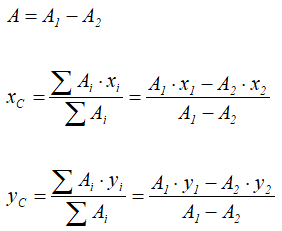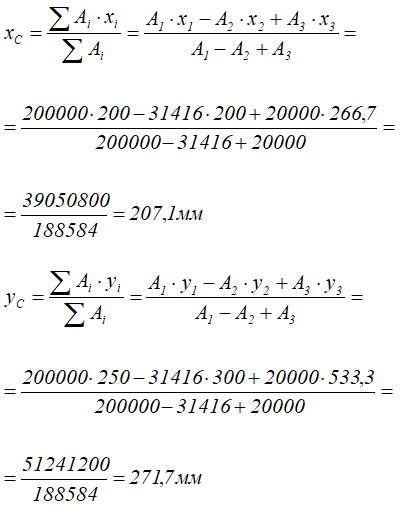
Определение координат центра тяжести x_C и y_C плоских фигур нестандартной формы выполняется при решении задач для последующих расчетов остальных геометрических характеристик, например, таких как радиусы и осевые моменты инерции поперечных сечений.

Рассмотрим способы и пример определения координат положения центра тяжести фигуры нестандартной формы.

Способы определения координат центра тяжести

Способы определения координат центров тяжести твердых объёмных тел и плоских фигур можно получить исходя из полученных ранее общих формул для расчета положения центра тяжести.

Существует 5 способов расчета координат положения центра тяжести:

Аналитический (путем интегрирования).
Метод симметрии. Если тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
Экспериментальный. (метод подвешивания тела).
Этот способ подходит в основном для плоских и линейных тел.
Разбиение. Тело или фигура разбивается на конечное число частей (простых тел или фигур), для каждой из которых положение центра тяжести C и площадь A известны.
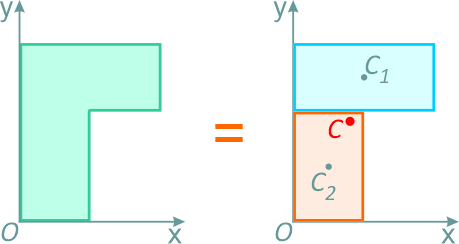
Например, проекцию тела на плоскость xOy (рисунок 1.8) можно представить в виде двух плоских фигур с площадями A₁ и A₂ (A = A₁+ A₂).

Рисунок 1.8

Центры тяжести этих фигур находятся в точках C₁(x₁, y₁) и C₂(x₂, y₂). Тогда координаты центра тяжести тела равны:
Дополнение (Метод отрицательных площадей или объемов).
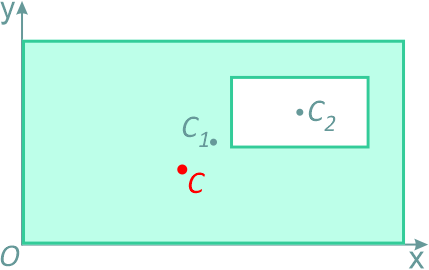
Это частный случай предыдущего способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны.

Например, необходимо найти координаты центра тяжести плоской фигуры (рисунок 1.9):

Рисунок 1.9

Тогда координаты центра тяжести фигуры с отверстием можно определить по формулам:

При решении задач по определению координат центра тяжести плоских фигур и объемных тел применяются последние два способа (разбиение и дополнение).

Пример определения координат центра тяжести сложной фигуры в нашем коротком видео:

Другие видео

Пример определения координат центра тяжести плоской фигуры

Задача
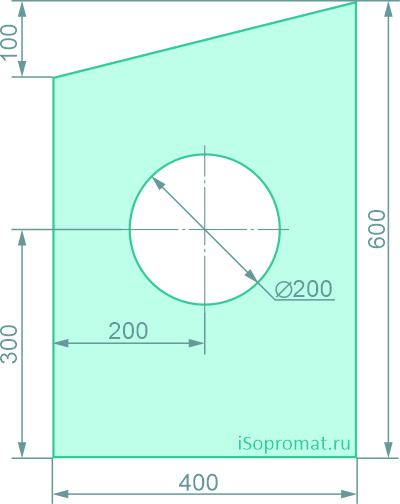
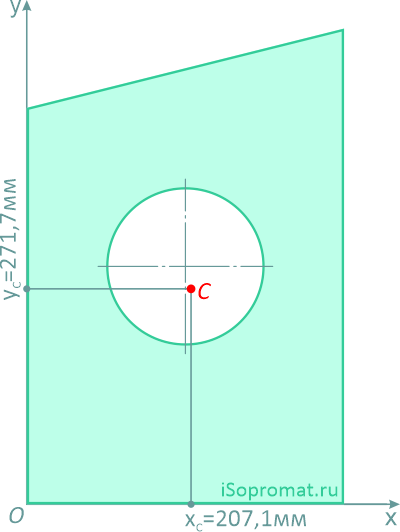
Определить координаты центра тяжести плоской фигуры с круглым отверстием

Решение
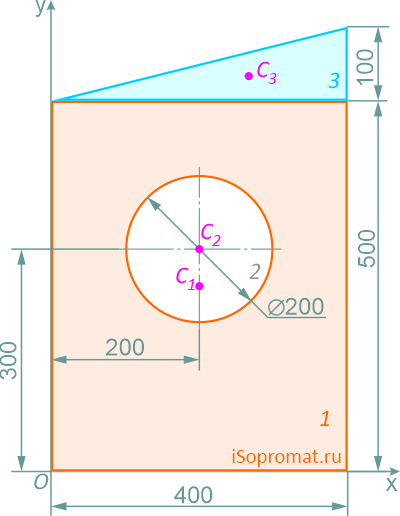
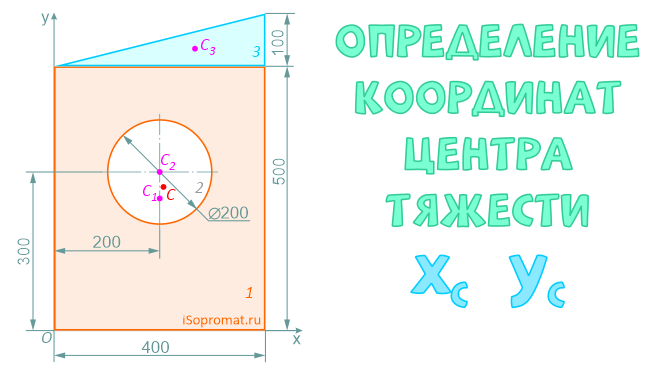
Разделим заданное сечение на простые фигуры – прямоугольник, круг и прямоугольный треугольник.
Через нижнюю левую точку фигуры проведем координатные оси x и y.

Рассчитаем необходимые для решения задачи площади A и координаты x,y центров тяжести C_i отдельных фигур:

Прямоугольник (фигура 1)
Площадь
A₁=400×500=200000 мм²
Положение центра тяжести
x₁=200мм
y₁=250мм

Круг (2) (вычитаемая фигура)
Площадь
A₂=π×200²/4=31416 мм²
Центр тяжести
x₂=200мм
y₂=300мм

Прямоугольный треугольник (3)
Площадь
A₃=400*100/2=20000 мм²
Положение центра тяжести треугольника находится на пересечении его медиан (на расстоянии 1/3 высоты от основания или 2/3 высоты от его вершин)
x₃=400×2/3=266,7мм
y₃=500+100×1/3=533,3мм

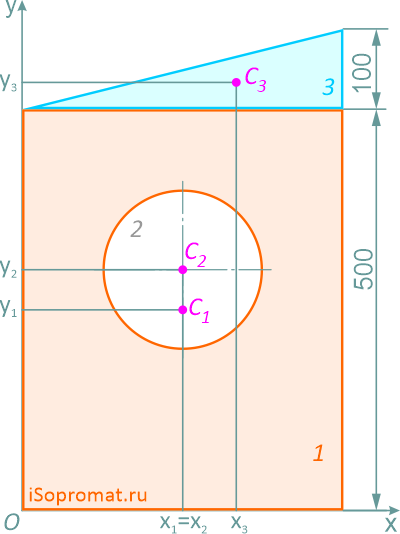
Координаты x и y центра тяжести C всей плоской фигуры определим по формулам:

Ответ: Таким образом, центр тяжести заданной фигуры находится в точке C с координатами x_C=207,1мм, y_C=271,7мм.

Другие примеры решения задач >
Центры тяжести простейших фигур >

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Источник

В этой статье посмотрим, как определяются координаты центра тяжести сложной фигуры — состоящей из простых. В задачах по сопромату часто приходится находить положение центра тяжести составных сечений, для дальнейшего вычисления моментов инерции и т. д.

Также часто, при изучении теоретической механики, студентам предлагается решить подобную задачу, и найти центр тяжести какой-нибудь фигуры.

Условие задачи

Предлагаю рассмотреть следующую фигуру:

Фигура, состоящая из нескольких простых фигур

В сопромате принято заштриховывать сечения тонкими линиями, вот так:

Штриховка на сечении, состоящем из нескольких фигур

В своих же уроках я буду использовать заливку. Так, штриховка не будет мешать наносить обозначения.

Разбивка сложной фигуры на простые

Как видишь, сечение состоит из прямоугольника, прямоугольного треугольника, четверти круга, а также имеет круглый вырез:

Отметим центры тяжести (С₁, С₂, С₃, С₄) каждой отдельной фигуры, с учётом справочной информации.

Открой эту страничку, и пока не закрывай, она нам ещё понадобится!

Покажем вспомогательные оси (x₀, y₀) для всего сечения, которые будем использовать для нахождения положения центра тяжести (C):

Введение вспомогательной системы координат для всего сечения

Как определить положение центра тяжести?

Чтобы определить координату центра тяжести сечения, например, вертикальное расстояние от оси x₀ до центра тяжести сечения (y_c):

Указание координаты от вспомогательной оси до центра тяжести

Нужно статический момент сечения относительно этой вспомогательной оси (x₀) разделить на площадь всего сечения (A):

Площадь всего сечения (A) найти просто – это алгебраическая сумма площадей всех фигур:

Статический момент сечения, относительно вспомогательной оси будет равен алгебраической сумме статических моментов каждой фигуры (с учётом знака):

где A_i – площадь отдельной фигуры;
y_i – расстояние от центра тяжести отдельной фигуры до вспомогательной оси (x₀).

Координата центра тяжести (x_c), находится аналогично:

Определение площади сечения

Для начала предлагаю сделать самое простое, используя формулы, указанные на этой странице, найти площадь всего сечения (A):

Сечение, для которого рассчитывается площадь

Как видишь, круглый вырез, нужно учесть с «минусом», что очевидно.

Определение расстояний от вспомогательных осей до центров тяжести отдельных фигур

Найдём расстояния от вспомогательных осей (x₀, y₀) до центров тяжести отдельных фигур, опять же, используя нашу шпаргалку:

Определение статических моментов

Определяем статические моменты сечения относительно вспомогательных осей (x₀, y₀):

Важно! Статические моменты могут быть и отрицательными.

Определение координат центра тяжести

И, наконец, определяем положение центра тяжести всего сечения (C):

Покажем центр тяжести всего сечения (C):

Указание найденного центра тяжести сечения

Если остались какие-то вопросы по данному уроку, можешь смело задавать их в комментариях. Также, другие уроки, на сайте – ssopromat.ru, по определению геометрических характеристик, можешь найти здесь.

Источник

Обратите внимание, на этом сайте есть онлайн-сервис для вычисления центра тяжести и моментов инерции составных сечений, которые состоят из прокатных профилей (двутавр, уголок и т.д.) и из простых фигур.

Часто при расчете элементов строительных конструкций приходится определять геометрические характеристики профилей, составленных из элементарных геометрических фигур (прямоугольник, круг и т.п.) и прокатных профилей. Рассмотрим подробно пример расчета.

Необходимо определить геометрические характеристики составного сечения (рис.), который состоит из уголка 20/12,5/1,2, уголка 14/1 и прямоугольника 20х2см.

Определение собственных характеристик отдельных профилей – составляющих сечения

Собственные характеристики прокатных профилей определяются из сортамента.

Для неравнополочного уголка 20/12,5/1,2:

– высота и ширина уголка h = 20 см, b = 12,5 см;

– площадь $A$= 37,9 см2;

– собственные осевые моменты инерции ${I_x}$=1570 см4, ${I_y}$= 482 см4;

– собственный центробежный момент инерции ${I_{xy}}$=505 см4;

– координаты центра тяжести ${x_c}$= 2,83 см, ${y_c}$= 6,51 см.

Для равнополочного уголка 14/1:

– высота и ширина уголка h = b = 14 см;

– площадь $A$= 27,3 см2;

– собственные осевые моменты инерции ${I_x}$= ${I_y}$= 512 см4;

– собственный центробежный момент инерции ${I_{xy}}$=301 см4;

– координаты центра тяжести ${x_c}$= ${y_c}$= 3,82 см.

Для прямоугольника 20х2см:

– высота и ширина прямоугольника h = 20 см, b = 2 см;

– площадь $A$= 20∙2 = 40 см²;

– собственные осевые моменты инерции ${I_x} = frac{{2 cdot {{20}^3}}}{{12}} = 1330$ см⁴, ${I_y} = frac{{20 cdot {2^3}}}{{12}} = 13,3$см⁴;

– собственный центробежный момент инерции ${I_{xy}}$= 0, так как профиль имеет ось симметрии.

Определение центра тяжести сечения

Общая площадь всего сечения A = 37,9+27,3+40 = 105см2.

Проводим вспомогательные оси $X$ и $Y$ и определяем относительно них центр тяжести сечения:

${X_c} = frac{{sum {{X_i} cdot {A_i}} }}{A} = frac{{{text{37}}{text{,9}} cdot {text{( — 13}}{text{,5) + 27}}{text{,3}} cdot {text{( — 3}}{text{,82) + 40}} cdot {text{1}}}}{{{text{105}}}}{text{ = — 5}}{text{,49}}$см;

${Y_c} = frac{{sum {{Y_i} cdot {A_i}} }}{A} = frac{{{text{37}}{text{,9}} cdot {text{( — 2}}{text{,83) + 27}}{text{,3}} cdot {text{10}}{text{,2 + 40}} cdot {text{10}}}}{{105}} = 5,44$.

При этом в координатах центров тяжести составных обязанности’обязательно учитываем знак. Откладываем оси, которые проходят через центр тяжести –центральные оси $Xc$ и ${Y_c}$.

Определение центральных моментов инерции

Осевые и центробежный моменты инерции сечения определяем по формулам перехода между параллельными осями. Для этого находим и показываем на чертеже расстояния между центральными осями всего сечения и собственными осями каждой из фигур.

$Ix = sum {left( {I{x_i} + A cdot {b^2}} right) = {text{482 + 8}}{text{,2}}{{text{7}}^{text{2}}} cdot {text{37}}{text{,9 + 512 + 4}}{text{,7}}{{text{6}}^{text{2}}} cdot {text{27}}{text{,3 + 1330 + 4}}{text{,5}}{{text{6}}^{text{2}}} cdot {text{40 = 6360}}} $см4;

$Iy = sum {left( {I{y_i} + A cdot {a^2}} right)} = {text{1570 + 8}}{text{,0}}{{text{1}}^{text{2}}} cdot {text{37}}{text{,9 + 512 + 1}}{text{,6}}{{text{7}}^{text{2}}} cdot {text{27}}{text{,3 + 13}}{text{,3 + 6}}{text{,4}}{{text{9}}^{text{2}}} cdot {text{40 = 6280}}$см4;

${I_{xy}} = sum {left( {{I_{xy}}_i + A cdot a cdot b} right)} = $

$ = 505 + ( — 8,01) cdot ( — 8,27) cdot 37,9 — 301 + 1,67 cdot 4,76 cdot 27,3 + 0 + 6,49 cdot 4,56 cdot 40 = 4120$см4.

При этом обязанности’обязательно учитываем размещения фигур относительно рассматриваемых осей. Так, при определении момента инерции ${I_x}$ в формулу подставляем собственный момент инерции неравнополочного уголка относительно оси, которая параллельна оси ${X_c}$, в сортаменте это ось $Y$, и наоборот.

Определение положения главных осей и главных моментов инерции

Угол поворота главных осей относительно осей, для которых известны моменты инерции, определяется по формуле

[tg,2alpha = frac{{2 cdot {I_{xy}}}}{{{I_y} — {I_x}}} = frac{{2 cdot 4120}}{{6280 — 6360}} = — 97] $alpha = frac{{arctg( — 97)}}{2} = — 44,7^circ $.

Если $alpha > 0$, главные оси откладываются против часовой стрелки, и наоборот.

Главные моменты инерции определяются так

${I_{x0}} = {I_x} cdot {cos ^2}alpha + {I_y} cdot {sin ^2}alpha — {I_{xy}} cdot sin 2alpha = $

$ = 6360 cdot {cos ^2}( — 44,7^circ ) + 6280 cdot {sin ^2}( — 44,7^circ ) — 4120 cdot sin ( — 2 cdot 44,7^circ ) = 10430$см4.

${I_{y0}} = {I_y} cdot {cos ^2}alpha + {I_x} cdot {sin ^2}alpha + {I_{xy}} cdot sin 2alpha = $

$ = 6280 cdot {cos ^2}( — 44,7^circ ) + 6360 cdot {sin ^2}( — 44,7^circ ) + 4120 cdot sin ( — 2 cdot 44,7^circ ) = 2210$см4.

Центробежный момент инерции относительно главных осей равен нулю.

Радиусы инерции. Моменты сопротивления

Радиусы инерции сечения

${i_x} = sqrt[{}]{{frac{{{I_x}}}{A}}} = sqrt[{}]{{frac{{10430}}{{105}}}} = 9,96$см, ${i_y} = sqrt[{}]{{frac{{{I_y}}}{A}}} = sqrt[{}]{{frac{{2210}}{{105}}}} = 4,58$см.

Моменты сопротивления сечения определяем относительно центральных осей. Для этого необходимо определить расстояния ${x_{max }}$ и ${y_{max }}$ до максимально удаленных точек от главных осей. Сначала необходимо по чертежам определить, какие точки являются наиболее удаленными. В нашем случае это точки $A$ и $B$ (рис.). Искомые расстояния можно определить, имея координаты этих точек в центральных (не возвращенных осям).

${x_{max }} = {x_A} cdot cos left( alpha right) + {y_A} cdot sin left( alpha right)$

${y_{max }} = {y_B} cdot cos left( alpha right) — {x_B} cdot sin left( alpha right)$

XА= –8,53см YA=8,57см

XB= –14,5см YB= –18см

xmax = –12,1см ymax = –23см

Моменты сопротивления

${W_x} = frac{{{I_x}}}{{{y_{max }}}} = frac{{10430}}{{23}} = 454$см3; ${W_y} = frac{{{I_y}}}{{{x_{max }}}} = frac{{2210}}{{12.1}} = 183$см3.

Источник

h 2

b h

I x =

∫ y

dA = ∫ y

b dy = b

[

− (−

)] =

−h 2

−h

3 8

h 2

yc = h 3

b 2

2b 3

Рис. 6.5

Аналогичным путем для момента инерции относительно оси другой

симметрии y

можно получить выражение I y =

b3 h

. Заметим,

что в выраже—

ниях для I x и I y

в куб возводится размер, перпендикулярный оси, относитель—

но которой вычисляется геометрическая характеристика.

Для прямоугольного треугольного сечения имеем (рис. 6.5, б)

h − y

или

= b

h − y

Площадь

элементарной

полоски

h − y

dA = b

dy = b

dy . Тогда

h − y

b h

A = ∫dA =

∫b

−

= [h − ( )] =

dy = h y

− y

b h

S x

∫ y dA = ∫

y b

dy =

−

[3 h

−

2 h

] =

6 h

b h2

аналогично

b h

h − y

b h

I x

∫ y

dA = ∫ y

−

[4 h

− 3

] =

Поскольку ось x

центральная и параллельна случайной оси x1 , то спра—

ведливо

соотношение

I x = I x

+ ( yc )2

или

b h3

= I x + (

b h

или

				6
I x	=	b h3		. Аналогично относительно другой центральной оси y получаем

	36
I y	=	b3 h	. Здесь в куб возводится размер, перпендикулярный оси, относитель—

	36

но которой вычисляется геометрическая характеристика.

Равнобедренный треугольник (оси xoy на рис. 6.6, а) можно представить в виде двух одинаковых прямоугольных треугольников (оси x1o1 y1 ). Тогда согласно формулам параллельного переноса имеем

I x	= 2 I x = 2	(b 2) h3	=	b h3		,

	1	36	36

I y	= 2 [I y	+ ( yc )2 A] = 2 [	h (b 2)3	+ (b 6)2	1		b	h] =	h b3	.

	1					36	2	2	48

	Для круглого сечения, относительно любой оси, проходящей через центр

круга, мы будем иметь одно и тоже значение осевого момента инерции I x . Тогда

I ρ = I y + I x = 2 I x . Чтобы получить формулу для полярного момента инерции

сечения относительно центра, выделим из круга элементарное кольцо толщиной dρ , радиусом ρ и площадью dA = 2πρ dρ (рис. 6.6, б) и вычислим интеграл

		R		ρ	4	R	=	π R	4		π R	4	π d	4
I ρ = ∫ ρ	2	dA = ∫ ρ	2				, отсюда I x	=	=	.

		2πρ dρ = 2π	4		2	4	64
A		0			0

	y			α d
		dA	dρ
y1	y1
ρ
	h	x	x
o		x, x1

o1	o	h 3
	1

b 6	b 6	d = 2R		d

b 2	b 2
а		б		в
		Рис. 6.6

Моменты инерции (полярный и осевой) сечения, имеющего форму кругового кольца с наружным диаметром d и внутренним (α d ) (рис. 6.6, в), можно определить как разности между соответствующими моментами инерции наружного и внутреннего кругов:

			7
I ρ = π d 4	− π (α d )4	= π d 4	(1 − α 4 ) , I x	= π d 4	− π (α d )4	= π d 4	(1 − α 4 ) .
32	32	32		64	64	64

Вычисления моментов инерции сложных сечений с одной осью симметрии

Способ вычисления моментов инерции сложных сечений основан на том, что любой интеграл можно рассматривать как сумму интегралов и, следовате— льно, момент инерции любого сечения вычислять как сумму моментов инерции отдельных его частей.

Поэтому для вычисления моментов инерции сложное сечение разбивает— ся на ряд простых частей (фигур) с таким расчетом, чтобы их геометрические характеристики можно было вычислить по известным формулам или найти по специальным справочным таблицам.

Для каждой простой фигуры выбирается прямоугольная центральная сис— тема координат, причем все они принимаются параллельными друг другу для того, чтобы затем путем параллельного переноса осей можно было подсчитать моменты инерции всех частей относительно системы координат, общей для всего сложного сечения, которая совпадает с главными центральными осями..

Поскольку конечной целью вычисления геометрических характеристик сложного сечения является определение его главных центральных моментов инерции и положения главных центральных осей инерции, то следующим этапом вычисления является определение координат центра тяжести заданного сечения по формуле

∑Sxi

A y + A y

+ … A y

( i = 1, 2,… n ),

1 1

∑ A

A + A + … A

где

n –

количество простых фигур;

xk – вспомогательная ось, относительно

которой определяются координаты центра тяжести сложной фигуры; yi – рас— стояние от вспомогательной оси xk до центра тяжести i простой фигуры.

Ограничимся рассмотрением сложных сечений, имеющих хотя бы одну ось симметрии, поскольку такие типы сечений получили наибольшее распро— странение в технике и строительстве. В этом случае определение положения главных центральных осей инерции сечения значительно упрощается. Вторая главная центральная ось (первая – ось симметрии) будет перпендикулярна оси симметрии и пройдет через центр тяжести заданного сечения.

Вопросы для самопроверки

1.Что называется статическим моментом сечения относительно оси? Какую размерность он имеет?

2.Что называется осевым, полярным и центробежным моментами инерции сечения? Какую размерность они имеют?

3.Чему равен статический момент относительно оси, проходящей через центр тяжести сечения? Какие оси называются центральными?

4.Что называется центром тяжести сечения?

5.Как определяются координаты центра тяжести простого и сложного сечения?

6.Чему равна сумма осевых моментов инерции сечения относительно двух взаимно перпендикулярных осей?

7.Как в некоторых случаях без расчетов можно определить знак центробежного момента инерции для заданного сечения.

8.Как связаны между собой осевые моменты инерции сечения относительно двух параллельных осей, одна из которых центральная?

9.Какие оси называются главными центральными? В каких случаях без вычис— ления можно установить положение главной центральной оси инерции?

10.Чему равны главные центральные моменты инерции для прямоугольника и круга?

Лекция № 7

Кручение стержней круглого поперечного сечения. Построение эпюр крутящих моментов. Напряжения и деформации

Основные понятия

Кручением называется такой вид деформации, при котором в попереч— ных сечениях бруса возникает только один внутренний силовой фактор – кру— тящий момент ( M кр , другое обозначение – M z ).

Кручение возникает в валах, винтовых пружинах, в элементах простран— ственных конструкций и т.п.

Валом обычно называется стержень, испытывающий деформацию круче— ния совместно с изгибом.

Деформация кручения наблюдается, если прямой брус нагружен внешни— ми моментами (парами сил M ), плоскости действия которых перпендикулярны

кего продольной оси

Вчистом виде деформация кручения встречается редко, обычно присут— ствуют и другие внутренние силовые факторы (изгибающие моменты, продоль— ные силы).

Внешние крутящие моменты передаются на вал в местах посадки на него шкивов, зубчатых колес, там, где поперечная нагрузка смещена относительно оси вала.

Мы будем рассматривать прямой брус только в состоянии покоя или равномерного вращения. В этом случае алгебраическая сумма всех внешних скручивающих моментов, приложенных к брусу, будет равна нулю.

При расчете брусьев, испытывающий деформацию кручения, на проч— ность и жесткость при статическом действии нагрузки надо решить две основ— ные задачи. Это определение напряжений (от M кр ), возникающих в брусе, и

нахождение угловых перемещений в зависимости от внешних скручивающих моментов.

Крутящий момент

В ряде случаев величины внешних скручивающих моментов определяют— ся по величине потребляемой мощности и по скорости вращения вала. Если вал делает в минуту n оборотов, то угол поворота вала за 1 секунду (1 с), выражен—

ный в радианах, равен		n	2π =	π n	. Работа скручивающего момента M за 1 с,
60
	30
т. е. мощность N , передаваемая валом, равна произведению величины момен—
та на угол поворота вала (в радианах) за 1 с:
N = M π n , откуда	M (кГ м) =	30 N (кГ м c)	.

30					π n(об мин)

Если мощность N задана в лошадиных силах ( л. с. ), то

M (кГ м) =

30 75 N

= 716,2

N (л.с.)

или M (н м) = 7024

N (л.с.)

n(об мин)

π n

n(об мин)

Если мощность N

задана в киловаттах, то, учитывая,

что 1 л. с. равна

0,736 квт , получаем

M (кГ м) = 973,6

N (квт)

или M (н м) = 9548

N (квт)

n(об мин)

Крутящие моменты

M кр

( M z ),

возникающие в поперечных сечениях

бруса, определяются по внешним скручивающим моментам

M с помощью

метода сечений.

В простейшем случае, когда брус нагружен только двумя внешними мо—

ментами (эти моменты из условия равновесия вала ∑ M = 0 всегда равны друг

другу по величине и направлены в противоположные стороны), как показано на
рис. 7.1, крутящий момент M кр в любом поперечном сечении бруса (на участке
между внешними моментами) по величине равен внешнему моменту M = M .
						1	2
M	Ι	M	M	M	M	M
	1	2	1	z	z		2
			z				z

Рис. 7.1

В более сложных случаях, когда к прямому брусу приложено несколько внешних моментов, крутящие моменты M кр в поперечных сечениях различных

участков бруса неодинаковы.

На основании метода сечений крутящий момент в произвольном попе— речном сечении бруса численно равен алгебраической сумме внешних скручивающих моментов, приложенных к брусу по одну сторону от рас— сматриваемого сечения.

При расчетах на прочность знак крутящего момента не имеет никакого значения, но для удобства построения эп. M кр примем следующее правило

знаков: крутящий момент считается положительным, если при взгляде в торец отсеченной части бруса действующий на него момент представляется направленным по ходу часовой стрелки (рис. 7.2).

+ M кр			− M кр

Рис. 7.2

На рис. 7.3, а изображен стержень, жестко защемленный в правом конце— вом сечении, к которому приложены три внешних скручивающих момента.

M1 = 200 Н м	M 3	= 500 Н м
а
z	M 2 = 300 Н м	z3
1		z2
	a	c
	b

			400
		200	эп.М кр (Н м)
б
	100
		Рис. 7.3
В нашем случае крутящие	моменты	M кр в их поперечных сечениях

удобно выражать через внешние моменты, приложенные со стороны свободно— го конца стержня.

Это позволяет определять крутящие моменты, не вычисляя реактивного

момента, возникающего в заделке.	1−1	( 0 ≤ z1 ≤ a )
Крутящий момент	M кр	в сечении	численно	равен
M1 = 200 н м и, согласно принятому правилу знаков, положителен.
Крутящий момент	M кр	в сечении	2 − 2	( 0 ≤ z2 ≤ b )	численно	равен
алгебраической сумме моментов M1 и M 2 ,	т.е. M	= 200 − 300 = −100 нм, а его
				кр
знак зависит от соотношения этих моментов.
Аналогичным образом вычисляется крутящий момент	M кр в сечении
3 − 3 ( 0 ≤ z3 ≤ c ): M = 200 − 300 + 500 = 400 нм .
кр

График, показывающий изменение крутящих моментов по длине вала, называется эпюрой крутящих моментов. На рис. 7.3, б показана такая эпюра для стержня, изображенного на рис. 7.3, а.

Каждая ордината эп. M кр в принятом масштабе равна величине крутя—

щего момента, действующего в том поперечном сечении стержня, которому соответствует эта ордината.

В сечении, в котором к стержню приложен внешний скручивающий момент, ордината эпюры изменяется скачкообразно на величину, равную значению этого момента.

Следует учитывать, что наибольший внешний скручивающий момент, приложенный к брусу, не всегда равен наибольшему крутящему моменту, по которому ведется расчет бруса на прочность и жесткость.

Напряжения и деформации

Рассмотрим прямой брус с поперечным сечением в виде круга, нагружен— ный на концах скручивающими моментами M (рис. 7.4, а).

				y		τ
				x
					τ
а	M	γ	ϕ	z	б
τ
	M
					γ
	z	dz				τ

			L

Рис. 7.4

Для наглядного представления характера деформации бруса при круче— нии проводится следующий опыт. На цилиндрическую поверхность бруса нано— сится равномерная сетка линий, состоящая из окружностей и образующих. Как видно, поворот правого торцевого сечения относительно неподвижного левого на угол ϕ (назовем его углом закручивания стержня) вызывает поворот продольных волокон на угол γ (угол сдвига), поскольку на величину γ иска— жаются углы ортогональной сетки продольных и поперечных рисок модели

(рис. 7.4, б).

Отношение угла закручивания ϕ к длине участка L называется относи—

тельным углом закручивания, который обозначается θ = ϕ , или в дифференци—

альной форме θ = ddzϕ .

При деформации все образующие остаются параллельными друг другу и сдвигаются на один и тот же угол γ (рис. 7.4, а), а прямоугольники, нанесенные на поверхность бруса сетки, становятся параллелограммами (рис. 7.4, б). При этом длина L остается постоянной ( L = const ), что говорит об отсутствии нормальных напряжений в поперечном сечении бруса (σ z = 0 ).

Все это позволяет сделать следующее предположение, которое будет в дальнейшем принято при выводе формул: материал бруса на поверхности нахо—

дится в состоянии чистого сдвига, где γ = Gτ .

Теория кручения брусьев, имеющих круглое сплошное поперечное сече— ние, основана на следующих предположениях:

1.Поперечные сечения бруса, плоские и нормальные к его оси до деформации, остаются плоскими и нормальными к ней и после деформации (справедлива гипотеза плоских сечений или гипотеза Бернулли).

2.Расстояния (вдоль оси бруса) между поперечными сечениями не изменяются, следовательно ε z = 0 .

3. Контуры поперечных сечений и их радиусы не деформируются. Это озна— чает, что поперечные сечения ведут себя как жесткие круговые пластинки, поворачивающиеся при деформировании относительно оси стержня z . Отсюда следует, что любые деформации в плоскости пластинки равны нулю, в том чис— ле и ε x = ε y = 0 .

4. Материал стержня подчиняется закону Гука. Поскольку ε x = ε y = ε z = 0 , то и

σ x = σ y = σ z = 0 . Это означает, что в поперечных сечениях стержня возникают

лишь касательные напряжения τ , а вследствие закона парности касательных напряжений, равные им напряжения действуют и в сопряженных продольных сечениях. Следовательно напряженное состояние стержня – чистый сдвиг.

Формулы, выведенные на основе этих положений, совпадают с формула— ми, полученные точными методами теории упругости, и подтверждаются экспериментально.

Поскольку задача по определению напряжений является статически неопределимой, т. е. неизвестных больше чем независимых уравнений равно— весия, то для получения дополнительных уравнений необходимо рассмотреть геометрическую и физическую стороны задачи.

Геометрическая сторона задачи.

Двумя смежными сечениями вырежем элемент стержня длиной dz и, поскольку нас интересуют деформации элемента, левое сечение его будем считать неподвижным (рис. 7.5, а, б).

ϕz

+ dϕz

γ ρ

dϕ

С1

Рис. 7.5

При повороте правого сечения на угол dϕ

в соответствии с гипотезой о

недеформируемости радиусов,

правый конец волокна СС

(отстоящий от оси

элемента на величину полярного радиуса ρ)

будет перемещаться по дуге С С ,

вызывая поворот волокна на угол сдвига

					6
		γ ρ = С С СС = ρ dϕz = ρ dθ .
			1	2	1	dz

Статическая сторона задачи.
Рассмотрим две элементарные площадки dA поперечного сечения бруса,
расположенные на общем диаметре на равных расстояниях ρ от центра тяжес—
ти круглого сечения	о (рис. 7.6, а).
y		τ max			τ	max	σ1 = τ max	y	τ max

τ ρ dA		M z			σ 3				τ ρ	x
	dA	x						M
о
dA			ρ		τ max					z
					τ ρ		z

ρ	ρ	τ max			σ1				ρ	τ max

R	R	τ ρ =	M	z	ρ	σ 3	= −τ max

			I ρ

Рис. 7.6

Силы, действующие на каждую из этих площадок, равны (τ ρ dA ), распо—

ложены в плоскости поперечного сечения бруса и направлены перпендикуляр— но к диаметру в противоположные стороны. Они образуют элементарную пару сил.

Таких пар возникает в поперечном сечении бесконечное множество. Все они приводятся к одному моменту, действующему в плоскости поперечного сечения и представляющего собой крутящий момент M z , который из условия

статики будет равен:

M z = ∫τ ρ ρ dA.

Физическая сторона задачи.

Величина касательных напряжений, на основании закона Гука при

сдвиге, равна

τ ρ = G γ ρ .

Синтез.

Итак, после рассмотрения трех сторон задачи, мы получили следующую совместную систему из трех уравнений (условие равновесия, геометрическое и физическое уравнения).

Решая эту систему мы получаем все необходимые формулы для опреде— ления напряжений и деформаций, а также геометрические характеристики, которые соответствуют деформации кручения.

Соседние файлы в предмете Сопротивление материалов

Источник