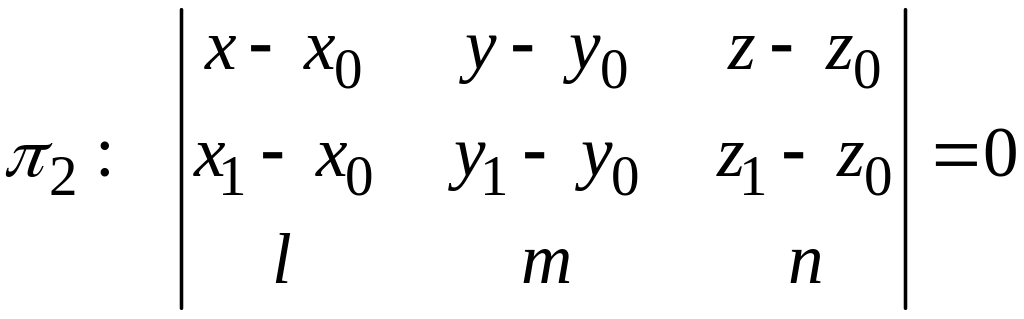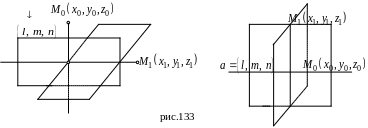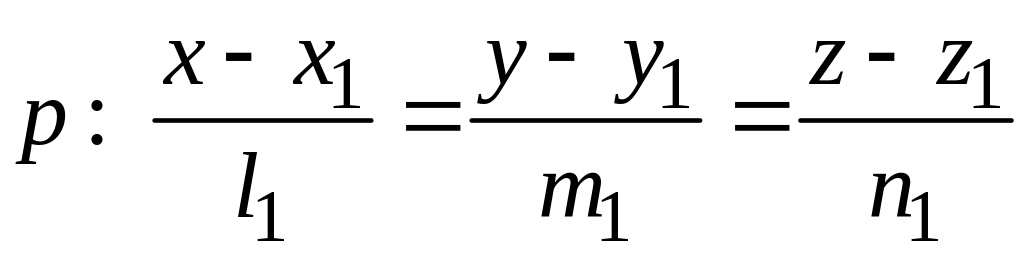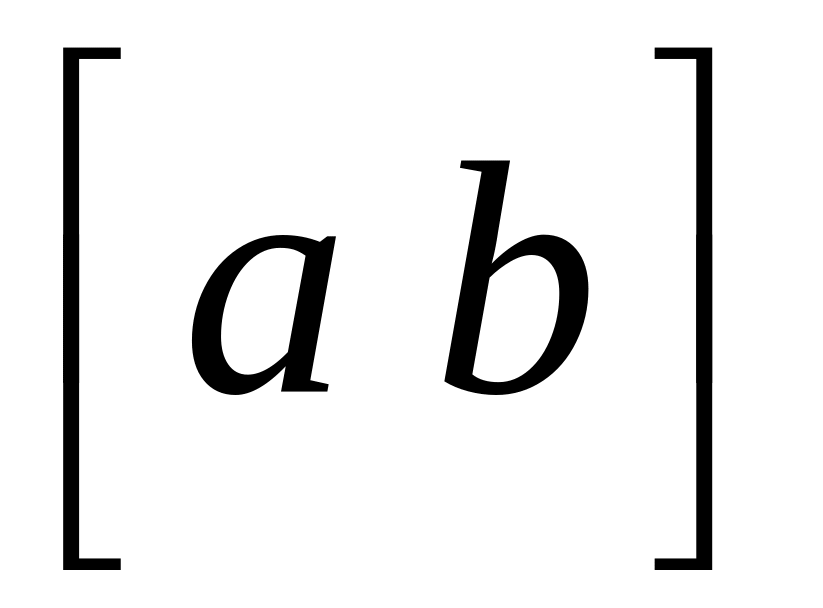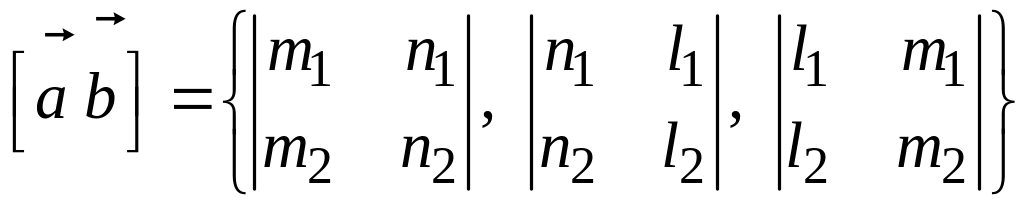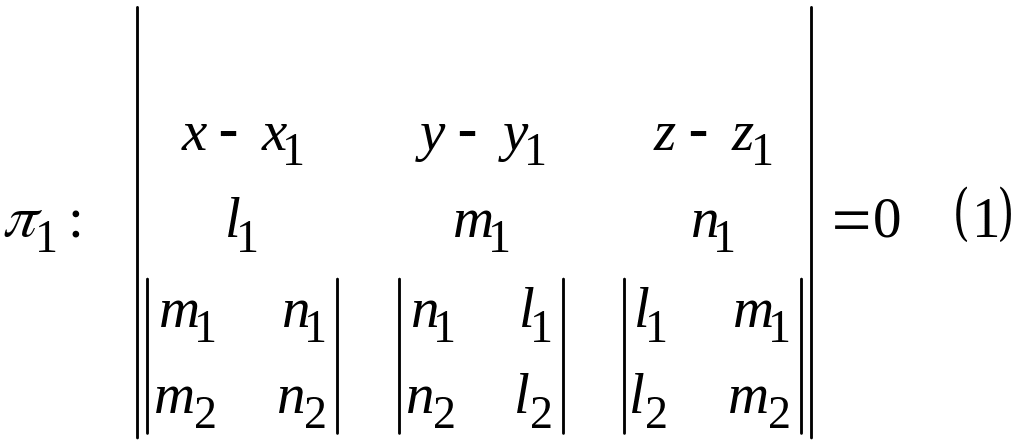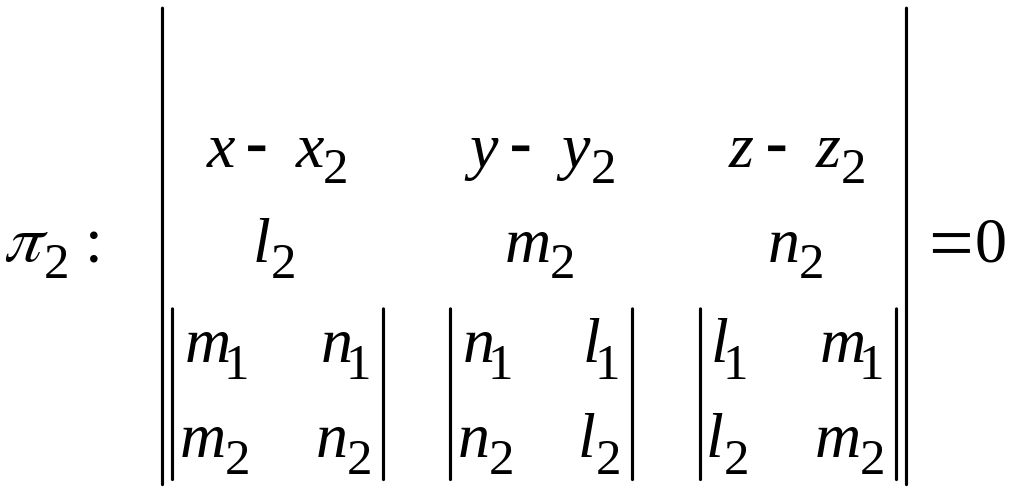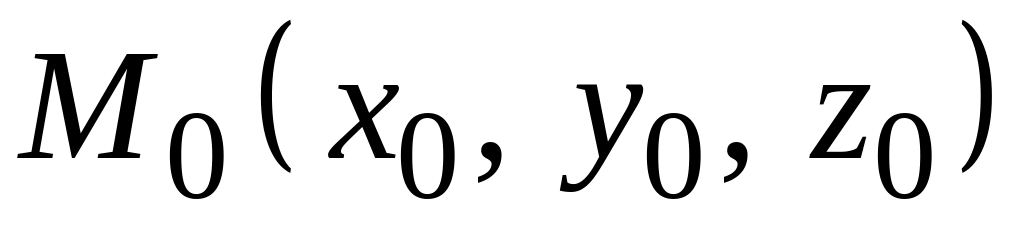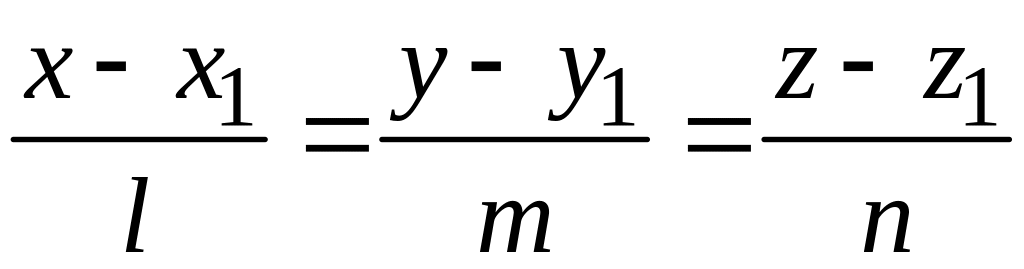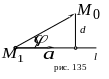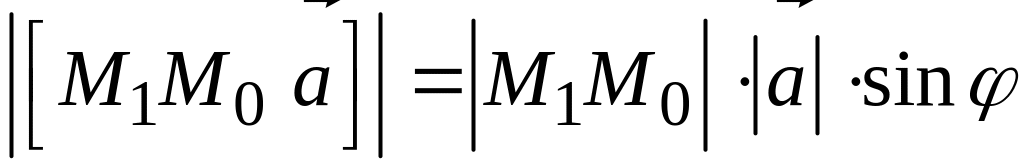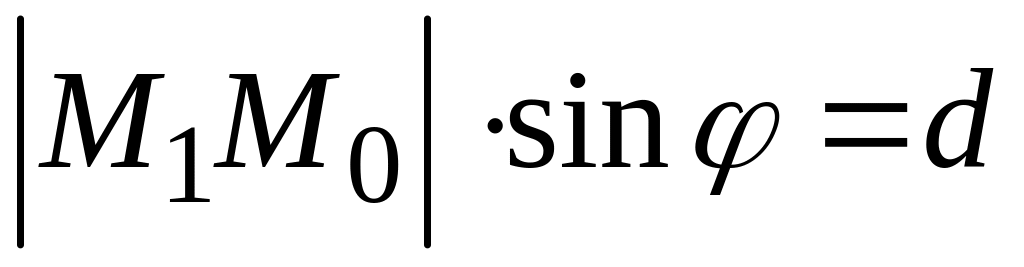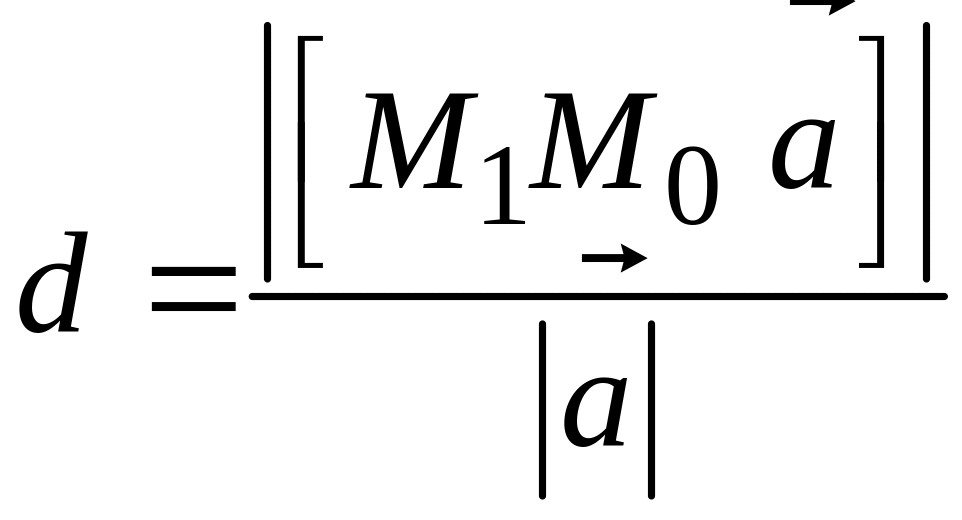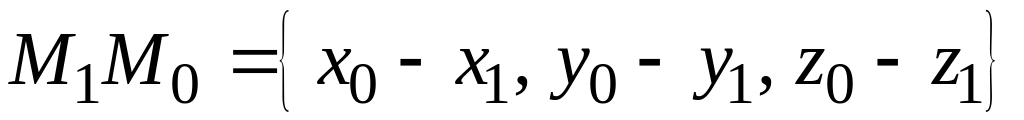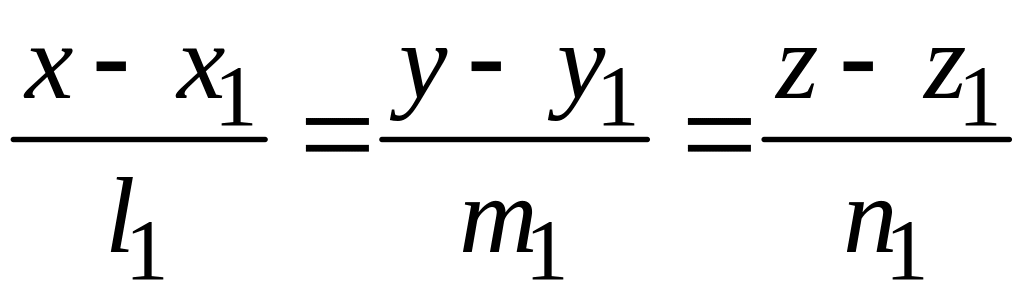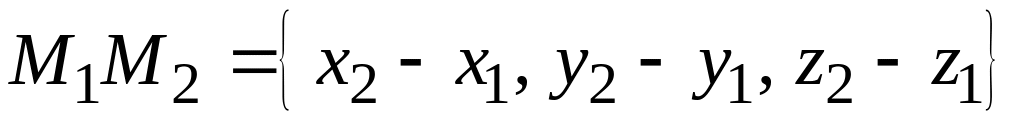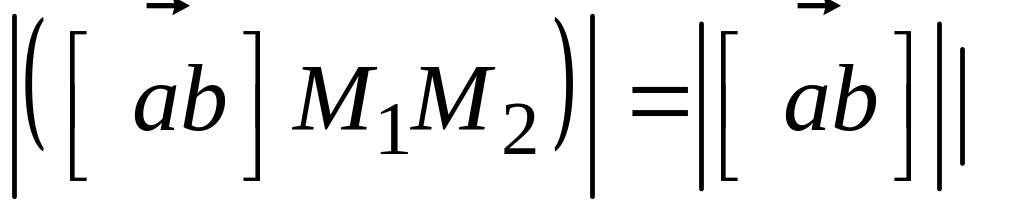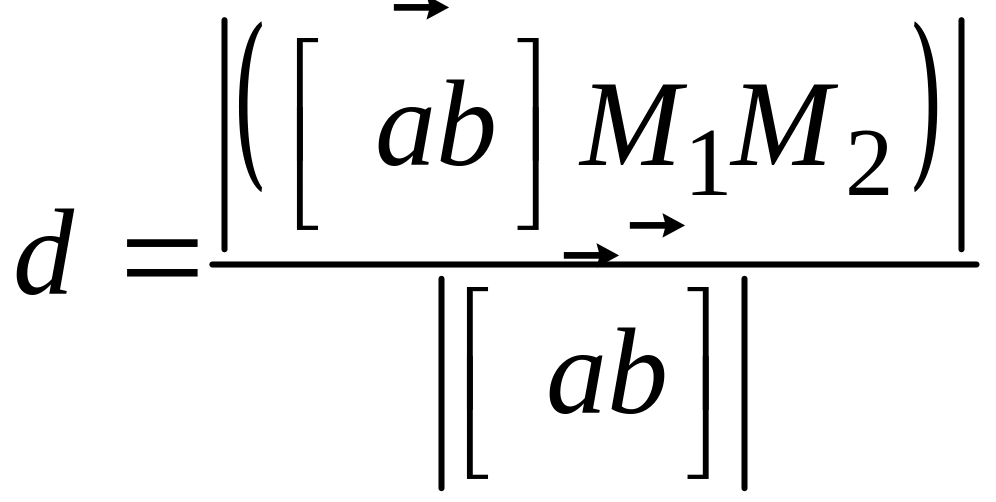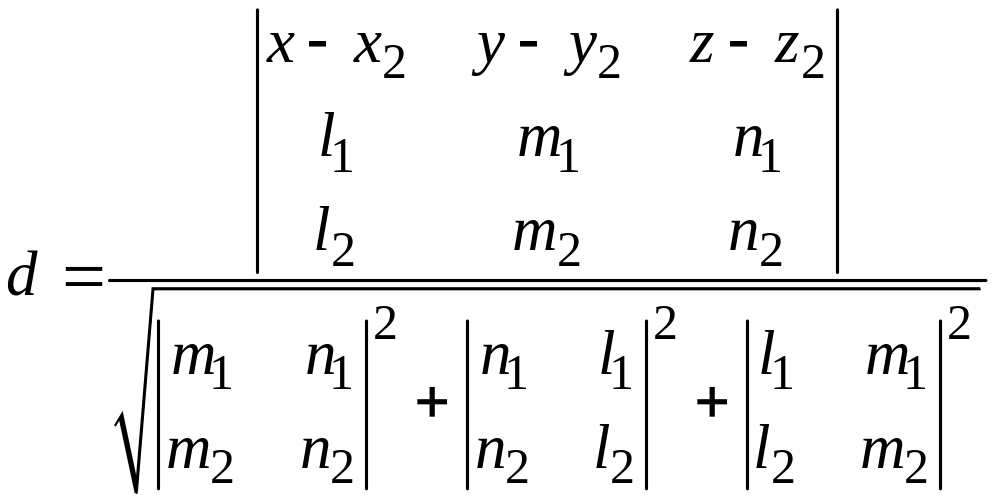Как найти координаты конца перпендикуляра

Уравнение перпендикулярной прямой

Альтернативная формула
Прямая, проходящая через точку M₁(x₁; y₁) и перпендикулярная прямой Ax+By+C=0 , представляется уравнением

назначение сервиса . Онлайн-калькулятор предназначен для составления уравнения перпендикулярной прямой (см. также как составить уравнение параллельной прямой).

Пример №1 . Составить уравнение прямой, проходящей через точку (2; -1) и перпендикулярной 4x-9y=3 .
Решение. Данную прямую можно представить уравнением y = 4 /₉x – 1 /₃ (a = 4 /₉). Уравнение искомой прямой есть y+1 = -9/4(x-2) , т.е. 9x+4y-14=0 .

Пример №2 . Решая пример 1 (A=4, B=-9) по формуле (2), найдем 4(y+1)+9(x-2)=0 , т.е. 9x+4y-14=0 .

Пример №3 . Составить уравнение прямой, проходящей через точку (-3, -2) перпендикулярно прямой 2y+1=0 .
Решение. Здесь A=0, B=2. Формула (2) дает -2(x+3)=0, т.е. x+3=0 . Формула (1) неприменима, так как a=0 .

Вычисление расстояния между двумя прямыми и координат концов общего перпендикуляра.

Координаты концов общего перпендикуляра к двум скрещивающимся или пересекающимся прямым.

В пространстве даны четыре точки:

Прямые AB и CS являются скрещивающимися или пересекающимися.
Найти координаты концов общего перпендикуляра к прямым AB и CS

Пусть выполняются пять условий:

1. Точка M(xm, ym, zm) принадлежит прямой AB ;
2. Точка N(xn, yn, z6) принадлежит прямой CS ;
3. Прямая MN перпендикулярна прямой AB ;
4. Прямая MN перпендикулярна прямой СS ;
5. Прямые AB и СS не являются параллельными;

Тогда отрезок [MN] является общим перпендикуляром к прямым AB и CS, а длина отрезка [MN] является кратчайшим расстоянием между прямыми AB и CS.

Выполняются пять следующие пять условий:

Координаты параллельных (коллинеарных) векторов пропорциональны.

Скалярное произведение перпендикулярных (ортогональных) векторов равно нулю.

Векторное произведение неколлинеарных векторов не равно нулевому вектору. Модуль векторного произведения неколлинеарных векторов строго больше нуля.

По условию, так как прямые AB и CS не параллельны, векторное произведение векторов

Выполняются следующие пять условий:

Выражаем из первых двух уравнений xm, ym, zm, xn, yn, zn

Находим координаты вектора MN

Подставляя xm, ym, zm, xn, yn, zn в третье и четвёртое уравнение, найдём m и n:

Получаем систему двух уравнений с двумя неизвестными m, n:

Имеем следующую систему из двух уравнений с двумя неизвестными m, n:

Так как квадрат скалярного произведения неколлинеарных векторов всегда строго меньше произведения квадратов модулей этих векторов, главный определитель этой системы:

Поэтому данная система имеет единственное решение.

Координаты концов общего перпендикуляра [MN] к двум скрещивающимся прямым. Отрезок [MN] перпендикулярен AB и перпендикулярен SC

Координаты точки M(xm, ym, zm), лежащей на прямой AB:

Координаты точки N(xn, yn, zn), лежащей на прямой SC:

Координаты концов общего перпендикуляра к скрещивающимся (или пересекающимся) прямым AB и CS:

Расстояние между непараллельными прямыми.

Два способа вычисления расстояния между непараллельными прямыми.

Расстояние между непараллельными прямыми AB и SC может быть найдено по формуле:

Расстояние между непараллельными прямыми AB и SC может быть найдено вторым способом, как высота параллелепипеда, сторонами основания которого являются [AB] и [SC], а боковым ребром является [AS].

Перенеся начало вектора SC в точку A, построим параллелепипед на векторах AB, SC, AS, объём которого равен модулю смешанного произведения векторов AB, SC, AS, а площадь основания равна модулю векторного произведения векторов AB и SC. Расстояние между прямыми AB и SC равно высоте этого параллелепипеда, построенного на векторах AB, SC, AS:

Векторное произведение векторов AB и SC имеет координаты:

Модуль векторного произведения векторов AB и SC:

Модуль смешанного произведения векторов AS, AB, SC:

Кратчайшее расстояние между прямыми AB и CS может быть найдено по формуле:

Расстояние между параллельными прямыми AB и CS

Расстояние между параллельными прямыми AB и CS равно расстоянию от точки S(xs, ys, zs) до прямой AB.

Существуют также два способа нахождения расстояния между двумя параллельными прямыми, то есть два способа нахождения расстояния от точки до прямой. Сначала найдём координаты проекции точки на прямую. Прямая AB задана координатами двух её точек

Точка K является проекцией точки S на прямую AB.

Найти координаты точки K

Для нахождения координат точки K используем условия:

1. Векторы AK и AB – коллинеарны, их координаты пропорциональны;
2. Векторы SK и AB ортогональны, и их скалярное произведение равно нулю ;

Из первого уравнения

Подставляя xk, yk, zk во второе уравнение, находим t:

Координаты проекции точки S на прямую AB, то есть координаты точки K(xk, yk, zk):

Расстояние между точкой S и прямой AB может быть найдено по формуле:

Расстояние между точкой S и прямой AB может быть найдено вторым способом, как высота параллелограмма, сторонами которого являются [AB] и [AS].

Векторное произведение векторов AB и AS имеет координаты:

Модуль векторного произведения векторов AB и AS:

Модуль вектора AB:

Расстояние между точкой S и прямой AB может быть найдено по формуле:

Программа «Вычисление расстояния между двумя прямыми и координат концов общего перпендикуляра».

Выдаётся точное значение координат координат концов общего перпендикуляра к прямым AB и CS виде несократимой рациональной дроби c/r.
Выдаётся точное значение расстояния между двумя прямыми в виде c*sqrt(p)/r

Дробь c/r является несократимой рациональной дробью, а подкоренное выражение p не содержит в качестве своих делителей квадраты натуральных чисел.

Результат можно вывести в файл.

Для перевода курсора в следующее поле и вычисления результата используйте клавишу Enter.

Уравнение прямой, проходящей через заданную точку перпендикулярно заданной прямой

В данной статье научимся составлять уравнения прямой, проходящей через заданную точку на плоскости перпендикулярно заданной прямой. Изучим теоретические сведения, приведем наглядные примеры, где необходимо записать такое уравнение.

Принцип составления уравнения прямой, проходящей через заданную точку плоскости перпендикулярно заданной прямой

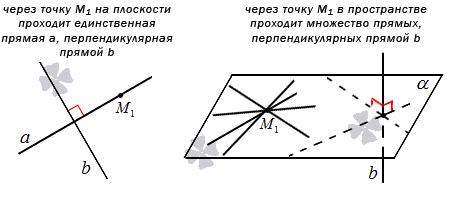
Перед нахождением уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой. Теорема рассматривается в средней школе. Через заданную точку, лежащую на плоскости, можно провести единственную прямую, перпендикулярную данной. Если имеется трехмерное пространство, то количество таких прямых увеличится до бесконечности.

Если плоскость α проходит через заданную точку М 1 перпендикулярно к заданной прямой b , то прямые, лежащие в этой плоскости, в том числе и проходящая через М 1 являются перпендикулярными заданной прямой b .

Отсюда можно прийти к выводу, что составление уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой применимо только для случая на плоскости.

Задачи с трехмерным пространством подразумевают поиск уравнения плоскости, проходящей через заданную точку перпендикулярно к заданной прямой.

Если на плоскости с системой координат О х у z имеем прямую b , то ей соответствует уравнение прямой на плоскости, задается точка с координатами M 1 ( x 1 , y 1 ) , а необходимо составить уравнение прямой a , которая проходит через точку М 1 , причем перпендикулярно прямой b .

По условию имеем координаты точки М 1 . Для написания уравнения прямой необходимо иметь координаты направляющего вектора прямой a , или координаты нормального вектора прямой a , или угловой коэффициент прямой a .

Необходимо получить данные из заданного уравнения прямой b . По условию прямые a и b перпендикулярные, значит, направляющий вектор прямой b считается нормальным вектором прямой a . Отсюда получим, что угловые коэффициенты обозначаются как k b и k a . Они связаны при помощи соотношения k b · k a = — 1 .

Получили, что направляющий вектор прямой b имеет вид b → = ( b x , b y ) , отсюда нормальный вектор — n a → = ( A 2 , B 2 ) , где значения A 2 = b x , B 2 = b y . Тогда запишем общее уравнение прямой, проходящее через точку с координатами M 1 ( x 1 , y 1 ) , имеющее нормальный вектор n a → = ( A 2 , B 2 ) , имеющее вид A 2 · ( x — x 1 ) + B 2 · ( y — y 1 ) = 0 .

Нормальный вектор прямой b определен и имеет вид n b → = ( A 1 , B 1 ) , тогда направляющий вектор прямой a является вектором a → = ( a x , a y ) , где значения a x = A 1 , a y = B 1 . Значит осталось составить каноническое или параметрическое уравнение прямой a , проходящее через точку с координатами M 1 ( x 1 , y 1 ) с направляющим вектором a → = ( a x , a y ) , имеющее вид x — x 1 a x = y — y 1 a y или x = x 1 + a x · λ y = y 1 + a y · λ соответственно.

После нахождения углового коэффициента k b прямой b можно высчитать угловой коэффициент прямой a . Он будет равен — 1 k b . Отсюда следует, что можно записать уравнение прямой a , проходящей через M 1 ( x 1 , y 1 ) с угловым коэффициентом — 1 k b в виде y — y 1 = — 1 k b · ( x — x 1 ) .

Полученное уравнение прямой, проходящее через заданную точку плоскости перпендикулярно заданной. Если того требуют обстоятельства, можно переходить к другому виду данного уравнения.

Решение примеров

Рассмотрим составление уравнения прямой, проходящей через заданную точку плоскости и перпендикулярно заданной прямой.

Записать уравнение прямой а, которая проходит через точку с координатами M 1 ( 7 , — 9 ) и перпендикулярна прямой b , которое задано каноническим уравнением прямой x — 2 3 = y + 4 1 .

Из условия имеем, что b → = ( 3 , 1 ) является направляющим вектором прямой x — 2 3 = y + 4 1 . Координаты вектора b → = 3 , 1 являются координатами нормального вектора прямой a , так как прямые a и b взаимно перпендикулярны. Значит, получаем n a → = ( 3 , 1 ) . Теперь необходимо записать уравнение прямой, проходящее через точку M 1 ( 7 , — 9 ) , имеющее нормальный вектор с координатами n a → = ( 3 , 1 ) .

Получим уравнение вида: 3 · ( x — 7 ) + 1 · ( y — ( — 9 ) ) = 0 ⇔ 3 x + y — 12 = 0

Полученное уравнение является искомым.

Ответ: 3 x + y — 12 = 0 .

Составить уравнение прямой, которая проходит через начало координат системы координат О х у z , перпендикулярно прямой 2 x — y + 1 = 0 .

Имеем, что n b → = ( 2 , — 1 ) является нормальным вектором заданной прямой. Отсюда a → = ( 2 , — 1 ) — координаты искомого направляющего вектора прямой.

Зафиксируем уравнение прямой, проходящую через начало координат с направляющим вектором a → = ( 2 , — 1 ) . Получим, что x — 0 2 = y + 0 — 1 ⇔ x 2 = y — 1 . Полученное выражение является уравнение прямой, проходящей через начало координат перпендикулярно прямой 2 x — y + 1 = 0 .

Ответ: x 2 = y — 1 .

Записать уравнение прямой, проходящей через точку с координатами M 1 ( 5 , — 3 ) перпендикулярно прямой y = — 5 2 x + 6 .

Из уравнения y = — 5 2 x + 6 угловой коэффициент имеет значение — 5 2 . Угловой коэффициент прямой, которая перпендикулярна ей имеет значение — 1 — 5 2 = 2 5 . Отсюда делаем вывод, что прямая, проходящая через точку с координатами M 1 ( 5 , — 3 ) перпендикулярно прямой y = — 5 2 x + 6 , равна y — ( — 3 ) = 2 5 · x — 5 ⇔ y = 2 5 x — 5 .

Как найти основание перпендикуляра опущенного из точки на прямую

Перпендикуляр, опущенный из точки на прямую

(не проходящую через ), представляется уравнениями

или в векторной форме уравнениями

Взятое отдельно, уравнение (2) представляет плоскость (рис. 175), проведенную через перпендикулярно (§ 155), а уравнение (3) — плоскость проведенную через точку и прямую

Замечание. Если прямая проходит через точку то уравнение (3) обращается в тождество (через точку, взятую на прямой можно провести бесчисленное множество перпендикуляров , § 120). Пример. Найти уравнение перпендикуляра, опущенного из точки (1; 0; 1) на прямую

Найти также основание перпендикуляра. Решение. Уравнения (1а) можно записать в симметричном виде (§ 151) так:

Искомый перпендикуляр представляется уравнениями

или после упрощений

Координаты основания К перпендикуляра найдем, решив систему трех уравнений (16), (2в). Уравнение должно удовлетворяться само собой. Получаем .

Замечание. Система трех уравнений (1б), (3в) имеет бесчисленное множество решений (так как плоскость проходит через прямую а не пересекает ее).

Проекция точки на прямую

Пусть необходимо спроектировать точку на прямую Ах+Ву+С=0. проекцией точки на прямую является основание перпендикуляра, опущенного из точки на прямую. Нормалью к данной прямой является вектор . Составим уравнение проецирующей прямой. Она проходит через точку и параллельна вектору . Подставив координаты точки и вектора в каноническое уравнение прямой , получим: . Теперь необходимо найти координаты точки пересечения данной прямой и проектирующей, для чего объединим их в систему: решение этой системы есть координаты точки, являющейся проекцией точки на прямую

Пример: Даны вершины треугольника : ; ; . Найти:

1) уравнение высоты, опущенной из вершины ;

2) точку пересечения высоты и стороны ;

3) точку пересечения медиан треугольника .

Решение: 1) Составим уравнение высоты , проходящей через точку перпендикулярно вектору :

2) Составим уравнение стороны :

Найдем точку пересечения высоты и стороны .Обозначим эту точку N, она является проекцией точки А на сторону ВС. Для нахождения точки N, решим следующую систему уравнений:

Перпендикуляр к прямой

Что такое перпендикуляр к прямой? Как построить перпендикуляр к прямой? Сколько перпендикуляров можно провести из точки к прямой? Что такое наклонная? Что называется проекцией наклонной? Об этом — ниже.

Перпендикуляр, опущенный из точки A на прямую a — это отрезок, лежащий на прямой, перпендикулярной прямой a, один конец которого — точка A, второй — точка пересечения этих двух прямых.

Как построить перпендикуляр к прямой?

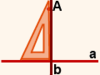
На рисунке 1 изображены прямая a и точка A, не лежащая на прямой a.

Чтобы построить перпендикуляр, воспользуемся угольником.

Угольник располагаем так,

чтобы одна сторона прямого угла проходила вдоль прямой a,

а вторая — через точку A.

Если провести через точку A вдоль стороны угольника прямую,

то получим прямую b, перпендикулярную данной прямой a.

Нам нужно построить перпендикуляр, то есть отрезок — часть этой прямой.

Соединим точку A с точкой на пересечении прямых a и b

(назовем вторую точку B).

Отрезок AB — перпендикуляр, проведенный из точки A к прямой a.

Точка B называется основанием перпендикуляра.

Расстояние от точки до прямой измеряется длиной перпендикуляра.

Расстояние от точки A до прямой a (рисунок 4) равно длине отрезка AB.

Из данной точки к данной прямой можно провести только один перпендикуляр.

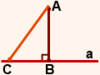
Любой другой отрезок, который соединяет точку A с точкой на прямой a, называется наклонной.

Наклонной, проведенной из точки A к прямой a, называется отличный от перпендикуляра отрезок, соединяющий точку A с некоторой точкой на прямой a.

На рисунке 5 AC — наклонная, проведенная из точки A к прямой a.

Точка C называется основанием наклонной AC.

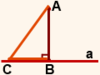
Отрезок, который соединяет основание перпендикуляра с основанием данной наклонной, называется проекцией этой наклонной на прямую.

На рисунке 6 BC — проекция наклонной AC на прямую a.

Перпендикуляр часто встречается при решении задач, связанных с треугольниками. В частности, определение высоты треугольника опирается на перпендикуляр.

Светило науки — 12 ответов — 0 раз оказано помощи

Уравнение
перпендикуляра, опущенного из точки

на
прямую, заданную каноническими уравнениями

относительно
декартовой прямоугольной системы
координат, можно записать в виде
пересечения двух плоскостей:

,

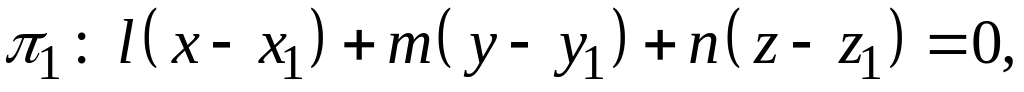
т
ак
как первое из этих уравнений выражает
плоскость, проходящую через точку

перпендикулярно данной прямой, а второе
– плоскость, проходящую через данную
точку

и данную прямую. Эти две плоскости
пересекаются по прямой, проходящей
через точку

и пересекающей данную прямую под углом

(рис. 133).

§ 92. Уравнение общего перпендикуляра к двум неколлинеарным прямым

Пусть
две прямые p
и
q
заданы своими каноническими уравнениями:

,

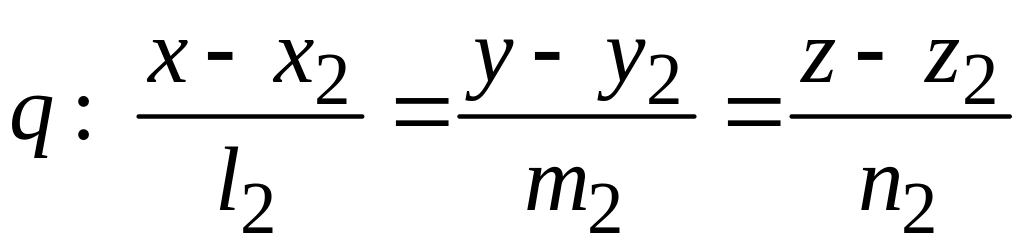
относительно
декартовой прямоугольной системы
координат. Предположим, что направляющие
векторы этих прямых

и

неколлинеарны,
т.е. что данные прямые или скрещиваются,
или пересекаются. Пусть l
– прямая, которая пересекает обе прямые
под углом

.

Тогда
за направляющий вектор прямой l
можно взять векторное произведение

направляющих векторов данных прямых:

.

Общий перпендикуляр l
к двум данным прямым можно определить
как прямую, по которой пересекается
плоскость

,
проходящая через прямую р
компланарно вектору

,
с плоскостью

,
проходящей через прямую q
компланарно

,
(рис.134). Уравнение плоскости

,
имеет вид:

Так как
эта плоскость проходит через точку

прямой р,
и коллинеарна векторам

и

.

Аналогично составляется уравнение
плоскости

:

.
(2)

Общий
перпендикуляр l
к данным прямым выражается уравнениями
(1) и (2).

§ 93. Расстояние от точки до прямой в пространстве

Пусть
в пространстве заданы точка

и прямая l
каноническими уравнениями

.

относительно
декартовой прямоугольной системы
координат.

Расстояние
d
от точки

до прямой l
можно определить как высоту параллелограмма,
сторонами которого служит вектор

и направляющий вектор

прямой l
отложенный от точки

этой прямой. Поэтому для определения
расстояния d
рассмотрим модуль векторного произведения:

.

Но

,
следовательно (рис. 135),

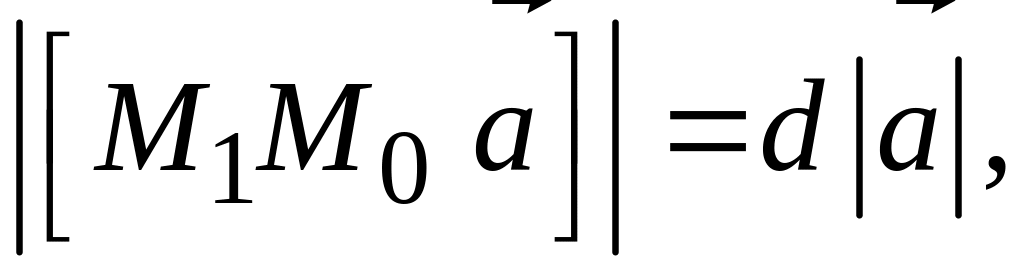
откуда

.

Так как

,

то

Потому

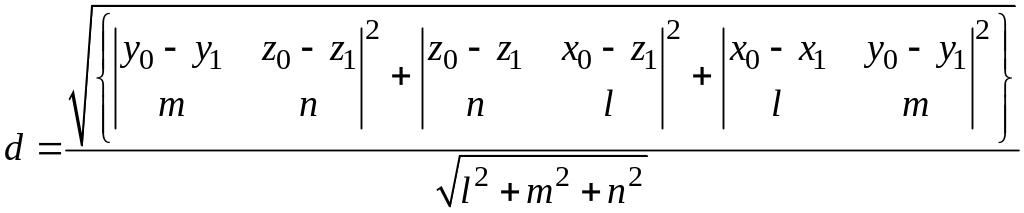
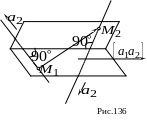
§ 94. Кротчайшее расстояние между двумя прямыми

Если две прямые скрещиваются, т.е. не
лежат в одной плоскости, то кротчайшее
расстояние между ними (как доказывается
в элементарной геометрии) есть длина
отрезка общего перпендикуляра к этим
двум прямым, концы которого лежат на
этих прямых. Отсюда следует, что кротчайшее
расстояние между двумя скрещивающимися
прямыми равно величине ортогональной
проекции любого отрезка

концы которого лежат на этих прямых
(рис. 136) на любую прямую, перпендикулярную
к данным; это очевидно при проектировании
точек

и

на общий перпендикуляр к данным прямым;
величина проекции не изменится, если
спроектировать отрезок на любую прямую,
параллельную этому перпендикуляру.
Пусть две скрещивающиеся прямые заданы
каноническими уравнениями

,

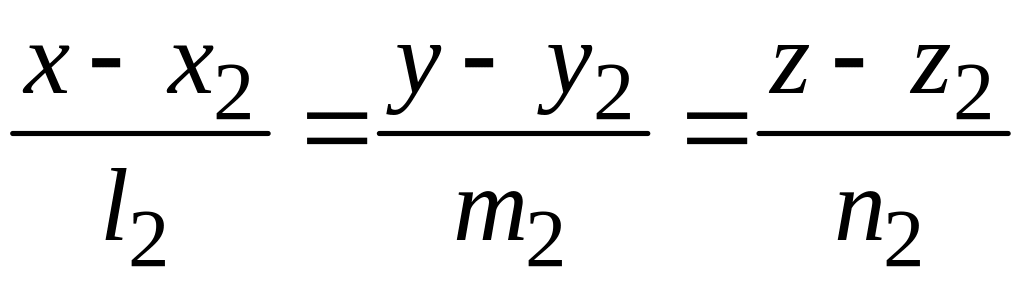
относительно
декартовой прямоугольной системы
координат. Кратчайшее расстояние между
ними равно абсолютной величине проекции
вектора

,

начало

конец которого

лежат соответственно на первой и второй
прямых, на прямую, параллельную вектору

,

перпендикулярному
направляющим векторам:

;

данных прямых.

Так как

пр.

,

то
кротчайшее расстояние d
между двумя скрещивающимися вычисляется
по формуле

,

или в координатах

.

Отметим, что эта формула верна и для
двух пересекающихся прямых: числитель
обратится в нуль, а знаменатель отличен
от нуля, и мы получим d
= 0 в соответствии с определением
кротчайшего расстояния между двумя
пересекающимися прямыми.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #