ЦЕЛЕУКАЗАНИЕ ПО КВАДРАТАМ КООРДИНАТНОЙ СЕТКИ
Координатная сетка весьма широко используется при работе на карте. Основное ее назначение — облегчить и упростить определение прямоугольных координат точек местности при целеуказании по карте.
Вместе с тем она облегчает ориентирование на карте и указание на ней местоположения различных объектов при докладах, постановке задач, передаче распоряжений и составлении донесений. Наконец, она помогает быстро оценивать по карте на глаз расстояния и определять азимуты направлений.
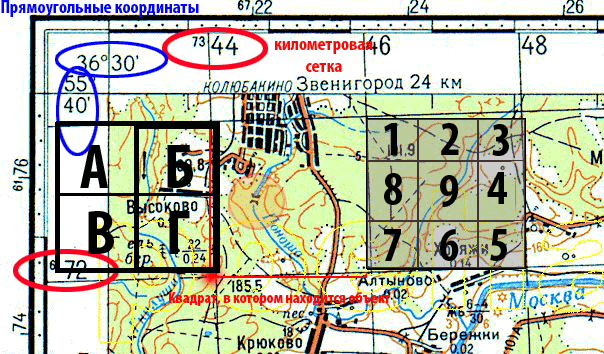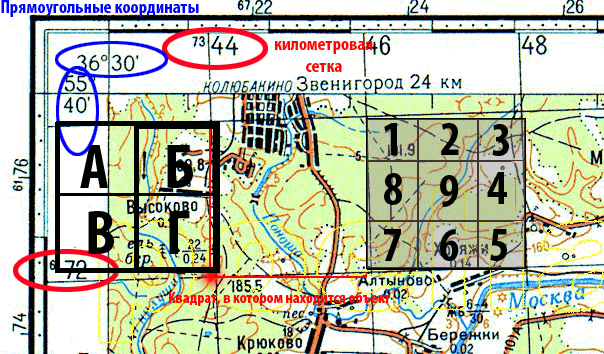
Чтобы указать приближенно местоположение какого-нибудь пункта на карте, достаточно назвать квадрат сетки, в котором он расположен. Для этого надо прочитать за рамкой карты оцифровка вертикальной и горизонтальной километровых линий, образующих нижний левый (юго-западный) угол квадрата.
При этом необходимо обязательно соблюдать следующее правило: сначала прочитывать и называть оцифровку (номер) горизонтальной километровой линии, а затем вертикальной, т.е. сначала называть абсциссу Х, потом ординату Y.═
Например, командир, ориентирующий по карте своих подчиненных в обстановке, указывая местоположение пешеходного моста через ручей южнее деревни Колюбакино , скажет: Квадрат семьдесят два, сорок четыре: мостик через ручей. В письменных же донесениях и других документах этот пункт будет обозначаться так: Мостик через ручей (7244).
При целеуказании по квадратам километровой сетки достаточно указать квадрат, в котором расположена цель. Квадрат указывается цифровыми обозначениями километровых линий, пересечением которых образован его юго-западный (нижний левый) угол. Правила указания ═ квадрата карты при целеуказании, были приведены ранее.
При этом цифры пишутся и произносятся слитно, без разделения на Х и Y. Например, ЦЕЛЬ мостик, 7244 ( семьдесят два, сорок четыре). Если требуется уточнить положение цели в квадрате, то он делится мысленно на 4 или 9 частей (улитка»), из которых каждая обозначается в первом случае буквами, а во втором — цифрами. В этом случае называют квадрат, в котором находится цель, и добавляют букву или цифру, уточняющую положение цели внутри квадрата. Например, ЦЕЛЬ — мостик, 7244-А (цель — мостик, 7244-8).
Точность определения по карте прямоугольных координат точек ограничивается не только ее масштабом, но и величиной погрешностей, допускаемых при съемке или составлении карты в нанесении на нее различных точек и объектов местности.
Наиболее точно, с ошибкой, не превышающей 0,2 мм, на карту наносятся геодезические пункты и наиболее резко выделяющиеся на местности и видимые издали предметы, имеющие значение ориентиров и определяемые как геодезические пункты (отдельные колокольни, фабричные трубы, постройки башенного типа). Поэтому координаты таких точек, возможно, определять по карте примерно с той же точностью, с какой они на нее наносятся (т. е. с ошибкой 10 — 15 м для карты масштаба 1:50000 и 20 — 30 м для карты масштаба 1:100000).
Имеем исходные данные: по широте (Latitude) 1 градус равен 110.574 км, по долготе (Longitude) 1 градус равен 111.32 км, следовательно, чтобы определить в каких диапазонах должны быть координаты геоточки входящей в квадрат — нужно сторону квадрата поделить на соответствующее значение по широте и долготе. Например:
Заданный квадрат со стороной 5 км
Исходная точка (центр) имеет координату 55.751635, 37.618900
половина длины квадрата в радианах по широте: (5 / 110.574) / 2 = 0,022609293
половина высоты квадрата в радианах по долготе: (5 / 111.32) / 2 = 0,022457779
Получается, что в заданный квадрат будут входить все геоточки, у которых разница с заданным центром находится в диапазоне ±0,022609293 (по широте) и ±0,022457779 (по долготе).
С помощью этого калькулятора Вы можете рассчитать
значение квадрата (QTH-локатора) по географическим координатам.
Инструкция
— Определите координаты по карте. Чем точней тем лучше.
— Введите широту и долготу (можно с десятичными знаками).
— Нажмите «Рассчитать».
* Ваш результат — это 6 первых знаков.
| Широта (гмс) | ||
|
|
||
| Долгота (гмс) | ||
| Квадрат |
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Смотрите также
Прямоугольные координаты
(плоские) — линейные величины (абсцисса X и ордината У), определяющие положение точки на плоскости (карте) относительно двух
взаимно перпендикулярных осей X и У. Абсцисса X и ордината У точки А — расстояния от начала
координат до оснований перпендикуляров, опущенных из точки А на соответствующие оси, с указанием знака.
В топографии и геодезии ориентирование производится по северу со счетом углов по ходу часовой стрелки. Поэтому для сохранения знаков тригонометрических
функций положение осей координат, принятое в математике, повернуто на 90° (за ось X принята вертикальная линия, за ось У —
горизонтальная).
Прямоугольные координаты (Гаусса) на топографических картах
применяются по координатным зонам, на которые делится поверхность Земли при изображении ее на картах в проекции Гаусса. Координатные зоны — части земной
поверхности, ограниченные меридианами с долготой, кратной 6°. Счет зон идет от Гринвичского меридиана с запада на восток. Первая зона ограничена
меридианами 0 и 6°, вторая — 6° и 12°, третья —12° и 18° и т.д. (например, территория СССР располагалась в 29 зонах: от 4-й до 32-й включительно).
Протяженность каждой зоны с севера на юг составляет примерно 20 000 км. Ширина зоны на экваторе равна примерно 670 км, на широте 40° — 510 км, на широте
50° — 430 км, на широте 60° — 340 км.
Все топографические карты в пределах одной зоны имеют общую систему прямоугольных координат. Началом координат в каждой зоне служит точка пересечения
среднего (осевого) меридиана зоны с экватором (рис.2.1), средний меридиан зоны соответствует оси абсцисс (X), а экватор — оси
ординат (Y).
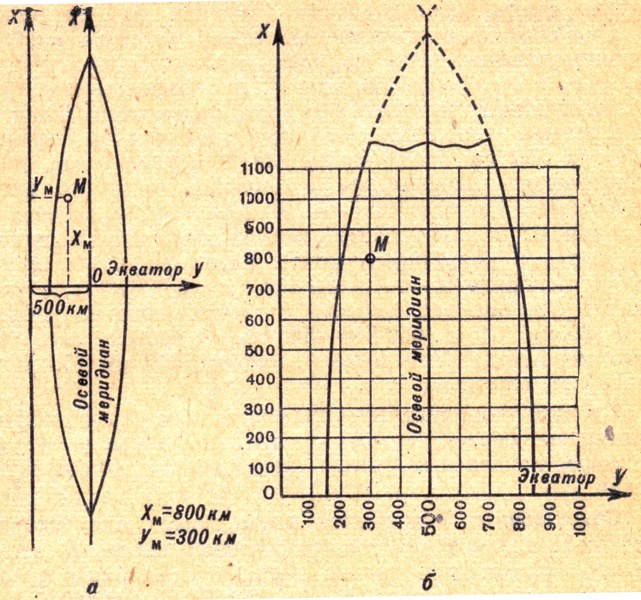
Рис. 2.1 Система прямоугольных координат на топографических картах:
а – одной зоны;
б – части зоны
При таком расположении координатных осей абсциссы точек, расположенных южнее экватора, и ординаты точек, расположенных западнее среднего меридиана, будут
иметь отрицательные значения. Для удобства пользования координатами на топографических картах принят условный счет ординат, исключающий отрицательные
значения координаты У. Это вызвано тем, что отсчет ординат идет не от нуля, а от величины 500 км, т.е. начало координат в каждой зоне как бы
перенесено на 500 км влево вдоль оси У.
Кроме того, для однозначного определения положения точки по прямоугольным координатам на земном шаре к значению координаты у слева приписывается
номер зоны (однозначное или двузначное число). Если, например, точка имеет координаты х = 5 650 450; у = 3 620 840, то это значит, что
она расположена в третьей зоне на удалении 120 км 840 м (620 840 — 500 000) к востоку от среднего меридиана зоны и на удалении 5 650 км 450 м к
северу от экватора.
Полные координаты
— прямоугольные координаты, указанные полностью, без каких-либо сокращений. В примере, приведенном выше, даны полные координаты точки.
Сокращенные координаты
применяются для ускорения целеуказания по топографической карте. В этом случае указывают только десятки и единицы километров и метры, например, х = 50 450; у = 20 840. Сокращенные координаты нельзя применять, если район действий охватывает пространство протяженностью более 100 км
по широте или долготе.
Координатная (километровая) сетка
(рис.2.2) — сетка квадратов на топографических картах, образованная горизонтальными и вертикальными линиями, проведенными параллельно осям прямоугольных
координат через определенные интервалы: на карте масштаба 1:25000 — через 4 см, на картах масштабов 1:50000, 1:100000 и 1:200000 — через 2 см. Эти линии
называются километровыми.
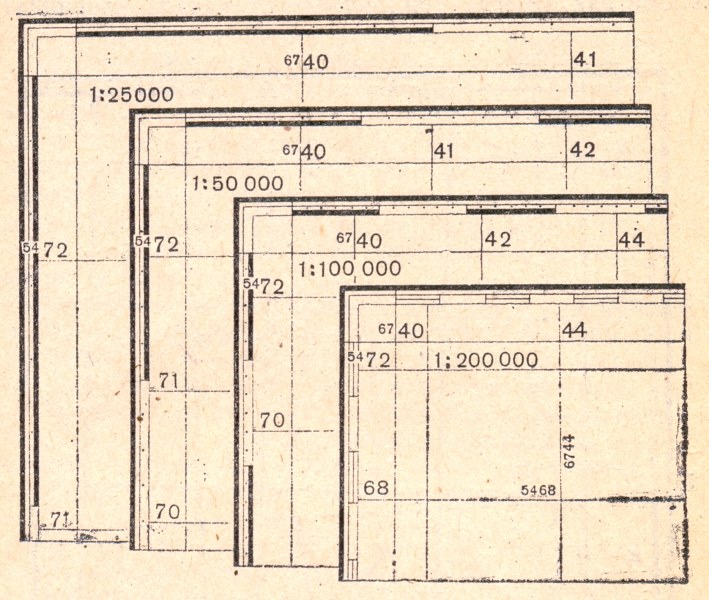
Рис. 2.2 Координатная (километровая) сетка на топографических картах различных масштабов
На карте масштаба 1:500000 координатная сетка полностью не показывается, наносятся только выходы километровых линий по сторонам рамки (через 2 см). При
необходимости по этим выходам координатная сетка может быть прочерчена на карте.
Координатная сетка используется для определения прямоугольных координат и нанесения на карту точек, объектов, целей по их координатам, для целеуказания и
отыскания на карте различных объектов (пунктов), для ориентирования карты на местности, измерения дирекционных углов, приближенного определения расстояний
и площадей.
Километровые линии на картах подписываются у их выходов за рамкой листа и в девяти местах внутри листа карты. Ближайшие к углам рамки километровые линии,
а также ближайшее к северо-западному углу пересечение линий подписываются полностью, остальные сокращенно, двумя цифрами (указываются только десятки и
единицы километров). Подписи у горизонтальных линий соответствуют расстояниям от оси ординат (от экватора) в километрах. Например, подпись 6082 в правом
верхнем углу (рис.2.3) показывает, что данная линия отстоит от экватора на удалении 6 082 км.
Подписи у вертикальных линий обозначают номер зоны (одна или две первые цифры) и расстояние в километрах (всегда три цифры) от начала координат, условно
перенесенного к западу от среднего меридиана на 500 км. Например, подпись 4308 в левом верхнем углу означает: 4 — номер зоны, 308 — расстояние от условного
начала координат в километрах.
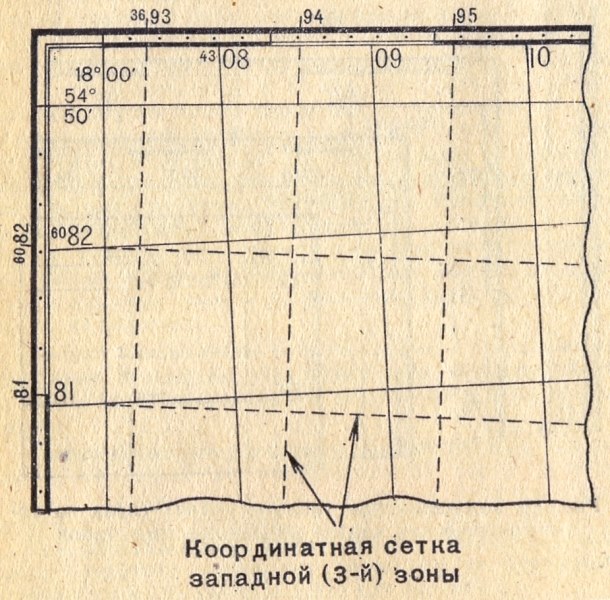
Рис. 2.3 Дополнительная координатная сетка
Дополнительная координатная (километровая) сетка
предназначается для преобразования координат одной зоны в систему координат другой, соседней зоны. Она может быть нанесена на топографических картах
масштабов 1:25000, 1:50000, 1:100000 и 1:200000 по выходам километровых линий в смежной западной или восточной зоне. Выходы километровых линий в виде
черточек с соответствующими подписями даются на картах, расположенных на протяжении 2° к востоку и западу от граничных меридианов зоны.
На рис.2.3 черточки на внешней стороне западной рамки с подписями 81 6082 и на северной стороне рамки с подписями 3693 94 95 обозначают выходы километровых
линий в системе координат смежной (третьей) зоны. При необходимости дополнительная координатная сетка прочерчивается на листе карты путем соединения
одноименных черточек на противоположных сторонах рамки. Вновь построенная сетка является продолжением километровой сетки листа карты смежной зоны и должна
полностью совпадать (смыкаться) с ней при склейке карты.
Определение прямоугольных координат точек по карте
. Вначале измеряют по перпендикуляру расстояние от точки до нижней километровой линии, по масштабу определяют его действительную величину в метрах и
приписывают справа к подписи километровой линии. При длине отрезка более километра вначале суммируют километры, а затем также приписывают число метров
справа. Это будет координата х (абсцисса). Таким же образом определяют и координату у (ординату), только расстояние от точки измеряют до
левой стороны квадрата.
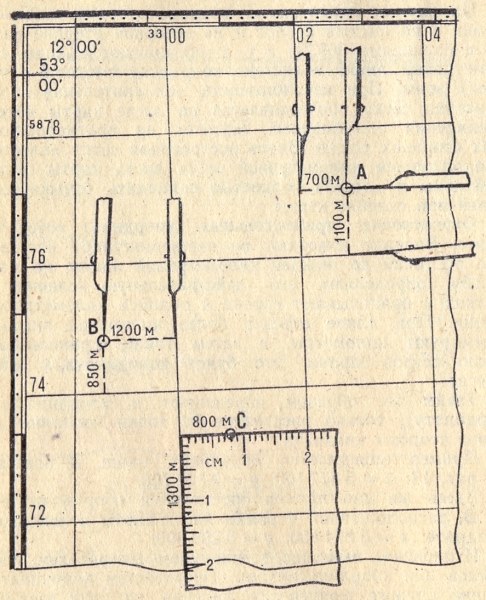
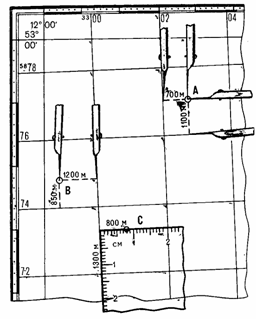
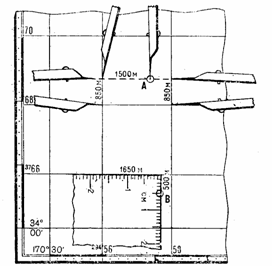
Пример определения координат точки А показан на рис.2.4: х = 5 877 100; у = 3 302 700. Здесь же дан пример определения координат
точки В, расположенной у рамки листа карты в неполном квадрате: х = 5 874 850; у = 3 298 800.
Рис. 2.4 Определение прямоугольных координат точек по карте
Измерения выполняют циркулем-измерителем, линейкой или координатомером. Простейшим координатомером служит офицерская линейка, на двух взаимно
перпендикулярных краях которой имеются миллиметровые деления и надписи х и у.
При определении координат координатомер накладывают на квадрат, в котором располагается точка, и, совместив вертикальную шкалу с его левой стороной, а
горизонтальную — с точкой, как показано на рис.2.4, снимают отсчеты.
Отсчеты в миллиметрах (десятые миллиметра отсчитывают на глаз) в соответствии с масштабом карты преобразуют в действительные величины — километры и
метры, а затем величину, полученную по вертикальной шкале, суммируют (если она больше километра) с оцифровкой нижней стороны квадрата или приписывают к
ней справа (если величина меньше километра). Это будет координата х точки.
Таким же образом получают и координату у — величину, соответствующую отсчету по горизонтальной шкале, только суммирование производят с оцифровкой
левой стороны квадрата.
На рис.2.4 показан пример определения прямоугольных координат точки С: х = 5 873 300; у = 3 300 800.
Нанесение точек на карту по прямоугольным координатам. Прежде всего, по координатам в километрах и оцифровкам километровых линий находят на карте квадрат,
в котором должна быть расположена точка.
Квадрат местонахождения точки на карте масштаба 1:50000, где километровые линии проведены через 1 км, находят непосредственно по координатам объекта в
километрах. На карте масштаба 1:100000 километровые линии проведены через 2 км и подписаны четными числами, поэтому если одна или две координаты точки в.
километрах нечетные числа, то нужно находить квадрат, стороны которого подписаны числами на единицу меньше соответствующей координаты в километрах.
На карте масштаба 1:200000 километровые линии проведены через 4 км и подписаны числами, кратными 4. Они могут быть меньше соответствующей координаты
точки на 1, 2 или 3 км. Например, если даны координаты точки (в километрах) х = 6755 и у = 4613, то стороны квадрата будут иметь оцифровки 6752 и
4612.
После нахождения квадрата, в котором расположена точка, рассчитывают удаление ее от нижней стороны квадрата и полученное расстояние откладывают в
масштабе карты от нижних углов квадрата вверх. К полученным точкам прикладывают линейку и от левой стороны квадрата также в масштабе карты откладывают
расстояние, равное удалению объекта от этой стороны.
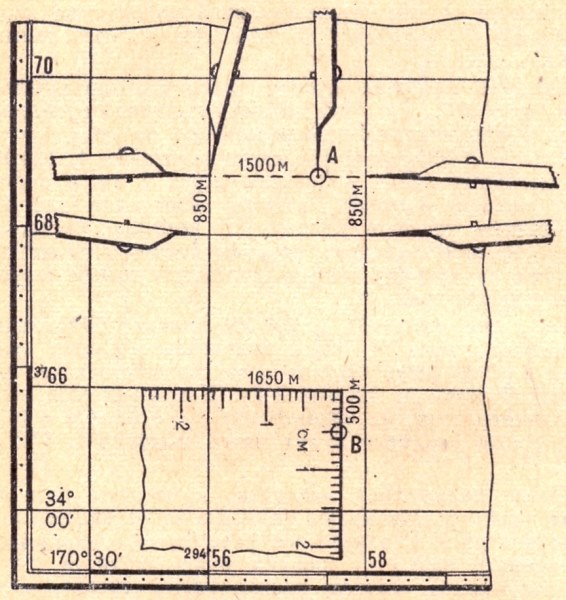
На рис.2.5 показан пример нанесения на карту точки А по координатам х = 3 768 850, у = 29 457 500.
Рис. 2.5 Нанесение точек на карту по прямоугольным координатам
При работе с координатомером вначале также находят квадрат, в котором расположена точка. На этот квадрат накладывают координатомер, совмещают его
вертикальную шкалу с западной стороной квадрата так, чтобы против нижней стороны квадрата был отсчет, соответствующий координате х. Затем, не
изменяя положения координатомера, находят на горизонтальной шкале отсчет, соответствующий координате у. Точка против отсчета покажет ее
местоположение, соответствующее данным координатам.
На рис.2.5 показан пример нанесения на карту точки В, расположенной в неполном квадрате, по координатам х = 3 765 500; у = 29 457 650.
В данном случае координатомер наложен так, что горизонтальная шкала его совмещена с северной стороной квадрата, а отсчет против западной его стороны
соответствует разности координаты у точки и оцифровки этой стороны (29 457 км 650 м — 29 456 км = 1 км 650 м). Отсчет, соответствующий разности
оцифровки северной стороны квадрата и координаты х (3766 км — 3765км 500 м), отложен по вертикальной шкале вниз. Местоположение точки В
будет против штриха у отсчета 500 м.
Напомним, что географические координаты (широта и долгота) – это угловые величины, определяющие
положение объектов на земной поверхности и на карте. При этом широта точки — это угол, составленный плоскостью экватора и нормалью к поверхности земного
эллипсоида, проходящей через данную точку. Счет широт ведется по дуге меридиана от экватора к полюсам от 0 до 90°; в северном полушарии широты называют
северными (положительными), в южном — южными (отрицательными).
Долгота точки — это двугранный угол между плоскостью Гринвичского меридиана и плоскостью меридиана данной точки. Счет долготы ведется по дуге экватора
или параллели в обе стороны от начального меридиана, от 0 до 180°. Долготу точек, расположенных к востоку от Гринвича до 180°, называют восточной
(положительной), к западу — западной (отрицательной).
Географическая (картографическая, градусная) сетка
— изображение на карте линий параллелей и меридианов; используется для определения географических (геодезических) координат точек (объектов) и
целеуказания. На топографических картах линии параллелей и меридианов являются внутренними рамками листов; их широта и долгота подписываются на углах
каждого листа. Географическая сетка полностью показывается лишь на топографических картах масштаба 1:500000 (параллели проведены через 30′, а меридианы —
через 20′) и 1:1000000 (параллели проведены через 1°, а меридианы — через 40′). Внутри каждого листа карты на линиях параллелей и меридианов подписаны их
широта и долгота, которые позволяют определять географические координаты на большой склейке карт.
На картах масштабов 1:25000, 1:50000, 1:100000 и 1:200000 стороны рамок разделены на отрезки, равные в градусной мере 1′. Минутные отрезки оттенены через
один и разделены точками (за исключением карты масштаба 1:200000) на части по 10″. Кроме того, внутри каждого листа карт масштабов 1:50000 и 1:100000
показывается пересечение средних параллели и меридиана и дается их оцифровка в градусах и минутах, а вдоль внутренней рамки даны выходы минутных делений
штрихами длиной 2—3 мм, по которым можно прочертить параллели и меридианы на карте, склеенной из нескольких листов.
Если территория, на которую создана карта, находится в западном полушарии, то в северо-западном углу рамки листа правее подписи долготы меридиана
помещается надпись «К западу от Гринвича».
Определение географических координат точки по карте производится по ближайшим к ней параллели и меридиану, широта и долгота которых известны. Для этого на
картах, масштабов 1:25000 — 1:200000 следует предварительно провести южнее точки параллель и западнее — меридиан, соединив линиями соответствующие штрихи
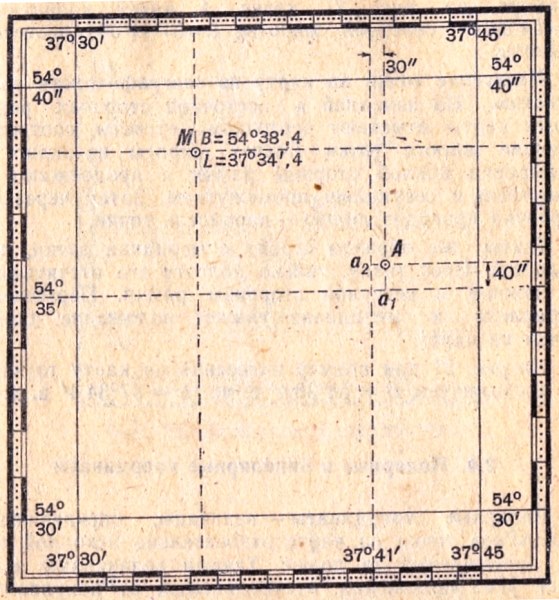
по сторонам рамки листа (рис.2.6). Затем от проведенных линий берут отрезки до определяемой точки (Аа1 Аа2), прикладывают
их к градусным шкалам на сторонах рамки и производят отсчеты. В примере на рис.1.2.6 точка А имеет координаты В = 54°35’40» северной широты, L = 37°41’30» восточной долготы.
Нанесение точки на карту по географическим координатам
. На западной и восточной сторонах рамки листа карты отмечают черточками отсчеты, соответствующие широте точки. Отсчет широты начинают от оцифровки южной
стороны рамки и продолжают по минутным и секундным промежуткам. Затем через эти черточки проводят линию — параллель точки.
Таким же образом строят и меридиан точки, проходящий через точку, только долготу его отсчитывают по южной и северной сторонам рамки. Пересечение параллели
и меридиана укажет положение данной точки на карте. На рис.2.6 дан пример нанесения на карту точки М по координатам В = 54°38,4′ с.ш., L = 37°34,4′ в.д.
Рис. 2.6 Определение географических координат по карте и нанесение точек на карту по географическим координатам
Как было указано выше, в силу особенностей формы, внутреннего строения и движения в пространстве земной эллипсоид имеет истинные (географические) и
магнитные полюса, не совпадающие друг с другом.
Северный и Южный географические полюсы — это точки, через которые проходит ось вращения земного шара, а Северный и Южный магнитные полюсы – это полюсы
гигантского магнита, которым, собственно, является Земля, причем Северный магнитный полюс (≈ 74°с.ш., 100°з.д.) и Южный магнитный полюс (≈ 69°ю.ш.,
144°в.д.) постепенно дрейфуют и, соответственно, не имеют постоянных координат. В этой связи важно понимать, что магнитная стрелка компаса указывает именно
на магнитный, а не на истинный (географический) полюс.
Таким образом, существуют истинный и магнитный полюсы, не совпадающие между собой, соответственно этому существуют истинный (географический) и магнитный меридианы. И от того и от другого можно отсчитывать направление
на нужный объект: в одном случае наблюдатель будет иметь дело с истинным азимутом, в другом — с магнитным.
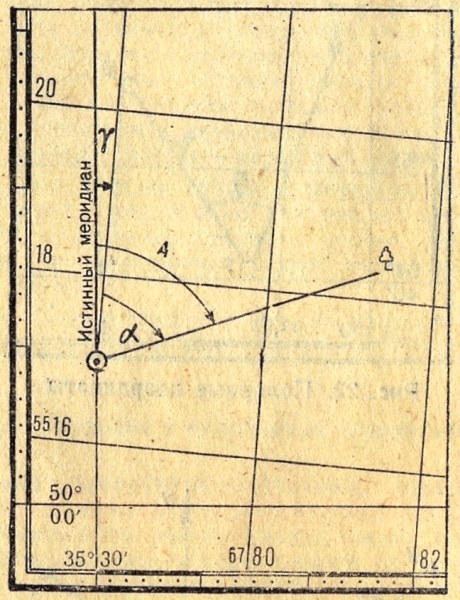
Рис. 2.7 Истинный азимут А, дирекционный угол α, и сближение меридианов γ
Истинный азимут
— это угол А (рис.2.7), измеряемый по ходу часовой стрелки от 0 до 360° между северным направлением истинного (географического)
меридиана и направлением на определяемый пункт.
Магнитный азимут
— это угол Ам, измеряемый по ходу часовой стрелки от 0 до 360° между заданным (выбранным) направлением и направлением
на Север на местности.
Обратный азимут
— азимут (истинный, магнитный) направления, противоположного определяемому (прямому). Он отличается от прямого на 180°, и его можно отсчитать по компасу
против указателя у прорези.
Понятно, что истинный и магнитный азимуты отличаются, как минимум, на ту же самую величину, на которую магнитный меридиан отличается от истинного. Эта
величина называется магнитным склонением. Другими словами, магнитное склонение – угол δ ( дельта) между истинным и магнитным меридианами.
На величину магнитного склонения оказывают влияние различные магнитные аномалии (залежи руд, подземные потоки и т.д.), суточные, годовые и вековые
колебания, а также временные возмущения под действием магнитных бурь. Величина магнитного склонения и его годовые изменения указаны на каждом листе
топографической карты. Суточное колебание магнитного склонения достигает 0,3° и при точных измерениях магнитного азимута учитывается по графику поправок,
составленному в зависимости от времени суток. На картах масштабов 1:500000 и 1:1000000 показываются районы магнитных аномалий, и в каждом из них
подписывается значение амплитуды колебания магнитного склонения. Если стрелка компаса отклоняется от истинного меридиана к востоку, магнитное склонение
называют восточным (положительным), если стрелка отклоняется к западу, склонение называют западным (отрицательным). Соответственно, восточное склонение
часто обозначают знаком «+», западное — знаком «—».
Дирекционный угол
— это угол α (альфа), измеряемый на карте по ходу часовой стрелки от 0 до 360° между северным направлением вертикальной
линии координатной сетки и направлением на определяемый пункт. Другими словами, дирекционный угол — это угол между заданным (выбранным) направлением и
направлением на Север на карте (рис.2.7). Дирекционные углы измеряются по карте, а также определяются по измеренным на местности
магнитным или истинным азимутам.
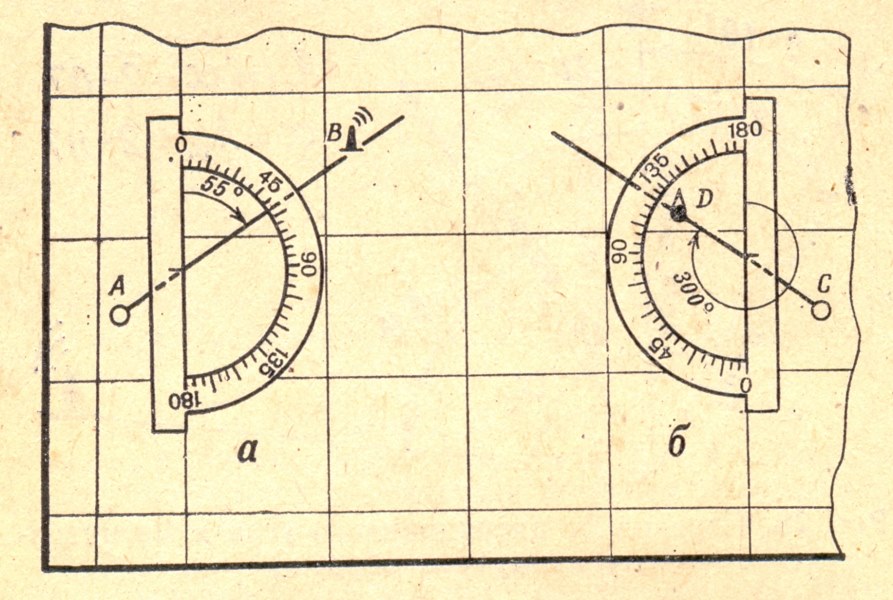
Рис. 2.8 Измерение дирекционного угла транспортиром
Измерение и построение дирекционных углов на карте производится с помощью транспортира (рис.2.8).
Чтобы измерить на карте дирекционный угол какого-нибудь направления, надо наложить на нее транспортир так, чтобы середина его линейки, отмеченная
штрихом, совпала с точкой пересечения определяемого направления с вертикальной километровой линией сетки, а край линейки (т.е. деления 0 и 180° на
транспортире) совместился с этой линией. Затем следует отсчитать по шкале транспортира угол по ходу часовой стрелки от северного направления километровой
линии до определяемого направления.
Для построения на карте в какой-либо точке дирекционного угла проводят через эту точку прямую, параллельную вертикальным линиям километровой сетки,
и от этой прямой строят заданный дирекционный угол.
Следует учитывать, что средняя ошибка измерения угла транспортиром, имеющимся на офицерской линейке, составляет 0,5°.
Значения истинного азимута и дирекционного угла отличаются друг от друга на величину сближения меридианов. Сближение меридианов —
угол ? (гамма) между северным направлением истинного меридиана данной точки и вертикальной линией координатной сетки
(рис.2.7). Сближение меридианов отсчитывается от северного направления истинного меридиана до северного направления вертикальной линии сетки. Для точек,
расположенных восточнее среднего меридиана зоны, величина сближения положительная, а для точек, расположенных западнее, — отрицательная. Величина
сближения меридианов на осевом меридиане зоны равна нулю и возрастает с удалением от среднего меридиана зоны и от экватора, при этом ее максимальное
значение не превышает 3°.
Сближение меридианов, указываемое на топографических картах, относится к средней (центральной) точке листа; величина ее в пределах листа карты масштаба
1:100000 на средних широтах у западной или восточной рамки может отличаться на 10-15′ от значения, подписанного на карте.
Переход от дирекционного угла к магнитному азимуту и обратно
может производиться различными способами: по формуле, с учетом годового изменения магнитного склонения, по графической схеме. Удобен переход через поправку
направления. Необходимые данные для этого имеются на каждом листе карты масштабов 1:25000—1:200000 в специальной текстовой справке и графической схеме,
помещаемых на полях листа в левом нижнем углу (рис.2.9).
Рис. 2.9 Данные о величине поправки направления
При этом в специальной текстовой справке ключевой фразой является: «Поправка в дирекционный угол при переходе к магнитному азимуту плюс (минус)…»,
также важен угол между «стрелочкой» и «вилочкой»:
-
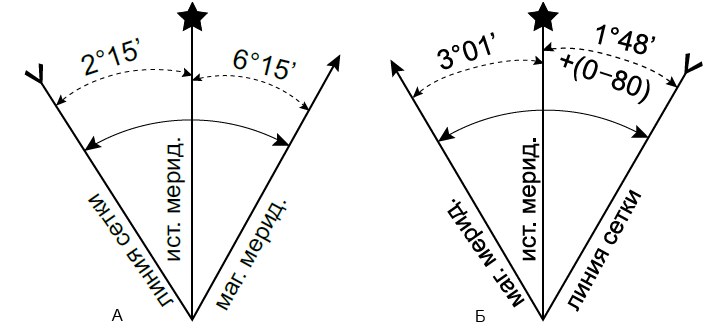
если «вилочка» слева, а «стрелочка» справа (рис.2.10-А), то склонение восточное и при переходе от дирекционного угла к азимуту
поправка (2°15′ + 6°15′ = 8°30′) от величины измеренного дирекционного угла отнимается (соответственно, при
переходе от азимута к дирекционному углу, поправка прибавляется); -
если «вилочка» справа, а «стрелочка» слева (рис.2.10-Б), то склонение западное и при переходе от дирекционного угла к азимуту
поправка (3°01′ + 1°48′ = 4°49′) к величине измеренного дирекционного угла прибавляется (соответственно, при
переходе от азимута к дирекционному углу, поправка отнимается).
Рис. 2.10 Внесение поправки
Внимание!
Невнесение поправки в дирекционный угол или магнитный азимут, особенно при больших расстояниях и крупных масштабах карт, ведет к значительным ошибкам в
определении координат, промежуточных и конечных точек маршрута.
Книга найдена на
http://www.geolink-group.com/tourclub/ — спасибо создателям
Вы можете заказать 2CD
с картами Юга России
Содержание книги
1.11.
ОПРЕДЕЛЕНИЕ ПРЯМОУГОЛЬНЫХ КООРДИНАТ ПО КАРТЕ И НАНЕСЕНИЕ ОБЪЕКТОВ НА КАРТУ
ПО КООРДИНАТАМ
Определение прямоугольных координат
объекта по карте циркулем.
Циркулем измеряют по перпендикуляру расстояние от данного объекта до нижней
километровой линии и по масштабу определяют его действительную величину.
Затем эту величину в метрах приписывают справа к подписи километровой линии,
а при длине отрезка более километра вначале суммируют километры, а затем
также приписывают число метров справа. Это будет координата объекта Х
(абсцисса).
Таким же приемом определяют и
координату Y
(ординату), только расстояние от объекта измеряют до левой стороны квадрата,
При отсутствии циркуля расстояния измеряют линейкой или полоской бумаги
Рис. 18.
Определение прямоугольных координат объектов по карте
Пример определения координат объекта
А показан на рис. 18:
Х=
5 877100; У == 3 302 700.
Здесь же дан пример определения
координат объекта В, расположенного у рамки листа карты в неполном
квадрате:
Х=
5 874 850;
Y
= 3 298 800.
Определение прямоугольных координат
координатомером.
Коор-динатомер — приспособление для отсчета координат. Наиболее
распространен коордииатомер в виде прямого угла прозрачной линейки, по
сторонам которого нанесены миллиметровые деления. Такого типа координатомер
имеется на командирской линейке.
При определении координат коордпнатомер
накладывают на квадрат, в котором располагается объект и, совместив
вертикальную шкалу с его левой стороной, а горизонтальную — с объектом, как
показано на рис. 18, снимают отсчеты.
Отсчеты в миллиметрах (десятые
миллиметра отсчитывают на глаз) в соответствии с масштабом карты преобразуют
в действительные величины — километры и метры, а затем величину, полученную
по вертикальной шкале, суммируют (если она больше километра) с оцифровкой
нижней стороны квадрата или приписывают к ней справа (если величина меньше
километра). Это будет координата Х объекта.
Таким же порядком получают и координату
Y
— величину, соответствующую
отсчету по горизонтальной шкале, только суммирование производят с оцифровкой
левой стороны квадрата.
На рис. 18 показан пример определения
прямоугольных координат объекта С: Х -= 5 873 300; У = 3 300 800.
Нанесение объекта на карту по
прямоугольным координатам циркулем или линейкой. Прежде всего по координатам
объекта в километрах и оцифровкам километровых линий находят на карте
квадрат, в котором должен быть расположен объект.
Квадрат местонахождения объекта на
карте масштаба 1:50 000, где километровые линии проведены через 1 км,
находят непосредственно по координатам объекта в километрах.
На карте масштаба 1: 100 000
километровые линии проведены через 2 км и подписаны четными числами,
поэтому если одна или две координаты объекта в километрах нечетные числа, то
нужно находить квадрат, стороны которого подписаны числами на единицу меньше
соответствующей координаты в километрах.
‘ На карте масштаба 1:200 000 километровые
линии проведены через 4 км, поэтому стороны нужного квадрата будут
подписаны числами, кратными четырем, меньшими соответствующей координаты
объекта в километрах на один, два или три километра. Например, если даны
координаты объекта (в километрах): Х==6755 и У=4613, то стороны квадрата
будут иметь оцифровки: 6752 и 4612. После нахождения квадрата, в котором
расположен объект, рассчитывают удаление объекта от нижней стороны квадрата
и откладывают его в масштабе карты от нижних углов квадрата вверх. К
полученным точкам прокладывают линейку и от левой стороны квадрата, также в
масштабе карты, откладывают расстояние, равное удалению объекта от этой
стороны.
На рис. 19 показан пример нанесения на
карту объекта А по координатам: Х=3 768 850, У=29 457 500.
Рис. 19.
Нанесение объектов на карту по прямоугольным координатам
Нанесение объекта на карту
координатомером,
выгравированным на командирской линейке. По координатам объекта в километрах
и оцифровке километровых линий определяют квадрат, в котором находится
объект. На этот квадрат накладывают координатомер так же, как и при
определении координат (см. рис. 18), совмещают его вертикальную шкалу с
западной стороной квадрата так, чтобы против нижней стороны квадрата был
отсчет, соответствующий координате Х в масштабе карты минус оцифровка
этой стороны квадрата. Затем, не изменяя положения координатомера, находят
на горизонтальной шкале отсчет, соответствующий (также В масштабе карты)
раэности координаты
Y
объекта и оцифровки западной стороны квадрата. Точка против штриха у этого
отсчета будет соответствовать положению объекта на карте.
На рис. 19 показан пример нанесения на
карту объекта В, расположенного в неполном квадрате, по координатам:
Х =
3 765 500; У = 29 45750.
В данном случае координатомер наложен так, чтобы горизонтальная шкала его
была совмещена с северной стороной квадрата, а отсчет против западной его
стороны соответствовал разности координаты
Y
объекта и оцифровки этой стороны (29457 км 650 м—29456 км=1
км 650 м). Отсчет, соответствующий разности оцифровки северной
стороны квадрата и координате
Y
объекта (3766 км — 3765 км 500 м), отложен по
вертикальной шкале вниз. Точка против штриха у отсчета 500 м будет
указывать положение объекта на карте.
Вы
можете заказать 2CD с картами Юга России