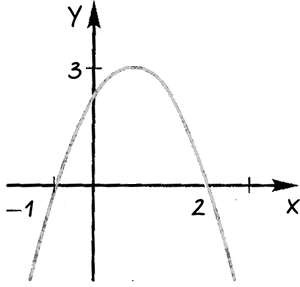Как найти координаты точек пересечения графика функции: примеры решения
Ирина Алексеевна Антоненко
Эксперт по предмету «Математика»
Задать вопрос автору статьи
В практике и в учебниках наиболее распространены нижеперечисленные способы нахождения точки пересечения различных графиков функций.
Первый способ
Первый и самый простой – это воспользоваться тем, что в этой точке координаты будут равны и приравнять графики, а из того что получится можно найти $x$. Затем найденный $x$ подставить в любое из двух уравнений и найти координату игрек.
Пример 1
Найдём точку пересечения двух прямых $y=5x + 3$ и $y=x-2$, приравняв функции:
$5x = x- 2$;
$4x = -2$;
$x=-frac{1}{2}$
Теперь подставим полученный нами икс в любой график, например, выберем тот, что попроще — $y=x-2$:
$y=-frac{1}{2} – 2 = — 2frac12$.
Точка пересечения будет $(-frac{1}{2};- 2frac12)$.
Второй способ
Второй способ заключается в том, что составляется система из имеющихся уравнений, путём преобразований одну из координат делают явной, то есть, выражают через другую. После это выражение в приведённой форме подставляется в другое.
Пример 2
Узнайте, в каких точках пересекаются графики параболы $y=2x^2-2x-1$ и пересекающей её прямой $y=x+1$.
Решение:
Составим систему:
$begin{cases} y=2x^2-2x-1 \ y= x + 1 \ end{cases}$
Второе уравнение проще первого, поэтому подставим его вместо $y$:
$x+1 = 2x^2 – 2x-1$;
$2x^2 – 3x – 2 = 0$.
Вычислим, чему равен x, для этого найдём корни, превращающие равенство в верное, и запишем полученные ответы:
$x_1=2; x_2 = -frac{1}{2}$
Подставим наши результаты по оси абсцисс по очереди во второе уравнение системы:
$y_1= 2 + 1 = 3; y_2=1 — frac{1}{2} = frac{1}{2}$.
Точки пересечения будут $(2;3)$ и $(-frac{1}{2}; frac{1}{2})$.
Третий способ
«Как найти координаты точек пересечения графика функции: примеры решения» 👇
Перейдём к третьему способу — графическому, но имейте в виду, что результат, который он даёт, не является достаточно точным.
Для применения метода оба графика функций строятся в одном масштабе на одном чертеже, и затем выполняется визуальный поиск точки пересечения.
Данный способ хорош лишь в том случае, когда достаточно приблизительного результата, а также если нет каких-либо данных о закономерностях рассматриваемых зависимостей.
Пример 3
Найдите точку пересечения графиков на общем рисунке.
Рисунок 1. Точка пересечения двух функций. Автор24 — интернет-биржа студенческих работ
Решение:
Тут всё просто: ищем точки пересечения пунктиров, опущенных с графиков с осями абсцисс и ординат и записываем по порядку. Здесь точка пересечения равна $(2;3)$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 07.05.2023
Координаты точки пересечения графиков функций
Как найти?
- Чтобы найти координаты точки пересечения графиков функций нужно приравнять обе функции друг к другу, перенести в левую часть все члена, содержащие $ x $, а в правую остальные и найти корни, полученного уравнения.
- Второй способ заключается в том, что нужно составить систему уравнений и решить её путём подстановки одной функции в другую
- Третий способ подразумевает графическое построение функций и визуальное определение точки пересечения.
Случай двух линейных функций
Рассмотрим две линейные функции $ f(x) = k_1 x+m_1 $ и $ g(x) = k_2 x + m_2 $. Эти функции называются прямыми. Построить их достаточно легко, нужно взять любые два значения $ x_1 $ и $ x_2 $ и найти $ f(x_1) $ и $ (x_2) $. Затем повторить тоже самое и с функцией $ g(x) $. Далее визуально найти координату точки пересечения графиков функций.
Следует знать, что линейные функции имеют только одну точку пересечения и только тогда, когда $ k_1 neq k_2 $. Иначе, в случае $ k_1=k_2 $ функции параллельны друг другу, так как $ k $ — это коэффициент угла наклона. Если $ k_1 neq k_2 $, но $ m_1=m_2 $, тогда точкой пересечения будет $ M(0;m) $. Это правило желательно запомнить для ускоренного решения задач.
| Пример 1 |
| Пусть даны $ f(x) = 2x-5 $ и $ g(x)=x+3 $. Найти координаты точки пересечения графиков функций. |
| Решение |
|
Как это сделать? Так как представлены две линейные функции, то первым делом смотрим на коэффициент угла наклона обеих функций $ k_1 = 2 $ и $ k_2 = 1 $. Замечаем, что $ k_1 neq k_2 $, поэтому существует одна точка пересечения. Найдём её с помощью уравнения $ f(x)=g(x) $: $$ 2x-5 = x+3 $$ Переносим слагаемые с $ x $ в левую часть, а остальные в правую: $$ 2x — x = 3+5 $$ $$ x = 8 $$ Получили $ x=8 $ абциссу точки пересечения графиков, а теперь найдём ординату. Для этого подставим $ x = 8 $ в любое из уравнений хоть в $ f(x) $, либо в $ g(x) $: $$ f(8) = 2cdot 8 — 5 = 16 — 5 = 11 $$ Итак, $ M (8;11) $ — является точкой пересечения графиков двух линейных функций. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ M (8;11) $$ |
| Пример 2 |
| Дано $ f(x)=2x-1 $ и $ g(x) = 2x-4 $. Найти точки пересечения графиков функций. |
| Решение |
| Как найти? Опять же обращаем внимание на то, что угловые коэффициенты равны $ k_1 = k_2 = 2 $. Это означает, что линейные функции параллельны между собой, поэтому у них нет точек пересечения! |
| Ответы |
| Графики функций параллельны, нет точек пересечения. |
Случай двух нелинейных функций
| Пример 3 |
| Найти координаты точки пересечения графиков функций: $ f(x)=x^2-2x+1 $ и $ g(x)=x^2+1 $ |
| Решение |
|
Как быть с двумя нелинейными функциями? Алгоритм простой: приравниваем уравнения друг к другу и находим корни: $$ x^2-2x+1=x^2+1 $$ Разносим по разным сторонам уравнения члены с $ x $ и без него: $$ x^2-2x-x^2=1-1 $$ $$ -2x=0 $$ $$ x=0 $$ Найдена абцисса искомой точки, но её недостаточно. Ещё нехватает ординаты $ y $. Подставляем $ x = 0 $ в любое из двух уравнений условия задачи. Например: $$ f(0)=0^2-2cdot 0 + 1 = 1 $$ $ M (0;1) $ — точка пересечения графиков функций |
| Ответ |
| $$ M (0;1) $$ |
В предыдущем уроке мы подробно разобрали,
как построить параболу.
В этом уроке мы разберем, как решать типовые задачи на квадратичную функцию.
Как найти нули квадратичной функции
Запомните!
Чтобы найти координаты точек нулей функции, нужно
в исходную функцию подставить вместо «y» число
ноль.
Рассмотрим задачу.
Найти нули квадратичной
функции «y = x2 − 3».
Подставим в исходную функцию вместо «y» ноль и решим полученное
квадратное уравнение.
0 = x2 − 3
x2 − 3 = 0
x1;2 =
| 0 ± √02 − 4 · 1 · (−3) |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
x1;2 = ±√3
Ответ: нули функции «y = x2 − 3» :
x1 = √3;
x2 = −√3 .
Как найти при каких значениях
«x» квадратичная функция принимает заданное
числовое значение
Запомните!
Чтобы найти при каких значениях «x» квадратичная функция принимает заданное числовое значение,
нужно:
- вместо «y» подставить в функцию заданное числовое значение;
- решить полученное квадратное уравнение относительно «x».
Рассмотрим задачу.
При каких значениях «x» функция
«y = x2 − x − 3» принимает значение
«−3».
Подставим в исходную функцию
«y = x2 − x − 3» вместо «y = −3» и
найдем «x».
y = x2 − x − 3
−3 = x2 − x − 3
x2 − x − 3 = −3
x2 − x − 3 + 3 = 0
x2 − x = 0
x1;2 =
| 1 ± √12 − 4 · 1 · 0 |
| 2 · 1 |
x1;2 =
x1;2 =
| x1 = | x2 = |
| x1 = | x2 = |
| x1 = 1 | x2 = 0 |
Ответ: при «x = 0» и
«x = 1» функция «y = x2 − x − 3»
принимает значение «y = −3».
Как найти координаты точек пересечения параболы и прямой
Запомните!
Чтобы найти точки пересечения параболы с прямой нужно:
- приравнять правые части функций (те части функций, в которых содержатся «x»);
- решить полученное уравнение относительно «x»;
- подставить полученные числовые значения «x»
в любую из функций и найти координаты точек по оси «Оy».
Рассмотрим задачу.
Найти координаты точек пересечения параболы «y = x2»
и прямой «y = 3 − 2x».
Приравняем правые части функций и решим
полученное уравнение относительно «x».
x2 = 3 − 2x
x2 − 3 + 2x = 0
x2 + 2x − 3 = 0
x1;2 =
| −2 ± √22 − 4 · 1 · (−3) |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
| x1 = | x2 = |
| x1 = | x2 = |
| x1 = 1 | x2 = −3 |
Теперь подставим в любую из заданных функций (например, в
«y = 3 − 2x») полученные
числовые значения «x», чтобы найти координаты
«y» точек пересечения.
1) x = −3
y = 3 − 2x
y(−3) = 3 − 2 · (−3) = 3 − (−6) = 3 + 6 = 9
(·) A (−3; 9) — первая точка пересечения.
2) x = 1
y = 3 − 2x
y(1) = 3 − 2 · 1 = 3 − 2 = 1
(·) B (1; 1) — вторая точка пересечения.
Запишем полученные точки пересечения с их координатами в ответ.
Ответ: точки пересечения параболы
«y = x2»
и прямой «y = 3 − 2x»:
(·) A (−3; 9) и
(·) B (1; 1).
Как определить, принадлежит ли точка графику функции параболы
Запомните!
Чтобы проверить принадлежность точки параболе нет необходимости строить график функции.
Достаточно подставить координаты точки в формулу функции (координату по оси
«Ox» вместо
«x», а координату по оси
«Oy» вместо «y») и выполнить арифметические расчеты.
- Если получится верное равенство, значит, точка принадлежит графику функции.
- Если получится неверное равенство, значит, точка
не принадлежит графику функции.
Рассмотрим задачу:
Не строя графика функции «y = x2», определить, какие точки принадлежат ему:
(·) А(2; 6),
(·) B(−1; 1).
Подставим в функцию
«y = x2»
координаты точки (·) А(2; 6).
y = x2
6 = 22
6 = 4
(неверно)
Значит, точка (·) А(2; 6)
не принадлежит графику функции
«y = x2».
Подставим в функцию
«y = x2»
координаты точки (·) B(−1; 1).
y = x2
1 = (−)12
1 = 1
(верно)
Значит, точка (·) B(−1; 1)
принадлежит графику функции
«y = x2».
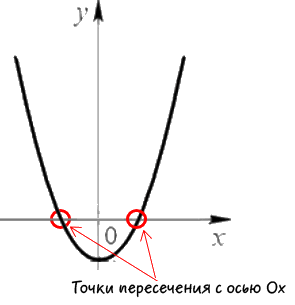
Как найти точки пересечения параболы с осями координат
Рассмотрим задачу
Найти координаты точек пересечения параболы
«y = x2 −3x + 2» с осями координат.
Сначала определим точки пересечения функции с осью «Ox».
На графике функции эти точки выглядят так:
Как видно на рисунке выше, координата «y» точек пересечения с осью «Ox»
равна нулю, поэтому подставим «y = 0» в
исходную функцию «y = x2 −3x + 2»
и найдем их координаты по оси «Ox».
0 = x2 −3x + 2
x2 −3x + 2 = 0
x1;2 =
| 3 ± √32 − 4 · 1 · 2 |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
| x1 = | x2 = |
| x1 = | x2 = |
| x1 = 2 | x2 = 1 |
Запишем координаты точек пересечения графика с осью «Ox»:
(·) A (2; 0) и
(·) B (1; 0).
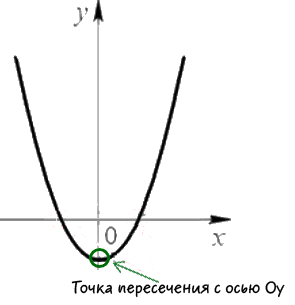
Теперь найдем координаты точки пересечения с осью «Oy».
Как видно на рисунке выше, координата «x»
точки пересечения с осью «Oy» равна нулю.
Подставим «x = 0»
в исходную функцию
«y = x2 −3x + 2»
и найдем координату точки по оси
«Oy».
y(0) = 02 − 3 · 0 + 2 = 2
Выпишем координаты полученной точки: (·) C (0; 2)
Запишем в ответ все координаты точек пересечения параболы с осями.
Ответ: точки пересечения с осью «Ox»:
(·) A (2; 0) и
(·) B (1; 0).
С осью «Oy»: (·)C (0; 2).
Как определить при каких значениях x функция принимает
положительные или
отрицательные значения
Напоминаем, что когда в задании говорится «функция принимает
значения» — речь идет о
значениях«y».
Другими словами, необходимо ответить на вопрос: при каких значениях
«x», координата
«y» положительна или отрицательна.
Запомните!
Чтобы по графику функции определить, где функция принимает положительные или отрицательные значения нужно:
- провести прямые через точки в местах, где график пересекает ось «Ox»;
- определить положительные или отрицательные значения принимает функция на промежутках между проведенными прямыми;
- записать ответ для каждого промежутка относительно «x».
Рассмотрим задачу.
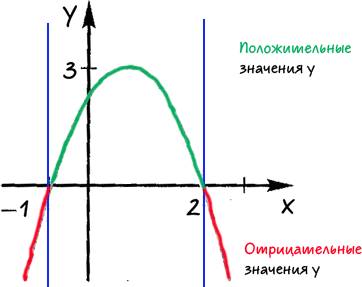
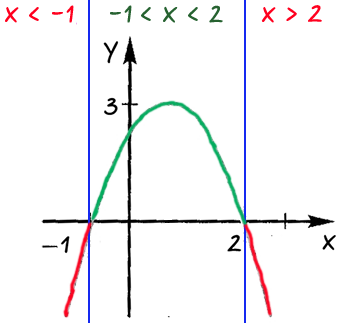
С помощью графика квадратичной функции, изображенного на рисунке, ответить:
При каких значениях «x» функция принимает 1) положительные значения; 2) отрицательные значения.
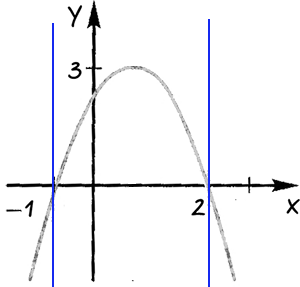
Проведем через точки, где график функции пересекает ось «Ox» прямые.
Определим области, где функция принимает отрицательные или положительные значения.
Подпишем над каждой полученной областью, какие значения принимает
«x» в каждой из выделенных областей.
Ответ: при «x < −1» и
«x > 2» функция принимает отрицательные значения;
при «−1 < x < 2» функция принимает
положительные значения.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Как найти точку пересечения прямой и параболы
Задачи по поиску точек пересечения каких-нибудь фигур идеологически просты. Сложности в них бывают только из-за арифметики, так как именно в ней допускаются различные опечатки и ошибки.

Инструкция
Данная задача решается аналитически, поэтому можно вовсе не рисовать графики прямой и параболы. Часто это дает большой плюс в решении примера, так как в задаче могут быть даны такие функции, что их проще и быстрее не нарисовать.
Согласно учебникам по алгебре парабола задается функцией вида f(x)=ax^2+bx+c, где a,b,c – это вещественные числа, притом коэффициент a отличен он нуля. Функция g(x)=kx+h, где k,h – это вещественные числа, определяет прямую на плоскости.
Точка пересечения прямой и параболы – это общая точка обеих кривых, поэтому в ней функции примут одинаковые значение, то есть f(x)=g(x). Данное утверждение позволяет записать уравнение: ax^2+bx+c=kx+h, которое даст возможность найти множество точек пересечения.
В уравнении ax^2+bx+c=kx+h необходимо перенести все слагаемые в левую часть и привести подобные: ax^2+(b-k)x+c-h=0. Теперь остается решить полученное квадратное уравнение.
Все найденные «иксы» – это еще не ответ на задачу, так как точку на плоскости характеризуют два вещественных числа (x,y). Для полного завершения решения необходимо вычислить соответствующие «игрики». Для этого нужно подставить «иксы» либо в функцию f(x), либо в функцию g(x), ведь для точки пересечения верно: y=f(x)=g(x). После этого вы найдете все общие точки параболы и прямой.
Для закрепления материала очень важно рассмотреть решение на примере. Пусть парабола задается функцией f(x)=x^2-3x+3, а прямая – g(x)=2x-3. Составьте уравнение f(x)=g(x), то есть x^2-3x+3=2x-3. Перенося все слагаемые в левую часть, и приводя подобные, получите: x^2-5x+6=0. Корни данного квадратного уравнения: x1=2, x2=3. Теперь найдите соответствующие «игрики»: y1=g(x1)=1, y2=g(x2)=3. Таким образом, найдены все точки пересечения: (2,1) и (3,3).
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Загрузить PDF
Загрузить PDF
Точка пересечения с осью Y – это точка, в которой график функции пересекает ось ординат. Найти такую точку можно несколькими способами, в зависимости от начальной информации.
-
1
Запишите значение углового коэффициента и координаты точки. Угловой коэффициент характеризует угол наклона графика по отношению к оси X. Координаты точки, лежащей на графике, записываются в виде (х,у). Если вам не даны координаты и угловой коэффициент, воспользуйтесь другим методом.
- Пример 1. Дана прямая, на которой лежит точка А (3,4) и угловой коэффициент которой равен 2. Найдите точку пересечения этой прямой с осью Y.
-
2
Запишите линейную функцию. Ее график представляет собой прямую. Линейная функция имеет вид у = kх + b, где k – угловой коэффициент, b – координата «у» точки пересечения с осью Y.
-
3
В функцию подставьте значение углового коэффициента. Подставьте данное значение вместо k.
-
Пример 1. y = kx + b
k = 2
y = 2x + b
-
Пример 1. y = kx + b
-
4
Вместо «х» и «у» подставьте данные координаты точки. Если даны координаты точки, лежащей на прямой, подставьте их в функцию вместо х и у.
-
Пример 1. Точка А (3,4) лежит на прямой. То есть х = 3, у = 4.
Подставьте эти значения в y = 2x + b
4 = 2*3 + b
-
Пример 1. Точка А (3,4) лежит на прямой. То есть х = 3, у = 4.
-
5
Найдите значение b. Напомним, что b – это координата «у» точки пересечения с осью Y. В уравнении b является единственной переменной, которую нужно обособить и найти ее значение.
-
Пример 1. 4 = 2*3 + b
4 = 6 + b
4 — 6 = b
-2 = b
Координата «у» точки пересечения с осью Y равна -2 (у = -2).
-
Пример 1. 4 = 2*3 + b
-
6
Ответ запишите в виде пары координат точки пересечения прямой с осью Y. Точка лежит на пересечении прямой и оси Y; координата «х» любой точки, лежащей на оси Y, равна 0, поэтому координата «х» точки пересечения всегда равна 0 (х = 0).
- Пример 1. Точка пересечения прямой с осью Y имеет координаты (0,-2).
Реклама
-
1
Запишите координаты двух точек, лежащих на прямой. Если координаты обеих точек не даны, воспользуйтесь другим методом. Координаты каждой точки записываются в виде (х,у).
-
2
Пример 2. Прямая проходит через точки А(1,2) и В(3,-4). Найдите точку пересечения этой прямой с осью Y.
-
3
Найдите вертикальное и горизонтальное расстояние между двумя точками. Угловой коэффициент равен тангенсу угла наклона прямой, образуемого с осью Х, и вычисляется как отношение вертикального расстояния между двумя точками к горизонтальному расстоянию между двумя точками.
- Вертикальное расстояние – это разность координат «у» двух точек.
- Горизонтальное расстояние – это разность координат «х» двух точек.
-
Пример 2. Координаты «у» двух точек: 2 и -4, поэтому вертикальное расстояние: -4 — 2 = -6.
Координаты «х» двух точек (в том же порядке): 1 и 3, поэтому вертикальное расстояние: 3 — 1 = 2.
-
4
Разделите вертикальное расстояние на горизонтальное, чтобы найти угловой коэффициент. Найденные значение подставьте в формулу: угловой коэффициент = вертикальное расстояние / горизонтальное расстояние.
- Пример 2. k = -6/2 = -3.
-
5
Запишите линейную функцию. Ее график представляет собой прямую. Линейная функция имеет вид у = kх + b, где k – угловой коэффициент, b – координата «у» точки пересечения с осью Y. Подставьте известное значение углового коэффициента k и координаты точки (х,у), чтобы найти b.
-
6
В функцию подставьте значение углового коэффициента и координаты точки. Вычисленное значение углового коэффициента подставьте вместо k. Координаты любой из данных точек подставьте вместо «х» и «у».
-
Пример 2. y= kх + b
k = -3, поэтому у = -3x + b
На прямой лежит точка А (1,2), поэтому 2 = -3*1 + b.
-
Пример 2. y= kх + b
-
7
Найдите значение b. В уравнении b является единственной переменной, которую нужно обособить и найти ее значение. Напомним, что координата «х» точки пересечения всегда равна 0.
-
Пример 2. 2 = -3*1 + b
2 = -3 + b
5 = b
Координаты точки пересечения прямой с осью Y равны (0,5).
Реклама
-
Пример 2. 2 = -3*1 + b
-
1
Запишите уравнение прямой. Если дано уравнение, описывающее прямую, можно найти точку ее пересечения с осью Y.
- Пример 3. Найти точку пересечения прямой, которая задана уравнением х + 4y = 16, с осью Y.
- Примечание: уравнение, приведенное в примере 3, описывает прямую. В конце этого раздела приведен пример квадратного уравнения (в котором переменная возводится в квадрат).
-
2
Вместо «х» подставьте 0. Напомним, что точка пересечения лежит на пересечении прямой и оси Y; координата «х» любой точки, лежащей на оси Y, равна 0, поэтому координата «х» точки пересечения всегда равна 0 (х = 0). Подставьте х = 0 в уравнение прямой.
-
Пример 3. x + 4y = 16
х = 0
0 + 4y = 16
4y = 16
-
Пример 3. x + 4y = 16
-
3
Найдите «у». Так вы вычислите координату «у» точки пересечения с осью Y.
-
Пример 3. 4y = 16
у = 4
Координаты точки пересечения прямой с осью Y равны (0,4).
-
Пример 3. 4y = 16
-
4
Проверьте ответ, построив график (если хотите). График постройте как можно более точно. Точка, в которой прямая пересекает ось Y, является точкой пересечения.
-
5
Найдите точку пересечения в случае квадратного уравнения. Переменная (в большинстве случаев «х») в квадратном уравнении возводится в квадрат. В квадратное уравнение также подставляется х = 0, но имейте в виду, что квадратное уравнение описывает параболу, которая может пересекать ось Y в одной или двух точках или вообще не пересекать ось ординат. Это значит, что задача будет иметь 1 или 2 решения или вообще не иметь решений.
Реклама
Советы
- В случае более сложного уравнения постарайтесь обособить члены с переменной «у» на одной стороне уравнения.
- В некоторых странах в уравнении y = kx + b переменные k и b обозначаются по-другому.[1]
Это не меняет значения линейной функции. - Вычисляя угловой коэффициент, вычитайте координаты «х» и координаты «у» в любом порядке, но если какая-то точка считается первой, то и ее координаты должны считаться первыми.[2]
Например, даны координаты двух точек: (1,12) и (3, 7). Угловой коэффициент вычисляется двумя способами:
Реклама
Похожие статьи
Об этой статье
Эту страницу просматривали 50 796 раз.