Как найти координаты перпендикуляра опущенного на плоскость

Уравнение перпендикуляра опущенного из вершины на плоскость

Прямая и плоскость

Даны канонические уравнения прямой

Пример. Найти проекцию точки А (2; –1; 3) на плоскость x + 2 y – z – 3 =0.

Решение. Проекцию точки А на плоскость найдем как точку пересечения плоскости перпендикуляром, опущенным из точки А на данную плоскость. Составим уравнение перпендикуляра, опущенного из точки А (2; –1; 3) на плоскость x + 2 y – z – 3 = 0:

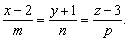
Из условия перпендикулярности прямой и плоскости имеем ,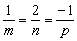

т.е. m = 1, n = 2, p = –1. Уравнения перпендикуляра примут вид

.

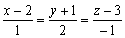
Чтобы найти точку пересечения прямой и плоскости, нужно решить систему из уравнений прямой и плоскости:

или или

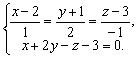
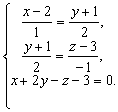
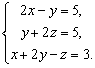
Решая указанную систему, получим координаты проекции точки А на данную плоскость: (3; 1; 2).

Расстояние от точки до плоскости

Формула для вычисления расстояния от точки до плоскости

Если задано уравнение плоскости A x + B y + C z + D = 0 , то расстояние от точки M(M _x , M _y , M _z ) до плоскости можно найти, используя следующую формулу:

d =	|A·M x + B·M y + C·M z + D|
√ A 2 + B 2 + C 2

Примеры задач на вычисление расстояния от точки до плоскости

Решение. Подставим в формулу коэффициенты плоскости и координаты точки

d = |2·0 + 4·3 + (-4)·6 — 6| √ 4 + 16 + 16 = |0 + 12 — 24 — 6| √ 36 = |-18| 6 = 3

Ответ: расстояние от точки до плоскости равно 3.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Уравнение перпендикуляра опущенного из вершины на плоскость

Расстояние от точки до плоскости .

Расстояние от произвольной точки М₀(х₀, у₀, z ₀ ) до плоскости Ах+Ву+С z + D =0 равно:

Пример. Найти уравнение плоскости, зная, что точка Р(4; -3; 12) – основание перпендикуляра, опущенного из начала координат на эту плоскость.

Таким образом, A = 4/13; B = -3/13; C = 12/13, воспользуемся формулой:

Пример. Найти уравнение плоскости, проходящей через две точки P (2; 0; -1) и

Q (1; -1; 3) перпендикулярно плоскости 3х + 2у – z + 5 = 0.

Вектор нормали к плоскости 3х + 2у – z + 5 = 0 параллелен искомой плоскости.

Пример. Найти уравнение плоскости, проходящей через точки А(2, -1, 4) и

В(3, 2, -1) перпендикулярно плоскости х + у + 2 z – 3 = 0.

Искомое уравнение плоскости имеет вид: Ax + By + Cz + D = 0, вектор нормали к этой плоскости ( A , B , C ). Вектор (1, 3, -5) принадлежит плоскости. Заданная нам плоскость, перпендикулярная искомой имеет вектор нормали (1, 1, 2). Т.к. точки А и В принадлежат обеим плоскостям, а плоскости взаимно перпендикулярны, то

Таким образом, вектор нормали (11, -7, -2). Т.к. точка А принадлежит искомой плоскости, то ее координаты должны удовлетворять уравнению этой плоскости, т.е. 11 × 2 + 7 × 1 — 2 × 4 + D = 0; D = -21.

Итого, получаем уравнение плоскости: 11 x — 7 y – 2 z – 21 = 0.

Пример. Найти уравнение плоскости, зная, что точка Р(4, -3, 12) – основание перпендикуляра, опущенного из начала координат на эту плоскость.

Находим координаты вектора нормали = (4, -3, 12). Искомое уравнение плоскости имеет вид: 4 x – 3 y + 12 z + D = 0. Для нахождения коэффициента D подставим в уравнение координаты точки Р:

16 + 9 + 144 + D = 0

Итого, получаем искомое уравнение: 4 x – 3 y + 12 z – 169 = 0

Пример. Даны координаты вершин пирамиды А₁(1; 0; 3), A ₂ (2; -1; 3), A ₃ (2; 1; 1),

Сначала найдем вектор нормали к грани А₁А₂А₃ как векторное произведение векторов и.

= (2-1 ; 1-0; 1-3) = (1; 1; -2);

Найдем угол между вектором нормали и вектором .

-4 – 4 = -8.

Искомый угол g между вектором и плоскостью будет равен g = 90 0 — b .

5) Найти объем пирамиды.

(ед 3 ).

Воспользуемся формулой уравнения плоскости, проходящей через три точки.

2 x + 2 y + 2 z – 8 = 0

При использовании компьютерной версии “Курса высшей математики” можно запустить программу, которая решит рассмотренный выше пример для любых координат вершин пирамиды.

Угол между плоскостями.

Угол между двумя плоскостями в пространстве j связан с углом между нормалями к этим плоскостям j ₁ соотношением: j = j ₁ или j = 180 0 — j ₁ , т.е.

cos j = ± cos j ₁ .

Определим угол j ₁ . Известно, что плоскости могут быть заданы соотношениями:

, где

( A ₁ , B ₁ , C ₁ ), ( A ₂ , B ₂ , C ₂ ). Угол между векторами нормали найдем из их скалярного произведения:

.

Таким образом, угол между плоскостями находится по формуле:

Выбор знака косинуса зависит от того, какой угол между плоскостями следует найти – острый, или смежный с ним тупой.

Условия параллельности и перпендикулярности

На основе полученной выше формулы для нахождения угла между плоскостями можно найти условия параллельности и перпендикулярности плоскостей.

Для того, чтобы плоскости были перпендикулярны необходимо и достаточно, чтобы косинус угла между плоскостями равнялся нулю. Это условие выполняется, если:

.

Плоскости параллельны, векторы нормалей коллинеарны: ïï .Это условие выполняется, если: .

Каноническое уравнение перпендикуляра на плоскость

Прямая и плоскость

Даны канонические уравнения прямой

Пример. Найти проекцию точки А (2; –1; 3) на плоскость x + 2 y – z – 3 =0.

Решение. Проекцию точки А на плоскость найдем как точку пересечения плоскости перпендикуляром, опущенным из точки А на данную плоскость. Составим уравнение перпендикуляра, опущенного из точки А (2; –1; 3) на плоскость x + 2 y – z – 3 = 0:

Из условия перпендикулярности прямой и плоскости имеем ,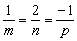

т.е. m = 1, n = 2, p = –1. Уравнения перпендикуляра примут вид

.

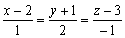
Чтобы найти точку пересечения прямой и плоскости, нужно решить систему из уравнений прямой и плоскости:

или или

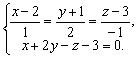
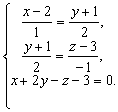
Решая указанную систему, получим координаты проекции точки А на данную плоскость: (3; 1; 2).

Уравнение прямой, проходящей через данную точку и перпендикулярной данной плоскости онлайн

С помощю этого онлайн калькулятора можно построить уравнение прямой, проходящей через данную точку и перпендикуляной данной плоскости. Дается подробное решение с пояснениями. Для построения уравнения прямой введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Уравнение прямой, проходящей через данную точку и перпендикулярной данной плоскости

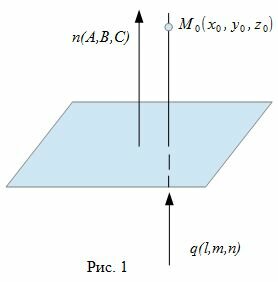
Наша цель построить уравнение прямой, проходящей через данную точку M₀ и перпендикулярной к данной плоскости Ax+By+Cz+D=0.

Общее уравнение плоскости имеет вид:

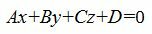(1)

где n(A,B,C)− называется нормальным вектором плоскости.

Уравнение прямой, проходящей через точку M₀(x₀, y₀, z₀) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:

(2)

Для того, чтобы прямая (2) была ортогональна плоскости (1), направляющий вектор q(l, m, n) прямой (2) должен быть коллинеарным нормальному вектору n(A,B,C) плоскости (1)(Рис. 1). Следовательно, в качестве направляющего вектора прямой (2) можно взять нормальный вектор плоскости (1) .

Таким образом, уравнение прямой, проходящей через точку M₀(x₀, y₀, z₀) и ортогональный плоскости (1) имеет следующий вид:

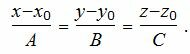(3)

Пример 1. Построить прямую, проходящую через точку M₀(5, -4, 4) и перпендикулярной плоскости

Общее уравнение плоскости имеет вид (1), где :

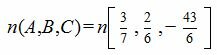(4)

Подставляя координаты точки M₀(5, -4, 4) и координаты нормального вектора плоскости (4) в (3), получим:

Перпендикулярные плоскости, условие перпендикулярности плоскостей

Данная статья посвящена перпендикулярным плоскостям. Будут даны определения, обозначения вместе с примерами. Будет сформулирован признак перпендикулярности плоскостей и условие, при котором он выполним. Будут рассмотрены решения подобных задач на примерах.

Перпендикулярные плоскости – основные сведения

При наличии угла между пересекающимися прямыми можно говорить об определении перпендикулярных плоскостей.

При условии, что угол между перпендикулярными прямыми равен 90 градусов, их называют перпендикулярными.

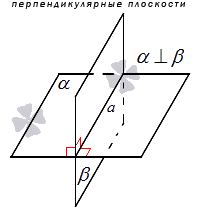
Обозначение перпендикулярности принято писать знаком « ⊥ ». Если в условии дано, что плоскости α и β перпендикулярные, тогда запись принимает вид α ⊥ β . На рисунке ниже показано подробно.

Когда в улови дано, что плоскость α и β перпендикулярны, это значит, что α перпендикулярна β и наоборот. Такие плоскости называют взаимно перпендикулярными. Например, стена и потолок в комнате являются взаимно перпендикулярными, так как при пересечении дают прямой угол.

Перпендикулярность плоскостей – признак и условие перпендикулярности

На практике можно встретить задания, где необходимо определить перпендикулярность заданных плоскостей. Для начала нужно определить угол между ними. Если он равен 90 градусам, тогда они считаются перпендикулярными из определения.

Для доказательства перпендикулярности двух плоскостей применяют признак перпендикулярности двух плоскостей. Формулировка содержит понятия перпендикулярная прямая и плоскость. Напишем точное определение признака перпендикулярности в виде теоремы.

Если одна из двух заданных плоскостей пересекает прямую, перпендикулярную другой плоскости, то заданные плоскости перпендикулярны.

Доказательство имеется в учебнике по геометрии за 10 — 11 класс, где есть подробное описание. Из признака следует, что, если плоскость перпендикулярна линии пересечения двух заданных плоскостей, то она перпендикулярна к каждой из этих плоскостей.

Существует необходимое и достаточное условия для доказательства. Рассмотрим их для перпендикулярности двух заданных плоскостей, которое применяется в качестве проверки их перпендикулярности, находящихся в прямоугольной системе координат трехмерного пространства. Чтобы доказательство имело силу, необходимо применить определение нормального вектора плоскости, который способствует доказать необходимое и достаточное условие перпендикулярности плоскостей.

Для того, чтобы перпендикулярность пересекающихся плоскостей была явной, необходимо и достаточно, чтобы нормальные векторы заданных плоскостей пересекались под прямым углом.

Пусть в трехмерном пространстве задана прямоугольная система координат. Если имеем n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) , являющимися нормальными векторами заданных плоскостей α и β , то необходимым и достаточным условием перпендикулярности векторов n 1 → и n 2 → примет вид

n 1 → , n 2 → = 0 ⇔ A 1 · A 2 + B 1 · B 2 + C 1 · C 2 = 0

Отсюда получаем, что n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) — нормальные векторы заданных плоскостей, а для действительности перпендикулярности α и β необходимо и достаточно, чтобы скалярное произведение векторов n 1 → и n 2 → было равным нулю, а значит, принимало вид n 1 → , n 2 → = 0 ⇔ A 1 · A 2 + B 1 · B 2 + C 1 · C 2 = 0 .

Рассмотрим подробнее на примерах.

Определить перпендикулярность плоскостей, заданных в прямоугольной системе координат O x y z трехмерно пространства, заданного уравнениями x — 3 y — 4 = 0 и x 2 3 + y — 2 + z 4 5 = 1 ?

Для нахождения ответа на вопрос о перпендикулярности для начал необходимо найти координаты нормальных векторов заданных плоскостей, после чего можно будет выполнить проверку на перпендикулярность.

x — 3 y — 4 = 0 является общим уравнением плоскости, из которого можно сразу преобразовать координаты нормального вектора, равные n 1 → = ( 1 , — 3 , 0 ) .

Для определения координаты нормального вектора плоскости x 2 3 + y — 2 + z 4 5 = 1 перейдем от уравнения плоскости в отрезках к общему.

x 2 3 + y — 2 + z 4 5 ⇔ 3 2 x — 1 2 y + 5 4 z — 1 = 0

Тогда n 2 → = 3 2 , — 1 2 , 5 4 — это координаты нормального вектора плоскости x 2 3 + y — 2 + z 4 5 = 1 .

Перейдем к вычислению скалярного произведения векторов n 1 → = ( 1 , — 3 , 0 ) и n 2 → = 3 2 , — 1 2 , 5 4 .

Получим, что n 1 → , n 2 → = 1 · 3 2 + ( — 3 ) · — 1 2 + 0 · 5 4 = 3 .

Видим, что оно не равно нулю, значит, что заданные векторы не перпендикулярны. Отсюда следует, что плоскости также не перпендикулярны. Условие не выполнено.

Ответ: плоскости не перпендикулярны.

Прямоугольная система координат O x y z имеет четыре точки с координатами A — 15 4 , — 7 8 , 1 , B 17 8 , 5 16 , 0 , C 0 , 0 , 3 7 , D — 1 , 0 , 0 . Проверить, перпендикулярны ли плоскости А В С и A B D .

Для начала необходимо рассчитать скалярное произведение векторов данных плоскостей. Если оно равно нулю, только в этом случае можно считать, что они перпендикулярны. Находим координаты нормальных векторов n 1 → и n 2 → плоскостей А В С и A B D .

Из заданных координат точек вычислим координаты векторов A B → , A C → , A D → . Получаем, что:

A B → = 47 8 , 19 16 , — 1 , A C → = 15 4 , 7 8 , — 4 7 , A D → = 11 4 , 7 8 , — 1 .

Нормальный вектор плоскости А В С является векторным произведением векторов A B → и A C → , а для A B D векторное произведение A B → и A D → . Отсюда получим, что

n 1 → = A B → × A C → = i → j → k → 47 8 19 16 — 1 15 4 7 8 — 4 7 = 11 56 · i → — 11 28 · j → + 11 16 · k → ⇔ n 1 → = 11 56 , — 11 28 , 11 16 n 2 → = A B → × A D → = i → j → k → 47 8 19 16 — 1 11 4 7 8 — 1 = — 5 16 · i → + 25 8 · j → + 15 8 · k → ⇔ n 2 → = — 5 16 , 25 8 , 15 8

Приступим к нахождению скалярного произведения n 1 → = 11 56 , — 11 28 , 11 16 и n 2 → = — 5 16 , 25 8 , 15 8 .

Получим: n 1 → , n 2 → = 11 56 · — 5 16 + — 11 28 · 25 8 + 11 16 · 15 8 = 0 .

Если оно равно нулю, значит векторы плоскостей А В С и A B D перпендикулярны, тогда и сами плоскости перпендикулярны.

Ответ: плоскости перпендикулярны.

Можно было подойти к решению иначе и задействовать уравнения плоскостей А В С и A B D . После нахождения координат нормальных векторов данных плоскостей можно было бы проверить на выполнимость условие перпендикулярности нормальных векторов плоскостей.

Министерство
образования и науки Российской Федерации

Калужский
филиал федерального государственного
бюджетного образовательного учреждения
высшего профессионального образования

«Московский
государственный технический университет

имени
Н.Э. Баумана»

кафедра

Высшая
математика

Учебное пособие по курсу аналитической геометрии «Решение типовых задач»

Составил:
Влайков Н.Д.

Рецензент:
к.ф.-м.н. Савотин А.И.

г.
Калуга, 2011 г.

Содержание.

1. Уравнение
   прямой и плоскости в пространстве
   стр. 2

2. Уравнения
   кривых второго порядка
   стр.7

3. Матричные
   уравнения
   стр. 8

4. Решение
   СЛАУ
   стр. 10

5. Задачи
   для самостоятельного решения
   стр. 14

6. Список
   рекомендуемой литературы
   стр. 16

1. Уравнение плоскости и прямой в пространстве.

Даны
координаты четырех точек в пространстве
.

Найти:

1. Уравнение
   плоскости, проходящей через точки
   .

2. Уравнение
   и длину перпендикуляра, опущенного из
   т.
   на
   плоскость, проходящую через точки
   .

3. Расстояние
   от т.
   
   до прямой, проходящей через точки
   .

4. Точку,
   симметричную точке
   ,
   относительно прямой, проходящей через
   точки
   .

5. Выполнить
   чертеж.

Решение.

1.1.
Уравнение плоскости, проходящей через
три заданные точки,

,

имеет
вид:

.
Для наших точек:
.
Вычислим определитель:
следовательно,
уравнение искомой плоскости
.

1.2.
Составим уравнение перпендикуляра,
опущенного из т.
на
плоскость, проходящую через точки
.
Запишем это уравнение в каноническом
виде:
,
где
—
координаты точки, принадлежащей прямой,
а в знаменателях записаны соответствующие
координаты направляющего вектора
.
Координаты точки,
принадлежащей прямой, нам известны. В
качестве направляющего вектора, возьмем
нормальный вектор плоскости. Т.е.
_.

Запишем
уравнение перпендикуляра:
.

Длина
перпендикуляра может быть найдена как
расстояние от т.
до плоскости

по формуле:
,
где
,,—
координаты нормального вектора плоскости,
а

— координаты точки
.

.

1.3. Расстояние от т. До прямой, проходящей через точки .

а)
Общий вид уравнения прямой проходящей
через две заданные точки
,имеет
вид:
.
Для наших точек:

;
;

б)
Теперь найдем расстояние от точки
до
прямой
.
Для этого составим уравнение плоскости

,
проходящей через т.
,
перпендикулярно прямой
.
Уравнение плоскости, проходящей через
т.
,
с нормальным вектором

имеет вид:
.

Координаты
т.
известны,
а в качестве нормального вектора можно
выбрать направляющий вектор прямой
:

.
Подставим координаты в уравнение:
;
раскрыв скобки и приведя подобные
слагаемые получим уравнение плоскости

.

в)
Найдем координаты точки
—
точки пересечения прямой
и
плоскости
.
Точка
—
будет являться основанием перпендикуляра
опущенного из т.

на прямую
.
Т.к. т.

принадлежит и прямой и плоскости, ее
координаты должны удовлетворять двум
уравнениям, следовательно, координаты
можно найти, решив систему:

_;

Для
этого перейдем к параметрическому
уравнению прямой
:

;
выразим

через
параметр
:.

Подставим
в уравнение плоскости

и решим его:
;

.
Найдем

из системы:
;;.

Следовательно,
координаты т.
.

г)
Расстояние от т.

до прямой, проходящей через точки

можно найти как расстояние между точками

и

по формуле:
.

.

1.4.
Найдем координаты т.
,
симметричной точке
,
относительно прямой, проходящей через
точки
.
Координаты точки

можно найти из условия: т.
—
середина отрезка

(т.к. прямая
).
Координаты середины отрезка можно найти
по формулам:
,

,

.
Следовательно, координаты т.

можно
найти так:
,

,

.

Т.е.

,

,

.

.

1.5.
Построим несколько поясняющих чертежей:

1.5.1.
Построим
точки
.
Для примера построим т.

Рис
1.1 Точка

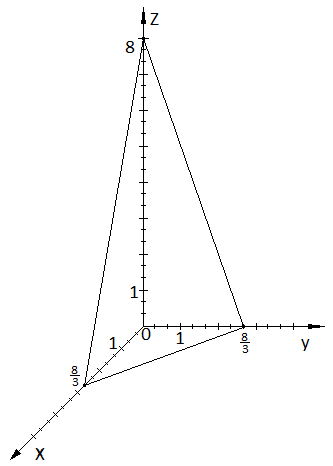
1.5.2.
На рис 1.2 построим плоскость
,
приведя общее уравнение к уравнению
плоскости в отрезках:
;

;

Рис
1.2 плоскость
.

1.5.3.
Изобразим прямую
:

Рис
1.3 прямая

1.5.4.
Построим точку
:

Рис
1.4 Точка
.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Условие

Решение

Написать комментарий

Найдем расстояние От данной точки до данной плоскости

. (1)

Искомое расстояние мы найдем по формуле

(2)

Где — координаты основания перпендикуляра, опущенного из точки на плоскость (1). Найдем координаты .

Во-первых, они удовлетворяют уравнению (1), т. к. точка лежит на этой плоскости:

(3)

Во-вторых, вектор по построению перпендикулярен к плоскости (1) и, значит, коллинеарен с нормальным вектором плоскости (1). Следовательно, их соответственные координаты пропорциональны

(4)

Выразим из (4) через

(5)

Перепишем равенства (5) в виде

(6)

Подставим эти выражения в (3). Получим

(7)

Преобразуем его относительно , будем иметь

(8)

Подставим выражения (5) в (2)

(9)

Далее в (9) подставим выражение (8), получим

Или

(10)

Следовательно, чтобы найти расстояние от данной точки до данной плоскости (1), достаточно подставить в левую часть уравнения (1) координаты данной точки , результат разделить на квадратный корень из суммы квадратов коэффициентов уравнения (1) при текущих координатах и взять абсолютную величину частного.

< Предыдущая		Следующая >