Как найти координаты по азимуту

расчёт координат от точки по азимуту?

//$lat - текущая широта, $lng - текущая долгота
//$dist - расстояние между искомыми точками
//$ang - азимут на искомую точку

$newlat=sin($lat * PI / 180)*cos($dist * PI / 180)+cos($lat * PI / 180)*sin($dist * PI / 180)*cos($ang * PI / 180);
$newlat=$lat+(asin($newlat));

$newlng=sin($dist * PI / 180)*sin($ang * PI / 180)/(cos($lat * PI / 180)*cos($dist * PI / 180)-sin($lat * PI / 180)*sin($dist * PI / 180)*cos($ang * PI / 180));
$newlng=$lng+(atan($newlng));

LAT1 = LAT + L * COS(AZIMUT * PI / 180) / (6371000 * PI / 180)
LON1 = LON + L * SIN(AZIMUT * PI / 180) / COS(LAT * PI / 180) / (6371000 * PI / 180)

$phi = 62.8356; $lyambda = 61.2193; $A = 328.7625; $L = 1008.18; $R = 6371; $s = $L/$R;

$grad = pi()/180;
$phi1 = asin(cos($s*$grad)*sin($phi*$grad)+sin($s*$grad)*cos($phi*$grad)*cos($a*$grad)*180/pi();
echo $phi1;

***62.970788480261***

$lyambda1 = $lyambda + atan(sin($s*$grad)*sin($A*$grad)/(cos($s*$grad)*cos($phi*$grad)-sin($s*$grad)*sin($phi*$grad)*cos($A*$grad)))*180/pi();
echo $lyambda1;

***61.038719442206***

Географические
координаты точки А, широту и долготу
определяют, пользуясь минутными шкалами
рамок карты. Из точки А опускают
перпендикуляры на рамки карты и в местах
пересечения со шкалой берут отсчеты:
западная или восточная – широта, северная
или южная – долгота ( см. рисунок).

Задание:
самостоятельно определить географические
координаты точки Б.

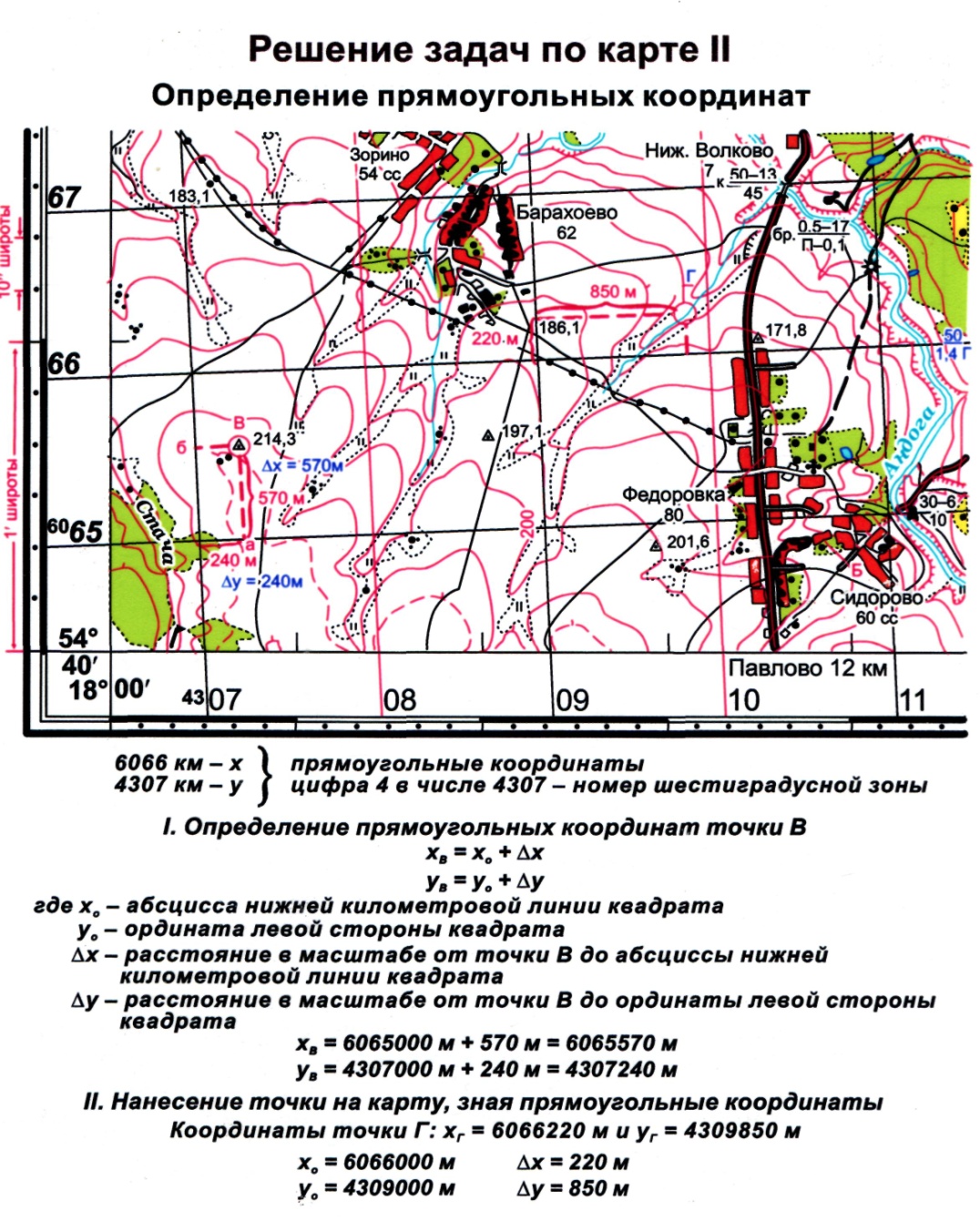
рис.

Прямоугольные
координаты точки В х и уопределяют
относительно километровых линий сетки.
Для этого измеряют расстояние по
перпендикулярам до ближайших километровых
линий.

Задание:
Самостоятельно определить координаты
точки Г.

Расстояние
между точками определяют с помощью
линейного или поперечного масштаба.
Криволинейные отрезки измеряют
курвиметром.

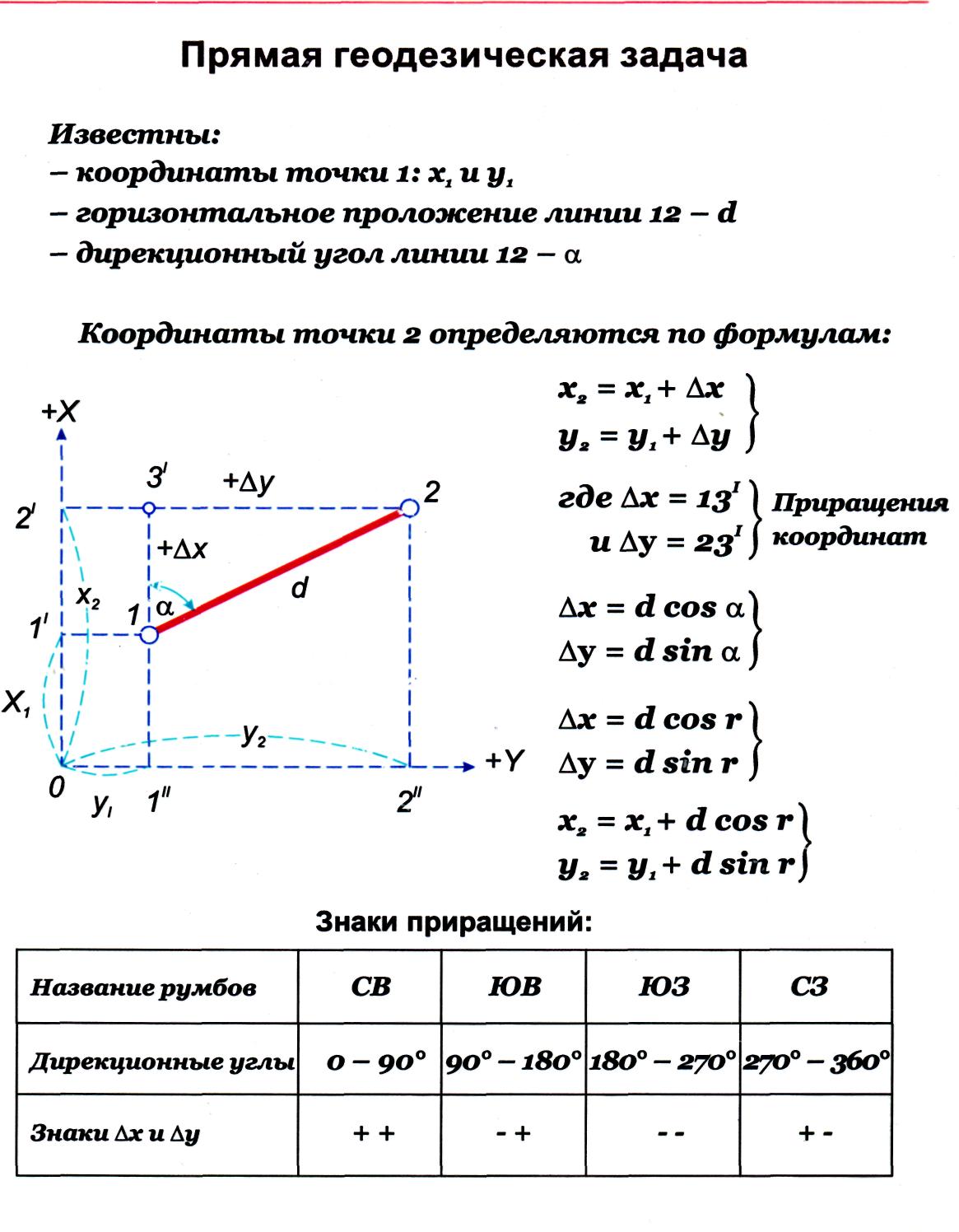
Тема 3. Прямая и обратная геодезическая задача.

При
производстве строительных работ
создается разбивочная основа в виде
строительной сетки. Пункт Государственной
геодезической сети выносится на
территорию строительства для обеспечения
исходными данными всех геодезических
работ. Решение прямой геодезической
задачи позволяет определить координаты
всех точек, расположенных в зоне
строительства.

В
геодезии принята система плос­ких
прямоугольных координат, в которой
относительно оси XX,
совпадающей
с направлением меридиана, и оси YY,
перпендику­лярной
к оси XX,
определяют
положение каждой точки, т. е. её координаты
х
и у; при
этом счет четвертей идет по ходу часовой
стрелки,
согласно возрастанию азимутов и
дирекционных углов .

При
составлении планов ситуацию накладывают
от опорных точек
и линий, их соединяющих. Поэтому на
бумагу сначала на­носят
опорные точки по их координатам. Так
как число этих точек
весьма велико, то при геодезических
работах часто решают прямую
задачу на координаты. Она состоит в том,
что по извест­ным
координатам данной точки, а также
дирекционному углу и горизонтальному
проложению линии от этой точки до
определяе­мой вычисляют координаты
определяемой точки.

ПРИМЕР.

Решить
прямую геодезическую задачу, т.е Пример

определить
прямоугольные координаты точки 2 через
координаты точки 1
по следующим данным:

Кординаты
точки 1 — X,
= 4250 м. У,=6730 м;

Расстояние между
точками d =120,10
м; направление линии, т.е
дирекционный угол 48°30′ =r.

Для определения
координат точки 2 сначала нужно найти
приращение координат –ΔХ и ΔУ,затем
сами координаты Х₂;У_2
.

Решение:

1.Определяем приращение
координат ΔХ =d^.
cosr
= 120,10^.
0,6626 =79,51 м

ΔУ= d^.
sinr
=12,10 ^.
0,7490 =89,95 м

х

ΔУ

х₂ 2

ΔХ

r d

х₁ 1

0 у₁ у₂ у

2. Определяем
координаты точки 2

Х₂=
Х₁+ΔХ
= 4250 +79,51 + 4329,51 м

У₂=У₁+
ΔУ =6730 + 89,95 + 6819,95 м

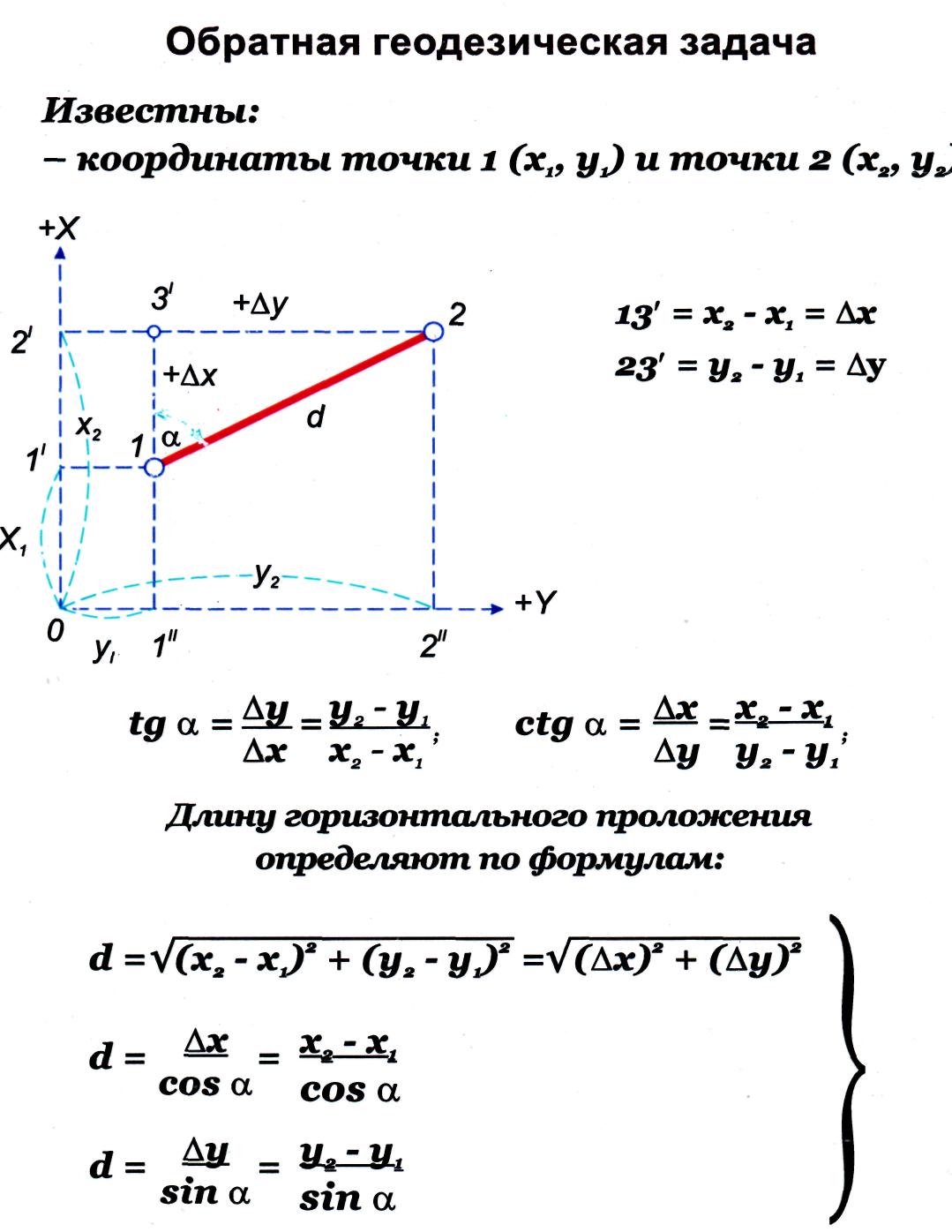
В практике прикладной
геодезии для нужд проектирования и
выноса проекта на местность приходиться
определять значения дирекционного угла
и длинны стороны по известным координатам
её конечных точек. Это и составляет
сущность решения обратной геодезической
задачи.

Решение обратной
геодезической задачи состоит в том,
что, зная координаты опорных точек,
можно вычислить дирекционный угол и
расстояние между данными точками.

Пример.

Решить
обратную геодезическую задачу, т.е.
найти расстояниеd
между точками и направление этой линии
( румб, азимут), если координаты точки1
Х₁=
320,5 м, У₁
= 780,2 м; координаты т очки 2 Х₂=
230,7 м, У₂
=900,1 м.

Решение.

1.
Определяем приращение координатΔХ =
Х₂-Х₁
= 230,7 -320,5 =
-89,8 м

ΔХ
= У₂
–У₁
=900,1 – 780,2 = 119,9 м

Знаки
приращений говорят, что линия расположена
во второй четверти (ЮВ)

Знаки
приращения координат можно определить
по следующей схеме:

СЗ
С х

СВ

З +ΔХ
— ΔУ +ΔХ + ΔУ В

у -ΔХ
— ΔУ -ΔХ + ΔУ у

ЮЗ ЮВ

Ю
х

Они
зависят от четверти, в которой расположена
линия.

2.
Величина румба определяется по формуле

tg
r=

=

= 1, 3352

ctgr
=

=

=
0,74,89

По
таблицам Брадиса находим величину румба
— 53⁰ 10ʹ

3.
Расстояние между точками найдем по
теореме Пифагора:

d=


ΔХ²+
ΔУ² =

89,8²
+ 119,9²
=
22440,05
= 149,8 м

Контрольные
вопросы:

1.
Какие знаки у приращения координат ΔХ
и ΔУ, если наименование румба ЮЗ?

а)
–ΔХ, –ΔУ; б)+ ΔХ, +ΔУ; в)–ΔХ,+ΔУ; г))+
ΔХ,–ΔУ;

2.
Найдите координаты точки 2, если координаты
точки 1 Х= 10, У=5 и приращение ΔХ = 20, ΔУ
=15.

а)
30, 20; б) 20, 30; в) 20, 40; г) 30, 40;

3.
Решить обратную геодезическую задачу:
найти расстояние между двумя точками
и румб линии, если координаты начала и
конца линии Х₁=
320,5 м, У₁ =
780,2 м; Х₂ 230,7
м,

У₂
= 900,1 м.

а);
160,7 м, 60⁰ 20ʹ; б)149,8 м, 53⁰ 10ʹ; в) 120, 9 м, 58⁰
45ʹ; г) 456,7м, 45⁰ 15ʹ;

4.
Решить прямую геодезическую задачу:
определить прямоугольные координаты
точки 2 через координаты точки 1 по
следующим данным: Х₁
= 4250м, У₁=
6730м, расстояние d – 120, 1 м, дирекционный
угол — 48⁰30ʹ.

а)
Х₂
=2570 м,У₂
=4820м; б)Х₂
=357 м,У₂
=724 м; в) Х₂
=695м, У₂₌
611 м; г) Х₂
=4329,5 м, У₂
= 6819,9 м.

Тема:
Ориентирование

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

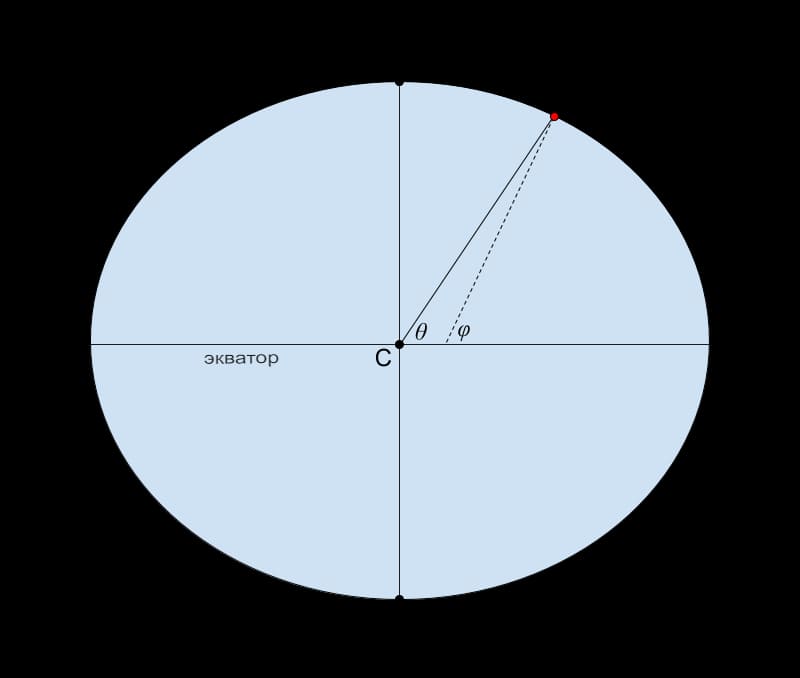
Первое, что делает калькулятор, — это преобразует обе точки, точку A и точку B, в декартовы ( x, y, z  ) координаты. Это осложняется тем, что Земля не является идеальной сферой. Из-за вращения Земля выпячивается на экваторе, образуя форму, известную как сплюснутый сфероид . Расстояние между полюсами равно 6357 км, а расстояние диаметра, проходящего через экватор, равно 6378 км. Рассмотрим эту диаграмму, на которой выпуклость преувеличена для иллюстрации:

Здесь X — точка на поверхности Земли, N — северный полюс, S — южный полюс, C — центр Земли. Экватор представлен горизонтальной линией, проходящей через С. Представьте , что вы стоите в точке X. Пунктирная линия, касательная к Земле, указывает на ваш местный горизонт.

Перпендикулярно вашему горизонту проходит еще одна пунктирная линия, уходящая в землю. Там, где эта пунктирная линия касается плоскости земного экватора, вы видите угол, отмеченный φ (греческая буква phi ). Этот угол называется геодезической широтой . Именно такую ​​широту сообщает GPS.

Действительно, геодезическая широта — это классический вид широты, используемый с древних времен. Грубо говоря, это широта, измеренная астрономами: это угол Северного небесного полюса (точки на небе рядом с Полярной звездой) над вашим местным горизонтом. Если вы стоите на северном полюсе Земли, Полярная звезда будет прямо вверху или на 90 градусов выше горизонта. Точно так же, если вы стоите на экваторе, Полярная звезда будет на горизонте или на 0 градусов выше горизонта. Таким образом, геодезическую широту может измерить непосредственно любой моряк при ясном ночном небе.

Однако, чтобы вычислить декартовы координаты X относительно центра C Земли, калькулятору нужна геоцентрическая широта , обозначенная на диаграмме θ (греческая буква theta ). Это угол между экватором и X , как видно из C. Преобразование основано на стандарте Всемирной геодезической системы WGS 84.

Точно так же и расстояние от центра Земли до данной точки на ее поверхности является переменным. Функция вычисляет это расстояние как функцию геодезической широты, также используя WGS 84.

Интересно отметить, что геоцентрическая и геодезическая широты одинаковы, когда вы находитесь на экваторе: обе равны 0 градусов. Оба вида широты также одинаковы, если вы находитесь на любом из полюсов Земли: +90 или -90 градусов. Но они расходятся в разной степени в других местах на Земле.

Калькулятор вычисления декартовых координат точки с учетом ее геодезической широты, долготы и высоты. Эта функция также вычисляет вектор нормали в заданной точке, то есть направление вверх, перпендикулярное горизонту наблюдателя, для правильной поправки на высоту над средним уровнем моря. Результирующие компоненты вектора все выражены в метрах.

Для завершения вычислений калькулятор использует хитрость. Он поворачивает систему координат так, что точка наблюдения (точка A) находится на условном экваторе и нулевом меридиане. Другими словами, представьте, что вы вращаете глобус, который держите в руках, так, что ваша точка наблюдения теперь находится на экваторе и обращена прямо к вам. Координаты теперь идеально расположены для расчета углов азимута и высоты, как их видит наблюдатель в точке А:

• Ось X указывает прямо вверх (от центра земного шара).
• Ось Y указывает точно на восток.
• Ось Z указывает точно на север.

После поворота системы координат вы можете провести линию от точки А на повернутом глобусе к точке Б на том же повернутом глобусе через трехмерное пространство. Эта линия обычно проходит через Землю, предполагая, что и A, и B находятся на поверхности Земли или вблизи нее. Используя комбинацию функций тригонометрии и скалярных произведений векторов, калькулятор определяет азимутальный угол и угол высоты. Он использует формулу Пифагора для определения расстояния по прямой между точками.

Этот калькулятор азимута позволит вам рассчитать азимут по широте и долготе. Он подскажет вам, в каком направлении вам нужно указать компас, и каково кратчайшее расстояние между двумя точками с известными географическими координатами. Эта статья включает в себя краткое объяснение используемых нами формул — они могут оказаться полезными, если вы планируете определять азимут вручную.