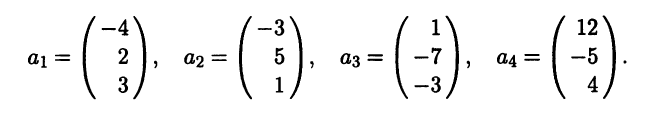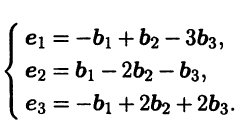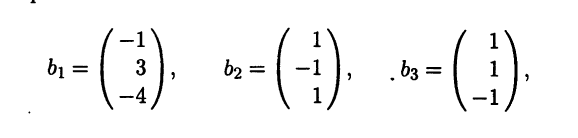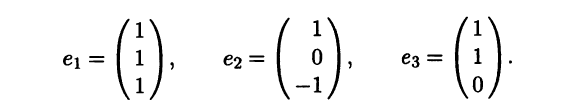Матрица перехода
3 июля 2022
Матрица перехода — это просто квадратная матрица, в столбцах которой записаны координаты новых базисных векторов. У такой матрицы много важных свойств, которые сформулированы и доказаны в первой части урока — теоретической. Этой теории хватит для любого экзамена или коллоквиума.
Вторая часть урока — практическая. В ней разобраны все типовые задачи, которые встречаются на контрольных, зачётах и экзаменах.
Содержание
- Определение матрицы перехода
- Свойства матрицы перехода
- Теорема о замене координат
- Задача 1. Базисы трёхмерного пространства
- Задача 2. Базисы в поле вычетов
- Задача 3. Пространство многочленов
- Задача 4. Матрица перехода при симметрии
- Задача 5. Матрица поворота
Если вы учитесь в серьёзном университете (МГУ, Бауманка и т.д.), то обязательно изучите первые три пункта. А если вам нужны только задачи, сразу переходите к пункта 4—6.
1. Определение матрицы перехода
Пусть дано $n$-мерное линейное пространство $L$. Пусть также $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ и $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ — два базиса в $L$.
Определение. Матрица перехода ${{T}_{eto f}}$ от базиса $e=left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ к базису $f=left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ — это квадратная матрица порядка $n$, где по столбцам записаны координаты нового базиса $f$ в старом базисе $e$:
[{{T}_{eto f}}=left[ begin{array}{c|c|c|c}{{t}_{1,1}} & {{t}_{2,1}} & cdots & {{t}_{n,1}} \{{t}_{1,2}} & {{t}_{2,2}} & cdots & {{t}_{n,1}} \cdots & cdots & cdots & cdots \{{t}_{1,n}} & {{t}_{2,n}} & cdots & {{t}_{n,n}} \end{array} right]]
Обратите внимание на нумерацию элементов ${{t}_{i,j}}$: первый индекс обозначает номер столбца, т.е. номер нового базисного вектора, а второй отвечает за координаты этого вектора в старом базисе. Так, во втором столбце записаны координаты вектора ${{f}_{2}}$:
[{{f}_{2}}={{left[ {{t}_{2,1}},{{t}_{2,2}},ldots ,{{t}_{2,n}} right]}^{T}}]
Или, что то же самое, разложение вектора ${{f}_{2}}$ по базису $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$:
[{{f}_{2}}={{t}_{2,1}}{{e}_{1}}+{{t}_{2,2}}{{e}_{2}}+ldots +{{t}_{2,n}}{{e}_{n}}]
Да, такая нумерация не является обязательной. Но она очень распространена именно в записи матриц перехода: первый индекс отвечает за номер базисного вектора, второй — за номер координаты этого вектора.
Пример 1. В некотором базисе $e=left{ {{e}_{1}},{{e}_{2}},{{e}_{3}} right}$ векторного пространства ${{mathbb{R}}^{3}}$ даны три вектора:
[{{f}_{1}}={{left( 1,0,1 right)}^{T}},quad {{f}_{2}}={{left( 2,1,0 right)}^{T}},quad {{f}_{3}}={{left( 0,3,1 right)}^{T}}]
[begin{align}{{f}_{1}} &={{left( 1,0,1 right)}^{T}}, \ {{f}_{2}} &={{left( 2,1,0 right)}^{T}}, \ {{f}_{3}} &={{left( 0,3,1 right)}^{T}} \ end{align}]
Убедитесь, что система векторов $f=left{ {{f}_{1}},{{f}_{2}},{{f}_{3}} right}$ образует базис в ${{mathbb{R}}^{3}}$, найдите матрицу перехода ${{T}_{eto f}}$.
Решение. Система векторов будет базисом, если эти векторы линейно независимы, а их количество совпадает с размерностью пространства. Поскольку у нас три вектора и $dim{{mathbb{R}}^{3}}=3$, осталось проверить линейную независимость. Составим матрицу из столбцов с координатами векторов ${{f}_{1}}$, ${{f}_{2}}$ и ${{f}_{3}}$:
[left[ begin{matrix}1 & 2 & 0 \ 0 & 1 & 3 \ 1 & 0 & 1 \ end{matrix} right]]
Вообще-то это и есть матрица перехода ${{T}_{eto f}}$, но сначала надо установить линейную независимость. Поэтому выполним элементарные преобразования строк:
[left[ begin{matrix} 1 & 2 & 0 \ 0 & 1 & 3 \ 1 & 0 & 1 \ end{matrix} right]begin{matrix} \ \ -1cdot left[ 1 right] \ end{matrix}sim left[ begin{array}{crc} 1 & 2 & 0 \ 0 & 1 & 3 \ 0 & -2 & 1 \ end{array} right]begin{matrix} -2cdot left[ 2 right] \ \ +2cdot left[ 2 right] \ end{matrix}sim left[ begin{array}{ccr} 1 & 0 & -6 \ 0 & 1 & 3 \ 0 & 0 & 7 \ end{array} right]]
[begin{align} & left[ begin{matrix} 1 & 2 & 0 \ 0 & 1 & 3 \ 1 & 0 & 1 \ end{matrix} right]begin{matrix} \ \ -1cdot left[ 1 right] \ end{matrix} \ & left[ begin{array}{crc} 1 & 2 & 0 \ 0 & 1 & 3 \ 0 & -2 & 1 \ end{array} right]begin{matrix} -2cdot left[ 2 right] \ \ +2cdot left[ 2 right] \ end{matrix} \ & left[ begin{array}{ccr} 1 & 0 & -6 \ 0 & 1 & 3 \ 0 & 0 & 7 \ end{array} right] \ end{align}]
Получили верхнетреугольную матрицу без нулей на главной диагонали. Ранг такой матрицы равен 3, поэтому система $left{ {{f}_{1}},{{f}_{2}},{{f}_{3}} right}$ линейно независима и образует базис. Матрица перехода от базиса $e$ к базису $f$ уже известна:
[{{T}_{eto f}}=left[ begin{matrix} 1 & 2 & 0 \ 0 & 1 & 3 \ 1 & 0 & 1 \ end{matrix} right]]
1.1. Зачем нужна матрица перехода
Матрица перехода нужна для того, чтобы компактно и наглядно выражать новый базис через старый. В самом деле, разложим векторы $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ нового базиса по старому базису $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$:
[begin{align}{{f}_{1}} &={{x}_{1,1}}{{e}_{1}}+{{x}_{2,1}}{{e}_{2}}+ldots +{{x}_{n,1}}{{e}_{n}} \ {{f}_{2}} &={{x}_{1,2}}{{e}_{1}}+{{x}_{2,2}}{{e}_{2}}+ldots +{{x}_{n,2}}{{e}_{n}} \ & cdots \ {{f}_{n}} &={{x}_{1,n}}{{e}_{1}}+{{x}_{2,n}}{{e}_{2}}+ldots +{{x}_{n,n}}{{e}_{n}} \ end{align}]
Получили систему из $n$ уравнений, которые в матричном виде можно представить так:
[left[ begin{matrix} {{f}_{1}} & cdots & {{f}_{n}} \ end{matrix} right]=left[ begin{matrix} {{e}_{1}} & cdots & {{e}_{n}} \ end{matrix} right]cdot left[ begin{matrix} {{x}_{1,1}} & cdots & {{x}_{1,n}} \ cdots & cdots & cdots \ {{x}_{n,1}} & cdots & {{x}_{n,n}} \ end{matrix} right]]
[left[ {{f}_{1}} cdots {{f}_{n}} right]=left[ {{e}_{1}} cdots {{e}_{n}} right]cdot left[ begin{matrix} {{x}_{1,1}} & cdots & {{x}_{1,n}} \ cdots & cdots & cdots \ {{x}_{n,1}} & cdots & {{x}_{n,n}} \ end{matrix} right]]
Обратите внимание: ${{f}_{1}},ldots ,{{f}_{n}}$ и ${{e}_{1}},ldots ,{{e}_{n}}$ — это именно векторы, а не числа. Такие наборы принято записывать строками — в отличие от вектор-столбцов, элементами которых как раз выступают обычные числа.
Последний множитель — это и есть матрица перехода ${{T}_{eto f}}$, поэтому всё произведение можно записать более компактно:
[left[ begin{matrix} {{f}_{1}} & cdots & {{f}_{n}} \ end{matrix} right]=left[ begin{matrix} {{e}_{1}} & cdots & {{e}_{n}} \ end{matrix} right]cdot {{T}_{eto f}}]
2. Свойства матрицы перехода
Мы разберём три простых свойства, а далее отдельным разделом будет ещё одно — уже более серьёзное.
2.1. Переход от базиса к этому же базису
Свойство 1. При переходе от базиса $e$ к этому же базису $e$ матрица перехода ${{T}_{eto e}}=E$.
Для доказательства достаточно рассмотреть формулы
[begin{align}{{f}_{1}} &={{x}_{1,1}}{{e}_{1}}+{{x}_{2,1}}{{e}_{2}}+ldots +{{x}_{n,1}}{{e}_{n}} \ {{f}_{2}} &={{x}_{1,2}}{{e}_{1}}+{{x}_{2,2}}{{e}_{2}}+ldots +{{x}_{n,2}}{{e}_{n}} \ &cdots \ {{f}_{n}} &={{x}_{1,n}}{{e}_{1}}+{{x}_{2,n}}{{e}_{2}}+ldots +{{x}_{n,n}}{{e}_{n}} \ end{align}]
А затем положить ${{f}_{1}}={{e}_{1}}$, ${{f}_{2}}={{e}_{2}}$, …, ${{f}_{n}}={{e}_{n}}$. Тогда:
[begin{align} {{f}_{1}} &={{e}_{1}}=1cdot {{e}_{1}}+0cdot {{e}_{2}}+ldots +0cdot {{e}_{n}} \ {{f}_{2}} &={{e}_{2}}=0cdot {{e}_{1}}+1cdot {{e}_{2}}+ldots +0cdot {{e}_{n}} \ &cdots \ {{f}_{n}} &={{e}_{n}}=0cdot {{e}_{1}}+0cdot {{e}_{2}}+ldots +1cdot {{e}_{n}} \ end{align}]
Указанное выражение однозначно, поскольку $e$ — базис. Следовательно, матрица перехода равна
[{{T}_{eto f}}=left[ begin{array}{c|c|c|c} 1 & 0 & cdots& 0 \ 0 & 1 & cdots& 0 \ cdots& cdots& cdots& cdots \ 0 & 0 & cdots& 1 \ end{array} right]=E]
Итак, ${{T}_{eto f}}=E$, что и требовалось доказать.
2.2. Обратный переход
Свойство 2. Если ${{T}_{eto f}}$ — матрица перехода от базиса $e$ к базису $f$, то ${{T}_{fto e}}={{left( {{T}_{eto f}} right)}^{-1}}$ матрица обратного перехода, от базиса $f$ к базису $e$.
В самом деле, базисы $e$ и $f$ связаны с матрицей перехода по формуле
[left[ {{f}_{1}},ldots ,{{f}_{n}} right]=left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot {{T}_{eto f}}]
Поскольку матрица ${{T}_{eto f}}$ невырожденная, существует обратная к ней матрица ${{left( {{T}_{eto f}} right)}^{-1}}$. Домножим на эту матрицу обе части формулы, связывающей базисы $e$ и $f$:
[left[ {{f}_{1}},ldots ,{{f}_{n}} right]cdot {{left( {{T}_{eto f}} right)}^{-1}}=left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot {{T}_{eto f}}cdot {{left( {{T}_{eto f}} right)}^{-1}}]
[begin{align}left[ {{f}_{1}},ldots ,{{f}_{n}} right] &cdot {{left( {{T}_{eto f}} right)}^{-1}}= \ &=left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot {{T}_{eto f}}cdot {{left( {{T}_{eto f}} right)}^{-1}} \ end{align}]
Упрощаем эту формулу и получаем
[left[ {{e}_{1}},ldots ,{{e}_{n}} right]=left[ {{f}_{1}},ldots ,{{f}_{n}} right]cdot {{left( {{T}_{eto f}} right)}^{-1}}]
Итак, мы получили формулу перехода от базиса $f$ к базису $e$. Следовательно, ${{left( {{T}_{eto f}} right)}^{-1}}$ — матрица такого перехода, что и требовалось доказать.
2.3. Переход через транзитный базис
Пусть ${{T}_{eto f}}$ — матрица перехода от базиса $e$ к базису $f$ линейного пространства $L$, а ${{T}_{fto g}}$ — матрица перехода от базиса $f$ к базису $g$ того же линейного пространства $L$.
Тогда матрица перехода ${{T}_{eto g}}$ от базиса $e$ к базису $g$ находится по формуле
[{{T}_{eto g}}={{T}_{eto f}}cdot {{T}_{fto g}}]
Для доказательства достаточно записать формулы для выражения базисов $f$ и $g$, а затем подставить одну формулу в другую. По условию теоремы, базис $f$ выражается через базис $e$ по формуле
[left[ {{f}_{1}},ldots ,{{f}_{n}} right]=left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot {{T}_{eto f}}]
Кроме того, базис $g$ выражается через базис $f$ по формуле
[left[ {{g}_{1}},ldots ,{{g}_{n}} right]=left[ {{f}_{1}},ldots ,{{f}_{n}} right]cdot {{T}_{fto g}}]
Подставим первое выражение во второе и получим
[begin{align}left[ {{g}_{1}},ldots ,{{g}_{n}} right] &=left[ {{f}_{1}},ldots ,{{f}_{n}} right]cdot {{T}_{fto g}}= \ &=left( left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot {{T}_{eto f}} right)cdot {{T}_{fto g}}= \ & =left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot left( {{T}_{eto f}}cdot {{T}_{fto g}} right) end{align}]
[begin{align}& left[ {{g}_{1}},ldots ,{{g}_{n}} right]= \ =& left[ {{f}_{1}},ldots ,{{f}_{n}} right]cdot {{T}_{fto g}}= \ =& left( left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot {{T}_{eto f}} right)cdot {{T}_{fto g}}= \ =& left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot left( {{T}_{eto f}}cdot {{T}_{fto g}} right) end{align}]
Мы получили прямое выражение базиса $g$ через базис $e$, причём матрица перехода равна
[{{T}_{eto g}}={{T}_{eto f}}cdot {{T}_{fto g}}]
Это именно та формула, которую и требовалось доказать.
2.4. Невырожденные матрицы
И ещё одно важное свойство:
Свойство 4. Пусть дана произвольная квадратная невырожденная матрица
[T=left[ begin{matrix}{{a}_{1,1}} & {{a}_{1,2}} & cdots & {{a}_{1,n}} \ {{a}_{2,1}} & {{a}_{2,2}} & cdots & {{a}_{2,n}} \ cdots & cdots & cdots & cdots \ {{a}_{n,1}} & {{a}_{n,2}} & cdots & {{a}_{n,n}} \ end{matrix} right]]
Пусть $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ — произвольный базис линейного пространства $L$. Тогда система векторов $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$, полученных по формуле
[begin{align}{{f}_{1}}&={{a}_{1,1}}{{e}_{1}}+{{a}_{2,1}}{{e}_{2}}+ldots +{{a}_{n,1}}{{e}_{n}} \ {{f}_{2}}&={{a}_{1,2}}{{e}_{1}}+{{a}_{2,2}}{{e}_{2}}+ldots +{{a}_{n,2}}{{e}_{n}} \ & cdots \ {{f}_{n}}&={{a}_{1,n}}{{e}_{1}}+{{a}_{2,n}}{{e}_{2}}+ldots +{{a}_{n,n}}{{e}_{n}} \ end{align}]
тоже будет базисом $L$.
Иначе говоря, всякая квадратная невырожденная матрица $T$ является матрицей перехода от данного базиса $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ к некоторому новому базису $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ линейного пространства $L$.
Обратите внимание: поскольку изначально мы не знаем, что $T$ — матрица перехода, её элементы пронумерованы стандартным образом: первый индекс отвечает за строку, а второй — за столбец. Однако это нисколько не помешает нам доказать теорему.
Для доказательства того, что $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ — базис линейного пространства $L$, нужно доказать два утверждения:
- 1.Система векторов $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ — линейно независима.
- 2.Ранг этой системы векторов совпадает с размерностью пространства $L$.
Поскольку количество векторов в системе $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ совпадает с количеством базисных векторов $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$, т.е. равно $n=dim L$, достаточно лишь проверить линейную независимость.
Рассмотрим линейную комбинацию векторов $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ и предположим, что она равна нулю:
[{{lambda }_{1}}{{f}_{1}}+{{lambda }_{2}}{{f}_{2}}+ldots +{{lambda }_{n}}{{f}_{n}}=0]
В матричном виде это выглядит так:
[left[ {{f}_{1}},ldots ,{{f}_{n}} right]cdot left[ begin{align}& {{lambda }_{1}} \ & cdots\ & {{lambda }_{n}} \ end{align} right]=0]
По условию теоремы векторы $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ раскладываются по базису $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ с коэффициентами, записанными в столбцах матрицы $T$. В матричном виде это выглядит так:
[left[ {{f}_{1}},ldots ,{{f}_{n}} right]=left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot T]
Подставляем полученное выражение для $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ в предыдущее матричное уравнение и получаем
[left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot Tcdot left[ begin{align}& {{lambda }_{1}} \ & cdots \ & {{lambda }_{n}} \ end{align} right]=0]
Поскольку $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ — базис линейного пространства $L$, такое равенство возможно лишь при условии
[Tcdot left[ begin{matrix} {{lambda }_{1}} \ cdots \ {{lambda }_{n}} \ end{matrix} right]=left[ begin{matrix} 0 \ cdots \ 0 \ end{matrix} right]]
Это матричное уравнение можно рассматривать как систему из $n$ однородных уравнений относительно переменных ${{lambda }_{1}},ldots ,{{lambda }_{n}}$. И поскольку по условию теоремы матрица $T$ невырожденная, это СЛАУ имеет лишь одно решение — тривиальное:
[{{lambda }_{1}}={{lambda }_{2}}=ldots ={{lambda }_{n}}=0]
Получаем, что система векторов $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ линейно независима, а количество векторов совпадает с размерностью линейного пространства $L$. Следовательно, эта система — базис, что и требовалось доказать.
3. Замена координат в новом базисе
До сих пор мы рассуждали лишь о том, как координаты новых базисных векторов $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ выражаются через координаты старых базисных векторов $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$. Но что будет с координатами одного и того же вектора линейного пространства $L$ при переходе от одного базиса к другому?
Ответ даёт следующая теорема.
3.1. Формулировка теоремы
Теорема. Пусть $e=left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ и $f=left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ — базисы линейного пространства $L$ над полем $K$. Пусть ${{T}_{eto f}}$ — матрица перехода от базиса $e$ к $f$:
[{{T}_{eto f}}=left[ begin{matrix}{{a}_{1,1}} & cdots& {{a}_{1,n}} \ cdots& cdots& cdots \ {{a}_{n,1}} & cdots & {{a}_{n,n}} \ end{matrix} right]]
Тогда координаты произвольного вектора $hin L$ пересчитываются по формуле
[{{left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]}_{e}}={{T}_{eto f}}cdot {{left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]}_{f}}]
Ещё раз: если произвольный вектор $hin L$ в новом базисе $f$ имеет координаты
[{{left[ h right]}_{f}}=left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]]
то в старом базисе $e$ этот же вектор $hin L$ имеет координаты
[{{left[ h right]}_{e}}=left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]={{T}_{eto f}}cdot left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]]
Т.е. для векторов всё наоборот: не новые координаты выражаются через старые, а старые — через новые. Впрочем, никто не мешает найти матрицу $T_{eto f}^{-1}$ и записать
[left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]=T_{eto f}^{-1}cdot left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]]
Но такая запись предполагает дополнительное действие — нахождение обратной матрицы.
3.2. Доказательство
Сначала «соберём» матрицу ${{T}_{eto f}}$. Для этого разложим векторы $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ по базису $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$:
[left{ begin{align}{{f}_{1}} &={{a}_{1,1}}{{e}_{1}}+{{a}_{2,1}}{{e}_{2}}+ldots +{{a}_{n,1}}{{e}_{n}} \ {{f}_{2}} &={{a}_{1,2}}{{e}_{1}}+{{a}_{2,2}}{{e}_{2}}+ldots +{{a}_{n,2}}{{e}_{n}} \ & cdots \ {{f}_{n}} &={{a}_{1,n}}{{e}_{1}} +{{a}_{2,n}}{{e}_{2}}+ldots +{{a}_{n,n}}{{e}_{n}} \ end{align} right.]
В матричной форме эту систему линейных уравнений можно записать так:
[left[ begin{matrix} {{f}_{1}} \ {{f}_{2}} \ cdots \ {{f}_{n}} \ end{matrix} right]=left[ begin{matrix} {{a}_{1,1}} & {{a}_{2,1}} & cdots & {{a}_{n,1}} \ {{a}_{1,2}} & {{a}_{2,2}} & cdots & {{a}_{n,2}} \ cdots & cdots & cdots & cdots \ {{a}_{1,n}} & {{a}_{2,n}} & cdots & {{a}_{n,n}} \ end{matrix} right]cdot left[ begin{matrix} {{e}_{1}} \ {{e}_{2}} \ cdots \ {{e}_{n}} \ end{matrix} right]]
Транспонируем обе стороны равенства, учитывая, что произведение справа транспонируется по правилу ${{left( Acdot B right)}^{T}}={{B}^{T}}cdot {{A}^{T}}$:
[left[ begin{matrix}{{f}_{1}} & cdots & {{f}_{n}} \ end{matrix} right]=left[ begin{matrix} {{e}_{1}} & cdots & {{e}_{n}} \ end{matrix} right]cdot left[ begin{matrix} {{a}_{1,1}} & {{a}_{1,2}} & cdots & {{a}_{1,n}} \ {{a}_{2,1}} & {{a}_{2,2}} & cdots & {{a}_{2,n}} \ cdots & cdots & cdots & cdots \ {{a}_{n,1}} & {{a}_{n,2}} & cdots & {{a}_{n,n}} \ end{matrix} right]]
[left[ {{f}_{1}} cdots {{f}_{n}} right]=left[ {{e}_{1}} cdots {{e}_{n}} right]cdot left[ begin{matrix} {{a}_{1,1}} & cdots & {{a}_{1,n}} \ cdots & cdots & cdots \ {{a}_{n,1}} & cdots & {{a}_{n,n}} \ end{matrix} right]]
Квадратная матрица справа — это и есть матрица перехода ${{T}_{eto f}}$. Поэтому матричное уравнение можно переписать так:
[left[ begin{matrix}{{f}_{1}} & cdots& {{f}_{n}} \ end{matrix} right]=left[ begin{matrix}{{e}_{1}} & cdots& {{e}_{n}} \ end{matrix} right]cdot {{T}_{eto f}}]
Теперь возьмём произвольный вектор $hin L$ и разложим его по базисам $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ и $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$:
[begin{align}h &={{x}_{1}}{{e}_{1}}+{{x}_{2}}{{e}_{2}}+ldots +{{x}_{n}}{{e}_{n}}= \ &={{y}_{1}}{{f}_{1}}+{{y}_{2}}{{f}_{2}}+ldots +{{y}_{n}}{{f}_{n}} end{align}]
Вновь перейдём к матричной форме. Сначала учтём, что координаты векторов принято записывать в виде вектор-столбцов:
[{{left[ h right]}_{e}}=left[ begin{matrix} {{x}_{1}} \ {{x}_{2}} \ cdots \ {{x}_{n}} \ end{matrix} right]quad {{left[ h right]}_{f}}=left[ begin{matrix} {{y}_{1}} \ {{y}_{2}} \ cdots \ {{y}_{n}} \ end{matrix} right]]
Тогда левую и правую часть уравнения можно представить как произведение строк с базисными векторами и указанных вектор-столбцов с координатами:
[left[ begin{matrix} {{e}_{1}} & cdots & {{e}_{n}} \ end{matrix} right]cdot left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]=left[ begin{matrix} {{f}_{1}} & cdots & {{f}_{n}} \ end{matrix} right]cdot left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]]
[left[ {{e}_{1}} cdots {{e}_{n}} right]cdot left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]=left[ {{f}_{1}} cdots {{f}_{n}} right]cdot left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]]
Но выше мы выражали строку векторов $left[ {{f}_{1}},ldots ,{{f}_{n}} right]$ через строку $left[ {{e}_{1}},ldots ,{{e}_{n}} right]$ и матрицу перехода ${{T}_{eto f}}$. Подставим это выражение в наше матричное уравнение:
[left[ begin{matrix} {{e}_{1}} & cdots & {{e}_{n}} \ end{matrix} right]cdot left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]=left[ begin{matrix} {{e}_{1}} & cdots & {{e}_{n}} \ end{matrix} right]cdot {{T}_{eto f}}cdot left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]]
[left[ {{e}_{1}} cdots {{e}_{n}} right]cdot left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]=left[ {{e}_{1}} cdots {{e}_{n}} right]cdot {{T}_{eto f}}cdot left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]]
Уберём слева и справа первый множитель — строку $left[ {{e}_{1}},ldots ,{{e}_{n}} right]$. Получим уравнение, связывающее координаты вектора в разных базисах:
[left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]={{T}_{eto f}}cdot left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]]
Это именно та формула, которую и требовалось доказать.
Задача 1. Базисы трёхмерного пространства
Задача. Убедитесь, что системы векторов
[{{a}_{1}}={{left( 1,2,1 right)}^{T}},quad {{a}_{2}}={{left( 2,3,2 right)}^{T}},quad {{a}_{3}}={{left( 1,-1,2 right)}^{T}}]
[begin{align}{{a}_{1}} &={{left( 1,2,1 right)}^{T}}, \ {{a}_{2}} &={{left( 2,3,2 right)}^{T}}, \ {{a}_{3}} &={{left( 1,-1,2 right)}^{T}} \ end{align}]
и
[{{b}_{1}}={{left( 1,3,1 right)}^{T}},quad {{b}_{2}}={{left( 1,-1,3 right)}^{T}},quad {{b}_{3}}={{left( 2,2,1 right)}^{T}}]
[begin{align}{{b}_{1}} &={{left( 1,3,1 right)}^{T}}, \ {{b}_{2}} &={{left( 1,-1,3 right)}^{T}}, \ {{b}_{3}} &={{left( 2,2,1 right)}^{T}} \ end{align}]
являются базисами в векторном пространстве ${{mathbb{R}}^{3}}$. Найдите матрицу перехода ${{T}_{ato b}}$. Найдите координаты в базисе $a$ вектора $x$, который в базисе $b$ имеет координаты ${{left( 0,3,2 right)}^{T}}$.
Решение
Чтобы доказать, что система векторов образует базис, достаточно составить матрицу $A$ из координат этих векторов, а затем вычислить её определитель $det A$. И если $det Ane 0$, то векторы линейно независимы. А поскольку их количество совпадает с размерностью линейного пространства, такие векторы образуют базис.
Рассмотрим систему векторов $a=left{ {{a}_{1}},{{a}_{2}},{{a}_{3}} right}$. Составим из них матрицу, расположив координаты по столбцам. Получим матрицу перехода ${{T}_{eto a}}$ от некого исходного базиса $e$ (в котором как раз и даны координаты векторов ${{a}_{i}}$ и ${{b}_{i}}$ в условии задачи) к базису $a$:
[{{T}_{eto a}}=left[ begin{array}{ccr} 1 & 2 & 1 \ 2 & 3 & -1 \ 1 & 2 & 2 \ end{array} right]]
Определитель этой матрицы отличен от нуля:
[det {{T}_{eto a}}=-1ne 0]
Следовательно, $left{ {{a}_{1}},{{a}_{2}},{{a}_{3}} right}$ — базис пространства ${{mathbb{R}}^{3}}$.
Теперь составим матрицу из векторов $b=left{ {{b}_{1}},{{b}_{2}},{{b}_{3}} right}$. Получим матрицу перехода ${{T}_{eto b}}$:
[{{T}_{eto b}}=left[ begin{array}{crc} 1 & 1 & 2 \ 3 & -1 & 2 \ 1 & 3 & 1 \ end{array} right]]
Определитель этой матрицы вновь отличен от нуля:
[det {{T}_{eto b}}=12ne 0]
Следовательно, $left{ {{b}_{1}},{{b}_{2}},{{b}_{3}} right}$ — тоже базис пространства ${{mathbb{R}}^{3}}$.
Осталось найти матрицу перехода ${{T}_{ato b}}$. Заметим, что эту матрицу можно выразить так:
[begin{align}{{T}_{ato b}} &={{T}_{ato e}}cdot {{T}_{eto b}}= \ &={{left( {{T}_{eto a}} right)}^{-1}}cdot {{T}_{eto b}}end{align}]
Мы внедрили «транзитный» базис $e$ и вместо прямого перехода $ato b$ рассмотрели цепочку $ato eto b$. Это стандартный и очень распространённый приём, но из-за этого появился новый элемент $T_{eto a}^{-1}$ — матрица, обратная к ${{T}_{eto a}}$. Найдём $T_{eto a}^{-1}$ методом присоединённой матрицы:
[left[ {{T}_{eto a}}|E right]sim ldots sim left[ E|T_{eto a}^{-1} right]]
Напомню, что элементарные преобразования в присоединённых матрицах выполняются только над строками. Если вы забыли, как всё это работает, см. урок «Обратная матрица». В нашем случае получим:
[left[ begin{array}{ccr|ccc}1 & 2 & 1 & 1 & 0 & 0 \ 2 & 3 & -1 & 0 & 1 & 0 \ 1 & 2 & 2 & 0 & 0 & 1 \end{array} right]begin{matrix} , \ -2cdot left[ 1 right] \ -1cdot left[ 1 right] \ end{matrix}]
Мы «зачистили» первый столбец. Теперь «зачистим» последний:
[left[ begin{array}{crr|rcc} 1 & 2 & 1 & 1 & 0 & 0 \ 0 & -1 & -3 & -2 & 1 & 0 \ 0 & 0 & 1 & -1 & 0 & 1 \ end{array} right]begin{matrix} -1cdot left[ 3 right] \ +3cdot left[ 3 right] \ , \ end{matrix}]
Остался лишь средний. Разберёмся и с ним:
[left[ begin{array}{crc|rcr} 1 & 2 & 0 & 2 & 0 & -1 \ 0 & -1 & 0 & -5 & 1 & 3 \ 0 & 0 & 1 & -1 & 0 & 1 \ end{array} right]begin{matrix} +2cdot left[ 2 right] \ |cdot left( -1 right) \ , \ end{matrix}]
Получили единичную матрицу слева от вертикальной черты. Значит, справа стоит искомая матрица $T_{eto a}^{-1}$:
[left[ begin{array}{ccc|rrr} 1 & 0 & 0 & -8 & 2 & 5 \ 0 & 1 & 0 & 5 & -1 & -3 \ 0 & 0 & 1 & -1 & 0 & 1 \ end{array} right]]
Теперь у нас есть всё, чтобы найти матрицу перехода ${{T}_{ato b}}$:
[{{T}_{ato b}}={{left( {{T}_{eto a}} right)}^{-1}}cdot {{T}_{eto b}}=left[ begin{array}{rrr} -8 & 2 & 5 \ 5 & -1 & -3 \ -1 & 0 & 1 \ end{array} right]cdot left[ begin{array}{crc} 1 & 1 & 2 \ 3 & -1 & 2 \ 1 & 3 & 1 \ end{array} right]]
[begin{align}{{T}_{ato b}} &={{left( {{T}_{eto a}} right)}^{-1}}cdot {{T}_{eto b}}= \ &=left[ begin{array}{rrr} -8 & 2 & 5 \ 5 & -1 & -3 \ -1 & 0 & 1 \ end{array} right]cdot left[ begin{array}{crc} 1 & 1 & 2 \ 3 & -1 & 2 \ 1 & 3 & 1 \ end{array} right] end{align}]
После несложных вычислений получаем матрицу перехода от базиса $a$ к базису $b$:
[{{T}_{ato b}}=left[ begin{array}{rrr} 3 & 5 & -7 \ -1 & -3 & 5 \ 0 & 2 & -1 \ end{array} right]]
Осталось найти координаты вектора $x$, который в базисе $b$ имеет координаты ${{left( 0,3,2 right)}^{T}}$. Вспомним формулу, выражающую координаты в старом базисе через координаты в новом базисе:
[{{left[ x right]}_{a}}={{T}_{ato b}}cdot {{left[ x right]}_{b}}]
Подставляем в эту формулу матрицу ${{T}_{ato b}}$ и вектор-столбец ${{left[ x right]}_{b}}={{left[ 0,3,2 right]}^{T}}$:
[{{left[ x right]}_{a}}=left[ begin{array}{rrr} 3 & 5 & -7 \ -1 & -3 & 5 \ 0 & 2 & -1 \ end{array} right]cdot left[ begin{matrix} 0 \ 3 \ 2 \ end{matrix} right]=left[ begin{matrix} 1 \ 1 \ 4 \ end{matrix} right]]
Итак, вектор $x$ в базисе $a$ имеет координаты ${{left( 1,1,4 right)}^{T}}$. Задача решена.
Альтернативное решение
Можно найти матрицу ${{T}_{ato b}}$ заметно быстрее, если использовать алгоритм решения матричных уравнений. Заметим, что нам требуется найти произведение
[{{T}_{ato b}}={{A}^{-1}}cdot B]
С другой стороны, для нахождения такого произведения достаточно составить присоединённую матрицу вида $left[ A|B right]$ и цепочкой элементарных преобразований свести её к виду
[left[ A|B right]sim ldots sim left[ E|{{A}^{-1}}cdot B right]]
Другими словами, справа от вертикальной черты мы получим искомую матрицу перехода ${{T}_{ato b}}$!
На практике это выглядит так. Записываем присоединённую матрицу $left[ A|B right]$:
[left[ begin{array}{ccr|crc} 1 & 2 & 1 & 1 & 1 & 2 \ 2 & 3 & -1 & 3 & -1 & 2 \ 1 & 2 & 2 & 1 & 2 & 1 \ end{array} right]]
И после элементарных преобразований получим
[left[ begin{array}{ccc|rrr} 1 & 0 & 0 & 3 & 5 & -7 \ 0 & 1 & 0 & -1 & -3 & 5 \ 0 & 0 & 1 & 0 & 2 & -1 \ end{array} right]]
Для экономии места я пропустил промежуточные шаги. Попробуйте сделать их самостоятельно — это очень полезная практика.
Если же вы хотите разобраться, как это работает (и почему вдруг справа возникает матрица вида ${{A}^{-1}}cdot B$), см. урок «Матричные уравнения». А мы идём дальше.
Задача 2. Базисы в поле вычетов
Найдите матрицу перехода от базиса
[{{a}_{1}}={{left( 1,1,1 right)}^{T}},quad {{a}_{2}}={{left( 2,1,1 right)}^{T}},quad {{a}_{3}}={{left( 3,2,1 right)}^{T}}]
[begin{align}{{a}_{1}} &={{left( 1,1,1 right)}^{T}}, \ {{a}_{2}} &={{left( 2,1,1 right)}^{T}}, \ {{a}_{3}} &={{left( 3,2,1 right)}^{T}} \ end{align}]
к базису
[{{b}_{1}}={{left( 0,4,3 right)}^{T}},quad {{b}_{2}}={{left( 3,3,2 right)}^{T}},quad {{b}_{3}}={{left( 2,2,1 right)}^{T}}]
[begin{align}{{b}_{1}} &={{left( 0,4,3 right)}^{T}}, \ {{b}_{2}} &={{left( 3,3,2 right)}^{T}}, \ {{b}_{3}} &={{left( 2,2,1 right)}^{T}} \ end{align}]
арифметического линейного пространства $mathbb{Z}_{5}^{3}$.
Решение
Эта задача проще предыдущей, поскольку поле вычетов ${{mathbb{Z}}_{5}}$ является конечным и состоит всего из пяти элементов — представителей смежных классов:
[{{mathbb{Z}}_{5}}=left{ 0,1,2,3,4 right}]
Как и в предыдущей задаче, рассмотрим систему векторов $a=left{ {{a}_{1}},{{a}_{2}},{{a}_{3}} right}$ и составим из них матрицу ${{T}_{eto a}}$:
[{{T}_{eto a}}=left[ begin{matrix} 1 & 2 & 3 \ 1 & 1 & 2 \ 1 & 1 & 1 \ end{matrix} right]]
Определитель $det {{T}_{eto a}}=1ne 0$, поэтому $left{ {{a}_{1}},{{a}_{2}},{{a}_{3}} right}$ — базис.
Аналогично, рассмотрим систему $b=left{ {{b}_{1}},{{b}_{2}},{{b}_{3}} right}$ и составим матрицу ${{T}_{eto b}}$:
[{{T}_{eto b}}=left[ begin{matrix} 0 & 3 & 2 \ 4 & 3 & 2 \ 3 & 2 & 1 \ end{matrix} right]]
Определитель $det {{T}_{eto b}}=4ne 0$, поэтому $left{ {{b}_{1}},{{b}_{2}},{{b}_{3}} right}$ — базис.
Выразим искомую матрицу ${{T}_{ato b}}$ через «транзитный» базис $e$:
[begin{align}{{T}_{ato b}} &={{T}_{ato e}}cdot {{T}_{eto b}}= \ &={{left( {{T}_{eto a}} right)}^{-1}}cdot {{T}_{eto b}} end{align}]
Найдём $T_{eto a}^{-1}$ через присоединённую матрицу:
[left[ begin{array}{ccc|ccc} 1 & 2 & 3 & 1 & 0 & 0 \ 1 & 1 & 2 & 0 & 1 & 0 \ 1 & 1 & 1 & 0 & 0 & 1 \ end{array} right]]
После цепочки элементарных преобразований над строками (попробуйте выполнить их самостоятельно!) получим
[left[ begin{array}{ccc|ccc} 1 & 0 & 0 & 4 & 1 & 1 \ 0 & 1 & 0 & 1 & 3 & 1 \ 0 & 0 & 1 & 0 & 1 & 4 \ end{array} right]]
Итак, мы нашли матрицу $T_{eto a}^{-1}$:
[T_{eto a}^{-1}=left[ begin{matrix} 4 & 1 & 1 \ 1 & 3 & 1 \ 0 & 1 & 4 \ end{matrix} right]]
Осталось вычислить искомую матрицу перехода ${{T}_{ato b}}$:
[{{T}_{ato b}}={{left( {{T}_{eto a}} right)}^{-1}}cdot {{T}_{eto b}}=left[ begin{matrix} 4 & 1 & 1 \ 1 & 3 & 1 \ 0 & 1 & 4 \ end{matrix} right]cdot left[ begin{matrix} 0 & 3 & 2 \ 4 & 3 & 2 \ 3 & 2 & 1 \ end{matrix} right]=left[ begin{matrix} 2 & 2 & 1 \ 0 & 4 & 4 \ 1 & 1 & 1 \ end{matrix} right]]
[begin{align}{{T}_{ato b}} &={{left( {{T}_{eto a}} right)}^{-1}}cdot {{T}_{eto b}}= \ &=left[ begin{matrix} 4 & 1 & 1 \ 1 & 3 & 1 \ 0 & 1 & 4 \ end{matrix} right]cdot left[ begin{matrix} 0 & 3 & 2 \ 4 & 3 & 2 \ 3 & 2 & 1 \ end{matrix} right]= \ &=left[ begin{matrix} 2 & 2 & 1 \ 0 & 4 & 4 \ 1 & 1 & 1 \ end{matrix} right] end{align}]
По аналогии с предыдущей задачей, матрицу ${{T}_{ato b}}$ можно найти и через элементарные преобразования присоединённой матрицы $left[ A|B right]$. Результат будет точно такой же, но мы сэкономим пару строк вычислений и несколько минут времени.
Задача 3. Пространство многочленов
Убедитесь, что системы многочленов
[begin{align}e &=left{ 1,t-1,{{left( t-1 right)}^{2}} right} \ f &=left( 1,t+1,{{left( t+1 right)}^{2}} right) \ end{align}]
являются базисами в пространстве ${{P}_{3}}$ многочленов степени не выше 2. Найдите матрицу перехода ${{T}_{eto f}}$. Разложите по степеням $left( t-1 right)$ многочлен ${{left( t+1 right)}^{2}}+left( t+1 right)+1$.
Решение
Стандартным базисом в пространстве многочленов является система многочленов $p=left{ {{p}_{1}},{{p}_{2}},{{p}_{3}} right}$, где
[{{p}_{1}}=1quad {{p}_{2}}=tquad {{p}_{3}}={{t}^{2}}]
Выразим через базис $p$ многочлены из системы $e$:
[begin{align} & {{e}_{1}}=1={{p}_{1}} \ & {{e}_{2}}=t-1={{p}_{2}}-{{p}_{1}} \ & {{e}_{3}}={{left( t-1 right)}^{2}}={{t}^{2}}-2t+1={{p}_{3}}-2{{p}_{2}}+{{p}_{1}} end{align}]
[begin{align}{{e}_{1}} &=1={{p}_{1}} \ {{e}_{2}} &=t-1={{p}_{2}}-{{p}_{1}} \ {{e}_{3}} &={{left( t-1 right)}^{2}}= \ &={{t}^{2}}-2t+1= \ &={{p}_{3}}-2{{p}_{2}}+{{p}_{1}} end{align}]
Следовательно, матрица перехода ${{T}_{pto e}}$ выглядит так:
[{{T}_{pto e}}=left[ begin{array}{crr} 1 & -1 & 1 \ 0 & 1 & -2 \ 0 & 0 & 1 \ end{array} right]]
Аналогично, выразим через базис $p$ многочлены из системы $f$:
[begin{align} & {{f}_{1}}=1={{p}_{1}} \ & {{f}_{2}}=t+1={{p}_{2}}+{{p}_{1}} \ & {{f}_{3}}={{left( t+1 right)}^{2}}={{t}^{2}}+2t+1={{p}_{3}}+2{{p}_{2}}+{{p}_{1}} end{align}]
[begin{align}{{f}_{1}} &=1={{p}_{1}} \ {{f}_{2}} &=t+1={{p}_{2}}+{{p}_{1}} \ {{f}_{3}} &={{left( t+1 right)}^{2}}= \ &={{t}^{2}}+2t+1= \ &={{p}_{3}}+2{{p}_{2}}+{{p}_{1}} end{align}]
Получим матрицу перехода ${{T}_{pto f}}$:
[{{T}_{pto f}}=left[ begin{matrix} 1 & 1 & 1 \ 0 & 1 & 2 \ 0 & 0 & 1 \ end{matrix} right]]
Обе матрицы оказались верхнетреугольными, их определители отличны от нуля:
[begin{align} det {{T}_{pto e}} &=1cdot 1cdot 1=1 \ det {{T}_{pto f}} &=1cdot 1cdot 1=1 \ end{align}]
Следовательно системы многочленов $e$ и $f$ действительно являются базисами пространства ${{P}_{3}}$.
Теперь найдём матрицу перехода ${{T}_{eto f}}$. Для этого нам даже не потребуется искать обратную матрицу. Достаточно заметить, что векторы ${{f}_{1}}$ и ${{f}_{2}}$ легко раскладываются по базису $e$:
[begin{align}{{f}_{1}} &=1={{e}_{1}} \ {{f}_{2}} &=t+1=left( t-1 right)+2={{e}_{2}}+2{{e}_{1}} \ end{align}]
С вектором ${{f}_{3}}$ вычислений будет чуть больше:
[begin{align}{{f}_{3}} &={{left( t+1 right)}^{2}}= \ &={{left( t-1 right)}^{2}}+4t= \ &={{left( t-1 right)}^{2}}+4left( t-1 right)+4= \ &={{e}_{3}}+4{{e}_{2}}+4{{e}_{1}} end{align}]
Итого матрица перехода ${{T}_{eto f}}$ примет вид
[{{T}_{eto f}}=left[ begin{matrix} 1 & 2 & 4 \ 0 & 1 & 4 \ 0 & 0 & 1 \ end{matrix} right]]
Теперь разложим многочлен ${{left( t+1 right)}^{2}}+left( t+1 right)+1$ по базису $e$. Сначала перепишем этот многочлен так:
[begin{align}hleft( t right) &=1+left( t+1 right)+{{left( t+1 right)}^{2}}= \ &={{f}_{1}}+{{f}_{2}}+{{f}_{3}} end{align}]
Следовательно, в базисе $f$ многочлен $hleft( t right)$ имеет координаты ${{left( 1,1,1 right)}^{T}}$. Но тогда по теореме о замене координат этот же многочлен в базисе $e$ имеет координаты
[{{left[ h right]}_{e}}={{T}_{eto f}}cdot {{left[ h right]}_{f}}=left[ begin{matrix} 1 & 2 & 4 \ 0 & 1 & 4 \ 0 & 0 & 1 \ end{matrix} right]cdot left[ begin{matrix} 1 \ 1 \ 1 \ end{matrix} right]=left[ begin{matrix} 7 \ 5 \ 1 \ end{matrix} right]]
[begin{align}{{left[ h right]}_{e}} &={{T}_{eto f}}cdot {{left[ h right]}_{f}}= \ &=left[ begin{matrix} 1 & 2 & 4 \ 0 & 1 & 4 \ 0 & 0 & 1 \ end{matrix} right]cdot left[ begin{matrix} 1 \ 1 \ 1 \ end{matrix} right]=left[ begin{matrix} 7 \ 5 \ 1 \ end{matrix} right] end{align}]
Другими словами, многочлен $hleft( t right)$ имеет вид
[hleft( t right)={{left( t-1 right)}^{2}}+5left( t-1 right)+7]
Это и есть искомое разложение многочлена ${{left( t+1 right)}^{2}}+left( t+1 right)+1$ по степеням $left( t-1 right)$.
Альтернативное решение
Искомое разложение можно получить и без привлечения матриц перехода. Достаточно применить схему Горнера или выделить нужные степени напрямую:
[begin{align}hleft( t right) &={{left( t+1 right)}^{2}}+left( t+1 right)+1= \ &={{left( t-1 right)}^{2}}+4t+t+1+1= \ &={{left( t-1 right)}^{2}}+5left( t-1 right)+5+2= \ &={{left( t-1 right)}^{2}}+5left( t-1 right)+7 end{align}]
Как видим, результат получился тем же самым, а времени потрачено меньше. Однако уже в пространстве ${{P}_{4}}$ многочленов степени не выше 4 сложность решения через матрицы и через выделение степеней будет сопоставимой. А дальше матрицы начнут выигрывать.
Смысл линейной алгебры — дать универсальные алгоритмы, которые работают с объектами любой природы, если эти объекты подчиняются аксиомам линейного пространства.
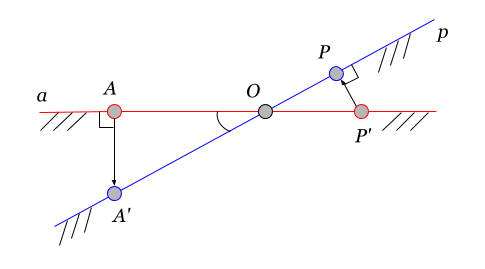
Задача 4. Матрица перехода при симметрии
Базис $b$получается из базиса
[{{a}_{1}}={{left( 2,1,3 right)}^{T}},quad {{a}_{2}}={{left( 1,1,-1 right)}^{T}},quad {{a}_{3}}={{left( 2,-1,-1 right)}^{T}}]
[begin{align}{{a}_{1}} &={{left( 2,1,3 right)}^{T}}, \ {{a}_{2}} &={{left( 1,1,-1 right)}^{T}}, \ {{a}_{3}} &={{left( 2,-1,-1 right)}^{T}} \ end{align}]
пространства ${{V}_{3}}$ симметрией относительно плоскости $2x+y+3z=0$. Найти матрицу перехода ${{T}_{ato b}}$.
Решение
Из курса аналитической геометрии мы знаем, что если плоскость задана уравнением
[ax+by+cz+d=0]
то вектор-нормаль $n$ имеет координаты
[n=left( a,b,c right)]
Тогда для плоскости $2x+y+3z=0$ нормаль имеет координаты $n=left( 2,1,3 right)$, что в точности совпадает с вектором ${{a}_{1}}$. Следовательно, при симметрии относительно плоскости этот вектор просто перейдёт в противоположный: ${{b}_{1}}=-{{a}_{1}}$.
Далее заметим, что векторы ${{a}_{2}}$ и ${{a}_{3}}$ лежат в плоскости симметрии, поскольку при подстановке их координат уравнение плоскости обращается в верное числовое равенство:
[begin{align}{{a}_{2}}={{left( 1,1,-1 right)}^{T}} &Rightarrow 2cdot 1+1+3cdot left( -1 right)=0 \ {{a}_{3}}={{left( 2,-1,-1 right)}^{T}} &Rightarrow 2cdot 2-1+3cdot left( -1 right)=0 \ end{align}]
[begin{align}{{a}_{2}}=&{{left( 1,1,-1 right)}^{T}}Rightarrow \ & Rightarrow 2cdot 1+1+3cdot left( -1 right)=0 \ {{a}_{3}}=&{{left( 2,-1,-1 right)}^{T}}Rightarrow \ & Rightarrow 2cdot 2-1+3cdot left( -1 right)=0 \ end{align}]
Следовательно, при симметрии эти векторы переходят сами в себя: ${{b}_{2}}={{a}_{2}}$, ${{b}_{3}}={{a}_{3}}$. Матрица перехода имеет вид
[{{T}_{ato b}}=left[ begin{array}{rcc} -1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1 \ end{array} right]]
Важное замечание. симметрия предполагает использование проекций и углов, что в конечном счёте сводится к скалярному произведению. Однако мы пока не знаем, что такое скалярное произведение в линейном пространстве.
Полноценное определение скалярного произведения будет намного позже — см. урок «Евклидово пространство». А пока будем считать, что скалярное произведение векторов $a$ и $b$ определено стандартным образом:
[left( a,b right)=left| a right|cdot left| b right|cdot cos alpha ]
Геометрическая интерпретация
Симметрию на плоскости и в пространстве удобно представлять графически. Пусть $alpha $ — плоскость, относительно которой выполняется симметрия. Тогда векторы $left{ {{a}_{1}},{{a}_{2}},{{a}_{3}} right}$ будут выглядеть так:
Из приведённого рисунка сразу видно, что при симметрии вектор ${{a}_{1}}$ перейдёт в противоположный, а векторы ${{a}_{2}}$ и ${{a}_{3}}$ останутся на месте.
Задача 5. Матрица поворота
Базис $e=left{ i,j,k right}$ пространства ${{V}_{3}}$ поворачивается на 180° вокруг прямой $l$, заданной системой
[left{ begin{align}x-y &=0 \ z &=0 \ end{align} right.]
Затем полученный базис $f$ поворачивается на 90° в отрицательном направлении вокруг нового положения вектора $j$. В результате получается базис $g=left{ {{i}_{2}},{{j}_{2}},{{k}_{2}} right}$.
Найдите матрицу перехода ${{T}_{eto g}}$. Найдите в базисе $e$ координаты вектора $h$, который в новом базисе $g$ имеет координаты $left( 1,1,1 right)$.
Решение
Вращение базиса и матрица поворота — это очень важная тема, по которой есть отдельный урок — «Матрица поворота». Но сейчас вращение совсем простое, поэтому обойдёмся без специальных матриц.
Вновь обратимся к геометрической интерпретации. Рассмотрим исходный базис $e=left{ i,j,k right}$ трёхмерного пространства:
Также на этом рисунке изображена прямая $l$, которая задаётся требованиями $z=0$ и $x=y$. Эта лежит в плоскости $Oxy$ и является биссектрисой первой координатной четверти.
Очевидно, что при повороте пространства на 180° относительно прямой $l$ базисные векторы $i$ и $j$ просто поменяются местами, а вектор $k$ перейдёт в противоположный:
Другими словами, ${{i}_{1}}=j$, ${{j}_{1}}=i$, ${{k}_{1}}=-k$, поэтому матрица перехода от базиса $e=left{ i,j,k right}$ к базису $f=left{ {{i}_{1}},{{j}_{1}},{{k}_{1}} right}$ примет вид
[{{T}_{eto f}}=left[ begin{array}{ccr} 0 & 1 & 0 \ 1 & 0 & 0 \ 0 & 0 & -1 \ end{array} right]]
Далее поворот осуществляется вокруг нового положения вектора $j$, т.е. вокруг вектора ${{j}_{1}}$. Вновь обратимся к чертежу. В этот раз нам уже не нужны координатные оси — нас интересуют лишь векторы ${{i}_{1}}$, ${{j}_{1}}$ и ${{k}_{1}}$, а также ось вращения:
Обратите внимание: в задаче сказано, что базис вращается на 90° в отрицательном направлении. Если мы смотрим на плоскость, образованную векторами ${{i}_{1}}$ и ${{k}_{1}}$, с вершины вектора ${{j}_{1}}$ (как на картинке), то отрицательное направление — это по часовой стрелке (отмечено зелёным), а положительное —против часовой стрелки (отмечено красным).
Все эти тонкости (положительное и отрицательное направление, правые и левые тройки векторов) детально описаны в уроке про матрицы поворота. Сейчас не будем подробно разбираться в них, а просто нарисуем результат:
Итак, ${{i}_{2}}={{k}_{1}}$, ${{j}_{2}}={{j}_{1}}$ и ${{k}_{2}}=-{{i}_{1}}$, поэтому матрица перехода от базиса $f=left{ {{i}_{1}},{{j}_{1}},{{k}_{1}} right}$ к базису $g=left{ {{i}_{2}},{{j}_{2}},{{k}_{2}} right}$ имеет вид
[{{T}_{fto g}}=left[ begin{array}{ccr} 0 & 0 & -1 \ 0 & 1 & 0 \ 1 & 0 & 0 \ end{array} right]]
Теперь мы можем найти матрицу ${{T}_{eto g}}$ через транзитный базис $f$:
[{{T}_{eto g}}={{T}_{eto f}}cdot {{T}_{fto g}}=left[ begin{array}{ccr} 0 & 1 & 0 \ 1 & 0 & 0 \ 0 & 0 & -1 \ end{array} right]cdot left[ begin{array}{ccr} 0 & 0 & -1 \ 0 & 1 & 0 \ 1 & 0 & 0 \ end{array} right]=left[ begin{array}{rcr} 0 & 1 & 0 \ 0 & 0 & -1 \ -1 & 0 & 0 \ end{array} right]]
[begin{align}{{T}_{eto g}} &={{T}_{eto f}}cdot {{T}_{fto g}}= \ &=left[ begin{array}{ccr} 0 & 1 & 0 \ 1 & 0 & 0 \ 0 & 0 & -1 \ end{array} right]cdot left[ begin{array}{ccr} 0 & 0 & -1 \ 0 & 1 & 0 \ 1 & 0 & 0 \ end{array} right]= \ &=left[ begin{array}{rcr} 0 & 1 & 0 \ 0 & 0 & -1 \ -1 & 0 & 0 \ end{array} right] end{align}]
Кроме того, нам известны координаты вектора $h$ в базисе $g$:
[h={{left( 1,1,1 right)}^{T}}]
Тогда в базисе $e$ координаты этого же вектора равны
[{{left[ h right]}_{e}}={{T}_{eto g}}cdot {{left[ h right]}_{g}}=left[ begin{array}{rcr} 0 & 1 & 0 \ 0 & 0 & -1 \ -1 & 0 & 0 \ end{array} right].left[ begin{matrix} 1 \ 1 \ 1 \ end{matrix} right]=left[ begin{array}{r} 1 \ -1 \ -1 \ end{array} right]]
[begin{align}{{left[ h right]}_{e}} &={{T}_{eto g}}cdot {{left[ h right]}_{g}}= \ &=left[ begin{array}{rcr} 0 & 1 & 0 \ 0 & 0 & -1 \ -1 & 0 & 0 \ end{array} right].left[ begin{matrix} 1 \ 1 \ 1 \ end{matrix} right]=left[ begin{array}{r} 1 \ -1 \ -1 \ end{array} right] end{align}]
Итак, мы нашли матрицу перехода ${{T}_{eto g}}$ и координаты вектора $h$ в исходном базисе. Задача решена.
Смотрите также:
- Критерий Сильвестра для квадратичных функций
- Работа с формулами в задаче B12
- Тест к уроку «Площади многоугольников на координатной сетке» (легкий)
- Показательные функции в задаче B15
- Задача B5: площадь кольца
- Случай четырехугольной пирамиды
Координаты и преобразования координат в линейном пространстве
Координаты векторов в данном базисе линейного пространства
Пусть — базис линейного пространства
. Каждый вектор
можно разложить по базису (см. теорему 8.1), т.е. представить в виде
, причем коэффициенты
в разложении определяются однозначно. Эти коэффициенты
называются координатами вектора
в базисе
(или относительно базиса
). Координаты
вектора
— это упорядоченный на бор чисел, который представляется в виде матрицы-столбца
и называется координатным столбцом вектора
(в данном базисе). Вектор и его координатный столбец обозначаются одной и той же буквой полужирной или светлой соответственно.
Если базис (как упорядоченный набор векторов) представить в виде символической матрицы-строки , то разложение вектора
по базису
можно записать следующим образом:
(8.6)
Здесь умножение символической матрицы-строки на числовую матрицу-столбец
производится по правилам умножения матриц.
При необходимости, если речь идет о разных базисах, у координатного столбца указывается обозначение базиса, относительно которого получены координаты, например, — координатный столбец вектора
в базисе
.
Из теоремы 8.1 следует, что равные векторы имеют равные соответствующие координаты (в одном и том же базисе), и наоборот, если координаты векторов (в одном и том же базисе) соответственно равны, то равны и сами векторы.
Линейные операции в координатной форме
Пусть — базис линейного пространства
, векторы
и
имеют в этом базисе координаты
и
соответственно, т.е.
(8.7)
Складывая эти равенства, получаем .
т.е. при сложении векторов их координаты складываются.
Умножая второе равенство в (8.7) на число , получаем
т.е. при умножении вектора на число все его координаты умножаются на это число.
Другими словами, сумма векторов имеет координаты
, а произведение
имеет координаты
. Разумеется, что все координаты получены в одном базисе
.
Замечания 8.5
1. Нетрудно показать, что координатный столбец линейной комбинации векторов
равен линейной комбинации
координатных столбцов
этих векторов.
2. Если система векторов линейно зависима (линейно независима), то их координатные столбцы, полученные относительно одного базиса, образуют линейно зависимую (соответственно, линейно независимую) систему. Это следует из равносильности равенств и
. Например, если в этих равенствах не все коэффициенты равны нулю, т.е. система векторов
и система
их координатных столбцов линейно зависимы одновременно.
3. Все свойства линейной зависимости и линейной независимости векторов переносятся без изменений на их координатные столбцы, полученные в одном и том же базисе. И наоборот, свойства для матриц-столбцов, переносятся на векторы, если матрицы-столбцы считать их координатными столбцами.
4. Выбрав в n-мерном вещественном линейном пространстве некоторый базис, можно установить взаимно однозначное соответствие: каждому вектору поставить в соответствие его координатный столбец (в вы бранном базисе), и наоборот, каждому координатному столбцу поставить в соответствие вектор. Другими словами, любой фиксированный базис n-мерного вещественного линейного пространства позволяет установить взаимно однозначное соответствие между всеми векторами вещественно го пространства
и всеми столбцами n-мерного арифметического пространства
. Это соответствие обозначается
. Для n-мерного комплексного линейного пространства
аналогичное взаимно однозначное соответствие устанавливается с пространством
.
Преобразование координат вектора при замене базиса
Пусть заданы два базиса пространства и
. Базис
будем условно называть «старым», а базис
— «новым». Пусть известны разложения каждого вектора нового базиса по старому базису:
(8.8)
Записывая по столбцам координаты векторов в базисе
, составляем матрицу:
(8.9)
Квадратная матрица , составленная из координатных столбцов векторов нового базиса
в старом базисе
, называется матрицей перехода от старого базиса к новому. При помощи матрицы перехода (8.9) формулы (8.8) можно записать в виде:
(8.10)
Умножение символической матрицы-строки на матрицу перехода
в (8.10) производится по правилам умножения матриц.
Пусть в базисе вектор
имеет координаты
, а в базисе
— координаты
, т.е.
или, короче,
Подставляя в правую часть последнего равенства выражение (8.10), получаем — два разложения вектора
в одном и том же базисе
. Коэффициенты этих разложений должны совпадать (по теореме 8.1), так как это координаты одного и того же вектора в одном базисе. Поэтому
(8.11)
Формула (8.11) устанавливает связь координат вектора в разных базисах: координатный столбец вектора в старом базисе получается в результате умножения матрицы перехода на координатный столбец вектора в новом базисе.
Пример 8.3. В пространстве многочленов степени не выше второй даны две системы многочленов:
Доказать, что каждая система является базисом пространства . Найти матрицу
перехода от базиса
к базису
. Определить координаты квадратного трехчлена
относительно базисов
и
.
Решение. Система многочленов является стандартным базисом пространства
. Докажем, что система
является базисом. По ступим следующим образом. Найдем координатные столбцы
этих многочленов в стандартном базисе. Раскладывая по базису
, получаем
Составим из этих столбцов матрицу . Ранг этой матрицы равен 3, так как
. Следовательно, столбцы
линейно независимы, тогда и многочлены
линейно независимы (см. пункт 2 замечаний 8.5). Итак, многочлены
являются базисом пространства
, а матрица
— искомая матрица перехода от базиса
к базису
. Осталось найти координаты многочлена
в этих базисах. Раскладывая
по базисам, находим
Проверим результат, вычисляя по формуле (8.11):
Результаты совпадают.
Свойства матрицы перехода от одного базиса к другому
1. Пусть имеются три базиса пространства
и известны матрицы перехода:
от базиса
к базису
;
от
к
;
от
к
. Тогда
(8.12)
Действительно, запишем связь (8.10) для данных базисов:
Подставляя первое выражение во второе равенство, получаем . Сравнивая с третьим равенством, приходим к (8.12).
2. Если — матрица перехода от базиса
к базису
, то матрица
обратима и обратная матрица
является матрицей перехода от базиса
к базису
. Координаты вектора
в базисах
и
связаны формулами:
В самом деле, пусть — матрица перехода от базиса
к базису
. Учитывая, что матрица перехода от базиса
к базису
— единичная, применяем свойство 1 к трем базисам
. Для трех базисов
аналогично получаем:
. Следовательно,
.
3. Всякая обратимая квадратная матрица n-го порядка может служить матрицей перехода от одного базиса n-мерного линейного пространства к другому базису.
Пример 8.4. В двумерном арифметическом пространстве даны два базиса:
и
. Найти матрицу
перехода от базиса
к базису
и координаты вектора
в каждом из базисов.
Решение. Рассмотрим стандартный базис пространства
. Находим координаты векторов
в стандартном базисе. Раскладываем вектор
В стандартном базисе пространства
координатный столбец
совпадает с вектором
. Для других векторов аналогично получаем
. Из координатных столбцов составим матрицы перехода (8.9) от стандартного базиса
к данным базисам
и
По свойству 1 матриц перехода имеем . .По свойству 2:
. Поэтому
В стандартном базисе пространства
координатный столбец
совпадает с вектором
. Найдем координаты этого вектора в базисе
(по свойству 2 матрицы перехода):
В самом деле, справедливо разложение
Найдем координаты вектора в базисе
двумя способами
Полученный результат подтверждает разложение:
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Изменение координат вектора при изменении
базиса
Пусть в
-мерном
линейном пространстве
выбран
базис
,
который мы будем для удобства называть
«старый» и другой базис
,
который мы будем называть «новый».
Возьмем призвольный вектор
из
.
Его координатный столбец в старом базисе
обозначим

а в новом —

Нам нужно выяснить, как связаны друг с
другом координаты в старом и в новом
базисе. Для этого нам сначала нужно
«связать» друг с другом старый и
новый базисы. Запишем разложения новых
базисных векторов по старому базису
Составим матрицу, столбцами которой
служат координатные столбцы векторов
нового базиса
Эта матрица называется матрицей перехода
от старого базиса к новому.
Замечание
18.1 Матрица перехода
всегда невырождена, то есть
.
Предложение
18.5 Координатные
столбцы в старом базисе и в новом базисе
связаны формулой
|
|
(18.1) |
где справа стоит произведение матрицы
перехода
на
матрицу-столбец.
Доказательство.
Так как
—
координатный столбец вектора
в
новом базисе, то
Заменив векторы
их
разложениями по старому базису, получим
В силу предложения
14.3 изменим порядок суммирования
Здесь мы получили разложение вектора
по
старому базису, причем координата
вектора с номером
равна

Элемент с номером
столбца
будет
иметь такой же вид. Следовательно,
формула (18.1)
доказана.
Пример 18.4
Пусть
,
то есть
—
трехмерное векторное пространство.
Пусть задан ортонормированный базис
i, j, k. Выберем другой (новый)
базис
Возьмем вектор
.
Найдем его координаты в новом базисе.
Выпишем матрицу перехода, ее столбцы —
это координаты новых базисных векторов
Пусть
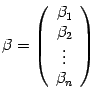
координатный столбец вектора
в
новом базисе. Тогда
|
|
(18.2) |
откуда
Найдем матрицу
по
формуле (14.14).
Находим определитель
Находим алгебраические дополнения
Следовательно,
Находим координаты вектора
Таким образом, новые координаты вектора
:
,
,
,
.
Тот же самый результат можно было
получить, записав формулу (18.2)
в виде системы уравнений
Решив эту систему, например, методом
Гаусса, найдем новые координаты
,
,
.
Соседние файлы в папке Анал_Геом
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В линейном пространстве все базисы равноправны. Тот или иной базис выбирают исходя из конкретных обстоятельств, а может быть, и вообще произвольно. Иногда удобно использовать для представления элементов линейного пространства несколько базисов, но тогда естественным образом возникает задача преобразования координат векторов, которое связано с изменением базиса.
Пусть в n-мерном линейном пространстве L заданы два базиса: старый b = (b1 … bn) и новый с = (с1 … сn). Любой вектор можно разложить по базису Ь. В частности, каждый вектор из базиса с может быть представлен в виде линейной комбинации векторов базиса b:
ci = α1ib1 + … + αnibn, i = 1,n.
Запишем эти представления в матричной форме:
или
c = bU,
где
Определение 1.6. Матрицу (1.7) называют матрицей перехода от старого базиса b к новому базису с.
Согласно данному определению, i-й столбец матрицы пе-рехода есть столбец координат i-го вектора нового базиса в старом. Поэтому говорят, что матрица перехода состоит из координат векторов нового базиса в старом, записанных по столбцам.
Обсудим некоторые свойства матрицы перехода.
1°. Матрица перехода невырождена и всегда имеет обратную.
◄ Действительно, столбцы матрицы перехода — это столбцы координат векторов нового базиса в старом. Следовательно, они, как и векторы базиса, линейно независимы. Значит, матрица U невырожденная и имеет обратную матрицу U-1 [III]. ►
2°. Если в n-мерном линейном пространстве задан базис b, то для любой невырожденной квадратной матрицы U порядка п существует такой базис с в этом линейном пространстве, что U будет матрицей перехода от базиса b к базису с.
◄ Из невырожденности матрицы U следует, что ее ранг равен n, и поэтому ее столбцы, будучи базисными, линейно независимы. Эти столбцы являются столбцами координат векторов системы с = bU. Линейная независимость столбцов матрицы U равносильна линейной независимости системы векторов с. Так как система с содержит n векторов, причем линейное пространство n-мерно, то, согласно теореме 1.4, эта система является базисом. ►
Пример 1.15. Пусть b = (b1 b2 b3) — базис линейного пространства. Тогда система векторов c1 = 2b1, c2 = — b2, c3 = b3 тоже является базисом в этом линейном пространстве. Это следует из того, что
(c1 c2 c3) = (b1 b2 b3)U,
где диагональная матрица U = diag(2, -1, 1) невырождена.
3°. Если U — матрица перехода от старого базиса b к новому базису с линейного пространства, то U-1 — матрица перехода от базиса с к базису b.
◄ Матрица U невырождена, и поэтому из равенства с = bU следует, что cU-1 = b. Последнее равенство означает, что столбцы матрицы U-1 являются столбцами координат векторов базиса b относительно базиса с, т.е., согласно определению 1.6, U-1 — это матрица перехода от базиса с к базису b. ►
4°. Если в линейном пространстве заданы базисы b, с и d, причем U — матрица перехода от базиса b к базису с, а V — матрица перехода от базиса с к базису d, то произведение этих матриц UV — матрица перехода от базиса b к базису d.
◄ Согласно определению 1.6 матрицы перехода, имеем равенства
с = bU, d = cV,
откуда
d = cV = (bU)V = b(UV),
т.е. UV — матрица перехода от базиса b к базису d. ►
Рассмотрим теперь, как преобразуются координаты про-извольного вектора в линейном пространстве при переходе от старого базиса к новому. Выберем произвольный вектор х ∈ L и разложим его в старом базисе:
Разложение того же вектора в новом базисе имеет вид
Найдем связь между старыми координатами х вектора х и новыми его координатами х’. Из соотношений (1.8), (1.9) следует, что bх = сх’. Учитывая, что с = bU, получаем bх = (bU)x’, или bх = b(Ux’). Последнее равенство можно рассматривать как запись двух разложений одного и того же вектора х в данном базисе b. Разложениям соответствуют столбцы координат х и Ux’, которые, согласно теореме 1.2 о единственности разложения вектора по базису, должны быть равны:
x = Ux’, или х’ = U-1x.
Итак, чтобы получить координаты вектора в старом базисе, необходимо столбец координат этого вектора в новом базисе умножить слева на матрицу перехода из старого базиса в новый. Матрица перехода из старого базиса в новый позволяет пересчитывать новые координаты в старые.
Пример 1.16. Рассмотрим в V2 ортонормированный базис b = (i j) из векторов i, j. Обозначим через е = (e1 е2) новый базис, который получается поворотом старого базиса b на заданный угол φ. Исходя из заданного угла поворота мы можем найти координаты векторов e1, e2 нового базиса относительно старого (рис. 1.2):
Эти разложения позволяют составить матрицу перехода U из старого базиса b в новый е, а также обратную матрицу:
Найденные матрицы перехода U (из старого базиса в новый) и U-1 (из нового базиса в старый) позволяют записать соотношения между старыми х1, х2 и новыми х’1, х’2 координатами произвольного вектора x из V2:
x’1 = x1cosφ + x2sinφ x1 = x’1cosφ + x’2sinφ
x’2 = -x1sinφ + x2cosφ x2 = x’1sinφ + x’2cosφ .
Например, вектор x = i + j в старом базисе имеет координаты х1 = 1, x2 = 1, а в новом базисе — х’1 = cosφ + sinφ, х’2 = — sinφ + соsφ.
Пример 1.17. Пусть в линейном пространстве V3 заданы два правых ортонормированных базиса: старый (i j к) и новый (i’ j’ k’). Тогда старый базис можно преобразовать в новый при помощи трех поворотов вокруг координатных осей прямоугольной системы координат, определяемой ортонормированным базисом.
Рассмотрим единичный вектор s, который одновременно лежит в плоскостях пар векторов i, j и i’ ,j’. Повернем базис (i j к) вокруг оси вектора k на некоторый угол ψ так, что вектор i совпадет с вектором s. Отметим, что вектор s ортогонален и вектору k, и вектору k’, так как является линейной комбинацией и пары i, j, и пары i’, j’. Значит, поворотом вокруг оси вектора s на некоторый угол ϑ можно добиться совмещения вектора k с вектором k’. Наконец, поворотом вокруг оси вектора k’ на некоторый угол φ совместим вектор s с вектором i’ (рис. 1.3).
Матрица перехода, соответствующая первому повороту вокруг оси вектора k, имеет вид
Матрица перехода А2, соответствующая повороту уже нового базиса вокруг оси вектора s на угол ϑ, похожа на предыдущую:
Наконец, матрица перехода, соответствующая третьему повороту вокруг оси вектора k’ имеет вид
Согласно свойству 4°, матрица перехода U из старого базиса (i j k) в новый базис (i’ j’ k’) равна U = U1U2U3 и может быть записана в виде
Дополнение 1.1. Линейное пространство над полем Р
Мы ввели понятие линейного пространства как множества произвольной природы, на котором заданы две операции: сложение элементов множества и умножение элемента множества на число. Согласно замечанию 1.1, под числами можно понимать как действительные числа, так и комплексные. Обе операции должны подчиняться аксиомам линейного пространства, при этом происхождение этих операций совершенно несущественно.
Этот подход можно развивать, давая понятию «число» расширительное толкование. Само понятие числа характеризуется в первую очередь тем, что над числами можно выполнять четыре арифметические операции. Если наличие четырех арифметических операций взять за основу, мы придем к алгебраической структуре, называемой полем. Напомним, что в самом широком толковании алгебраическая структура (алгебраическая система) — это некоторое множество, на котором задана одна или несколько алгебраических операций, подчиняющихся некоторому набору аксиом. Алгебраическая операция (внутренний закон композиции, [I-4.1]) на множестве X — это такой закон, или правило, который любому упорядоченному набору x1,…, хn элементов множества X (операндов) ставит в соответствие единственный элемент того же множества (результат этой операции). Наиболее распространены бинарные алгебраические операции, имеющие два операнда (т.е. n = 2).
Определение 1.7. Полем называют множество Р произвольной природы, на котором заданы две бинарные алгебраические операции, условно сложение (+) и умножение (•), подчиняющиеся следующим аксиомам поля:
а) сложение коммутативно: а + b = b + а;
б) сложение ассоциативно: (а + b) + с = а + (b + с);
в) существует такой элемент 0 ∈ Р (нулевой элемент, или нуль), что а + 0 = а для любого элемента a ∈ Р;
г) каждый элемент a ∈ Р имеет противоположный (симметричный) элемент (-а), такой, что а + (-а) = 0;
д) умножение коммутативно: а • b = b • а;
е) умножение ассоциативно: (а • b) • с = а • (b • с);
ж) существует такой элемент е ∈ Р (единичный), что а • e = а для любого а ∈ Р;
з) каждый элемент а ∈ Р, а ≠ 0, имеет обратный элемент а-1, такой, что а • а-1 = е;
и) умножение дистрибутивно относительно сложения: (а + b) • с = (а • с) + (b • с).
Отметим, что первые четыре аксиомы поля, относящиеся к операции сложения, совпадают с соответствующими аксиомами линейного пространства. Так же как и в линейном пространстве, исходя из аксиом в) и г) строим операцию вычитания, полагая, например, что, по определению,
а — b = а + (-b).
Аксиомы ж) и з), относящиеся к умножению, аналогичны аксиомам в) и г). Они позволяют определить операцию деления:
а/Ь = а • b-1, b ≠ 0.
Сложение и умножение задаются в поле априори, их называют основными операциями, а вычитание и деление, которые базируются на свойствах основных операций, называют дополнительными операциями.
Аксиомы поля позволяют с его элементами оперировать так же, как и с числами. Сохраняются основные правила пре-образования выражений. В записи выражений используют те же соглашения, что и в записи числовых выражений. Знак операции умножения опускают, если сомножители обозначены буквами, т.е. вместо а • b пишут ab. В выражениях действует приоритет операций умножения и деления по отношению к сложению и вычитанию. Если в выражении записаны несколько операций подряд, то сперва выполняются более приоритетные операции. Операции одного приоритета выполняются в порядке слева направо. Например, в выражении a + bc — d/f сперва следует операция умножения bс, затем деления d/f, затем сложения, последней выполняется операция вычитания.
Операция умножения на число в линейном пространстве на самом деле не опирается на специфические свойства дей-ствительных чисел. Важно лишь, что числа можно умножать (используется в аксиомах д) и е) линейного пространства) и складывать (аксиома ж)). Операция сложения вообще оперирует только элементами линейного пространства. Поэтому можно, опираясь на то же определение 1.1, ввести линейное пространство над произвольным полем Р. Такое линейное пространство определяют как множество произвольной природы, на котором заданы две операции: сложение, подчиняющееся аксиомам а)-г) линейного пространства, и умножение элементов линейного пространства на элементы поля Р, подчиняющееся аксиомам д)-з) линейного пространства.
В качестве поля Р чаще всего рассматривают поле действительных чисел R и поле комплексных чисел С. Это объясняет введенную ранее терминологию (» линейное пространство над полем действительных чисел «, «линейное пространство над полем комплексных чисел», см. замечание 1.1).
Пример 1.18. Рассмотрим однородную СЛАУ
с комплексными коэффициентами. Множество ее решений представляет собой комплексное линейное пространство. Размерность и базис этого пространства мы определим, если найдем фундаментальную систему решений этой СЛАУ. Решаются системы с комплексными коэффициентами по той же схеме, что и СЛАУ с действительными коэффициентами. Записываем матрицу СЛАУ и при помощи элементарных преобразований строк приводим ее к ступенчатому виду. Чтобы упростить вычисления, используем умножение строк на комплексные числа, сопряженные к элементам первого столбца:
Видим, что ранг матрицы СЛАУ равен двум, а значит, линейное пространство решений одномерно. В качестве базис-ных неизвестных можно взять х1, x2, тогда х3 — свободное неизвестное. Полагая х3 = 1, находим x2 = 1, х1 = 2. Таким образом, фундаментальная система решений рассматриваемой СЛАУ имеет один вектор x(1) = (2 1 1)T , а общее решение имеет вид
где С — произвольное комплексное число. #
Далее мы будем рассматривать линейные пространства только над полем действительных чисел.
Вопросы и задачи
- Может ли линейное пространство состоять из: а) двух элементов; б) одного элемента; в) 100 элементов?
- Выясните, образует ли линейное пространство:
- Пусть множество М состоит из одного элемента а. Определим операции сложения и умножения на действительное число α соответственно равенствами: а + а = а, αа = а. Является ли М линейным пространством?
- Предположим, что множество М состоит из всевозможных упорядоченных пар действительных чисел x = (α1,α2). Пусть на этом множестве заданы следующие операции: а) если
x = (α1,α2), у = (β1,β2), то x + у = (α1 + β1, α2 + β2); б) если γ ∈ R и х ∈ М, то γx = (γα1,α2). Является ли М линейным пространством? - Является ли линейным пространством множество всех действительных чисел, если операции сложения ⊕ и умножения
на число ввести следующим образом: x ⊕ у = x + у, a
x = |а|x?
- Докажите, что множество матриц-столбцов высоты n образует линейное пространство относительно матричных операций сложения и умножения.
- В линейном пространстве V3 заданы три вектора
- Пусть в линейным пространстве L задана линейно независимая система из п векторов. При каких условиях можно утверждать, что dimL = n?
- Докажите, что dimV2 = 2, dimV3 = 3
- Найдите размерность линейного пространства, состоящего из решений системы линейных однородных уравнений [III]. Как связаны между собой понятия: а) базис и фундаментальная система решений; б) размерность линейного пространства решений и ранг матрицы системы?
- Векторы a1, a2, а3, a4 линейного пространства L заданы своими координатами в некотором базисе:
- Выясните, образуют ли векторы
- Найдите координаты вектора х в базисе е = (e1 е2 е3), если известны его координаты (-1 4 3)T в базисе b = (b1 b2 b3), а базисы связаны соотношениями
- В линейном пространстве две системы векторов b = (b1 b2 b3) и е = (e1 е2 е3) заданы своими координатами в некотором базисе:
- Найдите размерность dimMnm(R) линейного пространства матриц типа m×n с элементами из R.
- Является ли матрица
- Какой вид имеет матрица перехода от старого базиса к новому, если матрица перехода от нового базиса к старому является: а) треугольной; б) симметрической; в) кососимметрической?
- Может ли в пространстве V3 матрица перехода быть кососимметрической?
- При каких условиях векторы а, b, a×b в пространстве V3 образуют базис?
- Докажите, что в линейном пространстве Кn[х] многочлены (x — a)k, k = 0,n, а = const, образуют базис. Найти координаты произвольно взятого многочлена р(х) ∈ Кn[х] в этом базисе.
а) множество всех векторов данной плоскости, не парал-лельных данной прямой, относительно линейных операций над векторами;
б) множество всех векторов плоскости с началом в начале системы координат, расположенных в правой полуплоскости, относительно обычных операций сложения и умножения векторов;
в) множество кососимметрических матриц третьего порядка относительно операции сложения матриц и умножения матрицы на число;
г) множество функций вида acost + bsint, t ∈ (- ∞,∞), a,b ∈ R, относительно обычных операций сложения функций и умножения функции на число;
д) множество многочленов степени п относительно обычных операций сложения многочленов и умножения многочлена на число.
a1 = {l;4;3}, a2 = {3;3;2}, a3 = {8;1;3}.
Выясните, является ли система этих векторов линейно зависи-мой. Если система линейно зависима, то найдите зависимость между векторами (нулевую нетривиальную линейную комбинацию этих векторов).
Является ли система этих векторов линейно зависимой? Дайте ответ, не проводя вычислений.
a1 = (1, 0, 0, 0), a2 = (1, 1, 0, 0),
a3 = (1, 1, 1, 0), a4 = (1, 1, 1, 1)
базис в линейном арифметическом пространстве R4?
Докажите, что эти системы являются базисами. Найдите: а) матрицу U = Рbe перехода от базиса b к базису е; б) матрицу Рeb обратного перехода от базиса е к базису b; в) координаты вектора е2 в обоих базисах; г) координаты вектора х = -3b1 — 5b2 + 2b3 в базисе е.
матрицей перехода от одного базиса трехмерного линейного пространства к его другому базису?
-
Линейные операции над векторами
-
Базис. Cкалярное произведение
-
Векторное и смешанное произведения векторов
-
Декартова система координат. прямая на плоскости
-
Плоскость в пространстве
-
Прямая в пространстве
-
Кривые второго порядка — I
-
Кривые второго порядка — II
-
Поверхности второго порядка
-
Матрицы и операции с ними
-
Обратная матрица
-
Ранг матрицы
-
Системы линейных алгебраических уравнений
-
Свойства решений однородных и неоднородных СЛАУ
Время на прочтение
9 мин
Количество просмотров 9.4K
Под преобразованием базиса системы координат понимается замена одного набора базовых вершин (реперов) на другой. По сравнению с обычной системой координат на векторах изменение системы координат на точечном базисе имеет особенности, связанные с тем, что базисы могут принадлежать разным пространствам.
В предыдущей части было рассмотрено определение базиса низкой размерности в пространстве высокой размерности и показано, каким образом можно определять дистанции между вершинами, не принадлежащими пространству базиса. При замене базиса требование сохранения метрических свойств системы координат также является ключевым.
Основные матрицы
Под матрицами преобразования (матрицами перехода) обычно понимают такие матрицы, при умножении на которые координат элемента (вершины) в старом базисе, получаются ее координаты в новом. На основании данных матриц преобразуются также метрические тензоры из одного базиса в другой.
Матрицы преобразования базисов содержат сравнительные характеристики двух базисов. Среди данных матриц выделятся инвариантные матрицы — их значения не зависят от выбора базиса. Например, матрица дистанций между вершинами является инвариантной.
Прямые матрицы перехода
Набор исходных базовых вершин обозначим как
(старый базис), новый набор как
(новый базис). Для преобразования координат должна быть задана матрица перехода — описание координат вершин нового базиса в старом. Такими координатами могут быть как ди-координаты вершин, так и би-координаты. Матрицу перехода в ди-координатах обозначим как
. Строка матрицы — это координаты вершины нового базиса
в старом
, соответственно столбец — это ди-координаты вершины старого базиса относительно нового.
Матрица перехода должна быть квадратной, следовательно одних координат вершин недостаточно — их количество меньше, чем количество компонент координат (из-за наличия скалярной компоненты в координатах). Поэтому необходимо добавить в данную матрицу ди-координаты вектора нормали [0; 1, 1,… 1]. После чего матрица перехода в ди-координатах становится похожей по форме на мажорный грамиан. Назовем матрицу
дистанционным тензором преобразования координат (ДТП):
Дистанционный тензор преобразования является инвариантом — его значения не зависят от базиса. При обратном переходе (от
к
) значения даной матрицы просто транспонируются (строки и столбцы меняются местами).
Поскольку ДТП — это ди-координаты, то умножая их на лапласиан (ЛМТ), можно получить би-координаты
. Структура би-координат матрицы перехода:
Первая строка данной матрицы — это би-координаты нормали:
.
В отличие от ДТП значения би-координат матрицы перехода зависят от того, для какого базиса они получены — для старого или нового. Выбор базиса определяет матрицу ЛМТ. Для определенности би-координаты перехода в базисе
обозначим как
, а в базисе
как
. Тогда имеют место следующие тождества. Для исходного базиса:
,
и для нового:
,
Здесь
и
— лапласиан и грамиан исходного базиса. Соответственно
и
— метрические тензоры нового базиса.
При переходе от одного базиса к другому требуется определить метрические тензоры нового базиса, если заданы матрицы преобразования.
Обратные матрицы перехода
Матрицы перехода
и
обратимы при условии отличного от нуля детерминанта матрицы перехода:
или
Нулевой детерминант матрицы преобразования означает ортогональность базисов. В ортогональном базисе невозможно выразить метрику проекций. Будем считать базисы неортогональными. Тогда обратные матрицы перехода выражаются через прямые следующим образом:
Матрица
— представляет собой би-координаты вершин старого базиса
относительно вершин нового
. То есть обращение би-координат дает взаимные би-координаты.
Матрица
— это лапласовский тензор преобразования базиса (ЛТП). Ее структура аналогична структуре лапласиана (ЛМТ):
Здесь главный минор
— это симметричный лапласиан. В окаймлении барицентрические координаты обратных проекций ортоцентров двух базисов (симплексов). Ортоцентр исходного базиса выражена в барицентрических координатах нового —
, а ортоцентр нового в координатах исходного —
.
Что понимается под «обратными проекциями», будет пояснено далее.
В углу лапласовского тензора находится скаляр
. Его значение отражает скалярное произведение двух базисов — нового и старого. Чтобы раскрыть его смысл, рассмотрим две ситуации — 1) базисы принадлежат одному и тому же пространству и 2) базисы принадлежат разным пространствам.
Скалярное произведение базисов одного пространства
В общем пространстве скалярное произведение базисов выражается через нормы ортоцентров (
и
) и расстояния между ортоцентрами (
):
Данная формула подобна выражению для скалярного произведения пар с общей вершиной (3.8). Поэтому можно считать соотношение (5.5) определением скалярного произведения ортоцентров.
На рисунке показана геометрическая интерпретация скалярного произведения ортоцентров (окружностей). Слева — определение через скалярное произведение смежных пар
и
. Если окружности пересекаются, то у них есть общий элемент
— элемент смежности пар.
Скалярное произведение элементов можно определить через их взаимные степени (показано на рисунке справа). Геометрическое определение степени точки дано во 2-й части. Согласно (2.9) степень точки
относительно элемента выражается через дистанцию от точки до элемента
и норму элемента
:
Можно обобщить данное определение, если вместо точки использовать другой элемент. Тогда взаимной степенью двух элементов
и
является следующая скалярная величина
:
Данная формула известна как произведение Дарбу. На правом рисунке показано построение точек, значение дистанции между которыми равно взаимной степени элементов:
По своим свойствам взаимная степень элементов обобщает свойства степени точки, то есть определяет их взаимное расположение. Если элементы находятся вне друг друга, то их взаимная степень положительна, если пересекаются — отрицательна. Под пересечением здесь понимается ситуация, при которой точки касания
(или
) находятся внутри элемента
(или
соответственно) (на рисунке взаимная степень элементов положительна).
Тогда скалярное произведение (5.5) — это взаимная полустепень элементов (и наоборот). Напомним (2.10), что под полустепенью понимается степень, деленная на (-2):
Если центры элементов совпадают (
), то их скалярное произведение будет равно их средней норме:
Скалярное произведение базисов разных пространств
Если базисы принадлежат разным пространствам, то геометрическая интерпретация их скалярного произведения
усложняется. Приведем вначале алгебраические тождества. Они аналогичны подобным для составляющих лапласовского тензора, приведенных в первой части.
Скалярное произведение базисов может выражено через отношение детерминантов дистанционной матрицы перехода и ее главного минора (см. 5.1.1):
Связь взаимной нормы базисов и барицентрических координат обратных проекций их ортоцентров:
— для вершин базиса
.
— для вершин базиса
.
Разберемся, что такое обратная проекция точки. Допустим, что у нас есть точка
, принадлежащая базису
. Тогда ее обратной проекцией на базис
будет такая точка
, что перпендикуляр, опущенный из нее на базис
, пересекается с ним в исходной точке
.
На рисунке обратной проекцией точки
на пространство
является точка
, а обратной проекцией точки
на пространство
— точка
. Точки
и
— это ортоцентры базисов
и
соответственно.
Понятие обратной проекции применимо также к нормам элементов. Норма при обратной проекции становится больше исходной (в отличие от прямой проекции). На рисунке дистанция
— это норма ортоцентра базиса
. Обратной проекцией на базис
будет дистанция:
.
Соответственно обратной проекцией нормы базиса
на базис
будет дистанция
.
Обозначая дистанцию между обратными проекциями центров как
, получаем следующее выражение для скалярного произведения базисов разных пространств:
Видим, что по форме оно совпадает со взаимной нормой базисов одного пространства (5.5), но вместо дистанций используются их обратные проекции на взаимный базис. Если базисы принадлежат одному пространству, то угол между пространствами становится нулевым, и формула (5.9) переходит в (5.5).
Все приведенные формулы применимы также и к пространству графа. В графе нет описанных сфер (базиса), но есть связность. Тогда скалярное произведение базисов графа должно отражать их взаимную связность.
Расчет нового базиса
Здесь также рассмотрим две ситуации: 1) новый и старый базис принадлежат одному и тому же пространству и 2) принадлежат разным пространствам. Первый случай как правило относится к обычному геометрическому пространству (при смене базиса тут редко меняется его пространство), второй — к пространству графа.
Определить принадлежность элемента (вершины) пространству базиса можно по его норме в данном пространстве. Если равна нулю, то элемент принадлежит пространству.
Единое пространство базисов
Для получения грамиана нового базиса
необходимо умножить ди-координаты элементов нового базиса
на би-координаты
. Полученная матрица будет матрицей скалярных произведений в новом базисе
(см. 4.4.2 в предыдущей части). Таким образом если пространства базисов совпадают, то матрица норм вершин нового базиса относительно старого — это и есть грамиан нового базиса:
Мы пометили данный грамиан штрихом, чтобы помнить об условии общего пространства базисов. Лапласиан нового базиса (ЛМТ) можно получить обращением грамиана (ДМТ):
Координаты элемента в новом базисе могут быть выражены через координаты в старом и матрицы перехода. Ди-координаты
:
Би-координаты элемента в новом базисе
:
Все приведенные выражения аналогичны формулам изменения координат и в обычных (векторных) системах координат. В пределах общего пространства использование точечного базиса аналогично использованию векторного.
Пример преобразования базиса
На КДПВ показан основной базис
из 3-х вершин (A, B, C) и новый базис
, образованный вершинами (P, Q, R). Значения ДМТ основного базиса есть в первой статье:
begin{array}{c | c c c c}
Gm_{aa} & * & A & B & C \
hline
* & 0 & 1 & 1 & 1 \
A & 1 & 0 & -4.5 & -8 \
B & 1 & -4.5 & 0 & -12.5 \
C & 1 & -8 & -12.5 & 0 \
end{array}
Звездочкой обозначена скалярная компонента. Значение лапласиана (ЛМТ) можно получить обращением грамиана (ДМТ).
Дистанционную матрицу перехода считаем заданной. Ее вид:
begin{array}{c | c c c c}
Dm_{pa} & * & A & B & C \
hline
* & 0 & 1 & 1 & 1 \
P & 1 & -1.0 & -2.5 & -13.0 \
Q & 1 & -6.5 & -2.0 & -6.5 \
R & 1 & -12.5 & -2.0 & -20.5 \
end{array}
Значения би-координат матрицы перехода получаем по формуле (5.2.1):
begin{array}{c | c c c c}
Ba_p{}^a & * & A & B & C \
hline
* & 1 & 0 & 0 & 0 \
P & -1.5 & 0.91(6) & 0.(3) & -0.25 \
Q & 2.0 & -0.5 & 1.0 & 0.50 \
R & -5.0 & -0.(6) & 1.(6) & 0.0 \
end{array}
Скалярной компонентой (значения первого столбца) би-координат являются орбитали. Сумма барицентрических компонент равна 1.
Лапласовский тензор преобразования (5.3.1):
begin{array}{c | c c c c}
Lt^{ap} & * & P & Q & R \
hline
* & 2.15 & 0.30 & 1.15 & -0.45 \
A & 0.058(3) & 0.11(6) & -0.0(6) & -0.05 \
B & 0.9(6) & -0.0(6) & -0.0(3) & 0.10 \
C & -0.025 & -0.05 & 0.10 & -0.05 \
end{array}
Вектор
— это барицентрические координаты ортоцентра старого базиса (симплекса ABC) относительно вершин нового (PQR). Соответственно, вектор
— наоборот, барицентрические координаты ортоцентра симплекса PQR относительно вершин старого базиса.
Используя (5.10.1), получаем грамиан нового базиса:
begin{array}{c | c c c c}
Gm’_{pp} & * & P & Q & R \
hline
* & 0 & 1 & 1 & 1 \
P & 1 & 0 & -6.5 & -8.5 \
Q & 1 & -6.5 & 0 & -4.0 \
R & 1 & -8.5 & -4.0 & 0 \
end{array}
Базисы в разных пространствах
Если базисы находятся в разных пространствах, то формула (5.10.1) будет давать неверные значения полудистанций между вершинами нового базиса. В предыдущей части было показано, что в общем случае для нахождения правильных дистанций между вершинами необходимо к матрице норм прибавить фундаментальную матрицу
(4.5):
Следовательно, при преобразовании базиса к базису из другого пространства необходимо наряду с матрицами перехода задать фундаментальную матрицу нового базиса (относительно исходного).
Для задания фундаментальной матрицы полезно вспомнить ее геометрический смысл (см. 4.6.1). Элемент фундаментальной матрицы — это скалярное произведение нормалей, направленных к вершинам из их проекций на пространство базиса. В частном (но практически важном) случае общего надпространства элемент фундаментальной матрицы вычисляется как произведение расстояний от заданных элементов до пространства базиса.
Скалярное произведение обратных проекций
В пространстве графа значения фундаментальной матрицы можно получить через матрицу смежности между старым и новым базисом
. Элементами данной матрицы является вес связей между вершинами двух базисов. Если матрица известна и обратима, то можно получить обратную матрицу смежности:
Полученная матрица (как и матрица смежности) является инвариантом — ее значения не зависят от выбора базиса. Значения элементов матрицы
отражают скалярное произведение обратных проекций между вершинами двух базисов. На рисунке представлена поясняющая схема.
Здесь точка A принадлежит базису
, а точка P — базису
. Штрихами помечены обратные проекции точек на смежный базис. Тогда значение элемента матрицы — это скалярное произведение векторов
и
:
Можно выразить данное соотношение через расстояния от вершин до гиперплоскости пересечения пространств (на рисунке — точка O) и угол между пространствами
:
Из формулы (5.13.2′) видно, что если базисы ортогональны
, то элементы скалярного произведения обращаются в бесконечность.
Итоговые формулы преобразования базисов
Удобно привести размерность матрицы скалярных произведений проекций
к размерности остальных матриц перехода, окаймив ее нулями. Тогда фундаментальная матрица базиса
определяется как
Объединяя все вместе, получаем конечное выражение для грамиана нового базиса
:
Симметричным образом выражается исходный базис при заданных матрицах преобразования:
Здесь
и
— би-координаты матриц перехода (5.2.1) и (5.2.2).
— общая дистанционная матрица преобразования:
Данная матрица является инвариантом, состоит из двух частей — дистанционного тензора преобразования
и добавки, связанной с некомпланарностью пространств базисов, — матрицы скалярных произведений проекций
.
Лапласовский тензор базисов получается обращением ДМТ (5.15). Задача определения связи базисов решена.
Подводим итоги. Тяжелая формульная часть серии в целом завершена. Приведены основные понятия и тождества. Точечные базисы — это полезный и мощный инструмент для различных прикладных задач. В заключительной статье рассмотрим базис простейшей структуры — в виде звезды.









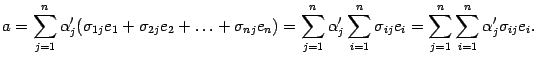
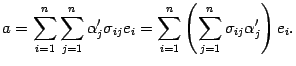

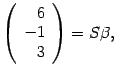





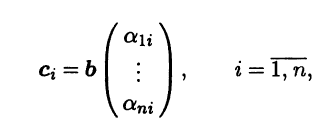
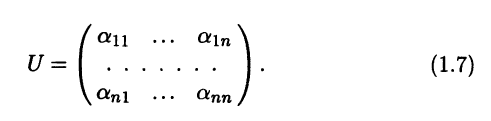
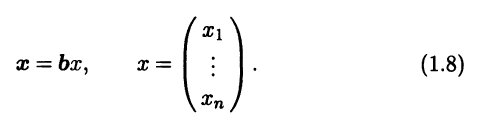
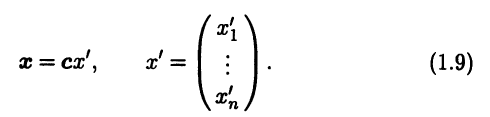
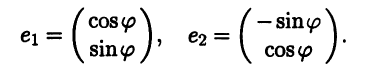
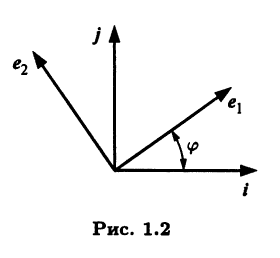
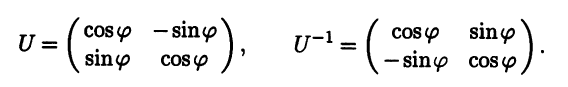
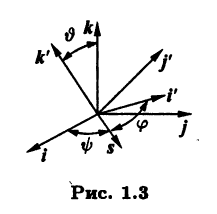
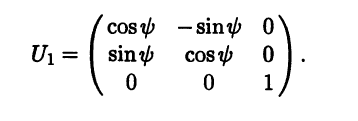
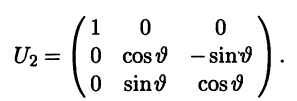
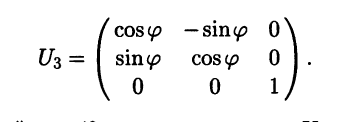
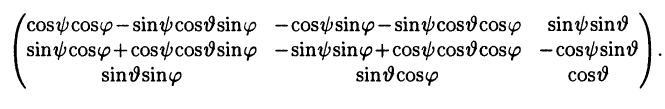
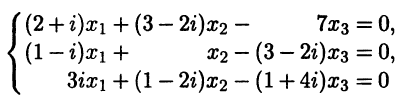
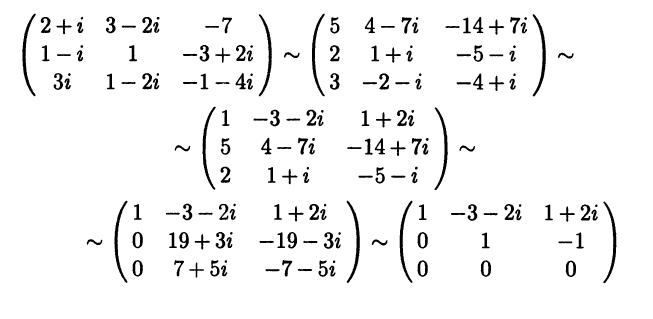
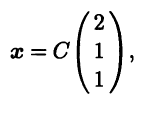
 на число ввести следующим образом: x ⊕ у = x + у, a
на число ввести следующим образом: x ⊕ у = x + у, a