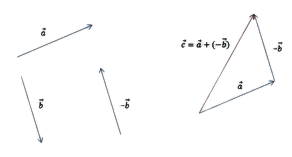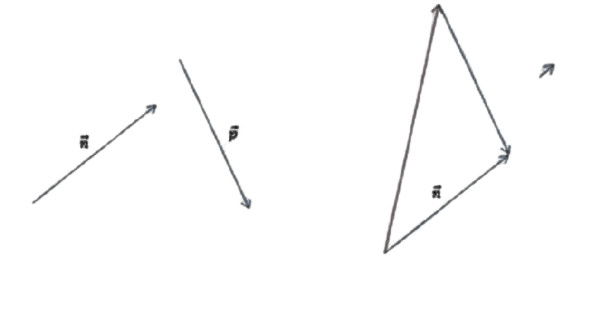Как найти координаты разности векторов формула - Исправление недочетов и поиск решений вместе с Examum.ru

Содержание:

Формула
Примеры нахождения разности векторов

Формула

Чтобы найти разность векторов $bar{a}-bar{b}$, заданных на плоскости координатами $bar{a}=left(a_{x} ; a_{y}right)$ и $bar{b}=left(b_{x} ; b_{y}right)$, необходимо вычесть из
координат первого вектора соответствующие
координаты второго, то есть

$$bar{a}-bar{b}=left(a_{x}-b_{x} ; a_{y}-b_{y}right)$$

В случае если векторы заданы в пространстве, то есть $bar{a}=left(a_{x} ; a_{y} ; a_{z}right)$ и $bar{b}=left(b_{x} ; b_{y} ; b_{z}right)$, то их разность равна

$$bar{a}-bar{b}=left(a_{x}-b_{x} ; a_{y}-b_{y} ; a_{z}-b_{z}right)$$

Примеры нахождения разности векторов

Пример

Задание. Найти разность векторов $bar{a}-bar{b}$, где
$bar{a}=(3 ; 0)$ и $bar{b}=(1 ; 2)$

Решение. Для нахождения разности векторов
$bar{a}$ и
$bar{b}$, вычтем их соответствующие координаты:

$$bar{a}-bar{b}=(3 ; 0)-(1 ; 2)=(3-1 ; 0-2)=(2 ;-2)$$

Ответ. $bar{a}-bar{b}=(2 ;-2)$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти разность векторов
$bar{a}-bar{b}-bar{c}$, заданных в трехмерном пространстве своими координатами $bar{a}=(2 ;-3 ; 1), bar{b}=(1 ; 0 ;-2)$ и $bar{c}=(-1 ; 2 ; 3)$

Решение. Для нахождения искомой разности векторов вычтем их соответствующие координаты:

$$begin{aligned} bar{a}-bar{b}-bar{c}=(2 ;-3 ; 1)-(1 ; 0 ;-2)-(-1 ; 2 ; 3)=& \=(2-1-(-1) ;-3-0-2 ; 1-(-2)-3)=(2 ;-5 ; 0) end{aligned}$$

Ответ. $begin{aligned} bar{a}-bar{b}-bar{c}=(2 ;-5 ; 0) end{aligned}$

Читать дальше: как найти проекцию вектора.

Источник

Как найти разность векторов

ФОРМУЛА

Чтобы найти разность векторов(
overline{a}-overline{b}
), заданных на плоскости координатами (
overline{a}=left(a_{x} ; a_{y}right)quad{и}quad overline{b}=left(b_{x} ; b_{y}right)
) , необходимо вычесть из координат первого вектора соответствующие координаты второго, т.е.

(
overline{a}-overline{b}=left(a_{x}-b_{x} ; a_{y}-b_{y}right)
)

Если векторы заданы в пространстве, то есть (
tilde{a}=left(a_{x} ; a_{y} ; a_{z}right)quad{и}quad overline{b}=left(b_{x} ; b_{y} ; b_{z}right)
)тогда их различие

(
overline{a}-overline{b}=left(a_{x}-b_{x} ; a_{y}-b_{y} ; a_{z}-b_{z}right)
)

ПРИМЕР

Задание: Найти разность векторов (
overline{a}-overline{b}, text { где } overline{a}=(3 ; 0)quad{и}quad overline{b}=(1 ; 2)
)

Решение: Для нахождения разности векторов (
overline{a}quad иquad overline{b}
) вычитаем их соответствующие координаты: (
overline{a}-overline{b}=(3 ; 0)-(1 ; 2)=(3-1 ; 0-2)=(2 ;-2)
)

Ответ: (
overline{a}-overline{b}=(2 ;-2)
)

ПРИМЕР

Задание: Найти разность векторов (
overline{a}-overline{b}-overline{c}
) , заданных в трехмерном пространстве их координатами (
overline{a}=(2 ;-3 ; 1), overline{b}=(1 ; 0 ;-2)
) и (
overline{c}=(-1 ; 2 ; 3)
)

Решение: Чтобы найти нужную разницу векторов, вычтите их соответствующие координаты:

(
overline{a}-overline{b}-overline{c}=(2 ;-3 ; 1)-(1 ; 0 ;-2)-(-1 ; 2 ; 3)=
)

(
=(2-1-(-1) ;-3-0-2 ; 1-(-2)-3)=(2 ;-5 ; 0)
)

Ответ: (
overline{a}-overline{b}-overline{c}=(2 ;-5 ; 0)
)

Источник

Решение. Для нахождения разности векторов $bar$ и $bar$, вычтем их соответствующие координаты:

Решение. Для нахождения искомой разности векторов вычтем их соответствующие координаты:

Остались вопросы?

Здесь вы найдете ответы.

Поможем выполнить
любую работу

Все еще сложно?

Наши эксперты помогут разобраться

Не получается написать работу самому?

Доверь это кандидату наук!

Ищещь ответ на вопрос с которым нужна помощь?

Определение разности двух векторов

В математике и физике студентам и школьникам зачастую попадаются задачи на векторные величины и на выполнение различных операций над ними. В чём же отличие векторных величин от привычных нам скалярных, единственная характеристика которых — это численное значение? В том, что они обладают направлением.
[block >

Определения векторной математики

Введём главные определения, используемые при выполнении линейных операций.

Вектором называют направленный (имеющий точку начала и точку конца) отрезок.
Длина (модуль) — это длина направленного отрезка.
Коллинеарными называют такие два вектора, которые либо параллельны одной и той же прямой, либо одновременно лежат на ней.
Противоположно направленными векторами называют коллинеарные и при этом направленные в разные стороны. Если же их направление совпадает, то они являются сонаправленными.
Вектора являются равными, когда они сонаправлены и одинаковы по модулю.
Суммой двух векторов a и b является такой вектор c, начало которого совпадает с началом первого, а конец — с концом второго при условии, что b начинается в той же точке, в которой заканчивается a.
Разностью векторов a и b называют сумму a и (—b), где (—b) — противоположно направленный к вектору b. Также определение разности двух векторов может быть дано следующее: разностью c пары векторов a и b называют такой c, который при сложении с вычитаемым b образует уменьшаемое a.

Аналитический метод

Аналитический способ подразумевает получение координат разности по формуле без построения. Возможно выполнить вычисление для плоского (двухмерного), объёмного (трёхмерного) или же n-мерного пространства.

Для двухмерного пространства и векторных величин a <a₁; a₂> и b <b₁; b₂> расчёты будут иметь следующий вид: c <c₁; c₂> = <a₁ — b₁; a₂ — b₂>.

В случае с добавлением третьей координаты расчёт будет проводиться аналогично, и для a <a₁; a₂; a₃> и b <b₁; b₂; b₃> координаты разности будут также получены попарным вычитанием: c <c₁; c₂; c₃> = <a₁ — b₁; a₂ — b₂; a₃ — b₃>.

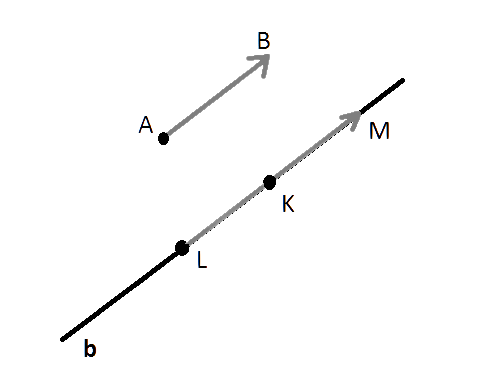
Вычисление разности графически

Для того чтобы построить разность графическим способом, следует воспользоваться правилом треугольника. Для этого необходимо выполнить следующую последовательность действий:

По заданным координатам построить векторы, для которых нужно найти разность.
Совместить их концы (т. е. построить два направленных отрезка, равных заданным, которые будут оканчиваться в одной и той же точке).
Соединить начала обоих направленных отрезков и указать направление; результирующий будет начинаться в той же точке, где начинался вектор, являющийся уменьшаемым, и заканчиваться в точке начала вычитаемого.

[block > Результат операции вычитания показан на рисунке ниже.

Также существует метод построения разности, незначительно отличающийся от предыдущего. Его суть заключается в применении теоремы о разности векторов, которая формулируется следующим образом: для того чтобы найти разность пары направленных отрезков, достаточно найти сумму первого из них с отрезком, противоположно направленным ко второму. Алгоритм построения будет иметь следующий вид:

Построить исходные направленные отрезки.
Тот, что является вычитаемым, необходимо отразить, т. е. построить противоположно направленный и равный ему отрезок; затем совместить его начало с уменьшаемым.
Построить сумму: соединить начало первого отрезка с концом второго.

Результат такого решения изображён на рисунке:

Решение задач

Для закрепления навыка разберём несколько заданий, в которых требуется рассчитать разность аналитически или графически.

Задача 1. На плоскости заданы 4 точки: A (1; —3), B (0; 4), C (5; 8), D (—3; 2). Определить координаты вектора q = AB — CD, а также рассчитать его длину.

Решение. Вначале следует найти координаты AB и CD. Для этого из координат конечных точек вычтем координаты начальных. Для AB началом является A (1; —3), а концом — B (0; 4). Рассчитаем координаты направленного отрезка:

Аналогичный расчёт выполняется для CD:

Теперь, зная координаты, можно найти разность векторов. Формула для аналитического решения плоских задач была рассмотрена ранее: для c = a — b координаты имеют вид <c₁; c₂> = <a₁ — b₁; a₂ — b₂>. Для конкретного случая можно записать:

Чтобы найти длину q, воспользуемся формулой | q | = √(q₁² + q₂²) = √((— 9)² + (— 1)²) = √(81 + 1) = √82 ≈ 9,06.
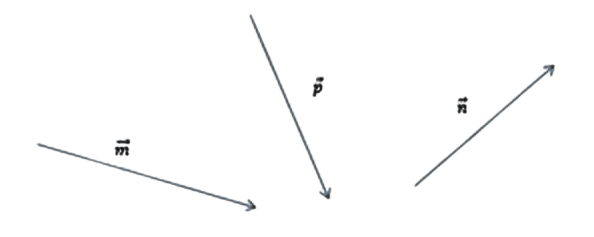
[block > Задача 2. На рисунке изображены векторы m, n и p.

Необходимо построить для них разности: p — n; m — n; m — n — p. Выяснить, какая из них обладает наименьшим модулем.

Решение. В задаче требуется выполнить три построения. Рассмотрим каждую часть задания более подробно.

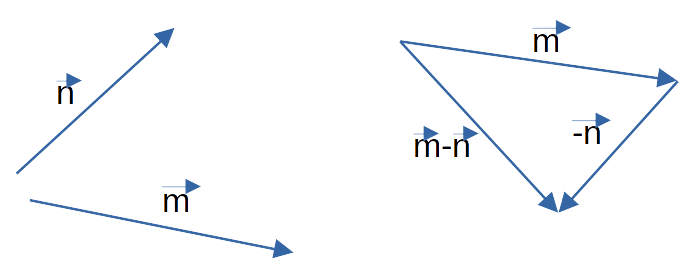
Часть 1. Для того чтобы изобразить p — n, воспользуемся правилом треугольника. Для этого при помощи параллельного переноса соединим отрезки так, чтобы совпала их конечная точка. Теперь соединим начальные точки и определим направление. В нашем случае вектор разности начинается там же, где и вычитаемый n.

Часть 2. Изобразим m — n. Теперь для решения воспользуемся теоремой о разности векторов. Для этого следует построить вектор, противоположный n, а затем найти его сумму с m. Полученный результат будет выглядеть так:

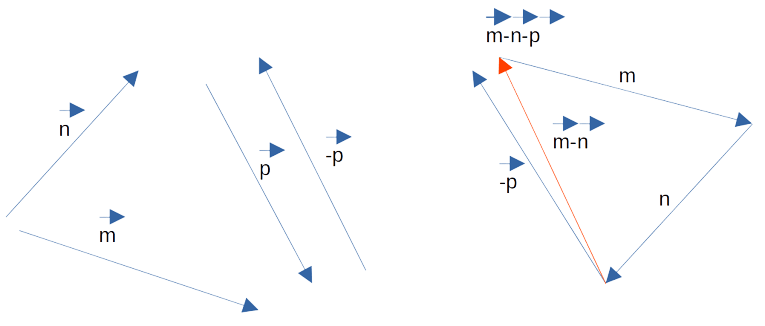
[block > Часть 3. Для того чтобы найти разность m — n — p, следует разбить выражение на два действия. Поскольку в векторной алгебре действуют законы аналогичные законам арифметики, то возможны варианты:

m — (n + p): в этом случае вначале строится сумма n + p, которая затем вычитается из m;
(m — n) — p: здесь сначала нужно найти m — n, а затем отнять от этой разности p;
(m — p) — n: первым действием определяется m — p, после чего из полученного результата нужно вычесть n.

Так как в предыдущей части задачи мы уже нашли разность m — n, нам остаётся лишь вычесть из неё p. Построим разность двух данных векторов при помощи теоремы о разности. Ответ показан на изображении ниже (красным цветом обозначен промежуточный результат, а зелёным — окончательный).

Остаётся определить, модуль какого из отрезков является наименьшим. Вспомним, что понятия длины и модуля в векторной математике являются идентичными. Оценим визуально длины p — n, m — n и m — n — p. Очевидно, что самым коротким и обладающим наименьшим модулем является ответ в последней части задачи, а именно m — n — p.
[block > [block >

Сумма и разность векторов

В данной публикации мы рассмотрим, как найти сумму и разность векторов, приведем геометрическую интерпретацию, а также формулы, свойства и примеры этих действий.

Сумма векторов

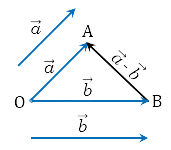
Сложение векторов выполняется по правилу треугольника.

Геометрическая интерпретация:

Суммой a и b является вектор c , начало которого совпадает с началом a , а конец – с концом b . При этом конец вектора a должен совпадать с началом вектора b .

Для сложения векторов также используется правило параллелограмма.

Два неколлинеарных вектора a и b можно привести к общему началу, и в этом случае их суммой является вектор c , совпадающий с диагональю параллелограмма и берущий начало в той же точке, что и исходные векторы.

Формула сложения векторов

Элементы вектора c равняются попарной сумме соответствующих элементов a и b .

» data-lang=»default» data-override=»<«emptyTable»:»»,»info»:»»,»infoEmpty»:»»,»infoFiltered»:»»,»lengthMenu»:»»,»search»:»»,»zeroRecords»:»»,»exportLabel»:»»,»file»:»default»>» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>

Для плоских задач	a + b = x + b_x; a_y + b_y>
Для трехмерных задач	a + b = x + b_x; a_y + b_y; a_z + b_z>
Для n-мерных векторов	a + b = 1 + b₁; a₂ + b₂; . a_n + b_n>

Свойства сложения векторов

1. Коммутативность: a + b = b + a

2. Ассоциативность: ( a + b ) + c = a + ( b + c )

3. Прибавление к нулю: a + 0 = a

4. Сумма противоположных векторов: a + (- a ) = 0

Примечание: Вектор – a коллинеарен и равен по длине a , но имеет противоположное направление, из-за чего называется противоположным.

Разность векторов

Для вычитания векторов также применяется правило треугольника.

Если из вектора a вычесть b , то получится c , причем должно соблюдаться условие:

Формула вычитания векторов

Элементы вектора c равны попарной разности соответствующих элементов a и b .

Для плоских задач	a — b = x — b_x; a_y — b_y>
Для трехмерных задач	a — b = x — b_x; a_y — b_y; a_z — b_z>
Для n-мерных векторов	a — b = 1 — b₁; a₂ — b₂; . a_n — b_n>

Примеры задач

Задание 1
Вычислим сумму векторов и .

Задание 2
Найдем разность векторов и .

источники:

Определение разности двух векторов

Сумма и разность векторов

Источник

Для того, чтобы уяснить, что собой представляет разность векторов, введём понятие откладывания вектора от определённой точки и понятие суммы векторов.

Определение

Если некоторая точка A является началом вектора a, то говорят, что он является отложенным от точки A.

Теорема. От каждой точки можно отложить только один вектор, имеющий заданный модуль и направление. Докажем эту теорему.

Доказательство:

В случае, когда вектор нулевой, то теорема очевидна. Нулевые вектора в одной и той же точки совпадают между собой, т. е. являются одним и тем же вектором.

Сделаем построение. Точкой A обозначим начало вектора a, а точкой B его конец. Пусть у нас имеется некоторая точка K. Проведём через неё прямую b, которая параллельна вектору a. Отложим на данной прямой равные по своей абсолютной величине вектору a отрезки KL и KM. Из векторов, образованных этими отрезками искомым можно назвать только сонаправленный с a.

Единственность нашего вектора следует из того, что мы построили и видим.

Теорема доказана.

Определение

Суммой векторов a и b называется вектор с тем же началом, что вектор a и концом, как у вектора b. При этом вектор b должен начинаться в той же самой точке, в которой заканчивается вектор a.

Равные векторы, начинающиеся в разных точках, нередко обозначают одной и той же буквой. Иногда про подобные векторы говорят, как об одном и том же векторе, отложенном из разных мест.

Разность векторов

Определение

Разностью векторов a и b называется сумма вектора a c вектором, который противоположно направлен к вектору b.

По-другому это определение можно сформулировать следующим образом: разностью двух векторов a и b называется вектор c, который при сложении с вычитаемым b образует уменьшаемое, т. е. вектор a.

Формулами это записывается так:

b + c = a

a – b = c

Как найти разность векторов аналитическим способом

В двухмерном пространстве векторов a {x₁, y₁} и b {x₂, y₂} разность векторов можно вычислить, как показано ниже:

c {x₃, y₃} = {x₁ — x₂, y₁ — y₂}.

Вычитание векторов в 3-мерном пространстве выглядит следующим образом:

c {x₃; y₃; z₃} = {x₁ — x₂, y₂ — y₂, z₁ — z₂}.

Как найти разность векторов графическим способом

Нужно воспользоваться правилом треугольника. Последовательность действий следующая:

Постройте по координатам векторы, для которых требуется найти разность;
Совместите концы построенных векторов. Для этого нужно построить два равных заданным направленных отрезка, концы у которых будут в одной и той же точке;
Соедините начала построенных отрезков и укажите их направление. Вектор c, называемый разностью векторов, будет иметь своё начало в той же точке, где начинается вектор, именуемый уменьшаемым и заканчивается в точке начала вычитаемого. Смотрите рисунок ниже.

Есть ещё один способ графического нахождения разности векторов. Он предусматривает следующий порядок действий:

Постройте исходные направленные отрезки;
Отразите вычитаемый отрезок. Для этого постройте противоположно направленный и равный ему отрезок и затем совместите начало этого отрезка с уменьшаемым;
Постройте сумму, т. е. соедините начало первого отрезка и конец второго.

Нет времени решать самому?

Наши эксперты помогут!

Примеры вычисления разности векторов

Примеры

Вычислить вектор c, который представляет собой разность вектора a ={1;
2} и вектора b = {4; 8}.

Решение:

Действуем по выше указанному правилу

a — b = {1 — 4; 2 — 8} = {-3; -6}

Ответ: с{-3; -6}.

Вычислить вектор c, который является разностью векторов a = {1; 2; 5} и
b = {4; 8; 1}.

Решение:

Почти всё делается, как в уже рассмотренном примере, только добавляется третья координата.

a — b = {1 — 4; 2 — 8; 5 — 1} = {-3; -6; 4}

Ответ: c {-3; -6; 4}.

На рисунке векторы

Требуется построить разности: p — n, m —
n,m — n — p и найти ту из них, которая
имеет наименьший модуль.

Решение:

Для изображения p — n проще всего воспользоваться правилом треугольника. Параллельным переносом
отрезки
следует соединить таким образом, чтобы совпали их конечные точки. Далее нужно соединить начальные точки и
определить направление. В нашем случае вектор разности берёт своё начало там же, где и вычитаемый n.

Для изображения m — n правильнее будет воспользоваться вторым графическим способом нахождения разности
векторов. Сначала построим вектор противоположный n и найдём его суммы с вектором m.

Для нахождения разности m — n — p разобьём это выражение на два действия. Возможны следующие варианты:

m — (n + p). Сначала нужно построить сумму,
затем уже вычесть её из m;
(m — n) — p. Сначала находим m — n,
осле этого от полученной разности отнимаем p;
(m— p) — n. Сначала определяем m — p, затем от
полученного результата отнимаем n.

Из вычислений выше нам известна разность m — n. Для получения решения нам нужно вычесть из неё
p.
Используя определение 3 построим разность векторов на рисунке. На нём изображён окончательный результат
и промежуточный.

Теперь нужно определить наименьший модуль. В нашем случае для этого можно лишь визуально оценить длины p — n,
m — n и m — n — p. Из построения сразу видно, что наименьшим модулем обладает вектор разности m — n —
p.

Источник

Вычитание векторов

Содержание:

Как происходит вычитание векторов
Как производится вычитание векторов по координатам
Основные правила вычисления
- Правило треугольника
- Правило параллелограмма
Примеры задач на понятие разности векторов

Как происходит вычитание векторов

Определение

Вычитание векторов — это арифметическое действие в геометрии, при котором из одного вектора отнимают другой.

Чтобы вычесть (overrightarrow b) из (overrightarrow а), нужно найти такой (overrightarrow с), сложение которого с вектором (overrightarrow b) составляло бы (overrightarrow а).

Таким образом, формула разности будет выглядеть так:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

(overrightarrow а-overrightarrow b=overrightarrow а+left(-overrightarrow bright))

Если задан (overrightarrow а), то можно построить противоположный ему (-overrightarrow а), равный по длине, но противоположно направленный. Тогда происходит сведение двух противоположно направленных векторов к нулевому:

(overrightarrow а+left(-overrightarrow аright)=0)

Как производится вычитание векторов по координатам

Если необходимо произвести вычитание векторов по координатам, то следует просто вычесть соответствующие точки. То есть если из (overrightarrow а) отнимается (overrightarrow b), то из X₁ отнимаем X_2, из Y₁ Y₂ и из Z₁ Z₂.

Проиллюстрируем координатное пространство:

Вычитание векторов по координатам

Основные правила вычисления

Для того, чтобы найти значение разности векторов, можно использовать несколько способов.

Правило треугольника

Чтобы графически продемонстрировать разность, необходимо отложить от произвольной точки вектор (overrightarrow а), из его начала (overrightarrow b). Тогда вектор, начало которого совпадает с концом ( overrightarrow b), а конец — с концом (overrightarrow a), и будет искомым вектором разности (overrightarrow a;-;overrightarrow b). Проиллюстрируем это:

Правило треугольника

Правило параллелограмма

Если два неколлинеарных, то есть непараллельных вектора (overrightarrow а) и (overrightarrow b) имеют общее начало, то их разностью является вектор, совпадающий с диагональю параллелограмма, построенного на (overrightarrow а) и (overrightarrow b), причем начало этой диагонали совпадает с концом (overrightarrow b), а конец — с концом (overrightarrow а).

Если векторы (overrightarrow а) и (overrightarrow b) заданы в некотором промежутке:

(overrightarrow a=left(а_1;а_2right),;overrightarrow b=left(b_1;b_2right))

то, чтобы найти координаты их разности (overrightarrow a;-;overrightarrow b), необходимо от точек (overrightarrow a) отнять соответствующие точки (overrightarrow b):

(overrightarrow a;-;overrightarrow b=left(a_1;a_2right)-left(b_1;b_2right)=left(a_1-b_1;a_2-b_2right))

Проиллюстрируем правило многоугольника:

Правило параллелограмма

Примеры задач на понятие разности векторов

Задача 1

Дано

(overrightarrow a;=left(2;-1right),;overrightarrow b=left(0;2right))

Найти: (overrightarrow с=2overrightarrow a-3overrightarrow b;)

Решение

Найдем координаты (2overrightarrow a) и (3overrightarrow b). Для этого умножим каждую на два и три:

(2overrightarrow а=2timesleft(2;-1right)=left(2times2;2timesleft(-1right)right)=left(4;-2right), 3overrightarrow b=3timesleft(0;2right)=left(3times0;3times2right)=left(0;6right))

Тогда искомый вектор:

(overrightarrow с=2overrightarrow a-3overrightarrow b=left(4;-2right)-left(0;6right)=left(4-0;;-2-6right)=left(4;-8right))

Ответ: (overrightarrow с=left(4;-8right).)

Задача 2

Дано

(Аleft(1;-1;0right),;Вleft(2;3;-1right),;Сleft(0;-1;0right),;Dleft(1;0;2right))

Найти: координаты (overrightarrow{AB}-overrightarrow{CD}.)

Решение

Для начала найдем проекции (overrightarrow{AB}) и (overrightarrow{CD}).

Для этого от координат конца вектора, то есть точек B и D, нужно отнять соответствующие проекции его начала, то есть точек А и С.

(overrightarrow{AB}=left(2-1;3-left(-1right);-1-0right)=left(1;4;-1right),;overrightarrow{CD}=left(1-0;0-left(-1right);2-0right)=left(1;1;2right))

Тогда для нахождения координат разности (overrightarrow{AB}-overrightarrow{CD}), от координат первого вычтем координаты второго:

(overrightarrow{AB}-overrightarrow{CD}=left(1;4;-1right)-left(1;1;2right)=left(1-1;4-1;-1-2right)=left(0;3;-3right))

Ответ: (overrightarrow{AB}-overrightarrow{CD}=left(0;3;-3right))

Насколько полезной была для вас статья?

Рейтинг: 3.00 (Голосов: 4)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Текст с ошибкой:

Расскажите, что не так

Поиск по содержимому

Источник