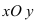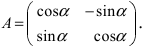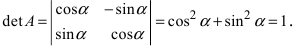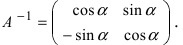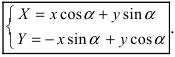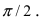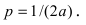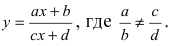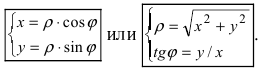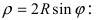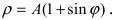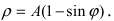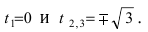Как найти координаты точек при параллельном переносе

Если при параллельном переносе одна точка переходит в другую точку, какую информацию можно получить из этих данных, если координаты обеих точек известны?

Параллельный перенос, при котором точка A (x;y) переходит в точку

A1 (x1; y1), задаётся формулами:

1) При параллельном переносе точка A (-2;7) переходит в точку B (4;-3). Найти формулы параллельного переноса.

Решение:

Чтобы найти числа a и b в формулах параллельного переноса, подставим в них координаты точек A и B:

x=-2, y=7; x1=4, y1=-3:

Отсюда a=6, b= -4. Следовательно, формулы параллельного переноса

2) При параллельном переносе точка A (-9; 4) переходит в точку B (2; -2). В какую точку при этом параллельном переносе переходит точка C (0; 7)?

Решение:

Сначала найдём формулы параллельного переноса, который переводит точку A в точку B. Для этого в формулы подставим координаты точек A и B:

Отсюда a=11, b=-6. Значит, данный параллельный перенос задаётся формулами

Чтобы найти, в какую точку переходит C, подставим её координаты x=0, y=7 в формулы параллельного переноса и найдём x1и y1:

Таким образом, точка C переходит в точку (11; 1).

Ответ: (11; 1).

3) Найти координаты точки, являющейся образом точки A (-8; 5) при параллельном переносе на вектор

Решение:

x=-8; y=5; a1=3; a2=4:

Ответ: (5;9).

Содержание:

Преобразования декартовой системы координат

Параллельный перенос и поворот системы координат

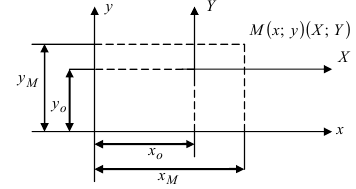
1. Параллельный перенос системы координат. Пусть на плоскости две декартовы системы координат, причем соответствующие оси параллельны и сонаправлены (Рис.46):

Рис. 46. Параллельный перенос одной системы координат относительно другой системы.

Систему координат

Пример:

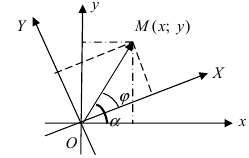
Дана точка М(3;2) и начало новой системы координат 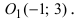Вычислить положение точки М в новой системе отсчета.

Решение:

Используя формулы, определяющие параллельный перенос одной системы отсчета относительно другой, получим 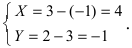Следовательно, точка М в новой системе отсчета имеет координаты М(4; -1).

2. Поворот системы координат. Пусть даны две системы координат (старая и новая), имеющие общее начало отсчета и повернутые относительно друг друга на угол 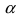(Рис. 47):

Рис. 47. Поворот одной системы координат относительно другой системы с общим началом координат двух систем.

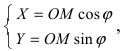
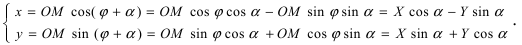
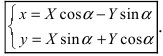
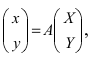
Получим формулы, связывающие старые и новые координаты произвольной точки М(х; у). Из рисунка видно, что в новой системе координат координаты точки равны а координаты этой точки в старой системе координат равны Таким образом формулы перехода от новых координат произвольной точки М к старым имеет вид В матричном виде эти равенства можно записать в виде где матрица перехода

Найдем обратное преобразование системы координат, найдем матрицу 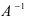обратную к матрице А:

Найдем алгебраические дополнения всех элементов

Запишем обратную матрицу

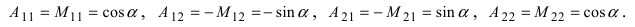
Определение: Унитарными преобразованиями называются такие преобразования, для которых определитель матрицы преобразования равен 1.

Определение: Ортогональными преобразованиями называются такие преобразования, для которых обратная матрица к матрице преобразования совпадает с транспонированной матрицей преобразования.

Таким образом, имеем 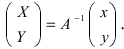Следовательно, формулы перехода от старой системы отсчета к новой системе отсчета имеют вид:

Пример:

Найти координаты точки М(1; 2) в новой системе координат, повернутой относительно старой системы отсчета на угол

Решение:

Воспользуемся полученными формулами 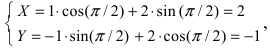т.е. в новой системе координат точка имеет координаты М(2; -1).

Рассмотрим применение преобразования координат:

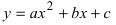
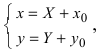
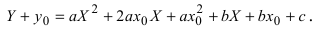
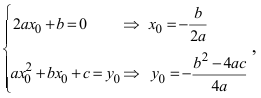
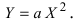
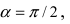
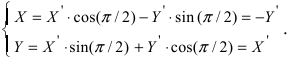
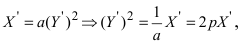
а) Преобразовать уравнение параболы к каноническому виду. Проведем параллельный перенос системы координат получим Выберем начало отсчета новой системы координат так, чтобы выполнялись равенства тогда уравнение принимает вид Выполним поворот системы координат на угол тогда Подставим найденные соотношения в уравнение параболы где параметр параболы

Пример:

Преобразовать уравнение параболы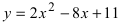 к каноническому виду.

Решение:

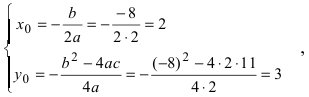
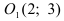
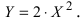
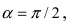
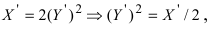
Найдем начало отсчета новой системы координат после параллельного переноса т.е. точка — начало координат новой системы отсчета. В этой системе уравнение параболы имеет вид Проведем поворот системы отсчета на угол тогда

следовательно, параметр параболы р = 1/4.

б) Выяснить, какую кривую описывает функция

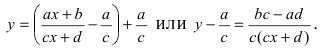
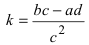
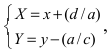
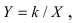
Проведем следующее преобразование Производя параллельный перенос системы координат, вводя обозначение

и новые координаты получим уравнение которое описывает равнобочную гиперболу.

• Заказать решение задач по высшей математике

Полярные координаты. Замечательные кривые

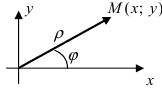
Пусть полярная ось совпадает с осью абсцисс Ох, а начало полярной оси (полюс полярной системы координат) совпадает с началом координат декартовой системы отсчета (Рис. 48). Любая точка М(х;у) в полярной системе координат характеризуется длиной радиус-вектора, соединяющего эту точку с началом отсчета и углом 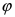между радиус-вектором и полярной осью (угол отсчитывается против часовой стрелки).

Рис. 48. Полярная система координат.

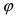
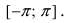
Главными значениями угла являются значения, лежащие в интервале Из рисунка видно, что декартовы и полярные координаты связаны формулами

Рассмотрим замечательные кривые в полярной системе координат:

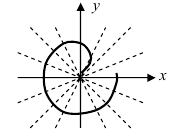
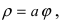
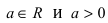
1. Спираль Архимеда где число (Рис. 49). Для построения кривой в полярной системе координат, разобьем декартову плоскость лучами с шагом по углу и на каждом луче отложим ему соответствующее значение р.

Рис. 49. Спираль (улитка) Архимеда.

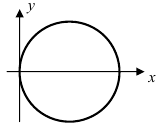
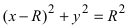
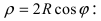
2. Уравнение окружности: уравнение описывает окружность с центром в точке A(R; 0) и радиусом R (Рис. 50). В полярной системе координат уравнение принимает вид

Рис. 50. Окружность с центром в точке A(R; 0) и радиусом R.

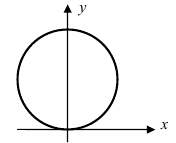
3. Уравнение 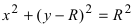описывает окружность с центром в т. А(0; R) и радиусом R (Рис. 51). В полярной системе координат уравнение принимает вид

Рис. 51. Окружность с центром в точке А(0; R) и радиусом R.

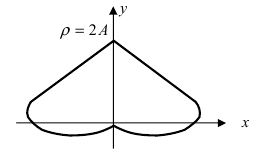
4. Кардиоиды:

Рис. 52. Кардиоида

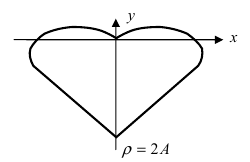
Рис. 53. Кардиоида

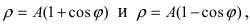
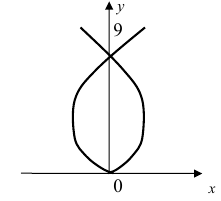
Аналогично выглядят кардиоиды но они вытянуты вдоль оси абсцисс Ох.

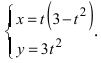
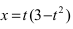
5. Петля: Величина равна нулю при

Для первого корня у = 0, а для второго и третьего — у = 9 . Следовательно, петля имеет вид

Рис. 54. Петля.

Сегодня на уроке мы вспомним, какое отображение
плоскости на себя мы называли параллельным переносом, введём понятие
параллельного переноса в пространстве. Проверим, будет ли параллельный перенос
движением пространства.

Вернёмся в планиметрию и вспомним, что параллельным
переносом мы называли преобразование, при котором каждая точка фигуры
перемещается в одном и том же направлении и на одно и то же расстояние. Мы
говорили, что для того, чтобы задать перенос достаточно задать вектор.

Другими словами, параллельным переносом на
вектор  называется
отображение плоскости на себя, при котором каждая точка  отображается
в такую точку ,
что вектор  равен
вектору .

То, что параллельный перенос является примером
движения плоскости, мы уже доказывали. Давайте вспомним это доказательство.

Пусть при параллельном переносе на вектор  точки
 и
 отображаются
в точки  и
.
Так как векторы  и
,
то значит, эти векторы равны между собой .
То есть они параллельны  и
их длины равны, поэтому четырёхугольник  –
параллелограмм. Следовательно, ,
то есть расстояние между точками  и
 равно
расстоянию между точками  и
.

Случай, когда точки  и
 лежат
на прямой параллельной вектору ,
вы можете рассмотреть самостоятельно. Но и в этом случае расстояние между
точками  и
 будет
равно расстоянию между точками  и
.

Таким образом, параллельный перенос сохраняет
расстояние между точками и поэтому представляет собой движение. Это
движение можно представить себе как сдвиг всей плоскости в направлении данного
вектора  на
его длину.

В планиметрии мы говорили, что параллельный перенос
обладает некоторыми свойствами.

Свойства параллельного переноса:

·              
При
параллельном переносе отрезок переходит в равный ему отрезок.

·              
Угол
переходит в равный ему угол.

·              
Окружность
переходит в равную ей окружность.

·              
Любой
многоугольник переходит в равный ему многоугольник.

·              
Параллельные
прямые переходят в параллельные прямые.

·              
Перпендикулярные
прямые переходят в перпендикулярные прямые.

Теперь давайте определим, что мы будем понимать под
параллельным переносом в пространстве.

Определение:

Параллельным переносом на вектор  называется
такое отображение пространства на себя, при котором любая точка  переходит
в такую точку  что
.

Проверим, будет ли параллельный перенос в
пространстве примером движения пространства.

При параллельном переносе точки пространства  и
 переходят
в такие точки  и
,
что вектора  и
.

Сложим по правилу треугольника векторы

Поскольку левые части равенств равны, значит, равны
и правые части равенств.

Значит, можно записать, что .

Заменим вектора  и
 на
вектор .
Получим, что .
Отсюда получаем, что вектор .
Поскольку векторы равны, значит, равны и их длины, то есть .
То есть расстояние между точками при параллельном переносе в пространстве
сохраняется, значит, параллельный перенос в пространстве также является
движением, но уже не плоскости, а пространства.

Сформулируем свойства параллельного переноса.

Свойства параллельного переноса:

·                  
Параллельный
перенос является примером движения пространства.

·                  
При
параллельном переносе точки смещаются по параллельным или совпадающим прямым на
одно и то же расстояние.

·                  
При
параллельном переносе прямая переходит в параллельную прямую (или сама в себя).

·                  
Каковы
бы не были две точки  и
,
существует, и притом единственный, параллельный перенос, при котором точка  переходит
в точку .

·                  
При
параллельном переносе в пространстве каждая плоскость переходит либо в себя,
либо в параллельную ей плоскость.

Движение в пространстве обладает теми же свойствами,
что и движение плоскости.

Свойства движения пространства:

·                  
Движение
сохраняет расстояние между точками.

·                  
При
любом движении пространства отрезок отображается на отрезок, прямая – в прямую,
плоскость – в плоскость.

Решим несколько задач.

Задача:
начертить отрезок  и
вектор .
Построить отрезок ,
который получится из отрезка параллельным
переносом на вектор .

Решение:
для того, чтобы построить отрезок ,
отобразим точку  в
точку ,
точку  в
точку  с
помощью параллельного переноса. Тогда соединив точки ,
 мы
получим отрезок .

Задача:
начертить треугольник  и
вектор .
Построить треугольник ,
который получится из треугольникa
параллельным
переносом на вектор .

Решение:
отобразим с помощью параллельного переноса точки ,
,
 в
точки ,
,.
Соединив полученные точки, мы получим искомый треугольник .

Задача:
начертить пятиугольник  и
вектор .
Построить пятиугольник ,
который получится из пятиугольника параллельным
переносом на вектор .

Решение:
решать эту задачу будем аналогично тому, как мы решали предыдущую задачу.
Отобразим каждую вершину пятиугольника с помощью параллельного переноса на
вектор .
Соединим получившиеся точки и получим искомый пятиугольник .

Итоги:

Сегодня на уроке мы вспомнили, что мы понимали под
параллельным переносом в планиметрии. Ввели понятие параллельного переноса в пространстве.
Сформулировали основные свойства параллельного переноса, движения пространства.