Как найти точку пересечения окружностей
Геометрические задачи, решаемые аналитически при помощи приемов алгебры, являются неотъемлемой частью программы школьного обучения. Кроме логического и пространственного мышления они развивают понимание ключевых взаимосвязей между сущностями окружающего мира и абстракциями, применяемыми людьми для формализации отношений между ними. Нахождение точек пересечения простейших геометрических фигур — один из типов подобных задач.
Инструкция
Предположим, что даны две окружности, заданные своими радиусами R и r, а также координатами их центров — соответственно (x1, y1) и (x2, y2). Требуется вычислить, пересекаются ли эти окружности, и если да, то найти координаты точек пересечения.Для простоты можно предположить, что центр одной из заданных окружностей совпадает с началом координат. Тогда (x1, y1) = (0, 0), а (x2, y2) = (a, b). Также имеет смысл предполагать, что a ≠ 0 и b ≠ 0.
Таким образом, координаты точки (или точек) пересечения окружностей, если они есть, должны удовлетворять системе из двух уравнений:x^2 + y^2 = R^2,
(x — a)^2 + (y — b)^2 = r^2.
После раскрытия скобок уравнения приобретают вид:x^2 + y^2 = R^2,
x^2 + y^2 — 2ax — 2by + a^2 + b^2 = r^2.
Теперь первое уравнение можно вычесть из второго. Таким образом, квадраты переменных исчезают, и возникает линейное уравнение: -2ax — 2by = r^2 — R^2 — a^2 — b^2. С его помощью можно выразить y через x:y = (r^2 — R^2 — a^2 — b^2 — 2ax)/2b.
Если подставить найденное выражение для y в уравнение окружности, задача сводится к решению квадратного уравнения: x^2 + px + q = 0, гдеp = -2a/2b,
q = (r^2 — R^2 — a^2 — b^2)/2b — R^2.
Корни этого уравнения позволят найти координаты точек пересечения окружностей. Если уравнение неразрешимо в действительных числах, то окружности не пересекаются. Если корни совпадают между собой, то окружности касаются друг друга. Если корни различны, то окружности пересекаются.
Если a = 0 или b = 0, то исходные уравнения упрощаются. Например, при b = 0 система уравнений примет вид:x^2 + y2 = R^2,
(x — a)^2 + y^2 = r^2.
После вычитания первого уравнения из второго получается:- 2ax + a^2 = r^2 — R^2.Его решение: x = — (r^2 — R^2 — a2)/2a. Очевидно, что в случае b = 0 центры обеих окружностей лежат на оси абсцисс, и у точек их пересечения будет одинаковая абсцисса.
Это выражение для x можно подставить в первое уравнение окружности и получить квадратное уравнение относительно y. Его корни — ординаты точек пересечения, если таковые существуют. Аналогичным образом находится выражение для y, если a = 0.
Если a = 0 и b = 0, но при этом R ≠ r, то одна из окружностей заведомо находится внутри другой, и точки пересечения отсутствуют. Если же R = r, то окружности совпадают, и точек их пересечения бесконечно много.
Если ни у одной из двух окружностей центр не совпадает с началом координат, то их уравнения будут иметь вид:(x — x1)^2 + (y — y1)^2 = R^2,
(x — x2)^2 + (y — y2)^2 = r^2.Если перейти к новым координатам, получающимся из старых методом параллельного переноса: x′ = x + x1, y′ = y + y1, то эти уравнения приобретают вид:x′^2 + y′^2 = R^2,
(x′ — (x1 + x2))^2 + (y′ — (y1 + y2))^2 = r^2.Задача, таким образом, сводится к предыдущей. Найдя решения для x′ и y′, можно легко вернуться к изначальным координатам, обратив уравнения для параллельного переноса.
Источники:
- как найти точки пересечения окружности с прямой
Чтобы использовать калькулятор, введите координаты x и y центра и радиус каждой окружности.
Формулы для расчета приведены под калькулятором.
Точки пересечения двух окружностей
Первая окружность
Вторая окружность
Точность вычисления
Знаков после запятой: 2
Проверка расстояния между окружностями
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Пересечение окружностей
Сама по себе задача нахождения точек пересечения двух окружностей достаточно проста, однако предварительно надо проанализировать если ли вообще точки пересения у данных двух окружностей. Поэтому начать надо с вычисления расстояния d в декартовых координатах между центрами окружностей и сравнения его с радиусами окружностей r1 и r2.
При этом возможно следующие случаи (расстояние между центрами показано красным отрезком):
| Случай | Описание | Условие |
|---|---|---|
| Тривиальный случай — окружности совпадают (это одна и та же окружность) | ||
 |
Окружности не касаются друг друга | |
 |
Одна окружность содержится внутри другой и не касается ее | |
  |
Окружности пересекаются в двух точках | Не выполнено ни одно из условий выше |
  |
Окружности соприкасаются в одной точке | Частный случай предыдущего |
Если окружности действительно пересекаются, калькулятор использует следующие формулы (в-основном выведенные из теоремы Пифагора), проиллюстрированные рисунком ниже:
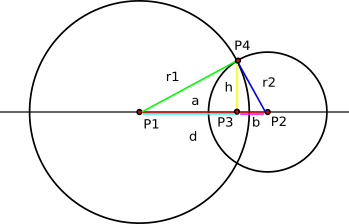
Сначала калькулятор находит отрезок a
и затем отрезок h
Чтобы найти точку P3, калькулятор использует следующую формулу (в векторном виде):
И наконец, чтобы найти точки пересечения, калькулятор использует следующие уравнения:
Первая точка:
Вторая точка:
Обратите внимание на разные знаки перед вторым слагаемым
По теме также можно посмотреть следующие ссылки (на английском языке): Circle-Circle Intersection и Circles and spheres
Как найти координаты точек пересечения двух окружностей
Пересечение двух окружностей
Этот онлайн калькулятор находит точки пересечения двух окружностей, если они существуют
Чтобы использовать калькулятор, введите координаты x и y центра и радиус каждой окружности.
Формулы для расчета приведены под калькулятором.
Точки пересечения двух окружностей
Первая окружность
Вторая окружность
Пересечение окружностей
Сама по себе задача нахождения точек пересечения двух окружностей достаточно проста, однако предварительно надо проанализировать если ли вообще точки пересения у данных двух окружностей. Поэтому начать надо с вычисления расстояния d в декартовых координатах между центрами окружностей и сравнения его с радиусами окружностей r1 и r2.
При этом возможно следующие случаи (расстояние между центрами показано красным отрезком):
| Случай | Описание | Условие |
|---|---|---|
| Тривиальный случай — окружности совпадают (это одна и та же окружность) | ||
| Окружности не касаются друг друга | r1 + r2″ /> | |
| Одна окружность содержится внутри другой и не касается ее | ||
| Окружности пересекаются в двух точках | Не выполнено ни одно из условий выше | |
| Окружности соприкасаются в одной точке | Частный случай предыдущего |
Если окружности действительно пересекаются, калькулятор использует следующие формулы (в-основном выведенные из теоремы Пифагора), проиллюстрированные рисунком ниже:
Сначала калькулятор находит отрезок a
Чтобы найти точку P3, калькулятор использует следующую формулу (в векторном виде):
И наконец, чтобы найти точки пересечения, калькулятор использует следующие уравнения:
Первая точка:
Обратите внимание на разные знаки перед вторым слагаемым
По теме также можно посмотреть следующие ссылки (на английском языке): Circle-Circle Intersection и Circles and spheres
Координаты пересечения двух окружностей
| Координаты центра первой окружности, через пробел |
| Радиус первой окружности |
| Координаты центра второй окружности, через пробел |
| Радиус второй окружности |
| Координата первого пересечения |
| Координата второго пересечения |
|
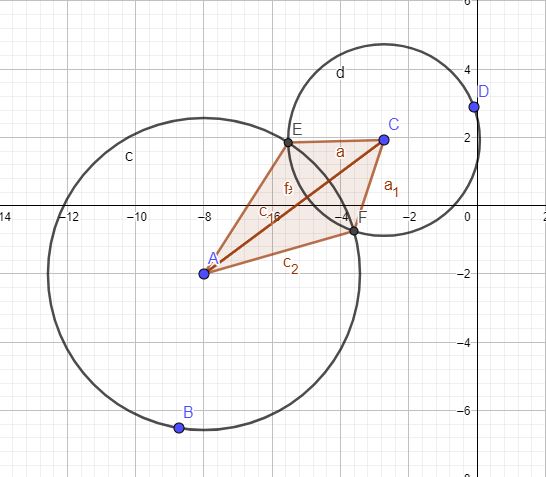
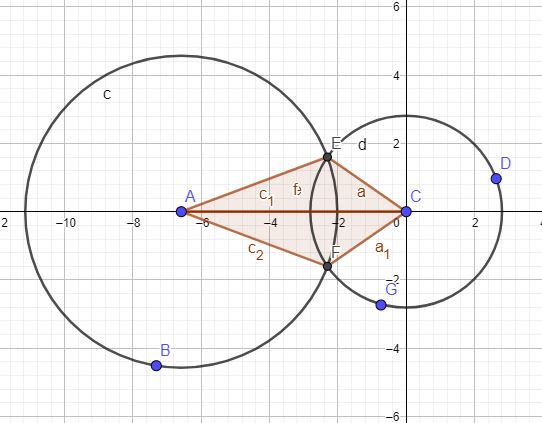
Продолжим изучение геометрии и в этом материале мы рассмотрим, как находить координаты пересечения двух окружностей, если заданы их уравнения. Определение координат двух окружностей на плоскости можно свести к более простым задачам которые мы можем уже решать или понимаем, как их решать. Пусть Две окружности заданы своими двумя уравнениями Повернем изображение на такой угол, что бы линия соединяющая центры окружностей, совпадала с осью абсцисс. Кроме этого перенесем всю схему таким образом, что бы центр одной из окружностей совпал с началом координат.
И алгоритм следующий: 1. Приводим ( линейным смещением) центр первой окружности к координатам (0,0) 3. Определяем угол (W) прямой, проходящей между точками A и C 4. Определяем два угла (psi_1) как сумму и (psi_2) как разность углов W и F 5. Взяв для каждого из углов (в п. 4), синус и умножив на радиус первой окружности мы узнаем координату Y , взяв косинус мы узнаем координату X. 6. Делаем для двух полученных координат, обратное смещение. Пересечение двух окружностейДаны две окружности, каждая определена координатами своего центра и радиусом. Требуется найти все их точки пересечения (либо одна, либо две, либо ни одной точки, либо окружности совпадают). РешениеПредположим, не теряя общности, что центр первой окружности — в начале координат (если это не так, то перенесём центр в начало координат, а при выводе ответа будем обратно прибавлять координаты центра). Тогда мы имеем систему двух уравнений: Вычтем из второго уравнения первое, чтобы избавиться от квадратов переменных: Таким образом, мы свели задачу о пересечении двух окружностей к задаче о пересечении первой окружности и следующей прямой: А решение последней задачи описано в соответствующей статье. Единственный вырожденный случай, который надо рассмотреть отдельно — когда центры окружностей совпадают. Действительно, в этом случае вместо уравнения прямой мы получим уравнение вида 0 = С, где C — некоторое число, и этот случай будет обрабатываться некорректно. Поэтому этот случай нужно рассмотреть отдельно: если радиусы окружностей совпадают, то ответ — бесконечность, иначе — точек пересечения нет. источники: http://abakbot.ru/online-2/460-cookr http://e-maxx.ru/algo/circles_intersection |
Координаты пересечения двух окружностей
| Координаты центра первой окружности, через пробел |
| Радиус первой окружности |
| Координаты центра второй окружности, через пробел |
| Радиус второй окружности |
| Координата первого пересечения |
| Координата второго пересечения |
Продолжим изучение геометрии и в этом материале мы рассмотрим, как находить координаты пересечения двух окружностей, если заданы их уравнения.
Определение координат двух окружностей на плоскости можно свести к более простым задачам которые мы можем уже решать или понимаем, как их решать.
Пусть Две окружности заданы своими двумя уравнениями
((x+8)^2+(y+2)^2=20.87)
((x+2.73)^2+(y-1.92)^2=10.87)
Повернем изображение на такой угол, что бы линия соединяющая центры окружностей, совпадала с осью абсцисс.
Кроме этого перенесем всю схему таким образом, что бы центр одной из окружностей совпал с началом координат.

( F=acos(cfrac{R_1^2-R_2^2+D^2}{2*R_1*D}))
И алгоритм следующий:
1. Приводим ( линейным смещением) центр первой окружности к координатам (0,0)
2. Определяем угол ( F=acos(cfrac{R_1^2-R_2^2+D^2}{2*R_1*D}))
3. Определяем угол (W) прямой, проходящей между точками A и C
4. Определяем два угла (psi_1) как сумму и (psi_2) как разность углов W и F
5. Взяв для каждого из углов (в п. 4), синус и умножив на радиус первой окружности мы узнаем координату Y , взяв косинус мы узнаем координату X.
6. Делаем для двух полученных координат, обратное смещение.
7. Две координаты получены. Задача решена.
Геометрические задачи, решаемые аналитически при помощи приемов алгебры, являются неотъемлемой частью программы школьного обучения. Кроме логического и пространственного мышления они развивают понимание ключевых взаимосвязей между сущностями окружающего мира и абстракциями, применяемыми людьми для формализации отношений между ними. Нахождение точек пересечения простейших геометрических фигур — один из типов подобных задач.
Предположим, что даны две окружности, заданные своими радиусами R и r, а также координатами их центров — соответственно (x1, y1) и (x2, y2). Требуется вычислить, пересекаются ли эти окружности, и если да, то найти координаты точек пересечения.Для простоты можно предположить, что центр одной из заданных окружностей совпадает с началом координат. Тогда (x1, y1) = (0, 0), а (x2, y2) = (a, b). Также имеет смысл предполагать, что a ≠ 0 и b ≠ 0.
Таким образом, координаты точки (или точек) пересечения окружностей, если они есть, должны удовлетворять системе из двух уравнений:x^2 + y^2 = R^2,
(x — a)^2 + (y — b)^2 = r^2.
После раскрытия скобок уравнения приобретают вид:x^2 + y^2 = R^2,
x^2 + y^2 — 2ax — 2by + a^2 + b^2 = r^2.
Теперь первое уравнение можно вычесть из второго. Таким образом, квадраты переменных исчезают, и возникает линейное уравнение: -2ax — 2by = r^2 — R^2 — a^2 — b^2. С его помощью можно выразить y через x:y = (r^2 — R^2 — a^2 — b^2 — 2ax)/2b.
Если подставить найденное выражение для y в уравнение окружности, задача сводится к решению квадратного уравнения: x^2 + px + q = 0, гдеp = -2a/2b,
q = (r^2 — R^2 — a^2 — b^2)/2b — R^2.
Корни этого уравнения позволят найти координаты точек пересечения окружностей. Если уравнение неразрешимо в действительных числах, то окружности не пересекаются. Если корни совпадают между собой, то окружности касаются друг друга. Если корни различны, то окружности пересекаются.
Если a = 0 или b = 0, то исходные уравнения упрощаются. Например, при b = 0 система уравнений примет вид:x^2 + y2 = R^2,
(x — a)^2 + y^2 = r^2.
После вычитания первого уравнения из второго получается:- 2ax + a^2 = r^2 — R^2.Его решение: x = — (r^2 — R^2 — a2)/2a. Очевидно, что в случае b = 0 центры обеих окружностей лежат на оси абсцисс, и у точек их пересечения будет одинаковая абсцисса.
Это выражение для x можно подставить в первое уравнение окружности и получить квадратное уравнение относительно y. Его корни — ординаты точек пересечения, если таковые существуют. Аналогичным образом находится выражение для y, если a = 0.
Если a = 0 и b = 0, но при этом R ≠ r, то одна из окружностей заведомо находится внутри другой, и точки пересечения отсутствуют. Если же R = r, то окружности совпадают, и точек их пересечения бесконечно много.
Если ни у одной из двух окружностей центр не совпадает с началом координат, то их уравнения будут иметь вид:(x — x1)^2 + (y — y1)^2 = R^2,
(x — x2)^2 + (y — y2)^2 = r^2.Если перейти к новым координатам, получающимся из старых методом параллельного переноса: x′ = x + x1, y′ = y + y1, то эти уравнения приобретают вид:x′^2 + y′^2 = R^2,
(x′ — (x1 + x2))^2 + (y′ — (y1 + y2))^2 = r^2.Задача, таким образом, сводится к предыдущей. Найдя решения для x′ и y′, можно легко вернуться к изначальным координатам, обратив уравнения для параллельного переноса.