Как найти координаты точки в базисе - Исправление недочетов и поиск решений вместе с Examum.ru

Пусть на плоскости задан ненулевой вектор , тогда для любого вектора , лежащего на этой же прямой, существует единственное вещественное число , такое, что

, (1)

При этом называют базисным вектором, – координатой относительно базиса .

Если на плоскости заданы два ненулевых, неколлинеарных вектора и , то для любого вектора , лежащего в этой же плоскости, существует единственная пара чисел и , таких, что

, (2)

При этом совокупность , называется базисом, – координатами относительно этого базиса. Подчеркнем, что так как и неколлинеарны, то они линейно независимы.

Если в пространстве заданы три ненулевых, некомпланарных (а, следовательно, линейно независимых) вектора , то для любого вектора существует единственная тройка чисел таких, что

, (3)

При этом совокупность называется базисом, – координатами относительно этого базиса.

Линейные комбинации вида (1), (2), (3) называют разложением вектора по базису.

Объединяя три случая, можно дать следующее определение:

Определение. Коэффициенты линейной комбинации, при помощи которой вектор выражается через базис, называются координатами вектора относительно этого базиса.

Теорема 5. Линейные операции над векторами сводятся к таким же операциям над их соответствующими координатами.

Введенные базисы на плоскости и в пространстве называют аффинными. Аффинный базис называется декартовым, если он состоит из единичных взаимно перпендикулярных векторов. Векторы декартова базиса обозначают . Координаты вектора относительно декартова базиса обозначают через .

Определение. Система, состоящая из произвольной точки 0 и векторного аффинного базиса пространства, называется аффинной системой координат этого пространства, точка 0 – начало аффинной системы координат.

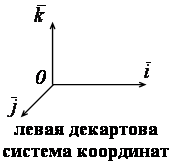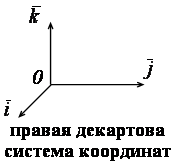Аффинная система координат называется декартовой, если ее векторный базис – декартов.

Определение. Радиус-вектором точки в аффинной или декартовой системе координат называется вектор , где – начало системы координат.

Определение. Координатами точки относительно некоторого базиса называются координаты ее радиус-вектора относительно этого базиса.

Теорема 6. Координаты вектора равны разностям соответствующих координат его конца и начала.

Пример 9. Заданы векторы и . Убедиться, что они коллинеарны и найти разложение по базису .

Решение. У коллинеарных векторов координаты пропорциональны. В нашем случае 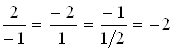, следовательно, .

Пример 10. Относительно некоторого базиса даны векторы , и . Убедиться, что векторы и можно взять за базис и найти координаты в этом базисе.

Решение. Координаты и не пропорциональны, следовательно, не параллелен , значит, они линейно независимы и их можно принять за базис. Обозначим искомые координаты через и , тогда . По теореме 5 получим систему из которой находим ; .

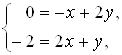
Пример 11. В декартовом базисе заданы векторы , , и .

1. Найти координаты вектора в базисе .

2. Убедиться, что векторы образуют базис.

3. Найти координаты вектора в базисе и написать разложение по этому базису.

Решение. 1. Вектор является линейной комбинацией векторов , следовательно, или .

2. Базис состоит из линейно независимых векторов, значит линейная комбинация векторов обратится в только если все коэффициенты этой линейной комбинации равны нулю. Найдем эти коэффициенты из условия , Или . Так как – линейно независимы, то это равенство возможно, если все коэффициенты обратятся в : , следовательно, – линейно независимы и образуют базис.

3. Разложение вектора по базису имеет вид: , где – координаты вектора в этом базисе. По теореме 5 имеем:

Решая эту систему, найдем , т. е. , .

Пример 12. Вектор отложен от точки . Конец его оказался в точке . Найти координаты точки .

Решение. Обозначим координаты точки через . По теореме 6: , , , откуда .

Пример 13. Даны точки , . Найти значения и , при которых точка , лежит на прямой .

Решение. Векторы и коллинеарны, следовательно , откуда , .

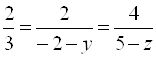
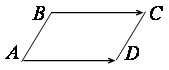
Пример 14. Даны три последовательные вершины параллелограмма , , . Найти координаты четвертой вершины .

Решение. Пусть , тогда , . Так как , то их соответствующие координаты равны, поэтому , , . Откуда .

< Предыдущая		Следующая >

Источник

Базис. Координаты вектора в базисе

Определим
понятие базиса на прямой, плоскости и
в пространстве.

Базисом
на прямойназывается любой ненулевой
векторна этой прямой. Любой другой вектор,
коллинеарный данной прямой, может быть
выражен через векторв виде.

Базисом
на плоскостиназываются любых два
линейно независимых вектораиэтой плоскости, взятые в определенном
порядке. Любой третий вектор,
компланарный плоскости, на которой
выбран базис,
может быть представлен в виде.

Базисом
в трехмерном пространстве называются
любые три некомпланарных вектора
,
взятые в определенном порядке. Такой
базис обозначается.
Пусть‑ произвольный вектор трехмерного
пространства, в котором выбран базис.
Тогда существуют числатакие, что:

(4.5)

Коэффициенты
называются координатами векторав базисе,
а формула (4.5) есть разложение векторапо данному базису.

Координаты
вектора в заданном базисе определяются
однозначно. Введение координат для
векторов позволяет сводить различные
соотношения между векторами к числовым
соотношениям между их координатами.
Координаты линейной комбинации векторов
равны таким же линейным комбинациям
соответствующих координат этих векторов.

Декартовы прямоугольные координаты в пространстве. Координаты точек. Координаты векторов. Деление отрезка в данном отношении

Д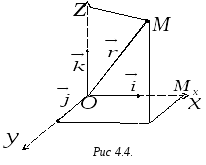екартова
прямоугольная система координат в
пространстве определяется заданием
единицы масштаба для измерения длин и
трех пересекающихся в точке взаимно
перпендикулярных осей, первая из которых
называется осью абсцисс,
вторая – осью ординат,
третья – осью аппликат;
точка‑ начало координат (Рис. 4.4).

Положение
координатных осей можно задать с помощью
единичных векторов
,
направленных соответственно по осям.
Векторыназываются основными или базисными
ортами и определяют базисв трехмерном пространстве.

Пусть
в пространстве дана точка
.
Проектируя ее на ось,
получим точку.
Первой координатойилиабсциссой точки
называется длина вектора,
взятая со знаком плюс, еслинаправлен
в ту же сторону, что и вектор,
и со знаком минус ‑ если в противоположную.
Аналогично проектируя точкуна осии,
определим ееординату
иаппликату
.Тройка чиселвзаимно однозначно соответствует точке.

Система
координат называется правой, если
вращение от осик осив ближайшую сторону видно с положительного
направления осисовершающимися против часовой стрелки,
илевой, если вращение от осик осив ближайшую сторону видно совершающимися
по часовой стрелке.

Вектор
,
направленный из начала координат в
точкуназываетсярадиус-вектором точки
,
т.е.:

(4.6)

Если
даны координаты точек
и,
то координаты вектораполучаются вычитанием из координат его
концакоординат начала:или.

Следовательно,
по формуле (4.5):

или

(4.7)

При
сложении (вычитании) векторов их
координаты складываются (вычитаются),
при умножении вектора на число все его
координаты умножаются на это число.

Длина
вектора
равна квадратному корню из суммы
квадратов его координат.

(4.8)

Длина
вектора
,заданного координатами своих концов,
т.е. расстояние между точками
и
вычисляется по формуле:

(4.9)

Если
иколлинеарны, то они отличаются друг от
друга скалярным множителем. Следовательно,
у коллинеарных векторов координаты
пропорциональны:

(4.10)

Пусть
точка
делит отрезок между точкамиив отношении,
тогда радиус-вектор точкивыражается через радиусы-векторыиего концов по формуле:.

Отсюда
получаются координатные формулы:

В
частности, если точка
делит отрезокпополам, тои,
т.е..

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Как найти координаты вектора в базисе

Решение:
Записываем матрицу перехода А:

и находим ее определитель
<>0
Видим, что ранг матрицы С равен трем. Из теоремы о базисном миноре векторы f₁ , f₂ , f₃ линейно независимы, а поэтому могут быть приняты в качестве базиса пространства R 3 .
Находим обратную матрицу А -1 .
Транспонированная матрица:

Обратная матрица А -1

Находим координаты вектора х относительно нового базиса.

Пример №1 . Даны векторы a<1;2;1>, b<2;-2;1>, c <1;-2;0>и d <0;3;1>. Установить, что векторы a , b , c образуют базис, и найти координаты вектора d в этом базисе.
Решение:
Соотношение, записанное для векторов d = αa + βb + γc, справедливо для каждой из проекций:
α*1 + β*2 + γ*1 = 0
α*2 — β*2 — γ*2 = 3
α*1 + β*1 + γ0 = 1 т.е. получена алгебраическая система трёх уравнений с тремя неизвестными. Решение системы удобнее вычислять методом Крамера или методом обратной матрицы:
α = 1/2; β = 1/2; γ = -3/2
следовательно, и вектор d имеет разложение в базисе a, b, c :
d = 1/2a + 1/2b — 3/2c

Пример №2 . Даны векторы . Показать, что векторы образуют базис трехмерного пространства и найти координаты вектора в этом базисе:

Пример №3 . Даны два линейных преобразования:
х’₁ = a₁₁x₁ + a₁₂x₂ + a₁₃x₃, х»₁ = b₁₁x’₁ + b₁₂x’₂ + b₁₃x’₃,
х’₂ = a21x1 + a22x2 + a23x3, х»₂ = b₂₁x’1 + b₂₂x’₂ + b₂₃x’₃,
х’₃ = a₃₁x₁ + a₃₂x₂ + a₃₃x₃, х»₃ = b₃₁x’₁ + b₃₂x’₂ + b₃₃x’₃,
Средствами матричного исчисления найти преобразование, выражающее х»₁, x»₂, x»₃ через х₁, х₂, х₃.
х’₁ = 4x₁ + 3x₂ + 5x₃, х»₁ = — x’₁ + 3x’₂ — 2x’₃,
х’₂ = 6x₁ + 7x₂ + x₃, х»₂ = — 4x’₁ + x’₂ + 2x’₃,
х’₃ = 9x₁ + x₂ + 8x₃, х»₃ = 3x’₁ — 4x’₂ + 5x’₃,
Решение. Используя калькулятор, получаем:
Обозначим:

Тогда матричное уравнение запишется в виде: A·X = B.
Вычислим определитель матрицы А:
∆ = 4*(7*8 — 1*1) — 6*(3*8 — 1*5) + 9*(3*1 — 7*5) = -182
Определитель матрицы А равен detA=-182
Так как A невырожденная матрица, то существует обратная матрица A -1 . Умножим слева обе части уравнения на A -1 : A -1 ·A·X = A -1 ·B, тогда получим E·X = A -1 ·B, или X = A -1 ·B.
Найдем обратную матрицу A -1 .

A -1 = -1/182

55	-19	-32
-39	-13	26
-57	23	10

Матрицу Х ищем по формуле:

X = A -1 ·B = -1/182

55	-19	-32
-39	-13	26
-57	23	10

75 /₁₈₂	-1 46 /₉₁	1 9 /₁₃
-13 /₁₄	1 2 /₇	-1
5 /₁₈₂	1 3 /₉₁	-1 2 /₁₃

Пример №4 . В декартовой прямой системе координат даны вершины пирамиды A(3,0,-1), B(-1,-2,-4), C(-1,2,4), D(7,-3,1). Найдите:
а) длину ребра AB;
б) косинус угла между векторами AB и AC ;
в) уравнение ребра AB;
г) уравнение грани ABC;
д) уравнение высоты, опущенной из вершины D на грань ABC;
е) координаты векторов e ₁= AB , e ₂= AC , e ₃= AD и докажите, что они образуют линейную независимую систему;
ж) координаты вектора MN , где M и N – середины ребер AD и DC соответственно;
з) разложение вектора MN по базису ( e ₁, e ₂, e ₃)

Решение. Пункты (а-д) решаются через онлайн калькулятор.

Задание 1 . Разложить вектор d =(8;-5) по векторам a =(1;-2) и b =(2;3).
Решение. Векторы a и b образуют базис на плоскости, так как они не коллинеарны (, то есть соответствующие координаты этих векторов не пропорциональны).
Следовательно, вектор d = α a +β b , где α и β – коэффициенты, которые надо найти.
Таким образом, имеем равенство
8i-5j=α(i-2j)+β(2i+3j)=(α+2β)i+ (-2α+3β)j.
В координатной форме это равенство примет вид
Решим полученную систему уравнений.

Базис и координаты вектора

Определение 5.7. Линейной комбинацией векторов а_1, а₂,…,а_nназывается выражение вида: k₁a₁ + k₂a₂ +…+k_na_n, (5.1)

Определение 5.8. Векторы а_1, а₂,…,а_nназываются линейно зависимыми, если найдутся такие числа k₁, k₂,…, k_n, не все равные нулю, что соответствующая линейная комбинация векторов равна нулю, т.е. k₁a₁ + k₂a₂ +…+ k_na_n = 0. (5.2)

Если же равенство (5.2) возможно только при всех k_i = 0, векторы называются линейно независимыми.

Замечание 1. Если система векторов содержит нулевой вектор, то она линейно зависима.

Замечание 2. Если среди n векторов какие-либо (n-1) линейно зависимы, то и все n векторов линейно зависимы.

Замечание 3. Необходимым и достаточным условием линейной зависимости двух векторов является их коллинеарность.

Определение 5.9. Векторы называютсякомпланарными, если они лежат либо в одной плоскости, либо в параллельных плоскостях.

Замечание 4. Необходимым и достаточным условием линейной зависимости трех векторов является их компланарность.

Замечание 5. Любые четыре вектора в трехмерном пространстве линейно зависимы.

Определение 5.10. Два линейно независимых вектора на плоскости ( или три линейно независимых вектора в пространстве) образуют базис, если любой вектор плоскости (пространства) может быть представлен в виде их линейной комбинации. Числовые коэффициенты этой линейной комбинации называютсякоординатами данного вектора в рассматриваемом базисе:

если a, b, c –базис и d = ka+ mb+ pc, то числа k, m, p есть координаты вектора d в базисе a, b, c.

1. Любые два неколлинеарных вектора образуют базис на плоскости, а любые три некомпланарных вектора – базис в пространстве.

2. Разложение данного вектора по данному базису единственно, т.е. его координаты в данном базисе определяются единственным образом.

3. При сложении двух векторов их координаты относительно любого базиса складываются.

4. При умножении вектора на число все его координаты умножаются на это число.

Определение 5.11. Проекцией вектора АВ на ось u называется длина направленного отрезка А / В / оси u, где А / и В / — основания перпендикуляров, опущенных из точек А и В на ось u.

Обозначение: пр_uа.

1. Пр_ua = |a| cosφ, где φ – угол между а и осью u.

2. При сложении двух векторов их проекции на любую ось складываются.

3. При умножении вектора на число его проекция на любую ось умножается на это число.

Замечание. Свойства 2 и 3 назовем линейными свойствами проекции.

Рассмотрим декартову систему координат, базис которой образуют в пространстве три попарно ортогональных единичных вектора i, j, k. Тогда любой вектор d может быть представлен в виде их линейной комбинации:

d = Xi + Yj +Zk. (5.3)

Определение 5.12. Числа X, Y, Z называются декартовыми координатами вектора d.

Замечание. Декартовы координаты вектора равны его проекциям на оси Ох, Оу и Оz декартовой системы координат.

Определение 5.13. Косинусы углов, образованных вектором о осями декартовой системы координат, называются его направляющими косинусами.

Свойства направляющих косинусов:

1. X = |d| cosα, Y = |d| cosβ, Z = |d| cosγ.

2. , , .

Векторное пространство: размерность и базис, разложение вектора по базису

В статье о n -мерных векторах мы пришли к понятию линейного пространства, порождаемого множеством n -мерных векторов. Теперь нам предстоит рассмотреть не менее важные понятия, такие как размерность и базис векторного пространства. Они напрямую связаны с понятием линейно независимой системы векторов, так что дополнительно рекомендуется напомнить себе основы и этой темы.

Введем некоторые определения.

Размерность векторного пространства – число, соответствующее максимальному количеству линейно независимых векторов в этом пространстве.

Базис векторного пространства – совокупность линейно независимых векторов, упорядоченная и в своей численности равная размерности пространства.

Рассмотрим некое пространство n -векторов. Размерность его соответственно равна n . Возьмем систему из n -единичных векторов:

e ( 1 ) = ( 1 , 0 , . . . , 0 ) e ( 2 ) = ( 0 , 1 , . . . , 0 ) e ( n ) = ( 0 , 0 , . . . , 1 )

Используем эти векторы в качестве составляющих матрицы A : она будет являться единичной с размерностью n на n . Ранг этой матрицы равен n . Следовательно, векторная система e ( 1 ) , e ( 2 ) , . . . , e ( n ) является линейно независимой. При этом к системе невозможно добавить ни одного вектора, не нарушив ее линейной независимости.

Так как число векторов в системе равно n , то размерность пространства n -мерных векторов равна n , а единичные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом указанного пространства.

Из полученного определения сделаем вывод: любая система n -мерных векторов, в которой число векторов меньше n , не является базисом пространства.

Если мы поменяем местами первый и второй вектор, получим систему векторов e ( 2 ) , e ( 1 ) , . . . , e ( n ) . Она также будет являться базисом n -мерного векторного пространства. Составим матрицу, взяв за ее строки векторы полученной системы. Матрица может быть получена из единичной матрицы перестановкой местами первых двух строк, ранг ее будет равен n . Система e ( 2 ) , e ( 1 ) , . . . , e ( n ) линейно независима и является базисом n -мерного векторного пространства.

Переставив местами в исходной системе другие векторы, получим еще один базис.

Мы можем взять линейно независимую систему неединичных векторов, и она также будет представлять собой базис n -мерного векторного пространства.

Векторное пространство с размерностью n имеет столько базисов, сколько существует линейно независимых систем из n -мерных векторов числом n.

Плоскость является двумерным пространством – ее базисом будут два любых неколлинеарных вектора. Базисом трехмерного пространства послужат три любых некомпланарных вектора.

Рассмотрим применение данной теории на конкретных примерах.

Исходные данные: векторы

a = ( 3 , — 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , — 1 , — 2 )

Необходимо определить, являются ли указанные векторы базисом трехмерного векторного пространства.

Решение

Для решения поставленной задачи исследуем заданную систему векторов на линейную зависимость. Составим матрицу, где строки – координаты векторов. Определим ранг матрицы.

A = 3 2 3 — 2 1 — 1 1 2 — 2 A = 3 — 2 1 2 1 2 3 — 1 — 2 = 3 · 1 · ( — 2 ) + ( — 2 ) · 2 · 3 + 1 · 2 · ( — 1 ) — 1 · 1 · 3 — ( — 2 ) · 2 · ( — 2 ) — 3 · 2 · ( — 1 ) = = — 25 ≠ 0 ⇒ R a n k ( A ) = 3

Следовательно, заданные условием задачи векторы линейно независимы, и их численность равна размерности векторного пространства – они являются базисом векторного пространства.

Ответ: указанные векторы являются базисом векторного пространства.

Исходные данные: векторы

a = ( 3 , — 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , — 1 , — 2 ) d = ( 0 , 1 , 2 )

Необходимо определить, может ли указанная система векторов являться базисом трехмерного пространства.

Решение

Указанная в условии задачи система векторов является линейно зависимой, т.к. максимальное число линейно независимых векторов равно 3. Таким образом, указанная система векторов не может служить базисом трехмерного векторного пространства. Но стоит отметить, что подсистема исходной системы a = ( 3 , — 2 , 1 ) , b = ( 2 , 1 , 2 ) , c = ( 3 , — 1 , — 2 ) является базисом.

Ответ: указанная система векторов не является базисом.

Исходные данные: векторы

a = ( 1 , 2 , 3 , 3 ) b = ( 2 , 5 , 6 , 8 ) c = ( 1 , 3 , 2 , 4 ) d = ( 2 , 5 , 4 , 7 )

Могут ли они являться базисом четырехмерного пространства?

Решение

Cоставим матрицу, используя в качестве строк координаты заданных векторов

A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7

По методу Гаусса определим ранг матрицы:

A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7

1 2 3 3 0 1 0 2 0 1 — 1 1 0 1 — 2 1

1 2 3 3 0 1 0 2 0 0 — 1 — 1 0 0 — 2 — 1

1 2 3 3 0 1 0 2 0 0 — 1 — 1 0 0 0 1 ⇒ ⇒ R a n k ( A ) = 4

Следовательно, система заданных векторов линейно независима и их численность равна размерности векторного пространства – они являются базисом четырехмерного векторного пространства.

Ответ: заданные векторы являются базисом четырехмерного пространства.

Исходные данные: векторы

a ( 1 ) = ( 1 , 2 , — 1 , — 2 ) a ( 2 ) = ( 0 , 2 , 1 , — 3 ) a ( 3 ) = ( 1 , 0 , 0 , 5 )

Составляют ли они базис пространства размерностью 4?

Решение

Исходная система векторов линейно независима, но численность векторов в ней недостаточна, чтобы стать базисом четырехмерного пространства.

Ответ: нет, не составляют.

Разложение вектора по базису

Примем, что произвольные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом векторного n-мерного пространства. Добавим к ним некий n -мерный вектор x → : полученная система векторов станет линейно зависимой. Свойства линейной зависимости гласят, что хотя бы один из векторов такой системы может линейно выражаться через остальные. Переформулируя это утверждение, можно говорить о том, что хотя бы один из векторов линейно зависимой системы может раскладываться по остальным векторам.

Таким образом, мы пришли к формулировке важнейшей теоремы:

Любой вектор n -мерного векторного пространства единственным образом раскладывается по базису.

Докажем эту теорему:

зададим базис n -мерного векторного пространства — e ( 1 ) , e ( 2 ) , . . . , e ( n ) . Сделаем систему линейно зависимой, добавив к ней n -мерный вектор x → . Этот вектор может быть линейно выражен через исходные векторы e :

x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) , где x 1 , x 2 , . . . , x n — некоторые числа.

Теперь докажем, что такое разложение является единственным. Предположим, что это не так и существует еще одно подобное разложение:

Отнимем от левой и правой частей этого равенства соответственно левую и правую части равенства x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) . Получим:

1 — x 1 ) · e ( 1 ) + ( x

2 — x 2 ) · e ( 2 ) + . . . ( x

Система базисных векторов e ( 1 ) , e ( 2 ) , . . . , e ( n ) линейно независима; по определению линейной независимости системы векторов равенство выше возможно только тогда, когда все коэффициенты ( x

2 — x 2 ) , . . . , ( x

n — x n ) будут равны нулю. Из чего справедливым будет: x 1 = x

n . И это доказывает единственный вариант разложения вектора по базису.

При этом коэффициенты x 1 , x 2 , . . . , x n называются координатами вектора x → в базисе e ( 1 ) , e ( 2 ) , . . . , e ( n ) .

Доказанная теория делает понятным выражение «задан n -мерный вектор x = ( x 1 , x 2 , . . . , x n ) »: рассматривается вектор x → n -мерного векторного пространства, и его координаты заданы в некотором базисе. При этом также понятно, что этот же вектор в другом базисе n -мерного пространства будет иметь другие координаты.

Рассмотрим следующий пример: допустим, что в некотором базисе n -мерного векторного пространства задана система из n линейно независимых векторов

e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )

а также задан вектор x = ( x 1 , x 2 , . . . , x n ) .

Векторы e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) в этом случае также являются базисом этого векторного пространства.

Предположим, что необходимо определить координаты вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) , обозначаемые как x

Вектор x → будет представлен следующим образом:

2 · e ( 2 ) + . . . + x

Запишем это выражение в координатной форме:

( x 1 , x 2 , . . . , x n ) = x

1 · ( e ( 1 ) 1 , e ( 1 ) 2 , . . . , e ( 1 ) n ) + x

2 · ( e ( 2 ) 1 , e ( 2 ) 2 , . . . , e ( 2 ) n ) + . . . + + x

n · ( e ( n ) 1 , e ( n ) 2 , . . . , e ( n ) n ) = = ( x

2 e 1 ( 2 ) + . . . + x

2 e 2 ( 2 ) + + . . . + x

n e 2 ( n ) , . . . , x

2 e n ( 2 ) + . . . + x

Полученное равенство равносильно системе из n линейных алгебраических выражений с n неизвестными линейными переменными x

n e 2 n ⋮ x n = x

Матрица этой системы будет иметь следующий вид:

e 1 ( 1 ) e 1 ( 2 ) ⋯ e 1 ( n ) e 2 ( 1 ) e 2 ( 2 ) ⋯ e 2 ( n ) ⋮ ⋮ ⋮ ⋮ e n ( 1 ) e n ( 2 ) ⋯ e n ( n )

Пусть это будет матрица A , и ее столбцы – векторы линейно независимой системы векторов e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) . Ранг матрицы – n , и ее определитель отличен от нуля. Это свидетельствует о том, что система уравнений имеет единственное решение, определяемое любым удобным способом: к примеру, методом Крамера или матричным методом. Таким образом мы сможем определить координаты x

n вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) .

Применим рассмотренную теорию на конкретном примере.

Исходные данные: в базисе трехмерного пространства заданы векторы

e ( 1 ) = ( 1 , — 1 , 1 ) e ( 2 ) = ( 3 , 2 , — 5 ) e ( 3 ) = ( 2 , 1 , — 3 ) x = ( 6 , 2 , — 7 )

Необходимо подтвердить факт, что система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) также служит базисом заданного пространства, а также определить координаты вектора х в заданном базисе.

Решение

Система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) будет являться базисом трехмерного пространства, если она линейно независима. Выясним эту возможность, определив ранг матрицы A , строки которой – заданные векторы e ( 1 ) , e ( 2 ) , e ( 3 ) .

Используем метод Гаусса:

A = 1 — 1 1 3 2 — 5 2 1 — 3

1 — 1 1 0 5 — 8 0 3 — 5

1 — 1 1 0 5 — 8 0 0 — 1 5

R a n k ( A ) = 3 . Таким образом, система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) линейно независима и является базисом.

Пусть в базисе вектор x → имеет координаты x

3 . Связь этих координат определяется уравнением:

3 e 1 ( 3 ) x 2 = x

3 e 2 ( 3 ) x 3 = x

Применим значения согласно условиям задачи:

Решим систему уравнений методом Крамера:

∆ = 1 3 2 — 1 2 1 1 — 5 — 3 = — 1 ∆ x

1 = 6 3 2 2 2 1 — 7 — 5 — 3 = — 1 , x

1 ∆ = — 1 — 1 = 1 ∆ x

2 = 1 6 2 — 1 2 1 1 — 7 — 3 = — 1 , x

2 ∆ = — 1 — 1 = 1 ∆ x

3 = 1 3 6 — 1 2 2 1 — 5 — 7 = — 1 , x

Так, вектор x → в базисе e ( 1 ) , e ( 2 ) , e ( 3 ) имеет координаты x

Ответ: x = ( 1 , 1 , 1 )

Связь между базисами

Предположим, что в некотором базисе n-мерного векторного пространства даны две линейно независимые системы векторов:

c ( 1 ) = ( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) c ( 2 ) = ( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) ⋮ c ( n ) = ( c 1 ( n ) , e 2 ( n ) , . . . , c n ( n ) )

e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )

Указанные системы являются также базисами заданного пространства.

n ( 1 ) — координаты вектора c ( 1 ) в базисе e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) , тогда связь координат будет задаваться системой линейных уравнений:

1 ( 1 ) e 1 ( 1 ) + c

2 ( 1 ) e 1 ( 2 ) + . . . + c

n ( 1 ) e 1 ( n ) с 2 ( 1 ) = c

1 ( 1 ) e 2 ( 1 ) + c

2 ( 1 ) e 2 ( 2 ) + . . . + c

n ( 1 ) e 2 ( n ) ⋮ с n ( 1 ) = c

1 ( 1 ) e n ( 1 ) + c

2 ( 1 ) e n ( 2 ) + . . . + c

В виде матрицы систему можно отобразить так:

( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) = ( c

n ( 1 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

Сделаем по аналогии такую же запись для вектора c ( 2 ) :

( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) = ( c

n ( 2 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

И, далее действуя по тому же принципу, получаем:

( c 1 ( n ) , c 2 ( n ) , . . . , c n ( n ) ) = ( c

n ( n ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

Матричные равенства объединим в одно выражение:

c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n ) = c

n ( n ) · e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n )

Оно и будет определять связь векторов двух различных базисов.

Используя тот же принцип, возможно выразить все векторы базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) через базис c ( 1 ) , c ( 2 ) , . . . , c ( n ) :

e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n ) = e

n ( n ) · c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n )

Дадим следующие определения:

n ( n ) является матрицей перехода от базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 )

к базису c ( 1 ) , c ( 2 ) , . . . , c ( n ) .

n ( n ) является матрицей перехода от базиса c ( 1 ) , c ( 2 ) , . . . , c ( n )

к базису e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) .

источники:

http://lektsii.org/5-20526.html

http://zaochnik.com/spravochnik/matematika/vektory/vektornoe-prostranstvo/

Источник

Координаты и преобразования координат в линейном пространстве

Координаты векторов в данном базисе линейного пространства

Пусть $mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_n$ — базис линейного пространства . Каждый вектор mathbf{v}in V можно разложить по базису (см. теорему 8.1), т.е. представить в виде $mathbf{v}=v_1 mathbf{e}_1+v_2 mathbf{e}_2+ldots+v_n mathbf{e}_n$ , причем коэффициенты v_1,v_2,ldots,v_n в разложении определяются однозначно. Эти коэффициенты называются координатами вектора в базисе $mathbf{e}_1, mathbf{e}_2, ldots, mathbf{e}_n$ (или относительно базиса $mathbf{e}_1, mathbf{e}_2, ldots,mathbf{e}_n$ ). Координаты v_1,v_2,ldots, v_n вектора mathbf{v} — это упорядоченный на бор чисел, который представляется в виде матрицы-столбца $v=begin{pmatrix}v_1&cdots&v_nend{pmatrix}^T$ и называется координатным столбцом вектора (в данном базисе). Вектор и его координатный столбец обозначаются одной и той же буквой полужирной или светлой соответственно.

Если базис (как упорядоченный набор векторов) представить в виде символической матрицы-строки $(mathbf{e})= (mathbf{e}_1,ldots,mathbf{e}_n)= begin{pmatrix}mathbf{e}_1& cdots& mathbf{e}_nend{pmatrix}$ , то разложение вектора mathbf{v} по базису можно записать следующим образом:

$mathbf{v}= v_1 mathbf{e}_1+v_2 mathbf{e}_2+cdots+v_n mathbf{e}_n= begin{pmatrix}mathbf{e}_1&cdots& mathbf{e}_nend{pmatrix}!cdot! begin{pmatrix}v_1\vdots\v_nend{pmatrix}= (mathbf{e})v.$

(8.6)

Здесь умножение символической матрицы-строки (mathbf{e}) на числовую матрицу-столбец {v} производится по правилам умножения матриц.

При необходимости, если речь идет о разных базисах, у координатного столбца указывается обозначение базиса, относительно которого получены координаты, например, $mathop{v}limits_{(mathbf{e})}$ — координатный столбец вектора {v} в базисе $(mathbf{e})= (mathbf{e}_1,ldots,mathbf{e}_n)$ .

Из теоремы 8.1 следует, что равные векторы имеют равные соответствующие координаты (в одном и том же базисе), и наоборот, если координаты векторов (в одном и том же базисе) соответственно равны, то равны и сами векторы.

Линейные операции в координатной форме

Пусть $mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_n$ — базис линейного пространства , векторы mathbf{u} и mathbf{v} имеют в этом базисе координаты $u=begin{pmatrix}u_1&cdots&u_nend{pmatrix}^T$ и $v=begin{pmatrix} v_1&cdots&v_n end{pmatrix}^T$ соответственно, т.е.

$mathbf{u}= u_1 mathbf{e}_1+u_2 mathbf{e}_2+ldots+u_n mathbf{e}_n,quad mathbf{v}= v_1 mathbf{e}_1+v_2 mathbf{e}_2+ldots+v_n mathbf{e}_n.$

(8.7)

Складывая эти равенства, получаем $mathbf{u}+mathbf{v}= (u_1+v_1)mathbf{e}_1+ (u_2+v_2)mathbf{e}_2+ ldots+(u_n+v_n)mathbf{e}_n$ .

т.е. при сложении векторов их координаты складываются.

Умножая второе равенство в (8.7) на число lambda , получаем $lambda mathbf{v}= (lambda v_1)mathbf{e}_1+(lambda v_2)mathbf{e}_2+ldots+ (lambda v_n)mathbf{e}_n,$

т.е. при умножении вектора на число все его координаты умножаются на это число.

Другими словами, сумма векторов mathbf{u}+mathbf{v} имеет координаты u+v , а произведение lambdamathbf{v} имеет координаты lambda v . Разумеется, что все координаты получены в одном базисе $(mathbf{e})=(mathbf{e}_1,ldots,mathbf{e}_n)$ .

Замечания 8.5

1. Нетрудно показать, что координатный столбец линейной комбинации alphacdot mathbf{a}+betacdot mathbf{b}+ldots+omegacdot mathbf{z} векторов mathbf{a}, mathbf{b},ldots,mathbf{z} равен линейной комбинации alphacdot a+betacdot b+ ldots+omegacdot z координатных столбцов a,b,ldots,z этих векторов.

2. Если система векторов линейно зависима (линейно независима), то их координатные столбцы, полученные относительно одного базиса, образуют линейно зависимую (соответственно, линейно независимую) систему. Это следует из равносильности равенств alphacdot mathbf{a}+betacdot mathbf{b}+ldots+omegacdot mathbf{z} и alphacdot a+betacdot b+ ldots+omegacdot z . Например, если в этих равенствах не все коэффициенты равны нулю, т.е. система векторов mathbf{a}, mathbf{b},ldots,mathbf{z} и система a,b,ldots,z их координатных столбцов линейно зависимы одновременно.

3. Все свойства линейной зависимости и линейной независимости векторов переносятся без изменений на их координатные столбцы, полученные в одном и том же базисе. И наоборот, свойства для матриц-столбцов, переносятся на векторы, если матрицы-столбцы считать их координатными столбцами.

4. Выбрав в n-мерном вещественном линейном пространстве некоторый базис, можно установить взаимно однозначное соответствие: каждому вектору поставить в соответствие его координатный столбец (в вы бранном базисе), и наоборот, каждому координатному столбцу поставить в соответствие вектор. Другими словами, любой фиксированный базис n-мерного вещественного линейного пространства позволяет установить взаимно однозначное соответствие между всеми векторами вещественно го пространства и всеми столбцами n-мерного арифметического пространства $mathbb{R}^n$ . Это соответствие обозначается $Vleftrightarrow mathbb{R}^n$ . Для n-мерного комплексного линейного пространства аналогичное взаимно однозначное соответствие устанавливается с пространством $mathbb{C}^n$ .

Преобразование координат вектора при замене базиса

Пусть заданы два базиса пространства $Vcolon,(mathbf{e})= (mathbf{e}_1, mathbf{e}_2, ldots,mathbf{e}_n)$ и $(mathbf{e}')= (mathbf{e}'_1, mathbf{e}'_2, ldots, mathbf{e}'_n)$ . Базис будем условно называть «старым», а базис — «новым». Пусть известны разложения каждого вектора нового базиса по старому базису:

$mathbf{e}'_i=s_{1i}cdot mathbf{e}_1+s_{2i}cdot mathbf{e}_2+ldots+ s_{ni}cdot mathbf{e}_n, quad i=1,2,ldots,n.$

(8.8)

Записывая по столбцам координаты векторов $(mathbf{e}'_1, mathbf{e}'_2, ldots, mathbf{e}'_n)$ в базисе (mathbf{e}) , составляем матрицу:

$S=begin{pmatrix}s_{11}&cdots&s_{1n}\ vdots&ddots&vdots\ s_{n1}&cdots& s_{nn}end{pmatrix}!.$

(8.9)

Квадратная матрица , составленная из координатных столбцов векторов нового базиса (mathbf{e}') в старом базисе (mathbf{e}) , называется матрицей перехода от старого базиса к новому. При помощи матрицы перехода (8.9) формулы (8.8) можно записать в виде:

$begin{pmatrix}mathbf{e}'_1&cdots&mathbf{e}'_nend{pmatrix}= begin{pmatrix} mathbf{e}_1&cdots&mathbf{e}_nend{pmatrix}!cdot SquadLeftrightarrowquad (mathbf{e}')=(mathbf{e})cdot S.$

(8.10)

Умножение символической матрицы-строки (mathbf{e}) на матрицу перехода в (8.10) производится по правилам умножения матриц.

Пусть в базисе (mathbf{e}) вектор mathbf{v} имеет координаты v_1,v_2,ldots,v_n , а в базисе (mathbf{e}') — координаты v'_1,v'_2, ldots,v'_n , т.е.

$mathbf{v}= v_1 mathbf{e}_1+v_2 mathbf{e}_2+ldots+v_n mathbf{e}_n= v'_1 mathbf{e}_1+v'_2 mathbf{e}_2+ldots+v'_n mathbf{e}_n$ или, короче, mathbf{v}= (mathbf{e})v=(mathbf{e}')v'

Подставляя в правую часть последнего равенства выражение (8.10), получаем mathbf{v}=(mathbf{e})v=(mathbf{e})S,v' — два разложения вектора в одном и том же базисе . Коэффициенты этих разложений должны совпадать (по теореме 8.1), так как это координаты одного и того же вектора в одном базисе. Поэтому

$mathop{mathbf{v}}limits_{(mathbf{e})}= Scdot mathop{mathbf{v'}}limits_{(mathbf{e}')}quad Leftrightarrowquad begin{pmatrix} v_1\vdots\v_n end{pmatrix}= begin{pmatrix}s_{11}&cdots&s_{1n}\ vdots&cdots& vdots\ s_{n1}&cdots& s_{nn}end{pmatrix}!cdot! begin{pmatrix}v'_1\vdots\ v'_nend{pmatrix}!.$

(8.11)

Формула (8.11) устанавливает связь координат вектора в разных базисах: координатный столбец вектора в старом базисе получается в результате умножения матрицы перехода на координатный столбец вектора в новом базисе.

Пример 8.3. В пространстве $P_2(mathbb{R})$ многочленов степени не выше второй даны две системы многочленов:

$mathbf{e}_1=1,quad mathbf{e}_2=x,quad mathbf{e}_3=x^2,quad mathbf{f}_1=(x+1)^2, quad mathbf{f}_2=(x-1)^2,quad mathbf{f}_3=x^2.$

Доказать, что каждая система является базисом пространства $P_2(mathbb{R})$ . Найти матрицу перехода от базиса (mathbf{e}) к базису (mathbf{f}) . Определить координаты квадратного трехчлена $mathbf{p}=x^2-x+1$ относительно базисов и .

Решение. Система многочленов $mathbf{e}=1,~mathbf{e}_2=x,~ mathbf{e}_3=x^2$ является стандартным базисом пространства $P_2(mathbb{R})$ . Докажем, что система $mathbf{f}_1=(x+1)^2,$ $mathbf{f}_2=(x-1)^2,$ $mathbf{f}_3=x^2$ является базисом. По ступим следующим образом. Найдем координатные столбцы f_1,,f_2,,f_3 этих многочленов в стандартном базисе. Раскладывая по базису (mathbf{e}) , получаем

$begin{aligned}mathbf{f}_1&=(x+1)^2=x^2+2x+1= 1cdot mathbf{e}_1+2cdot mathbf{e}_2+1cdot mathbf{e}_3quad Rightarrowquad f_1=begin{pmatrix}1&2&1 end{pmatrix}^T;\[5pt] mathbf{f}_2&=(x-1)^2=x^2-2x+1= 1cdot mathbf{e}_1-2cdot mathbf{e}_2+ 1cdot mathbf{e}_3quad Rightarrowquad f_1=begin{pmatrix}1&-2&1end{pmatrix}^T;\[5pt] mathbf{f}_3&=x^2=0cdot mathbf{e}_1+0cdot mathbf{e}_2+1cdot mathbf{e}_3quad Rightarrow quad f_3=begin{pmatrix}0&0&1end{pmatrix}^T. end{aligned}$

Составим из этих столбцов матрицу $s=begin{pmatrix}1&1&0\ 2&-2&0\ 1&1&1 end{pmatrix}$ . Ранг этой матрицы равен 3, так как det{S}=-4ne0 . Следовательно, столбцы f_1,,f_2,,f_3 линейно независимы, тогда и многочлены $mathbf{f}_1,, mathbf{f}_2,,mathbf{f}_3$ линейно независимы (см. пункт 2 замечаний 8.5). Итак, многочлены $mathbf{f}_1,, mathbf{f}_2,,mathbf{f}_3$ являются базисом пространства $P_2(mathbb{R})$ , а матрица — искомая матрица перехода от базиса (mathbf{e}) к базису (mathbf{f}) . Осталось найти координаты многочлена $mathbf{p}=x^2-x+1$ в этих базисах. Раскладывая по базисам, находим

$begin{gathered} mathbf{p}=x^2-x+1= 1cdot mathbf{e}_1-1cdot mathbf{e}_2+1cdot mathbf{e}_3quad Rightarrowquad mathop{mathbf{p}}limits_{(mathbf{e})}= begin{pmatrix}1&-1&1 end{pmatrix}^T;\[5pt] mathbf{p}=x^2-x+1=frac{(x+1)^3+3(x-1)^2}{4}= frac{1}{4}cdot mathbf{f}_1+frac{3}{4}cdot mathbf{f}_2+ 0cdot mathbf{f}_3quad Rightarrowquad mathop{mathbf{p}}limits_{(mathbf{f})}= begin{pmatrix}dfrac{1}{4}& dfrac{3}{4}&0 end{pmatrix}^T. end{gathered}$

Проверим результат, вычисляя $mathop{mathbf{p}}limits_{(mathbf{e})}$ по формуле (8.11):

$mathop{mathbf{p}}limits_{(mathbf{e})}= Scdot mathop{mathbf{p}}limits_{(mathbf{f})}= begin{pmatrix}1&1&0\ 2&-2&0\ 1&1&1 end{pmatrix}!cdot! begin{pmatrix}1/4\3/4\0 end{pmatrix}= begin{pmatrix}1\-1\1 end{pmatrix}!.$

Результаты совпадают.

Свойства матрицы перехода от одного базиса к другому

1. Пусть имеются три базиса (mathbf{e}),,(mathbf{f}),,(mathbf{g}) пространства и известны матрицы перехода: $mathop{S}limits_{(mathbf{e})to(mathbf{f})}$ от базиса к базису ; $mathop{S}limits_{(mathbf{f})to(mathbf{g})}$ от к ; $mathop{S}limits_{(mathbf{e})to(mathbf{g})}$ от к . Тогда

$mathop{S}limits_{(mathbf{e})to(mathbf{g})}= mathop{S}limits_{(mathbf{e})to(mathbf{f})}cdot mathop{S}limits_{(mathbf{f})to(mathbf{g})}.$

(8.12)

Действительно, запишем связь (8.10) для данных базисов:

$(mathbf{f})= (mathbf{e})cdot mathop{S}limits_{(mathbf{e})to(mathbf{f})};qquad (mathbf{g})= (mathbf{f})cdot mathop{S}limits_{(mathbf{f})to(mathbf{g})};qquad (mathbf{g})= (mathbf{e})cdot mathop{S}limits_{(mathbf{e})to (mathbf{g})}.$

Подставляя первое выражение во второе равенство, получаем $(mathbf{g})= (mathbf{e})cdot mathop{S}limits_{(mathbf{e})to(mathbf{f})}cdot mathop{S}limits_{(mathbf{f})to(mathbf{g})}$ . Сравнивая с третьим равенством, приходим к (8.12).

2. Если — матрица перехода от базиса (mathbf{e}) к базису (mathbf{f}) , то матрица обратима и обратная матрица $S^{-1}$ является матрицей перехода от базиса к базису . Координаты вектора mathbf{v} в базисах и связаны формулами:

$mathop{mathbf{v}}limits_{(mathbf{e})}= Scdot mathop{mathbf{v}}limits_{(mathbf{f})},qquad mathop{mathbf{v}}limits_{(mathbf{f})}= S^{-1}cdot mathop{mathbf{v}}limits_{(mathbf{e})}.$

В самом деле, пусть — матрица перехода от базиса (mathbf{f}) к базису (mathbf{e}) . Учитывая, что матрица перехода от базиса к базису — единичная, применяем свойство 1 к трем базисам (mathbf{e}),(mathbf{f}),(mathbf{e})colon,E=ST . Для трех базисов (mathbf{f}),,(mathbf{e}),,(f) аналогично получаем: E=TS . Следовательно, $T=S^{-1}$ .

3. Всякая обратимая квадратная матрица n-го порядка может служить матрицей перехода от одного базиса n-мерного линейного пространства к другому базису.

Пример 8.4. В двумерном арифметическом пространстве $mathbb{R}^2$ даны два базиса: $mathbf{f}_1= begin{pmatrix}3\2 end{pmatrix}!,$ $mathbf{f}_2= begin{pmatrix}1\1end{pmatrix}$ и $mathbf{g}_1= begin{pmatrix}1\2 end{pmatrix}!,$ $mathbf{g}_2=begin{pmatrix}-1\1 end{pmatrix}$ . Найти матрицу $mathop{S}limits_{(mathbf{f})to(mathbf{g})}$ перехода от базиса к базису и координаты вектора $mathbf{v}=begin{pmatrix}6\9end{pmatrix}$ в каждом из базисов.

Решение. Рассмотрим стандартный базис $mathbf{e}_1= begin{pmatrix}1\0end{pmatrix}!,~ mathbf{e}_2=begin{pmatrix}0\1 end{pmatrix}$ пространства $mathbb{R}^2$ . Находим координаты векторов $mathbf{f}_1,, mathbf{f}_2,,mathbf{g}_1,,mathbf{g}_2$ в стандартном базисе. Раскладываем вектор $mathbf{f}_1:$

$mathbf{f}_1=begin{pmatrix}3\2end{pmatrix}= 3cdot! begin{pmatrix}1\0 end{pmatrix}+ 2cdot! begin{pmatrix}0\1end{pmatrix}= 3cdot mathbf{e}_1+2cdot mathbf{e}_2quad Rightarrowquad f_1=begin{pmatrix}3\2end{pmatrix}!.$

В стандартном базисе (mathbf{e}) пространства $mathbb{R}^2$ координатный столбец f_1 совпадает с вектором $mathbf{f}_1$ . Для других векторов аналогично получаем $f_2=begin{pmatrix}1\1end{pmatrix}!,$ $g_1=begin{pmatrix}1\2end{pmatrix}!,$ $g_2=begin{pmatrix}-1\1end{pmatrix}$ . Из координатных столбцов составим матрицы перехода (8.9) от стандартного базиса (mathbf{e}) к данным базисам (mathbf{f}) и (mathbf{g}):

$mathop{S}limits_{(mathbf{e})to(mathbf{f})}= begin{pmatrix}3&1\ 2&1 end{pmatrix}!,quad mathop{S}limits_{(mathbf{e})to(mathbf{g})}= begin{pmatrix}1&-1\ 2&1 end{pmatrix}!.$

По свойству 1 матриц перехода имеем $mathop{S}limits_{(mathbf{f})to(mathbf{g})}= mathop{S}limits_{(mathbf{f})to(mathbf{e})}cdot mathop{S}limits_{(mathbf{e})to(mathbf{g})}$ . .По свойству 2: $mathop{S}limits_{(mathbf{f})to(mathbf{e})}= mathop{S^{-1}}limits_{(mathbf{e})to(mathbf{f})}$ . Поэтому

$mathop{S}limits_{(mathbf{f})to(mathbf{g})}= mathop{S^{-1}}limits_{(mathbf{e})to(mathbf{f})}cdot mathop{S}limits_{(mathbf{e})to(mathbf{g})}= begin{pmatrix}3&1\2&1 end{pmatrix}^{-1}!cdot! begin{pmatrix}1&-1\ 2&1end{pmatrix}= begin{pmatrix}1&-1\-2&3 end{pmatrix}!cdot! begin{pmatrix}1&-1\ 2&1 end{pmatrix}= begin{pmatrix}-1&-2\ 4&5 end{pmatrix}!.$

В стандартном базисе (mathbf{e}) пространства $mathbb{R}^2$ координатный столбец $mathop{v}limits_{(mathbf{e})}=begin{pmatrix}6\9 end{pmatrix}$ совпадает с вектором mathbf{v} . Найдем координаты этого вектора в базисе (mathbf{f}) (по свойству 2 матрицы перехода):

$mathop{v}limits_{(mathbf{f})}= mathop{S^{-1}}limits_{(mathbf{e})to(mathbf{f})}cdot mathop{v}limits_{(mathbf{e})}= begin{pmatrix}3&1\2&1 end{pmatrix}^{-1}!cdot! begin{pmatrix}6\9 end{pmatrix}= begin{pmatrix}1&-1\ -2&3 end{pmatrix}!cdot! begin{pmatrix}6\9 end{pmatrix}= begin{pmatrix}-3\15 end{pmatrix}!.$

В самом деле, справедливо разложение

$mathbf{v}= begin{pmatrix}6\9 end{pmatrix}= -3cdot! begin{pmatrix}3\2 end{pmatrix}+ 15cdot! begin{pmatrix}1\1 end{pmatrix}= -3cdot mathbf{f}_1+15cdot mathbf{f}_2.$

Найдем координаты вектора mathbf{v} в базисе (mathbf{g}) двумя способами

$begin{aligned}mathop{mathbf{v}}limits_{(mathbf{g})}&= mathop{S^{-1}}limits_{(mathbf{f})to(mathbf{g})}cdot mathop{mathbf{v}}limits_{(mathbf{f})}= begin{pmatrix}-1&-2\ 4&5end{pmatrix}^{-1}!cdot! begin{pmatrix}-3\15 end{pmatrix}= frac{1}{3}cdot! begin{pmatrix}5&2\ -4&-1 end{pmatrix}!cdot! begin{pmatrix}-3\15 end{pmatrix}= begin{pmatrix}5\-1 end{pmatrix}!;\[5pt] mathop{mathbf{v}}limits_{(mathbf{g})}&= mathop{S^{-1}}limits_{(mathbf{e})to(mathbf{g})}cdot mathop{mathbf{v}}limits_{(mathbf{e})}= begin{pmatrix}1&-1\ 2&1end{pmatrix}^{-1}!cdot! begin{pmatrix}6\9 end{pmatrix}= frac{1}{3}cdot! begin{pmatrix}1&1\ -2&1 end{pmatrix}!cdot! begin{pmatrix}6\9 end{pmatrix}= begin{pmatrix}5\-1 end{pmatrix}!end{aligned}$

Полученный результат подтверждает разложение:

$mathbf{v}= begin{pmatrix}6\9 end{pmatrix}= 5cdot! begin{pmatrix}1\2 end{pmatrix}+(-1)cdot! begin{pmatrix}-1\1end{pmatrix}= 5cdot mathbf{f}_1+(-1)cdot mathbf{f}_2.$

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

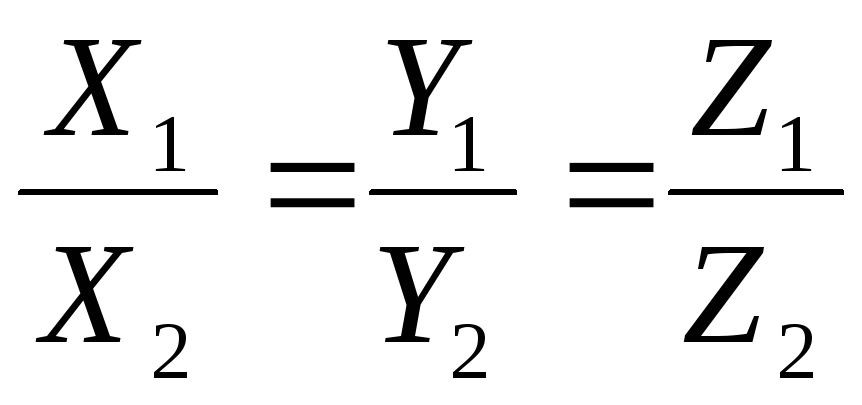Источник