Введение системы координат
30 мая 2011
Метод координат — это, конечно, очень хорошо, но в настоящих задачах C2 никаких координат и векторов нет. Поэтому их придется вводить. Да-да, вот так взять и ввести: указать начало отсчета, единичный отрезок и направление осей x, y и z.
Самое замечательное свойство этого метода заключается в том, что не имеет никакого значения, как именно вводить систему координат. Если все вычисления будут правильными, то и ответ будет правильным.
Тем не менее, приведу некоторые рекомендации, как лучше ввести систему координат для самых часто встречающихся в задаче C2 многогранников. С указанием конкретных точек. Во всех случаях упор делается на минимизацию объема вычислений.
Координаты куба
Если в задаче C2 будет куб — считайте, что вам повезло. Это самый простой многогранник, все двугранные углы которого равны 90°.
Система координат также вводится очень просто:
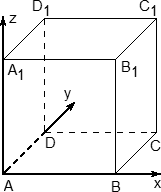
- Начало координат — в точке A;
- Чаще всего ребро куба не указано, поэтому принимаем его за единичный отрезок;
- Ось x направляем по ребру AB, y — по ребру AD, а ось z — по ребру AA1.
Обратите внимание: ось z направляется вверх! После двумерной системы координат это несколько непривычно, но на самом деле очень логично.
Итак, теперь у каждой вершины куба есть координаты. Соберем их в таблицу — отдельно для нижней плоскости куба:
| Точка | A | B | C | D |
| Координаты | (0; 0; 0) | (1; 0; 0) | (1; 1; 0) | (0; 1; 0) |
И для верхней:
| Точка | A1 | B1 | C1 | D1 |
| Координаты | (0; 0; 1) | (1; 0; 1) | (1; 1; 1) | (0; 1; 1) |
Несложно заметить, что точки верхней плоскости отличаются соответствующих точек нижней только координатой z. Например, B = (1; 0; 0), B1 = (1; 0; 1). Главное — не запутаться!
Координаты трехгранной призмы
Призма — это уже намного веселее. При правильном подходе достаточно знать координаты только нижнего основания — верхнее будет считаться автоматически.
В задачах C2 встречаются исключительно правильные трехгранные призмы (прямые призмы, в основании которых лежит правильный треугольник). Для них система координат вводится почти так же, как и для куба. Кстати, если кто не в курсе, куб — это тоже призма, только четырехгранная.
Итак, поехали! Вводим систему координат:
- Начало координат — в точке A;
- Сторону призмы принимаем за единичный отрезок, если иное не указано в условии задачи;
- Ось x направляем по ребру AB, z — по ребру AA1, а ось y расположим так, чтобы плоскость OXY совпадала с плоскостью основания ABC.
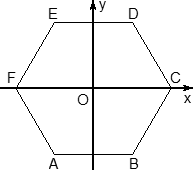
Здесь требуются некоторые пояснения. Дело в том, что ось y НЕ совпадает с ребром AC, как многие считают. А почему не совпадает? Подумайте сами: треугольник ABC — равносторонний, в нем все углы по 60°. А углы между осями координат должны быть по 90°, поэтому сверху картинка будет выглядеть так:
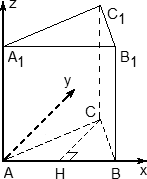
Надеюсь, теперь понятно, почему ось y не пойдет вдоль AC. Проведем в этом треугольнике высоту CH. Треугольник ACH — прямоугольный, причем AC = 1, поэтому AH = 1 · cos A = cos 60°; CH = 1 · sin A = sin 60°. Эти факты нужны для вычисления координат точки C.
Теперь взглянем на всю призму вместе с построенной системой координат:
Получаем следующие координаты точек:
Как видим, точки верхнего основания призмы снова отличаются от соответствующих точек нижнего лишь координатой z. Основная проблема — это точки C и C1. У них есть иррациональные координаты, которые надо просто запомнить. Ну, или понять, откуда они возникают.
Координаты шестигранной призмы
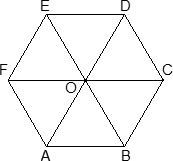
Шестигранная призма — это «клонированная» трехгранная. Можно понять, как это происходит, если взглянуть на нижнее основание — обозначим его ABCDEF. Проведем дополнительные построения: отрезки AD, BE и CF. Получилось шесть треугольников, каждый из которых (например, треугольник ABO) является основанием для трехгранной призмы.
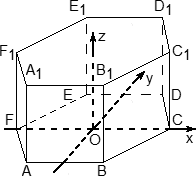
Теперь введем собственно систему координат. Начало координат — точку O — поместим в центр симметрии шестиугольника ABCDEF. Ось x пойдет вдоль FC, а ось y — через середины отрезков AB и DE. Получим такую картинку:
Обратите внимание: начало координат НЕ совпадает с вершиной многогранника! На самом деле, при решении настоящих задач вы обнаружите, что это очень удобно, поскольку позволяет значительно уменьшить объем вычислений.
Осталось добавить ось z. По традиции, проводим ее перпендикулярно плоскости OXY и направляем вертикально вверх. Получим итоговую картинку:
Запишем теперь координаты точек. Предположим, что все ребра нашей правильной шестигранной призмы равны 1. Итак, координаты нижнего основания:
Координаты верхнего основания сдвинуты на единицу по оси z:
Координаты четырехугольной пирамиды
Пирамида — это вообще очень сурово. Мы разберем только самый простой случай — правильную четырехугольную пирамиду, все ребра которой равны единице. Однако в настоящих задачах C2 длины ребер могут отличаться, поэтому ниже приведена и общая схема вычисления координат.
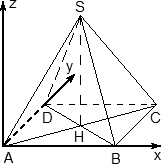
Итак, правильная четырехугольная пирамида. Это такая же, как у Хеопса, только чуть поменьше. Обозначим ее SABCD, где S — вершина. Введем систему координат: начало в точке A, единичный отрезок AB = 1, ось x направим вдоль AB, ось y — вдоль AD, а ось z — вверх, перпендикулярно плоскости OXY. Для дальнейших вычислений нам потребуется высота SH — вот и построим ее. Получим следующую картинку:
Теперь найдем координаты точек. Для начала рассмотрим плоскость OXY. Здесь все просто: в основании лежит квадрат, его координаты известны. Проблемы возникают с точкой S. Поскольку SH — высота к плоскости OXY, точки S и H отличаются лишь координатой z. Собственно, длина отрезка SH — это и есть координата z для точки S, поскольку H = (0,5; 0,5; 0).
Заметим, что треугольники ABC и ASC равны по трем сторонам (AS = CS = AB = CB = 1, а сторона AC — общая). Следовательно, SH = BH. Но BH — половина диагонали квадрата ABCD, т.е. BH = AB · sin 45°. Получаем координаты всех точек:
Вот и все с координатами пирамиды. Но не с координатами вообще. Мы рассмотрели лишь самые распространенные многогранники, однако этих примеров достаточно, чтобы самостоятельно вычислить координаты любых других фигур. Поэтому можно приступать, собственно, к методам решения конкретных задач C2.
Смотрите также:
- Четырехугольная пирамида в задаче C2
- Метод координат в пространстве
- Сложение и вычитание дробей
- Не пишите единицы измерения в задаче B12
- Как решать простейшие логарифмические уравнения
- Задача B4: транзит нефти
Векторы в пространстве и метод координат
Существует два способа решения задач по стереометрии
Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.
Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.
Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.
Система координат в пространстве
Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.
Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.
Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:
Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.
Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора:
Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:
Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма
Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и
.
Сумма векторов:
Разность векторов:
Произведение вектора на число:
Скалярное произведение векторов:
Косинус угла между векторами:
Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.
1. В кубе ABCDA1B1C1D1 точки E и K — середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.
Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:
Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.
Прямые AE и BK — скрещиваются. Найдем угол между векторами и
. Для этого нужны их координаты.
Запишем координаты векторов:
и найдем косинус угла между векторами и
:
2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.
Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.
Координаты точек A, B и C найти легко:
Из прямоугольного треугольника AOS найдем
Координаты вершины пирамиды:
Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.
Найдем координаты векторов и
:
и угол между ними:
Покажем теперь, как вписать систему координат в треугольную призму.
3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D — середина ребра A1B1. Найдите косинус угла между прямыми AD и BC1
Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.
Запишем координаты точек:
Точка D — середина A1B1. Значит, пользуемся формулами для координат середины
отрезка.
Найдем координаты векторов и
, а затем угол между ними:
Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.
Плоскость в пространстве задается уравнением:
Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.
Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.
Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
Покажем, как это делается.
Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).
Уравнение плоскости выглядит так:
Подставим в него по очереди координаты точек M, N и K.
Для точки M:
То есть A + C + D = 0.
Для точки N:
Аналогично для точки K:
Получили систему из трех уравнений:
.
В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.
Пусть, например, D = −2. Тогда:
;
.
Выразим C и B через A и подставим в третье уравнение:
.
Решив систему, получим:
Уравнение плоскости MNK имеет вид:
Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:
Вектор — это нормаль к плоскости MNK.
Уравнение плоскости, проходящей через заданную точку имеет вид:
Угол между плоскостями равен углу между нормалями к этим плоскостям:
Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.
Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.
Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.
4. В кубе ABCDA1B1C1D1 точки E и F — середины ребер соответственно A1B1 и A1D1. Найдите тангенс угла между плоскостями AEF и BDD1.
Строим чертеж. Видно, что плоскости AEF и BDD1 пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD1.
Сначала — нормаль к плоскости BDD1. Конечно, мы можем подставить координаты точек B, D и D1 в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD1 — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.
Итак, первый вектор нормали у нас уже есть:
Напишем уравнение плоскости AEF.
Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.
Упростим систему:
.
Пусть С = -1. Тогда A = B = 2.
Уравнение плоскости AEF:
Нормаль к плоскости AEF:
Найдем угол между плоскостями:
5. Основание прямой четырехугольной призмы BCDA1B1C1D1 — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3.
Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 
Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».
Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?
«Расстояние между прямыми A1C1 и BD равно √3». Прямые A1C1 и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A1C1 и BD — это, очевидно, OO1, где O — точка пересечения диагоналей нижнего основания, O1 — точка пересечения диагоналей верхнего. А отрезок OO1 и равен высоте параллелепипеда.
Итак, AA1 = √3
Плоскость AA1 D1 D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор
.
Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B1D». Но позвольте, если плоскость перпендикулярна прямой B1D — значит, B1D и есть нормаль к этой плоскости! Координаты точек B1 и D известны:
Координаты вектора — тоже:
Находим угол между плоскостями, равный углу между нормалями к ним:
Зная косинус угла, находим его тангенс по формуле
Получим:
Ответ:
Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.
Пусть — вектор, лежащий на прямой m (или параллельный ей),
— нормаль к плоскости α.
Находим синус угла между прямой m и плоскостью α по формуле:
6. В кубе ABCDA1B1C1D1 точка E — середина ребра A1B1. Найдите синус угла между прямой AE и плоскостью BDD1.
Как всегда, рисуем чертеж и выбираем систему координат
Находим координаты вектора .
Нужно ли нам уравнение плоскости BDD1? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .
Найдем угол между прямой и плоскостью:
Ответ:
Расстояние от точки M с координатами x0, y0 и z0 до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:
7. В основании прямоугольного параллелепипеда BCDA1B1C1D1 лежит прямоугольник ABCD со сторонами AB = , AD =
. Высота параллелепипеда AA1 =
. Найдите расстояние от точки A до плоскости A1DB.
Построим чертеж и выпишем координаты точек:
Запишем уравнение плоскости A1DB. Вы помните, как это делается — по очереди подставляем координаты точек A1, D и B в уравнение Ax + Be + Cz + D
Решим эту систему. Выберем
Тогда
Уравнение плоскости A1DB имеет вид:
Дальше все просто. Находим расстояние от точки A до плоскости A1DB:
В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Векторы в пространстве и метод координат» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.05.2023
1. Система координат в пространстве.
Выберем начало координат. Проведем три взаимно перпендикулярные оси х, y и z . Выберем масштаб.
Получилась система координат в трехмерном пространстве.
Каждая точка характеризуется тремя числами — координатами по x, y и z. Запись M(−1;
3;
2)
означает,
что координата точки M по
x (абсцисса) равна −1, координата
по y (ордината) равна 3, а координата по z (аппликата) равна 2.
Векторы в пространстве определяются так же, как и на плоскости.
Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами
x, y и z:
ﺂ؟(xa; ya; za)
Чтобы найти
координаты
вектора, так же, как и на плоскости, из
координаты конца надо вычесть координату начала.
1.
2.
Если точка M – середина отрезка AB,
то ее координаты находятся по формуле:
3.
4. 
 – сумма векторов.
– сумма векторов.
5. – разность векторов.
6. – произведение вектора на число.
7. — скалярное произведение векторов
8. 
векторами.
2. Введение системы координат.
Метод
координат – это, конечно, очень хорошо, но в настоящих задачах C2
никаких координат и векторов нет, поэтому их надо вводить.
Самое
замечательное свойство заключается в том, что не имеет никакого значения как
именно вводить систему координат. Если все вычисления будут правильными, то и
ответ будет правильным.
2.1
Координаты куба.
Система координат вводится очень просто:
1. Начало
координат – в точке A
2. Если
ребро куба не указано, то принимаем его за единичный отрезок;
3. Ось
x
направляем по ребру АВ, у – по ребру АD, а
ось z
– по ребру AA1 .
Теперь
у каждой вершины куба есть координаты:
A
(0; 0; 0), B (1; 0; 0), C
(1; 1; 0), D (0; 1; 0),
A1 (0; 0;1) B
(1; 0; 1) C1
(1; 1; 1), D1
(0; 1; 1).
2.2 Координаты
правильной треугольной призмы
A
(1; 0; 0), B, C
(0; 0; 0), A1 (1;
0; 1), B1 , C1 (0; 0; 1).
2.3
Координаты правильной шестиугольной призмы
, , , ,
, , ,
, , ,
, .
2.4 Координаты
правильной четырехугольной пирамиды
Введем
систему координат с началом в точке А
A (0; 0; 0), B (1;
0; 0), C (1; 1; 0), D (0; 1; 0), H (0,5;
0,5; 0).
Найдем
координаты точки S. Рассмотрим треугольники ASH и ABH
1. AS = AB =
1 по условию;
2. Угол AHS = AHB =
90°, поскольку SH — высота, а AH ⊥ HB как диагонали
квадрата;
3. Сторона AH — общая.
Следовательно,
прямоугольные треугольники ASH и ABH равны по одному
катету и гипотенузе. Значит, SH = BH =
0,5 · BD. Но BD — диагональ квадрата
со стороной 1. Поэтому имеем:
Итак,
координаты точки S:

случай, если боковые ребра пирамиды не равны ребрам основания.
В этом случае рассмотрим треугольник AHS:
Треугольник AHS — прямоугольный,
причем гипотенуза AS — это одновременно и боковое
ребро исходной пирамиды SABCD. Катет: AH =
0,5 · AC. Оставшийся катет SH найдем по теореме
Пифагора. Это и будет координата z для
точки S.
3. Матрицы и
определители второго и третьего порядка.
Определение:
Таблица, составленная из четырёх чисел называется
квадратной матрицей второго порядка. Числа называют
элементами матрицы.
Определение:
Число ∆ называется определителем или детерминантом матрицы.
∆=
Определитель третьего порядка можно вычислить так:
4. Метод
координат в пространстве
4.1 Угол
между прямыми.
Вычисление
направляющих векторов для прямых.
В задаче С2
прямые всегда задаются парой точек. Если ввести систему координат и рассмотреть
вектор с началом и концом в этих точках, получим направляющий вектор для
прямой.

α-угол
между прямыми
3.1 Угол
между двумя прямыми – это угол между их направляющими векторами.

В единичном
кубе ABCDA1B1C1D1
найдите угол между прямыми AE и BF, где E –
середина ребра A1B1,
где Е – середина ребра А1В1 а F –
середина ребра B1C1.
Решение
(1 способ)
K—
середина A1D1 AK║BF
угол KAE = φ
По теореме
Пифагора
По
теореме косинусов для ∆ AKE
KE² = AE²
+ AK²
— 2 * AE
*AK
* cos φ
cos φ=0,8
φ=arccos0.8
Решение
(2 способ)
С
помощью векторов и координат легко найти угол между прямыми.
 |
А
если требуется найти угол между плоскостями или между прямой и плоскостью, то
для этого нам понадобится уравнение плоскости в пространстве.
4.2
Плоскость в пространстве задается уравнением.
Ax+By+Cz+D=0,
где A,
B
и С – координаты вектора, перпендикулярного этой плоскости. Его называют
нормалью к плоскости.
Чтобы
написать уравнение плоскости, берем координаты трех принадлежащих ей точек.
Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
Напишем
уравнение плоскости, проходящей через точки M (1;
0; 1), N(2;
-2; 0) и К (4; 1; 2)
Уравнение
плоскости выглядит так:
Ax+By+Cz+D=0
Получим
систему из трех уравнений:
В ней
четыре неизвестных: A, B,
С и D.
Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило –
простое вместо одной из переменных можно взять любое число, не равное нулю.
Решив систему, получим:
A=- B=-
C=
Уравнение
плоскости MNK имеет вид:
Умножим
обе части уравнения на -3. Тогда коэффициенты станут целыми:
x+4y+7z+6-0
Вектор
(1; 4; -7) – это нормаль к плоскости MNK.
Если
плоскость проходит через начало координат, то D=0
(так как D≠0 не позволит получить верное числовое
равенство).
Уравнение
плоскости, проходящей, через заданную точку имеет
вид:
Уравнение плоскости можно составить и с помощью определителя третьего
порядка :
Пусть имеем точки
,
Тогда уравнение плоскости, проходящей через эти
три точки ,будет иметь вид:

4.3
Угол между плоскостями равен углу между нормалями к
этим плоскостям:
cos φ=
При
пересечении двух плоскостей образуется четыре угла . Мы
берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения –
чтобы косинус угла был неотрицателен.
Задача
2
В кубе ABCDA1B1C1D1 точки E и F с
середины ребер соответственно A1B1 и
A1D1. Найдите косинус угла между плоскостями AEF и BDD1.
Видно, что плоскости AEF и BDD1 пересекаются где-то вне куба. В классическом решении пришлось бы
строить пересечения. Но координатный метод значительно всё
упрощает. Достаточно отметить координаты нужных точек и найти
угол между нормалями
к плоскостям
AEF и BDD1.
A(0;
0; 0), C(1; 1; 0)
Сначала
– нормаль к плоскости BDD1.
Мы можем подставить координаты точек B, D
и D1 в уравнение плоскости и найти координаты
вектора нормали. А можно увидеть нужную нормаль на чертеже. Ведь плоскость BDD1 – это диагональное сечение куба. Вектор перпендикулярен этой плоскости.
Итак,
первый вектор нормали у нас уже есть:
Напишем
уравнение плоскости AEF.
A E
F
Составим уравнение плоскости:

Уравнение
плоскости AEF: 2x+2y—z=0
Нормаль
к плоскости AEF: (2;
2; -1)
Найдем
угол между плоскостями:

Угол между прямой и плоскостью
Задача
3.
В
правильной четырехугольной пирамиде SABCD, все
ребра которой равны 1, найдите угол между прямой DE, где E-середина
апофемы SF
грани ASB
грани и плоскостью ASC

OB —
вектор нормали плоскости ASC
DE —
направляющий вектор прямой
OB — — вектор нормали
плоскости ASC
DE — — вектор направляющей
вектор прямой DE
 |

4.5
Расстояние от точки до плоскости
Задача
4
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1
, все рёбра которой равны 1, найдите расстояние от точки E
до прямой B1C1.
Решение
(1 способ)
1) Рассмотрим ΔCDE:
по теореме косинусов:
СЕ2 = 2СD2
— 2CD2 cos120° = 2 + 2*1/2 = 3 =>
CE =
2) Рассмотрим ΔС1СЕ: он
прямоугольный, т.к. С1С перпендикулярна плоскости нижнего основания
=> CC1
перпендикулярна СЕ.
По теореме Пифагора:
С1Е2 = ()2 + 12
= 4, С1Е = 2
3) Рассмотрим ΔBCE:
он прямоугольный , т.к. 120° — 60°:2 = 90° (из ΔCDE)
ВЕ2 = ()2 + 12
= 4, ВЕ = 2
4) Рассмотрим ΔВВ1Е: он прямоугольный,
т.к. ВВ1 перпендикулярна ВЕ,
по теореме Пифагора:
В1Е2 = В1В2
+ ВЕ2 = 4 + 1 = 5, ВЕ =
5) Рассмотрим ΔВ1С1Е:
С1Е = 2, С1В1
= 1, В1Е = , т.е. 22 + 12
= ()2. Таким образом,
по теореме обратной теореме Пифагора, ΔВ1С1Е –
прямоугольный, угол В1С1Е = 90°

– это длина С1Е = 2
2
способ
1)
Поместим призму в прямоугольную систему координат, расположив координатные оси,
как показано на рисунке. СС1, СВ и СЕ попарно перпендикулярны,
поэтому можно направить вдоль них координатные оси. Получаем координаты:
С1 (0;0;1),
Е (;0;0), В1 (0;1;1)
2) Найдем координаты
векторов С1В1 и С1Е:
С1В1
(0;1;0), С1Е (;0;-1).
3) Найдем косинус угла
между С1В1 и С1Е, используя скалярное
произведение векторов С1В1 и С1Е:
cosβ = = 0 => β
= 90° => C1E
– искомое расстояние.
4) С1Е = =2
4.6 Расстояние между скрещивающимися прямыми
в пространстве — это длина их общего перпендикуляра. Общий перпендикуляр скрещивающихся прямых — отрезок с
концами на этих прямых, перпендикулярный обеим этим прямым.
Если прямые в пространстве пересекаются, расстояние между ними считается равным
0.
Пусть есть не
пересекающиеся в пространстве прямые a и b.
Построим плоскости α и β так, чтобы эти плоскости были
параллельны, плоскость α содержала в себе прямую a, плоскость β содержала в себе прямую b.
Расстоянием между прямыми a и b будет расстояние между плоскостями α и β.
←Метод координат
Задача 1
Задача 2
Задача 3
Задача1:
Основанием призмы АВСА1В1С1 является правильный треугольник АВС со стороной 6. Боковое ребро АА1 призмы равно 6 и образует со сторонами АВ и АС углы по 600.
Определите:
а) угол между прямыми АА1 и СВ1;
б) расстояние от точки B1 до плоскости А1СВ;
Наша заданная призма не прямая, а наклонная, так как ребро АА1 не перпендикулярно основанию. Это обстоятельство в значительной степени усложняет решение задачи Две боковые грани у нее не привычные прямоугольники, а ромбы со стороной, равной 6. Почему? Потому что боковые ребра у призмы параллельны, а в нашей задаче они еще и равны ребрам основания призмы. Третья боковая грань — прямоугольник, а в данной задаче — квадрат, так как все ребра призмы равны.
Конечно же ее, эту задачу, можно решить геометрически, что мы и сделаем, частично.


. Это квадрат по условию, а следовательно,
. Тогда угол между прямыми будет
= ∠M1OB1 = 45°.

Мы же пойдем другим путем, присоединим к нашей призме систему координат, определим координаты узловых точек и найдем, все что нужно по координатам прямых и плоскостей. (Кликните, чтобы увеличить чертеж).
Чтобы сделать рисунок более понятным, я закрасила грани и основания разным цветом. Предлагаю посмотреть на призму в проекциях на координатные плоскости, как бы со всех сторон. Соответственно на рисунке 1 смотрим на плоскость х0у, на рисунке 2 — z0y, а на рисунках 3 и 4 — плоскость z0x слева и справа от призмы.
Переходим к расчету координат узловых точек. Вспомним, что наша призма состоит их двух треугольников (основания призмы), двух ромбов (боковые грани) и квадрата (третья боковая грань). 
Боковая грань АА1С1С — ромб углом 600, а следовательно, его диагональ равна стороне. А это значит, что точка А1 равноудалена от точек А и С. Точно также можно рассмотреть грань АА1В1В.

Координата z для нижнего основания призмы равна 0, а для верхнего определяем его из рисунка2, где АА1 — гипотенуза треугольника, а высота (она же координата z) — катет. Координата
Итак, точки и их координаты: Нижнее основание
В верхнем основании каждая точка сдвигается на вдоль оси Ох, и координата
Переходим к следующему вопросу

до плоскости А1СВ определим по формуле
Осталась «самая ерунда» — найти эти самые A, B, C и D. Ну что ж, ищем.
Для этого составляем и решаем систему уравнений, основываясь на точках плоскости:
.
Складываем второе и третье уравнение, получаем:
Из второго уравнения: ,
Из первого уравнения:
Подставляем В и находим С :
(Кстати, уравнение нашей плоскости будет . )
Теперь ищем расстояние от точки до плоскости:
Ответ: 45º,

Дан куб АВСDА1В1С1D1 c ребром 2.
- а) Докажите, что плоскости A1BD и B1D1C параллельны
- б) Найдите расстояние между плоскостями A1BD и B1D1C.
С первым пунктом все просто: Плоскости параллельны, потому что пересекающиеся прямые их попарно параллельны.
Переходим к пункту б). Координаты точек будут
Составляем систему уравнения плоскости с координатами точек, через которые она проходит, чтобы определить коэффициенты А B, C и D:
Получаем: ,
,
Уравнение плоскости B1D1C будет
Домножим на 2, чтобы избавиться от дробей
Получается, что у первого уравнения . Но если плоскости параллельны, а они у нас параллельны, их уравнения имеют одинаковые коэффициенты А, В, и С, но разные D. Ищем
Для этого подставляем в уравнение плоскости B1D1C вместо D=1
, будет
, а вместо x, y, z — координаты точки, например, A1( 2; 0; 2 ), принадлежащей плоскости A1BD. Получим
Получается, что
Подставляем в формулу для определения расстояния между параллельными плоскостями
Ответ:
Задача 3→
Нахождение координат вектора через координаты точек
Отложим от начала координат единичные векторы, то есть векторы, длины которых равны единице. Направление вектора i → должно совпадать с осью O x , а направление вектора j → с осью O y .
Векторы i → и j → называют координатными векторами.
Координатные векторы неколлинеарны. Поэтому любой вектор p → можно разложить по векторам p → = x i → + y j → . Коэффициенты x и y определяются единственным образом. Коэффициенты разложения вектора p → по координатным векторам называются координатами вектора p → в данной системе координат.
Координаты вектора записываются в фигурных скобках p → x ; y . На рисунке вектор O A → имеет координаты 2 ; 1 , а вектор b → имеет координаты 3 ; — 2 . Нулевой вектор представляется в виде 0 → 0 ; 0 .
Если векторы a → и b → равны, то и y 1 = y 2 . Запишем это так: a → = x 1 i → + y 1 j → = b → = x 2 i → + y 2 j → , значит x 1 = x 2 , y 1 = y 2 .
Таким образом, координаты равных векторов соответственно равны.
Если точка координат не совпадает с его началом системы координат, тогда рассмотрим задачу. Пусть в декартовой системе координат на O x y заданы координаты точек начала и конца A B → : A x a , y a , B x b , y b . Найти координаты заданного вектора.
Изобразим координатную ось.
Из формулы сложения векторов имеем O A → + A B → = O B → , где O – начало координат. Отсюда следует, что A B → = O B → — O A → .
O A → и O B → – это радиус-векторы заданных точек А и В, значит координаты точек имеют значения O A → = x a , y a , O B → = x b , y b .
По правилу операций над векторами найдем A B → = O B → — O A → = x b — x a , y b — y a .
Нахождение в трехмерном пространстве проходит по такому же принципу, только для трех точек.
Для нахождения координат вектора, необходимо найти разность его точек конца и начала.
Найти координаты O A → и A B → при значении координат точек A ( 2 , — 3 ) , B ( — 4 , — 1 ) .
Для начала определяется радиус-вектор точки A . O A → = ( 2 , — 3 ) . Чтобы найти A B → , нужно вычесть значение координат точек начала из координат точек конца.
Получаем: A B → = ( — 4 — 2 , — 1 — ( — 3 ) ) = ( — 6 , 2 ) .
Ответ: O A → = ( 2 , — 3 ) , A B → = ( — 6 , — 2 ) .
Задано трехмерное пространство с точкой A = ( 3 , 5 , 7 ) , A B → = ( 2 , 0 , — 2 ) . Найти координаты конца A B → .
Подставляем координаты точки A : A B → = ( x b — 3 , y b — 5 , z b — 7 ) .
По условию известно, что A B → = ( 2 , 0 , — 2 ) .
Известно, что равенство векторов справедливо тогда, когда координаты равны соответственно. Составим систему уравнений: x b — 3 = 2 y b — 5 = 0 z b — 7 = — 2
Отсюда следует, что координаты точки B A B → равны: x b = 5 y b = 5 z b = 5
Ответ: B ( 5 , 5 , 5 ) .
Векторы в пространстве и метод координат
Существует два способа решения задач по стереометрии
Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.
Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.
Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.
Система координат в пространстве
Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.
Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.
Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:
Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.
Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:
Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма
Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и
.
Произведение вектора на число:
Скалярное произведение векторов:
Косинус угла между векторами:
Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.
1. В кубе ABCDA1B1C1D1 точки E и K — середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.
Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:
Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.
Прямые AE и BK — скрещиваются. Найдем угол между векторами и
. Для этого нужны их координаты.
Запишем координаты векторов:
и найдем косинус угла между векторами и
:
2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.
Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.
Координаты точек A, B и C найти легко:
Из прямоугольного треугольника AOS найдем
Координаты вершины пирамиды:
Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.
Найдем координаты векторов и
и угол между ними:
Покажем теперь, как вписать систему координат в треугольную призму:
3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D — середина ребра A1B1. Найдите косинус угла между прямыми AD и BC1
Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.
Запишем координаты точек:
Точка D — середина A1B1. Значит, пользуемся формулами для координат середины
отрезка.
Найдем координаты векторов и
, а затем угол между ними:
Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.
Плоскость в пространстве задается уравнением:
Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.
Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.
Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
Покажем, как это делается.
Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).
Уравнение плоскости выглядит так:
Подставим в него по очереди координаты точек M, N и K.
То есть A + C + D = 0.
Аналогично для точки K:
Получили систему из трех уравнений:
В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.
Пусть, например, D = −2. Тогда:
Выразим C и B через A и подставим в третье уравнение:
Решив систему, получим:
Уравнение плоскости MNK имеет вид:
Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:
Вектор — это нормаль к плоскости MNK.
Уравнение плоскости, проходящей через заданную точку имеет вид:
Угол между плоскостями равен углу между нормалями к этим плоскостям:
Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.
Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.
Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.
4. В кубе ABCDA1B1C1D1 точки E и F — середины ребер соответственно A1B1 и A1D1. Найдите тангенс угла между плоскостями AEF и BDD1.
Строим чертеж. Видно, что плоскости AEF и BDD1 пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD1.
Сначала — нормаль к плоскости BDD1. Конечно, мы можем подставить координаты точек B, D и D1 в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD1 — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.
Итак, первый вектор нормали у нас уже есть:
Напишем уравнение плоскости AEF.
Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.
Пусть С = -1. Тогда A = B = 2.
Уравнение плоскости AEF:
Нормаль к плоскости AEF:
Найдем угол между плоскостями:
5. Основание прямой четырехугольной призмы BCDA1B1C1D1 — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3.
Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 
Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».
Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?
«Расстояние между прямыми A1C1 и BD равно √3». Прямые A1C1 и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A1C1 и BD — это, очевидно, OO1, где O — точка пересечения диагоналей нижнего основания, O1 — точка пересечения диагоналей верхнего. А отрезок OO1 и равен высоте параллелепипеда.
Плоскость AA1 D1 D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор
.
Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B1D». Но позвольте, если плоскость перпендикулярна прямой B1D — значит, B1D и есть нормаль к этой плоскости! Координаты точек B1 и D известны:
Координаты вектора — тоже:
Находим угол между плоскостями, равный углу между нормалями к ним:
Зная косинус угла, находим его тангенс по формуле
Получим:
Ответ:
Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.
Пусть — вектор, лежащий на прямой m (или параллельный ей),
— нормаль к плоскости α.
Находим синус угла между прямой m и плоскостью α по формуле:
6. В кубе ABCDA1B1C1D1 точка E — середина ребра A1B1. Найдите синус угла между прямой AE и плоскостью BDD1.
Как всегда, рисуем чертеж и выбираем систему координат
Находим координаты вектора .
Нужно ли нам уравнение плоскости BDD1? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .
Найдем угол между прямой и плоскостью:
Ответ:
Расстояние от точки M с координатами x0, y0 и z0 до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:
7. В основании прямоугольного параллелепипеда BCDA1B1C1D1 лежит прямоугольник ABCD со сторонами AB = , AD =
. Высота параллелепипеда AA1 =
. Найдите расстояние от точки A до плоскости A1DB.
Построим чертеж и выпишем координаты точек:
Запишем уравнение плоскости A1DB. Вы помните, как это делается — по очереди подставляем координаты точек A1, D и B в уравнение Ax + Be + Cz + D
Решим эту систему. Выберем
Тогда
Уравнение плоскости A1DB имеет вид:
Дальше все просто. Находим расстояние от точки A до плоскости A1DB:
В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.
Координаты точки и координаты вектора. Как найти координаты вектора
Вы будете перенаправлены на Автор24
Прямоугольная система координат
Чтобы определить понятие координат точек, нам необходимо ввести систему координат, в которой мы и будем определять ее координаты. Одна и та же точка в разных системах координат может иметь различные координаты. Здесь мы будем рассматривать прямоугольную систему координат в пространстве.
Возьмем в пространстве точку $O$ и введем для нее координаты $(0,0,0)$. Назовем ее началом системы координат. Проведем через нее три взаимно перпендикулярные оси $Ox$, $Oy$ и $Oz$, как на рисунке 1. Эти оси будут называться осями абсцисс, ординат и аппликат, соответственно. Осталось только ввести масштаб на осях (единичный отрезок) – прямоугольная система координат в пространстве готова (рис. 1)
Рисунок 1. Прямоугольная система координат в пространстве. Автор24 — интернет-биржа студенческих работ
Координаты точки
Теперь разберем, как определяют в такой системе координаты любой точки. Возьмем произвольную точку $M$ (рис. 2).
Рисунок 2. Произвольная точка. Автор24 — интернет-биржа студенческих работ
Построим на координатных осях прямоугольный параллелепипед, так, что точки $O$ и $M$ противоположные его вершины (рис. 3).
Рисунок 3. Построение прямоугольного параллелепипеда. Автор24 — интернет-биржа студенческих работ
Готовые работы на аналогичную тему
Тогда точка $M$ будет иметь координаты $(X,Y,Z)$, где $X$ – значение на числовой оси $Ox$, $Y$ – значение на числовой оси $Oy$, а $Z$ – значение на числовой оси $Oz$.
Необходимо найти решение следующей задачи: написать координаты вершин параллелепипеда, изображенного на рисунке 4.
Рисунок 4. Параллелепипед. Автор24 — интернет-биржа студенческих работ
Решение.
Точка $O$ начало координат, следовательно, $O=(0,0,0)$.
Точки $Q$, $N$ и $R$ лежат на осях $Ox$, $Oz$ и $Oy$, соответственно, значит
Точки $S$, $L$ и $M$ лежат в плоскостях $Oxz$, $Oxy$ и $Oyz$, соответственно, значит
Точка $P$ имеет координаты $P=(2,2.5,1.5)$
Координаты вектора по двум точкам и формула нахождения
Чтобы узнать, как найти вектор по координатам двух точек, необходимо рассмотреть введенную нами ранее систему координат. В ней от точки $O$ по направлению оси $Ox$ отложим единичный вектор $overline$, по направлению оси $Oy$ — единичный вектор $overline$, а единичный вектор $overline$ нужно направлять по оси $Oz$.
Для того чтобы ввести понятие координат вектора, введем следующую теорему (здесь ее доказательство мы рассматривать не будем).
Произвольный вектор в пространстве может быть разложен по трем любым векторам, которые не лежат в одной плоскости, причем коэффициенты в таком разложении будут единственным образом определены.
Математически это выглядит следующим образом:
Так как векторы $overline$, $overline$ и $overline$ построены на координатных осях прямоугольной системы координат, то они, очевидно, не будут принадлежать одной плоскости. Значит любой вектор $overline<δ>$ в этой системе координат, по теореме 1, может принимать следующий вид
Три вектора $overline$, $overline$ и $overline$ будут называться координатными векторами.
Коэффициенты перед векторами $overline$, $overline$ и $overline$ в разложении (1) будут называться координатами этого вектора в заданной нами системе координат, то есть
Линейные операции над векторами
Теорема о сумме: Координаты суммы любого числа векторов определяются суммой их соответствующих координат.
Доказательство.
Будем доказывать эту теорему для 2-х векторов. Для 3-х и более векторов доказательство строится аналогичным образом. Пусть $overline<α>=(α_1,α_2,α_3)$, $overline<β>=(β_1,β_2 ,β_3)$.
Эти вектора можно записать следующим образом
$overline<α>=α_1overline+ α_2overline+α_3overline$, $overline<β>=β_1overline+ β_2overline+β_3overline$
$overline<α>+overline<β>=α_1overline+α_2overline+α_3overline+β_1overline+ β_2overline+β_3overline=(α_1+β_1 )overline+(α_2+β_2 )overline+(α_3+β_3)overline$
Замечание: Аналогично, находится решение разности нескольких векторов.
Теорема о произведении на число: Координаты произведения произвольного вектора на действительное число определяется произведением координат на это число.
Доказательство.
Возьмем $overline<α>=(α_1,α_2,α_3)$, тогда $overline<α>=α_1overline+α_2overline+α_3overline$, а
$loverline<α>=l(α_1overline+ α_2overline+α_3overline)=lα_1overline+ lα_2overline+lα_3overline$
Пусть $overline<α>=(3,0,4)$, $overline<β>=(2,-1,1)$. Найти $overline<α>+overline<β>$, $overline<α>-overline<β>$ и $3overline<α>$.
Решение.
$3overline<α>=(3cdot 3,3cdot 0,3cdot 4)=(9,0,12)$
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 20 07 2021
http://ege-study.ru/ru/ege/materialy/matematika/vektory-v-prostranstve-i-metod-koordinat/
http://spravochnick.ru/geometriya/metod_koordinat_v_prostranstve/koordinaty_tochki_i_koordinaty_vektora_kak_nayti_koordinaty_vektora/


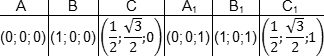
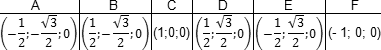
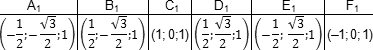




































![Rendered by QuickLaTeX.com [begin{Bmatrix}{Acdot 0 +Bcdot(2sqrt3) + Ccdot(2sqrt6) + 1 = 0}\{Acdot (-3) +Bcdot(3sqrt3) + Ccdot 0 + 1 = 0}\{Acdot 3 +Bcdot(3sqrt3) + Ccdot(0) + 1 = 0}]](https://zagalina.ru/wp-content/ql-cache/quicklatex.com-d115b61682a5d2ee56d7fabc1618cc31_l3.png)
![Rendered by QuickLaTeX.com [begin{Bmatrix}{0 +{2sqrt3}B + {2sqrt6}C + 1 = 0}\{-3 A +{3sqrt3}B + 0 + 1 = 0}\{ 3A +{3sqrt3}B + 0 + 1 = 0}]](https://zagalina.ru/wp-content/ql-cache/quicklatex.com-921144cc9bde2114a0dd63f0639e6d23_l3.png)
![Rendered by QuickLaTeX.com [rho = frac{left|{0cdot(-3) + (- frac{sqrt3}{9})cdot{5sqrt3} + ( - frac{sqrt6}{36}){2sqrt6} +1}right|}{sqrt{0^2 + (- frac{sqrt3}{9})^2 + ( - frac{sqrt6}{36})^2}}]](https://zagalina.ru/wp-content/ql-cache/quicklatex.com-222e7df421ba651701a3246873301ec8_l3.png)
![Rendered by QuickLaTeX.com [begin{Bmatrix}{Acdot 0 +Bcdot 0 + Ccdot2 + 1 = 0}\{Acdot 2 +Bcdot 2 + Ccdot2 + 1 = 0}\{Acdot 0 +Bcdot 2 + Ccdot0 + 1 = 0}]](https://zagalina.ru/wp-content/ql-cache/quicklatex.com-4f63c767d36a6caea7db6c894ff1a888_l3.png)
![Rendered by QuickLaTeX.com [begin{Bmatrix}{ 0 +0 + 2C + 1 = 0}\{2A +2B + 2C+ 1 = 0}\{ 0 +2B + 0 + 1 = 0}]](https://zagalina.ru/wp-content/ql-cache/quicklatex.com-422ccbd82afdce0e43ad5abbcb87cce3_l3.png)


