Как найти вершину треугольника?
Для того чтобы найти координаты вершины равностороннего треугольника, если известны координаты двух других его вершин, нужно воспользоваться одним из предложенных способов.
1 способ (графический)
- В системе координат отмечаем две заданные вершины.
- Ставим ножку циркуля в одну из построенных точек.
- Проводим окружность с радиусом, равным расстоянию между отмеченными вершинами.
- Таким же образом чертим вторую окружность с тем же радиусом, но из второй отмеченной точки.
- Точки пересечения проведённых окружностей определяют вершины треугольников (их получится два).
- Определяем координаты полученных точек, исходя из полученного чертежа.
Данный способ позволяет точно построить третью вершину. Однако определение координат является приблизительным. Метод хорошо использовать для иллюстрации.
2 способ (аналитический)
Решение задачи основано на применении формулы нахождения расстояния между двумя точками: d(A(x1;y1);B(x2;y2))=√((x2-x1)^2+(y2-y1)^2)
- Пусть имеются вершины A(x1;y1) и B(x2;y2) треугольника АВС. Обозначим координаты третьей вершины x и y (то есть, С(x;y))
- Составляем соотношения
AC=√((x-x1)^2+(y-y1)^2)
BC=√((x-x2)^2+(y-y2)^2)
AB=√((x2-x1)^2+(y2-y1)^2) - Учитывая, что треугольник равносторонний, составляем систему уравнений:
AC=BC
AC=AB
Или система уравнений:
√((x-x1)^2+(y-y1)^2)= √((x-x2)^2+(y-y2)^2)
√((x-x1)^2+(y-y1)^2)= √((x2-x1)^2+(y2-y1)^2) - Методом подстановки решаем полученную систему.
Теперь вы знаете, как найти вершину треугольника.
Внимание! Оба случая применимы только для равностороннего треугольника.
Для равнобедренного или любого другого произвольного треугольника для нахождения координат третьей вершины требуются дополнительные данные (например, значение некоторых отрезков или углов).
Уравнение описанной окружности
Как составить уравнение описанной около треугольника окружности по координатам его вершин? Как найти координаты центра описанной окружности? Как найти радиус описанной окружности, зная координаты вершин треугольника?
Решение всех этих задач сводится к одной — написать уравнение окружности, проходящей через три данные точки. Для этого достаточно подставить координаты точек (вершин треугольника) в уравнение окружности. Получим систему из трёх уравнений с тремя неизвестными: координатами центра и радиусом окружности.
Составить уравнение описанной окружности для треугольника с вершинами в точках A(2;1), B(6;3), C(9;2).
Подставив координаты вершин треугольника в уравнение окружности
получим систему уравнений
Вычтем из первого уравнения системы второе:
Теперь из второго уравнения системы вычтем третье:
Приравняем правые части равенств b=-2a+10 и b=3a-20:
Подставим в первое уравнение системы a=6 и b=-2:
a и b — координаты центра окружности, R — её радиус. Таким образом, точка (6;-2) — центр описанной около треугольника ABC окружности, радиус R=5, а уравнение описанной окружности
Для решения аналогичной задачи для четырёхугольника либо многоугольника достаточно знать координаты трёх его вершин.
Прямая на плоскости
Построение графика функции методом дифференциального исчисления
Экстремум функции двух переменных
Пример . В задачах даны координаты точек A , B , C . Требуется: 1) записать векторы AB и AC в системе орт и найти модули этих векторов; 2) найти угол между векторами AB и AC .
Решение.
1) Координаты векторов в системе орт. Координаты векторов находим по формуле:
X=xj-xi; Y=yj-yi
здесь X , Y координаты вектора; xi , yi — координаты точки Аi ; xj , yj — координаты точки Аj
Например, для вектора AB: X=x2-x1=12-7=5 ; Y=y2-y1=-1-(-4)=3
AB(5;3), AC(3;5), BC(-2;2)
2) Длина сторон треугольника. Длина вектора a(X;Y) выражается через его координаты формулой:
3) Угол между прямыми. Угол между векторами a1(X1;Y1) , a2(X2;Y2) можно найти по формуле:
где a1a2=X1X2+Y1Y2
Найдем угол между сторонами AB и AC
γ = arccos(0.88) = 28.07 0

Уравнение прямой AB . Каноническое уравнение прямой: 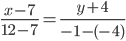
y= 3 /5x- 41 /5 или 5y-3x+41=0
Вариантов много. Например:
1. Найти середину отрезка AB, назовём точкой S.
2. Найти высоту треугольника. Учитывая, что треугольник равнобедренный, высота является срединным перпендикуляром.
3. Построить вектор, параллельный AB с длиной, равной высоте треугольника.
4. Повернуть его на 90 градусов влево или вправо.
5. Перенести начало вектора в точку S.
1) Строим из точки A окружность с радиусом AC
(x-xA)^2 + (y-yA)^2 = R^2 = AC^2
2) Строим из точки B окружность с радиусом BC
(x-xB)^2 + (y-yB)^2 = R^2 = BC^2
3) Решаем систему уравнений, получаем 0(пересечений нет), 1(пересечение в одной точке, касание) или 2 действительных корня(пересечение в 2х точках). Это и есть возможные варианты точки C.
Можно найти x, а потом подставить в любое из уравнений и получить y, или же наоборот.
Как определить координаты вершин треугольника
Стороны треугольника заданы уравнениями:
Найти координаты вершин треугольника.
Координаты вершины A найдем, решая систему, составленную из уравнений сторон AB и AC:
Систему двух линейных уравнений с двумя неизвестными решаем способами, известными из элементарной алгебры, и получаем
Вершина A имеет координаты
Координаты вершины B найдем, решая систему из уравнений сторон AB и BC:
получаем .
Координаты вершины C получим, решая систему из уравнений сторон BC и AC:
Вершина C имеет координаты .
Вершина треугольника – определение
В геометрии нередко рассматривают такое понятие, как «вершина треугольника». Это точка пересечения двух сторон данной фигуры. Практически в каждой задаче встречается это понятие, поэтому имеет смысл рассмотреть его более подробно.
Определение вершины треугольника
В треугольнике есть три точки пересечения сторон, образующие три угла. Их называют вершинами, а стороны, на которые они опираются – сторонами треугольника.
Рис. 1. Вершина в треугольнике.
Вершины в треугольниках обозначают большими латинскими буквами. Поэтому чаще всего в математике стороны обозначают двумя заглавными латинскими буквами, по названию вершин, которые входят в стороны. Например стороной АВ называют сторону треугольника, соединяющую вершины А и В.
Рис. 2. Обозначение вершин в треугольнике.
Характеристики понятия
Если взять произвольно ориентированный в плоскости треугольник, то на практике очень удобно выразить его геометрические характеристики через координаты вершин этой фигуры. Так, вершину А треугольника можно выразить точкой с определенными числовыми параметрами А(х; y).
Зная координаты вершин треугольника можно найти точки пересечения медиан, длину высоты, опущенную на одну из сторон фигуры, и площадь треугольника.
Для этого используются свойства векторов, изображаемых в системе декартовой системе координат, ведь длина стороны треугольника определятся через длину вектора с точками, в которых находятся соответствующие вершины этой фигуры.
Использование вершины треугольника
При любой вершине треугольника можно найти угол, который будет смежным внутреннему углу рассматриваемой фигуры. Для этого придется продлить одну из сторон треугольника. Поскольку сторон при каждой вершин две, то и внешних углов при каждой вершине два. Внешний угол равен сумме двух внутренних углов треугольника, несмежных с ним.
Рис. 3. Свойство внешнего угла треугольника.
Если построить при одной вершине два внешних угла, то они будут равны, как вертикальные.
Что мы узнали?
Одним из важных понятий геометрии при рассмотрении различных типов треугольников является вершина. Это точка, где пересекаются две стороны угла данной геометрической фигуры. Ее обозначают одной из больших букв латинского алфавита. Вершину треугольника можно выразить через координаты x и y, это помогает определять длину стороны треугольника как длину вектора.
Определить треугольник по координатам
Решить треугольник Онлайн по координатам
1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
A ( ; ), B ( ; ), C ( ; )
Примечание: дробные числа записывайте
через точку, а не запятую.
Округлять до -го знака после запятой.
Координаты вершин треугольника векторы
Решить треугольник Онлайн по координатам
1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
A ( ; ), B ( ; ), C ( ; )
Примечание: дробные числа записывайте
через точку, а не запятую.
Округлять до -го знака после запятой.
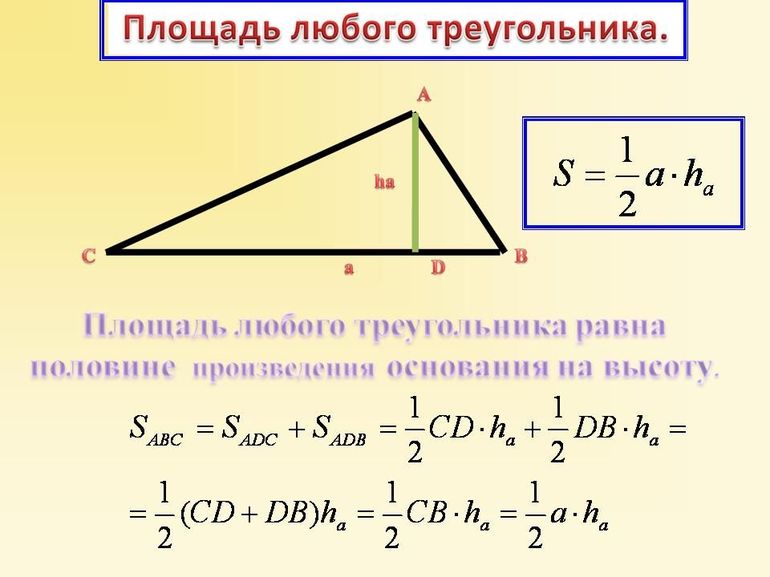
Площадь треугольника по координатам вершин — формулы для расчета
Самый простой многоугольник и вектор
Чтобы найти площадь треугольника через векторы и известные координаты его вершин, необходимо подробнее познакомиться с этими геометрическими объектами. Знание их свойств позволяет легко вычислять разные характеристики изучаемой фигуры, включая периметр, высоту, углы при вершинах и другие. При этом используются универсальные математические операции, которые можно применять с успехом не только для треугольника, но и для других многоугольников.
Фигура на плоскости
Треугольник в геометрии представляет собой самый простой многоугольник, который лежит всегда в одной плоскости, даже если фигура рассматривается в трехмерном пространстве. Состоит он из сторон и вершины.
Сторон и вершин у фигуры по три. Сторона является отрезком, а вершина — это точка пересечения этих отрезков. Для нее характерен определенный угол. Все углы треугольника являются разными в общем случае, их сумма всегда соответствует 180°. Однако, существуют специальные типы фигуры, для которых либо два угла равны друг другу (равнобедренный), либо все три (равносторонний). В задачах называют треугольники по имени их трех вершин, обозначенных латинскими буквами, например, ABC или NPQ.
Для треугольника важное значение имеют следующие отрезки:
- делящий противоположную углу сторону пополам — медиана;
- разделяющий угол при вершине на два равных — биссектриса;
- падающий под прямым углом на противоположную углу сторону — высота.
Высота, например, используется для расчета площади фигуры. Для равностороннего треугольника все эти отрезки совпадают друг с другом для любой вершины, а для равнобедренного они одинаковы лишь для угла, образованного равными сторонами.
Направленный отрезок
Вектором называют линейный элемент, который имеет начало и конец. Для его определения удобнее всего использовать координатную плоскость. Она представляет собой две направленные оси, имеющие шкалу и пересекающиеся под углом 90°. Точка пересечения является началом координат и обозначается буквой O (0; 0). Здесь каждая из цифр указывает точку пересечение перпендикуляра, опущенного из рассматриваемого объекта к каждой из двух осей.
Если начало A (x0; y0) и конец B (x1; y1) вектора известны, тогда легко можно вычислить его собственные координаты. Делается это так:
AB- = B-A = (x1-x0; y1-y0).
Иными словами, чтобы получить вектор AB-, следует из соответствующих координат его конца вычесть его начало. Эта операция эквивалентна параллельному перемещению AB- в начало координатной плоскости, что говорит о существовании бесконечного количества одинаковых AB-векторов.
Направленные отрезки можно складывать, вычитать и умножать. Для каждой из операций существуют определенные правила. Если для сложения и вычитания речь идет о геометрических особенностях, то в случае умножения применяются исключительно алгебраические выражения. Вектор a- можно умножить на b- двумя принципиально разными способами:
- Скалярно: (a-*b-). В этом случае мы получаем число. Правило умножения записывается следующим образом: (a-*b-) = |a-|*|b-|*cos (ab)=x1*x2+y1*y2. Здесь знаком модуля (||) обозначены длины соответствующих отрезков, cos (ab) — это косинус угла между a- и b-, при этом a-(x1; y1), b-(x2; y2). Этот тип произведения можно использовать для вычисления углов между направленными отрезками, а также для определения объема фигур в пространстве.
- Векторно: [a-*b-]. Результатом этой операции является вектор, который перпендикулярен исходным, его направление (вверх или вниз) принято определять по правилу правой руки: четыре пальца должны быть направлены от конца a- к концу b-, тогда оттопыренный большой палец укажет направление их векторного произведения. Длина этого перпендикулярного вектора определяется так: [a-*b-] = |a-|*|b-|*sin (ab) = x1*y2-x2*y1. Векторное произведение используют для вычисления площадей фигур.
Методы вычисления площади по координатам
Задачи на вычисление площадей, периметров или объемов фигур по известным координатам их вершин являются типичными для школьного курса геометрии. В связи с развитием современных технологий школьники часто ищут в интернете, как решить треугольник онлайн по координатам. Тем не менее, существует ряд простых способов, которые позволяют быстро найти площадь фигуры, если известно расположение трех его вершин на координатной плоскости.
Универсальный подход
Этот метод можно применять всегда, независимо от того, какой тип треугольника рассматривается. Известно, что площадь фигуры вычисляется, как произведение половины стороны на опущенную на нее высоту: S = ½*a*h.
Пусть имеются координаты вершин заданного треугольника ABC:
Тогда координаты его векторов AB- и AC- выразятся так:
Если провести высоту h треугольника ABC к любой из этих сторон, например, к AC, то ее длина может быть рассчитана с использованием тригонометрической функции синуса:
Здесь α является углом между векторами-сторонами AB- и AC-. Тогда формулу площади можно переписать в следующем виде: S = ½*a*h = ½*AC* AB*sin (α).
Можно заметить, что записанное выражение является не чем иным, как векторным произведением для AB- и AC-, поэтому можно переписать формулу для S так:
S = ½*[ AB-* AC- ] = ½*((x2-x1)*(y3-y1) — (y2-y1)*(x3-x1)).
Можно аналогично показать, что подобные выражения получаются для пар векторов AC-, BC- и AB-, BC-.
Рекомендуется не запоминать конечные выражения для площади треугольника, поскольку они являются несколько громоздкими, и при их использовании ученики могут запутаться. Для решения подобного рода задач достаточно понять свойства векторов и единственную универсальную формулу для S для любого типа треугольников.
Любопытно отметить, что векторное произведение при вычислении площади можно применять не только для треугольников, но и для любых четырехугольников. Так, в случае параллелограмма рассматриваемая характеристика будет точно равна векторному произведению любых смежных (непараллельных) его сторон.
Использование формулы Герона
Этот способ также может считаться универсальным, поскольку он применим к любым типам треугольников. В работе Герона Александрийского, которая называется «Метрика» и относится к I веку нашей эры, впервые было обнаружено выражение, позволяющее по длинам сторон рассматриваемой фигуры определить ее площадь. Формула имеет следующий вид:
Здесь p — полупериметр, a, b, c — длины сторон.
Последовательность этапов решения задачи можно выразить таким образом:
- Необходимо определить координаты векторов, образующих стороны треугольника.
- Затем, следует вычислить длины их сторон.
- Посчитать полупериметр фигуры.
- Применить формулу Герона.
Ключевым этапом является определение длины вектора. Пусть AB- имеет координаты (x1; y1), тогда его длина вычисляется так:
|AB-| = (x1 2 + y1 2 )^0,5.
Длина любого вектора как на плоскости, так и в пространстве, вычисляется, как сумма квадратов всех его координат, взятых под корень.
Очевидно, что можно записать общее выражение для площади треугольника через координаты с использованием формулы Герона, но оно будет слишком громоздким, поэтому нет никакого смысла запоминать его.
Другие способы
Существуют эмпирические правила, которые можно запомнить и легко решать задачи на определение площади треугольника. Пусть координаты его вершин задаются так: A (x1; y1), B (x2; y2), C (x3; y3). Предположим, что порядок вершин A, B, C расположен против часовой стрелки, тогда существуют следующие правила определения площади ABC:
- Можно воспользоваться формулой: S = ½*(x1*(y2-y3) + x2*(y3-y1) + x3*(y1-y2)). То есть выбирается первая координата вершины и умножается на разность вторых координат двух других вершин, возникающих против хода стрелки часов от первой. Затем, все три члена складываются и делятся на 2.
- Матричный способ. Необходимо выписать в столбик пары координат каждой вершины против часовой стрелки и завершить координатами исходной. После этого следует сложить три попарных произведения первой и второй координат двух соседних вершин, а затем, вычесть три попарных произведений второй и первой координат тех же вершин. Результат поделить пополам. Например: (x1; y1) (x2; y2) (x3; y3) (x1; y1). S = ½*(x1*y2 + x2*y3 + x3*y1 — y1*x2 — y2*x3 — y3*x1).
Решение задачи
Дана фигура АВС. Найдите площадь треугольника, вершины которого имеют координаты A (1; -3), B (2; 5), C (-2; -2).
Для нахождения решения следует обратиться за помощью к универсальному способу. Сначала необходимо выбрать два вектора, образующих стороны треугольника. Пусть это будут AB- и BC-. Теперь нужно знать их координаты. Они равны:
Чтобы рассчитать площадь, достаточно вычислить полупроизведение векторное для выбранных направленных отрезков: S = ½*[AB-*BC-] = ½*(1*(-7)-8*(-4)) = 12,5 квадратных единиц.
Таким образом, существует несколько методик вычисления площади треугольника, если известны координаты его вершин. Все они сводятся к использованию свойств векторов и известных формул. Существуют также выражения, которые следует запомнить, чтобы решать подобные задачи.
Площадь треугольника по координатам вершин — формулы для расчета
Использование координатной плоскости в математике является удобным изобретением для расчета различных геометрических характеристик фигур. Одной из них является площадь треугольника. По координатам вершин фигуры это свойство можно рассчитать несколькими различными способами.
Самый простой многоугольник и вектор
Чтобы найти площадь треугольника через векторы и известные координаты его вершин, необходимо подробнее познакомиться с этими геометрическими объектами. Знание их свойств позволяет легко вычислять разные характеристики изучаемой фигуры, включая периметр, высоту, углы при вершинах и другие. При этом используются универсальные математические операции, которые можно применять с успехом не только для треугольника, но и для других многоугольников.
Фигура на плоскости
Треугольник в геометрии представляет собой самый простой многоугольник, который лежит всегда в одной плоскости, даже если фигура рассматривается в трехмерном пространстве. Состоит он из сторон и вершины.
Сторон и вершин у фигуры по три. Сторона является отрезком, а вершина — это точка пересечения этих отрезков. Для нее характерен определенный угол. Все углы треугольника являются разными в общем случае, их сумма всегда соответствует 180°. Однако, существуют специальные типы фигуры, для которых либо два угла равны друг другу (равнобедренный), либо все три (равносторонний). В задачах называют треугольники по имени их трех вершин, обозначенных латинскими буквами, например, ABC или NPQ.
Для треугольника важное значение имеют следующие отрезки:
- делящий противоположную углу сторону пополам — медиана;
- разделяющий угол при вершине на два равных — биссектриса;
- падающий под прямым углом на противоположную углу сторону — высота.
Высота, например, используется для расчета площади фигуры. Для равностороннего треугольника все эти отрезки совпадают друг с другом для любой вершины, а для равнобедренного они одинаковы лишь для угла, образованного равными сторонами.
Направленный отрезок
Вектором называют линейный элемент, который имеет начало и конец. Для его определения удобнее всего использовать координатную плоскость. Она представляет собой две направленные оси, имеющие шкалу и пересекающиеся под углом 90°. Точка пересечения является началом координат и обозначается буквой O (0; 0). Здесь каждая из цифр указывает точку пересечение перпендикуляра, опущенного из рассматриваемого объекта к каждой из двух осей.
Если начало A (x0; y0) и конец B (x1; y1) вектора известны, тогда легко можно вычислить его собственные координаты. Делается это так:
AB- = B-A = (x1-x0; y1-y0).
Иными словами, чтобы получить вектор AB-, следует из соответствующих координат его конца вычесть его начало. Эта операция эквивалентна параллельному перемещению AB- в начало координатной плоскости, что говорит о существовании бесконечного количества одинаковых AB-векторов.
Направленные отрезки можно складывать, вычитать и умножать. Для каждой из операций существуют определенные правила. Если для сложения и вычитания речь идет о геометрических особенностях, то в случае умножения применяются исключительно алгебраические выражения. Вектор a- можно умножить на b- двумя принципиально разными способами:
Методы вычисления площади по координатам
Задачи на вычисление площадей, периметров или объемов фигур по известным координатам их вершин являются типичными для школьного курса геометрии. В связи с развитием современных технологий школьники часто ищут в интернете, как решить треугольник онлайн по координатам. Тем не менее, существует ряд простых способов, которые позволяют быстро найти площадь фигуры, если известно расположение трех его вершин на координатной плоскости.
Универсальный подход
Этот метод можно применять всегда, независимо от того, какой тип треугольника рассматривается. Известно, что площадь фигуры вычисляется, как произведение половины стороны на опущенную на нее высоту: S = ½*a*h.
Пусть имеются координаты вершин заданного треугольника ABC:
Тогда координаты его векторов AB- и AC- выразятся так:
Если провести высоту h треугольника ABC к любой из этих сторон, например, к AC, то ее длина может быть рассчитана с использованием тригонометрической функции синуса:
Здесь α является углом между векторами-сторонами AB- и AC-. Тогда формулу площади можно переписать в следующем виде: S = ½*a*h = ½*AC* AB*sin (α).
Можно заметить, что записанное выражение является не чем иным, как векторным произведением для AB- и AC-, поэтому можно переписать формулу для S так:
S = ½*[ AB-* AC- ] = ½*((x2-x1)*(y3-y1) — (y2-y1)*(x3-x1)).
Можно аналогично показать, что подобные выражения получаются для пар векторов AC-, BC- и AB-, BC-.
Рекомендуется не запоминать конечные выражения для площади треугольника, поскольку они являются несколько громоздкими, и при их использовании ученики могут запутаться. Для решения подобного рода задач достаточно понять свойства векторов и единственную универсальную формулу для S для любого типа треугольников.
Любопытно отметить, что векторное произведение при вычислении площади можно применять не только для треугольников, но и для любых четырехугольников. Так, в случае параллелограмма рассматриваемая характеристика будет точно равна векторному произведению любых смежных (непараллельных) его сторон.
Использование формулы Герона
Этот способ также может считаться универсальным, поскольку он применим к любым типам треугольников. В работе Герона Александрийского, которая называется «Метрика» и относится к I веку нашей эры, впервые было обнаружено выражение, позволяющее по длинам сторон рассматриваемой фигуры определить ее площадь. Формула имеет следующий вид:
Здесь p — полупериметр, a, b, c — длины сторон.
Последовательность этапов решения задачи можно выразить таким образом:
Ключевым этапом является определение длины вектора. Пусть AB- имеет координаты (x1; y1), тогда его длина вычисляется так:
|AB-| = (x1 2 + y1 2 )^0,5.
Длина любого вектора как на плоскости, так и в пространстве, вычисляется, как сумма квадратов всех его координат, взятых под корень.
Очевидно, что можно записать общее выражение для площади треугольника через координаты с использованием формулы Герона, но оно будет слишком громоздким, поэтому нет никакого смысла запоминать его.
Другие способы
Существуют эмпирические правила, которые можно запомнить и легко решать задачи на определение площади треугольника. Пусть координаты его вершин задаются так: A (x1; y1), B (x2; y2), C (x3; y3). Предположим, что порядок вершин A, B, C расположен против часовой стрелки, тогда существуют следующие правила определения площади ABC:
Решение задачи
Дана фигура АВС. Найдите площадь треугольника, вершины которого имеют координаты A (1; -3), B (2; 5), C (-2; -2).
Для нахождения решения следует обратиться за помощью к универсальному способу. Сначала необходимо выбрать два вектора, образующих стороны треугольника. Пусть это будут AB- и BC-. Теперь нужно знать их координаты. Они равны:
Чтобы рассчитать площадь, достаточно вычислить полупроизведение векторное для выбранных направленных отрезков: S = ½*[AB-*BC-] = ½*(1*(-7)-8*(-4)) = 12,5 квадратных единиц.
Таким образом, существует несколько методик вычисления площади треугольника, если известны координаты его вершин. Все они сводятся к использованию свойств векторов и известных формул. Существуют также выражения, которые следует запомнить, чтобы решать подобные задачи.
Расчет треугольника по координатам вершин
Этот онлайн калькулятор по введенным координатам вершин вычисляет параметры треугольника: длины сторон, углы, периметр и площадь.
Этот онлайн калькулятор предназначен для быстрого вычисления ряда характеристик треугольника по координатам его вершин. Вы вводите координаты вершин A, B и C. Калькулятор рассчитывает по координатам следующие величины:
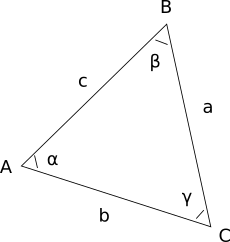
- длину стороны a — стороны, противолежащей вершине А
- длину стороны b — стороны, противолежащей вершине B
- длину стороны c — стороны, противолежащей вершине C
- значение угла α при вершине A
- значение угла β при вершине B
- значение угла γ при вершине C
- периметр треугольника
- площадь треугольника
Если нужно что-то еще, пишите в комментариях, добавим. Формулы расчета значений треугольника описаны под калькулятором.
http://sprint-olympic.ru/uroki/matematika-uroki/15500-vershina-treygolnika-opredelenie.html
http://b4.cooksy.ru/articles/opredelit-treugolnik-po-koordinatam
| Автор | Сообщение | ||||
|---|---|---|---|---|---|
|
|||||
|
Здравствуйте, уважаемые форумчане. Помогите пожалуйста с формулой Как найти координаты третьей вершины треугольника по длинам трёх сторон и двум координатам вершин? Известны координаты точек А(x1,y1), С(x2,y2). Использовать для вычислений Косинус и Синус угла АСВ и смещение прямой АС относительно системы координат нельзя из-за получающейся огромной погрешности при вычислениях. Я про формулу такого вида: x3 = x2 + a*cosС, y3 = y2 + a*sinС
|
||||
| Вернуться к началу |
|
||||
|
Avgust |
|
||
|
Точка А — центр окружности радиусом с Точка С — центр окружности радиусом a Пересечение двух окружностей дадут точку B, то есть ее координаты. Всего-то нужно решить систему относительно [math]x,[/math] и [math]y[/math] [math](y-y_1)^2+(x-x_1)^2=c^2[/math] [math](y-y_2)^2+(x-x_2)^2=a^2[/math] Получим два решения при допустимых соотношениях параметров (при которых треугольник может существовать) Последний раз редактировалось Avgust 26 мар 2013, 09:10, всего редактировалось 1 раз. |
|||
| Вернуться к началу |
|
||
| За это сообщение пользователю Avgust «Спасибо» сказали: panda |
|||
|
panda |
|
||
|
Спасибо за ответ. А не могли бы вы оформить его в виде формулы?
|
|||
| Вернуться к началу |
|
||
|
Avgust |
|
||
|
Формулы я получил. Но они такие громоздкие, что писать полчаса надо. Вот численно элементарно делается. Например, зададим параметры пифагорова треугольника: Тогда по команде Maple solve({(y-y1)^2+(x-x1)^2 = c^2, (y-y2)^2+(x-x2)^2 = a^2}, [x, y]); получим два решения: 1) [math]x=4 , ; , y=0[/math] 2) [math]x=frac{28}{25}, ; , y=frac{96}{25}[/math] Графическое представление этой задачи:
|
|||
| Вернуться к началу |
|
||
| За это сообщение пользователю Avgust «Спасибо» сказали: panda |
|||
|
Avgust |
|
||
|
Я добавил рисунок… x:=(1/2)*((y1-y2)*sqrt(-(-x1^2+2*x2*x1-x2^2+(-c+a-y1+y2)*(-c+a+y1-y2))*(-x1^2+2*x2*x1-x2^2+(c+a-y1+y2)*(c+a+y1-y2))*(x1-x2)^2)+(x1^3-x1^2*x2+(y2^2-2*y1*y2-c^2+y1^2+a^2-x2^2)*x1-x2*(a^2-c^2-x2^2-y2^2+2*y1*y2-y1^2))*(x1-x2))/((x1-x2)*(x1^2-2*x2*x1+x2^2+(y1-y2)^2)); y := (-sqrt(-(-x1^2+2*x2*x1-x2^2+(-c+a-y1+y2)*(-c+a+y1-y2))*(-x1^2+2*x2*x1-x2^2+(c+a-y1+y2)*(c+a+y1-y2))*(x1-x2)^2)+y1^3-y1^2*y2+(a^2+x1^2-c^2+x2^2-2*x2*x1-y2^2)*y1+y2^3+(x2^2-2*x2*x1+c^2-a^2+x1^2)*y2)/(2*y1^2-4*y1*y2+2*y2^2+2*(x1-x2)^2); Второе решение: x := (1/2)*((-y1+y2)*sqrt(-(-x1^2+2*x2*x1-x2^2+(-c+a-y1+y2)*(-c+a+y1-y2))*(x1-x2)^2*(-x1^2+2*x2*x1-x2^2+(c+a-y1+y2)*(c+a+y1-y2)))+(x1-x2)*(x1^3-x1^2*x2+(y1^2-2*y1*y2+y2^2+a^2-c^2-x2^2)*x1-x2*(-c^2-x2^2+a^2-y1^2+2*y1*y2-y2^2)))/((x1^2-2*x2*x1+x2^2+(y1-y2)^2)*(x1-x2)); y := (sqrt(-(x1-x2)^2*(-x1^2+2*x2*x1-x2^2+(c+a+y1-y2)*(c+a-y1+y2))*(-x1^2+2*x2*x1-x2^2+(-c+a+y1-y2)*(-c+a-y1+y2)))+y1^3-y1^2*y2+(a^2+x1^2-c^2+x2^2-2*x2*x1-y2^2)*y1+y2^3+(x2^2-2*x2*x1+c^2-a^2+x1^2)*y2)/(2*y1^2-4*y1*y2+2*y2^2+2*(x1-x2)^2); Формулы проверил — работают отлично. Вот если бы их суметь упростить!
|
|||
| Вернуться к началу |
|
||
| За это сообщение пользователю Avgust «Спасибо» сказали: amjava, panda, Realdreamer |
|||
|
Realdreamer |
|
||
|
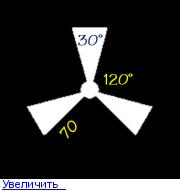
Уважаемые математики Пишу программу, но к сожалению не очень силен в математических науках. Нужно как раз вершины треугольника Вообще в итоге мне нужно написать симуляцию работы вентилятора. Крутится то я его заставлю. Пытался сам найти, но видимо не так запрос формирую.
|
|||
| Вернуться к началу |
|
||
|
Realdreamer |
|
||
|
vvvv Координат всего должно быть 9 для каждой оси, но в таблице их 10 В итоге я пошёл по другому пути a = 70 и разделил её пополам. Получил координату по Y в обе стороны y1 = sqrt(a ** 2 — b ** 2) А потом по формуле окружности просто сдвинул на 120 градусов влево и вправо xn1 = sin(120 — 15) * a xn1 = sin(-120 — 15) * a От меня вам всё равно спасибо что откликнулись!
|
|||
| Вернуться к началу |
|
||
|
39 / 28 / 8 Регистрация: 14.04.2012 Сообщений: 249 |
|
|
1 |
|
Как найти координаты третьей вершины треугольника, зная все стороны и две вершины?07.07.2013, 16:27. Показов 98196. Ответов 19
Добрый день, подскажите как найти координаты третьей вершины треугольника?
0 |
|
107 / 102 / 9 Регистрация: 29.06.2013 Сообщений: 369 |
|
|
07.07.2013, 17:10 |
2 |
|
Зная то, что расстояние между двумя точками равно: Откуда и найдем координаты 3-ей точки
2 |
|
39 / 28 / 8 Регистрация: 14.04.2012 Сообщений: 249 |
|
|
07.07.2013, 17:18 [ТС] |
3 |
|
А как вывести из формулы нужную?
0 |
|
107 / 102 / 9 Регистрация: 29.06.2013 Сообщений: 369 |
|
|
07.07.2013, 17:44 |
4 |
|
Например, можно произвести смещение точки А в начало координат.
0 |
|
39 / 28 / 8 Регистрация: 14.04.2012 Сообщений: 249 |
|
|
07.07.2013, 17:46 [ТС] |
5 |
|
Извени, но я не понимаю…
0 |
|
1767 / 971 / 180 Регистрация: 24.02.2013 Сообщений: 2,790 Записей в блоге: 12 |
|
|
07.07.2013, 19:38 |
6 |
|
А так понимаете?
0 |
|
39 / 28 / 8 Регистрация: 14.04.2012 Сообщений: 249 |
|
|
07.07.2013, 20:07 [ТС] |
7 |
|
Рисунок не доступен пишет.
0 |
|
4216 / 3411 / 396 Регистрация: 15.06.2009 Сообщений: 5,818 |
|
|
07.07.2013, 21:35 |
8 |
|
Известны координаты точек А(x1,y1), С(x2,y2). Условие некорректно — переопределено. Две заданных вершины тем самым уже определяют и длину одной стороны.
0 |
|
39 / 28 / 8 Регистрация: 14.04.2012 Сообщений: 249 |
|
|
07.07.2013, 23:27 [ТС] |
9 |
|
Условие некорректно — переопределено. Две заданных вершины тем самым уже определяют и длину одной стороны. Длина и координаты две разные вещи.
0 |
|
2525 / 1751 / 152 Регистрация: 11.08.2012 Сообщений: 3,349 |
|
|
07.07.2013, 23:52 |
10 |
|
Длина и координаты две разные вещи. А Том Ардер другого и не утверждал. Читайте внимательнее.
0 |
|
1767 / 971 / 180 Регистрация: 24.02.2013 Сообщений: 2,790 Записей в блоге: 12 |
|
|
08.07.2013, 11:23 |
11 |
|
Решение
Добрый день, подскажите как найти координаты третьей вершины треугольника? Вот картинка. Миниатюры
3 |
|
39 / 28 / 8 Регистрация: 14.04.2012 Сообщений: 249 |
|
|
08.07.2013, 14:48 [ТС] |
12 |
|
А как вы выделили x и y из формулы?
0 |
|
1767 / 971 / 180 Регистрация: 24.02.2013 Сообщений: 2,790 Записей в блоге: 12 |
|
|
09.07.2013, 09:13 |
13 |
|
Справа на картинке записана система двух уравнениий — уравнений окружностей.Решив систему, получаем координаты двух точек. т.е. точек В может быть две.
0 |
|
39 / 28 / 8 Регистрация: 14.04.2012 Сообщений: 249 |
|
|
09.07.2013, 14:03 [ТС] |
14 |
|
проблема в том, что я не знаю как решить уравнение окружностей(
0 |
|
107 / 102 / 9 Регистрация: 29.06.2013 Сообщений: 369 |
|
|
09.07.2013, 14:11 |
15 |
|
Раскройте скобки, вычтите из 1 уравнения другое. Уйдут квадраты, выразите одну переменную через другую. Подставите в 1 исходное.
0 |
|
1767 / 971 / 180 Регистрация: 24.02.2013 Сообщений: 2,790 Записей в блоге: 12 |
|
|
09.07.2013, 15:16 |
16 |
|
Только проще сначала вычесть из первого уравнение второе, затем воспользоваться формулой разности квадратов.
1 |
|
0 / 0 / 0 Регистрация: 10.04.2016 Сообщений: 7 |
|
|
28.04.2016, 22:07 |
17 |
|
А можно решить как-нибудь без системы уравнений?
0 |
|
0 / 0 / 0 Регистрация: 08.04.2019 Сообщений: 6 |
|
|
10.04.2019, 13:19 |
18 |
|
Я тоже был бы не против без системы уравнений
0 |
|
1471 / 826 / 140 Регистрация: 12.10.2013 Сообщений: 5,456 |
|||||
|
10.04.2019, 21:50 |
19 |
||||
|
del Для чего тут система уравнений?
Нормализуем вектор AC и множим на длину AB стороны и крутим матрицей поворота в 2д на нужный угол. Угол треугольника найти по трем сторонам. Эх раньше бы и рис и формулы кинул…но теперь лень =). Может кто из гуру не полениться…
0 |
|
pro4vayder 1 / 1 / 0 Регистрация: 25.05.2016 Сообщений: 2 |
||||
|
04.11.2020, 09:49 |
20 |
|||
|
Прошу глянуть решение здесь. Ответ выше был близок к ответу, но человеку далекому от математики (мне) — это не особо было понятно. P.S решение выводит 2 ответа точек пересечения Кликните здесь для просмотра всего текста http://algolist.ru/maths/geom/… rcle2d.php
1 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
04.11.2020, 09:49 |
|
20 |



![[ left{ begin{array}{l} (2 - a)^2 + (1 - b)^2 = R^2 , \ (6 - a)^2 + (3 - b)^2 = R^2 , \ (9 - a)^2 + (2 - b)^2 = R^2 . \ end{array} right. ]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-82dd95fa041ab9c8ca35f00eaea5d2ba_l3.png)

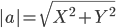
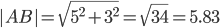
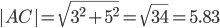
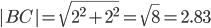
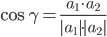
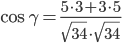
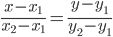
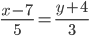























 Сообщение было отмечено как решение
Сообщение было отмечено как решение
