Как найти координаты треугольника если известны длины

Раз уж вы нашли косинус и синус угла в треугольнике — дальше вы можете просто повернуть на этот угол вектор одной из сторон и получить направление второй стороны, а дальше нужно лишь изменить длину вектора.

Но есть и решение в векторах, вообще без тригонометрии.

---

Рассмотрим задачу в общем виде: у нас заданы вершины A и B, нам надо найти третью вершину треугольника С зная прилежащие к ней стороны — AC=a и BC=b соответственно. Построим окружности нужных радиусов с центрами в точках A и B, и тогда точка C как раз будет на их пересечении:

Обозначим через rA, rB и rC радиус-векторы точек. Тогда получаем следующую систему уравнений:

(rC-rA)² = a²
(rC-rB)² = b²

Решив её относительно rC можно получить ответ. Для решения первым делом вычтем одно уравнение из другого, чтобы избавиться от квадрата rC:

(rC-rA)² - (rC-rB)² = a² - b²
(rC² - 2rCrA + rA²) - (rC² - 2rCrB + rB²) = a² - b²
2rC(rB-rA) + rA² - rB² = a² - b²
2rC(rB-rA) = a² - b² - (rA² - rB²)

У нас получилось, внезапно или не очень, уравнение прямой в одном из своих форм. Этой прямой по построению принадлежат точки C и C’ — значит, это уравнение прямой CC’. Кстати, разности rB — rA будет в дальнейшем встречаться часто, поэтому обозначим её как AB (потому что это и есть вектор стороны AB).

В принципе, на этом этапе можно перейти от векторного вида к координатному, выразить через это уравнение переменную y через x или наоборот, подставить в любое уравнение окружности и решить обыкновенное квадратное уравнение. Однако, любого кто так попытается сделать, ожидает засада под названием «сингулярность»: если прямая CC’ вертикальная, то при попытке выразить y через x в формуле будет деление на ноль, а если она горизонтальная — деление на ноль будет при попытке выразить x через y.

Можно было бы просто разобрать два случая, но есть вариант лучше. Для этого надо перейти к параметрическому виду уравнения прямой СС’. Напомню, что параметрический вид уравнения прямой выглядит вот так:

r = r0 + t u

Чтобы получить параметрическое уравнение прямой, нужно знать направляющий вектор и любую точку на этой прямой. Точки C и С’ мы узнать не можем (точнее можем, но если узнаем — задача будет уже решена), поэтому попытаемся найти точку пересечения прямых CC’ и AB.

Это сделать не так сложно как кажется, потому что у нас есть уравнение прямой CC’ и мы можем составить параметрическое уравнение прямой AB:

r = rA + tAB
2r·AB = a² - b² - (rA² - rB²)

Подставим первое уравнение во второе и решим его относительно переменной t:

2(rA + tAB)·AB = a² - b² - (rA² - rB²)

2rA·AB + 2t AB² = a² - b² - (rA² - rB²)

t = (a² - b² - rA² + rB² - 2rA·AB) / 2AB²

t = (a² - b² - rA² + rB² + 2rA² - 2rA·rB) / 2AB²

t = (a² - b² + rA² + rB² - 2rA·rB) / 2AB²

t = (a² - b² + (rA - rB)²) / 2AB²

t = (a² - b² + AB²) / 2AB²

Осталось подставить эту переменную обратно в параметрическое уравнение:

t = (a² - b² + AB²) / 2AB²
r0 = rA + tAB

Формула выглядит страшно, но не имеет сингулярностей пока A и B — разные точки. Даже в случае некорректных начальных данных у тут будет какое-то решение.

Кстати, для проверки корректности формулы можно подставить сюда вырожденные треугольники: при a=0, b=AB точка r0 окажется равна rA; а при a=AB, b=0 точка r0 окажется равна rB. Пока всё нормально.

И так, у нас есть точка r0, осталось найти направляющий вектор прямой CC’. Ну, это тоже просто: надо лишь взять вектор AB и повернуть его на прямой угол в любую сторону. Это делается тоже просто, если вектор AB был с координатами (xB — xA, yB — yA) — то повёрнутый будет с координатами (-yB + yA, xB — xA). Почему так — объясняется по ссылке, которую я уже приводил ранее. Обозначим его через AB^.

Ну, теперь у нас есть параметрическое уравнение прямой CC’ и уравнение одной из окружностей, осталось их пересечь и мы найдём точки C и C’.

rC = r0 + k AB^
(rC-rA)² = a²

И снова мы можем просто подставить одно уравнение в другое (вот почему я так люблю параметрические уравнения прямых в задачах на геометрию!):

(r0-rA + k AB^)² = a²

k² AB^² + 2k AB^ (r0-rA) + (r0-rA)² - a² = 0

Тут есть и дальнейшие упрощения: вектор r0—rA сонаправлен AB, а потому при умножении на AB^ будет чистый ноль, можно и не считать. Кстати, длина вектора AB^ равна длине вектора AB, что тоже позволяет чуть упростить формулу.

Суммируя всё что написано выше, получаем следующую систему уравнений:

t = (a² - b² + AB²) / 2AB²
k² AB² = a² - t² AB²
r0 = rA + t AB
rC = r0 + k AB^

Осталось решить примитивное квадратное уравнение:

t = (a² - b² + AB²) / 2AB²
k = ± sqrt(a² / AB² - t²)
rC = rA + t AB + k AB^

Дальше осталось перейти от векторов к координатам и решение готово.

Автор	Сообщение
	Заголовок сообщения: Координаты третьей вершины треугольника Добавлено: 26 мар 2013, 05:26
Начинающий Зарегистрирован: 26 мар 2013, 05:23 Сообщений: 2 Cпасибо сказано: 3 Спасибо получено: 0 раз в 0 сообщении Очков репутации: 1	Здравствуйте, уважаемые форумчане. Помогите пожалуйста с формулой Как найти координаты третьей вершины треугольника по длинам трёх сторон и двум координатам вершин? Известны координаты точек А(x1,y1), С(x2,y2). длины сторон а, в, с необходимо вычислить координаты точки В(x3,y3) Использовать для вычислений Косинус и Синус угла АСВ и смещение прямой АС относительно системы координат нельзя из-за получающейся огромной погрешности при вычислениях. Я про формулу такого вида: x3 = x2 + a*cosС, y3 = y2 + a*sinС Последний раз редактировалось Andy 11 дек 2019, 10:12, всего редактировалось 1 раз. Название темы изменено модератором.
Вернуться к началу

Avgust	Заголовок сообщения: Re: Найти координаты третьей вершины треугольника по длинам трёх Добавлено: 26 мар 2013, 08:29
	Точка А — центр окружности радиусом с Точка С — центр окружности радиусом a Пересечение двух окружностей дадут точку B, то есть ее координаты. Всего-то нужно решить систему относительно [math]x,[/math] и [math]y[/math] [math](y-y_1)^2+(x-x_1)^2=c^2[/math] [math](y-y_2)^2+(x-x_2)^2=a^2[/math] Получим два решения при допустимых соотношениях параметров (при которых треугольник может существовать) Последний раз редактировалось Avgust 26 мар 2013, 09:10, всего редактировалось 1 раз.
Вернуться к началу
	За это сообщение пользователю Avgust «Спасибо» сказали: panda

panda	Заголовок сообщения: Re: Найти координаты третьей вершины треугольника по длинам трёх Добавлено: 26 мар 2013, 08:47
	Спасибо за ответ. А не могли бы вы оформить его в виде формулы?
Вернуться к началу

Avgust	Заголовок сообщения: Re: Найти координаты третьей вершины треугольника по длинам трёх Добавлено: 26 мар 2013, 09:34
	Формулы я получил. Но они такие громоздкие, что писать полчаса надо. Вот численно элементарно делается. Например, зададим параметры пифагорова треугольника: [math]x_1=0,;, y_1=0, ; , x_2=4,;, y_2=3 ,;, a=3, ;, c=4[/math] Тогда по команде Maple solve({(y-y1)^2+(x-x1)^2 = c^2, (y-y2)^2+(x-x2)^2 = a^2}, [x, y]); получим два решения: 1) [math]x=4 , ; , y=0[/math] 2) [math]x=frac{28}{25}, ; , y=frac{96}{25}[/math] Графическое представление этой задачи:
Вернуться к началу
	За это сообщение пользователю Avgust «Спасибо» сказали: panda

Avgust	Заголовок сообщения: Re: Найти координаты третьей вершины треугольника по длинам трёх Добавлено: 26 мар 2013, 10:00
	Я добавил рисунок… Вот формулы только для одного из решений: x:=(1/2)*((y1-y2)*sqrt(-(-x1^2+2*x2*x1-x2^2+(-c+a-y1+y2)*(-c+a+y1-y2))*(-x1^2+2*x2*x1-x2^2+(c+a-y1+y2)*(c+a+y1-y2))*(x1-x2)^2)+(x1^3-x1^2*x2+(y2^2-2*y1*y2-c^2+y1^2+a^2-x2^2)*x1-x2*(a^2-c^2-x2^2-y2^2+2*y1*y2-y1^2))*(x1-x2))/((x1-x2)*(x1^2-2*x2*x1+x2^2+(y1-y2)^2)); y := (-sqrt(-(-x1^2+2*x2*x1-x2^2+(-c+a-y1+y2)*(-c+a+y1-y2))*(-x1^2+2*x2*x1-x2^2+(c+a-y1+y2)*(c+a+y1-y2))*(x1-x2)^2)+y1^3-y1^2*y2+(a^2+x1^2-c^2+x2^2-2*x2*x1-y2^2)*y1+y2^3+(x2^2-2*x2*x1+c^2-a^2+x1^2)*y2)/(2*y1^2-4*y1*y2+2*y2^2+2*(x1-x2)^2); Второе решение: x := (1/2)*((-y1+y2)*sqrt(-(-x1^2+2*x2*x1-x2^2+(-c+a-y1+y2)*(-c+a+y1-y2))*(x1-x2)^2*(-x1^2+2*x2*x1-x2^2+(c+a-y1+y2)*(c+a+y1-y2)))+(x1-x2)*(x1^3-x1^2*x2+(y1^2-2*y1*y2+y2^2+a^2-c^2-x2^2)*x1-x2*(-c^2-x2^2+a^2-y1^2+2*y1*y2-y2^2)))/((x1^2-2*x2*x1+x2^2+(y1-y2)^2)*(x1-x2)); y := (sqrt(-(x1-x2)^2*(-x1^2+2*x2*x1-x2^2+(c+a+y1-y2)*(c+a-y1+y2))*(-x1^2+2*x2*x1-x2^2+(-c+a+y1-y2)*(-c+a-y1+y2)))+y1^3-y1^2*y2+(a^2+x1^2-c^2+x2^2-2*x2*x1-y2^2)*y1+y2^3+(x2^2-2*x2*x1+c^2-a^2+x1^2)*y2)/(2*y1^2-4*y1*y2+2*y2^2+2*(x1-x2)^2); Формулы проверил — работают отлично. Вот если бы их суметь упростить!
Вернуться к началу
	За это сообщение пользователю Avgust «Спасибо» сказали: amjava, panda, Realdreamer

Realdreamer	Заголовок сообщения: Re: Найти координаты третьей вершины треугольника по длинам трёх Добавлено: 10 дек 2019, 17:11
	Уважаемые математики Чтобы не плодить темы, разрешить поднять текущую. Пишу программу, но к сожалению не очень силен в математических науках. Нужно как раз вершины треугольника Но исходные данные немного другие. Есть длина стороны равностороннего треугольника и угол между ними. Строится всё из начала координат в сторону x (вверх) Вообще в итоге мне нужно написать симуляцию работы вентилятора. Крутится то я его заставлю. Нарисовать не могу (( вот такой должен получится. Стороны 70 Угол лопасти 30 град Угол между лопастями 120 Три лопасти. У меня получается есть только координаты центра. Чтобы нарисовать треугольники мне нужны остальные координаты вершин Пытался сам найти, но видимо не так запрос формирую.
Вернуться к началу

Realdreamer	Заголовок сообщения: Re: Найти координаты третьей вершины треугольника по длинам трёх Добавлено: 11 дек 2019, 16:20
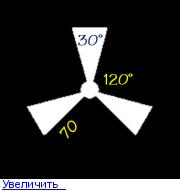
	vvvv Большое спасибо за потраченное время. К сожалению ваше решение только добавило мне вопросов (( Координат всего должно быть 9 для каждой оси, но в таблице их 10 Так же вижу на графике что есть координата с х = -70 но в таблице для Х такого значения нет. В итоге я пошёл по другому пути Нарисовал первую лопасть вверх от начала координат и посчитал основание равнобедренного треугольника зная его стороны и угол между ними a = 70 b = a * sin(30) / 2 и разделил её пополам. Получил координату по Y в обе стороны Лопасть это два прямоугольных треугольника в которых по теореме пифагора нашёл вторую сторону которая и является второй коорлинатой y1 = sqrt(a ** 2 — b ** 2) А потом по формуле окружности просто сдвинул на 120 градусов влево и вправо xn1 = sin(120 — 15) * a yn1 = cos(120 — 15) * a xn2 = sin(120 + 15) * a yn2 = cos(120 + 15) * a xn1 = sin(-120 — 15) * a yn1 = cos(-120 — 15) * a xn2 = sin(-120 + 15) * a yn2 = cos(-120 + 15) * a От меня вам всё равно спасибо что откликнулись!
Вернуться к началу

A ( ; ), B ( ; ), C ( ; )

Примечание: дробные числа записывайте
через точку, а не запятую.

Округлять до -го знака после запятой.

Как найти координаты точки?

О чем эта статья:

3 класс, 4 класс, 9 класс, 11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Понятие системы координат

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.

Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.

Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.

Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.

Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.

• Координатные оси — это прямые, образующие систему координат.
• Ось абсцисс Ox — горизонтальная ось.
• Ось ординат Oy — вертикальная ось.
• Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
• Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.

Оси координат делят плоскость на четыре угла — четыре координатные четверти.

У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:

• верхний правый угол — первая четверть I;
• верхний левый угол — вторая четверть II;
• нижний левый угол — третья четверть III;
• нижний правый угол — четвертая четверть IV;

• Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
• Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
• Если обе координаты отрицательны, то число находится в третьей четверти.
• Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.

Определение координат точки

Каждой точке координатной плоскости соответствуют две координаты.

Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.

Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.

Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.

Смотрим на график и фиксируем: A (1; 2) и B (2; 3).

Особые случаи расположения точек

В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:

1. Если точка лежит на оси Oy, то ее абсцисса равна 0. Например,
   точка С (0, 2).
2. Если точка лежит на оси Ox, то ее ордината равна 0. Например,
   точка F (3, 0).
3. Начало координат — точка O. Ее координаты равны нулю: O (0,0).
4. Точки любой прямой, которая перпендикулярна оси абсцисс, имеют одинаковые абсциссы.
5. Точки любой прямой, которая перпендикулярна оси ординат, имеют одинаковые ординаты.
6. Если точка лежит на оси абсцисс, то ее координаты будут иметь вид: (x, 0).
7. Если точка лежит на оси ординат, то ее координаты будут иметь вид: (0, y).

Способы нахождения точки по её координатам

Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.

Способ первый. Как определить положение точки D по её координатам (-4, 2):

1. Отметить на оси Ox, точку с координатой -4, и провести через нее прямую перпендикулярную оси Ox.
2. Отметить на оси Oy, точку с координатой 2, и провести через нее прямую перпендикулярную оси Oy.
3. Точка пересечения перпендикуляров и есть искомая точка D. Ее абсцисса равна -4, а ордината — 2.

Способ второй. Как определить положение точки D (-4, 2):

1. Сместить прямую по оси Ox влево на 4 единицы, так как у нас
   перед 4 стоит знак минус.
2. Подняться из этой точки параллельно оси Oy вверх на 2 единицы, так как у нас перед 2 стоит знак плюс.

Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:

Примеры решений по аналитической геометрии на плоскости

В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости об исследовании треугольника (заданного вершинами или сторонами): уравнения сторон, углы, площадь, уравнения и длины высот, медиан, биссектрис и т.п.

Решения задач о треугольнике онлайн

Задача 1. Даны вершины треугольника $A (-2, 1), B (3, 3), С (1, 0)$. Найти:
а) длину стороны $AB$;
б) уравнение медианы $BM$;
в) $cos$ угла $BCA$;
г) уравнение высоты $CD$;
д) длину высоты $СD$;
е) площадь треугольника $АВС$.

Задача 2. Найти длину высоты $AD$ в треугольнике с вершинами $A(3,2), B(2,-5), C(-6,-1)$ и написать уравнение перпендикуляра, опущенного из точки $C$ на прямую $AB$.

Задача 3. Даны вершины $A(1,1), B(7,5), C(4,5)$ треугольника. Найти:
1) длину стороны $AB$;
2) внутренний угол $A$ в радианах с точностью до 0,01;
3) уравнение высоты, проведенной через вершину $C$;
4) уравнение медианы, проведенной через вершину $C$;
5) точку пересечения высот треугольника;
6) длину высоты, опущенной из вершины $C$;
7) систему линейных неравенств, определяющую внутреннюю область треугольника.
Сделать чертеж.

Задача 4. Даны уравнения двух сторон треугольника $4x-5y+9=0$ и $x+4y-3=0$. Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке $P(3,1)$.

Задача 5. Даны две вершины $A(-3,3)$, $B(5,-1)$ и точка $D(4,3)$ пересечения высот треугольника. Составить уравнения его сторон.

Задача 6. Найти углы и площадь треугольника, образованного прямыми $у = 2х$, $y = -2х$ и $у = х + 6$.

Задача 7. Найти точку пересечения медиан и точку пересечения высот треугольника: $А(0, — 4)$, $В(3, 0)$ и $С(0, 6)$.

Задача 8. Вычислить координаты точек середины отрезков, являющихся медианами треугольника $ABC$, если $A(-6;1)$, $B(4;3)$, $C(10;8)$.