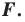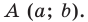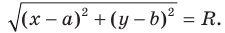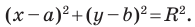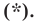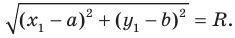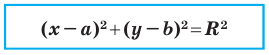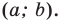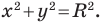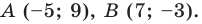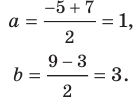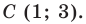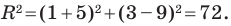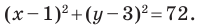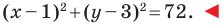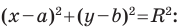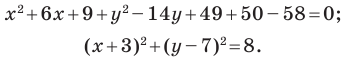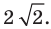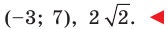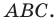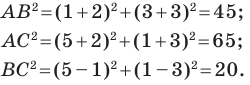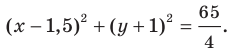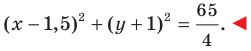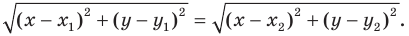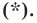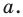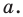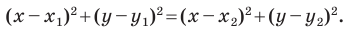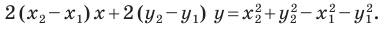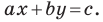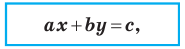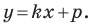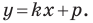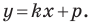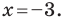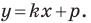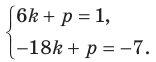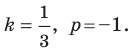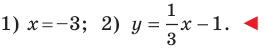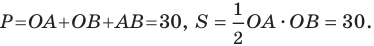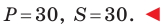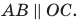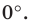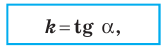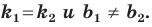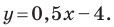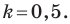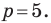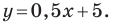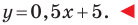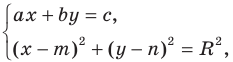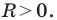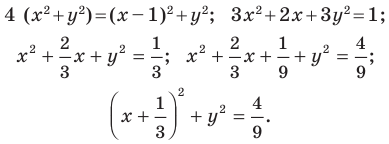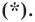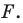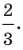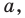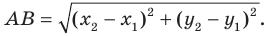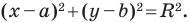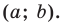Содержание:
Декартовы координаты на плоскости:
Изучая материал этой лекции, вы расширите свои знания о координатной плоскости.
Вы научитесь находить длину отрезка и координаты его середины, зная координаты его концов.
Сформируете представление об уравнении фигуры, выведете уравнения прямой и окружности.
Ознакомитесь с методом координат, позволяющим решать геометрические задачи средствами алгебры.
Расстояние между двумя точками с заданными координатами. Координаты середины отрезка
В 6 классе вы ознакомились с координатной плоскостью, то есть с плоскостью, на которой изображены две перпендикулярные координатные прямые (ось абсцисс и ось ординат) с общим началом отсчета (рис. 8.1). Вы умеете отмечать на ней точки по их координатам и наоборот, находить координаты точки, отмеченной на координатной плоскости.
Договорились координатную плоскость с осью
Координаты точки на плоскости 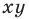
Вы знаете, как находить расстояние в между двумя точками, заданными своими координатами на координатной прямой. Для точек 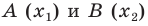
Научимся находить расстояние между точками 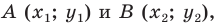
Рассмотрим случай, когда отрезок 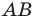
Через точки 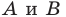
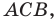
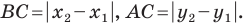
Тогда формулу расстояния между точками 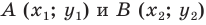
Докажите самостоятельно, что эта формула остается верной и для случая, когда отрезок 
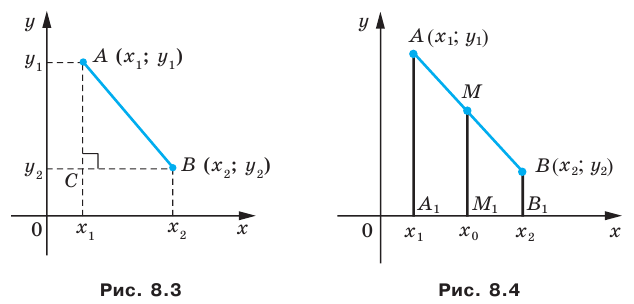
Пусть 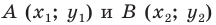
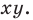
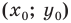
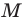
Рассмотрим случай, когда отрезок 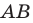
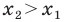
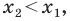
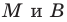
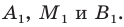
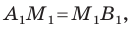
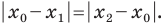
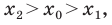
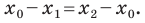

Формулы для нахождения координат середины отрезка остаются верными и для случая, когда отрезок 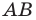
Пример №1
Докажите, что треугольник с вершинами в точках 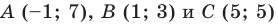
Решение:
Используя формулу расстояния между двумя точками, найдем стороны данного треугольника:
Следовательно, 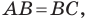
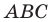
Поскольку 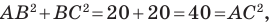
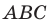
Пример №2
Точка 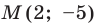
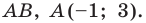
Решение:
Обозначим 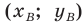
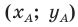
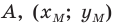
Поскольку 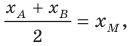
Аналогично
Ответ:
Пример №3
Докажите, что четырехугольник 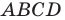
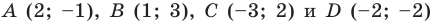
Решение:
Пусть точка 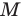
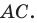
Следовательно,
Пусть точка 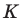
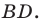
Следовательно,
Таким образом, точки 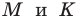
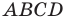
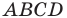
Найдем диагонали параллелограмма:
Следовательно, диагонали параллелограмма 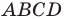
Уравнение фигуры. Уравнение окружности
Из курса алгебры 7 класса вы знаете, какую фигуру называют графиком уравнения. В этом пункте вы ознакомитесь с понятием уравнения фигуры.
Координаты 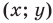
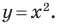
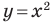
Определение. Уравнением фигуры 
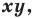
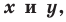
- если точка принадлежит фигуре
то ее координаты являются решением данного уравнения;
- любое решение
данного уравнения является координатами точки, принадлежащей фигуре
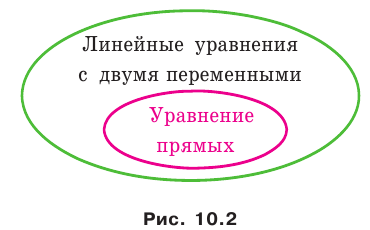
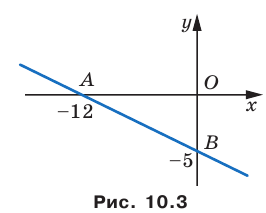
Например, уравнение прямой, изображенной на рисунке 9.2, имеет вид 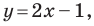
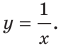
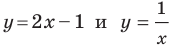
Если данное уравнение является уравнением фигуры 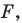
Пользуясь этими соображениями, выведем уравнение окружности радиуса 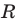
Пусть 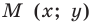
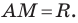
Отсюда
Мы показали, что координаты 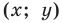
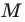
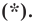
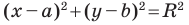
Пусть пара чисел 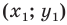
Тогда 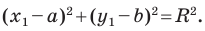
Это равенство показывает, что точка 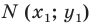
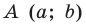
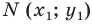
Итак, мы доказали следующую теорему.
Теорема 9.1. Уравнение окружности радиуса 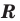
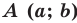
Верно и такое утверждение: любое уравнение вида 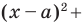
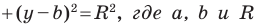
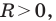
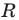
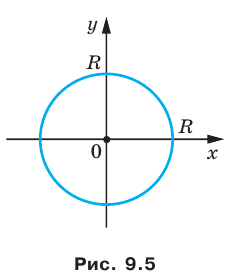
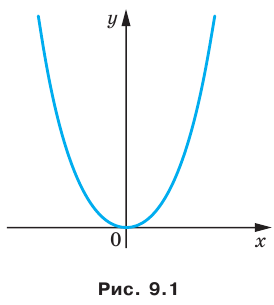
Если центром окружности является начало координат (рис. 9.5), то 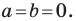
Пример №4
Составьте уравнение окружности, диаметром которой является отрезок 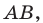
Решение:
Поскольку центр окружности является серединой диаметра, то можем найти координаты 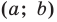
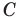
Следовательно,
Радиус окружности 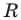
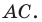
Следовательно, искомое уравнение имеет вид
Ответ:
Пример №5
Докажите, что уравнение 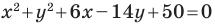
Решение:
Представим данное уравнение в виде
Следовательно, данное уравнение является уравнением окружности с центром в точке 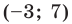
Ответ:
Пример №6
Докажите, что треугольник с вершинами в точках 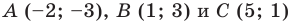
Решение:
Найдем квадраты сторон данного треугольника:
Поскольку 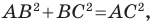
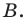
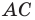
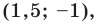
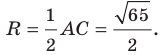
Ответ:
Уравнение прямой
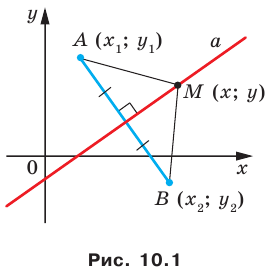
В предыдущем пункте, рассматривая окружность как ГМТ, равноудаленных от данной точки, мы вывели ее уравнение. Для того чтобы вывести уравнение прямой, рассмотрим ее как ГМТ, равноудаленных от двух данных точек.
Пусть 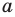
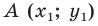
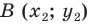
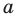
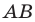
Пусть 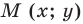
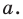
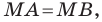
Мы показали, что координаты 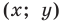
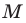
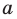
Теперь покажем, что любое решение уравнения 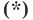
Пусть 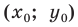
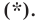
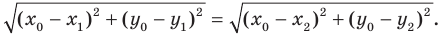
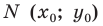
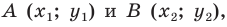
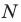
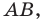
Итак, мы доказали, что уравнение 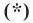
Однако из курса алгебры 7 класса вы знаете, что уравнение прямой выглядит гораздо проще, а именно: 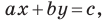
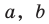
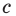
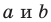
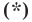
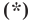
Раскроем скобки и приведем подобные слагаемые. Получим:
Обозначив 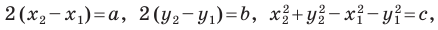
Поскольку точки 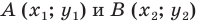
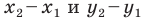
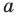
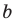
Итак, мы доказали следующую теорему.
Теорема 10.1. Уравнение прямой имеет вид?
где 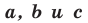
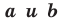
Верно и такое утверждение: любое уравнение вида 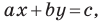
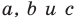
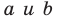
Если 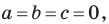
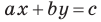
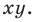
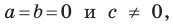
Из курса алгебры 7 класса вы знаете, что уравнение вида 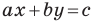
на уроках алгебры в 7 классе мы приняли без доказательства тот факт, что графиком линейной функции 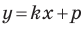
Перепишем уравнение 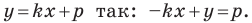
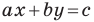
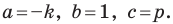
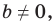
А любую ли прямую на плоскости можно задать уравнением вида 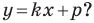
Дело в том, что прямая, перпендикулярная оси абсцисс, не может являться графиком функции, а следовательно, не может быть задана уравнением вида
Вместе с тем, если в уравнении прямой 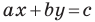
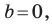
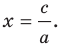
Если 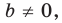
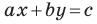
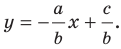
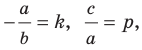
Следовательно, если 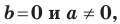
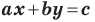
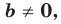
Уравнение невертикальной прямой удобно записывать в виде
Данная таблица подытоживает материал, рассмотренный в этом пункте.
Пример №7
Составьте уравнение прямой, проходящей через точки:
Решение:
1) Поскольку данные точки имеют равные абсциссы, то прямая 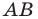
2) Поскольку данные точки имеют разные абсциссы, то прямая 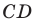
Подставив координаты точек 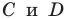
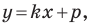
Решив эту систему уравнений, находим, что
Ответ:
Пример №8
Найдите периметр и площадь треугольника, ограниченного прямой 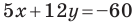
Решение:
Найдем точки пересечения данной прямой с осями координат.
С осью абсцисс: при 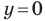
С осью ординат: при 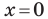
Следовательно, данная прямая и оси координат ограничивают прямоугольный треугольник 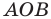
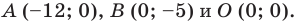
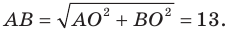
Ответ:
Угловой коэффициент прямой
Рассмотрим уравнение 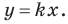
Покажем, что прямые 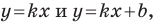
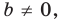
Точки 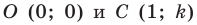
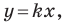
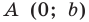
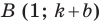
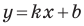
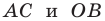
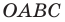
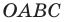
Теперь мы можем сделать такой вывод: если 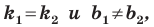
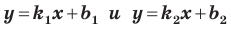
Пусть прямая 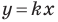
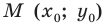
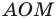
Если прямая 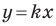
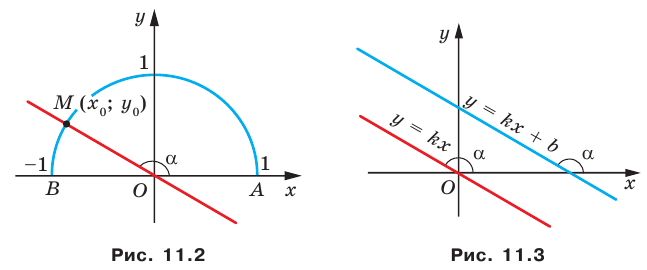
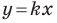
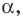
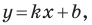
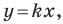
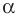
Рассмотрим прямую 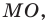
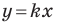
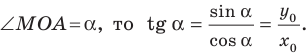
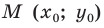
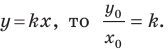
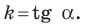
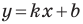
где 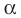
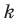
Если невертикальные прямые параллельны, то они образуют равные углы с положительным направлением оси абсцисс. Тогда тангенсы этих углов равны, следовательно, равны и их угловые коэффициенты. Таким образом,
если прямые 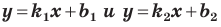
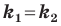
Выводы (1) и (2) объединим в одну теорему.
Теорема 11.1. Прямые 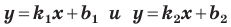
Пример №9
Составьте уравнение прямой, которая проходит через точку 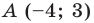
Решение:
Пусть уравнение искомой прямой 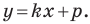
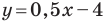
Следовательно, искомое уравнение имеет вид 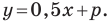
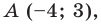
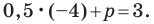
Искомое уравнение имеет вид
Ответ:
Метод координат
Мы часто говорим: прямая 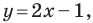
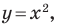
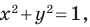
Проиллюстрируем сказанное на таком примере.
Из наглядных соображений очевидно, что прямая и окружность имеют не более двух общих точек. Однако это утверждение не является аксиомой, поэтому его надо доказывать.
Эта задача сводится к исследованию количества решений системы уравнений
где числа 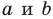
Решая эту систему методом подстановки, мы получим квадратное уравнение, которое может иметь два решения, одно решение или вообще не иметь решений. Следовательно, для данной системы существует три возможных случая:
- система имеет два решения — прямая и окружность пересекаются в двух точках;
- система имеет одно решение — прямая касается окружности;
- система не имеет решений — прямая и окружность не имеют общих точек.
С каждым из этих случаев вы встречались, решая задачи 10.17-10.19.
Метод координат особенно эффективен в тех случаях, когда требуется найти фигуру, все точки которой обладают некоторым свойством, то есть найти геометрическое место точек.
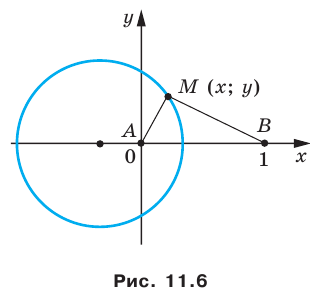
Отметим на плоскости две точки 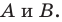
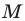
Это серединный перпендикуляр отрезка 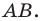
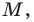
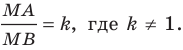
Плоскость, на которой отмечены точки 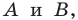
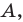
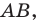
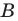
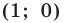
Пусть 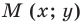
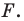
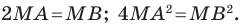
Следовательно, если точка 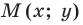
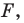
Пусть 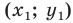
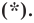
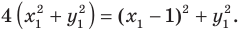
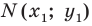
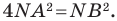
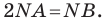
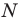
Таким образом, уравнением фигуры 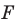
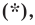
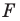
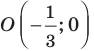
Мы решили задачу для частного случая, когда 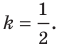
Как строили мост между геометрией и алгеброй
Идея координат зародилась очень давно. Ведь еще в старину люди изучали Землю, наблюдали звезды, а по результатам своих исследований составляли карты, схемы.
Во II в. до н. э. древнегреческий ученый Гиппарх впервые использовал идею координат для определения места расположения объектов на поверхности Земли.
Только в XIV в. французский ученый Николя Орем (ок. 1323-1382) впервые применил в математике идею Гиппарха: он разбил плоскость на клетки (как разбита страница вашей тетради) и стал задавать положение точек широтой и долготой.
Однако огромные возможности применения этой идеи были раскрыты лишь в XVII в. в работах выдающихся французских математиков Пьера Ферма и Рене Декарта. В своих трудах эти ученые показали, как благодаря системе координат можно переходить от точек к числам, от линий к уравнениям, от геометрии к алгебре.
Несмотря на то что П. Ферма опубликовал свою роботу на год раньше Р. Декарта, систему координат, которой мы сегодня пользуемся, называют декартовой. Р. Декарт в своей работе «Рассуждение о методе» предложил новую удобную буквенную символику, которой с незначительными изменениями мы пользуемся и сегодня. Вслед за Декартом мы обозначаем переменные последними буквами латинского алфавита 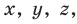
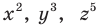
Справочный материал
Расстояние между двумя точками
Расстояние между точками 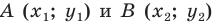
Координаты середины отрезка
Координаты 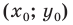
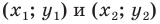
Уравнение фигуры
Уравнением фигуры 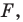
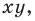
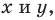
1) если точка принадлежит фигуре 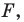
2) любое решение 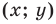
Уравнение окружности
Уравнение окружности радиуса 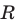
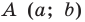
Любое уравнение вида 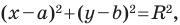
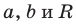
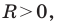
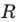
Уравнение прямой
Уравнение прямой имеет вид 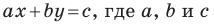
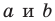
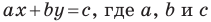
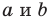
Если 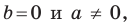
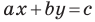
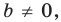
Угловой коэффициент прямой
Коэффициент 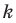
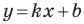
Необходимое и достаточное условие параллельности невертикальных прямых
Прямые 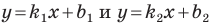
- Декартовы координаты в пространстве
- Геометрические преобразования в геометрии
- Планиметрия — формулы, определение и вычисление
- Стереометрия — формулы, определение и вычисление
- Перпендикулярность прямой и плоскости
- Взаимное расположение прямых в пространстве, прямой и плоскости
- Перпендикулярность прямых и плоскостей в пространстве
- Ортогональное проецирование
Illustration of a Cartesian coordinate plane. Four points are marked and labeled with their coordinates: (2, 3) in green, (−3, 1) in red, (−1.5, −2.5) in blue, and the origin (0, 0) in purple.
In geometry, a Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, called coordinate lines, coordinate axes or just axes (plural of axis) of the system. The point where they meet is called the origin and has (0, 0) as coordinates.
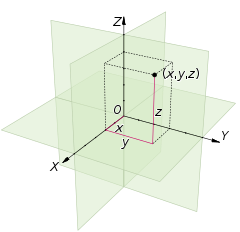
Similarly, the position of any point in three-dimensional space can be specified by three Cartesian coordinates, which are the signed distances from the point to three mutually perpendicular planes. More generally, n Cartesian coordinates specify the point in an n-dimensional Euclidean space for any dimension n. These coordinates are the signed distances from the point to n mutually perpendicular fixed hyperplanes.
Cartesian coordinate system with a circle of radius 2 centered at the origin marked in red. The equation of a circle is (x − a)2 + (y − b)2 = r2 where a and b are the coordinates of the center (a, b) and r is the radius.
Cartesian coordinates are named for René Descartes whose invention of them in the 17th century revolutionized mathematics by providing the first systematic link between geometry and algebra. Using the Cartesian coordinate system, geometric shapes (such as curves) can be described by equations involving the coordinates of points of the shape. For example, a circle of radius 2, centered at the origin of the plane, may be described as the set of all points whose coordinates x and y satisfy the equation x2 + y2 = 4.
Cartesian coordinates are the foundation of analytic geometry, and provide enlightening geometric interpretations for many other branches of mathematics, such as linear algebra, complex analysis, differential geometry, multivariate calculus, group theory and more. A familiar example is the concept of the graph of a function. Cartesian coordinates are also essential tools for most applied disciplines that deal with geometry, including astronomy, physics, engineering and many more. They are the most common coordinate system used in computer graphics, computer-aided geometric design and other geometry-related data processing.
History[edit]
The adjective Cartesian refers to the French mathematician and philosopher René Descartes, who published this idea in 1637 while he was resident in the Netherlands. It was independently discovered by Pierre de Fermat, who also worked in three dimensions, although Fermat did not publish the discovery.[1] The French cleric Nicole Oresme used constructions similar to Cartesian coordinates well before the time of Descartes and Fermat.[2]
Both Descartes and Fermat used a single axis in their treatments and have a variable length measured in reference to this axis. The concept of using a pair of axes was introduced later, after Descartes’ La Géométrie was translated into Latin in 1649 by Frans van Schooten and his students. These commentators introduced several concepts while trying to clarify the ideas contained in Descartes’s work.[3]
The development of the Cartesian coordinate system would play a fundamental role in the development of the calculus by Isaac Newton and Gottfried Wilhelm Leibniz.[4] The two-coordinate description of the plane was later generalized into the concept of vector spaces.[5]
Many other coordinate systems have been developed since Descartes, such as the polar coordinates for the plane, and the spherical and cylindrical coordinates for three-dimensional space.
Description[edit]
One dimension [edit]
Choosing a Cartesian coordinate system for a one-dimensional space—that is, for a straight line—involves choosing a point O of the line (the origin), a unit of length, and an orientation for the line. An orientation chooses which of the two half-lines determined by O is the positive and which is negative; we then say that the line «is oriented» (or «points») from the negative half towards the positive half. Then each point P of the line can be specified by its distance from O, taken with a + or − sign depending on which half-line contains P.
A line with a chosen Cartesian system is called a number line. Every real number has a unique location on the line. Conversely, every point on the line can be interpreted as a number in an ordered continuum such as the real numbers.
Two dimensions [edit]
A Cartesian coordinate system in two dimensions (also called a rectangular coordinate system or an orthogonal coordinate system[6]) is defined by an ordered pair of perpendicular lines (axes), a single unit of length for both axes, and an orientation for each axis. The point where the axes meet is taken as the origin for both, thus turning each axis into a number line. For any point P, a line is drawn through P perpendicular to each axis, and the position where it meets the axis is interpreted as a number. The two numbers, in that chosen order, are the Cartesian coordinates of P. The reverse construction allows one to determine the point P given its coordinates.
The first and second coordinates are called the abscissa and the ordinate of P, respectively; and the point where the axes meet is called the origin of the coordinate system. The coordinates are usually written as two numbers in parentheses, in that order, separated by a comma, as in (3, −10.5). Thus the origin has coordinates (0, 0), and the points on the positive half-axes, one unit away from the origin, have coordinates (1, 0) and (0, 1).
In mathematics, physics, and engineering, the first axis is usually defined or depicted as horizontal and oriented to the right, and the second axis is vertical and oriented upwards. (However, in some computer graphics contexts, the ordinate axis may be oriented downwards.) The origin is often labeled O, and the two coordinates are often denoted by the letters X and Y, or x and y. The axes may then be referred to as the X-axis and Y-axis. The choices of letters come from the original convention, which is to use the latter part of the alphabet to indicate unknown values. The first part of the alphabet was used to designate known values.
A Euclidean plane with a chosen Cartesian coordinate system is called a Cartesian plane. In a Cartesian plane one can define canonical representatives of certain geometric figures, such as the unit circle (with radius equal to the length unit, and center at the origin), the unit square (whose diagonal has endpoints at (0, 0) and (1, 1)), the unit hyperbola, and so on.
The two axes divide the plane into four right angles, called quadrants. The quadrants may be named or numbered in various ways, but the quadrant where all coordinates are positive is usually called the first quadrant.
If the coordinates of a point are (x, y), then its distances from the X-axis and from the Y-axis are |y| and |x|, respectively; where | · | denotes the absolute value of a number.
Three dimensions [edit]
A three dimensional Cartesian coordinate system, with origin O and axis lines X, Y and Z, oriented as shown by the arrows. The tick marks on the axes are one length unit apart. The black dot shows the point with coordinates x = 2, y = 3, and z = 4, or (2, 3, 4).
A Cartesian coordinate system for a three-dimensional space consists of an ordered triplet of lines (the axes) that go through a common point (the origin), and are pair-wise perpendicular; an orientation for each axis; and a single unit of length for all three axes. As in the two-dimensional case, each axis becomes a number line. For any point P of space, one considers a hyperplane through P perpendicular to each coordinate axis, and interprets the point where that hyperplane cuts the axis as a number. The Cartesian coordinates of P are those three numbers, in the chosen order. The reverse construction determines the point P given its three coordinates.
Alternatively, each coordinate of a point P can be taken as the distance from P to the hyperplane defined by the other two axes, with the sign determined by the orientation of the corresponding axis.
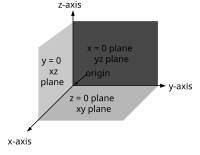
Each pair of axes defines a coordinate hyperplane. These hyperplanes divide space into eight octants. The octants are:
The coordinates are usually written as three numbers (or algebraic formulas) surrounded by parentheses and separated by commas, as in (3, −2.5, 1) or (t, u + v, π/2). Thus, the origin has coordinates (0, 0, 0), and the unit points on the three axes are (1, 0, 0), (0, 1, 0), and (0, 0, 1).
There are no standard names for the coordinates in the three axes (however, the terms abscissa, ordinate and applicate are sometimes used). The coordinates are often denoted by the letters X, Y, and Z, or x, y, and z. The axes may then be referred to as the X-axis, Y-axis, and Z-axis, respectively. Then the coordinate hyperplanes can be referred to as the XY-plane, YZ-plane, and XZ-plane.
In mathematics, physics, and engineering contexts, the first two axes are often defined or depicted as horizontal, with the third axis pointing up. In that case the third coordinate may be called height or altitude. The orientation is usually chosen so that the 90 degree angle from the first axis to the second axis looks counter-clockwise when seen from the point (0, 0, 1); a convention that is commonly called the right hand rule.
The coordinate surfaces of the Cartesian coordinates (x, y, z). The z-axis is vertical and the x-axis is highlighted in green. Thus, the red hyperplane shows the points with x = 1, the blue hyperplane shows the points with z = 1, and the yellow hyperplane shows the points with y = −1. The three surfaces intersect at the point P (shown as a black sphere) with the Cartesian coordinates (1, −1, 1).
Higher dimensions[edit]
Since Cartesian coordinates are unique and non-ambiguous, the points of a Cartesian plane can be identified with pairs of real numbers; that is, with the Cartesian product 


Generalizations[edit]
The concept of Cartesian coordinates generalizes to allow axes that are not perpendicular to each other, and/or different units along each axis. In that case, each coordinate is obtained by projecting the point onto one axis along a direction that is parallel to the other axis (or, in general, to the hyperplane defined by all the other axes). In such an oblique coordinate system the computations of distances and angles must be modified from that in standard Cartesian systems, and many standard formulas (such as the Pythagorean formula for the distance) do not hold (see affine plane).
Notations and conventions[edit]
The Cartesian coordinates of a point are usually written in parentheses and separated by commas, as in (10, 5) or (3, 5, 7). The origin is often labelled with the capital letter O. In analytic geometry, unknown or generic coordinates are often denoted by the letters (x, y) in the plane, and (x, y, z) in three-dimensional space. This custom comes from a convention of algebra, which uses letters near the end of the alphabet for unknown values (such as the coordinates of points in many geometric problems), and letters near the beginning for given quantities.
These conventional names are often used in other domains, such as physics and engineering, although other letters may be used. For example, in a graph showing how a pressure varies with time, the graph coordinates may be denoted p and t. Each axis is usually named after the coordinate which is measured along it; so one says the x-axis, the y-axis, the t-axis, etc.
Another common convention for coordinate naming is to use subscripts, as (x1, x2, …, xn) for the n coordinates in an n-dimensional space, especially when n is greater than 3 or unspecified. Some authors prefer the numbering (x0, x1, …, xn−1). These notations are especially advantageous in computer programming: by storing the coordinates of a point as an array, instead of a record, the subscript can serve to index the coordinates.
In mathematical illustrations of two-dimensional Cartesian systems, the first coordinate (traditionally called the abscissa) is measured along a horizontal axis, oriented from left to right. The second coordinate (the ordinate) is then measured along a vertical axis, usually oriented from bottom to top. Young children learning the Cartesian system, commonly learn the order to read the values before cementing the x-, y-, and z-axis concepts, by starting with 2D mnemonics (for example, ‘Walk along the hall then up the stairs’ akin to straight across the x-axis then up vertically along the y-axis).
Computer graphics and image processing, however, often use a coordinate system with the y-axis oriented downwards on the computer display. This convention developed in the 1960s (or earlier) from the way that images were originally stored in display buffers.
For three-dimensional systems, a convention is to portray the xy-plane horizontally, with the z-axis added to represent height (positive up). Furthermore, there is a convention to orient the x-axis toward the viewer, biased either to the right or left. If a diagram (3D projection or 2D perspective drawing) shows the x— and y-axis horizontally and vertically, respectively, then the z-axis should be shown pointing «out of the page» towards the viewer or camera. In such a 2D diagram of a 3D coordinate system, the z-axis would appear as a line or ray pointing down and to the left or down and to the right, depending on the presumed viewer or camera perspective. In any diagram or display, the orientation of the three axes, as a whole, is arbitrary. However, the orientation of the axes relative to each other should always comply with the right-hand rule, unless specifically stated otherwise. All laws of physics and math assume this right-handedness, which ensures consistency.
For 3D diagrams, the names «abscissa» and «ordinate» are rarely used for x and y, respectively. When they are, the z-coordinate is sometimes called the applicate. The words abscissa, ordinate and applicate are sometimes used to refer to coordinate axes rather than the coordinate values.[6]
Quadrants and octants[edit]
The four quadrants of a Cartesian coordinate system
The axes of a two-dimensional Cartesian system divide the plane into four infinite regions, called quadrants,[6] each bounded by two half-axes. These are often numbered from 1st to 4th and denoted by Roman numerals: I (where the coordinates both have positive signs), II (where the abscissa is negative − and the ordinate is positive +), III (where both the abscissa and the ordinate are −), and IV (abscissa +, ordinate −). When the axes are drawn according to the mathematical custom, the numbering goes counter-clockwise starting from the upper right («north-east») quadrant.
Similarly, a three-dimensional Cartesian system defines a division of space into eight regions or octants,[6] according to the signs of the coordinates of the points. The convention used for naming a specific octant is to list its signs; for example, (+ + +) or (− + −). The generalization of the quadrant and octant to an arbitrary number of dimensions is the orthant, and a similar naming system applies.
Cartesian formulae for the plane[edit]
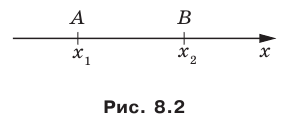
Distance between two points[edit]
The Euclidean distance between two points of the plane with Cartesian coordinates 

This is the Cartesian version of Pythagoras’s theorem. In three-dimensional space, the distance between points 

which can be obtained by two consecutive applications of Pythagoras’ theorem.[7]
Euclidean transformations[edit]
The Euclidean transformations or Euclidean motions are the (bijective) mappings of points of the Euclidean plane to themselves which preserve distances between points. There are four types of these mappings (also called isometries): translations, rotations, reflections and glide reflections.[8]
Translation[edit]
Translating a set of points of the plane, preserving the distances and directions between them, is equivalent to adding a fixed pair of numbers (a, b) to the Cartesian coordinates of every point in the set. That is, if the original coordinates of a point are (x, y), after the translation they will be
Rotation[edit]
To rotate a figure counterclockwise around the origin by some angle 
Thus:
Reflection[edit]
If (x, y) are the Cartesian coordinates of a point, then (−x, y) are the coordinates of its reflection across the second coordinate axis (the y-axis), as if that line were a mirror. Likewise, (x, −y) are the coordinates of its reflection across the first coordinate axis (the x-axis). In more generality, reflection across a line through the origin making an angle 
Thus:
Glide reflection[edit]
A glide reflection is the composition of a reflection across a line followed by a translation in the direction of that line. It can be seen that the order of these operations does not matter (the translation can come first, followed by the reflection).
General matrix form of the transformations[edit]
All affine transformations of the plane can be described in a uniform way by using matrices. For this purpose the coordinates 



where
is a 2×2 matrix and 
Among the affine transformations, the Euclidean transformations are characterized by the fact that the matrix 
and
This is equivalent to saying that A times its transpose is the identity matrix. If these conditions do not hold, the formula describes a more general affine transformation.
The transformation is a translation if and only if A is the identity matrix. The transformation is a rotation around some point if and only if A is a rotation matrix, meaning that it is orthogonal and
A reflection or glide reflection is obtained when,
Assuming that translations are not used (that is, 
where
With this trick, the composition of affine transformations is obtained by multiplying the augmented matrices.
Affine transformation[edit]
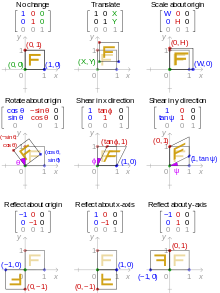
Effect of applying various 2D affine transformation matrices on a unit square (reflections are special cases of scaling)
Affine transformations of the Euclidean plane are transformations that map lines to lines, but may change distances and angles. As said in the preceding section, they can be represented with augmented matrices:
The Euclidean transformations are the affine transformations such that the 2×2 matrix of the 
The augmented matrix that represents the composition of two affine transformations is obtained by multiplying their augmented matrices.
Some affine transformations that are not Euclidean transformations have received specific names.
Scaling[edit]
An example of an affine transformation which is not Euclidean is given by scaling. To make a figure larger or smaller is equivalent to multiplying the Cartesian coordinates of every point by the same positive number m. If (x, y) are the coordinates of a point on the original figure, the corresponding point on the scaled figure has coordinates
If m is greater than 1, the figure becomes larger; if m is between 0 and 1, it becomes smaller.
Shearing[edit]
A shearing transformation will push the top of a square sideways to form a parallelogram. Horizontal shearing is defined by:
Shearing can also be applied vertically:
Orientation and handedness[edit]
In two dimensions[edit]
Fixing or choosing the x-axis determines the y-axis up to direction. Namely, the y-axis is necessarily the perpendicular to the x-axis through the point marked 0 on the x-axis. But there is a choice of which of the two half lines on the perpendicular to designate as positive and which as negative. Each of these two choices determines a different orientation (also called handedness) of the Cartesian plane.
The usual way of orienting the plane, with the positive x-axis pointing right and the positive y-axis pointing up (and the x-axis being the «first» and the y-axis the «second» axis), is considered the positive or standard orientation, also called the right-handed orientation.
A commonly used mnemonic for defining the positive orientation is the right-hand rule. Placing a somewhat closed right hand on the plane with the thumb pointing up, the fingers point from the x-axis to the y-axis, in a positively oriented coordinate system.
The other way of orienting the plane is following the left hand rule, placing the left hand on the plane with the thumb pointing up.
When pointing the thumb away from the origin along an axis towards positive, the curvature of the fingers indicates a positive rotation along that axis.
Regardless of the rule used to orient the plane, rotating the coordinate system will preserve the orientation. Switching any one axis will reverse the orientation, but switching both will leave the orientation unchanged.
In three dimensions[edit]
Fig. 7 – The left-handed orientation is shown on the left, and the right-handed on the right.
Fig. 8 – The right-handed Cartesian coordinate system indicating the coordinate planes.
Once the x— and y-axes are specified, they determine the line along which the z-axis should lie, but there are two possible orientation for this line. The two possible coordinate systems which result are called ‘right-handed’ and ‘left-handed’. The standard orientation, where the xy-plane is horizontal and the z-axis points up (and the x— and the y-axis form a positively oriented two-dimensional coordinate system in the xy-plane if observed from above the xy-plane) is called right-handed or positive.
3D Cartesian coordinate handedness
The name derives from the right-hand rule. If the index finger of the right hand is pointed forward, the middle finger bent inward at a right angle to it, and the thumb placed at a right angle to both, the three fingers indicate the relative orientation of the x-, y-, and z-axes in a right-handed system. The thumb indicates the x-axis, the index finger the y-axis and the middle finger the z-axis. Conversely, if the same is done with the left hand, a left-handed system results.
Figure 7 depicts a left and a right-handed coordinate system. Because a three-dimensional object is represented on the two-dimensional screen, distortion and ambiguity result. The axis pointing downward (and to the right) is also meant to point towards the observer, whereas the «middle»-axis is meant to point away from the observer. The red circle is parallel to the horizontal xy-plane and indicates rotation from the x-axis to the y-axis (in both cases). Hence the red arrow passes in front of the z-axis.
Figure 8 is another attempt at depicting a right-handed coordinate system. Again, there is an ambiguity caused by projecting the three-dimensional coordinate system into the plane. Many observers see Figure 8 as «flipping in and out» between a convex cube and a concave «corner». This corresponds to the two possible orientations of the space. Seeing the figure as convex gives a left-handed coordinate system. Thus the «correct» way to view Figure 8 is to imagine the x-axis as pointing towards the observer and thus seeing a concave corner.
Representing a vector in the standard basis[edit]
A point in space in a Cartesian coordinate system may also be represented by a position vector, which can be thought of as an arrow pointing from the origin of the coordinate system to the point.[10] If the coordinates represent spatial positions (displacements), it is common to represent the vector from the origin to the point of interest as 
where 


where 


There is no natural interpretation of multiplying vectors to obtain another vector that works in all dimensions, however there is a way to use complex numbers to provide such a multiplication. In a two-dimensional cartesian plane, identify the point with coordinates (x, y) with the complex number z = x + iy. Here, i is the imaginary unit and is identified with the point with coordinates (0, 1), so it is not the unit vector in the direction of the x-axis. Since the complex numbers can be multiplied giving another complex number, this identification provides a means to «multiply» vectors. In a three-dimensional cartesian space a similar identification can be made with a subset of the quaternions.
Applications[edit]
Cartesian coordinates are an abstraction that have a multitude of possible applications in the real world. However, three constructive steps are involved in superimposing coordinates on a problem application.
- Units of distance must be decided defining the spatial size represented by the numbers used as coordinates.
- An origin must be assigned to a specific spatial location or landmark, and
- the orientation of the axes must be defined using available directional cues for all but one axis.
Consider as an example superimposing 3D Cartesian coordinates over all points on the Earth (that is, geospatial 3D). Kilometers are a good choice of units, since the original definition of the kilometer was geospatial, with 10,000 km equaling the surface distance from the equator to the North Pole. Based on symmetry, the gravitational center of the Earth suggests a natural placement of the origin (which can be sensed via satellite orbits). The axis of Earth’s rotation provides a natural orientation for the X, Y, and Z axes, strongly associated with «up vs. down», so positive Z can adopt the direction from the geocenter to the North Pole. A location on the equator is needed to define the X-axis, and the prime meridian stands out as a reference orientation, so the X-axis takes the orientation from the geocenter out to 0 degrees longitude, 0 degrees latitude. With three dimensions, and two perpendicular axes orientations pinned down for X and Z, the Y-axis is determined by the first two choices. In order to obey the right-hand rule, the Y-axis must point out from the geocenter to 90 degrees longitude, 0 degrees latitude. From a longitude of −73.985656 degrees, a latitude 40.748433 degrees, and Earth radius of 40,000/2π km, and transforming from spherical to Cartesian coordinates, one can estimate the geocentric coordinates of the Empire State Building, (x, y, z) = (1,330.53 km, 4,635.75 km, 4,155.46 km). GPS navigation relies on such geocentric coordinates.
In engineering projects, agreement on the definition of coordinates is a crucial foundation. One cannot assume that coordinates come predefined for a novel application, so knowledge of how to erect a coordinate system where there previously was no such coordinate system is essential to applying René Descartes’ thinking.
While spatial applications employ identical units along all axes, in business and scientific applications, each axis may have different units of measurement associated with it (such as kilograms, seconds, pounds, etc.). Although four- and higher-dimensional spaces are difficult to visualize, the algebra of Cartesian coordinates can be extended relatively easily to four or more variables, so that certain calculations involving many variables can be done. (This sort of algebraic extension is what is used to define the geometry of higher-dimensional spaces.) Conversely, it is often helpful to use the geometry of Cartesian coordinates in two or three dimensions to visualize algebraic relationships between two or three of many non-spatial variables.
The graph of a function or relation is the set of all points satisfying that function or relation. For a function of one variable, f, the set of all points (x, y), where y = f(x) is the graph of the function f. For a function g of two variables, the set of all points (x, y, z), where z = g(x, y) is the graph of the function g. A sketch of the graph of such a function or relation would consist of all the salient parts of the function or relation which would include its relative extrema, its concavity and points of inflection, any points of discontinuity and its end behavior. All of these terms are more fully defined in calculus. Such graphs are useful in calculus to understand the nature and behavior of a function or relation.
See also[edit]
- Horizontal and vertical
- Jones diagram, which plots four variables rather than two
- Orthogonal coordinates
- Polar coordinate system
- Regular grid
- Spherical coordinate system
- Cartesian coordinate robot
References[edit]
- ^ Bix, Robert A.; D’Souza, Harry J. «Analytic geometry». Encyclopædia Britannica. Retrieved 6 August 2017.
- ^ Kent, Alexander J.; Vujakovic, Peter (4 October 2017). The Routledge Handbook of Mapping and Cartography. Routledge. ISBN 9781317568216.
- ^ Burton 2011, p. 374.
- ^ A Tour of the Calculus, David Berlinski.
- ^ Axler, Sheldon (2015). Linear Algebra Done Right – Springer. Undergraduate Texts in Mathematics. p. 1. doi:10.1007/978-3-319-11080-6. ISBN 978-3-319-11079-0.
- ^ a b c d «Cartesian orthogonal coordinate system». Encyclopedia of Mathematics. Retrieved 6 August 2017.
- ^ Hughes-Hallett, Deborah; McCallum, William G.; Gleason, Andrew M. (2013). Calculus : Single and Multivariable (6 ed.). John wiley. ISBN 978-0470-88861-2.
- ^ Smart 1998, Chap. 2
- ^ Brannan, Esplen & Gray 1998, pg. 49
- ^ Brannan, Esplen & Gray 1998, Appendix 2, pp. 377–382
- ^ David J. Griffiths (1999). Introduction to Electrodynamics. Prentice Hall. ISBN 978-0-13-805326-0.
Sources[edit]
- Brannan, David A.; Esplen, Matthew F.; Gray, Jeremy J. (1998), Geometry, Cambridge: Cambridge University Press, ISBN 978-0-521-59787-6
- Burton, David M. (2011), The History of Mathematics/An Introduction (7th ed.), New York: McGraw-Hill, ISBN 978-0-07-338315-6
- Smart, James R. (1998), Modern Geometries (5th ed.), Pacific Grove: Brooks/Cole, ISBN 978-0-534-35188-5
Further reading[edit]
- Descartes, René (2001). Discourse on Method, Optics, Geometry, and Meteorology. Translated by Paul J. Oscamp (Revised ed.). Indianapolis, IN: Hackett Publishing. ISBN 978-0-87220-567-3. OCLC 488633510.
- Korn GA, Korn TM (1961). Mathematical Handbook for Scientists and Engineers (1st ed.). New York: McGraw-Hill. pp. 55–79. LCCN 59-14456. OCLC 19959906.
- Margenau H, Murphy GM (1956). The Mathematics of Physics and Chemistry. New York: D. van Nostrand. LCCN 55-10911.
- Moon P, Spencer DE (1988). «Rectangular Coordinates (x, y, z)». Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions (corrected 2nd, 3rd print ed.). New York: Springer-Verlag. pp. 9–11 (Table 1.01). ISBN 978-0-387-18430-2.
- Morse PM, Feshbach H (1953). Methods of Theoretical Physics, Part I. New York: McGraw-Hill. ISBN 978-0-07-043316-8. LCCN 52-11515.
- Sauer R, Szabó I (1967). Mathematische Hilfsmittel des Ingenieurs. New York: Springer Verlag. LCCN 67-25285.
External links[edit]
- Cartesian Coordinate System
- Weisstein, Eric W. «Cartesian Coordinates». MathWorld.
- Coordinate Converter – converts between polar, Cartesian and spherical coordinates
- Coordinates of a point Interactive tool to explore coordinates of a point
- open source JavaScript class for 2D/3D Cartesian coordinate system manipulation
2.
Системы координат
2.1.
Декартова система координат
Две
перпендикулярные оси на плоскости с
общим началом и одинаковой масштабной
единицей образуют декартову
прямоугольную систему координат на
плоскости.
Одна
из осей называется осью
Ox,
или осью абсцисс,
другая – осью Oy,
или осью ординат.
Эти оси называют также координатными
осями.
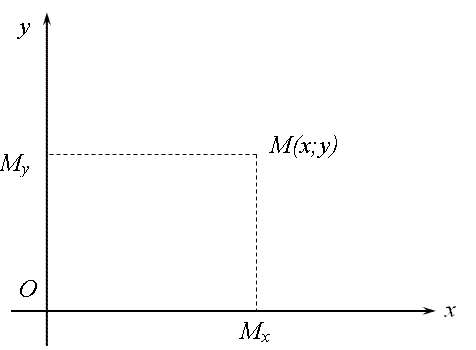
Обозначим
через Mx
и My
соответственно проекции произвольной
точки M плоскости на оси Ox
и Oy.
Декартовыми
прямоугольными координатами x и y точки
M
будем называть соответственно величины
направленных отрезков
и

— если
направления
и Ox
совпадают, то координата x
равна длине
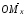
— если
противоположны, то x
равна длине

взятой со знаком «минус». Применяется
обозначение M(x,
y).
Аналогично
определяется координата y.
Три
взаимно перпендикулярные оси в
пространстве с общим началом и одинаковой
масштабной единицей образуют декартову
прямоугольную систему координат в
пространстве.
Одна
из осей называется осью
Ox,
или осью абсцисс,
другую – осью Oy,
или осью ординат,
третья – осью Oz
или осью аппликат.
Эти оси называют также координатными
осями в пространстве.
Декартовы
прямоугольные координаты точки в
пространстве определяются так же как
и на плоскости .
2.2.
Полярная система координат
Полярная
система на плоскости задается точкой
О, называемой полюсом,
лучом ОР, называемым полярной
осью
и вектором
единичной длины и того же направления,
что и луч ОР.
Возьмем
на плоскости точку М. Положение точки
М определяется двумя числами: её
расстоянием r=|ОМ|
от полюса О и углом j,
образованным отрезком ОМ с полярной
осью; при этом отсчет углов ведется в
направлении, противоположном движению
часовой стрелки.
Числа
r,
j
называются полярными координатами
точки М. Пишут
М(r;
j).
При этом r
называется полярным радиусом, j
– полярным углом. Рассматривают главные
значение полярного угла – из полуинтервала
[0; 2p).
Полярные координаты связаны с
прямоугольными следующим образом (на
рисунке полярная ось совпадет с осью
абсцисс):
полярный
радиус вычисляется по формуле

угол
j
в зависимости от значений x,
y
определяется
по формулам
j
= arctg(y/x),
если x
>
0, y
³
0;
j
= p
– arctg(y/x),
если x
<
0, y
<
0 или x
<
0, y
³
0;
j
= 2p
+ arctg(y/x),
если x
>
0, y
<
0;
j
= p/2,
если x
=
0, y
>
0;
j
= 3p/2,
если x
=
0, y
<
0.
Для
начала координат О r=0,
а угол j
может быть произвольным.
Если
же точка М задана в полярных координатах
(r;
j),
а полярная ось совпадает с осью абсцисс,
то
x
= r
cos j, y
= r
sin j.
2.3.
Представление векторов в декартовой
системе координат
Рассмотрим
в пространстве декартову систему
координат Oxyz.
Выделим на координатных осях Оx,
Оy
и Oz
единичные векторы (орты) и обозначим их



Выберем
произвольный вектор
и совместим его начало с началом координат
=

Найдем проекции ax,
ay,
az
вектора
на координатные оси Оx,
Оy
и Oz.
Для этого проведем через конец вектора
плоскости параллельно координатным
плоскостям. Точки пересечения этих
плоскостей с осями координат обозначим
соответственно М1,
М2,
М3.
Получим прямоугольный параллелепипед.
Имеем

+

Но
=
ax
=
ay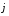
=
az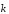
откуда

ax
ay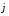
az
Поскольку
векторы
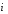
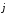
некомпланарные, то представление
вектора
в виде линейной комбинации (1) единственно.
Формула
(1) является основной в векторном
исчислении и называется разложением
вектора по ортам координатных осей.
Числа ax,
ay,
az
называются координатами вектора

то есть координаты вектора – это его
проекции на соответствующие координатные
оси.
Векторное
равенство (1) часто записывают в
символическом виде:
=
(ax,
ay,
az).
Модуль
вектора
равен
Пусть
углы вектора
с осями Оx,
Оy
и Oz,
соответственно, равны α,
β и
γ.
Тогда
Следовательно:
Числа
cosα,
cosβ
и
cosγ
называются
направляющими
косинусами
вектора

Очевидно, что
сos2α
+ cos2β
+ cos2γ
= 1.
Пусть
в пространстве задана прямоугольная
декартова система координат Оxyz.
Для любой точки М координаты вектора
называются координатами точки М.
Вектор
называется радиус-вектором
точки М, и обозначается
=
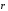
Следовательно, координаты точки – это
координаты её радиус-вектора

y,
z)
или

x
y
z
Координаты точки М записываются: М(x,
y,
z).
Даны
две точки А(x1,
y1,
z1)
и В(x2,
y2,
z2).
Тогда


(x2
–
x1,
y2
–
y1,
z2
–
z1).
Все
приведенные выше определения и
утверждения, касающиеся представления
векторов в координатной форме, справедливы
и для векторов на плоскости: в этом
случае будут фигурировать не три, а лишь
две координаты.
2.4.
Действия над векторами в декартовой
системе координат
Равенство
векторов.
Два
вектора
и

тогда и только тогда, если

Линейные
операции над векторами.
Пусть
векторы

(ax,
ay,
az)
и

(bх;
by;
bz)
заданы своими проекциями на оси координат
Оx,
Оy
и Oz:
=
ax
ay
az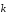
=
bх
by
+ bz
Операции
над векторами сводятся к соответствующим
линейным операциям над проекциями этих
векторов, то можно записать:
1)
±
= (ах
±
bх)
+ (аy
±
by
)
+ (аz
±
bz)
или
±
= (ах
±
bх;
аy
± by
; аz
± bz)
2)
λ
= λax
λay
λaz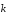
λ
= (λах;
λаy;
λаz)
Коллинеарность
векторов
Теорема
1.
Два заданных вектора
= (ax,
ay,
az)
и
= (bх;
by;
bz)
коллинеарные, если найдется такое
действительное число l,
что будет справедливо векторное равенство

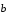
При этом число l
определяется единственным образом.
Равенство


представить в виде пропорции
Таким
образом проекции коллинеарных векторов
пропорциональны. Верно и обратное
утверждение: два вектора, имеющие
пропорциональные координаты, коллинеарны.
Представление
скалярного произведения в координатной
форме
Даны
два вектора

ay,
az)
и

by;
bz).
Их скалярное произведение в координатной
форме:
(

= ax
bх
+
ay
by
+
az
bz
.
Все
приведенные в этом пункте определения
и утверждения, справедливы и для векторов
на плоскости: в этом случае будут
фигурировать не три, а лишь две координаты.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Математика
6 класс
Урок № 79
Декартова система координат на плоскости
Перечень рассматриваемых вопросов:
- прямоугольная система координат;
- координатная плоскость;
- координатная ось, координата точки;
- изображение точек с действительными координатами на плоскости.
Тезаурус
Координатная плоскость. Зададим на плоскости две оси координат, расположив их под прямым углом. Координатные оси пересекаются в точке, являющейся началом отсчёта для каждой из них.
Ось х называют осью абсцисс – расположена горизонтально, направлена вправо. Ось у называют осью ординат – расположена вертикально, направлена вверх.
Оси координат разделяют плоскость на 4 угла, которые называются координатными четвертями.
Координаты точки М (х; у), где х – абсцисса, у – ордината точки.
Обязательная литература:
- Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.
Дополнительная литература:
- Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.
Теоретический материал для самостоятельного изучения
Зададим на плоскости две оси координат, расположив их под прямым углом. Единичные отрезки осей возьмём равными друг другу.
Ось х называют осью абсцисс – расположена горизонтально, направлена вправо. Ось у называют осью ординат – расположена вертикально, направлена вверх.
Положительное направление на осях указывается стрелкой.
Точку пересечения осей называют началом координат.
Оси взаимно перпендикулярны, поэтому заданную таким образом систему координат называют прямоугольной.
Оси координат разделяют плоскость на 4 угла – координатные четверти. Обозначают римскими цифрами как показано на рисунке.
Одним из первых, кто начал широко использовать прямоугольную систему координат в своих исследованиях, был французский философ и математик Рене Декарт, поэтому её часто называют декартовой системой координат.
Пусть A – произвольная точка координатной плоскости. Проведём через точку A прямые, параллельные осям координат. Прямая, параллельная оси y, пересечёт ось x в точке A1, а прямая, параллельная оси x, пересечёт ось y в точке A2. Координату точки A1 на оси x называют абсциссой точки A. Координату точки A2 на оси y называют ординатой точки A. Абсциссу x и ординату y точки A называют координатами точки A.
Координаты точки, записывают в круглых скобках рядом с буквой, обозначающей эту точку: М (х; у).
Важно!
х – первая координата
у – вторая координата
Поменять местами х и у нельзя – получится другая точка.
Поэтому пару координат (x; y) точки A называют упорядоченной парой чисел.
Если на плоскости задана прямоугольная система координат хOу, то:
– каждой точке плоскости поставлена в соответствие упорядоченная пара чисел (координаты точки);
– разным точкам плоскости соответствуют разные упорядоченные пары чисел;
– каждая упорядоченная пара чисел соответствует одной точке плоскости.
То есть установлено взаимно однозначное соответствие между точками плоскости и упорядоченными парами чисел.
Алгоритм построения точки на координатной плоскости
Построим точку А(3; 6).
Введём прямоугольную систему координат.
На каждой оси откладываем заданные координаты х и у (x > 0 и y > 0, значит, точка A расположена в I координатной четверти).
Проводим перпендикуляры к оси х и оси у.
Точка их пересечения – искомая точка.
В(– 4; 5) – имеет отрицательную абсциссу и положительную ординату, значит, расположена во II четверти.
С(– 8; – 4) – имеет обе отрицательные координаты, значит, расположена в III четверти.
D(9; – 2) – имеет положительную абсциссу и отрицательную ординату, значит, расположена в IV четверти.
F(6; 0), E(– 5; 0) – точки лежат на оси абсцисс.
H(0; – 5) – точка лежит на оси ординат.
O(0; 0) – начальная точка системы координат.
В географии положение объектов на земной поверхности определяется двумя координатами: широтой и долготой.
В концертном зале своё кресло можно найти по номеру ряда и места.
В шахматах каждой клетке соответствует буква столбца и цифра ряда.
Разбор заданий тренировочного модуля
Тип 1. Ввод с клавиатуры пропущенных элементов в тексте
Построить прямую АВ, если А(3; 2), В(– 3; – 4).
Найти:
1) координаты точек пересечения прямой AB с осями;
2) координаты середины отрезка AB.
Шаг 1. Строим точки А и В по их координатам.
Шаг 2. Проводим прямую АВ.
Шаг 3. Находим точки пересечения с осями координат, обозначаем их буквами M и N. Определяем их координаты:
М (1; 0), N (0; – 1).
Шаг 4. Находим по графику середину отрезка АВ, это точка N (0; – 1).
Ответ: координаты точек пересечения прямой AB с осями: М (1; 0), N (0; – 1), координаты середины отрезка AB: N (0; – 1).
Тип 2. Нарисуйте фигуру, последовательно соединяя точки
(0; 4), (– 2; – 2), (3; 2), (– 3; 2), (2; – 4), (0; 4).

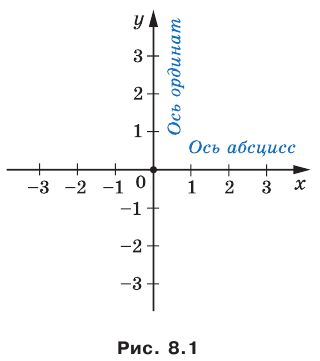
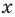
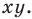
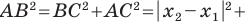
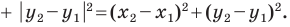

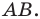
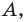
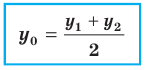
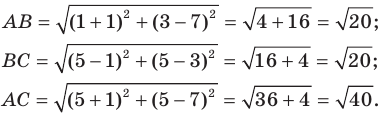

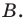
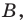
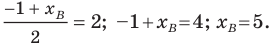
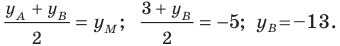
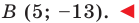
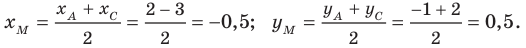
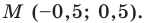
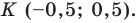
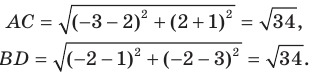

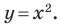
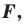 то ее координаты являются решением данного уравнения;
то ее координаты являются решением данного уравнения;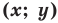 данного уравнения является координатами точки, принадлежащей фигуре
данного уравнения является координатами точки, принадлежащей фигуре