Как найти координаты вектора имея две точки - Исправление недочетов и поиск решений вместе с Examum.ru

1.5.1. Как найти вектор по двум точкам?

Задача 1

Даны две точки плоскости и . Найти координаты вектора

Решение: по соответствующей формуле:

Как вариант, можно использовать следующую запись:

Эстеты решат и так:

Лично я привык к первой версии записи.

Ответ:

По условию не требовалось строить чертежа (что характерно для задач аналитической геометрии), но в целях пояснения

важного момента, не поленюсь:

И момент здесь таков:
в чём различие между координатами точек и координатами векторов?

Координаты точек – это обычные координаты в прямоугольной системе координат (единичные векторы тут

вообще ни при чём). Откладывать точки на координатной плоскости, думаю, все умеют ещё с 5-6 класса. Каждая точка обладает

строгим местом на плоскости, и перемещать их куда-либо нельзя.

Координаты же вектора – это его разложение по базису , в данном случае . Любой вектор является свободным, поэтому при желании мы легко можем переобозначить

его через и отложить от какой-нибудь другой точки

плоскости. Следует отметить, что для векторов можно вообще не строить оси, прямоугольную систему координат, нужен лишь базис,

в данном случае ортонормированный базис плоскости .
Записи координат точек и координат

вектора формально одинаковы, но смысл

координат абсолютно разный, и вам следует хорошо понимать эту разницу. Данное отличие, разумеется, справедливо и

для пространства.

Дамы и господа, набиваем руку:

Задача 2

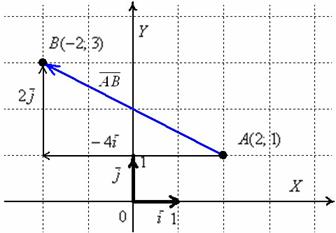
а) Даны точки и . Найти векторы и .
б) Даны точки и . Найти векторы и .
в) Даны точки и . Найти векторы и .
г) Даны точки . Найти векторы .

Пожалуй, достаточно…. Не пропускаем! Решаем письменно и «от руки»! Чертежи делать не нужно (коль скоро, не требовалось).

Решения и ответы в конце книги.

Для проверки вычислений удобно использовать Геометрический калькулятор, приложенные к данному

курсу. Дабы избежать нелепых ошибок а-ля «2 + 2 = 5». А подобные «затмения» бывают. Даже у профессоров. Отвлёкся – и

студентка сбежала

1.5.2. Как найти длину отрезка?

1.4. Координаты вектора на плоскости и в пространстве

| Оглавление |

Автор: Aлeксaндр Eмeлин

Источник

Координаты вектора по двум точкам

Чтобы найти координаты вектора по двум точкам нужно найти разность между координатами конца и начала вектора. Пусть даны две точки $ A(x_1;y_1) $ и $ B(x_2;y_2) $Вектор $ overline{AB} $ для плоской задачи можно найти по формуле: $$ overline{AB} = (x_2-x_1; y_2-y_1) $$

В случае, если точки расположены в пространстве $ A(x_1;y_1;z_1) $ и $ B(x_2;y_2;z_2) $, то координаты вектора $ overline{AB} $ расчитываются по формуле: $$ overline{AB} = (x_2-x_1; y_2-y_1; z_2-z_1) $$

Следует обратить внимание, что координаты вычисляются именно с помощью вычитания начальной точки из конечной, но не наоборот. То есть векторы $ overline{AB} $ и $ overline{BA} $ имеют разные координаты: $$ overline{AB} neq overline{BA} $$

Пример 1

Даны точки $ A(2;1;-3) $ и $ B(1;0;2) $. Найти координаты векторов $ overline{AB} $ и $ overline{BA} $

Решение

Как найти координаты вектора по двум точкам? Согласну правилу нужно из конечной точки вычесть начальную. Так как вектор $ overline{AB} $ имеет начало в точке $ A $, а конец в $ B $, то получаем:

$$ overline{AB} = (1-2;0-1;2-(-3)) = (-1; -1; 5) $$

Теперь посмотрим на вектор $ overline{BA} $, в котором начало в точке $ B $, а конец в $ A $. Поэтому имеем:

$$ overline{BA} = (2-1;1-0;-3-2)=(1;1;-5) $$

Как видим, векторые разные, и координаты их тоже отличаются.

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ overline{AB} = (-1;-1;5) $$ $$ overline{BA} = (1;1;-5) $$

Источник

Марина Николаевна Ковальчук

Эксперт по предмету «Геометрия»

Задать вопрос автору статьи

Прямоугольная система координат

Чтобы определить понятие координат точек, нам необходимо ввести систему координат, в которой мы и будем определять ее координаты. Одна и та же точка в разных системах координат может иметь различные координаты. Здесь мы будем рассматривать прямоугольную систему координат в пространстве.

Возьмем в пространстве точку $O$ и введем для нее координаты $(0,0,0)$. Назовем ее началом системы координат. Проведем через нее три взаимно перпендикулярные оси $Ox$, $Oy$ и $Oz$, как на рисунке 1. Эти оси будут называться осями абсцисс, ординат и аппликат, соответственно. Осталось только ввести масштаб на осях (единичный отрезок) – прямоугольная система координат в пространстве готова (рис. 1)

Рисунок 1. Прямоугольная система координат в пространстве. Автор24 — интернет-биржа студенческих работ

Координаты точки

Теперь разберем, как определяют в такой системе координаты любой точки. Возьмем произвольную точку $M$ (рис. 2).

Рисунок 2. Произвольная точка. Автор24 — интернет-биржа студенческих работ

Построим на координатных осях прямоугольный параллелепипед, так, что точки $O$ и $M$ противоположные его вершины (рис. 3).

Рисунок 3. Построение прямоугольного параллелепипеда. Автор24 — интернет-биржа студенческих работ

«Координаты точки и координаты вектора. Как найти координаты вектора» 👇

Тогда точка $M$ будет иметь координаты $(X,Y,Z)$, где $X$ – значение на числовой оси $Ox$, $Y$ – значение на числовой оси $Oy$, а $Z$ – значение на числовой оси $Oz$.

Пример 1

Необходимо найти решение следующей задачи: написать координаты вершин параллелепипеда, изображенного на рисунке 4.

Рисунок 4. Параллелепипед. Автор24 — интернет-биржа студенческих работ

Решение.

Точка $O$ начало координат, следовательно, $O=(0,0,0)$.

Точки $Q$, $N$ и $R$ лежат на осях $Ox$, $Oz$ и $Oy$, соответственно, значит

$Q=(2,0,0)$, $N=(0,0,1.5)$, $R=(0,2.5,0)$

Точки $S$, $L$ и $M$ лежат в плоскостях $Oxz$, $Oxy$ и $Oyz$, соответственно, значит

$S=(2,0,1.5)$, $L=(2,2.5,0)$, $R=(0,2.5,1.5)$

Точка $P$ имеет координаты $P=(2,2.5,1.5)$

Координаты вектора по двум точкам и формула нахождения

Чтобы узнать, как найти вектор по координатам двух точек, необходимо рассмотреть введенную нами ранее систему координат. В ней от точки $O$ по направлению оси $Ox$ отложим единичный вектор $overline{i}$, по направлению оси $Oy$ — единичный вектор $overline{j}$, а единичный вектор $overline{k}$ нужно направлять по оси $Oz$.

Для того чтобы ввести понятие координат вектора, введем следующую теорему (здесь ее доказательство мы рассматривать не будем).

Теорема 1

Произвольный вектор в пространстве может быть разложен по трем любым векторам, которые не лежат в одной плоскости, причем коэффициенты в таком разложении будут единственным образом определены.

Математически это выглядит следующим образом:

$overline{δ}=moverline{α}+noverline{β}+loverline{γ}$

Так как векторы $overline{i}$, $overline{j}$ и $overline{k}$ построены на координатных осях прямоугольной системы координат, то они, очевидно, не будут принадлежать одной плоскости. Значит любой вектор $overline{δ}$ в этой системе координат, по теореме 1, может принимать следующий вид

$overline{δ}=moverline{i}+noverline{j}+loverline{k}$ (1)

где $n,m,l∈R$.

Определение 1

Три вектора $overline{i}$, $overline{j}$ и $overline{k}$ будут называться координатными векторами.

Определение 2

Коэффициенты перед векторами $overline{i}$, $overline{j}$ и $overline{k}$ в разложении (1) будут называться координатами этого вектора в заданной нами системе координат, то есть

$overline{δ}=(m,n,l)$

Линейные операции над векторами

Теорема 2

Теорема о сумме: Координаты суммы любого числа векторов определяются суммой их соответствующих координат.

Доказательство.

Будем доказывать эту теорему для 2-х векторов. Для 3-х и более векторов доказательство строится аналогичным образом. Пусть $overline{α}=(α_1,α_2,α_3)$, $overline{β}=(β_1,β_2 ,β_3)$.

Эти вектора можно записать следующим образом

$overline{α}=α_1overline{i}+ α_2overline{j}+α_3overline{k}$, $overline{β}=β_1overline{i}+ β_2overline{j}+β_3overline{k}$

$overline{α}+overline{β}=α_1overline{i}+α_2overline{j}+α_3overline{k}+β_1overline{i}+ β_2overline{j}+β_3overline{k}=(α_1+β_1 )overline{i}+(α_2+β_2 )overline{j}+(α_3+β_3)overline{k}$

Следовательно

$overline{α}+overline{β}=(α_1+β_1,α_2+β_2,α_3+β_3)$

Теорема доказана.

Замечание 1

Замечание: Аналогично, находится решение разности нескольких векторов.

Теорема 3

Теорема о произведении на число: Координаты произведения произвольного вектора на действительное число определяется произведением координат на это число.

Доказательство.

Возьмем $overline{α}=(α_1,α_2,α_3)$, тогда $overline{α}=α_1overline{i}+α_2overline{j}+α_3overline{k}$, а

$loverline{α}=l(α_1overline{i}+ α_2overline{j}+α_3overline{k})=lα_1overline{i}+ lα_2overline{j}+lα_3overline{k}$

Значит

$koverline{α}=(lα_1,lα_2,lα_3)$

Теорема доказана.

Пример 2

Пусть $overline{α}=(3,0,4)$, $overline{β}=(2,-1,1)$. Найти $overline{α}+overline{β}$, $overline{α}-overline{β}$ и $3overline{α}$.

Решение.

$overline{α}+overline{β}=(3+2,0+(-1),4+1)=(5,-1,5)$

$overline{α}-overline{β}=(3-2,0-(-1),4-1)=(1,1,3)$

$3overline{α}=(3cdot 3,3cdot 0,3cdot 4)=(9,0,12)$

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Простейшие задачи Как найти вектор по двум точкам?

Если
даны две точки плоскости
и
,
то вектор
имеет
следующие координаты:

Если
даны две точки пространства
и
,
то вектор
имеет
следующие координаты:

То
есть, из
координат конца вектора нужно
вычесть соответствующие координаты начала
вектора.

Пример

Даны
две точки плоскости
и
.
Найти координаты вектора

Решение: по
соответствующей формуле:

Как
вариант, можно было использовать
следующую запись:

Можно
и так:

Обязательно
нужно понимать различие
между координатами точек и координатами
векторов:

Координаты
точек –
это обычные координаты в прямоугольной
системе координат. Каждая точка обладает
строгим местом на плоскости, и перемещать
их куда-либо нельзя.

Координаты
же вектора –
это его разложение по базису
,
в данном случае
.
Любой вектор является свободным, поэтому
при необходимости мы легко можем отложить
его от какой-нибудь другой точки
плоскости. Интересно, что для векторов
можно вообще не строить оси, прямоугольную
систему координат, нужен лишь базис, в
данном случае ортонормированный базис
плоскости
.

Записи
координат точек и координат векторов
вроде бы схожи:
,
а смысл
координат абсолютно разный,
и следует хорошо понимать эту разницу.

Пример

Даны
точки
.
Найти векторы
.

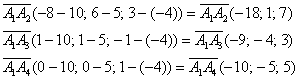
Как найти длину отрезка?

Если
даны две точки плоскости
и
,
то длину отрезка
можно
вычислить по формуле

Если
даны две точки пространства
и
,
то длину отрезка
можно
вычислить по формуле

Примечание: Формулы
останутся корректными, если переставить
местами соответствующие координаты:
и
,
но более стандартен первый вариант

Пример

Даны
точки
и
.
Найти длину отрезка
.

Ответ:

Если
дан вектор плоскости
,
то его длина вычисляется по формуле
.

Если
дан вектор пространства
,
то его длина вычисляется по формуле
.

Пример

Даны
точки
и
.
Найти длину вектора
.

Решение: Сначала
найдём вектор
:

По
формуле
вычислим
длину вектора:

Ответ:

Пример

а)
Даны точки
и
.
Найти длину вектора
.

б)
Даны векторы
,
,
и
.
Найти их длины.

а) Решение: найдём
вектор
:

Вычислим
длину вектора:

Ответ:

б) Решение:

Вычислим
длины векторов:

Действия с векторами в координатах

1) Правило
сложения векторов.
Рассмотрим два вектора плоскости
и
.
Для того, чтобы сложить векторы,
необходимо сложить
их соответствующие координаты:
.

Частный
случай – формула разности векторов:
.

Аналогичное
правило справедливо для суммы любого
количества векторов, например, найдём
сумму трёх векторов:

Если
речь идёт о векторах в пространстве, то
всё точно так же, только добавится
дополнительная координата. Если даны
векторы
,
то их суммой является вектор
.

2) Правило
умножения вектора на число.
Для того чтобы вектор
умножить
на число
,
необходимо каждую координату данного
вектора умножить на число
:

Для
пространственного вектора
правило
такое же:

Пример

Даны
векторы
и
.
Найти
и

Решение: Для
действий с векторами справедлив обычный
алгебраический приоритет: сначала
умножаем, потом складываем:

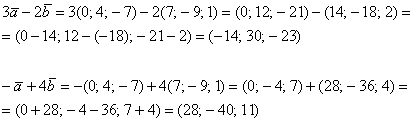
Ответ:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Онлайн калькулятор. Координаты вектора по двум точкам.

Этот онлайн калькулятор позволит вам очень просто найти значение координат вектора по двум точкам (зная его начальную и конечную точку) для плоских и пространственных задач.

Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на определение координат вектора по двум точкам и закрепить пройденый материал.

Калькулятор для вычисления координат вектора по двум точкам

Инструкция использования калькулятора для вычисления координат вектора по двум точкам

Ввод даных в калькулятор для вычисления координат вектора по двум точкам

В онлайн калькулятор можно вводить числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора для вычисления координат вектора по двум точкам

Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.

Теория. Координаты вектора по двум точкам

Например, вектор AB , заданный в пространстве координатами точек A(A _x , A _y , A _z ) и B(B _x , B _y , B _z ) можно найти использовав формулу:

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Нахождение координат вектора через координаты точек

Отложим от начала координат единичные векторы, то есть векторы, длины которых равны единице. Направление вектора i → должно совпадать с осью O x , а направление вектора j → с осью O y .

Векторы i → и j → называют координатными векторами.

Координатные векторы неколлинеарны. Поэтому любой вектор p → можно разложить по векторам p → = x i → + y j → . Коэффициенты x и y определяются единственным образом. Коэффициенты разложения вектора p → по координатным векторам называются координатами вектора p → в данной системе координат.

Координаты вектора записываются в фигурных скобках p → x ; y . На рисунке вектор O A → имеет координаты 2 ; 1 , а вектор b → имеет координаты 3 ; — 2 . Нулевой вектор представляется в виде 0 → 0 ; 0 .

Если векторы a → и b → равны, то и y 1 = y 2 . Запишем это так: a → = x 1 i → + y 1 j → = b → = x 2 i → + y 2 j → , значит x 1 = x 2 , y 1 = y 2 .

Таким образом, координаты равных векторов соответственно равны.

Если точка координат не совпадает с его началом системы координат, тогда рассмотрим задачу. Пусть в декартовой системе координат на O x y заданы координаты точек начала и конца A B → : A x a , y a , B x b , y b . Найти координаты заданного вектора.

Изобразим координатную ось.

Из формулы сложения векторов имеем O A → + A B → = O B → , где O – начало координат. Отсюда следует, что A B → = O B → — O A → .

O A → и O B → – это радиус-векторы заданных точек А и В, значит координаты точек имеют значения O A → = x a , y a , O B → = x b , y b .

По правилу операций над векторами найдем A B → = O B → — O A → = x b — x a , y b — y a .

Нахождение в трехмерном пространстве проходит по такому же принципу, только для трех точек.

Для нахождения координат вектора, необходимо найти разность его точек конца и начала.

Найти координаты O A → и A B → при значении координат точек A ( 2 , — 3 ) , B ( — 4 , — 1 ) .

Для начала определяется радиус-вектор точки A . O A → = ( 2 , — 3 ) . Чтобы найти A B → , нужно вычесть значение координат точек начала из координат точек конца.

Получаем: A B → = ( — 4 — 2 , — 1 — ( — 3 ) ) = ( — 6 , 2 ) .

Ответ: O A → = ( 2 , — 3 ) , A B → = ( — 6 , — 2 ) .

Задано трехмерное пространство с точкой A = ( 3 , 5 , 7 ) , A B → = ( 2 , 0 , — 2 ) . Найти координаты конца A B → .

Подставляем координаты точки A : A B → = ( x b — 3 , y b — 5 , z b — 7 ) .

По условию известно, что A B → = ( 2 , 0 , — 2 ) .

Известно, что равенство векторов справедливо тогда, когда координаты равны соответственно. Составим систему уравнений: x b — 3 = 2 y b — 5 = 0 z b — 7 = — 2

Отсюда следует, что координаты точки B A B → равны: x b = 5 y b = 5 z b = 5

Ответ: B ( 5 , 5 , 5 ) .

Нахождение координат вектора

В данной публикации мы рассмотрим формулы, с помощью которых можно найти координаты вектора, заданного координатами его начальной и конечной точек, а также разберем примеры решения задач по этой теме.

Нахождение координат вектора

Для того, чтобы найти координаты вектора AB , нужно из координат его конечной точки (B) вычесть соответствующие координаты начальной точки (A).

Формулы для определения координат вектора

» data-lang=»default» data-override=»<«emptyTable»:»»,»info»:»»,»infoEmpty»:»»,»infoFiltered»:»»,»lengthMenu»:»»,»search»:»»,»zeroRecords»:»»,»exportLabel»:»»,»file»:»default»>» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>

Для плоских задач	AB = x — A_x; B_y — A_y>
Для трехмерных задач	AB = x — A_x; B_y — A_y; B_z — A_z>
Для n-мерных векторов	AB = 1 — A₁; B₂ — A₂; . B_n — A_n>

Примеры задач

Задание 1
Найдем координаты вектора AB , если у его точек следующие координаты: , .

Задание 2
Определим координаты точки B вектора , если координаты точки .

Решение:
Координаты точки B можно вывести из формулы для расчета координат вектора:
B_x = AB _x + A_x = 6 + 2 = 8.
B_y = AB _y + A_y = 14 + 5 = 19.

источники:

http://zaochnik.com/spravochnik/matematika/vektory/nahozhdenie_kordinat_vectora/

Нахождение координат вектора

Источник