Как найти координаты вектора умноженного на число

Умножение вектора на число

Навигация по странице:

• Геометрическая интерпретация умножения вектора на число.
• Алгебраическая интерпретация умножения вектора на число.
• Формулы умножения вектора на число
  • для плоских задач
  • для пространственных задач
  • для n -мерного вектора
• Свойства вектора умноженного на число
• Примеры задач на умножение вектора и числа
  • плоская задача
  • пространственных задача

Геометрическая интерпретация.

Произведение ненулевого вектора на число — это вектор, коллинеарный данному (сонаправленный данному, если число положительное, имеющий противоположное направление, если число отрицательное), а его модуль равен модулю данного вектора, умноженному на модуль числа.

Алгебраическая интерпретация. Произведение ненулевого вектора на число — это вектор, координаты которого равны соответствующим координатам данного вектора, умноженным на число.

Формулы умножения вектора на число

Формула умножения вектора на число для плоских задач

В случае плоской задачи произведение вектора a = {a_x ; a_y} и числа k можно найти воспользовавшись следующей формулой:

k · a = {k · a_x ; k · a_y}

Формула умножения вектора на число для пространственных задач

В случае пространственной задачи произведение вектора a = {a_x ; a_y ; a_z} и числа k можно найти воспользовавшись следующей формулой:

k · a = {k · a_x ; k · a_y ; k · a_z}

Формула умножения n -мерного вектора

В случае n-мерного пространства произведение вектора a = {a₁ ; a₂; … ; a_n} и числа k можно найти воспользовавшись следующей формулой:

k · a = {k · a₁; k · a₂; … ; k · a_n}

Свойства вектора умноженного на число

Если вектор b равен произведению ненулевого числа k и ненулевого вектора a, то есть b = k · a, тогда:

• b || a — вектора b и a параллельны

• a↑↑b, если k > 0 — вектора b и a сонаправленные, если число k > 0

• a↑↓b, если k < 0 — вектора b и a противоположно направленные, если число k < 0

• |b| = |k| · |a| — модуль вектора b равен модулю вектора a умноженному на модуль числа k

Примеры задач на умножение вектора и числа

Пример умножения вектора на число для плоских задачи

Пример 1. Найти произведение вектора a = {1; 2} на 3.

Решение: 3 · a = {3 · 1; 3 · 2} = {3; 6}.

Пример умножения вектора на число для пространственных задачи

Пример 2. Найти произведение вектора a = {1; 2; -5} на -2.

Решение: (-2) · a = {(-2) · 1; (-2) · 2; (-2) · (-5)} = {-2; -4; 10}.

В данной публикации мы рассмотрим, каким образом вектор можно умножить на число (геометрическая интерпретация и алгебраическая формула). Также перечислим свойства этого действия и разберем примеры задач.

• Геометрическая интерпретация произведения

• Формула умножения вектора на число

• Свойства произведения вектора и числа

• Примеры задач

Геометрическая интерпретация произведения

Если вектор a умножить на число m, то получится вектор b, при этом:

• b || a
• |b| = |m| · |a|
• b ↑↑ a, если m > 0, b ↑↓ a, если m < 0

Таким образом, произведением ненулевого вектора на число является вектор:

• коллинеарный исходному;
• сонаправленный (если число больше нуля) или имеющий противоположное направление (если число меньше нуля);
• Длина равняется длине иходного вектора, умноженной на модуль числа.

Формула умножения вектора на число

Произведение ненулевого вектора на число – это вектор, координаты которого равняются соответствующим координатам исходного вектора, умноженным на заданное число.

Для плоских задач	a · m = {ax · m; ay · m}
Для трехмерных задач	a · m = {ax · m; ay · m; az · m}
Для n-мерных векторов	a · m = {a1 · m; a2 · m; … an · m}

Свойства произведения вектора и числа

Для любых произвольных векторов и чисел:

• (m ± n) · a = m · a ± n · a
• m · (a ± b) = m · a ± m · b
• m · (n · a) = (m · n) · a = n · (m · a)
• 1 · a = a
• 0 · a = 0

Примеры задач

Задание 1
Найдем произведение вектора a = {5; 11} и числа 4.

Решение:
4 · a = {4 · 5; 4 · 11} = {20; 44}

Задание 2
Умножим вектор b = {2; -4; 7} на число -6.

Решение:
-6 · b = {(-6) · 2; (-6) · (-4); (-6) · 7} = {-12; 24; -42}.

Содержание:

• Координаты вектора
• Направляющие косинусы
• Сумма двух векторов, заданных координатами
• Умножение вектора на число
• Основное свойство направляющих косинусов

Для решения задач с векторами необходимо определить вектор на плоскости или в пространстве, то есть дать информацию о его направлении
и длине.

Координаты вектора

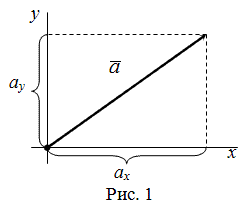
Пусть задана прямоугольная декартова система координат (ПДСК) $x O y$
и произвольный вектор $overline{a}$, начало которого совпадает
с началом системы координат (рис. 1).

Сумма двух векторов, заданных координатами

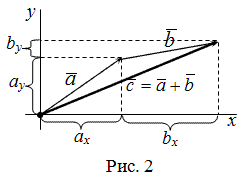
Пусть заданы $overline{a}=left(a_{x} ; a_{y}right)$ и $overline{b}=left(b_{x} ; b_{y}right)$,
тогда вектор $overline{c}=overline{a}+overline{b}$ имеет координаты
$left(a_{x}+b_{x} ; a_{y}+b_{y}right)$ (рис. 2).

Умножение вектора на число

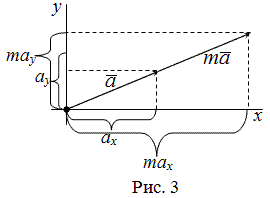
Если задан $overline{a}=left(a_{x} ; a_{y}right)$, то тогда вектор
$m overline{a}$ имеет координаты
$m overline{a}=left(m a_{x} ; m a_{y}right)$, здесь
$m$ — некоторое число (рис. 3).

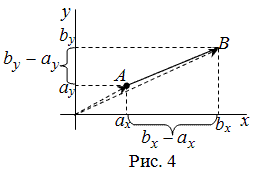
Рассмотрим далее случай, когда начало вектора не совпадает с началом системы координат. Предположим, что в ПДСК заданы две
точки $Aleft(a_{x} ; a_{y}right)$ и $Bleft(b_{x} ; b_{y}right)$.
Тогда координаты вектора $overline{A B}=left(x_{1} ; y_{1}right)$ находятся по формулам (рис. 4):

$x_{1}=b_{x}-a_{x}, y_{1}=b_{y}-a_{y}$

Направляющие косинусы

Направление вектора однозначно задается направляющими косинусами. Для
единичного вектора направляющие косинусы
равны его координатам.

Если в пространстве задан вектор $overline{a}=left(a_{x} ; a_{y} ; a_{z}right)$, то
его направляющие косинусы вычисляются по формулам:

$cos alpha=frac{a_{x}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}, cos beta=frac{a_{y}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}, cos gamma=frac{a_{z}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}$

Здесь $alpha$, $beta$ и
$gamma$ — углы, которые составляет вектор с положительными
направлениями осей $O x$, $O y$ и
$O z$ соответственно.

Основное свойство направляющих косинусов

Если известны направляющие косинусы вектора $overline{a}=left(a_{x} ; a_{y}right)$,
то его координаты могут быть найдены по формулам:

$a_{x}=|overline{a}| cos alpha, a_{y}=|overline{a}| cos beta$

Аналогичные формулы имеют место и в трехмерном случае — если известны направляющие косинусы вектора
$overline{a}=left(a_{x} ; a_{y} ; a_{z}right)$,
то его координаты могут быть найдены по формулам:

$a_{x}=|overline{a}| cos alpha, a_{y}=|overline{a}| cos beta, a_{z}=|overline{a}| cos gamma$

Читать дальше: длина (модуль) вектора.

ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ В КООРДИНАТНОЙ ФОРМЕ

1. При умножении вектора на число все его координаты
   умножаются на это число, т.е. если .

   Действительно,
   используя свойства операций умножения вектора на число и сложении векторов
   будем иметь

   .

   При сложении векторов их соответствующие
   координаты складываются, т.е. если .

   Доказательство очевидно.

   Условие
   коллинеарности двух векторов в
   коорднинатной форме.

   Два вектора коллинеарны тогда и только
   тогда, когда их соответствующие координаты пропорциональны. Т.е. если , то.

   Доказательство:

   1. Пусть вектор коллинеарен , тогда найдется λ такое, что . Значит, и . Поскольку
      разложение вектора по элементам базиса единственно, то .
   2. Пусть выполняется равенство . Обозначим коэффициент пропорциональности через λ. Тогда и, следовательно,
      , т.е. . Теорема доказана.

      Пример.

      1. Даны векторы . Найти вектор .

         .

      2. Найти координаты вектора в базисе, образованном
         векторами , , .

         Обозначим координаты вектора в новом базисе . Тогда в новом базисе будем иметь:

         

         Итак, .

      

      Рассмотрим две произвольные точки и . Найдем координаты вектора .

      Очевидно, что . Но по определению координат вектора и . Следовательно,

      

      Таким образом, чтобы найти координаты вектора , нужно из координат его конца вычесть соответствующие
      координаты начала.

      Примеры.

      1. Заданы точкиA(1; -2; 3), B(2; 0; -1). Найти вектор .

         

      2. Даны A(-2; 3; 1), В(-1; 2; 0), С(0; 1; 1).
         Найти .

         

         

      3. Известно, что. Найти координаты точки D, если

         А(3; -4; -1), В(-4; 4; 1), С(-3; -5; 4).

         Пусть тогда

         . С другой стороны . Следовательно, должно выполняться равенство (x+3; y+5; z-4)=(5;10;-8).
         Отсюда

         x=2, y=5, z=-4, т.е. точка D имеет координаты D(2; 5; -4).

СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ И ЕГО СВОЙСТВА

Мы рассмотрели умножение вектора на число. Однако во многих задачах механики и
физики встречается операция умножения вектора на вектор. Но при этом результат
может быть как числом, так и вектором. Поэтому рассматривают два вида умножения
векторов: скалярное и векторное.

Пусть даны два вектора и , угол между, которыми равен .

Скалярным произведением
векторов и называется
число, равное произведению длин этих векторов на косинус угла между ними.
Скалярное произведение обозначается . Итак, .

Если один из векторов нулевой, то угол не определен, и скалярное
произведение по определения считается равным нулю.

Рассмотрим свойства скалярного
произведения.

1. Скалярное произведение двух
   векторов подчиняется коммутативному закону, т.е. для любых векторов и .

   Очевидно, из определения скалярного произведения:

   .

2. Для любого числа λ и любых векторов имеем:

   .

   Доказательство. Ограничимся случаем, когда λ > 0. В этом случае
   угол между векторами и совпадает с
   углом между векторами и , .

   Поэтому . Откуда

   Аналогично доказывается и равенство .

   Случай λ
   <0 рассмотреть самостоятельно.

3. Для любых векторов выполняется
   равенство .

   Доказательство. Используя определение скалярного произведения и
   свойства проекций вектора на ось, будем иметь

   

4. Для любого вектора выполняется
   соотношение.

   Действительно, так как , то .

   Из
   этого свойства в частности следует .

5. Скалярное произведение двух
   векторов равно нулю тогда и только тогда,когда равен нулю один из сомножителей или векторы перпендикулярны.

   Это свойство очевидно из определения скалярного произведения.

   Таким образом, необходимым и достаточным условием ортогональности двух
   векторов является равенство нулю их скалярного произведения.

   Пример. Дан вектор . Известно, что

   Найти .

   Имеем, т.е. .

   Найдем:

   Следовательно, .

Рассмотрим, как находится скалярное произведение векторов, если они заданы в координатной
форме. Пусть даны два вектора и .

Рассмотрим сначала все возможные скалярные произведения векторов друг на друга.

Поэтому

Итак, скалярное произведение векторов равно сумме произведений
соответствующих координат: .

Это соотношение позволяет вычислить длину вектора через его координаты:

.

Далее из определения скалярного произведения находим

.

Выражая скалярное произведение и длины векторов через их координаты,получим формулу для нахождения косинуса угла
между векторами

.

Условие ортогональности двух
векторов:

или .

Т.о., для того чтобы
два вектора были перпендикулярны необходимо и достаточно, чтобы сумма
произведений соответствующих координат этих векторов была равна нулю.

Примеры.

1. Пусть А(-1; 1; 0), B(3; 1; -2), . Найти:
   1. ;
   2. и ;
   3. .
      1. .
      2. .
      3. .
2. Найти в , если известны координаты его вершин A(1; 5; 6),

   

   B(5; 3; 10), C(2; 1; 14).

   

   

3. При каком значении m векторы и перпендикулярны?

   Условие ортогональности двух векторов .

   . Следовательно, m = 15.

ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ И ЕГО СВОЙСТВА

Введем сначала понятие ориентации тройки векторов.

Пусть даны три некомпланарных вектора с общим
началом, перечисленных в определенном порядке: первый – , второй – , третий – .

Тройка некомпланарных векторов называется правоориентированной
или просто правой, если из конца
третьего вектора кратчайший поворот от первого ко второму виден против часовой
стрелки. В противном случае тройку векторов называют левой, в этом случае если мы будем смотреть с конца вектора , то кратчайший поворот от к осуществляется
по часовой стрелке.

Векторным произведением векторов и называется
новый вектор , удовлетворяющий условиям:

1. Длина вектора равна площади
   параллелограмма, построенного на векторах и .



2. Вектор перпендикулярен
   плоскости этого параллелограмма.
3. Он направлен так, что векторы и образуют правую
   тройку векторов.

Векторное произведение векторов и обозначается
символом . Если хотя бы один из сомножителей равен нулю, то
векторное произведение по определению считают равным нулю

Векторное произведение обладает следующими свойствами:

1. Из определения следует, что
   длина векторного произведения численно равна площади параллелограмма,
   построенного на векторах, и, следовательно, находится по формуле:

   .

   Таким образом, и .

2. При перестановке
   сомножителей векторное произведение меняет свой знак .

   Действительно
   из определения векторного произведения следует, что векторы и имеют одинаковые модули, расположены на одной прямой,
   но направлены в противоположные стороны. Поэтому, векторы и являются
   противоположными векторами и поэтому .



3. Скалярный множитель можно
   выносить за знак векторного произведения, т.е. для
   любого числа λ и любых векторов

   .

   Доказательство этого свойства непосредственно следует из определения
   векторного произведения. Докажем для λ > 0. В этом случае . Тогда по определению векторного произведения

   

   Вектор перпендикулярен
   векторам и . Вектор также векторам и , т.к. векторы и , и лежат в одной
   плоскости. Следовательно, векторы и коллинеарны. Очевидно, что направления их также совпадают.
   Т. к. , и следовательно, , то .

   Поэтому .

   Аналогично проводится доказательство для случая λ < 0.

4. Для любых векторов имеет место
   равенство

   .

   Примем без доказательства.

5. Векторное произведение двух
   векторов равно нулевому вектору тогда и только тогда, когда один из
   сомножителей равен нулю или векторы коллинеарны.

   Действительно, если векторы коллинеарны, то , т.е. площадь
   параллелограмма, построенного на данных векторах,равна нулю.

   Таким образом, для того чтобы два
   ненулевых вектора были коллинеарны, необходимо и
   достаточно, чтобы их векторное произведение равнялось нулевому вектору.

   В частности .

Примеры.

1. Раскрыть скобки

   .

2. Найти площадь треугольника,
   построенного на векторах и , если известно, что и .

   .

   Найдем .

   .

Можно показать, что если и , то координаты векторного произведения векторов и находятся по формуле:

.

Примеры.

1. Найти векторное произведение векторов и .

   .

2. Найти площадь , если A(2; 3; 1), B(-1; -2; 0), C(-3; 0; 1).

   

3. Даны векторы . Найти параметры n, p, q если известно, что векторы и коллинеарны, а
   векторы и ортогональны.

   Так как векторы и коллинеарны, то . Векторы и ортогональны, поэтому . Итак, получили систему уравнений

   

Возможно ли умножение вектора на число

Произведением вектора (bar{a}), не равного нулю, на число (lambda ne 0) является вектор (lambda bar{a},) коллинеарный заданному, то есть он будет сонаправлен данному вектору (bar{a}), если (lambda>0), и противоположно направленным — если (lambda<0), а его модуль равен модулю данного вектора, умноженному на модуль числа:

(lambda >0:lambda bar{a}uparrow uparrow bar{a})

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

(lambda <0:lambda bar{a}uparrow downarrow bar{a})

(left|lambda bar{a}right|=left|lambda right|cdot left|bar{a}right|)

В том случае, когда вектор (bar{a}ne bar{0}) задают с помощью координат, то произведение этого вектора на число (lambda ne 0) является вектором (lambda bar{a}) с координатами, равными соответствующим координатам заданного вектора (bar{a}), умноженным на число (lambda:)

(bar{a}=left(a_{1} ;; a_{2} ;; a_{3} right)Rightarrow lambda bar{a}=left(lambda a_{1} ;; lambda a_{2} ;; lambda a_{3} right))

Особенность такого действия, как умножение вектора на число заключается в том, что число является простой численной формой величины, для которого отсутствует направление, а вектор определяется в качестве направленного отрезка, обладающего численным измерением и направлением.

Подобная операция, как и вычитание, нередко используется при решении задач в математике, геометрии и физике.

Произведение ненулевого вектора (vec{a}) на число k является таким вектором (vec{b}), длина которого составляет (left| vec{b}right|=left|k right|*left|vec{a} right|). При этом векторы (vec{a}) и (vec{b}) сонаправлены, если k больше или равно нулю, и противоположно направлены, когда k меньше нуля. Произведение нулевого вектора на любое число в результате позволяет получить ненулевой вектор.

Предположим, что существует некий вектор (vec{a}). В таком случае вектор (vec{2a}) является вектором, направленным в ту же сторону, но с длиной, которая в 2 раза превышает длину вектора (vec{a}). Длина его в два раза больше. Вектор (vec{-2a}) является вектором, который направлен противоположно вектору (vec{a}) и длиннее его в 2 раза.

Геометрическая и алгебраическая интерпретация умножения

Алгебраическая интерпретация: произведение ненулевого вектора на число представляет собой вектор с координатами, равными соответствующим координатам данного вектора, умноженным на число.

Яркий пример умножения вектора на число является второй закон Ньютона, который часто применяют при решении задач в физике. Если умножить обе части закона Ньютона на массу тела, то формула примет следующий вид:

(m*vec{a}=vec{F})

После того, как умножили массу данного тела в виде скаляра m на ускорение тела, выраженного вектором (vec{a}), в результате получили вектор (m*vec{a}). Данный вектор можно обозначить, как (vec{F}), который будет называться силой. Таким образом, под действием силы тело приобретает ускорение.

Рассматриваемая формула записана в векторном виде:

(m*vec{a}=vec{F})

В таком случае говорят не только о модулях, то есть длинах векторов. С помощью векторного вида можно определить направление вектора. Согласно рассмотренному ранее определению произведения вектора на число, результат подобной операции не влияет на направление вектора. Его нельзя повернуть на какой-либо угол путем умножения на число. Результат произведения отличается лишь длиной вектора. Таким образом, векторы (vec{a}) и (vec{F}) характеризуются одинаковым направлением, но отличается по длине. В данном случае длина векторов отличается в m раз.

Понятие, основные свойства

В том случае, когда вектор (vec{b}) равен произведению ненулевого числа k и ненулевого вектора (vec{a}), то есть (vec{b}=k*vec{a}), справедливы следующие утверждения:

• (vec{a}parallelvec{b}), то есть рассматриваемые вектора параллельны;
• (vec{a}) и (vec{b}) обладают одинаковым направлением при k больше нуля;
• (vec{a}) и (vec{b}) обладают разными направлениями при k меньше нуля.

Вектор можно умножить на число в виде скалярной величины. При этом в результате получится тоже вектор. После операции умножения длина заданного вектора изменится:

• длина вектора будет увеличена при умножении на число, модуль которого больше 1;
• длина вектора уменьшится в том случае, когда модуль числа меньше 1.

Если вектор умножить на положительное число, полученный вектор будет обладать таким же направлением, что и первоначальный. В том случае, когда предполагается произведение вектора на отрицательное число, полученный в результате вектор будет направлен в противоположную сторону.

В том случае, когда есть информация о координатах вектора, при умножении его на число следует умножить каждую координату рассматриваемого вектора на данное число.

(vec{a}=left{a_{x};a_{y} right})

Данная запись представляет собой координаты вектора (vec{a}.)

(k*vec{a}=left{k*a_{x};k*a_{y} right})

Формулы применяющиеся при перемножении вектора и числа

В случае умножения вектора на число удобно использовать формулу умножения, предназначенную для решения плоских задач. При этом произведение вектора (vec{a}=left{a_{x};a_{y} right}) и какого-то числа k вычисляют по формуле:

(k*vec{a}=left{k*a_{x};k*a_{y} right})

Если предполагается решить задачу пространственного типа на произведение вектора (vec{a}=left{a_{x};a_{y}; a_{z} right}) и числа, то целесообразно воспользоваться следующей закономерностью:

(k*vec{a}=left{k*a_{x};k*a_{y}; k*a_{z} right})

Предусмотрена формула умножения n-мерного вектора. Когда n-мерный вектор (vec{a}=left{a_{1};a_{2};…; a_{n} right}) умножают на число k, целесообразно воспользоваться формулой:

(k*vec{a}=left{k*a_{1};k*a_{2};…; k*a_{n} right})

Примеры задач с решением 

Задача 1

Дан вектор (vec{a}=left{1;2 right}). Необходимо найти произведение этого вектора на 3.

Решение

В данном случае целесообразно воспользоваться формулой для решения плоских задач:

(k*vec{a}=left{k*a_{x};k*a_{y} right})

Таким образом:

(3*vec{a}=left{3*1;3*2 right}=left{3;6 right})

Ответ: (left{3;6 right})

Задача 2

Задан пространственный вектор (vec{a}=left{1;2;-5 right}). Данный вектор необходимо умножить на число -2.

Решение

В случае пространственной задачи следует воспользоваться следующей формулой:

(k*vec{a}=left{k*a_{x};k*a_{y}; k*a_{z} right})

Подставив числовые значения, получим:

((-2)*vec{a}=left{(-2)*1;(-2)*2; (-2)*(-5) right}=left{-2;-4;10 right})

Ответ: (left{-2;-4;10 right})

Задача 3

Существует некий вектор (bar{a}=left(-1;; 2;; 3right)). Требуется найти произведение этого вектора на число 2.

Решение

Исходя из определения, для умножения заданного вектора на число (lambda =2) требуется каждую координату вектора (bar{a}) умножить на это число. Таким образом:

(2bar{a}=2cdot left(-1;; 2;; 3right)=left(2cdot left(-1right);; 2cdot 2;; 2cdot 3right)=left(-2;; 4;; 6right))

Ответ: (2cdot bar{a}=left(-2;; 4;; 6right))

Задача 4

Задан вектор (bar{a}=left(-2;; 4right)). Необходимо определить вектор (-3bar{a}).

Решение

В том случае, когда требуется найти искомое произведение, следует умножить каждую координату заданного вектора (bar{a}) на число (lambda =-3). В результате умножения вектора на число получим:

(-3bar{a}=-3cdot left(-2;; 4right)=left(-3cdot left(-2right);; -3cdot 4right)=left(6;; -12right))

Ответ: (-3bar{a}=left(6;; -12right))

Задача 5

Согласно анализу рассмотренных закономерностей, действия с векторами аналогичны действиям с алгебраическими выражениями. По этому принципу требуется упростить следующую запись:

(vec{p}=2(vec{a}-vec{b})+(vec{c}+vec{a})-3(vec{b}-vec{c}+vec{a}))

Решение

В первую очередь следует раскрыть скобки:

(vec{p}=2vec{a}-2vec{b}+vec{c}+vec{a}-3vec{b}+3vec{c}-3vec{a})

Далее необходимо привести подобные:

(vec{p}=2vec{a}+vec{a}-3vec{a}-2vec{b}-3vec{b}+vec{c}+3vec{c}=-5vec{b}+4vec{c})

Ответ: (-5vec{b}+4vec{c})

Задача 6

Имеется некий отрезок АВ. Точка С является серединой данного отрезка, точка О представляет собой произвольную точку плоскости. Также (vec{OA}=vec{a}) и (vec{OB}=vec{b}.) Требуется доказать, что:

(vec{OC}=1/2(vec{a}+vec{b}))

Решение 1

Используя правило треугольника, можно выразить вектор (vec{OC}) в виде суммы двух векторов:

(vec{OC}=vec{a}+vec{AC})

Кроме того, следует отметить, что:

(vec{OC}=vec{b}+vec{BC})

В результате получилась система двух уравнений:

(vec{OC}=vec{a}+vec{AC})

(vec{OC}=vec{b}+vec{BC})

Далее необходимо сложить уравнения системы:

(2vec{OC}=vec{a}+vec{AC}+vec{b}+vec{BC}=vec{a}+vec{b}+vec{AC}+vec{BC})

(vec{AC}+vec{BC}=vec{0})

Исходя из того, что С является серединой АВ, следует вывод: модули данных векторов равны, но они обладают разными направлениями. Таким образом, сумма векторов является нулевым вектором. В результате:

(2vec{OC}=vec{a}+vec{b})

При делении обеих частей уравнения на 2 получим:

(vec{OC}=1/2(vec{a}+vec{b}))

Уравнение доказано.

Решение 2

(vec{OC}=vec{a}+vec{AC}=vec{a}+1/2vec{AB}=vec{a}+1/2(vec{b}-vec{a}))

Следует раскрыть скобки и привести подобные:

(vec{OC}=vec{a}+1/2vec{b}-1/2vec{a}=vec{a}-1/2vec{a}+1/2vec{b}=1/2(vec{a}+vec{b}))

Уравнение доказано.

Задача 7

Требуется доказать, что средняя линия трапеции и ее основания параллельны друг другу, а также средняя линия трапеции равна половине суммы оснований.

Решение

Известно, что средней линией трапеции соединены ее боковые стороны. Основания трапеции параллельны друг другу. Согласно правилу многоугольника, можно выразить вектор vec{MN} как сумму векторов:

(vec{MN}=vec{MB}+vec{BC}+vec{CN})

С другой стороны:

(vec{MN}=vec{MA}+vec{AD}+vec{DN})

В результате получена система уравнений:

(vec{MN}=vec{MB}+vec{BC}+vec{CN})

(vec{MN}=vec{MA}+vec{AD}+vec{DN})

Следует сложить уравнения системы:

(2vec{MN}=vec{MB}+vec{BC}+vec{CN}+vec{MA}+vec{AD}+vec{DN}=vec{MB}+vec{MA}+vec{BC}+ vec{AD}+vec{CN}+vec{DN})

Векторы (vec{MB}) и (vec{MA}) обладают противоположными направлениями и в сумме дают нулевой вектор, так как М — середина АВ, то есть модули данных векторов равны, кроме того, они противонаправлены. Аналогично векторы (vec{CN}) и (vec{DN}) дают в сумме нулевой вектор. Таким образом, получаем:

(2vec{MN}=vec{BC}+vec{AD})

Затем можно поделить обе части уравнения на 2:

(vec{MN}=1/2(vec{BC}+vec{AD}))

В результате получено доказательство того, что средняя линия равна половине суммы оснований. Кроме того, прямая MN параллельна основаниям трапеции.