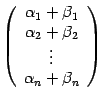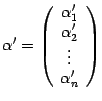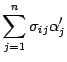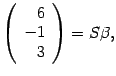Как найти координаты векторов в линейном пространстве

Координаты и преобразования координат в линейном пространстве

Координаты векторов в данном базисе линейного пространства

Пусть — базис линейного пространства . Каждый вектор можно разложить по базису (см. теорему 8.1), т.е. представить в виде , причем коэффициенты в разложении определяются однозначно. Эти коэффициенты называются координатами вектора в базисе (или относительно базиса ). Координаты вектора — это упорядоченный на бор чисел, который представляется в виде матрицы-столбца и называется координатным столбцом вектора (в данном базисе). Вектор и его координатный столбец обозначаются одной и той же буквой полужирной или светлой соответственно.

Если базис (как упорядоченный набор векторов) представить в виде символической матрицы-строки , то разложение вектора по базису можно записать следующим образом:

Здесь умножение символической матрицы-строки на числовую матрицу-столбец производится по правилам умножения матриц.

При необходимости, если речь идет о разных базисах, у координатного столбца указывается обозначение базиса, относительно которого получены координаты, например, — координатный столбец вектора в базисе .

Из теоремы 8.1 следует, что равные векторы имеют равные соответствующие координаты (в одном и том же базисе), и наоборот, если координаты векторов (в одном и том же базисе) соответственно равны, то равны и сами векторы.

---

Линейные операции в координатной форме

Пусть — базис линейного пространства , векторы и имеют в этом базисе координаты и соответственно, т.е.

Складывая эти равенства, получаем .

т.е. при сложении векторов их координаты складываются.

Умножая второе равенство в (8.7) на число , получаем

т.е. при умножении вектора на число все его координаты умножаются на это число.

Другими словами, сумма векторов имеет координаты , а произведение имеет координаты . Разумеется, что все координаты получены в одном базисе .

---

Замечания 8.5

1. Нетрудно показать, что координатный столбец линейной комбинации векторов равен линейной комбинации координатных столбцов этих векторов.

2. Если система векторов линейно зависима (линейно независима), то их координатные столбцы, полученные относительно одного базиса, образуют линейно зависимую (соответственно, линейно независимую) систему. Это следует из равносильности равенств и . Например, если в этих равенствах не все коэффициенты равны нулю, т.е. система векторов и система их координатных столбцов линейно зависимы одновременно.

3. Все свойства линейной зависимости и линейной независимости векторов переносятся без изменений на их координатные столбцы, полученные в одном и том же базисе. И наоборот, свойства для матриц-столбцов, переносятся на векторы, если матрицы-столбцы считать их координатными столбцами.

4. Выбрав в n-мерном вещественном линейном пространстве некоторый базис, можно установить взаимно однозначное соответствие: каждому вектору поставить в соответствие его координатный столбец (в вы бранном базисе), и наоборот, каждому координатному столбцу поставить в соответствие вектор. Другими словами, любой фиксированный базис n-мерного вещественного линейного пространства позволяет установить взаимно однозначное соответствие между всеми векторами вещественно го пространства и всеми столбцами n-мерного арифметического пространства . Это соответствие обозначается . Для n-мерного комплексного линейного пространства аналогичное взаимно однозначное соответствие устанавливается с пространством .

---

Преобразование координат вектора при замене базиса

Пусть заданы два базиса пространства и . Базис будем условно называть «старым», а базис — «новым». Пусть известны разложения каждого вектора нового базиса по старому базису:

Записывая по столбцам координаты векторов в базисе , составляем матрицу:

Квадратная матрица , составленная из координатных столбцов векторов нового базиса в старом базисе , называется матрицей перехода от старого базиса к новому. При помощи матрицы перехода (8.9) формулы (8.8) можно записать в виде:

Умножение символической матрицы-строки на матрицу перехода в (8.10) производится по правилам умножения матриц.

Пусть в базисе вектор имеет координаты , а в базисе — координаты , т.е.

или, короче,

Подставляя в правую часть последнего равенства выражение (8.10), получаем — два разложения вектора в одном и том же базисе . Коэффициенты этих разложений должны совпадать (по теореме 8.1), так как это координаты одного и того же вектора в одном базисе. Поэтому

Формула (8.11) устанавливает связь координат вектора в разных базисах: координатный столбец вектора в старом базисе получается в результате умножения матрицы перехода на координатный столбец вектора в новом базисе.

---

Пример 8.3. В пространстве многочленов степени не выше второй даны две системы многочленов:

Доказать, что каждая система является базисом пространства . Найти матрицу перехода от базиса к базису . Определить координаты квадратного трехчлена относительно базисов и .

Решение. Система многочленов является стандартным базисом пространства . Докажем, что система является базисом. По ступим следующим образом. Найдем координатные столбцы этих многочленов в стандартном базисе. Раскладывая по базису , получаем

Составим из этих столбцов матрицу . Ранг этой матрицы равен 3, так как . Следовательно, столбцы линейно независимы, тогда и многочлены линейно независимы (см. пункт 2 замечаний 8.5). Итак, многочлены являются базисом пространства , а матрица — искомая матрица перехода от базиса к базису . Осталось найти координаты многочлена в этих базисах. Раскладывая по базисам, находим

Проверим результат, вычисляя по формуле (8.11):

Результаты совпадают.

---

Свойства матрицы перехода от одного базиса к другому

1. Пусть имеются три базиса пространства и известны матрицы перехода: от базиса к базису ; от к ; от к . Тогда

Действительно, запишем связь (8.10) для данных базисов:

Подставляя первое выражение во второе равенство, получаем . Сравнивая с третьим равенством, приходим к (8.12).

2. Если — матрица перехода от базиса к базису , то матрица обратима и обратная матрица является матрицей перехода от базиса к базису . Координаты вектора в базисах и связаны формулами:

В самом деле, пусть — матрица перехода от базиса к базису . Учитывая, что матрица перехода от базиса к базису — единичная, применяем свойство 1 к трем базисам . Для трех базисов аналогично получаем: . Следовательно, .

3. Всякая обратимая квадратная матрица n-го порядка может служить матрицей перехода от одного базиса n-мерного линейного пространства к другому базису.

---

Пример 8.4. В двумерном арифметическом пространстве даны два базиса: и . Найти матрицу перехода от базиса к базису и координаты вектора в каждом из базисов.

Решение. Рассмотрим стандартный базис пространства . Находим координаты векторов в стандартном базисе. Раскладываем вектор

В стандартном базисе пространства координатный столбец совпадает с вектором . Для других векторов аналогично получаем . Из координатных столбцов составим матрицы перехода (8.9) от стандартного базиса к данным базисам и

По свойству 1 матриц перехода имеем . .По свойству 2: . Поэтому

В стандартном базисе пространства координатный столбец совпадает с вектором . Найдем координаты этого вектора в базисе (по свойству 2 матрицы перехода):

В самом деле, справедливо разложение

Найдем координаты вектора в базисе двумя способами

Полученный результат подтверждает разложение:

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Теорема доказана.

Теорема о произведении вектора на число: Координаты произведения вектора на число равны произведению соответствующих координат это число.

Доказательство.

Теорема доказана.

Пример задачи на нахождение координат вектора

Решение.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 05 04 2022

Координаты вектора в декартовой системе координат (ДСК)

Для начала дадим определение координат вектора в заданной системе координат. Чтобы ввести данное понятие, определим что мы называем прямоугольной или декартовой системой координат.

Прямоугольная система координат представляет из себя прямолинейную систему координат с взаимно перпендикулярными осями на плоскости или в пространстве.

С помощью введения прямоугольной системы координат на плоскости или в трехмерном пространстве становится возможным описывание геометрических фигур вместе с их свойствами при помощи уравнений и неравенств, то есть использовать алгебраические методы при решении геометрических задач.

Тем самым, мы можем привязать к заданной системе координат векторы. Это значительно расширит наши возможности при решении определенных задач

Прямоугольная система координат на плоскости обычно обозначается O x y , где O x и O y – оси коорднат. Ось O x называют осью абсцисс, а ось O y – осью ординат (в пространстве появляется ещё одна ось O z , которая перпендикулярна и O x и O y ).

Итак, нам дана прямоугольная декартова система координат O x y на плоскости если мы отложим от начала координат векторы i → и j → , направление которых соответственно совпадет с положительными направлениями осей O x и O y , и их длина будет равна условной единице, мы получим координатные векторы. То есть в данном случае i → и j → являются координатными векторами.

Координатные векторы

Векторы i → и j → называются координатными векторами для заданной системы координат.

Откладываем от начала координат произвольный вектор a → . Опираясь на геометрическое определение операций над векторами, вектор a → может быть представлен в виде a → = a x · i → + a y · j → , где коэффициенты a x и a y — единственные в своем роде, их единственность достаточно просто доказать методом от противного.

Разложение вектора

Разложением вектора a → по координатным векторам i → и j → на плоскости называется представление вида a → = a x · i → + a y · j → .

Коэффициенты a x и a y называются координатами вектора в данной системе координат на плоскости.

Координаты вектора в данной системе координат принято записывать в круглых скобках, через запятую, при этом заданные координаты следует отделять от обозначения вектора знаком равенства. К примеру, запись a → = ( 2 ; — 3 ) означает, что вектор a → имеет координаты ( 2 ; — 3 ) в данной системе координат и может быть представлен в виде разложения по координатным векторам i → и j → как a → = 2 · i → — 3 · j → .

Следует обратить внимание, что порядок записи координат, имеет важное значение, если вы запишите координаты вектора в другом порядке, вы получите совершенно другой вектор.

Опираясь на определения координат вектора и их разложения становится очевидным, что единичные векторы i → и j → имеют координаты ( 1 ; 0 ) и ( 0 ; 1 ) соответственно, и они могут быть представлены в виде следующих разложений i → = 1 · i → + 0 · j → ; j → = 0 · i → + 1 · j → .

Также имеет место быть нулевой вектор 0 → с координатами ( 0 ; 0 ) и разложением 0 → = 0 · i → + 0 · j → .

Равные и противоположные векторы

Векторы a → и b → равны тогда, когда их соответствующие координаты равны.

Противоположным вектором называется вектор противоположный данному.

Отсюда следует, что координаты такого вектора будут противоположны координатам данного вектора, то есть, — a → = ( — a x ; — a y ) .

Все вышеизложенное можно аналогично определить и для прямоугольной системы координат, заданной в трехмерном пространстве. В такой системе координат имеет место быть тройка координатных векторов i → , j → , k → , а произвольный вектор a → раскладывается не по двум, а уже по трем координатам, причем единственным образом и имеет вид a → = a x · i → + a y · j → + a z · k → , а коэффициенты этого разложения ( a x ; a y ; a z ) называются координатами вектора в данной (трехмерной) системе координат.

Следовательно, координатные векторы в трехмерном пространстве принимают также значение 1 и имеют координаты i → = ( 1 ; 0 ; 0 ) , j → = ( 0 ; 1 ; 0 ) , k → = ( 0 ; 0 ; 1 ) , координаты нулевого вектора также равны нулю 0 → = ( 0 ; 0 ; 0 ) , и в таком случае два вектора будут считаться равными, если все три соответствующие координаты векторов между собой равны a → = b → ⇔ a x = b x , a y = b y , a z = b z , и координаты противоположного вектора a → противоположны соответствующим координатам вектора a → , то есть, — a → = ( — a x ; — a y ; — a z ) .

Координаты радиус-вектора точки

Чтобы ввести данное определение, требуется показать в данной системе координат связь координат точки и координат вектора.

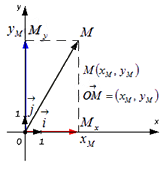
Пусть нам дана некоторая прямоугольная декартова система координат O x y и на ней задана произвольная точка M с координатами M ( x M ; y M ) .

Вектор O M → называется радиус-вектором точки M .

Определим, какие координаты в данной системе координат имеет радиус-вектор точки

Вектор O M → имеет вид суммы O M → = O M x → + O M y → = x M · i → + y M · j → , где точки M x и M y это проекции точки М на координатные прямые Ox и Oy соответственно (данные рассуждения следуют из определения проекция точки на прямую), а i → и j → — координатные векторы, следовательно, вектор O M → имеет координаты ( x M ; y M ) в данной системе координат.

Иначе говоря, координаты радиус-вектора точки М равны соответствующим координатам точки М в прямоугольной декартовой системе координат.

Аналогично в трехмерном пространстве радиус-вектор точки M ( x M ; y M ; z M ) разлагается по координатным векторам как O M → = O M x → + O M y → + O M z → = x M · i → + y M · j → + z M · k → , следовательно, O M → = ( x M ; y M ; z M ) .

Координаты и преобразования координат в линейном пространстве

Координаты векторов в данном базисе линейного пространства

Пусть — базис линейного пространства . Каждый вектор можно разложить по базису (см. теорему 8.1), т.е. представить в виде , причем коэффициенты в разложении определяются однозначно. Эти коэффициенты называются координатами вектора в базисе (или относительно базиса ). Координаты вектора — это упорядоченный на бор чисел, который представляется в виде матрицы-столбца и называется координатным столбцом вектора (в данном базисе). Вектор и его координатный столбец обозначаются одной и той же буквой полужирной или светлой соответственно.

Если базис (как упорядоченный набор векторов) представить в виде символической матрицы-строки , то разложение вектора по базису можно записать следующим образом:

Здесь умножение символической матрицы-строки на числовую матрицу-столбец производится по правилам умножения матриц.

При необходимости, если речь идет о разных базисах, у координатного столбца указывается обозначение базиса, относительно которого получены координаты, например, — координатный столбец вектора в базисе .

Из теоремы 8.1 следует, что равные векторы имеют равные соответствующие координаты (в одном и том же базисе), и наоборот, если координаты векторов (в одном и том же базисе) соответственно равны, то равны и сами векторы .

Линейные операции в координатной форме

Пусть — базис линейного пространства , векторы и имеют в этом базисе координаты и соответственно, т.е.

Складывая эти равенства, получаем .

т.е. при сложении векторов их координаты складываются .

Умножая второе равенство в (8.7) на число , получаем

т.е. при умножении вектора на число все его координаты умножаются на это число .

Другими словами, сумма векторов имеет координаты , а произведение имеет координаты . Разумеется, что все координаты получены в одном базисе .

1. Нетрудно показать, что координатный столбец линейной комбинации векторов равен линейной комбинации координатных столбцов этих векторов.

2. Если система векторов линейно зависима (линейно независима), то их координатные столбцы, полученные относительно одного базиса, образуют линейно зависимую (соответственно, линейно независимую) систему. Это следует из равносильности равенств и . Например, если в этих равенствах не все коэффициенты равны нулю, т.е. система векторов и система их координатных столбцов линейно зависимы одновременно.

3. Все свойства линейной зависимости и линейной независимости векторов переносятся без изменений на их координатные столбцы, полученные в одном и том же базисе. И наоборот, свойства для матриц-столбцов, переносятся на векторы, если матрицы-столбцы считать их координатными столбцами.

4. Выбрав в n-мерном вещественном линейном пространстве некоторый базис, можно установить взаимно однозначное соответствие: каждому вектору поставить в соответствие его координатный столбец (в вы бранном базисе), и наоборот, каждому координатному столбцу поставить в соответствие вектор. Другими словами, любой фиксированный базис n-мерного вещественного линейного пространства позволяет установить взаимно однозначное соответствие между всеми векторами вещественно го пространства и всеми столбцами n-мерного арифметического пространства . Это соответствие обозначается . Для n-мерного комплексного линейного пространства аналогичное взаимно однозначное соответствие устанавливается с пространством .

Преобразование координат вектора при замене базиса

Пусть заданы два базиса пространства и . Базис будем условно называть «старым», а базис — «новым». Пусть известны разложения каждого вектора нового базиса по старому базису:

Записывая по столбцам координаты векторов в базисе , составляем матрицу:

Квадратная матрица , составленная из координатных столбцов векторов нового базиса в старом базисе , называется матрицей перехода от старого базиса к новому. При помощи матрицы перехода (8.9) формулы (8.8) можно записать в виде:

Умножение символической матрицы-строки на матрицу перехода в (8.10) производится по правилам умножения матриц.

Пусть в базисе вектор имеет координаты , а в базисе — координаты , т.е.

Подставляя в правую часть последнего равенства выражение (8.10), получаем — два разложения вектора в одном и том же базисе . Коэффициенты этих разложений должны совпадать (по теореме 8.1), так как это координаты одного и того же вектора в одном базисе. Поэтому

Формула (8.11) устанавливает связь координат вектора в разных базисах: координатный столбец вектора в старом базисе получается в результате умножения матрицы перехода на координатный столбец вектора в новом базисе .

Пример 8.3. В пространстве многочленов степени не выше второй даны две системы многочленов:

Доказать, что каждая система является базисом пространства . Найти матрицу перехода от базиса к базису . Определить координаты квадратного трехчлена относительно базисов и .

Решение. Система многочленов является стандартным базисом пространства . Докажем, что система является базисом. По ступим следующим образом. Найдем координатные столбцы этих многочленов в стандартном базисе. Раскладывая по базису , получаем

Составим из этих столбцов матрицу . Ранг этой матрицы равен 3, так как . Следовательно, столбцы линейно независимы, тогда и многочлены линейно независимы (см. пункт 2 замечаний 8.5). Итак, многочлены являются базисом пространства , а матрица — искомая матрица перехода от базиса к базису . Осталось найти координаты многочлена в этих базисах. Раскладывая по базисам, находим

Проверим результат, вычисляя по формуле (8.11):

Свойства матрицы перехода от одного базиса к другому

1. Пусть имеются три базиса пространства и известны матрицы перехода: от базиса к базису ; от к ; от к . Тогда

Действительно, запишем связь (8.10) для данных базисов:

Подставляя первое выражение во второе равенство, получаем . Сравнивая с третьим равенством, приходим к (8.12).

2. Если — матрица перехода от базиса к базису , то матрица обратима и обратная матрица является матрицей перехода от базиса к базису . Координаты вектора в базисах и связаны формулами:

В самом деле, пусть — матрица перехода от базиса к базису . Учитывая, что матрица перехода от базиса к базису — единичная, применяем свойство 1 к трем базисам . Для трех базисов аналогично получаем: . Следовательно, .

3. Всякая обратимая квадратная матрица n-го порядка может служить матрицей перехода от одного базиса n-мерного линейного пространства к другому базису.

Пример 8.4. В двумерном арифметическом пространстве даны два базиса: и . Найти матрицу перехода от базиса к базису и координаты вектора в каждом из базисов.

Решение. Рассмотрим стандартный базис пространства . Находим координаты векторов в стандартном базисе. Раскладываем вектор

В стандартном базисе пространства координатный столбец совпадает с вектором . Для других векторов аналогично получаем . Из координатных столбцов составим матрицы перехода (8.9) от стандартного базиса к данным базисам и

По свойству 1 матриц перехода имеем . .По свойству 2: . Поэтому

В стандартном базисе пространства координатный столбец совпадает с вектором . Найдем координаты этого вектора в базисе (по свойству 2 матрицы перехода):

В самом деле, справедливо разложение

Найдем координаты вектора в базисе двумя способами

Полученный результат подтверждает разложение:

Примечание. Действия с векторами, осуществленные в примере 2.10,
можно выполнить на персональном компьютере. Для нахождения скалярного
произведения векторов в MS Excel используют функцию СУММПРОИЗВ( ), где в качестве
аргументов указываются адреса диапазонов элементов матриц, сумму произведений
которых необходимо найти. В MathCAD
скалярное произведение двух векторов выполняется при помощи соответствующего
оператора панели инструментов Matrix 

Координаты векторов

        Определение
18.4   Пусть

 —

-мерное
линейное пространство, вещественное
или комплексное,

 —
базис. Тогда произвольный вектор

из

представим
в виде линейной комбинации векторов
базиса:

Числа

называются
координатами вектора

в
базисе

.
Столбец

из
координат вектора называется координатным
столбцом вектора

.
        

        Предложение
18.3   Координаты вектора
в заданном базисе определяются однозначно.

        Доказательство.    
Предположим противное. Пусть

 —
базис, в котором у вектора

есть
два различных набора координат:

Тогда

то есть

Так как наборы координат различны, то
хотя бы один из коэффициентов справа
отличен от нуля. Следовательно, векторы

 —
линейно зависимы, что противоречит
определению базиса. Полученное
противоречие означает, что предположение
о наличии двух различных наборов
координат неверно.     

        Предложение
18.4   Пусть в

-мерном
пространстве

задан
базис

.
Тогда координатный столбец суммы
векторов равен сумме координатных
столбцов слагаемых, координатный столбец
произведения вектора на число равен
координатному столбцу вектора, умноженному
на это число.

Доказательство.    
Пусть векторы

и

имеют
координатные столбцы

и

соответственно.
Отсюда следует, что

Поэтому

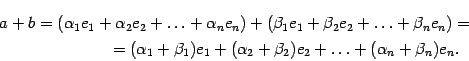
Это равенство означает, что координатный
столбец вектора

имеет
вид

.
Первая часть предложения доказана.
Доказательство второй части предоставляем
читателю.     

Из последнего
предложения следует, что как только в

-мерном
пространстве зафиксирован базис, каждый
вектор можно заменить его координатным
столбцом, и операциям сложения и умножения
на число соответствуют такие же операции
над их координатными столбцами. Таким
образом, каждое

-мерное
пространство является, с точки зрения
алгебры, копией пространства

в
вещественном случае, а в комплексном —
копией

.

Изменение
координат вектора при изменении базиса

Пусть в

-мерном
линейном пространстве

выбран
базис

,
который мы будем для удобства называть
«старый» и другой базис

,
который мы будем называть «новый».
Возьмем призвольный вектор

из

.
Его координатный столбец в старом базисе
обозначим

,
а в новом —

.
Нам нужно выяснить, как связаны друг с
другом координаты в старом и в новом
базисе. Для этого нам сначала нужно
«связать» друг с другом старый и
новый базисы. Запишем разложения новых
базисных векторов по старому базису

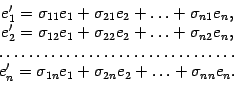
Составим матрицу, столбцами которой
служат координатные столбцы векторов
нового базиса

Эта матрица
называется матрицей перехода от
старого базиса к новому.

        Замечание
18.1   Матрица перехода
всегда невырождена, то есть

.
        

        Предложение
18.5   Координатные
столбцы в старом базисе и в новом базисе
связаны формулой

(18.1)

где справа стоит произведение матрицы
перехода

на
матрицу-столбец.

        Доказательство.    
Так как

 —
координатный столбец вектора

в
новом базисе, то

Заменив векторы

их
разложениями по старому базису, получим

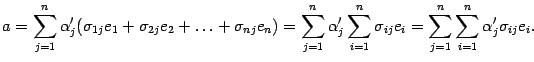
В силу предложения
14.3 изменим порядок суммирования

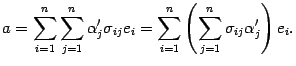
Здесь мы получили разложение вектора

по
старому базису, причем координата
вектора с номером

равна

.
Элемент с номером

столбца

будет
иметь такой же вид. Следовательно,
формула  (18.1)
доказана.     

        Пример 18.4
  Пусть

,
то есть

 —
трехмерное векторное пространство.
Пусть задан ортонормированный базис
i, j, k. Выберем другой (новый)
базис

Возьмем вектор

.
Найдем его координаты в новом базисе.

Выпишем матрицу
перехода, ее столбцы — это координаты
новых базисных векторов

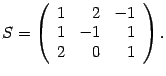
Пусть

 —
координатный столбец вектора

в
новом базисе. Тогда

(18.2)

откуда

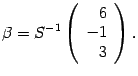
Найдем матрицу

по
формуле (14.14).
Находим определитель

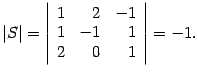
Находим алгебраические дополнения

Следовательно,

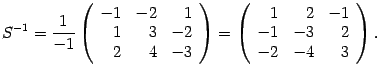
Находим координаты вектора

Таким образом, новые координаты вектора

:

,

,

,

.

Тот же самый
результат можно было получить, записав
формулу (18.2)
в виде системы уравнений

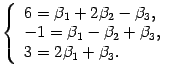
Решив эту систему, например, методом
Гаусса, найдем новые координаты

,

,

.
        

Вперед:
Матрица
линейного преобразования
Наверх:
Линейные
преобразования
Назад:
Линейные
преобразования
 

Определение и
примеры

Рассмотрим линейное
пространство

и
преобразование

этого
пространства, то есть закон, по которому
каждому вектору

из

соответствует
вектор

из
того же пространства. Вектор

называется
образом
вектора

и
обозначается

,
а вектор

называется
прообразом
вектора

.

        Определение
19.1  
Преобразование

линейного
пространства

называется
линейным,
если для любых векторов

и

и
любого числа

выполнены
равенства

(19.1)

то есть образ
суммы векторов равен сумме образов
слагаемых, образ вектора, умноженного
на число, равен произведению этого числа
на образ вектора.         

        Замечание
19.1   В этой
главе с каждым линейным преобразованием
будет связана матрица, которую мы будем
обозначать той же буквой, что и само
преобразование. Чтобы их различать, мы
для букв, обозначающих преобразование,
будем использовать так называемый
«каллиграфический» шрифт.         

Линейное
преобразование пространства

называют
также линейным
отображением
из

в

или
линейным
оператором
из

в

.

Исходя из
равенств (19.1)
легко проверить, что

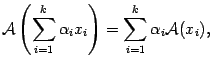
то есть образ
линейной комбинации векторов равен
линейной комбинации их образов.

Рассмотрим несколько
примеров линейных преобразований.

        Пример
19.1   Пусть

 —
двумерное векторное пространство, то
есть множество векторов плоскости.
Пусть

.
Это преобразование действует так: каждый
вектор оно переводит в вектор такого
же направления, но в два раза большей
длины. Если считать, что все векторы
имеют начало в начале координат, то
преобразование

можно
представить как растяжение плоскости
в два раза (рис. 19.1).

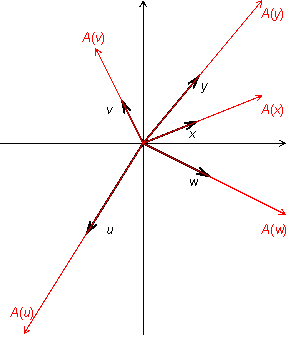
Рис.19.1.Преобразование растяжения

Проверим выполнение
равенств (19.1)

Равенства (19.1)
выполнены, следовательно, преобразование

является
линейным.         

        Пример
19.2   Пусть

 —
двумерное векторное пространство,

 —
поворот вектора по часовой стрелке на
угол

(рис.
19.2).

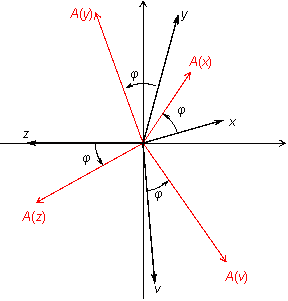
Рис.19.2.Преобразование поворота

Покажем, что это
— линейное преобразование.

Пусть

и

 —
два вектора. Тогда

 —
это диагональ параллелограмма со
стронами

,

(рис.
19.3).

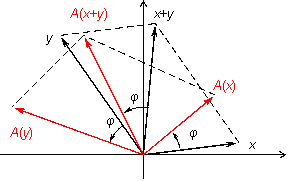
Рис.19.3.Образ суммы векторов

Если параллелограмм
повернуть как единое целое на угол

,
то его стороны станут векторами

и

,
диагональ будет вектором

.
С другой стороны, диагональ тоже
повернулась на угол

и
поэтому является вектором

.
Следовательно,

,
первое из условий (19.1)
выполнено.

Пусть

—
число. Из рисунка 19.4 очевидно, что

.

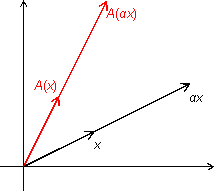
Рис.19.4.Образ вектора, умноженного на
число

Следовательно,
преобразование

 —
линейное.         

Упражнение19.1.1.
Пусть

 —
двумерное векторное пространство,

 —
некоторая прямая, проходящая через
начало координат,

 —
преобразование, переводящее каждый
вектор

в
вектор

симметричный
исходному относительно прямой

(рис.
19.5). Другими словами,

является
зеркальным отражением вектора

в
прямой

.

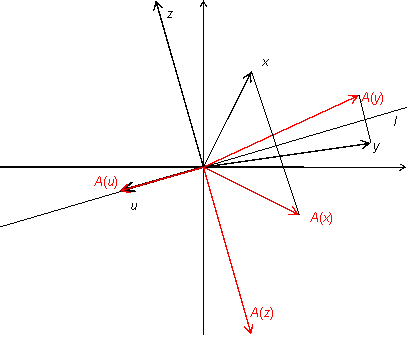
Рис.19.5.Преобразование отражения

Докажите, что

является
линейным преобразованием.

Упражнение19.1.2.
Пусть

 —
двумерное векторное пространство,

 —
некоторая прямая, проходящая через
начало координат,

 —
преобразование, переводящее каждый
вектор

в
его проекцию на прямую

(рис.
19.6).

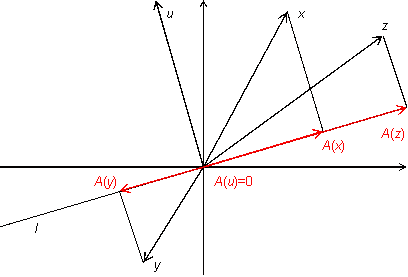
Рис.19.6.Преобразование проектирования

Докажите, что

является
линейным преобразованием.

        Пример
19.3   Пусть

 —
пространство всех многочленов,

 —
преобразование, которое переводит
вектор из

,
то есть многочлен, в производную этого
многочлена, которая естественно является
многочленом, то есть вектором из

.
Пусть

,
то есть

.
Тогда

Например, если

,
то

.
Покажем, что преобразование

является
линейным.

Пусть

,

 —
число. Тогда в силу свойства линейности
производной получим

Аналогично,

Следовательно,

 —
линейное преобразование.         

        Пример
19.4   Пусть

 —

-мерное
линейное пространство, Выберем в этом
пространстве базис

.
Тогда у любого вектора

есть
его координатный столбец

.
Пусть

 —
квадратная матрица порядка

.
Определим преобразование

следующим
образом:

является
вектором, координатный столбец которого
равен

(справа
стоит произведение матрицы

на
столбец

).
Покажем, что преобразование

 —
линейное.

Пусть

и

имеют
координатные столбцы

и

соответственно,
а их образы

и

 —
координатные столбцы

,
и

.
Тогда

Но выражение в
последнем равенстве справа является
координатным столбцом образа суммы
векторов

.
Следовательно,

.

Пусть

 —
произвольное число. Тогда координатный
столбец вектора

равен

,
координатный столбец образа вектора

то есть равен числу

,
умноженному на координатный столбец
образа вектора

.
Поэтому

.
Тем самым мы доказали, что преобразование

является
линейным.         

Очевидно, что
примерами линейных преобразований
могут служить тождественное
преобразование,
то есть преобразование, переводящее
каждый вектор в себя,

,
и нулевое
преобразование,
переводящее каждый вектор в нуль,

.

Легко проверяется,
что для любого линейного преобразования

образ
нуля равен нулю,

.
Действительно, в силу второго из
равенств (19.1)

Вперед:
Матрица
линейного преобразования
Наверх:
Линейные
преобразования
Назад:
Линейные
преобразования
 

Вперед: Координаты
векторов Наверх: Линейные
пространства Назад:
Определение
и примеры  

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Содержание:

1. n-мерный вектор и векторное пространство
2. Линейные (векторные) n — мерные пространства
3. Линейные операции над n — измеримыми векторами
4. Скалярное произведение двух векторов
5. Линейная зависимость и независимость векторов
6. Базис n -мерного пространства. Разложение вектора по базису
7. Переход к новому базису. Нахождение базисных решений системы линейных алгебраических уравнений
8. Однородная система уравнений. Особенности решения

n-мерный вектор и векторное пространство

Множество всех векторов, которые мы рассматривали на плоскости или в пространстве и для которых определены операции сложения векторов, умножение вектора на число являются простыми примерами векторного пространства.

Определение 1. Упорядоченное множество n действительных чисел, записанных в виде (a₁, a₂, a₃, …, a_n) называется n- мерным вектором. Числа a₁, a₂, a₃, …, a_n называются координатами вектора , то есть  =  (a₁, a₂, a₃, …, a_n).
Понятие n-мерного вектора широко используется в экономике, например, некоторый набор товаров можно охарактеризовать вектором  =  (a₁, a₂, a₃, …, a_n), а соответственно цены — вектором   = (b₁, b₂, b₃, …, b_n). 

Если у n-мерного вектора одна координата равна единице, а все остальные равны нулю, то такой вектор называется единичным. Очевидно, что существует n различных единичных векторов

исходящих из начала координат — точки О. Все определения и действия для двумерных и трехмерных векторов, заданных в координатной форме, распространяются и на n-мерные векторы (n ≥ 4).

Два  n-мерных вектора равны тогда и только тогда, когда их соответствующие компоненты равны.

Вектор  = (a₁, a₂, a₃, …, a_n)  и вектор   = (b₁, b₂, b₃, …, b_n) равны, когда a_i = b_i (i = 1, 2, 3, …, n).

Суммой двух n-мерных векторов   и   есть третий n-мерный вектор  ,  координаты которого равны сумме соответствующих одноименных координат векторов    и  , то есть с_i = a_i + b_i (i = 1, 2, 3, …, n).

Произведением вектора  на действительное число λ называется вектор , координаты которого d_i равны произведению числа λ на соответствующие координаты вектора  , то есть d_i = λa_i (i = 1, 2, 3, …, n).
Вектор, у которого все координаты равны нулю, называется нулевым вектором и обозначается

Операции над произвольными векторами удовлетворяют свойствам:
1.   — переместительный закон;
2.  — сочетательный закон;
3.  — сочетательный закон, относительно числового множителя;
4. — распределительный закон относительно суммы векторов;
5.  — распределительный закон относительно суммы числовых множителей.
6. Существует нулевой вектор , такой, что  для произвольного вектора  ;
7. Для произвольного вектора    существует противоположный вектор , такой, что

8.  , для любого вектора   (особая роль числового множителя 1).

Определение. Множество векторов с действительными координатами, в
котором определены операции сложения векторов и умножения вектора на число, удовлетворяющие выше приведенным восьми свойствам, называется векторным пространством.

Замечания. Если под векторами    и   можно рассматривать элементы произвольной природы, то соответствующее множество элементов называется линейным пространством.

Линейным пространством, например, множество всех алгебраических многочленов, степени которых не превышают натуральное число n. Если множество всех многочленов точно равно натуральному числу n, то не будет линейным пространством, потому что сумма двух многочленов может оказаться многочленом, степень которого меньше n.

Линейные (векторные) n — мерные пространства

Линейные -мерные пространства: основные определения:

В школьном курсе математики понятие вектора обозначалось как направленный отрезок. Положение (расположение) вектора на прямой плоскости  или в пространстве описывалось соответственно одним, двумя, тремя числами — координатами вектора. 

Математический подход к изучению различных явлений (процессов) окружающего мира, в том, числе и экономических, требует обобщения понятия вектора, связано с увеличением количества его координат. Такое обобщение не подразумевает геометрической интерnретации, но является удобным для математического моделирования.

Вектором размерности , или -мерных вектором , называется совокупность вещественных чисел  упорядоченных по номеру , а числа — его координатами. Обозначают п-мерные векторы маленькой буквой латинского алфавита с значком вектора — чертой — сверху, или выделяют ее жирным шрифтом, а координаты вектора записывают в круглых скобках в столбец или в строку:

Согласно определению -измеримый вектор можно рассматривать как матрицу-столбец размера , или как матрицу-строку размера  и, наоборот  названные матрицы — рассматривать как векторы. Итак, для -мерных векторов остаются в силе введенные для матриц определения и действия над матрицами.

Нулевым вектором , или ноль-вектором, называется -мерный вектор, все координаты которого равны нулю: 

Два вектора  и  одной размерности называются равными, если совпадают их координаты с одинаковыми индексами: 

Линейные операции над n — измеримыми векторами

1. Суммой -мерных векторов  и  называется вектор  той самой размерности, каждая координата которого определяется как сумма координат векторов-слагаемых, имеющих одинаковые индексы:

Следовательно: 

Следствие. Для любого вектора имеем: 

2. Произведением вектора со скаляром называется вектор , каждая координата которого является произведением координаты вектора с постоянной :

Следствие. Если  и скаляр  Для любого вектора  и скаляра  имеем: 

Векторы  и  называются противоположными друг другу, или взаимно противоположными, если иx соответствующие координаты отличаются множителем , то есть 

Суммой взаимно противоположных векторов есть нулевой вектор той же размерности.

Разность векторов  и  рассматривают как сумму вектора  и вектора , противоположного вектору 

Векторы  называются коллинеарными, если для любого  выполняется равенство . Согласно определению координаты коллинеарных векторов, имеют одинаковые индексы, пропорциональные: 

 где  или 

Если  то геометрически это означает, что векторы лежат на одной
прямой или на параллельных прямых.

В частном случае, когда , получаем равные векторы. Результатом выполнения линейных операций над -мерными векторами являются векторы той же размерности, что и выходные векторы. Как и действия над матрицами, линейные операции над векторами подчиняются ассоциативном (связующем), коммутативной (переставной) и дистрибутивному (распределительном) законам: 

где  -мерные векторы; — стали. 

Совокупность всех -мерных векторов с действительными координатами, для которых определены линейные операции (4.3) — (4.4), называется -мерных (линейными) векторным пространством и обозначается .

Скалярное произведение двух векторов

Аналогично тому, как рассматривался произведение матриц вводят понятие скалярного произведения векторов -мерного линейного пространства.  Напомним, что условием существования произведения матриц является равенство количества столбцов первой матрицы и количества строк дpyгoй матрицы. Это требование выполняется, если рассматривать произведение вектора строки на вектор-столбец , принадлежащих пространству одной размерности.

Скалярным произведением двух -мерных векторов называется число, равное сумме произведений иx одинаковых по номеру координат, и обозначается символом

Действие умножения для получения скалярного произведения обозначают точкой между векторами: 

Произведение называют скалярным квадратом вектора. 

На основе скалярного произведения приведем определение понятий, которые вводились для векторов размерностью , а именно длина вектора и угол между двумя векторами.

Длиной  или модулем, -мерного вектора называется арифметический квадратный корень из его скалярного квадрата: 

то есть 

Единичным -мерным вектором, или ортом, называется вектор , коллинеарной заданном вектора , длина которого равна единице: 

Возведение любого ненулевого вектора к единичному называется его нормированием.

Среди единичных векторов выделяют векторы, для которых одна из координат равна единице, а все остальные — нулю. Такие векторы обозначают маленькой буквой  с индексом, что указывает на номер координаты, равной единице. В пространстве существует различных -мерных единичных векторов:

В частности, в трехмерном пространстве эти векторы называются ортами координатных осей, они имеют собственные обозначения:

Кутом между двумя векторами и называется кут , который определяется соотношением: 

Согласно (4.9) скалярное произведение можно рассматривать как общую числовую характеристику двух векторов. 

Свойства скалярного произведения:

Линейное пространство, для которого определено скалярное произведение векторов со свойствами (4.10), называется евклидовым пространством.

В тeopии линейных пространств любое множество векторов одинаковой размерности называется системой векторов.

Пусть имеем систему, которая состоит из векторов, принадлежащих пространства . (Измеримость пространства обозначено через  в отличие от обозначения через количества векторов системы.) Систему векторов, имеющих размерность , можно рассматривать как матрицу размером , столбцами которой являются -мерные векторы, и наоборот:

С помощью этой системы векторов систему линейных алгебраических уравнений с неизвестными можно представить в вeктopний форме:

или кратко:

Действительно, если по правилам сложения векторов и умножения на скаляр умножить каждый вектор по координатам на а затем записать сумму результатов и приравнять координаты полученных векторов в левой и правой частях, то придем к системе линейных алгебраических уравнений ( 1.6). Решением такой системы будет -мерный вектор 

Замечания. На основе тeopии -мерных линейных пространств можно построить всю теорию матриц, в частности матричную алгебру, теорию систем линейных алгебраических уравнений и др. Поэтому линейной алгеброй, основы которой мы рассматриваем, называют раздел математики, объектом изучения которого являются линейные (векторные) пространства, а предметом — разработка соответствующих алгебраических методов для установления свойств пространств в целом и иx элементов в частности.

Линейная зависимость и независимость векторов

Пусть имеется система векторов , принадлежащие пространству  и действительные числа (скаляры) . Произвольное -мерный вектор , называют линейной комбинацией векторов системы, если его можно представить в виде суммы произведений чисел на вектор и :

Векторы называются линейно зависимыми, если хотя бы один из векторов системы является линейной комбинацией других. В противном случае, когда в системе векторов нет ни одного, который был бы линейной комбинацией других, векторы называются линейно независимыми.

Теорема 4.1 (про линейную зависимость системы векторов). Если среди чисел , где , не все равны нулю, и выполняется равенство

то система векторов  является линейно зависимой.

Доказательство. Пусть в равенстве (4.14) среди чисел существуют числа, отличающиеся от нуля. Выберем одно из них, неважно какое. Пусть этим числом будет . Умножим левую и правую части равенства (4.14) на 

Отсюда получаем: 

а согласно (4.13) это означает, что система векторов является линейно зависимой, поскольку вектор  является линейной комбинацией других векторов системы.

Последствие из теоремы 4.1 (о линейной независимости системы векторов).

Система векторов есть линейно независимой, если векторное равенство 

выполняется только в случае   (все числа равны нулю).

Доказательство. Предположим, что система векторов линейно независима, и при этом существуют , где . Тогда из теоремы 4.1 получим линейную зависимость системы векторов, которая противоречит условию.

Одной из основных задач теории линейных пространств является задача исследования системы векторов на линейную независимость, то есть выяснения вопрос о том, какова есть заданная система векторов — линейно зависимой или линейно независимой.

Решение этой задачи сводится к решению систем линейных уравнений.

Запишем равенство (4.14) в координатной форме:

выполним умножение векторов системы на скаляры найдем сумму полученных произведений и приравняем координаты векторов левой и правой частей равенства, что дает систему однородных линейных уравнений относительно постоянных :

По следствием из теоремы 4.1 система векторов линейно независимая, если система однородных уравнений (4.15) имеет только тривиальное решение: Если ранг основной матрицы системы равен числу неизвестных , то для этого необходимо и достаточно, чтобы ее определитель не равнялся нулю.

Проведем исследование на линейную независимость системы векторов:

Запишем векторное равенство:

Отсюда получаем систему уравнений:

Вычислим определитель основной матрицы системы:

Поскольку , однородная система линейных уравнений относительно коэффициентов имеет множество решений.

Преобразование основной матрицы системы по методу Жордана-Гаусса позволяет определить количество линейно независимых векторов в заданной системе векторов:

Ранг матрицы системы меньше количества векторов, поэтому система содержит только два линейно независимых вектора. По последнему преобразованию имеем:

Подставляя найденные коэффициенты в векторное равенство (4.14), получим

Таким образом, векторы и  является линейно зависимыми и любой из них можно представить в виде линейной комбинации двух других. Например, разделив последнее равенство на , определим вектор ; как линейную комбинацию векторов и :

В линейной алгебре широко применяется система п единичных векторов пространства , из которых согласно (4.11) можно образовать единичную матрицу -го порядка. Поскольку для любого определитель такой матрицы не равен нулю, то для пространства любой размерности система таких единичных векторов линейно независимой.

Рассмотрим питания о наибольшее количество векторов, которое может содержать линейно независимая система -мерных векторов.

Выберем из пространства произвольным образом систему векторов:

запишем векторное равенство

и соответствующую ей однородную линейную систему уравнений с неизвестными

Для ответа на поставленный вопрос будем исходить из сравнения количества векторов системы  с размерностью пространства , учитывая иx соотношение с рангом матрицы.

1. Если количество векторов больше измеримости пространства , то ранг основной матрицы однородной системы уравнений не будет превышать количество строк, а значит и количество неизвестных . В этом случае система имеет множество решений, среди которых есть и нетривиальные, то есть среди чисел существуют отличающиеся от нуля. Итак, по теореме 4.1 такая система векторов линейно зависима.

2. Если количество векторов равно размерности пространства , то такой системе уравнений соответствует квадратная основная матрица -го порядка. Система векторов будет линейно независимой, если определитель системы уравнений отличается от нуля .

Из проведенного анализа следует, что наибольшее количество линейно независимых векторов равно размерности линейного пространства.

Базис n -мерного пространства. Разложение вектора по базису

Понятие базис (от греч. basis — основа) является одним из фундаментальных понятий теории векторных пространств. Любая система линейно независимых -мерных векторов называется базисом линейного пространства . Определитель, состоящий из координат векторов базиса отличается от нуля, так как совокупность векторов содержит линейно независимых векторов и любой другой вектор является линейной комбинацией базисных векторов.

Теорема 4.2 (о разложении -мерного вектора по базису).

Произвольный вектор  с  можно представить в виде линейной комбинации векторов базиса и к тому же единственным способом.

Доказательство. Согласно определению линейной комбинации системы векторов (4.13) надо показать существование единого набора цифр , таких, что сумма произведений этих цифр с векторами базиса дает вектор :

Представим векторы  и вектор  через их координаты:

и запишем соответствующую систему линейных уравнений:

Поскольку определитель основной матрицы системы отличается от нуля (по условию векторы образуют базис пространства), то система уравнений совместима и имеет единственное решение, которым является набор чисел

Представление вектора в виде линейной комбинации векторов базиса (4 16) называется разложением вектора по базису, а числа коэффициентами разложения, или координатами вектора по этому базису.

Система -мерных единичных векторов называется единичным базисом . Единичный базис является частным случаем так называемых ортогональных базисов, то есть таких базисов, что скалярное произведение любых двух векторов с базиса равно нулю: Ортогональный базис из нормированных векторов называется ортонормированным.

Запись -мерного вектора в виде , то есть представление его в координатные форме, можно рассматривать как разложение вектора за ортонормированным базисом.

Определение базиса пространства и разложения вектора по базису можно выполнять одновременно, аналогично тому, как выбор базисных неизвестных и нахождения решений СЛАУ осуществляли при применении методов Гаусса и Жордана-Гаусса.

Осуществить разложение вектора  по векторам 

 если они образуют базис.

Для решения задачи представим вектор как линейную комбинацию векторов  и :

где  неизвестные коэффициенты разложения, или координаты вектора при условии, что вектор и образуют базис.

Представим векторы  и вектор через координаты и получим систему уравнений относительно координат вектора :

Проверку на линейную независимость векторов  и отыскания координат вектора по базису можно проводить одновременно.
Для этого запишем расширенную матрицу системы и проведем ее преобразования по методу Жордана-Гаусса:

Поскольку элементарными преобразования на месте основной матрицы системы получено единичную матрицу третьего порядка, то определитель исходной матрицы отличен от нуля, и система векторов   является линейно независимой, то есть она образует базис пространства . Вектор  можно разложить по этому базису единственным способом:

Следовательно, координатами вектора в базисе будут 

В другом базисе вектор будет иметь другие координаты. В ортонормированном базисе он выглядит так: то есть

Любой вектор с , заданный в координатной форме, можно рассматривать как его разложение по ортонормированному базису.

Переход к новому базису. Нахождение базисных решений системы линейных алгебраических уравнений

Представим произвольный вектор с  в виде линейной комбинации векторов базиса 

где  координаты вектора  в данном базисе.

Выясним, как можно осуществить переход от одного базиса линейного пространства к другому и найти координаты вектора в новом базисе за известными координатами вектора в начальном ортонормированном базисе.

Пусть в пространстве  есть два базиса: начальный и новый Каждый из векторов нового базиса можно представить в линейную комбинацию векторов начального базиса:

Запишем систему (4.17) в матричном виде:  где 

Неособенная матрица называется матрицей пepexoда от начального базиса к новому . Переход от нового базиса к первоначальному осуществляется по формуле: 

Можно показать, что зависимость между координатами вектора в разных базисах определяется формулами: 

где  вектор  с координатами в новом базисе 

Переход к новому базису широко используется в задачах линейного программирования и в других задачах математических методов в экономике.

Задан вектор в ортонормированном базисе векторов   и  Найдем координаты вектора в базисе из векторов   и  с помощью матрицы перехода. 

В предыдущем примере было показано, что векторы  образуют базис. Опишем связь между базисами с помощью системы векторных уравнений: 

Матрица перехода от базиса  и  к базису  и  является основной матрицей системы векторных уравнений:

Транспонируем матрицу :

Для нее существует обратная матрица, поскольку  Находим ее:

По соотношению (4.18) определяем координаты вектора в базисе векторов   и 

Рассмотрим разложение вектора по новому базису для нахождения базисных решений СЛАУ.

Запишем систему линейных алгебраических уравнений в векторной форме 

где коэффициентами при неизвестных системы являются векторы   которые образуют основную матрицу системы,  вектор-столбец свободных членов, — неизвестные системы, или коэффициенты разложения вектора по векторам .

Система линейных уравнений называется сводной к единичному базису, если среди векторов есть единичный базис. Система имеет единственное решение только в случае, если количество неизвестных системы совпадает с размерностью векторов и все векторы системы образуют базис 

В общем случае, если количество векторов, образующих базис, меньше количества векторов системы , то система линейных уравнений имеет множество решений, среди которых необходимо найти все базисные.

Таким образом, для нахождения всех базисных решений системы можно предложить такой алгоритм:
1) сводим систему линейных уравнений элементарными преобразованиями к единичному базису;
2) находим значения неизвестных, что соответствуют данном базису, то есть координаты вектора в этом базисе (свободные неизвестные возлагаем равными нулю)
3) выполняем преобразование системы уравнений с целью введения в базис других векторов системы. Тогда координаты вектора равны соответствующим неизвестным системы линейных уравнений в новом базисном решении и т. д.

Заметим, что максимальное количество базисных решений равно количеству сопряжений с векторов системы по , где — размерность пространства.

Найдем все базисные решения системы линейных уравнений

В векторной форме система уравнений имеет вид

где 

Среди заданных векторов  определим все возможные базисы и осуществим расписание вектора по каждому из этих базисов.

Есть четыре вектора двумерного пространства, среди которых необходимо определить базисные. Поскольку наибольшее количество линейно независимых векторов в этом пространстве равно двум, то все четыре вектора не могут быть линейно независимыми. Сводим систему линейных уравнений к единичному базису. Запишем матрицу коэффициентов системы в таблице 4.1 и выполним элементарные преобразования этой системы по методу Жордана-Гаусса.

Сведение системы уравнений к единичному базису                                       Таблица 4.1

По результатам последней операции получено единичную матрицу.

Следовательно, векторы и образуют единичный базис пространства. Координаты вектора в этом базисе  Для нахождения базисного решению системы положим тогда базисным решением системы будет По базису из векторов и можно разложить не только вектор , но и все другие векторы:

Количество базисов для данного примера определяется количеством соединений из четырех векторов по два , то есть равна шести. Преобразование системы по методу Жордана-Гаусса для нахождения других базисных решений приведены в таблице 4.2.

В таблице 4.2 первым из базисных решений системы приведено именно то, которое получили в таблице 4.1.

Нахождение базисных решений                                                                                  Таблица 4.2

Заметим, что среди шестерых базисных решений данной системы линейных уравнений только и имеют среди своих координат отрицательные, то есть эти решения не являются опорными.

В рамках учебной дисциплины Оптимизационные модели и методы изучается специальный алгоритм отбора только опорных решений системы, по которому в базис не вводятся векторы, которые в новом базисе превращают вектор на вектор, имеет отрицательное координаты.

Однородная система уравнений. Особенности решения

Рассмотрим векторный подход к нахождению общего решения систем линейных уравнений (1.9):

где основная матрица системы;

 матрица-столбец неизвестных;

 нулевая матрица-столбец.

В векторной форме система однородных линейных уравнений имеет вид:

где основная матрица системы;

 -измеримые векторы (столбцы матрицы 

вектор неизвестных;

 нулевой вектор.

Если ранг основной матрицы меньше количества неизвестных то однородная система уравнений имеет множество решений.

Пусть коэффициенты при неизвестных составляют базисный минор, другие неизвестные свободны. Если систему (4.20) решить относительно базисных неизвестных, то общее решение (по аналогии с (3.7)) будет иметь вид:

где линейные функции, отражающие законы зависимости базисных неизвестных от свободных неизвестных

По свойству 3 (п. 3.2) любая линейная комбинация решений однородной системы также является решением этой системы.

Фундаментальной системой решений однородной системы уравнений называется такая линейно независимая система векторов ранг основной матрицы системы), их линейные комбинации определяют все бесконечное множество решений системы.

Теорема 4.3 (пpo фундаментальную систему решений). Однородная система уравнений (4.20) имеет фундаментальную систему решений, количество векторов которой равно , где — ранг системы уравнений

Доказательство. Предоставим свободным неизвестным последовательно  значений, которые являются элементами столбцов единичной матрицы:

(Конечно, при получаем тривиальное решение.)

Выражения базисных неизвестных через свободные получим при равенстве (4.21), при этом получим частных решений системы: Эти решения линейно независимы, ведь матрица, составленная из координат всех векторов, включая единичную матриuю (4.22) порядка

Вектор 

где  как линейная комбинация решений системы (4.22) тоже будет и решением. 

Если числа , брать равными координатам векторов , которые соответствуют свободным неизвестным системы уравнений, то этот вектор опишет (отобразит) общее решение системы. 

Следовательно, для нахождения общего решения однородной системы уравнений выполняем следующее:

1. Выражает базисные неизвестные системы (4.20) через свободные.
2. Предоставляем значение свободным неизвестным системы согласно (4.21).
3. Подставляемые в (4.21) последовательно значение свободных неизвестных (4.22), находим базисные неизвестные, получая таким образом фундаментальную систему решений:
4. Записываем общее решение системы как линейную комбинацию фундаментальных решений (4.23).

Найдем фундаментальную систему решений однородной системы уравнений:

Чтобы выразить базисные неизвестные системы через свободные неизвестные, воспользуемся методом Жордана-Гаусса. Выполняем элементарные преобразования основной матрицы системы для получения в ней единичной матрицы:

Выбираем за базисные неизвестные , тогда  и  есть свободными. Общее решение системы (4.24) получим в виде:

Если свободным неизвестным последовательно предоставить значения а затем получим соответствующие частные решения системы и . Система векторов и   является фундаментальной системой решений.

Общее решение системы уравнений в векторной форме находим как линейную комбинацию фундаментальных решений, а именно:

где 

Тогда общее решение однородной системы уравнений, составленный из фундаментальных решений системы, имеет вид: 

Замечания. Аналогично можно представить общее решение и неоднородной системы уравнений, которая имеет множество решений.

Пусть система неоднородных уравнений 

совместима, но ранг матрицы системы меньше количества неизвестных . Тогда ее общее решение определяется формулой 

где  произвольное частичное решение неоднородной системы (4.25), а 

— общее решение (4.22) соответствующей однородной системы уравнений (4.20).

Найдем общее решение неоднородной системы уравнений:

Если праве части всех уравнений положить равными нулю, то получим однородной систему уравнений (4.24), общее решение которой определен в предыдущем примере:

где 

Найдем произвольный частное решение неоднородной системы. Например, возьмем свободные неизвестные равными нулю: , и найдем и , тогда . Таким образом, общим решением системы (4.27) является вектор:

где 

или 

Такое представление общего решения неоднородной системы линейных алгебраических уравнений обобщается на произвольные неоднородные системы, которые имеют множество решений.