I. Основные формулы:
1. Расстояние между точками А (,
), В
,
) равно
=
.
2. Угол между плоскостями. Если β – угол между плоскостями, заданными уравнениями х+
z+
=0 и
х+
z+
=0, то
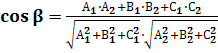
3. Расстояние от точки до плоскости. Если ρ – расстояние от точки (
,
), до плоскости
х+
z+D =0, то
ρ=.
4. Уравнение плоскости, проходящей через три заданные точки (
,
),
(
,
),
(
,
), в координатной форме:
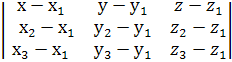
5. Если отрезок, концами которого служат точки А (,
), В
,
) разделен точкой С (х, у,
) в отношении λ, то координаты точки С определяются по формулам
Х = ; у=
; z=
.
II. Координаты вершин многогранников.
Определите координаты вершин многогранников:
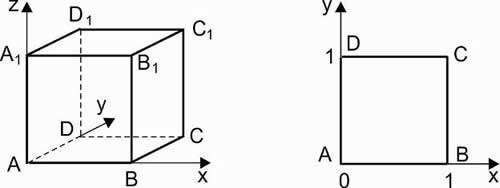
1. Единичный куб A…D1
Решение: координаты вершин А (0, 0, 0), А1 (0, 0, 1), В (1, 0, 0), В1 (1, 0, 1), D (0, 1, 0), D1 (0, 1, 1), С (1, 1, 0), С1 (1, 1, 1).
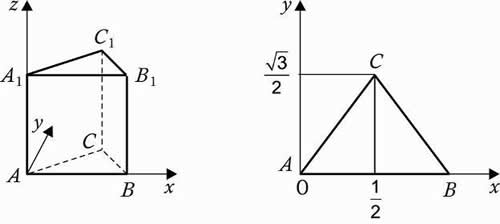
2. Правильная треугольная призма A…C1 , все ребра, которой равны 1.
Решение: координаты вершин: А (0, 0, 0), А1 (0, 0, 1), В (1, 0, 0), В1 (1, 0, 1), С (0,5; , 0), С1 (0,5;
, 1).
3. Правильная шестиугольная призма A…F1, все ребра которой равны 1.
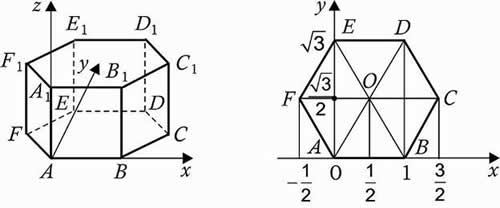
Решение: координаты вершин: А (0, 0, 0), А1 (0, 0, 1), В (1, 0, 0), В1 (1, 0, 1), С (1,5; , 0), С1 (1,5;
, 1), D (1,
(1,
Е (0,
,
(0,
,
F(-0,5 , 0),
(-0,5,
1).
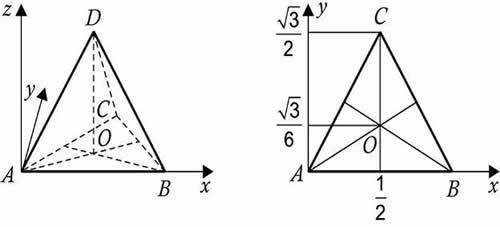
4. Правильная треугольная пирамида (тетраэдр) ABCD все ребра которой равны 1.
Решение: координаты вершин: А (0, 0, 0), В (1, 0, 0), С (0,5; , 0), D (0,5,
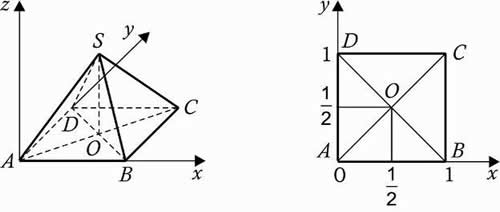
5. Правильная четырехугольная пирамида SABCD, все ребра которой равны 1.
Решение: координаты вершин: А (0, 0, 0), В (1, 0, 0), С (1, 1, 0), D (0, 1, 0 S (0,5; 0,5;
).
6. Правильная шестиугольная пирамида SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2.
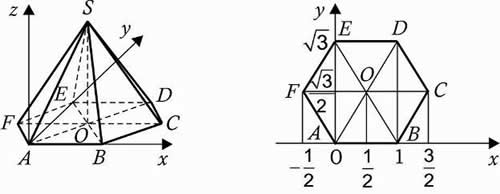
III. Решение задач.
Решение: координаты вершин: А (0, 0, 0), В (1, 0, 0), С (1,5; , 0), D (1,
Е (0,
, F (-05,
0), S (0,5;
).
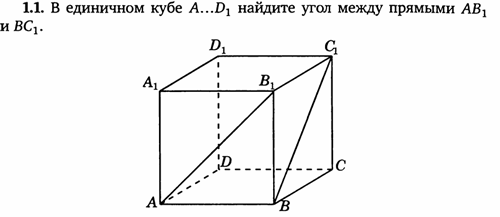
Решение:
- А (0, 0, 0), А1 (0, 0, 1), В (1, 0, 0), В1 (1, 0, 1), D (0, 1, 0), D1 (0, 1, 1), С (1, 1, 0), С1 (1, 1, 1).
- Найдем координаты векторов
(1, 0, 1) и
= (0, 1, 1)
- Найдем косинус угла между векторами
=
=
; α=60.
Ответ: 60.
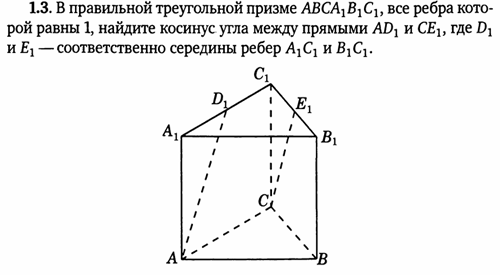
Решение:
- координаты вершин А (0, 0, 0), D1 (
,
, 1), С (0,5;
, 0), Е1 (
;
, 1).
- Найдем координаты векторов:
и
(
,
, 1)
- Найдем косинус угла между векторами
=
=0,7;
Ответ: 0,7.
Полностью текст работы приведен в Приложении.
Загрузить PDF
Загрузить PDF
В математике существует ряд задач, в которых требуется найти вершину. Например, вершину многогранника, вершину или несколько вершин области системы неравенств, вершину параболы или квадратного уравнения. Эта статья расскажет вам, как найти вершину в разных задачах.
-
1
Теорема Эйлера. Теорема утверждает, что в любом многограннике число его вершин плюс число его граней минус число его ребер всегда равно двум.[1]
- Формула, описывающая теорему Эйлера: F + V — E = 2
- F — число граней.
- V — число вершин.
- E — число ребер.
- Формула, описывающая теорему Эйлера: F + V — E = 2
-
2
Перепишите формулу, чтобы найти число вершин. Если вам дано число граней и число ребер многогранника, вы можете быстро найти число его вершин с помощью формулы Эйлера.
- V = 2 — F + E
-
3
Подставьте данные вам значения в эту формулу. В результате вы получите число вершин многогранника.
- Пример: найдите число вершин многогранника, у которого 6 граней и 12 ребер.
- V = 2 — F + E
- V = 2 — 6 + 12
- V = -4 + 12
- V = 8
Реклама
- Пример: найдите число вершин многогранника, у которого 6 граней и 12 ребер.
-
1
Постройте график решения (области) системы линейных неравенств. В определенных случаях на графике можно увидеть некоторые или все вершины области системы линейных неравенств. В противном случае вам придется найти вершину алгебраически.
- При использовании графического калькулятора вы можете посмотреть весь график и найти координаты вершин.
-
2
Преобразуйте неравенства в уравнения. Для того, чтобы решить систему неравенств (то есть найти «х» и «у»), вам необходимо вместо знаков неравенства поставить знак «равно».
- Пример: дана система неравенств:
- у < х
- у> — х + 4
- Преобразуйте неравенства в уравнения:
- у = х
- у = — х + 4
- Пример: дана система неравенств:
-
3
Теперь выразите любую переменную в одном уравнении и подставьте ее в другое уравнение. В нашем примере подставьте значение «у» из первого уравнения во второе уравнение.
- Пример:
- у = х
- у = — х + 4
- Подставляем у = х в у = — х + 4:
- х = — х + 4
- Пример:
-
4
Найдите одну из переменных. Сейчас у вас есть уравнение только с одной переменной «х», которую легко найти.
- Пример: х = — х + 4
- х + х = 4
- 2x = 4
- 2x/2 = 4/2
- х = 2
- Пример: х = — х + 4
-
5
Найдите другую переменную. Подставьте найденное значение «х» в любое из уравнений и найдите значение «у».
- Пример: у = х
- у = 2
- Пример: у = х
-
6
Найдите вершину. Вершина имеет координаты, равные найденным значениям «х» и «у».
- Пример: вершина области данной системы неравенств есть точка О(2,2).
Реклама
-
1
Разложите уравнение на множители. Есть несколько способов разложения квадратного уравнения на множители. В результате разложения вы получаете два двучлена, которые при перемножении приведут к исходному уравнению.
- Пример: дано квадратное уравнение
- 3×2 — 6x — 45
- Сначала вынесите за скобку общий множитель: 3(x2 — 2x — 15)
- Перемножьте коэффициенты «а» и «с»: 1 * (-15) = -15.
- Найдите два числа, результат умножения которых равен -15, а их сумма равна коэффициенту «b» (b = -2): 3 * (-5) = -15; 3 — 5 = -2.
- Подставьте найденные значения в уравнение ax2 + kx + hx + c: 3(x2 + 3x — 5x — 15).
- Разложите исходное уравнение: f(x) = 3 * (x + 3) * (x — 5)
- Пример: дано квадратное уравнение
-
2
Найдите точку (точки), в которой график функции (в данном случае парабола) пересекает ось абсцисс.[3]
График пересекает ось Х при f(x) = 0.- Пример: 3 * (x + 3) * (x — 5) = 0
- х +3 = 0
- х — 5 = 0
- х = -3; х = 5
- Таким образом, корни уравнения (или точки пересечения с осью Х): А(-3, 0 ) и В(5, 0)
- Пример: 3 * (x + 3) * (x — 5) = 0
-
3
Найдите ось симметрии. Ось симметрии функции проходит через точку, лежащую посередине между двумя корнями. При этом вершина лежит на оси симметрии.
- Пример: х = 1; это значение лежит посередине между -3 и +5.
-
4
Подставьте значение «х» в исходное уравнение и найдите значение «у». Эти значения «х» и «у» — координаты вершины параболы.
- Пример: у = 3×2 — 6x — 45 = 3(1)2 — 6(1) — 45 = -48
-
5
Запишите ответ.
- Пример: вершина данного квадратного уравнения есть точка О(1,-48)
Реклама
-
1
Перепишите исходное уравнение в виде[4]
: y = a(x — h)^2 + k, при этом вершина лежит в точке с координатами (h,k). Для этого нужно дополнить исходное квадратное уравнение до полного квадрата.- Пример: дана квадратичная функция у = — х^2 — 8x — 15.
-
2
Рассмотрите первые два члена. Вынесите за скобку коэффициент первого члена (при этом свободный член игнорируется).
- Пример: -1(х^2 + 8x) — 15.
-
3
Разложите свободный член (-15) на два числа так, чтобы одно из них дополнило выражение в скобках до полного квадрата. Одно из чисел должно быть равно квадрату половины коэффициента второго члена (из выражения в скобках).
- Пример: 8/2 = 4; 4*4 = 16; поэтому
- -1(х^2 + 8x + 16)
- -15 = -16 + 1
- у = -1 (х ^ 2 + 8x + 16) + 1
- Пример: 8/2 = 4; 4*4 = 16; поэтому
-
4
Упростите уравнение. Так как выражение в скобках есть полный квадрат, можно переписать это уравнение в следующем виде (если необходимо, проведите операции сложения или вычитания за скобками):
- Пример: у = -1(х + 4)^2 + 1
-
5
Найдите координаты вершины. Напомним, что координаты вершины функции вида y = a(x — h)^2 + k равны (h,k).
- k = 1
- h = -4
- Таким образом, вершина исходной функции есть точка О(-4,1).
Реклама
-
1
Найдите координату «х» по формуле: x = -b/2a (для функции вида y = ax^2 + bx + c). Подставьте значения «a» и «b» в формулу и найдите координату «х».
- Пример: дана квадратичная функция у = — х^2 — 8x — 15.
- х = -b/2a = -(-8)/(2*(-1)) = 8/(-2) = -4
- х = -4
-
2
Подставьте найденное значение «х» в исходное уравнение. Таким образом вы найдете «у». Эти значения «х» и «у» — координаты вершины параболы.
- Пример: у = — х^2 — 8x — 15 = -(-4 )^2 — 8(-4) — 15 = -(16) -(-32) — 15 = -16 + 32 — 15 = 1
- у = 1
- Пример: у = — х^2 — 8x — 15 = -(-4 )^2 — 8(-4) — 15 = -(16) -(-32) — 15 = -16 + 32 — 15 = 1
-
3
Запишите ответ.
- Пример: вершина исходной функции есть точка О(-4,1).
Реклама
Что вам понадобится
- Калькулятор
- Карандаш
- Бумага
Об этой статье
Эту страницу просматривали 11 682 раза.
Была ли эта статья полезной?


СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой

Была в сети 26.05.2023 23:49

Медведева Ирина Викторовна
учитель математики
50 лет
4 319
8 187
Местоположение
Россия, Калининградская область
Координаты вершин многогранников
13.10.2017 01:02
Сопровождение к уроку геометрии в 11 классе по теме «Координаты вершин многогранников». Рекомендуется использовать при изученни координатного метода решения задач и при поготовке к ЕГЭ
Просмотр содержимого документа
«Координаты вершин многогранников»
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы
Download Article
Download Article
There are multiple mathematical functions that use vertices. Polyhedrons have vertices, systems of inequalities can have one vertex or multiple vertices, and parabolas or quadratic equations can have a vertex, as well. Finding the vertex[1]
varies depending on the situation, but here’s what you need to know about finding vertices for each scenario.
-
1
Learn Euler’s Formula. Euler’s Formula, as it is used in reference to geometry and graphs, states that for any polyhedron that does not intersect itself, the number of faces plus the number of vertices, minus the number of edges, will always equal two.[2]
- Written out as an equation, the formula looks like: F + V — E = 2
- F refers to the number of faces
- V refers to the number of vertices, or corner points
- E refers to the number of edges
- Written out as an equation, the formula looks like: F + V — E = 2
-
2
Rearrange the formula to find the number of vertices. If you know how many faces and edges the polyhedron has, you can quickly count the number of vertices by using Euler’s Formula. Subtract F from both sides of the equation and add E to both sides, isolating V on one side.[3]
- V = 2 — F + E
Advertisement
-
3
Plug the numbers in and solve. All you need to do at this point is to plug the number of sides and edges into the equation before adding and subtracting like normal. The answer you get should tell you the number of vertices and complete the problem.[4]
- Example: For a polyhedron that has 6 faces and 12 edges…
- V = 2 — F + E
- V = 2 — 6 + 12
- V = -4 + 12
- V = 8
- Example: For a polyhedron that has 6 faces and 12 edges…
Advertisement
-
1
Graph the solutions of the system of linear inequalities. In some instances, graphing the solutions for all inequalities in the system can visually show you where some, if not all, of the vertices lie. When it does not, however, you will need to find the vertex algebraically.[5]
- If using a graphing calculator to graph the inequalities, you can usually scroll over to the vertices and find the coordinates that way.
-
2
Change the inequalities to equations. In order to solve for the system of inequalities, you will need to temporarily change the inequalities to equations, allowing you the ability to find values for x and y.[6]
- Example: For the system of inequalities:
- y < x
- y > -x + 4
- Change the inequalities to:
- y = x
- y = -x + 4
- Example: For the system of inequalities:
-
3
Substitute one variable for the other. While there are a couple of different ways you can solve for x and y, substitution is often the easiest to use. Plug the value of y from one equation into the other equation, effectively «substituting» y in the other equation with additional x values.
- Example: If:
- y = x
- y = -x + 4
- Then y = -x + 4 can be written as:
- x = -x + 4
- Example: If:
-
4
Solve for the first variable. Now that you only have one variable in the equation, you can easily solve for that variable, x, as you would in any other equation: by adding, subtracting, dividing, and multiplying.
- Example: x = -x + 4
- x + x = -x + x + 4
- 2x = 4
- 2x / 2 = 4 / 2
- x = 2
- Example: x = -x + 4
-
5
Solve for the remaining variable. Plug your new value for x into one of the original equations to find the value of y.
- Example: y = x
- y = 2
- Example: y = x
-
6
Determine the vertex. The vertex is simply the coordinate consisting of your new x and y values.[7]
- Example: (2, 2)
Advertisement
-
1
Factor the equation. Rewrite the quadratic equation in its factored form. There are several ways to factor out a quadratic equation, but when done, you should be left with two sets of parentheses that, when multiplied together, equal your original equation.
- Example: (using decomposition)
- 3×2 — 6x — 45
- Factor out the common factor: 3 (x2 — 2x — 15)
- Multiply the a and c terms: 1 * -15 = -15
- Find two numbers with a product that equals -15 and a sum that equals the b value, -2: 3 * -5 = -15; 3 — 5 = -2
- Substitute the two values into the equation ax2 + kx + hx + c: 3(x2 + 3x — 5x — 15)
- Factor the polynomial by grouping: f(x) = 3 * (x + 3) * (x — 5)
- Example: (using decomposition)
-
2
Find the point at which the equation crosses the x-axis.[8]
Whenever the function of x, f(x), equals 0, the parabola will cross the x-axis. This will occur when either set of factors equals 0.- Example: 3 * (x + 3) * (x — 5) = 0
- х +3 = 0
- х — 5 = 0
- х = -3 ; х = 5
- Therefore, the roots are: (-3, 0) and (5, 0)
- Example: 3 * (x + 3) * (x — 5) = 0
-
3
Calculate the midway point. The axis of symmetry for the equation[9]
will lie directly in between the two roots of the equation. You need to know the axis of symmetry since the vertex lies on it.- Example: x = 1; this value lies directly between -3 and 5
-
4
Plug the x value into the original equation. Plug the x value for your axis of symmetry into either equation for your parabola. The y value will be the y value for your vertex.[10]
- Example: y = 3×2 — 6x — 45 = 3(1)2 — 6(1) — 45 = -48
-
5
Write down the vertex point. At this point, your last calculated x and y values should give you the coordinates of your vertex.
- Example: (1, -48)
Advertisement
-
1
Rewrite the original equation in its vertex form. The «vertex» form of an equation is written as y = a(x — h)^2 + k, and the vertex point will be (h, k). Your current quadratic equation will need to be rewritten into this form, and in order to do that, you’ll need to complete the square.[11]
- Example: y = -x^2 — 8x — 15
-
2
Isolate the a value. Factor out the coefficient of the first term, a from the first two terms in the equation. Leave the final term, c, alone for now.[12]
- Example: -1 (x^2 + 8x) — 15
-
3
Find a third term for the parentheses. The third term must complete the set in the parentheses so that the values in parentheses form a perfect square. This new term is the squared value of half the coefficient of the middle term.
- Example: 8 / 2 = 4; 4 * 4 = 16; therefore,
- -1(x^2 + 8x + 16)
- Also keep in mind that what you do to the inside must also be done to the outside:
- y = -1(x^2 + 8x + 16) — 15 + 16
- Example: 8 / 2 = 4; 4 * 4 = 16; therefore,
-
4
Simplify the equation. Since your parentheses now form a perfect square, you can simplify the parenthetical portion to its factored form. Simultaneously, you can do any addition or subtraction needed to the values outside of the parentheses.[13]
- Example: y = -1(x + 4)^2 + 1
-
5
Figure out what the coordinates are based on the vertex equation. Recall that the vertex form of an equation is y = a(x — h)^2 + k, with (h, k) representing the coordinates of the vertex. You now have enough information to plug values into the h and k slots and complete the problem.
- k = 1
- h = -4
- Therefore, the vertex of this equation can be found at: (-4, 1)
Advertisement
-
1
Find the x coordinate of the vertex directly. When the equation of your parabola can be written as y = ax^2 + bx + c, the x of the vertex can be found using the formula x = -b / 2a. Simply plug the a and b values from your equation into this formula to find x.
- Example: y = -x^2 — 8x — 15
- x = -b / 2a = -(-8)/(2*(-1)) = 8/(-2) = -4
- x = -4
-
2
Plug this value into the original equation. By plugging a value for x into the equation, you can solve for y. This y value will be the y coordinate of your vertex.
- Example: y = -x^2 — 8x — 15 = -(-4)^2 — 8(-4) — 15 = -(16) — (-32) — 15 = -16 + 32 — 15 = 1
- y = 1
- Example: y = -x^2 — 8x — 15 = -(-4)^2 — 8(-4) — 15 = -(16) — (-32) — 15 = -16 + 32 — 15 = 1
-
3
Write down your vertex coordinates. The x and y values you have are the coordinates of your vertex point.
- Example: (-4, 1)
Advertisement
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Things You’ll Need
- Calculator
- Pencil
- Paper
References
About This Article
Article SummaryX
To find the vertex of a parabola with axis of symmetry, factor the quadratic equation and find the point at which the equation crosses the x-axis. Next, calculate the midway point, which will lie directly in between the two roots of the equation. Then, plug the x value into either equation for your parabola. Your calculated x and y values are the coordinates of the vertex. For tips on finding a vertex in other mathematical scenarios, read on!
Did this summary help you?
Thanks to all authors for creating a page that has been read 62,655 times.
Reader Success Stories
-
«So helpful.»
Did this article help you?
1.
11 класс
Метод координат в пространстве
ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ
В ПРОСТРАНСТВЕ
Найдите координаты всех вершин многогранника.
1. Дано: ABCDA1B1C1D1 – куб,
A (10; 0; 0).
2. Дано: ABCDA1B1C1D1 –
BD1 DB1 = M, M (1; 1; 1).
3. Дано: ABCDA1B1C1D1 – куб,
D (2; 2; 0).
4. Дано: ABCDA1B1C1D1 – куб,
AO = OB, C (–2; 4; 0).
5. Дано: ABCDA1B1C1D1 –
6. Дано: ABCD – квадрат,
прямоугольный параллелепипед,
FM = MC, M (0; 1; 2).
ABCD – квадрат, DC1 D1C = M, M
(0; 2; 3).
куб,
2.
7. Дано: ABCDA1B1C1D1 –
прямоугольный параллелепипед,
AB = 3, BC = 4, AA1 = 1.
8. Дано: AB = BC = AC =
9. Дано: (ABC) (ABD),
AB = BC = AC = BD = AD = 4.
10. Дано: ∆ABC – правильный,
AB = 4, AA1 = 3.
11. Дано: AD = DC = 10, AC = 12,
BM AC.
12. Дано: AB = 10, AC = 6,
ACB = 90 , DCB = 60 .
.
3.
Прямоугольная система координат в пространстве
1. А (10; 0; 0), B (0; 0; 0), C (0; 10; 0), D (10; 10; 0),
А1 (10; 0; 10), B1 (0; 0; 10), C1 (0; 10; 10), D1 (10; 10; 10).
2. А (2; 0; 0), B (0; 0; 0), C (0; 2; 0), D (2; 2; 0),
А1 (2; 0; 2), B1 (0; 0; 2), C1 (0; 2; 2), D1 (2; 2; 2).
3. А (2; –2; 0), B (–2; –2; 0), C (–2; 2; 0), D (2; 2; 0),
А1 (2; –2; 4), B1 (–2; –2; 4), C1 (–2; 2; 4), D1 (2; 2; 4).
4. А (2; 0; 0), B (–2; 0; 0), C (–2; 4; 0), D (2; 4; 0),
А1 (2; 0; 4), B1 (–2; 0; 4), C1 (–2; 4; 4), D1 (2; 4; 4).
5. А (2; –2; 0), B (–2; –2; 0), C (–2; 2; 0), D (2; 2; 0),
А1 (2; –2; 6), B1 (–2; –2; 6), C1 (–2; 2; 6), D1 (2; 2; 6).
6. А (2; 0; 0), B (0; 0; 0), C (0; 2; 0), D (2; 2; 0), F (0; 0; 4).
7. А (3; 0; 0), B (0; 0; 0), C (0; 4; 0), D (3; 4; 0),
А1 (3; 0; 1), B1 (0; 0; 1), C1 (0; 4; 1), D1 (3; 4; 1).
8. А (10; 0; 0), B (0; 0; 10), C (0; 10; 0), D (0; 0; 0).
9. А (2; 0; 0), B (–2; 0; 0), C (0; 0;
10. А (0; 0; 0), B (0; 4; 0), C (
C1 (
11. А (
), D (0; 0;
),
; 2; 0), А1 (0; 0; 3), B1 (0; 4; 3),
; 2; 3).
; 0; 0), B (0; 0; 0), C (0;
; 0), D (0; 0;
12. А (6; 8; 0), B (0; 0; 0), C (0; 8; 0), D (0; 0;
).
).
4.
НАХОЖДЕНИЕ КООРДИНАТ ВЕРШИН МНОГОГРАННИКОВ
Найдите координаты всех вершин многогранника.
1. Дано: ABCD – квадрат,
FCO = 45 , F (0; 0;
).
2. Дано: ABCD – квадрат,
FDCB = 45 , M (0; 6; 0).
3. Дано: ACB = 90 , BAC = 30 , 4. Дано: AB = 8, ACB = 90 ,
AB = 10, DB (ABC), DCB = 60 . BAC = 60 , DB (ABC),
DCB = 60 .
5. Дано: АB = AC = 25, BC = 30,
BO = OC, DAO = 45 .
6. Дано: AB = BC = AC = 6,
DBO = 60 , O – точка
пересечения высот ∆ABC.
5.
7. Дано: AB = BC = AC = 6,
АК ВC, BM AC, DMB = 60 .
8. Дано: ABCD – прямоугольник,
FB (ABC), FB = 3, FCDB = 30 ,
FADB = 45 .
9. Дано: AB = AC = 10, BC = 12,
DBCA = 45 .
10. Дано: ABCD – ромб, AC = 8, BD
= 6, FDCB = 45 .
11. Дано: ACB = 90 , AC = 4,
CB = 3, O – центр вписанной
окружности, DACB = 45 .
12. Дано: AB = AC = 10, BC = 12,
DBCA = 45 , O – центр вписанной
окружности.
6.
Нахождение координат вершин многогранников
1. А (0;
; 0), B (
; 0; 0), C (0; ; 0), D ( ; 0; 0), F (0; 0;
2. А (6; –6; 0), B (–6; –6; 0), C (–6; 6; 0), D (6; 6; 0), F (0; 0; 6).
3. А (0;
; 0), B (–5; 0; 0), C (0; 0; 0), D (–5; 0;
).
4. А (0; 0; 0), B (
; 4; 0), C (0; 4; 0), D (
; 4; 12).
5. А (0; –20; 0), B (–15; 0; 0), C (15; 0; 0), D (0; 0; 20).
6. А (
7. А (–3;
; –3; 0), B (
; 0), B (0;
; 0; 0), C (
; 0), C (3;
; 3; 0), D (0; 0; 6).
; 0), D (0; 0; 3).
8. А (3; 0; 0), B (0; 0; 0), C (0;
; 0), D (3;
; 0), F (0; 0; 3).
9. А (0; 0; 0), B (6; 8; 0), C (–6; 8; 0), D (0; 0; 8).
10. А (0; –4; 0), B (–3; 0; 0), C (0; 4; 0), D (3; 0; 0), F (0; 0; 2,4).
11. А (1; –3; 0), B (–2; 1; 0), C (1; 1; 0), D (0; 0; 1).
12. А (5; 0; 0), B (–3; 6; 0), C (–3; –6; 0), D (0; 0; 3).
).
7.
УГОЛ МЕЖДУ ВЕКТОРАМИ
1. Дано: DABC – правильный
тетраэдр.
2. Дано: ABCDA1B1C1D1 – куб.
Найдите:
Найдите:
,
,
,
,
.
.
3. Дано: DABC – правильный
тетраэдр.
4. Дано: FABCD – правильная
пирамида, BFD = 90 .
Найдите:
Найдите:
,
,
.
,
,
.
8.
5. Дано: ABCA1B1C1 – правильная
призма.
6. Дано: ABCDA1B1C1D1 – куб.
Найдите:
Найдите:
,
,
,
,
.
.
7. Дано: ABCDA1B1C1D1 – прямой
параллелепипед, BAD = 45 .
8. Дано: ABCDA1B1C1D1 – куб,
CM = MC1, CN = ND.
Найдите:
Найдите:
,
,
.
,
,
.
9.
9. Дано: ABCDA1B1C1D1 – куб,
AM = MB, BN = NB1,
B1P = PC1, C1K = KD1,
DL = LD1, AF = FD.
10. Дано: ABCA1B1C1 – призма,
CAA1 = BAA1 = 45 ,
AB = BC = AC = AA1.
Найдите:
Найдите:
,
,
,
,
.
11. Дано: FABCD – пирамида,
ABCD – квадрат, FB (ABC).
Найдите:
.
12. Дано: SABCDKF – пирамида, BS
(ABC), BS = AB, ABCDEF –
правильный шестиугольник.
,
Найдите:
,
,
.
, cos
.
10.
Угол между векторами
1. 60°, 120°, 90°.
2. 90°, 45°, 90°.
3. 90°, 180°, 90°.
4. 45°, 135°, 90°.
5. 120°, 90°, 180°.
6. 60°, 120°, 45°.
7. 180°, 135°, 0°.
8. 0°, 135°, 90°.
9. 120°, 60°, 90°.
10. 120°, 90°, 135°.
11. 90°, 90°, 90°.
12. 90°, 90°, –0,75.
11.
ЦИЛИНДР, КОНУС, ШАР
ЦИЛИНДР
1. Дано: R = 3, H = 8.
Найдите AC.
2. Дано: ABCD – квадрат,
SABCD = 12.
Найдите
3. Дано: R =
Найдите H.
, CAD = 60 .
5. Дано: Sосн = 3 , CAD = 30 .
Найдите H.
.
4. Дано: Sбок = 36 .
Найдите SABCD.
6. Дано: AC = 12, CAD = 60 .
Найдите
.
12.
7. Дано: H = 7, R = 5, AB OQ, 8. Дано: H = 12, R = 10,
AB || OQ, AB = BC, QK BC.
QK BC, QK = 3.
Найдите QK.
Найдите SABCD.
9. Дано: SABCD = 6.
Найдите Sбок.цил.
10. Дано: H = 5, R = 10,
AB OQ, AC = 13, QK BC.
Найдите QK.
11. Дано: H = 7, AB OQ,
AC = 25, QK BC, QK = 5.
Найдите R.
12. Дано: R = 13, QK BC,
QK = 5, CAD = 45 .
Найдите H.
13.
Цилиндр
1. 10.
2. 3.
3. 6.
4. 36.
5. 2.
6. 9.
7. 56.
8. 8.
9. 6 .
10. 8.
11. 13.
12. 24.
14.
ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ЦИЛИНДРА
Найдите Sбок.цил.
1. Дано: H = 10, AOD = 60 , 2. Дано: H = 10, AOD = 90 ,
OK AD, OK =
.
OK AD, OK =
.
3. Дано: H = 10, AOD = 120 ,
OK AD, OK = 5.
4. Дано: AOD = 60 , OK AD, OK
5. Дано: AC = 8, BC = 6,
AB = 10, AA1 = 4.
6. Дано: ABCA1B1C1 – правильная
=
, SABCD = 8.
призма, AB =
, AA1 = 5.
15.
7. Дано: ABCA1B1C1 – прямая 8. Дано: ABCDA1B1C1D1 – прямой
призма, AB = AC = 6, ABC = 120 , параллелепипед, ABCD – квадрат,
AA1 = 10.
AB =
, AA1 = 3.
9. Дано: ABCDA1B1C1D1 – куб,
10. Дано: ABCDA1B1C1D1 – куб, AC1
AC1 =
=
.
11. Дано: ABCDA1B1C1D1 –
прямой параллелепипед, AA1 = 3,
ABCD – ромб, BK DC, BK = 8.
.
12. Дано: H = 5, ABCD – ромб,
BAD = 30 , AB = 4.
Площадь боковой поверхности цилиндра
1. 160 .
2. 40 .
3. 200 .
4. 16 .
5. 40 .
6. 10 .
7. 120 .
8. 6 .
9. 36 .
10.
.
11. 24 .
12. 10 .
16.
КОНУС
1. Дано: l = 13, R = 5.
Найдите H.
2. Дано: ABC = 90 , l =
Найдите H.
3. Дано: ABC = 120 , l = 6.
Найдите H.
4. Дано: ABC = 60 , l = 10.
Найдите R.
5. Дано: R = 5, H = 12.
Найдите l.
6. Дано: ABC = 90 , R = 3.
Найдите SABC.
.
17.
7. Дано: l = 10, BAC = 60 .
Найдите R.
8. Дано: ABC = 60 , SABC =
Найдите l.
9. Дано: ABC = 120 ,
10. Дано: ∆ABC – равносторонний, l
= 12, R = 10, OK AC.
Найдите OK.
SABC =
.
Найдите l.
11. Дано: H = 12, OK AC,
OKB = 60 , OM BK.
Найдите ОM.
12. Дано: H = 12, OK AC,
OKB = 30 , AOC = 60 .
Найдите R.
.
18.
Конус
1. 12.
2. 3.
3. 3.
4. 5.
5. 13.
6. 9.
7. 5.
8. 8.
9. 8.
10. 8.
11. 6.
12. 24.
19.
ВПИСАННЫЙ ИЛИ ОПИСАННЫЙ КОНУС
1. Дано: ABCD – квадрат,
AB =
, H = 3.
Найдите Sбок. кон.
2. Дано: AB = AC = BC = 3, H = 1.
Найдите l.
3. Дано: AB = AC = BC = 6,
DO (ABC), DO = 1.
Найдите l.
4. Дано: ABC = 60 ,
Rопис. сферы = 6.
Найдите Sбок. кон.
5. Дано: ACB = 90 , AC = 3,
6. Дано: ABCD – квадрат,
SABCD = 64, H = 3.
Найдите Sбок. кон.
CB = 4, l =
Найдите H.
.
7. Дано: ABCD – ромб, BAD = 8. Дано: ABC = 90 , AC = 6,
BC = 8, H = 12.
= 30 , Sбок. кон = 20 , l = 5.
20.
Найдите SABCD.
Найдите Sбок. кон.
9. Дано: AB = AC = BC =
DC = 5.
Найдите H.
,
11. Дано: AC = 8, ABC = 30 ,
AD = 10.
Найдите Sбок. цил.
10. Дано: rвпис. сферы =
H = 3rсф.
Найдите Sбок. кон.
,
12. Дано: AC =
,
ABC = 120 , AD = 5.
Найдите Sбок. цил.
Вписанный или описанный конус
1. 20 .
2. 2.
3. 2.
4. 54 .
5. 2 (r = р – с).
6. 20 .
7. 128.
8. 65 .
9. 4.
10. 18 .
11. 80 (R = 8 по теореме синусов).
12. 15 .
21.
УСЕЧЕННЫЙ КОНУС
AFD – осевое сечение конуса;
ABCD – осевое сечение усеченного конуса;
r1 – радиус верхнего основания усеченного
конуса;
r2 – радиус нижнего основания усеченного
конуса;
h – высота усеченного конуса;
l – образующая усеченного конуса.
1. Дано: r1 = 3, r2 = 6, h = 4.
Найдите l.
2. Дано: r1 = 5, r2 = 11, l = 10.
Найдите h.
3. Дано: r1 = 3, r2 = 5,
BAO = 45 .
Найдите h.
4. Дано: r1 = 3, r2 = 7, l = 5.
Найдите SABCD.
5. Дано: OQ = QF, S1 = 16 .
Найдите r2.
6. Дано: S1 = 9 , S2 = 36 .
Найдите
7. Дано: OQ = QF,
Sбок. усеч =
.
.
8. Дано: OQ = QF, r2 = 2.
Найдите Sбок. усеч.
22.
Найдите r1.
9. Дано: OQ = QF.
10. Дано: FQ : QO = 1 : 2.
Найдите
Найдите
.
11. Дано: в усеченный конус
вписана сфера, l = 5, r2 = 4r1.
Найдите радиус вписанной сферы.
.
12. Дано: в усеченный конус
вписана сфера, r1= 9, r2 = 16.
Найдите SABCD.
Усеченный конус
1. 5.
2. 8.
3. 2.
4. 30.
5. 8.
6. 2.
7. 2.
8. 6 .
9. 0,75.
10. 1,125.
11. 2.
12. 600.
23.
СФЕРА
1. Дано: W = , OO1 ,
OO1 = 12, S = 25 .
Найдите Rсф.
2. Дано: W = , OO1 ,
OO1 = 8, C = 12 .
Найдите Sсф.
3. Дано: W = , OO1 ,
OO1 = 3, r = 4.
Найдите Sсф.
4. Дано: W = 1, W = 2, 1
2 = M, OO1 , OO2 , OO1 =
OO2 = 2, O1MO2 = 60 .
Найдите Rсф.
5. Дано: W = , OO1 ,
Sсф = 676 , OO1 = 5.
Найдите r .
6. Дано: W = , OO1 ,
Sсф = 100 , r = 3.
Найдите ρ(O, ).
24.
7. Дано: 1 W = 1,
= 25 , 2 W = 2,
8. Дано: 1 W = 1,
= 10 , 2 W = 2,
= 144 , 1 || 2, O1O2 = 17.
Найдите Sсф.
= 24 , 1 || 2, O1O2 = 7.
Найдите Sсф.
9. Дано: 1 W = A1,
2 W = A2, Sсф = 36 ,
( 1, 2) = 60°, 1 2 = a.
Найдите ρ(O, a).
10. Дано: 1 W = 1,
2 W = 2, 1 || 2,
11. Дано: 1 W = 1,
2 W = 2, 1 || 2,
12. Дано: 1 W = 1,
2 W = 2, 1 || 2,
OO1 : O1O2 : O2Q = 1 : 3 : 2,
OO1 = O1O2 =
Найдите
Rсф, Sсф = 36 .
.
OO1 = O1O2 =
Найдите Sсф.
= 55 .
Найдите Sсф.
= 5 .
25.
Сфера
1. 13.
2. 400 .
3. 100 .
4. 4.
5. 12.
6. 4.
7. 676 .
8. 676 .
9. 6.
10. 36 .
11. 13 .
12. 144 .
26.
ПЛОЩАДЬ ПОВЕРХНОСТИ СФЕРЫ
1. Дано: ABCD – квадрат, AB = 14,
все стороны касаются сферы,
Rсф = 25.
Найдите (O, (ABC)).
2. Дано: ∆ABC – правильный,
OO1 (ABC), OO1 = 3, все стороны
касаются сферы, Rсф = 6.
Найдите AB.
3. Дано: ABCD – квадрат, все
стороны касаются сферы, Rсф = 5,
OO1 (ABC), OO1 = 4.
Найдите AB.
4. Дано: ∆ABC, AB = AC = BC = 6,
все стороны касаются сферы,
Rсф = 2, OO1 (ABC).
Найдите OO1.
6. Дано: ∆ABC – правильный, все
5. Дано: ABCD – ромб, AB =
стороны касаются сферы,
, BAD = 60 , все стороны касаются
PABC =
, AO = BO = CO =
сферы, Rсф = 15, OO1 (ABC).
Найдите OO1.
= 26, OO1 (ABC).
Найдите OO1.
27.
7. Дано: ∆ABC, ACB = 90 ,
A W, B W, C W, AB = 24, OO1
(ABC), OO1 = 5.
Найдите Sсф.
8. Дано: ABCD – квадрат,
A W, B W, C W,
9. Дано: ∆ABC, ABC = 60 ,
10. Дано: ABCD – ромб, A W,
B W, C W, AB = 2,
AC =
, A W, B W,
C W, OO1 (ABC), Rсф = 5.
Найдите OO1.
11. Дано: ∆ABC, A W, B W,
C W, OO1 (ABC), OO1 = 12,
Rсф = 13, ABC = 30 .
Найдите AC.
AB =
, OO1 (ABC), OO1 = 6.
Найдите Sсф.
OO1 (ABC), OO1 =
Найдите Rсф.
.
12. Дано: ABCD – трапеция,
A W, B W, C W, D W,
AC = 4, ABC = 30 ,
OO1 (ABC), Rсф = 5.
Найдите OO1.
28.
Площадь поверхности сферы
1. 24.
2. 18.
3. 6.
4. 1.
5. 9.
6. 10.
7. 676 .
8. 400 .
9. 4.
10. 3.
11. 5.
12. 3.
29.
СФЕРА, ВПИСАННАЯ В ПИРАМИДУ
O1 – центр сферы, вписанной в пирамиду.
1. Дано: ∆ABC – правильный,
AB = 6, DK AB, DKC = 60 .
Найдите rсф.
2. Дано: ABCD – квадрат,
3. Дано: ∆ABC – правильный, DO1 :
O1O = 2 : 1, M – точка касания
вписанной сферы.
Найдите DKO.
4. Дано: ∆ABC – правильный,
M – точка касания вписанной
сферы, DM = KO.
Найдите DKO.
5. Дано: ABCDEK – правильный,
6. Дано: ∆ABC – правильный,
M – точка касания вписанной
Sосн =
, FM AK,
FMO = 60 . Найдите rсф.
AB =
, FK DC,
FKO = 60 . Найдите rсф.
сферы, KM =
. Найдите PABC.
30.
7. Дано: ABCD – квадрат,
M – точка касания вписанной
сферы, OFM = 30 .
Найдите
8. Дано: ABCD – квадрат,
M – точка касания вписанной
сферы, PABCD =
Найдите OKM.
, OO1 = 1.
.
9. Дано: ABCD – квадрат,
M – точка касания вписанной
сферы, AD = 6, FK = 5.
Найдите rсф.
10. Дано: ∆ABC – правильный, SABC
11. Дано: ABCD – ромб,
BAD = 60 , FK DC,
FKO = 60 , Sвпис. сф = 64 .
Найдите AD.
12. Дано: ABCD – трапеция,
AB = CD, BAD = 30 ,
Sвпис. сф = 4 , FK AD,
FKO = 60 . Найдите PABCD.
=
, M – точка касания
вписанной сферы, DKO = 30 .
Найдите DO.
31.
Сфера, вписанная в пирамиду
1. 1.
2. 3.
4. 60°.
5. 1.
7. 2.
8. 60°.
10. 1.
11. 16.
3. 60°.
6. 18.
9. 1,5.
12.
.
32.
СФЕРА, ОПИСАННАЯ ОКОЛО ПИРАМИДЫ
O1 – центр сферы, описанной около пирамиды.
1. Дано: ABCD – квадрат,
AF =
, BFD = 60 .
Найдите Rсф.
2. Дано: ∆ABC – правильный, FO1 :
O1O = 2 : 1.
Найдите FCO.
3. Дано: ∆ABC – правильный,
FC = 5, FO = 4.
Найдите Rсф.
4. Дано: ABCD – квадрат,
5. Дано: ABCD – квадрат,
Rсф = 2, FCO = 30 .
Найдите FC.
6. Дано: FO (ABC), O – центр
описанной около ∆ABC
окружности, FCO = 60 , Rсф = 4.
Найдите FC.
7. Дано: ABCD – квадрат,
AF = AC.
8. Дано: ABCD – квадрат,
AB =
, FC = 5.
Найдите Rсф.
AF = AC =
. Найдите Rсф.
33.
Найдите FO1C.
9. Дано: ∆ABC, O – центр
описанной вокруг ∆ABC
окружности,
DC = 10.
Найдите DO1 DO.
10. Дано: ∆ABC, O1
описанной
вокруг
окружности,
BC = 10, BAC = 30 .
Найдите DO1.
–
центр
∆ABC
11. Дано: ∆ABC, ACB = 90 ,
12. Дано: ∆ABC, AB = BC = AC =
AC = CB =
, DC (ABC),
DC = 6.
Найдите Rсф.
=
, AD = 8.
Найдите Rсф.
34.
Сфера, описанная около пирамиды
1. 2.
2. 60°.
4. .
5. 2.
3.
6.
.
.
7. 120°.
8. 3.
10. 10.
11. 5.
9. 50.
12. 5.
35.
СФЕРА, ВПИСАННАЯ В ПРИЗМУ
Сфера вписана в призму.
1. Дано: ∆ABC – правильный, 2. Дано: ∆ABC – правильный.
Найдите C1BC.
CN AB. Найдите ctg C1NC.
3. Дано: ∆ABC –
O1 – центр ABC.
Найдите C1O1C.
правильный, 4. Дано: ABCD – квадрат,
DC1 =
. Найдите rсф.
5. Дано: ABCD – ромб, AC = 12, BD 6. Дано: ABCD – ромб, AD = 4,
= 16. Найдите rсф.
BAD = 30 . Найдите AA1.
36.
7. Дано: ∆ABC – правильный,
rсф =
. Найдите AB.
8. Дано:
∆ABC
–
правильный,
AB =
. Найдите AA1.
9. Дано: ABCDA1B1C1D1 – куб,
Sсф = 64 . Найдите Sкуба.
10. Дано: ABCDEF – правильный,
11. Дано: ∆ABC, ACB = 90 ,
AC = 3, BC = 4. Найдите rсф.
12. Дано: ABCD – трапеция,
AB = CD, PABCD = 16,
BAD = 30 . Найдите rсф.
сумма всех ребер равна
Найдите rсф.
.
37.
Сфера, вписанная в призму
1. .
2. 30°.
3. 45°.
4. 2.
5. 4,8.
6. 2.
7. 6.
8. 12.
9. 384.
10.
.
11. 1.
12. 1.
38.
СФЕРА, ОПИСАННАЯ ОКОЛО ПРИЗМЫ
Сфера описана около призмы.
1. Дано: ABCD – прямоугольник,
AB =
, BC = 2, CC1 = 8.
Найдите Rсф.
2. Дано: ∆ABC, AB = AC = BC = 3,
Rсф = 2.
Найдите AA1.
3. Дано: ABCD – квадрат,
Rсф = 3, AA1 = 2.
Найдите AB.
4. Дано: ∆ABC, AB = AC = BC = 3,
AA1 = 2.
Найдите Rсф.
5. Дано: ∆ABC, AB = BC = 5, 6. Дано: ABCDEF – правильный,
AA1 = 8, Rсф = 5.
Найдите AB.
AC = 6, AA1 =
.
Найдите Rсф.
7. Дано:
∆ABC
Rсф = 10, Sосн =
–
.
правильный, 8. Дано: ∆ABC
Rсф = 7, AA1 = 2.
–
правильный,
39.
Найдите AA1.
Найдите AB.
9. Дано: ∆ABC, ACB =
AC = CB, AA1 = 12, Rсф = 10.
Найдите Sосн.
90 , 10. Дано: ∆ABC, ACB = 30 ,
Rсф = 5, CC1 = 8.
Найдите AB.
11. Дано: ABCD – трапеция, 12. Дано: ABCDA1B1C1D1 – куб,
BAD = 30 , Rсф = 25, AA1 = 48.
AB =
.
Найдите BD.
Найдите Rсф.
Сфера, описанная около призмы
1. 5.
4. 2.
7. 16.
10. 3.
2. 2.
3. 4.
5. .
6. 3.
8. 12.
9. 64.
11. 7.
12. 9.
40.
Объемы параллелепипеде, призмы, цилиндра
ОБЪЕМ ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА
ABCDA1B1C1D1 – прямоугольный параллелепипед.
Найдите объем параллелепипеда.
1. Дано: ABCD – квадрат,
AD = 4, DC1 = 5.
2. Дано: BB1D1D – квадрат,
BD = 10, AD = 8.
3. Дано: AB1C1D – квадрат,
AD = 5, AB = 4.
4. Дано: BD = BC1 = DC1 =
5. Дано: AA1 = 6, B1D =
AB1 = AD.
,
6. Дано: AB1C1D – квадрат,
BD =
, AD = 5.
.
41.
7. Дано: BD1 A1C, BD1 =
AB = 3.
,
8. Дано: AB = AD, A1C =
AA1 = 2.
,
9. Дано: AA1 = 2, AB = AD,
B1DB = 45 .
10. Дано: AB = 5, AD = 12,
B1DB = 45 .
11. Дано: AB1D = B1AB = 30 ,
B1D = 12.
12. Дано: B1D =
,
B1DC1 = 45 , sin C1DC = 0,8.
Объем прямоугольного параллелепипеда
1. 48.
4. 8.
7. 60.
10. 780.
2. 480.
3. 60.
5. 480.
6. 60.
8. 8.
9. 4.
11.
12. 60.
.
42.
ОБЪЕМ ПРЯМОГО ПАРАЛЛЕЛЕПИПЕДА
ABCDA1B1C1D1 – прямой параллелепипед.
Найдите объем параллелепипеда.
1. Дано: AB = 2, AD = 6, AA1 = 5,
BAD = 30 .
2. Дано: AB = AD = AA1 = 10, BAD
= 30 .
3. Дано: AC BD, AC = 6,
BD = 8, BOB1 = 45 .
4. Дано: AB = AD, BAD = 60 ,
5. Дано: AB = AD = 4, BAD = 60 ,
D1OD = 60 .
6. Дано: AB = AD = 4,
ABC = 120 , C1OC = 30 .
7. Дано: AB = AD, AD = 10,
BK AD, BK = 5, B1K = 13.
8. Дано: AB = 2, AD = 6,
BAD = 30 , BM AD,
B1MB = 45 .
B1DB = 45 , BB1 =
.
43.
9. Дано: AB = AD = 2,
BAD = 60 , BB1D1D – квадрат.
10. Дано: AB = AD, BAD = 60 , BD
11. Дано: AD = 7, AB =
,
BAD = 45 , BDB1 = 45 .
12. Дано: AB = AD, A1C = 5,
= DD1, B1D =
B1D =
.
, AA1 = 4.
Объем прямого параллелепипеда
1. 30.
2. 500.
4. 36.
5. 48.
3. 128.
6.
.
7. 600.
8. 6.
10.
.
11. 105.
9.
12. 6 (Sосн = Sромба =
.
d1d2).
44.
ОБЪЕМ ПРЯМОЙ ТРЕУГОЛЬНОЙ ПРИЗМЫ
ABCA1B1C1 – прямая треугольная призма.
Найдите объем призмы.
1. Дано: ACB = 90 , AC = CB,
AB1 = 10, BB1 = 8.
2. Дано: AB = AC, BAC = 120 ,
B1C = 8, B1CB = 60 .
3. Дано: AB = BC = 5, AC = 6,
B1M A1C1, MCB1 = 45 .
4. Дано: ACB = 90 , AC = 3,
AA1 = 4, ((AВ1C), (ABC)) = 45 .
5. Дано: ACB = 90 , A1C = BC,
AB = 10, AC = 6.
6. Дано: ACB = 90 , AC = 2,
A1C = 4, A1B = 5.
45.
7. Дано: ACB = 90 , AC = CB,
AM = MB, C1MC = 45 , CC1 = 6.
8. Дано: AB = BC = 10, AC = 16,
O – точка пересечения медиан
∆ABC, B1OB = 45 .
9. Дано: AB = BC = 10, AC = 12,
O – центр вписанной окружности,
B1OB = 45 .
10. Дано: AC = , BC = 2,
ACB = 30 , O – центр описанной
окружности, B1OB = 45 .
11. Дано: AC = 2, AB = 6,
BAC = 30 , ((ABC), (AB1C)) = 45 .
12. Дано: AB = 2, BC = 6,
ABC = 60 , ((ABC), (A1BC)) = 45 .
46.
Объем прямой треугольной призмы
1. 72.
7. 216.
2. 16.
3.
.
4. 24.
5.
.
6.
.
8. 192.
9. 240 (использовать формулу S = pr).
10.
(AB = 1 по теореме косинусов, R = 1 по теореме синусов).
11. 9. 12. 9.
47.
ОБЪЕМ ПРАВИЛЬНОЙ ТРЕУГОЛЬНОЙ ПРИЗМЫ
ABCA1B1C1 – правильная треугольная призма.
Найдите объем призмы.
1. Дано: C1M1 A1B1, MM1C1C –
квадрат, CC1 =
.
2. Дано: AM = MB, A1M1 = M1B1, AB
= 2, MM1C1C – квадрат.
3. Дано: AB = 2, AB1 A1B = M, BC1 4. Дано: AB = 6, M – точка
пересечения медиан ∆AC1B, MP
B1C = K, CC1 = 2MK.
(ABC), MP = 2.
5. Дано: в грань AA1B1B вписана
окружность единичного радиуса.
6. Дано: AA1 = 3, около грани
AA1B1B описана окружность,
R = 2,5.
48.
8. Дано: AM = MB, A1M1 = M1B1,
AA1 = 2, O – центр ∆ABC,
M1OC = 120 .
7. Дано: AA1 =
, O – центр
∆ABC, C1OC = 30 .
9. Дано: C1M1 A1B1, BC1 =
(BC1,(AA1B1)) = 45 .
11. Дано: CC1 =
(C1, AB) =
,
.
,
10. Дано: AB = 2,
((ABC),(AC1B)) = 45 .
12. Дано: CC1 =
,
(CC1,(AC1B)) = 30 .
49.
Объем правильной треугольной призмы
1. 24.
4.
2. 3.
5.
3.
.
6.
.
.
.
7. 162.
10. 3.
8.
.
11. 9.
9.
.
12. 27.
50.
ОБЪЕМ ПРАВИЛЬНОЙ ЧЕТЫРЕХУГОЛЬНОЙ ПРИЗМЫ
ABCDA1B1C1D1 – правильная четырехугольная призма.
Найдите объем призмы.
1. Дано: BB1 = BD = 2.
2. Дано: A1D = 4, B1D = 5.
3. Дано: CM : MC1 = 3 : 4,
BD = 6, ((ABC), (BDM)) = 45 .
4. Дано: в грань AA1D1D вписана
окружность единичного радиуса.
5. Дано: AB =
, около
прямоугольника AA1C1C описана
окружность, R = 2,5.
6. Дано: AB =
= 45 .
7. Дано: DB1 =
,
(DB1,(DD1C1)) = 30 .
8. Дано: AB =
,
(AC1, B1D) = 60°.
, (DB1,(ABC)) =
51.
9. Дано: AC BD = O, A1M =
10. Дано: AC BD = O,
= MB1, MO =
D1O =
, SABCD = 4.
11. Дано: AA1 = AB, DB1 =
.
, SABCD = 16.
12. Дано: AA1 = AB, AM = MD,
D1N = NC1, MN =
.
Объем правильной четырехугольной призмы
1. 4.
4. 8.
7. 4.
10. 80.
2.
.
3. 126.
5. 24.
6. 32.
8. 32.
9. 12.
11. 8.
12. 8.
52.
ОБЪЕМ ПРАВИЛЬНОЙ ШЕСТИУГОЛЬНОЙ ПРИЗМЫ
ABCDEKA1B1C1D1E1K1 – правильная шестиугольная призма.
Найдите объем призмы.
1. Дано: KK1 = KC = 4.
2. Дано: CE = EE1 =
4. Дано: AB = 2, C1KC = 30 .
3. Дано: KC1 =
,
(KC1, (ABC)) = 45 .
5. Дано: KB1 = 2, B1E =
7. Дано: K1D1 = K1E = ED1 =
.
6. Дано: KC1 =
.
.
, A1K =
8. Дано: KK1 = KE,
ρ(K1C1, DE) =
.
.
53.
9. Дано: AB = 2,
(KK1, DC1) = 45°.
10. Дано: AB = 4,
(KE1, CB1) = 90°.
11. Дано: AB = 2,
(KB1, CE1) = 90°.
12. Дано: AB = AA1,
ρ(D1, KE) =
.
54.
Объем правильной шестиугольной призмы
1.
.
4. 24.
7.
.
10.
2. 36.
5.
.
8.
.
11. 36.
3. 27.
6.
.
9.
.
12.
.
.
55.
ОБЪЕМ ЦИЛИНДРА
Найдите объем цилиндра.
1. Дано: ABCD – квадрат,
SABCD = 16.
2. Дано: AC =
3. Дано: BD OQ = M,
4. Дано: ON = 12, AM = MB,
MK OQ = N, NQ = 4, QK = 18.
BD =
, BMO = 30 .
, CAD = 45 .
5. Дано: AQ = 8, ON = NQ, 6. Дано: ABCD – осевое сечение, в
ABCD вписана окружность
NK AB = M, AM = 2, QK = 12.
единичного радиуса.
56.
7. Дано: в цилиндр вписана
правильная треугольная призма,
AB = 3, AA1 = 2.
8. Дано: цилиндр вписан в
правильную треугольную призму,
AB = 6, AA1 = 2.
9. Дано: Sосн = 25 , SABCD = 40.
10. Дано: концы отрезка AB лежат
на окружностях оснований
цилиндра, AB = 13, R = 10, (OQ,
AB) = 8.
11. Дано: AQD = 60 , OQ = 10, 12. Дано: AQD = 90 , OQ = 6,
(OQ, (ABC)) =
.
(OQ, (ABC)) =
.
57.
Объем цилиндра
1. 16 .
2. 2 .
3. 18 .
4. 576 .
5. 768 .
6. 2 .
7. 6 .
8. 6 .
9. 100 .
10. 500 .
11. 40 .
12. 24 .
58.
ОБЪЕМ НАКЛОННОЙ ПРИЗМЫ
(V = Sосн · H)
Найдите объем наклонной призмы.
1. Дано: ∆ABC – правильный,
AB = 2, AA1 = 8, (AA1,(ABC)) = 30 .
2. Дано: ∆ABC – правильный,
3. Дано: ∆ABC, ACB = 90 ,
AC = 6, BC = 8, (AA1B1) (ABC),
4. Дано: ∆ABC, ACB = 90 ,
AC = 6, BC = 8, AA1 = 13,
AA1 = BB1 = CC1.
(AA1,(ABC)) = 45 , CC1 =
.
AB =
, O – центр ∆ABC,
A1O (ABC), (AA1,(ABC)) = 60 .
5. Дано: ∆ABC – правильный,
AB = 4, AA1C1C – ромб,
A1C = 10, AC1 (ABC).
6. Дано: ∆ABC – правильный,
AB = AA1, BO = OC, A1O (ABC),
7. Дано: AC = AB = 10, BC = 12,
O – центр вписанной в основание
8. Дано: ACB = 90°, AC = 3,
CB = 4, O – центр вписанной в
.
59.
окружности, A1O (ABC),
AA1 = 13.
основание окружности, B1O
9. Дано: ABCD – ромб, AC = 8,
BD = 6, AC BD = O,
C1O (ABC), CC1 = 5.
10. Дано: AB = BC = AA1 = 2,
(BB1C1) (ABC), ((AA1B1),
(ABC)) = 30°.
11. Дано: ABCD – квадрат,
12. Дано: все грани
параллелепипеда – равные ромбы
со стороной 6 и острым углом 60°.
AB =
, B1O (ABC),
((BB1, (ABC)) = 45°.
(ABC), BB1 =
.
60.
Объем наклонной призмы (V = Sосн · H)
1.
.
4. 288.
2. 144.
5.
3. 48.
6.
.
.
7. 576.
10. 4.
8. 12.
11. 16.
9. 72.
12.
.
61.
ОБЪЕМ НАКЛОННОЙ ПРИЗМЫ
(V = S сеч · l)
Найдите объем призмы.
1. Дано: BB1 MN, BB1 NK,
MN NK, MN = 3, NK = 4,
MK = BB1.
2. Дано: AA1 (MNK), MN = MK = =
NK = 6, боковое ребро равно
высоте сечения.
3. Дано: AA1 (MNK), МК = 15, MN 4. Дано: AA1 (MNK), MNK =
= 14, NK = 13, AA1 = 2.
= 90°, MN = 6, NK = 8, боковое
ребро равно медиане треугольника,
проведенной к гипотенузе.
5. Дано: AA1 (MNK), MN MK,
MN = MK =
, боковое ребро
равно высоте треугольника,
проведенной к гипотенузе.
6. Дано: AA1 (MNK), MNK =
= 30°, MN = 8, MK = 6, боковое
ребро равно высоте треугольника к
стороне MK.
62.
7. Дано: AA1 (MNK), MNPK –
квадрат, MN = 2, боковое ребро
равно диагонали квадрата.
8. Дано: AA1 (MNK), MNPK –
квадрат, MP = 6, NK = 8, боковое
ребро равно стороне ромба.
9. Дано: AA1 (MNK), MNPK –
ромб, NMK = 60°, MN = 2,
боковое ребро равно меньшей
диагонали ромба.
10. Дано: AA1 (MNK), MNPK –
ромб, NMK = 60°, MN = 2,
боковое ребро равно большей
диагонали ромба.
11. Дано: AA1 (MNK), MNPK –
параллелограмм, NMK = 30°,
MN = 2, MK = 4, боковое ребро
равно высоте параллелограмма,
проведенной к большей стороне.
12. Дано: AA1 (MNK), MNPK –
параллелограмм, NMK = 30°,
MN = 2, MK = 4, боковое ребро
равно высоте параллелограмма,
проведенной к меньшей стороне.
63.
Объем наклонной призмы (V = S сеч · l)
1. 30.
2. 81.
4. 120.
5. 8.
7.
.
8. 120.
10. 12.
11. 4.
3. 168.
6. 48.
9.
12. 8.
.
64.
Объем пирамиды
ОБЪЕМ ПРАВИЛЬНОЙ ТРЕУГОЛЬНОЙ ПИРАМИДЫ
DABC – правильная треугольная пирамида. DO (ABC). DM BC. DK
AB.
Найдите объем пирамиды.
1. Дано: DO = 8, AD = 10.
2. Дано: DK = 5, DO = 4.
3. Дано: AB =
4. Дано: O1 и O2 – точки
пересечения медиан ∆ADB и ∆BDC,
, DC = 10.
O1O2 =
5. Дано: DM =
DMO = 45 .
,
, DC = 10.
6.Дано: DM =
MDO = 60 .
,
65.
7. Дано: AB =
MDO = 60 .
8. Дано: DO = 2,
((ABC), (BDC)) = 30 .
,
10. Дано: (DC, (ABC)) = 30 ,
9. Дано: DC =
,
(DC, (ABC)) = 45 .
DO =
11. Дано: ADB = BDC =
= ADC = 90 , AD =
.
.
12. Дано: AB =
ADB = 60°.
,
66.
Объем правильной треугольной пирамиды
1.
.
4.
.
7. 1.
2.
.
5. 72.
8.
3.
.
6. 27.
9. 18.
10. 54.
.
11.
12. 9.
.
67.
ОБЪЕМ ПРАВИЛЬНОЙ ЧЕТЫРЕХУГОЛЬНОЙ ПИРАМИДЫ
FABCD – правильная четырехугольная пирамида. FO (ABC).
Найдите объем пирамиды.
1. Дано: FC = 5, FO = 3.
2. Дано: AF = AC =
3. Дано: AF = AD = 6.
4. Дано: FM DC, FM = 5,
Sбок = 60.
5. Дано: FM DC, FO = 3,
OMF = 45 .
6. Дано: Sосн = 6, FAO = 60 .
.
68.
7. Дано: FM DC, FM = 4,
OMF = 30 .
8. Дано: AB =
cos =
9. Дано: FC =
11. Дано: AB =
DFC = 60 .
, FCO = 45 .
,
,
.
10. Дано: Sбок =
,
FM DC, OMF = 45 .
12. Дано: AF =
AFC = 90 .
,
Объем правильной четырехугольной пирамиды
1. 32.
2. 6.
3.
.
4. 48.
5. 36.
7. 32.
8. 192.
10. 36.
11. 18.
6. 6.
9. 144.
12. 18.
69.
ОБЪЕМ ПРАВИЛЬНОЙ ШЕСТИУГОЛЬНОЙ ПИРАМИДЫ
FABCDEK – правильная шестиугольная пирамида. FO (ABC).
Найдите объем пирамиды.
1. Дано: AF = FD = AD =
2. Дано: FE = FC = EC =
.
3. Дано: AB = 12,
ρ(F, DE) =
4. Дано: ρ(A, KE) =
.
, AF =
.
5. Дано: ρ(F, CE) = 2, FO =
.
6. Дано: ρ(E, (KFC)) =
FO =
.
,
.
70.
7. Дано: ρ(O, (EFC)) =
FO =
,
.
8. Дано: ρ(O, (EFD)) =
FO =
.
10. Дано: ρ(K, CD) =
9. Дано: ρ(O, AF) =
FO =
,
FD =
,
,
.
.
11. Дано: (FE, (KFC)) = α,
12. Дано: ρ(E, (AFK)) =
tg α =
, AB = 2.
FO =
.
,
71.
Объем правильной шестиугольной пирамиды
1.
2.
.
3. 216.
.
4. 6.
7. 6.
10. 6.
5. 6.
6. 6.
8. 2.
9. 1,5.
11. 6.
12. 2.
72.
ОБЪЕМ ПИРАМИДЫ, В ОСНОВАНИЕ КОТОРОЙ
МОЖНО ВПИСАТЬ ОКРУЖНОСТЬ
Найдите объем пирамиды.
1. Дано: DABC – пирамида,
ACB = 90 , AC = 5, CB = 12,
OM – радиус вписанной
окружности, DMO = 45 .
2. Дано: DABC – пирамида,
AC = 5, CB = 12, AB = 13,
((ADC),(ABC)) = ((BCD),(ABC)) =
= ((ABD),(ABC)) = 45 .
3. Дано: DABC – пирамида,
DM AC, DK AB, DN CB,
DMO = DNO = DKO = 45 ,
AC = 6, CB = 8, AB = 10.
4. Дано: DABC – пирамида,
AB = BC = 10, AC = 12,
((ADC),(ABC)) = ((BCD),(ABC)) =
= ((ABD),(ABC)) = 45 .
73.
5. Дано: FABCD – пирамида, ABCD
– ромб, AB = 12,
BAD = 30°, OM – радиус
вписанной окружности,
FO (ABC), FM CD, FM = 5.
6. Дано: FABCD – пирамида,
ABCD – ромб, ((ABC), (ABF)) =
= ((ABC), (BCF)) = ((ABC), (DCF)) =
= ((ABC), (ADF)) = α, tg α =
AC = 6, BD = 8.
,
7. Дано: FABCD – пирамида, ABCD 8. Дано: FABC – пирамида, каждая
– прямоугольник, каждая из
из апофем равна 5,
апофем равна 5,
AB = 13, BC = 14, AC = 15.
FO (ABC), FO = 3.
74.
9. Дано: FABC – пирамида, каждая 10. Дано: FABC – пирамида, каждая
из апофем составляет с высотой
из апофем равна
,
пирамиды угол α, ctg α = 0,3, AB =
AB = 5, AC = 8, BAC = 60°.
6, AC = 29, BC = 25.
11. Дано: FABC – пирамида, каждая
из боковых граней составляет с
плоскостью основания угол 45°, AB
= 5, AC = 16, BAC = 120°.
12. Дано: FABCD – пирамида,
ABCD – трапеция, AB = CD,
OM – радиус вписанной
окружности, AD = 32, BC = 18, FM
= 13.
Объем пирамиды, в основание которой
можно вписать окружность
1. 20.
2. 20.
3. 16.
4. 48.
5. 96.
6. 16.
7. 64.
8. 112.
9. 12.
10. 10.
11. 20.
12. 1000.
75.
ОБЪЕМ ПИРАМИДЫ, ОКОЛО ОСНОВАНИЯ КОТОРОЙ
МОЖНО ОПИСАТЬ ОКРУЖНОСТЬ
Найдите объем пирамиды.
1. Дано: DABC – пирамида,
ACB = 90 , AB = 10, AC = 8,
DO (ABC), DAO = DCO =
= DBO = 45 .
2. Дано: DABC – пирамида,
3. Дано: FABCD – пирамида,
AF = BF = CF = DF, ABCD –
прямоугольник, SABCD = 9,
AC BD = O, COD = 30 ,
FCO = 45 .
4. Дано: DABC – пирамида,
AD = CD = BD =
, AC = 1,
CB = 2, ACB = 60 .
ACB = 90 , AC = CB =
,
DAO = DCO = DBO = 60 .
76.
5. Дано: DABC – пирамида,
AD = DB = DC = 2, DO (ABC),
AOB = 120 , AB = 3, AC = BC.
6. Дано: DABC – пирамида,
AD = DB = DC, ACB = 90 ,
BAC = 30 , CB = 6, DO (ABC),
OM AC, DMO = 45 .
7. Дано: FABCD – пирамида, ABCD 8. Дано: FABC – пирамида,
– параллелограмм,
AF = BF = CF =
,
FO (ABC), AB = 6, AD = 8,
AC = BC = , ACB = 90°.
FAO = FBO = FCO =
FDO = 45 .
77.
9. Дано: FABC – пирамида,
10. Дано: FABC – пирамида,
AF = BF = CF =
,
AB = 3, AC = 6, BAC = 60°.
AF = BF = CF =
11. Дано: DABC – пирамида,
DO (ABC), DAO = DBO =
= DCO = 45 , CO = 6,
BAC = , ACB = .
12. Дано: DABC – пирамида,
DO (ABC), DO = 3, DAO =
= DBO = DCO = 45 ,
BAC = , ABC = .
AC = BC =
,
, ACB = 120°.
Объем пирамиды, около основания которой
можно описать окружность
1. 40.
4. 24.
2. 1.
5.
3. 9.
6.
.
.
7. 80.
10. 3.
8. 1.
11. 144 sin sin sin ( + ).
9. 9.
12. 18 sin sin sin ( + ).
78.
ОБЪЕМ ПИРАМИДЫ, У КОТОРОЙ ОДНО ИЗ БОКОВЫХ РЕБЕР
ПЕРПЕДИКУЛЯРНО ПЛОСКОСТИ ОСНОВАНИЯ
SB (ABC). Найдите объем пирамиды.
1. Дано: AB = 5, BC = 4, SB = 6.
2. Дано: AB = BC = 10,
AC = 12, SM AC.
3. Дано: AB = BC = AC =
SM AC, SMB = 60 .
4. Дано: SM AC, AC = 16,
SABC = 24, SMB = 45 .
5. Дано: AB = 10, AC = 8,
ACB = 90 , SАCB = 45 .
,
6. Дано: AC = AB = 6,
BAC = 150 , SАCВ = 45 .
79.
7. Дано: ABCD – прямоугольник,
SABC = 45 , SDCB = 60 ,
SB =
8. Дано: ABCD – квадрат,
BD = 6, BDS = 45 .
.
9. Дано: ABCD – ромб, AB = 6,
DAB = 30 , SK AD,
SKB = 45 .
10. Дано: ABCD – квадрат,
11. Дано: ABCD – квадрат,
12. Дано: ABCD – прямоугольник,
SABCD = 24, AC = 8, SACB = 45 .
AB =
, AC BD = O,
SOB = 30 .
AC =
, SAB = 60 .
80.
Объем пирамиды, у которой одно из боковых ребер
перпедикулярно плоскости основания
1. 20.
2. 96.
3. 9.
4. 24.
5. 48.
6. 9.
7. 27.
8. 36.
9. 18.
10. 3.
11. 2.
12. 24.
81.
ОБЪЕМ ПИРАМИДЫ С ГРАНЬЮ,
ПЕРПЕНДИКУЛЯРНОЙ ОСНОВАНИЮ
1. Дано: (ADB) (ABC), AB = BC
== AC = AD = BD = 2.
Найдите VDABC.
2. Дано: (ADB) (ABC), AB = BC =
= AC = AD = BD, VDABC = 1.
Найдите AB.
3. Дано: (ADB) (ABC), AC = CB, AD
= DB, ACB = 90 , ADB = 90 , AB =
6.
Найдите VDABC.
4. Дано: (ADB) (ABC), AC =
= CB = 2, ACB = 120 , CO AB,
DCO = 60 .
Найдите VDABC.
5. Дано: DO (ABC), O AB,
ACB = ADB = 90 , AD = 3,
6. Дано: (AFB) (ABC), ABCD –
квадрат, FDCB = 45 , AB = 3.
Найдите VFABCD.
DB = , AC = 2, BC =
Найдите VDABC.
.
82.
8. Дано: ABCD – ромб, AB = 6,
7. Дано: (AFB) (ABC), ABCD –
квадрат, AB = 3, VDABC = 18.
BAD = 30°, (AFB) (ABC),
Найдите tg α, где α = ((ABC), (FDC)). FDO = 45°.
Найдите VFABCD.
9. Дано: (ADB) (ABC), AB = 14,
AC = 15, BC = 13, DC = 13.
Найдите VDABC.
10. Дано: (ADB) (ABC), AB = 5,
11. Дано: (ADB) (ABC), AB = 5,
12. Дано: FO (ABC),
COD = 60°, OA = AD,
BC = 7, BAC = 60°, DC =
Найдите VDABC.
.
AC = 8, BAC = 60°, DC =
Найдите VDABC.
OB = BC, OF = DC =
Найдите VFABCD.
.
.
83.
Объем пирамиды с гранью, перпендикулярной основанию
1. 1.
4. 1.
7. 2.
10. 10.
2. 2.
3. 9.
5. .
6. 9.
8. 18.
9. 140.
11. 10.
12. 36.
84.
ОБЪЕМ УСЕЧЕННОЙ ПИРАМИДЫ
1. Дано: DABC – пирамида,
CD (ABC), CM = MD,
AK = KD, BN = ND,
VDABCD = 16. Найдите Vус. пир.
2. Дано: FABCD – пирамида,
AC || A1C1, BD = B1D1,
FO1 = O1O, Vус. пир = 49.
Найдите VFABCD.
3. Дано: FABCD – пирамида,
FB (ABC), AB || A1B1,
BC || B1C1, BB1 = B1F,
VFA1B1C1D1 = 2.
Найдите Vус. пир.
4. Дано: DABC – пирамида,
CD (ABC), CD = 4, CC1 = C1D,
AC = CB = 5, CK AB, CK = 3,
(A1B1C1) || (ABC).
Найдите VDA1B1C1.
5. Дано: FABC – пирамида, (A1B1C1)
|| (A2B2C2) || (ABC),
OO1 = O1O2 = O2F, VFABC = 27.
Найдите VA1B1C1A2B2C2.
6. Дано: FABC – пирамида, (A1B1C1)
|| (A2B2C2) || (ABC),
OO1 = O1O2 = O2F,
VA1B1C1A2B2C2 = 7. Найдите VABCA1B1C1.
85.
7. Дано: FABC – пирамида,
SABC = 16, S A1B1C1 = 9, OO1 = 6.
Найдите Vус. пир.
8. Дано: FABC – пирамида,
Vус. пир = 49, SABC = 25,
S A1B1C1 = 9. Найдите OO1.
9. Дано: FABC – пирамида,
10. Дано: FABC – пирамида,
VFA1B1C1=
VFABC.
ACB = 90°, AC = CB =
,
FO (ABC), FAO = FBO =
= FCO = 45°, (A1B1C1) || (ABC),
Найдите
.
. Найдите Vус. пир.
11. Дано: FABC – правильный
тетраэдр, CM AB, AK BC,
AK CM = O, NP || BC,
O NP, NL || BF, AB =
Найдите Vус. пир.
.
12. Дано: FABC – правильный тетраэдр,
CM AB, BK AC, ML || BF,
KL || CF, AB =
Найдите Vус. пир.
.
86.
Объем усеченной пирамиды
1. 14.
4. 2.
7. 74.
10. 21.
2. 56.
5. 7.
8. 3.
11.
.
3. 14.
6. 19.
9.
12.
.
.
87.
Объем конуса
ОБЪЕМ КОНУСА
Дан прямой круговой конус. ∆ABC 1. Дано: R = 6, BAO = 45 .
– осевое сечение.
Найдите Vконуса.
2. Дано: H = 3, BAO = 60 .
3. Дано: SABC = 9, ABC = 90 .
4. Дано: AB = 4, BAC = 30 .
5. Дано: H = 2, ABC = 120 .
88.
6. Дано: BC = 16, H = 4,
AM BC, AM = 3.
7. Дано: AC =
, ABC = 120 .
8. Дано: AB = BC = AC, H = 3.
9. Дано: OK BC, BK = 16,
KC = 9.
10. Дано: H = 4, cos = 0,6.
11. Дано: OM AB, OM = 6,
sin =
.
89.
Объем конуса
1. 72 .
2. 3 .
3. 9 .
4. 8 .
5. 8 .
6. 48 .
7. 8 .
8. 3 .
9. 1500 .
10. 12 .
11. 250 .
90.
ОБЪЕМ ВПИСАННОГО
ИЛИ ОПИСАННОГО КОНУСА
Найдите объем конуса.
1. Дано: Vцил = 81.
2. Дано: ABCDA1B1C1D1 – куб,
AB = 6.
3. Дано: ABCDA1B1C1D1 –
прямоугольный параллелепипед,
4. Дано: ABCDA1B1C1D1 – прямой
параллелепипед, AA1 = 3, AD = 4,
BAD = 30°.
AA1 = 3, AC =
.
5. Дано: DABC – правильная
пирамида, AC = 6, DC = 13.
6. Дано: DABC – пирамида,
AC = 6, ABC = 30°, DC = 10.
91.
7. Дано: DABC – пирамида,
ABC = 45°, AC =
, DC = 5.
8. Дано: DABC – пирамида,
DO (ABC), O AB, AC = 6,
BC = 8, AD = 13.
9. Дано: FABCD – правильная 10. Дано: FABCD – правильная
пирамида, Vпирамиды = 12.
пирамида, Vпирамиды = 12.
11. Дано:
DABC
–
пирамида, Vпирамиды =
правильная 12. Дано:
.
DABC
–
пирамида, Vпирамиды =
правильная
.
Объем вписанного или описанного конуса
1. 27.
2. 18 .
3. 4 .
4. .
7. 16 .
5. 4 .
8. 100 .
6. 96 (r = 6 по теореме синусов).
10. 6 .
11. .
9. 3 . 12. 4 .
92.
ОБЪЕМ УСЕЧЕННОГО КОНУСА
Дан усеченный конус. ABCD –
осевое сечение.
Найдите объем конуса.
1. Дано: r = 1, R = 6, AB = 5.
2. Дано: r = 4, R = 7, BAD = 45 .
3. Дано: AO = 6, BAO = OAQ = =
30 .
4. Дано: OQ = 3, AB = BO,
OAQ = 30 .
5. Дано: AD = 12, AC CD,
BAC = CAD.
93.
6. Дано: AB = BC = CD = 6,
AC CD.
7. Дано: BC = 6, AD = 12, в ABCD
можно вписать окружность.
8. Дано: AB = 5, BC = 2, в ABCD
можно вписать окружность.
9. Дано: AD = 8, PABCD = 20,
в ABCD можно вписать
окружность.
10. Дано: ABCQ – ромб, AD = 12.
11. Дано: AQB = BQC = CQD =
= 60°, AB = BC = 6.
Объем усеченного конуса
1. 31 .
4. 57 .
7.
2. 93 .
5.
.
8. 28 .
3. 57 .
6.
.
9. 28 .
.
10.
.
11.
.
94.
ОБЪЕМ УСЕЧЕННОГО КОНУСА
В конусе проведено сечение
параллельно основанию.
AQ = R, BO = r, FQ = H,
OQ = h, Sосн = S, Sсеч = S1.
1. Дано: BO = 1, AQ = 3,
Vконуса = 27.
Найдите Vусеч. конуса.
2. Дано: H = 6, h = 4, Vусеч. конуса = 52.
Найдите Vконуса.
3. Дано: R = 6, r = 3, H = 12.
Найдите Vусеч. конуса.
4. Дано: H = 12, h = 4, Vконуса = 54.
Найдите Vусеч. конуса.
5. Дано: h : H = 2 : 3.
Найдите
.
6. Дано: S1 : S2 = 1 : 9.
7. Дано:
Найдите
.
.
95.
Найдите
.
8. Дано: H = 9, R = 3, S1 = .
Найдите Vусеч. конуса.
9. Дано: S1 = 9 , S1 : S = 1 : 4,
H – h = 4.
Найдите Vусеч. конуса.
10. Дано: H = 9, S = 36 ,
FO : FQ = 2 : 3.
Найдите Vусеч. конуса.
11. Дано: H = 20, R = 25,
FO : FQ = 2 : 5.
Найдите Vусеч. конуса.
96.
Объем усеченного конуса
1. 26.
4. 38.
7.
.
2. 54.
5.
.
8. 26 .
3. 126 .
6.
.
9. 84 .
10. 76 .
11. 3900 .
97.
Объем шара и площадь сферы
ПЛОЩАДЬ СФЕРЫ
1. Дано: O – центр шара,
вписанного в цилиндр, ABCD –
осевое сечение цилиндра.
Найдите
.
2. Дано: O – центр шара,
вписанного в конус, ABC – осевое
сечение конуса, BAC = 60 , AB =
6.
Найдите Sсф.
3. Дано: O – центр шара,
вписанного в конус, ABC – осевое
сечение конуса, AC = 12, AB = 10.
Найдите Sсф.
4. Дано: ABCD – осевое сечение
цилиндра, O – центр шара,
описанного вокруг цилиндра, AB =
8, AD = 6. Найдите Sсф.
5. Дано: ABCD – осевое сечение
усеченного конуса, O – центр шара,
описанного вокруг усеченного
конуса, AC = 2, CDA = 30 .
Найдите Sсф.
6. Дано: O – центр шара,
описанного вокруг конуса, ABC –
осевое сечение конуса, AB = 2,
ABC = 120 . Найдите Sсф.
98.
7. Дано: O – центр шара,
вписанного в цилиндр, ABCD –
осевое сечение цилиндра, Sсф = 6.
Найдите Sбок. цил.
8. Дано: O – центр шара,
описанного вокруг конуса, ABC –
осевое сечение конуса, AB = BC = AC
9. Дано: O – центр шара,
описанного вокруг конуса, ABC –
осевое сечение конуса, AB = BC =
AC.
10. Дано: O – центр шара,
описанного вокруг конуса, ABC –
осевое сечение конуса, O лежит на
Найдите
=
.
Найдите Sсф.
основании конуса, Sбок. кон =
Найдите Sсф.
.
.
11. Дано: O – центр шара,
вписанного в усеченный конус,
ABCD – осевое сечение усеченного
конуса, AO1 = 2, BO2 = 1.
Найдите Sсф.
12. Дано: ABCD – осевое сечение
усеченного конуса, O – центр шара,
описанного вокруг усеченного
конуса, BC = 2, BAD = 30 .
Найдите Sсф.
99.
Площадь сферы
1. 1.
2. 12 .
4. 100 .
5. 16 .
7. 6.
8. 16 .
10. 4.
11. 8 .
3. 12 .
6. 48 .
9.
12. 112 .
.
100.
ОБЪЕМ ШАРА
1. Дано: O – центр шара, вписанного 2. Дано: O – центр шара,
в цилиндр, ABCD – осевое сечение вписанного в цилиндр, ABCD –
цилиндра.
осевое сечение цилиндра, Vш =
Найдите
.
.
Найдите Vцил.
3. Дано: ABC – осевое сечение
конуса, О – центр шара,
описанного вокруг конуса, AB = AC
= 3.
Найдите Vш.
4. Дано: ABC – осевое сечение
конуса, О – центр шара,
вписанного в конус, BAC = 2 , tg
α = 0,6,
AC = 10. Найдите Vш.
5. Дано: ABC – осевое сечение
конуса, О – центр шара,
вписанного в конус, AB = 10, AC =
12.
Найдите Vш.
6. Дано: ABC – осевое сечение
конуса, О – центр шара,
описанного вокруг конуса, ABC =
120 ,
AB =
. Найдите Vш.
101.
7. Дано: ABC – осевое сечение
8. Дано: ABC – осевое сечение
конуса, О – центр шара,
конуса, О – центр шара,
описанного вокруг конуса, Vш = 12. описанного вокруг конуса, диаметр
Найдите Vкон.
основания равен
, BAC = 60 .
Найдите Vш.
9. Дано: ABC – осевое сечение
конуса, О – центр шара,
вписанного в конус, BQ = 9, BO =
2QO.
Найдите Vш.
10. Дано: шар вписан в куб,
Vкуба = 216. Найдите Vш.
11. Дано: в цилиндр с водой
поместили шар, причем уровень
воды поднялся на 1. Rцил = 6.
Найдите Rш.
12. Дано: из цилиндра с водой
вынули шар, причем уровень воды
упал на 2. Rш = 6.
Найдите Rцил.
102.
Объем шара
1. 1,5.
2. 16 .
3.
.
4. 36 .
5. 36 .
7. 3.
8. 36 .
10. 36 .
11. 3.
6. 36 .
9. 36 .
12. 12.

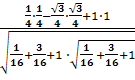 =0,7;
=0,7;











































