Как найти координаты вершин правильного шестиугольника - Исправление недочетов и поиск решений вместе с Examum.ru

	Найти вершин шестиугольника 20.01.2021, 18:03
20/01/21 4

kotenok gav	Re: Найти вершин шестиугольника 20.01.2021, 18:48
21/05/16 4294 Аделаида	Сначала найдите координаты точки (подсказка: какие координаты у центра тяжести треугольника?).

StepV	Re: Найти вершин шестиугольника 20.01.2021, 19:06
23/05/20 251 Беларусь	Здравствуйте, не могу понять как решается такая задача. Если это курс аналитической геометрии, то лучше решать этими методами. Тогда, т A начало прямоугольной и косоугольной системы координат. Надо: 1. Вычислить координаты всех точек в прямоугольной системе координат; 2. Найти матрицу пересчета из прямоугольной системы в косоугольную; 3. Пересчитать с помощью матрицы координаты всех точек. Для начала угол определить сможете?

Maximmmm	Re: Найти вершин шестиугольника 20.01.2021, 19:57
20/01/21 4

arseniiv

Re: Найти вершин шестиугольника

20.01.2021, 20:31

Заслуженный участник

27/04/09
28128

1. Вычислить координаты всех точек в прямоугольной системе координат;
2. Найти матрицу пересчета из прямоугольной системы в косоугольную;
3. Пересчитать с помощью матрицы координаты всех точек.

Выглядит очень неудобно. :-)

Я бы предложил достраивать чертёж: продолжать прямые, откладывать дальше на них отрезки и откладывать данные нам векторы. Тогда станет лучше видно, сколько раз отложенные целое число раз, куда они заведут, а потом останется просто поделить на какие-то числа ну и довести арифметикой дело до конца. Не обязательно стараться получить сразу только те точки, о которых спрашивается.

Пример: даёт нам точку , или $A + frac32 overrightarrow{AD}$ , и достроение чертежа вправо сделает это весьма наглядным. Значит, $D = A + frac23 (overrightarrow{AC} + overrightarrow{AE})$ , откуда координаты этой точки $(frac23, frac23)$ .

Выразив , теперь легко найти оставшиеся $B, F$ .

StepV	Re: Найти вершин шестиугольника 20.01.2021, 21:30
23/05/20 251 Беларусь	Выглядит очень неудобно. Задача явно учебная, поэтому тут важно не удобство, а какому курсу математики должно соответствовать решение. Если задачу задали по теме пересчет координат из одного базиса в другой, то пришлось бы решать именно по этому алгоритму.

arseniiv

Re: Найти вершин шестиугольника

20.01.2021, 22:14

Заслуженный участник

27/04/09
28128

Если задачу задали по теме пересчет координат из одного базиса в другой, то пришлось бы решать именно по этому алгоритму.

Но тогда очень вероятно дали бы координаты в исходном базисе уже готовые, чтобы не отвлекать. :-)

Модераторы: Модераторы Математики, Супермодераторы

Источник

Задание фигур в пространстве

Пусть
в пространстве введена система координат
Охуz.
Как мы показали, положение любой точки
однозначно определяется ее координатами.
Если Ф – некоторое множество точек (
фигура ), то всем ее точкам характерно
некоторое свойство, присущее только
точкам этой фигуры, а значит и для
координат точек этой фигуры выполняется
соотношение, присущее только точкам
этой фигуры.

Определение.
Пусть в
данной системе координат имеем некоторое
уравнение

F
(x,
y,
z)
= 0.
(1)

Уравнение
(1) называется уравнением фигуры Ф,
если координаты любой точки этой фигуры,
и только они, удовлетворяют этому
уравнению.

Следует
добавить, что уравнение (1) будет уравнением
фигуры Ф,
если выполняются два условия: 1) Если
М(
)

Ф, то координаты
(
)
удовлетворяют (1); 2) Если координаты (
)
удовлетворяют уравнению (1), то М(
)

Ф.

Под
уравнением фигуры мы понимаем не только
алгебраические уравнения, но и неравенства,
системы уравнений и неравенств, а также
их любые комбинации. Например, неравенство

(х
–- )²
+(у – )²
+ (z
– )²

R²

является
уравнением шара с центром в точке Q(;
;
)
и радиусом R.

Аналогично
определяется уравнение фигуры на
плоскости, только в системе координат
Оху.

Уравнение

является уравнением точек первой
четверти, причем точки, лежащие на осях
координат, не принадлежат данному
множеству.

Пример
1. Центр
О и вершина
А
правильного шестиугольника ABCDEF
имеют координаты О(–1;
2), А(1;
4). Найти
координаты остальных вершин.

Решение.
Так как точка
О является
серединой отрезка АD,
то находим координаты точки D.
Обозначим
D(х;
у), тогда
согласно (3) имеем:

Отсюда
получим: х
= – 3, у = 0. D(-3;
0).

Так
как данный шестиугольник правильный,
то АВО и
AFO
– правильные треугольники. Значит,
точки В
и F
являются точками, равноудаленные от
точек А
и О.
Пусть В(х;
у). Из условия
|AB|
= |OB|
= |OA|
получим |AВ|²
= |ОB|²
= |ОА|².
В координатной форме это выглядит так:

Следовательно,
B(
;3-
)
и
F
(–
;
3 +
).

Так
как точки Е
и С
симметричны точкам В
и F
относительно точки О,
то находим их координаты аналогично
тому, как мы находили координаты точки
D.
Обозначим Е(х;
у), тогда
согласно (3) имеем:

Отсюда
получим: х
= – (
+2),
у = 1+
.
Е(-(
+2);1+
).

Обозначим
С(х; у),
тогда согласно (3) имеем:

Отсюда
получим: х
=

-2,
у = 1-
.
С(
-2;
1-
).

Ответ:
С(
-2;
1-
),
Е(-(
+2);1+
),
B(
;3-
),
F
(–
;
3 +
),
D(–
3;0).

Пример
2. Найти
уравнение множества всех точек плоскости,
для каждой из которых сумма квадратов
расстояний до осей координат равна 5.

Решение.
Рассматриваем систему координат О
.
Обозначим заданное множество точек
F,
а М (х; у)
– произвольную точку плоскости.

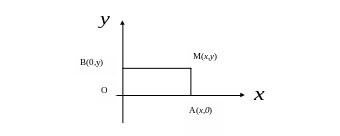
Тогда,
согласно условию задачи, получим

М

F

|MB|²
+ |MA|²
= 5.

В
координатах последнее уравнение имеет
вид

х²+
у²
= 5.

Получили
известное уравнение окружности с центром
в начале координат и радиусом равным

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

А мне нравится такое на комплексных числах считать. То же, что и с синусами, но элегантнее.
Вот пример на питоне:

from math import e, pi
f=lambda c, r, n=3, fi0=0: [c+r*e**(1j*(2*pi/n*i+fi0)) for i in range(n)]

Получим функцию f которая может рассчитать точки любого вписанного n-угольника:

>>> f(c=250+250j, r=250)
[(500+250j),
 (375+466.50635094610965j),
 (125.00000000000006+466.5063509461097j),
 250.00000000000003j,
 (124.99999999999989+33.49364905389041j),
 (374.99999999999983+33.49364905389024j)]

А если надо обяательно кортежами, а не комплексными точками. то вот:

>>> [(round(p.real), round(p.imag)) for p in f(c=250+250j, r=250, n=5, fi0=pi/2)]
[(250, 500), (12, 327), (103, 48), (397, 48), (488, 327)]

Тут, заметьте, пятиугольник, причем вершинкой вниз (при оси Y, направленной вниз).

Чтобы было понятно как это работает…
Представим, что центр окружности в нуле координат. Нам нужно 6 точек, смещенных относительно нуля на радиус под нужными углами: 0, 60, 120, 180, 240 и 300 градусов. В формулах мы. конечно используем радианы: pi — это 180 градусов.
Чтобы повернуть единичный вектор на какой-то угол, нужно его просто домножить на e в степени мнимая единица, умноженная на угол. Поскольку единичный вектор на комплексной плоскости это просто 1, то его даже писать не надо. Просто возводим e в нужную степень и получаем нужный вектор в виде комплексного числа. Осталось его домножить на требуемый радиус (он при этом удлинится: был длиной 1, а станет r) и добавить к нему желаемый центр (тоже в виде комплексного числа, где реальная часть — X, а мнимая — Y).
Вот и всё!
Красота же?..

Да, забыл сказать, что если нужно повернуть весь n-угольник на какой-то угол, то для этого есть там параметр fi0, который по умолчанию ноль.
c — это координаты центра в комплексной форме. Например если X=30, а Y=40, то c=30+40j.
n — это число вершин.
r — радиус.
И да, в javascript’е нет такого элегантного способа работать с комплексными числами, как в питоне. Но для js есть много библиотек для работы с комплексными числами. Будет не так компактно и красиво, как на питоне, но в целом всё точно так же в плане математики.

UPD: Исправил функцию. Там скобочек не хватало, поэтому поворот на fi0 работал неверно. Теперь все как надо.

Источник

Как можно рассчитать координаты вершин правильного шестиугольника (известен радиус описаннного круга, его центр)?

Вот попробовал сделать
center_x — X центра круга
center_y — Y центра круга
radius — радиус круга
Точка А: ( center_x — radius, center_y)
Точка B: ( center_x — (radius/2), ?)
Точка С: (center_x + (radius/2), ?)
Точка D: (center_x + radius, center_y)
Точка Е: (center_x + (radius/2, ?)
Тока F: (center_x — (radius/2), ?)

Как можно рассчитать y точек?

Добавлено через 38 минут
Разобрался, может кому понадобится:

C++

out << "Hexahedron(center(" << ring.m_x << ", " << ring.m_y << "); color " << ring.m_color; 
    out << "Point A(" << ring.m_x - ring.m_radius << ", " << ring.m_y << ");";
    out << "Point B(" << ring.m_x - (ring.m_radius/2) << ", " << ring.m_y + (((ring.m_x + ring.m_radius)*sqrt(3))/2 )<< ");";
    out << "Point C(" << ring.m_x + (ring.m_radius / 2) << ", " << ring.m_y + (((ring.m_x + ring.m_radius) * sqrt(3)) / 2) << ");";
    out << "Point D(" << ring.m_x + ring.m_radius << ", " << ring.m_y << ");";
    out << "Point E(" << ring.m_x + (ring.m_radius / 2) << ", " << ring.m_y - (((ring.m_x + ring.m_radius) * sqrt(3)) / 2) << ");";
    out << "Point F(" << ring.m_x - (ring.m_radius / 2) << ", " << ring.m_y - (((ring.m_x + ring.m_radius) * sqrt(3)) / 2) << ");";

Источник

Well, they are exactly the 8 ones obtained as permutations (instead of your said «16 combinations») of that given vertex pair.

Just as the vertices of the 3D cross-polytope, the octahedron, are the 6 ones obtained as permutations of $(0, 0, pmfrac1{sqrt2})$, or the vertices of the 2D cross-polytope, the square, are the 4 ones obtained as permutations of $(0, pmfrac1{sqrt2})$.

In fact, the general cross-polytope is just defined to be the convex hull of all points on all Cartesian axes (both directions each), which are $frac1{sqrt2}$ off.

Just as the general hypersphere is defined by the set of points, which bow to $||x||_2=sqrt{sum_i x_i^2}=const$, so the surface of the general cross-polytope would follow to $||x||_1=sum_i |x_i|=const$. Within your chosen scaling the latter constant happens to be dimension dependent, $const(D)=frac D{sqrt2}$. Thereby it is chosen such that the edge length of the thus constructed cross-polytope in any dimension would become unity. Btw. the surface of the general measure-polytope similarily would follow $||x||_{infty}=max_i |x_i|=const$.

— rk

Источник