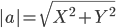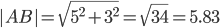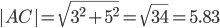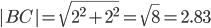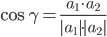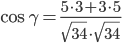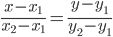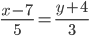Как найти координаты вершин равностороннего треугольника

Найдите координаты вершины С равностороннего треугольника АВС, если А (2; -3) и В (-2; 3).

Ваш ответ

решение вопроса

Похожие вопросы

• Все категории
• экономические 43,284
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,093
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Как найти вершину равностороннего треугольника

Ключевые слова: треугольник, сторона, угол, окружность вписанная, описанная

Треугольник — простейший многоугольник, имеющий 3 вершины и 3 стороны; часть плоскости, ограниченная тремя точками, не лежащими на одной прямой, и тремя отрезками, попарно соединяющими эти точки.

Вершины треугольника обычно обозначаются заглавными латинскими буквами (A, B, C), величины углов при соответственных вершинах — греческими буквами ($$alpha, beta, gamma$$), а длины противоположных сторон — прописными латинскими буквами (a, b, c).

Правильный треугольник или равносторонний треугольник — правильный многоугольник с тремя сторонами. Все стороны равны между собой, и все углы равны 60° (или $$frac<pi><3>$$).

Пусть t — сторона правильного треугольника, R — радиус описанной окружности, r — радиус вписанной окружности.

• Радиус вписанной окружности правильного треугольника, выраженный через его сторону $$r = frac<sqrt<3>><6>cdot t$$.
• Радиус описанной окружности правильного треугольника, выраженный через его сторону $$R = frac<sqrt<3>><3>cdot t$$.
• Периметр правильного треугольника равен $$P = 3t = 3 sqrt<3>R = 6sqrt<3>r$$.
• Высота правильного треугольника: $$h = frac<sqrt<3>><2>t$$.
• Площадь правильного треугольника рассчитывается по формулам: $$S = frac<sqrt<3>><4>t^ <2>= frac<3sqrt<3>><4>R^ <2>= 3 sqrt<3>r^<2>$$.

Свойства равностороннего треугольника: теория и пример задачи

В данной статье мы рассмотрим определение и свойства равностороннего (правильного) треугольника. Также разберем пример решения задачи для закрепления теоретического материала.

Определение равностороннего треугольника

Равносторонним (или правильным) называется треугольник, в котором все стороны имеют одинаковую длину. Т.е. AB = BC = AC.

Примечание: правильный многоугольник – это выпуклый многоугольник, имеющий равные стороны и углы между ними.

Свойства равностороннего треугольника

Свойство 1

В равностороннем треугольнике все углы равны 60°. Т.е. α = β = γ = 60°.

Свойство 2

В равностороннем треугольнике высота, проведенная к любой из сторон, одновременно является биссектрисой угла, из которого она проведена, а также медианой и серединным перпендикуляром.

CD – медиана, высота и серединный перпендикуляр к стороне AB, а также биссектриса угла ACB.

Свойство 3

В равностороннем треугольнике биссектрисы, медианы, высоты и серединные перпендикуляры, проведенные ко всем сторонам, пересекаются в одной точке.

Свойство 4

Центры вписанной и описанной вокруг равностороннего треугольника окружностей совпадают и находятся на пересечении медиан, высот, биссектрис и серединных перпендикуляров.

Свойство 5

Радиус описанной вокруг равностороннего треугольника окружности в 2 раза больше радиуса вписанной окружности.

• R – радиус описанной окружности;
• r – радиус вписанной окружности;
• R = 2r.

Свойство 6

В равностороннем треугольнике, зная длину стороны (условно примем ее за “a”), можно вычислить:

1. Высоту/медиану/биссектрису:

2. Радиус вписанной окружности:

3. Радиус описанной окружности:

4. Периметр:

5. Площадь:

Пример задачи

Дан равносторонний треугольник, сторона которого равна 7 см. Найдите радиус описанной вокруг и вписанной окружности, а также, высоту фигуры.

Решение
Применим формулы, приведеные выше, для нахождения неизвестных величин:

Как найти вершину треугольника?

Для того чтобы найти координаты вершины равностороннего треугольника, если известны координаты двух других его вершин, нужно воспользоваться одним из предложенных способов.

1 способ (графический)

1. В системе координат отмечаем две заданные вершины.
2. Ставим ножку циркуля в одну из построенных точек.
3. Проводим окружность с радиусом, равным расстоянию между отмеченными вершинами.
4. Таким же образом чертим вторую окружность с тем же радиусом, но из второй отмеченной точки.
5. Точки пересечения проведённых окружностей определяют вершины треугольников (их получится два).
6. Определяем координаты полученных точек, исходя из полученного чертежа.

Данный способ позволяет точно построить третью вершину. Однако определение координат является приблизительным. Метод хорошо использовать для иллюстрации.

2 способ (аналитический)

Решение задачи основано на применении формулы нахождения расстояния между двумя точками: d(A(x1;y1);B(x2;y2))=√((x2-x1)^2+(y2-y1)^2)

1. Пусть имеются вершины A(x1;y1) и B(x2;y2) треугольника АВС. Обозначим координаты третьей вершины x и y (то есть, С(x;y))
2. Составляем соотношения
   AC=√((x-x1)^2+(y-y1)^2)
   BC=√((x-x2)^2+(y-y2)^2)
   AB=√((x2-x1)^2+(y2-y1)^2)
3. Учитывая, что треугольник равносторонний, составляем систему уравнений:
   AC=BC
   AC=AB
   Или система уравнений:
   √((x-x1)^2+(y-y1)^2)= √((x-x2)^2+(y-y2)^2)
   √((x-x1)^2+(y-y1)^2)= √((x2-x1)^2+(y2-y1)^2)
4. Методом подстановки решаем полученную систему.

Теперь вы знаете, как найти вершину треугольника.

Внимание! Оба случая применимы только для равностороннего треугольника.
Для равнобедренного или любого другого произвольного треугольника для нахождения координат третьей вершины требуются дополнительные данные (например, значение некоторых отрезков или углов).

Уравнение описанной окружности

Как составить уравнение описанной около треугольника окружности по координатам его вершин? Как найти координаты центра описанной окружности? Как найти радиус описанной окружности, зная координаты вершин треугольника?

Решение всех этих задач сводится к одной — написать уравнение окружности, проходящей через три данные точки. Для этого достаточно подставить координаты точек (вершин треугольника) в уравнение окружности. Получим систему из трёх уравнений с тремя неизвестными: координатами центра и радиусом окружности.

Составить уравнение описанной окружности для треугольника с вершинами в точках A(2;1), B(6;3), C(9;2).

Подставив координаты вершин треугольника в уравнение окружности

получим систему уравнений

Вычтем из первого уравнения системы второе:

Теперь из второго уравнения системы вычтем третье:

Приравняем правые части равенств b=-2a+10 и b=3a-20:

Подставим в первое уравнение системы a=6 и b=-2:

a и b — координаты центра окружности, R — её радиус. Таким образом, точка (6;-2) — центр описанной около треугольника ABC окружности, радиус R=5, а уравнение описанной окружности

Для решения аналогичной задачи для четырёхугольника либо многоугольника достаточно знать координаты трёх его вершин.

Прямая на плоскости

Построение графика функции методом дифференциального исчисления

Экстремум функции двух переменных

Пример . В задачах даны координаты точек A , B , C . Требуется: 1) записать векторы AB и AC в системе орт и найти модули этих векторов; 2) найти угол между векторами AB и AC .
Решение.
1) Координаты векторов в системе орт. Координаты векторов находим по формуле:
X=x_j-x_i; Y=y_j-y_i
здесь X , Y координаты вектора; x_i , y_i — координаты точки А_i ; x_j , y_j — координаты точки А_j
Например, для вектора AB: X=x₂-x₁=12-7=5 ; Y=y₂-y₁=-1-(-4)=3
AB(5;3), AC(3;5), BC(-2;2)
2) Длина сторон треугольника. Длина вектора a(X;Y) выражается через его координаты формулой:




3) Угол между прямыми. Угол между векторами a₁(X₁;Y₁) , a₂(X₂;Y₂) можно найти по формуле:

где a₁a₂=X₁X₂+Y₁Y₂
Найдем угол между сторонами AB и AC

γ = arccos(0.88) = 28.07 0
Уравнение прямой. Прямая, проходящая через точки A₁(x₁; y₁) и A₂(x₂; y₂) , представляется уравнениями:

Уравнение прямой AB . Каноническое уравнение прямой: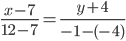
или
y= 3 /₅x- 41 /₅ или 5y-3x+41=0

Let $C = (a, b)$ be any given point in the plane, and let $r$ be any given positive real number. Then how to find the coordinates of the vertices of an equilateral triangle inscribed in the circle
$$
left{ (x, y) in mathbb{R}^2 colon (x-a)^2 + (y-b)^2 = r^2 right}?
$$

My Attempt:

Let $P$, $Q$, $R$ be the vertices one such equilateral triangle. Then we have
$$
triangle PCQ cong triangle QCR cong triangle RCP.
$$
So we have
$$
angle PCQ cong angle QCR cong angle RCP,
$$
which implies that
$$
m angle PCQ = m angle QCR = m angle RCP = frac{pi}{3}.
$$
Moreover, we also have
$$
vec{OP} = vec{OC} + vec{CP}.
$$
If $alpha$ is the angle that $vec{CP}$ makes with the positive $x$-axis, where $0 leq alpha < 2 pi$, then we have
$$
vec{OP} = (a + r cos alpha ) hat{i} + ( b + r sin alpha ) hat{j}.
$$
Thus we have
$$
P = big( a + r cos alpha, b + r sin alpha big).
$$
Since the angle between the vectors $vec{CP}$ and $vec{CQ}$ and the angle between $vec{CQ}$ and $vec{CR}$ is $frac{pi}{3}$, we have
$$
vec{OQ} = vec{OC} + vec{CQ} = left( a + r cos left( alpha + frac{pi}{3} right) right) hat{i} + left( b + r sin left( alpha + frac{pi}{3} right) right) hat{j},
$$
and therefore we have
$$
Q = left( a + r cos left( alpha + frac{pi}{3} right) , , , b + r sin left( alpha + frac{pi}{3} right) right).
$$
Similarly, we have
$$
R = left( a + r cos left( alpha + frac{2pi}{3} right) , , , b + r sin left( alpha + frac{2 pi }{3} right) right).
$$

Is my solution correct and clear enough? Or, are there any problems?

Элементы аналитической геометрии

§1. Метод координат на плоскости

1. Декартовы прямоугольные координаты

Выберем на плоскости
две взаимно перпендикулярные прямые:
Ох и Оу с
указанными на них положительными
направлениями.

Ох, Оу – координатные
оси.

О – начало координат

За положительное
направление на оси Ох примем направление
слева направо, а за положительное
направление на Оу — сверху вниз.

Возьмем некоторую
единицу масштаба, с помощью которой
будут производиться все измерения на
плоскости ХОУ.

Совокупность
координатных осей Ох, Оу и выбранная
единица масштаба называется
декартовой прямоугольной системой
координат на плоскости.

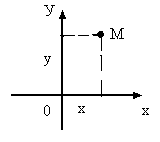
Произвольной точке
М на плоскости поставим в соответствии
два числа: абсциссу х, равную расстоянию
от точки М до оси Оу, взятому со знаком
«+», если точка М лежит правее оси Оу и
со знаком «-», если точка М лежит левее
оси Оу; ординату у равную расстоянию от
точки М до оси Ох, взятому со знаком «+»
, если М лежит выше Ох и со знаком «-»,
если М лежит ниже Ох.

Абсцисса х
и ордината у
называются декартовыми
прямоугольными
координатами
точки М и
обозначаются М (х; у).

Отметим, что каждой
точке плоскости соответствует пара
действительных чисел х
и у.
Верно и обратное, каждой паре действительных
чисел х
и у
соответствует 1 точка плоскости. Это
значит, что на плоскости положение
произвольной точки М полностью
определяется
ее координатами х
и у.

Координатные оси
Ох и Оу разбивают плоскость на I-ый
— IV-ый
координатные углы.

	I	II	III	IV
х	+			+
у	+	+		

2. Полярные координаты

Зафиксируем на
плоскости точку О и выходящую из нее
полупрямую Ор, а также выберем единицу
масштаба.

О– полюс

Ор
– полярная ось

Произвольной точке
М плоскости поставим в соответствие 2
числа: полярный радиус (г), равный
расстоянию от точки М до полюса О,
измеренному в выбранной единице масштаба.

Полярный угол 
(фи), 
измеряется в радианах:





Полюсу О соответствует
полярный г=0; полярный угол для него не
определен.

3. Связь между прямоугольной декартовой системой координат и полярной системой координат.

П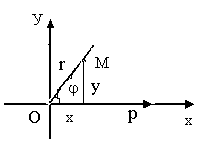усть
точка М задана в полярной системе
координат, т.е. она характеризуется
полярным радиусом г и полярным углом.
Найдем прямоугольные декартовые
координаты данной точки.

 OLM
– прямоугольный

cos

=
;sin

=

(1)

Пусть точка М
задана своими прямоугольными декартовыми
координатами. Найдем полярные координаты
данной точки

Дано х и у. Найти
r
и 

Из треугольника

OLM:

(2);

=arctg;

Формулы (1) и (2)
верны при любом расположении точки М.

Пример 1.

Дана точка А с
координатами: х = 1, у = 1. Найдем полярные
координаты точки А.

r==,tg==1
=arctg1
=.

Пример
2.

Даны полярные
координаты точки А: r=2,
=.
Найдем ее прямоугольные координаты.

Пользуясь формулами
(1), находим х=r·cos=r·cos=0,у=r·sin=r·sin=2.

4. Основные задачи, решаемые методом координат

I.
Задача о расстоянии между двумя точками.

Даны точка М₁
(х₁,
у₁)
и точка М₂
(х₂,
у₂).
Найти расстояние М₁М₂=d.

M₁NM₂
– прямоугольный.

По теореме Пифагора:
d
=

M₁N
= x₂
– x₁
(расстояние
между двумя точками на числовой оси)

NM₂
= y₂
– y₁

(3) d
=

Пример 3.

Дана точка А(-1;-2),
В(-4;2), d=АВ-?

Решение.

По формуле (3):
d===5.

II.
Задача о делении отрезка в данном
отношении.

Дано:

М₁
(х₁;
у₁),
М₂
(х₂;
у₂),

= .
М (х; у) -?

По
теореме Фалеса о пересечении сторон
угла параллельными прямыми будет
выполняться соотношение:

=

M₁N=x₂–x₁,
NM₂=y₂–y₁,
=,

 (x₂–x)=х-x₁,

x₂-х=х-x₁,
х+х=x₂+x₁,

(4) х=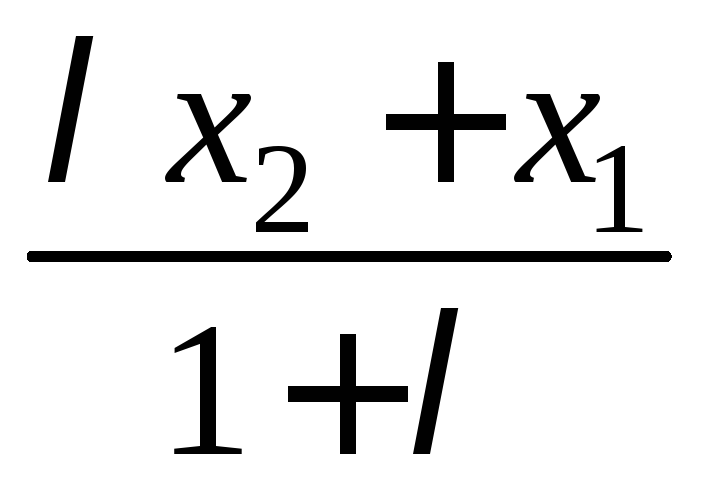; у=.

Пример 4.

М₁(1;1),
М₂
(4;7),
=2.
М (х; у) -?

Решение.

Применим формулы
(4). λ=2, х==3;
у==5М
(3; 5).

Решение задач

Задача 1.
Определить координаты вершин
равностороннего треугольника, лежащего
в I-ом
квадрате со стороной 10, если один из его
вершин совпадает с началом координат
(т.О), а основание треугольника расположено
на оси Ох.

Решение.

По условию О (0; 0),
С (10; 0). Так как треугольник равносторонний,
то В (5; y).

Найдем расстояние
ОВ по формуле (3).

10 =
,
100=25+y²,
у²
=75, у =

В = (5;
).

Задача
2. Найти
координаты вершин квадрата, если его
диагональ d
= 5 ед. длины.

Решение.

О (0;0) – точка
пересечения диагоналей,

Диагонали — на
осях координат

А (0; -2,5), С (0; 2,5), В
(2,5; 0), D
(-2,5; 0)

Задача 3.
На оси абсцисс найти точку, находящуюся
на расстоянии d
= 10 от точки А (2; 6).

Решение.

Так как точка М
лежит на оси Ох, то ее координаты М(х;
0). Применим формулу (3):10=,
(2-х)²+36=100,
(2-х)² =64,
2–х=8,

2-х=8x=-6,
2-х=-8x=10.

Или: х²–4х+4=64,
х²–4х-60=0,

D=16-4·1·(-60)=16+240=256

x_1,2=,x₁=10,
x₂=-6.

M₁
(10; 0) и M₂
(-6; 0)

Задача 4.
Найти точку М(х;у), равноудаленную от
точек О(0;0), А(-4;0) и В(0;8)

Решение.

ОМ=МА=МВ 
ОМ²=МА²=МВ²

ОМ²=х²+у²
, МВ²=х²+(у-8)²,
МА²=(х+4)²+у²

х²
+у²
=х²+(у-8)², х²+у²
=(х+4)²+у²,

у²
=у²-16у+64, х²=х²+8х+16,-

16y=64, -8х
= 16,

у=4, х
= -2,

М (-2; 4)

Задача
5. Вычислить
площадь равностороннего треугольника,
если заданы две его вершины: А (-3; 2) и С
(1; 6).

Решение.

S_=,
а=АС, АС=

S_=.

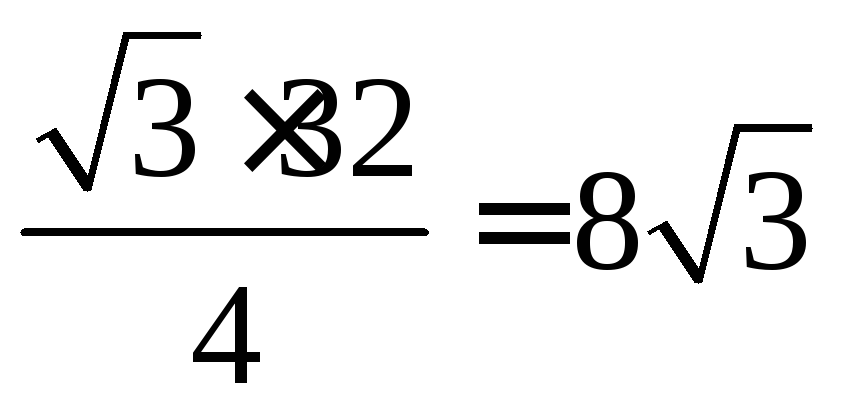
Задача 6.
Построить точки по их полярным координатам:
А(5;0), В(2;),
С(3;),
D(1;).

Решение.

Задача 7.
Найти полярные координаты точек А (1;
1), В (0; 2), С (-3; 3).

Решение.

А:r=;=arctg1=,
А,

B: r=2; 
=arctg0=,В,

C: r==;
=arctg(-1)=,С.

Задача 8.
Какие прямоугольные координаты имеют
точки, заданные полярными координатами
А(5; 0), В,
С?

Решение.

А:
х=r·cos=5·1
=5; у=r·sin=5·0=0;
А(5;0),

В: х=6·cos45^о
=6·=3;
у=6·=3;

В(3;3)

С: х=2·0=0;
у=2·1=2,
С(0;2).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Математические приемы для определения равностороннего треугольника по координатам его вершин

Равносторонний треугольник — это треугольник, у которого все стороны равны друг другу. Математические приемы для определения равностороннего треугольника по координатам его вершин основаны на использовании формулы расстояния между двумя точками на плоскости.

Для определения расстояния между двумя точками на плоскости используется формула расстояния между двумя точками в декартовой системе координат:

$d=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

где $d$ — расстояние между точками $(x_1,y_1)$ и $(x_2,y_2)$.

Для определения равностороннего треугольника по координатам его вершин необходимо измерить расстояния между всеми парами вершин. Если все три измерения будут одинаковы, то треугольник будет равносторонним.

Пример:

Пусть даны координаты вершин треугольника: $A(1,1)$, $B(5,6)$ и $C(9,1)$. Необходимо определить, является ли этот треугольник равносторонним.

1. Измеряем расстояния между всеми парами вершин:

$d_{AB}=sqrt{(5-1)^2+(6-1)^2}=5sqrt{2}$

$d_{AC}=sqrt{(9-1)^2+(1-1)^2}=8$

$d_{BC}=sqrt{(9-5)^2+(1-6)^2}=5sqrt{2}$

1. Если все три измерения будут одинаковы, то треугольник будет равносторонним. В данном случае, $d_{AB}=d_{BC}=5sqrt{2}$ и $d_{AC}=8$, поэтому данный треугольник не является равносторонним.

Таким образом, математические приемы для определения равностороннего треугольника по координатам его вершин основаны на использовании формулы расстояния между двумя точками на плоскости. Для определения равностороннего треугольника необходимо измерить расстояния между всеми парами вершин и проверить, являются ли они одинаковыми.