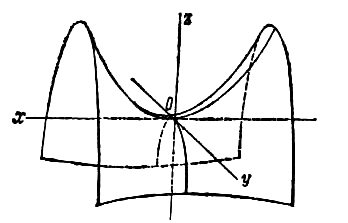
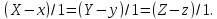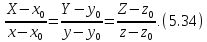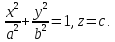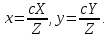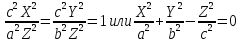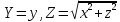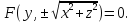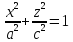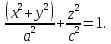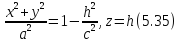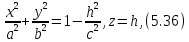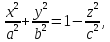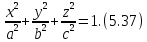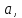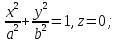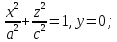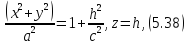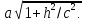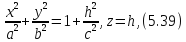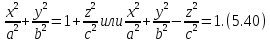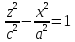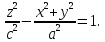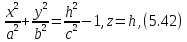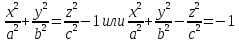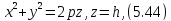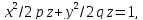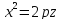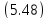Конусы: определение, сечения, построение
Конусом называется поверхность, определяемая в некоторой прямоугольной системе координат каноническим уравнением
(4.50)
где — положительные параметры, характеризующие конус, причем
.
Начало координат называется центром конуса (рис.4.44,а).
Конус является конической фигурой, поскольку вместе с любой своей точкой уравнению (4.50) удовлетворяют также все точки
при
луча
. Точка
является вершиной конуса (4.50), а любой луч
, принадлежащий конусу, является его образующей.
Плоские сечения конуса
Сечения конуса координатными плоскостями представляют собой пары пересекающихся прямых, удовлетворяющих в этих плоскостях уравнениям
(при
) или
(при
) соответственно.
Рассмотрим теперь сечение конуса плоскостями, параллельными плоскости . Подставляя
, где
— произвольная постоянная (параметр), в уравнение (4.50), получаем
При этому уравнению удовлетворяет одна вещественная точка — начало координат. При любом отличном от нуля значении параметра
уравнение определяет эллипс
с полуосями
. Следовательно, сечение конуса плоскостью
представляет с собой эллипс, центр которого лежит на оси аппликат, а вершины принадлежат координатным плоскостям
и
.
Таким образом, конус можно представить как поверхность, образованную эллипсами, центры которых лежат на оси аппликат, а вершины принадлежат координатным плоскостям и
(см. рис.4.44,а).
Круговой конус
При все сечения конуса плоскостями
становятся окружностями. Такой конус является фигурой вращения и называется прямым круговым конусом. Он может быть получен в результате вращения, например, прямой
(образующей) вокруг оси аппликат (рис.4.44,б).
Замечания 4.10.
1. Конус является линейчатой поверхностью, поскольку может быть получен при помощи перемещения прямой.
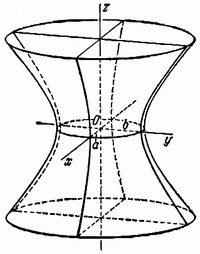
2. Конус, образованный асимптотами гипербол, получающихся при пересечении гиперболоида плоскостями, проходящими через ось , называется асимптотическим конусом этого гиперболоида. На рис.4.44,в изображен асимптотический конус для однополостного и двуполостного гиперболоидов.
3. Конус (4.50) может быть получен из прямого кругового конуса (у которого
) в результате двух сжатий (растяжений) к координатным плоскостям
и
.
4. Начало канонической системы координат является центром симметрии конуса, координатные оси — осями симметрии конуса, координатные плоскости — плоскостями симметрии конуса.
В самом деле, если точка принадлежит конусу, то точки с координатами
при любом выборе знаков также принадлежат конусу, поскольку их координаты удовлетворяют уравнению (4.50).
5. Рассмотрим сечение прямого кругового конуса плоскостями, не проходящими через его вершину, например, плоскостями
, где
— произвольная постоянная (параметр) — угловой коэффициент прямой
в плоскости
. Заметим, что образующие рассматриваемого конуса в плоскости
описываются уравнением
с угловым коэффициентом
. Подставляя
в уравнение конуса, получаем
Это уравнение проекции на координатную плоскость линии пересечения плоскости с конусом. Вычисляем инварианты
При имеем
. По таблице 3.2 определяем, что рассматриваемое сечение, которое пересекает все образующие прямого кругового конуса, является эллипсом. При
имеем
. По таблице 3.2 определяем, что рассматриваемое сечение, которое параллельно двум образующим кругового конуса, является гиперболой. При
имеем
. По таблице 3.2 определяем, что рассматриваемое сечение, которое параллельно одной образующей кругового конуса, является параболой. Поскольку при аффинных преобразованиях тип линий не изменяется, такой же вывод можно сделать для произвольного конуса (4.50):
– сечение конуса плоскостью, пересекающей все его образующие, является эллипсом (рис.4.45,а);
– сечение конуса плоскостью, параллельной двум его образующим, является гиперболой (рис.4.45,б);
– сечение конуса плоскостью, параллельной одной его образующей, является параболой (рис.4.45,в).
6. Конические сечения могут быть взяты в качестве эквивалентных определений эллипса, гиперболы, параболы.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
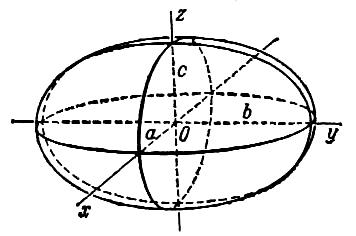
Эллипсоидом
называется поверхность, которая в некоторой
системе декартовых прямоугольных координат
определяется уравнением
(1).
Уравнение (1) называется каноническим
уравнением эллипсоида. Величины a,
b, c суть полуоси эллипсоида (рис. 1). Если все
они различны, эллипсоид называется трехосным; в
случае, когда какие-нибудь две из них одинаковы,
эллипсоид называется вытянутым, при a=b>c — сжатым. В случае, когда a=b=c, эллипсоид представляет
собой сферу.
Гиперболоидами называются
поверхности, которые в некоторой системе
декартовых прямоугольных координат
определяются уравнениями
, (2)
. (3)
Гиперболоид, определяемый уравнением
(2), называется однополостным (рис. 2); гиперболоид,
определяемый уравнением (3), — двуполостным (рис. 3);
уравнения (2) и (3) называются каноническими
уравнениями соответствующих гиперболоидов.
Величины a, b, c называются
полуосями гиперболоида. В случае однополостного
гиперболоида, заданного уравнением (2), только
первые из них (а и b) показаны
на рис. 2. В случае двуполостного гиперболоида,
заданного уравнением (3), одна из них (именно, с)
показана на рис. 3. Гиперболоиды, определяемые
уравнениями (2) и (3), при a=b
являются поверхностями вращения.
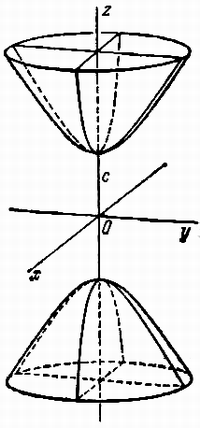
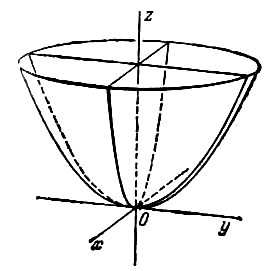
Параболоидами называются поверхности,
которые в некоторой системе декартовых
прямоугольных координат определяются
уравнениями
, (4)
, (5)
где p и q — положительные числа,
называемые параметрами параболоида. Параболоид,
определяемый уравнением (4), называется
эллиптическим (рис. 4); параболоид, определяемый
уравнением (5), — гиперболическим (рис. 5). Уравнения
(4) и (5) называют каноническими уравнениями
соответствующих параболоидов. В случае, когда p=q, параболоид, определяемый
уравнением (4), является поверхностью вращения
(вокруг Oz).
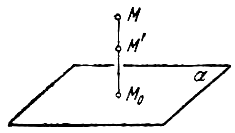
Рассмотрим теперь преобразование
пространства, которое называется равномерным
сжатием (или равномерным растяжением).
Выберем какую-нибудь плоскость;
обозначим ее буквой
. Зададим, кроме
того, некоторое положительное число q. Пусть М — произвольная точка
пространства, не лежащая на плоскости
,
— основание
перпендикуляра, опущенного на плоскость
из точки М. Переместим точку М по прямой
в
новое положение
так, чтобы имело
место равенство
и чтобы после перемещения точка
осталась с той же стороны от плоскости
,
где она была первоначально (рис. 6). Точно так же мы
поступим со всеми точками пространства, не
лежащими на плоскости
; точки, которые
расположены на плоскости
, оставим на своих
местах. Таким образом, все точки пространства, за
исключением тех, что лежат на плоскости
,
переместятся; при этом расстояние от каждой
точки до плоскости
изменится в
некоторое определенное число раз, общее для всех
точек. Описываемое сейчас перемещение точек
пространства называется его равномерным сжатием
к плоскости
; число q
носит название коэффициента сжатия.
Пусть дана некоторая поверхность F; при равномерном сжатии
пространства точки, которые ее составляют,
переместятся и в новых положениях сотавят
поверхность F’. Будем
говорить, что поверхность F’
получено из F в результате
равномерного сжатия пространства. Оказывается,
что многие поверхности второго порядка (все,
кроме гиперболического параболоида) можно
получить в результате равномерного сжатия из
поверхностей вращения).
ПРИМЕР. Доказать, что произвольный
трехосный эллипсоид
может быть получен из сферы
в результате двух последовательных
равномерных сжатий пространства к координатным
плоскостям: к плоскости Oxy с
коэффициентом сжатия
и к плоскости Oxz с коэффициентом сжатия
.
ДОКАЗАТЕЛЬСТВО. Пусть производится
равномерное сжатие пространства к плоскости Oxy с коэффициентом
и
пусть
— точка, в которую переходит при этом
точка
. Выразим координаты x’,
y’, z’ точки М’ через координаты x, y, z точки М. Так как прямая MM’ перпендикулярна к плоскости Oxy, то x’=x, y’=y.
С другой стороны, так как расстояние от точки М’
до плоскости Oxy равно
расстоянию от точки М до этой плоскости,
умноженному на число
, то
.
Таким образом, мы получаем искомые
выражения:
,
,
(6)
или
,
,
(7)
Предположим, что M(x; y; z)
— произвольная точка сферы
.
Заменим здесь x, y, z
их выражениями (7); получим
,
откуда
.
Следовательно, точка M’(x’;
y’; z’) лежит на эллипсоиде вращения.
Аналогично, мы должны осуществить сжатие
пространства к плоскости Oxz
по формулам
,
,
;
тогда получим трехосный эллипсоид и
именно тот, уравнение которого дано в условии
задачи.
Отметим еще, что однополостный
гиперболоид и гиперболический параболоид суть
линейчатые поверхности, то есть они состоят из
прямых; эти прямые называются прямолинейными
образующими указанных поверхностей.
Однополостный гиперболоид
имеет две системы прямолинейных
образующих, которые определяются уравнениями:
,
;
,
,
где
и
— некоторые
числа, не равные одновременно нулю.
Гиперболический параболоид
также имеет две системы прямолинейных
образующих, которые определяются уравнениями
,
;
,
.
Конической поверхностью, или конусом,
называется поверхность, которая описывается
движущейся прямой (образующей) при условии, что
эта прямая проходит через постоянную точку S и пересекает некоторую
определенную линию L. Точка S называется вершиной конуса;
линия L — направляющей.
Цилиндрической поверхностью, или
цилиндром, называется поверхность, которая
описывается движущейся прямой (образующей) при
услвоии, что эта прямая имеет постоянное
направление и пересекает некоторую определенную
линию L (направляющую).
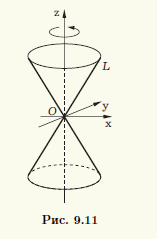
При вращении прямой L, пересекающейся с осью вращения, образуется прямой круговой конус (рис. 9.11). Точка пересечения вращающейся прямой с осью вращения остается неподвижной, ее называют вершиной конуса
.
Как и ранее, уравнение будем выводить в прямоугольной системе координат, ось Oz которой совпадает с осью вращения, а начало системы координат — с вершиной конуса. Ось Ox расположим так, чтобы прямая L находилась в координатной плоскости xOz и описывалась уравнением z = k1x. В этой системе координат уравнение поверхности вращения получается из уравнения прямой заменой x на ±√(х2 + у2) (см. 9.1). В результате такой замены получаем z = ±k1√(х2 + у2). Возведя уравнение в квадрат, придем к соотношению z2 = k21(x2 + у2), а разделив его на с2 = k21a2, получим каноническое уравнение прямого кругового конуса x2/a2 + y2/a2 + z2/c2
Преобразование сжатия прямого кругового конуса к координатной плоскости xOz с коэффициентом k дает эллиптический конус. Его уравнение имеет вид x2/a2 + k2y2/b2 = z2/c2 после переобозначения параметров,
x2/a2 + k2y2/b2 = z2/c2 (9.9)
Уравнение называют каноническим уравнением эллиптического конуса. Эллиптический конус при а = b совпадает с прямым круговым конусом, и оба они являются поверхностями второго порядка.
Конус
Конус (от др.-греч. κώνος «сосновая шишка»),— поверхность, образованная в пространстве множеством лучей (образующих конуса), соединяющих все точки некоторой плоской кривой (направляющей конуса) с данной точкой пространства (вершиной конуса).
Если направляющая конуса — замкнутая кривая, то коническая поверхность служит границей пространственного тела, которое также называют конусом (см. рисунок), а внутренность этой кривой называют основанием конуса, Если основание конуса представляет собой многоугольник, такой конус является пирамидой.
Иногда вместо лучей рассматривают прямые, тогда получается двойной конус, состоящий из двух симметричных относительно вершины частей.
Конус и связанные с ним конические сечения играют большую роль в математике, астрономии и других науках.
Связанные определения
- Боковая поверхность конуса — объединение образующих конуса; образующая поверхность конуса является конической поверхностью.
- Высота конуса — отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка).
- Угол раствора конуса — угол между двумя противоположными образующими (угол при вершине конуса, внутри конуса).
- Конусность — соотношение высоты и диаметра основания конуса.
Типы конусов
Прямой круговой конус
Прямой и косой круговые конусы с равным основанием и высотой: их объём одинаков
Усечённый прямой круговой конус
- Прямой конус — конус, основание которого имеет центр симметрии (например, является кругом или эллипсом) и ортогональная проекция вершины конуса на плоскость основания совпадает с этим центром; при этом прямая, соединяющая вершину и центр основания, называется осью конуса.
- Косой (или наклонный) конус — конус, у которого ортогональная проекция вершины на основание не совпадает с его центром симметрии.
- Круговой конус — конус, основание которого является кругом.
- Конус вращения, или прямой круговой конус (часто под конусом подразумевают именно его) — конус, который можно получить вращением (то есть тело вращения) прямоугольного треугольника вокруг прямой, содержащей катет треугольника (эта прямая является осью конуса).
- Конус, опирающийся на эллипс, параболу или гиперболу, называют соответственно эллиптическим, параболическим и гиперболическим конусом: последние два имеют бесконечный объём.
- Усечённый конус или конический слой — часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием.
- Равносторонний конус — конус вращения, образующая которого равна диаметру основания.
Свойства
- Если площадь основания конечна, то объём конуса также конечен и равен трети произведения высоты на площадь основания.
V = 1 3 S H , SH,> где S — площадь основания, H — высота. Таким образом, все конусы, опирающиеся на данное основание (конечной площади) и имеющие вершину, находящуюся на данной плоскости, параллельной основанию, имеют равный объём, поскольку их высоты равны.
- Центр тяжести любого конуса с конечным объёмом лежит на четверти высоты от основания.
- Телесный угол при вершине прямого кругового конуса равен
2 π ( 1 − cos α 2 ) , ight),> где α — угол раствора конуса.
- Площадь боковой поверхности прямого кругового конуса равна
S = π R t , а в общем случае S = t l 2 , <2>>,> где R — радиус основания, t = R 2 + H 2 +H^<2>>>> — длина образующей, l — длина границы основания. Полная площадь поверхности (то есть сумма площадей боковой поверхности и основания) равна S = π R ( t + R ) , для прямого кругового конуса и S = t l 2 + S , <2>>+S,> для произвольного, где S — площадь основания.
- Объём кругового (не обязательно прямого) конуса равен
V = 1 3 π R 2 H . pi R^<2>H.>
- Для усечённого кругового конуса (не обязательно прямого) объём равен:
V = 1 3 π H ( R 2 + R r + r 2 ) , pi H(R^<2>+Rr+r^<2>),> где R и r — радиусы соответственно нижнего и верхнего оснований, H — высота от плоскости нижнего основания,до верхнего основания.
- Для произвольного усечённого конуса (не обязательно прямого и кругового) объём равен:
V = 1 3 ( H 2 S 2 − H 1 S 1 ) , (H_<2>S_<2>-H_<1>S_<1>),> где S 1 > и S 2 > — площади соответственно верхнего (ближнего к вершине) и нижнего оснований, H 1 > и H 2 > — расстояния от плоскости соответственно верхнего и нижнего основания до вершины.
- Пересечение плоскости с прямым круговым конусом является одним из конических сечений (в невырожденных случаях — эллипсом, параболой или гиперболой, в зависимости от положения секущей плоскости).
Уравнение прямого кругового конуса
Уравнения, задающие боковую поверхность прямого кругового конуса с углом раствора 2Θ, вершиной в начале координат и осью, совпадающей с осью Oz:
- В сферической системе координат с координатами (r, φ, θ):
θ = Θ .
- В цилиндрической системе координат с координатами (r, φ, z):
z = r ⋅ ctg Θ Theta > или r = z ⋅ tg Θ . Theta .>
- В декартовой системе координат с координатами (x, y, z):
z = ± x 2 + y 2 ⋅ ctg Θ . +y^<2>>>cdot operatorname Theta .> Это уравнение в каноническом виде записывается как x 2 a 2 + y 2 a 2 − z 2 c 2 = 0 , >>>+>>>->>>=0,> где константы a, с определяются пропорцией c / a = cos Θ / sin Θ . Отсюда видно, что боковая поверхность прямого кругового конуса представляет собой поверхность второго порядка (она носит название коническая поверхность). В общем виде коническая поверхность второго порядка опирается на эллипс; в подходящей декартовой координатной системе (оси Ох и Оу параллельны осям эллипса, вершина конуса совпадает с началом координат, центр эллипса лежит на оси Oz) её уравнение имеет вид x 2 a 2 + y 2 b 2 − z 2 c 2 = 0 , >>>+>>>->>>=0,> причём a/c и b/c равны полуосям эллипса. В наиболее общем случае, когда конус опирается на произвольную плоскую поверхность, можно показать, что уравнение боковой поверхности конуса (с вершиной в начале координат) задаётся уравнением f ( x , y , z ) = 0 , где функция f ( x , y , z ) является однородной, то есть удовлетворяющей условию f ( α x , α y , α z ) = α n f ( x , y , z ) f(x,y,z)> для любого действительного числа α.
Развёртка
Прямой круговой конус как тело вращения образован прямоугольным треугольником, вращающимся вокруг одного из катетов, где h — высота конуса от центра основания до вершины — является катетом прямоугольного треугольника, вокруг которого происходит вращение. Второй катет прямоугольного треугольника r — радиус в основании конуса. Гипотенузой прямоугольного треугольника является l — образующая конуса.
В создании развёртки конуса могут использоваться всего две величины r и l. Радиус основания r определяет в развертке круг основания конуса, а сектор боковой поверхности конуса определяет образующая боковой поверхности l, являющаяся радиусом сектора боковой поверхности. Угол сектора φ в развёртке боковой поверхности конуса определяется по формуле:
Составить параметрическое уравнение кругового конуса
Глава 46. Поверхности второго порядка
Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением
(1).
Уравнение (1) называется каноническим уравнением эллипсоида. Величины a, b, c суть полуоси эллипсоида (рис. 1). Если все они различны, эллипсоид называется трехосным; в случае, когда какие-нибудь две из них одинаковы, эллипсоид называется вытянутым, при a=b>c — сжатым. В случае, когда a=b=c , эллипсоид представляет собой сферу.
Гиперболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями
, (2)
. (3)
Гиперболоид, определяемый уравнением (2), называется однополостным (рис. 2); гиперболоид, определяемый уравнением (3), — двуполостным (рис. 3); уравнения (2) и (3) называются каноническими уравнениями соответствующих гиперболоидов. Величины a, b, c называются полуосями гиперболоида. В случае однополостного гиперболоида, заданного уравнением (2), только первые из них (а и b ) показаны на рис. 2. В случае двуполостного гиперболоида, заданного уравнением (3), одна из них (именно, с) показана на рис. 3. Гиперболоиды, определяемые уравнениями (2) и (3), при a=b являются поверхностями вращения.
Параболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями
, (4)
, (5)
где p и q — положительные числа, называемые параметрами параболоида. Параболоид, определяемый уравнением (4), называется эллиптическим (рис. 4); параболоид, определяемый уравнением (5), — гиперболическим (рис. 5). Уравнения (4) и (5) называют каноническими уравнениями соответствующих параболоидов. В случае, когда p=q , параболоид, определяемый уравнением (4), является поверхностью вращения (вокруг Oz).
Рассмотрим теперь преобразование пространства, которое называется равномерным сжатием (или равномерным растяжением).
Выберем какую-нибудь плоскость; обозначим ее буквой . Зададим, кроме того, некоторое положительное число q . Пусть М — произвольная точка пространства, не лежащая на плоскости , — основание перпендикуляра, опущенного на плоскость из точки М. Переместим точку М по прямой в новое положение так, чтобы имело место равенство
и чтобы после перемещения точка осталась с той же стороны от плоскости , где она была первоначально (рис. 6). Точно так же мы поступим со всеми точками пространства, не лежащими на плоскости ; точки, которые расположены на плоскости , оставим на своих местах. Таким образом, все точки пространства, за исключением тех, что лежат на плоскости , переместятся; при этом расстояние от каждой точки до плоскости изменится в некоторое определенное число раз, общее для всех точек. Описываемое сейчас перемещение точек пространства называется его равномерным сжатием к плоскости ; число q носит название коэффициента сжатия.
Пусть дана некоторая поверхность F ; при равномерном сжатии пространства точки, которые ее составляют, переместятся и в новых положениях сотавят поверхность F ’. Будем говорить, что поверхность F ’ получено из F в результате равномерного сжатия пространства. Оказывается, что многие поверхности второго порядка (все, кроме гиперболического параболоида) можно получить в результате равномерного сжатия из поверхностей вращения).
ПРИМЕР. Доказать, что произвольный трехосный эллипсоид
может быть получен из сферы
в результате двух последовательных равномерных сжатий пространства к координатным плоскостям: к плоскости Oxy с коэффициентом сжатия и к плоскости Oxz с коэффициентом сжатия .
ДОКАЗАТЕЛЬСТВО. Пусть производится равномерное сжатие пространства к плоскости Oxy с коэффициентом и пусть — точка, в которую переходит при этом точка . Выразим координаты x’, y’, z ’ точки М’ через координаты x, y, z точки М. Так как прямая MM ’ перпендикулярна к плоскости Oxy , то x’=x, y’=y . С другой стороны, так как расстояние от точки М’ до плоскости Oxy равно расстоянию от точки М до этой плоскости, умноженному на число , то .
Таким образом, мы получаем искомые выражения:
, , (6)
, , (7)
Предположим, что M(x; y; z ) — произвольная точка сферы
.
Заменим здесь x, y, z их выражениями (7); получим
,
.
Следовательно, точка M’(x’; y’; z ’) лежит на эллипсоиде вращения. Аналогично, мы должны осуществить сжатие пространства к плоскости Oxz по формулам
, , ;
тогда получим трехосный эллипсоид и именно тот, уравнение которого дано в условии задачи.
Отметим еще, что однополостный гиперболоид и гиперболический параболоид суть линейчатые поверхности, то есть они состоят из прямых; эти прямые называются прямолинейными образующими указанных поверхностей.
имеет две системы прямолинейных образующих, которые определяются уравнениями:
, ;
, ,
где и — некоторые числа, не равные одновременно нулю. Гиперболический параболоид
также имеет две системы прямолинейных образующих, которые определяются уравнениями
, ;
, .
Конической поверхностью, или конусом, называется поверхность, которая описывается движущейся прямой (образующей) при условии, что эта прямая проходит через постоянную точку S и пересекает некоторую определенную линию L . Точка S называется вершиной конуса; линия L — направляющей.
Цилиндрической поверхностью, или цилиндром, называется поверхность, которая описывается движущейся прямой (образующей) при услвоии, что эта прямая имеет постоянное направление и пересекает некоторую определенную линию L (направляющую).
http://a-geometry.narod.ru/problems/problems_46.htm
Займемся
теперь изучением поверхностей. Их
уравнения после преобразований могут
быть приведены к виду
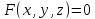
Мы будем предполагать, что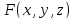
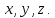
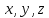
алгебраической поверхности.
Можно показать, что он не зависит от
выбора координатных осей. Ранее мы
убедились в том, что поверхностями 1-го
порядка являются плоскости. Займемся
исследованием поверхностей 2-го порядка.
Начнем
с цилиндрической поверхности.
Цилиндрической
называется поверхность,
образованная прямыми, называемыми
образующими,
параллельными
некоторой данной прямой и пересекающими
данную линию
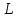
которая называетсянаправляющей.
Пусть направляющая цилиндрической
поверхности определяется уравнениями
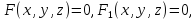
а
образующие уравнениями
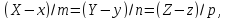
где
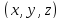
а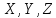
Исключая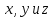
искомое уравнение цилиндрической
поверхности.
Пример
5.13.
Составить уравнение цилиндрической
поверхности, образующие которой
параллельны прямой
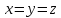
а направляющей служит прямая
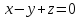
Рассмотрим канонические уравнения
образующих:
Обозначим
через 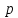
тогда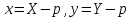
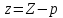
Подставляя эти значения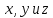
получим: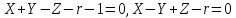
Исключив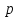
найдем: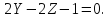
через данную направляющую и параллельной
прямой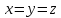
Конической
называется поверхность,
образованная прямыми (образующими
конуса), проходящими через данную
точку (вершину конуса) и пересекающими
данную линию (направляющую конуса).
Пусть
направляющая конуса задается уравнениями
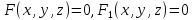
(5.33)
а
вершина конуса имеет координаты
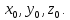
уравнения образующих конуса как прямых,
проходящих через точку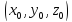
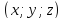
Исключая
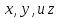
уравнение конической поверхности.
Пример
5.14.
Составить уравнение конуса с вершиной
в начале координат и направляющей
Канонические
уравнения образующих, проходящих через
вершину (0;0;0) конуса и точку
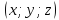
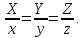
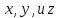
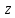
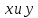

эти значения
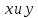
иметь:
Если
в рассмотренном примере
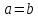
то направляющей будет окружность, и мы
получим круговой конус.
5.8. Поверхности вращения
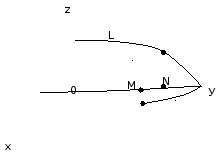
Рассмотрим
в плоскости Oyz некоторую линию L,
имеющую уравнение F(Y,Z)=0. Найдем уравнение
поверхности, полученной от вращения
этой линии вокруг оси Oy (рис.5.8).
Возьмем
произвольную точку M(x;y;z) этой поверхности
и проведем через нее плоскость,
перпендикулярную оси вращения Oy.
Очевидно, в пересечении этой плоскости
с нашей поверхностью получится
окружность с центром N на оси вращения.
Координаты точки N будут (0;y;0). Радиус
окружности MN как расстояние между
точками N и M равен
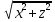
С другой стороны, ясно, что этот радиус
является абсолютной величиной аппликаты
той точки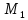
y. Следовательно, полагая в данном
уравнении
(координаты
точки
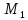
мы получим искомое уравнение поверхности
вращения:
Таким
образом, мы приходим к следующему
правилу:
чтобы
получить уравнение поверхности,
образованной вращением линии L, лежащей
в плоскости Oyz, вокруг оси Oy, надо в
уравнении этой линии заменить z на
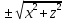
Рис.5.8.
Поверхность вращения.
Аналогичные
правила будут иметь место и по отношению
к поверхностям, полученным вращением
плоских линий вокруг других координатных
осей.
Уравнение
поверхности, полученной вращением
эллипса
вокруг
оси Oz, будет
Это
уравнение определяет поверхность,
называемую эллипсоидом
вращения.
Пересекая этот эллипсоид плоскостью
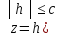
параллельной плоскости Oxy, получим в
сечении окружность, уравнения которой
будут:
и
радиус которой равен
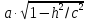
Следовательно,
при изменении
значения
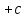
вращения.
Возьмем
теперь вместо окружности (5.35) эллипс
лежащий
в плоскости
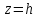
параллельной плоскости xOy, полуоси
которого
равны
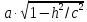
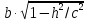
При изменении
уравнение которой получим, исключив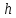
или
.
Поверхность,
определяемая уравнением (5.37) называется
эллипсоидом,
а величины
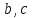
(рис.5.9).
Пересекая
эллипсоид координатными плоскостями
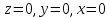
получим в сечении эллипсы:
Не
умаляя общности, мы можем считать, что
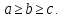
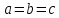
то уравнение (5.37) определяет сферу; если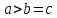
то — удлиненный эллипсоид вращения с
осью вращения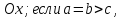
вращения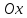
Если среди чисел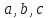
Рис.5.9.
Эллипсоид.
Рассмотрим
теперь гиперболоиды.
вокруг
оси
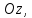
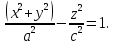
называемуюоднополостным
гиперболоидом
вращения.
Пересекая ее плоскостью
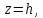
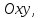
радиус
которой равен
Рис.
5.10. Однополостный гиперболоид.
Следовательно,
при изменении
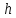
гиперболоид вращения.
Возьмем
теперь вместо окружности (5.38) эллипс:
лежащий
в плоскости
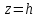
параллельной плоскости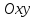
полуоси которого равны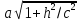
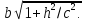
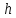
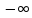
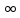
(рис.5.10), уравнение которой получим,
исключив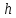
Поверхность,
задаваемая уравнением (5.40),
называется однополостным
гиперболоидом,
а величины
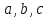
Вращая
гиперболу
вокруг
оси Oz, мы получим двуполостный
гиперболоид.
Его уравнение будет
Пересекая
его плоскостью
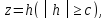
получим в сечении окружность
радиус
которой равен
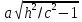
При изменении
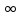
гиперболоида, а при изменении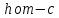
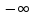
Возьмем
вместо окружности (5.41) эллипс
лежащий
в плоскости
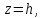
которого равны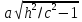
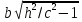
При изменении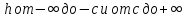
эллипс описывает двуполостную поверхность,
уравнение которой получим, исключая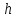
Поверхность
второго порядка, описываемая этим
уравнением называется двуполостным
гиперболоидом,
а величины
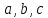
Параболоид
вращения получается вращением
параболы
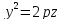
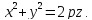
В
сечении его плоскостью
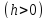
перпендикулярной оси вращения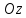
получается окружность, уравнения которой
будут
ее
радиус равен 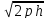
Следовательно, при изменении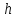
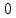
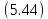
Возьмем
вместо окружности
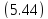
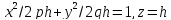
Здесь
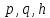
эллипса равны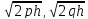
При изменении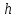
называемую эллиптическим параболоидом,
уравнение которого получается
исключением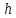
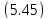
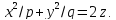
Простейшее
уравнение гиперболического
параболоида
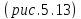
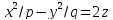
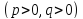
т.е.
отличается от уравнения
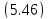
знаком при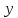
Плоскость координат пересекает эту
поверхность по параболе
для
которой ось
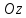
расположена в положительном направлении
оси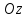
Плоскость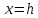
параллельная плоскости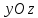
пересекает поверхность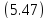
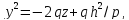
или
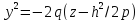
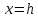
Из
этих уравнений видно, что эти параболы,
расположенные в плоскостях
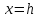
имеют один и тот же параметр, их оси
симметрии находятся в плоскости
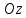
ветви парабол направлены вниз (в
отрицательном направлении оси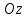
а их вершины имеют координатуz=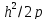
Вершины парабол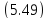
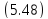
Таким
образом, гиперболический параболоид
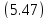
образованную движущейся параболой, ось
симметрии которой остается в плоскости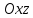
а вершина движется по параболе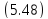
Плоскость параболы остается параллельной
плоскости
Пересекая
гиперболический параболоид
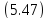
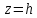
получим в сечении гиперболу,
уравнения которой: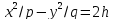
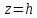
При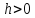
будет параллельна оси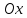
при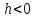
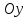
Так
как уравнение (5.47) содержит только
квадраты координат
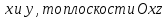
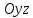
плоскостями симметрии для поверхности.
Среди
поверхностей второго порядка упомянем
еще конус с вершиной в начале координат,
направляющей линией которого является
эллипс, и цилиндры, направляющие линии
которых, лежащие в плоскости Oxy являются
эллипсами, гиперболами, параболами.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #