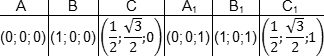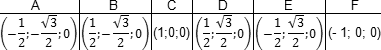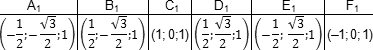Задание фигур в пространстве
Пусть
в пространстве введена система координат
Охуz.
Как мы показали, положение любой точки
однозначно определяется ее координатами.
Если Ф – некоторое множество точек (
фигура ), то всем ее точкам характерно
некоторое свойство, присущее только
точкам этой фигуры, а значит и для
координат точек этой фигуры выполняется
соотношение, присущее только точкам
этой фигуры.
Определение.
Пусть в
данной системе координат имеем некоторое
уравнение
F
(x,
y,
z)
= 0.
(1)
Уравнение
(1) называется уравнением фигуры Ф,
если координаты любой точки этой фигуры,
и только они, удовлетворяют этому
уравнению.
Следует
добавить, что уравнение (1) будет уравнением
фигуры Ф,
если выполняются два условия: 1) Если
М(
)
Ф, то координаты
(
)
удовлетворяют (1); 2) Если координаты (
)
удовлетворяют уравнению (1), то М(
)
Ф.
Под
уравнением фигуры мы понимаем не только
алгебраические уравнения, но и неравенства,
системы уравнений и неравенств, а также
их любые комбинации. Например, неравенство
(х
–- )2
+(у – )2
+ (z
– )2
R2
является
уравнением шара с центром в точке Q(;
;
)
и радиусом R.
Аналогично
определяется уравнение фигуры на
плоскости, только в системе координат
Оху.
Уравнение
является уравнением точек первой
четверти, причем точки, лежащие на осях
координат, не принадлежат данному
множеству.
Пример
1. Центр
О и вершина
А
правильного шестиугольника ABCDEF
имеют координаты О(–1;
2), А(1;
4). Найти
координаты остальных вершин.
Решение.
Так как точка
О является
серединой отрезка АD,
то находим координаты точки D.
Обозначим
D(х;
у), тогда
согласно (3) имеем:
,
.
Отсюда
получим: х
= – 3, у = 0. D(-3;
0).
Так
как данный шестиугольник правильный,
то АВО и
AFO
– правильные треугольники. Значит,
точки В
и F
являются точками, равноудаленные от
точек А
и О.
Пусть В(х;
у). Из условия
|AB|
= |OB|
= |OA|
получим |AВ|2
= |ОB|2
= |ОА|2.
В координатной форме это выглядит так:
Û
Следовательно,
B(
;3-
)
и
F
(–
;
3 +
).
Так
как точки Е
и С
симметричны точкам В
и F
относительно точки О,
то находим их координаты аналогично
тому, как мы находили координаты точки
D.
Обозначим Е(х;
у), тогда
согласно (3) имеем:
,
.
Отсюда
получим: х
= – (
+2),
у = 1+
.
Е(-(
+2);1+
).
Обозначим
С(х; у),
тогда согласно (3) имеем:
,
.
Отсюда
получим: х
=
-2,
у = 1-
.
С(
-2;
1-
).
Ответ:
С(
-2;
1-
),
Е(-(
+2);1+
),
B(
;3-
),
F
(–
;
3 +
),
D(–
3;0).
Пример
2. Найти
уравнение множества всех точек плоскости,
для каждой из которых сумма квадратов
расстояний до осей координат равна 5.
Решение.
Рассматриваем систему координат О
.
Обозначим заданное множество точек
F,
а М (х; у)
– произвольную точку плоскости.
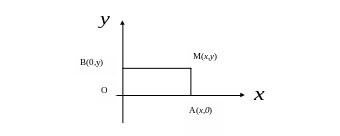
Тогда,
согласно условию задачи, получим
М
F
|MB|2
+ |MA|2
= 5.
В
координатах последнее уравнение имеет
вид
х2+
у2
= 5.
Получили
известное уравнение окружности с центром
в начале координат и радиусом равным
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
|
|
Найти вершин шестиугольника
|
|
20/01/21 |
|
|
|
|
|
kotenok gav |
Re: Найти вершин шестиугольника
|
|
21/05/16 |
Сначала найдите координаты точки
|
|
|
|
|
StepV |
Re: Найти вершин шестиугольника
|
|
23/05/20 |
Здравствуйте, не могу понять как решается такая задача. Если это курс аналитической геометрии, то лучше решать этими методами. Для начала угол
|
|
|
|
|
Maximmmm |
Re: Найти вершин шестиугольника
|
|
20/01/21 |
|
|
|
|
|
arseniiv |
Re: Найти вершин шестиугольника
|
||
27/04/09 |
1. Вычислить координаты всех точек в прямоугольной системе координат; Выглядит очень неудобно. Я бы предложил достраивать чертёж: продолжать прямые, откладывать дальше на них отрезки и откладывать данные нам векторы. Тогда станет лучше видно, сколько раз отложенные целое число раз, куда они заведут, а потом останется просто поделить на какие-то числа ну и довести арифметикой дело до конца. Не обязательно стараться получить сразу только те точки, о которых спрашивается. Пример: Выразив
|
||
|
|
|||
|
StepV |
Re: Найти вершин шестиугольника
|
|
23/05/20 |
Выглядит очень неудобно. Задача явно учебная, поэтому тут важно не удобство, а какому курсу математики должно соответствовать решение. Если задачу задали по теме пересчет координат из одного базиса в другой, то пришлось бы решать именно по этому алгоритму.
|
|
|
|
|
arseniiv |
Re: Найти вершин шестиугольника
|
||
27/04/09 |
Если задачу задали по теме пересчет координат из одного базиса в другой, то пришлось бы решать именно по этому алгоритму. Но тогда очень вероятно дали бы координаты в исходном базисе уже готовые, чтобы не отвлекать.
|
||
|
|
|||
Модераторы: Модераторы Математики, Супермодераторы
А мне нравится такое на комплексных числах считать. То же, что и с синусами, но элегантнее.
Вот пример на питоне:
from math import e, pi
f=lambda c, r, n=3, fi0=0: [c+r*e**(1j*(2*pi/n*i+fi0)) for i in range(n)]
Получим функцию f которая может рассчитать точки любого вписанного n-угольника:
>>> f(c=250+250j, r=250)
[(500+250j),
(375+466.50635094610965j),
(125.00000000000006+466.5063509461097j),
250.00000000000003j,
(124.99999999999989+33.49364905389041j),
(374.99999999999983+33.49364905389024j)]А если надо обяательно кортежами, а не комплексными точками. то вот:
>>> [(round(p.real), round(p.imag)) for p in f(c=250+250j, r=250, n=5, fi0=pi/2)]
[(250, 500), (12, 327), (103, 48), (397, 48), (488, 327)]Тут, заметьте, пятиугольник, причем вершинкой вниз (при оси Y, направленной вниз).
Чтобы было понятно как это работает…
Представим, что центр окружности в нуле координат. Нам нужно 6 точек, смещенных относительно нуля на радиус под нужными углами: 0, 60, 120, 180, 240 и 300 градусов. В формулах мы. конечно используем радианы: pi — это 180 градусов.
Чтобы повернуть единичный вектор на какой-то угол, нужно его просто домножить на e в степени мнимая единица, умноженная на угол. Поскольку единичный вектор на комплексной плоскости это просто 1, то его даже писать не надо. Просто возводим e в нужную степень и получаем нужный вектор в виде комплексного числа. Осталось его домножить на требуемый радиус (он при этом удлинится: был длиной 1, а станет r) и добавить к нему желаемый центр (тоже в виде комплексного числа, где реальная часть — X, а мнимая — Y).
Вот и всё!
Красота же?..
Да, забыл сказать, что если нужно повернуть весь n-угольник на какой-то угол, то для этого есть там параметр fi0, который по умолчанию ноль.
c — это координаты центра в комплексной форме. Например если X=30, а Y=40, то c=30+40j.
n — это число вершин.
r — радиус.
И да, в javascript’е нет такого элегантного способа работать с комплексными числами, как в питоне. Но для js есть много библиотек для работы с комплексными числами. Будет не так компактно и красиво, как на питоне, но в целом всё точно так же в плане математики.
UPD: Исправил функцию. Там скобочек не хватало, поэтому поворот на fi0 работал неверно. Теперь все как надо.

Задача №1. Построить точку, симметричную точке А (5; —3) относительно оси Оу.
Решение. Если две точки симметричны относительно какой-либо оси, то они лежат на одном перпендикуляре к этой прямой, по разные стороны и на одном расстоянии от нее. Поэтому через точку А проведем перпендикуляр АВ к оси Оу и отложим отрезок ВА’ равный по длине отрезку ВА.
Так как отрезок ВА’ откладываем в отрицательном направлении оси Ох, то ВА’= -ВА = -5. Следовательно, координаты точки А’ (—5; —3).
Задача №2. Найти точку, симметричную точке А (-2; 3) относительно биссектрисы I координатного угла.
Задача №3. Найти точку, симметричную точке А (3; 4) относительно начала координат.
Решения этих трех задач подробно объясняются в следующем видео:
Задача №4. Найти координаты вершин правильного шестиугольника, сторона которого равна а, зная, что начало координат помещено в центре шестиугольника, а ось абсцисс проходит через две противоположные вершины.
Решение этой задачи подробно изложено в следующем видео
Введение системы координат
30 мая 2011
Метод координат — это, конечно, очень хорошо, но в настоящих задачах C2 никаких координат и векторов нет. Поэтому их придется вводить. Да-да, вот так взять и ввести: указать начало отсчета, единичный отрезок и направление осей x, y и z.
Самое замечательное свойство этого метода заключается в том, что не имеет никакого значения, как именно вводить систему координат. Если все вычисления будут правильными, то и ответ будет правильным.
Тем не менее, приведу некоторые рекомендации, как лучше ввести систему координат для самых часто встречающихся в задаче C2 многогранников. С указанием конкретных точек. Во всех случаях упор делается на минимизацию объема вычислений.
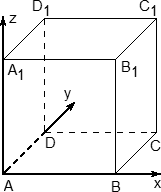
Координаты куба
Если в задаче C2 будет куб — считайте, что вам повезло. Это самый простой многогранник, все двугранные углы которого равны 90°.
Система координат также вводится очень просто:
- Начало координат — в точке A;
- Чаще всего ребро куба не указано, поэтому принимаем его за единичный отрезок;
- Ось x направляем по ребру AB, y — по ребру AD, а ось z — по ребру AA1.
Обратите внимание: ось z направляется вверх! После двумерной системы координат это несколько непривычно, но на самом деле очень логично.
Итак, теперь у каждой вершины куба есть координаты. Соберем их в таблицу — отдельно для нижней плоскости куба:
| Точка | A | B | C | D |
| Координаты | (0; 0; 0) | (1; 0; 0) | (1; 1; 0) | (0; 1; 0) |
И для верхней:
| Точка | A1 | B1 | C1 | D1 |
| Координаты | (0; 0; 1) | (1; 0; 1) | (1; 1; 1) | (0; 1; 1) |
Несложно заметить, что точки верхней плоскости отличаются соответствующих точек нижней только координатой z. Например, B = (1; 0; 0), B1 = (1; 0; 1). Главное — не запутаться!
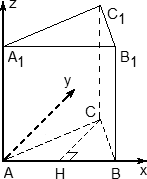
Координаты трехгранной призмы
Призма — это уже намного веселее. При правильном подходе достаточно знать координаты только нижнего основания — верхнее будет считаться автоматически.
В задачах C2 встречаются исключительно правильные трехгранные призмы (прямые призмы, в основании которых лежит правильный треугольник). Для них система координат вводится почти так же, как и для куба. Кстати, если кто не в курсе, куб — это тоже призма, только четырехгранная.
Итак, поехали! Вводим систему координат:
- Начало координат — в точке A;
- Сторону призмы принимаем за единичный отрезок, если иное не указано в условии задачи;
- Ось x направляем по ребру AB, z — по ребру AA1, а ось y расположим так, чтобы плоскость OXY совпадала с плоскостью основания ABC.
Здесь требуются некоторые пояснения. Дело в том, что ось y НЕ совпадает с ребром AC, как многие считают. А почему не совпадает? Подумайте сами: треугольник ABC — равносторонний, в нем все углы по 60°. А углы между осями координат должны быть по 90°, поэтому сверху картинка будет выглядеть так:
Надеюсь, теперь понятно, почему ось y не пойдет вдоль AC. Проведем в этом треугольнике высоту CH. Треугольник ACH — прямоугольный, причем AC = 1, поэтому AH = 1 · cos A = cos 60°; CH = 1 · sin A = sin 60°. Эти факты нужны для вычисления координат точки C.
Теперь взглянем на всю призму вместе с построенной системой координат:
Получаем следующие координаты точек:
Как видим, точки верхнего основания призмы снова отличаются от соответствующих точек нижнего лишь координатой z. Основная проблема — это точки C и C1. У них есть иррациональные координаты, которые надо просто запомнить. Ну, или понять, откуда они возникают.
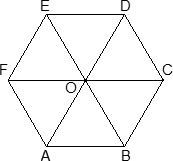
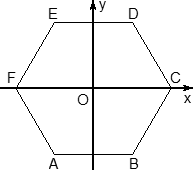
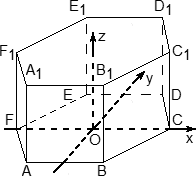
Координаты шестигранной призмы
Шестигранная призма — это «клонированная» трехгранная. Можно понять, как это происходит, если взглянуть на нижнее основание — обозначим его ABCDEF. Проведем дополнительные построения: отрезки AD, BE и CF. Получилось шесть треугольников, каждый из которых (например, треугольник ABO) является основанием для трехгранной призмы.
Теперь введем собственно систему координат. Начало координат — точку O — поместим в центр симметрии шестиугольника ABCDEF. Ось x пойдет вдоль FC, а ось y — через середины отрезков AB и DE. Получим такую картинку:
Обратите внимание: начало координат НЕ совпадает с вершиной многогранника! На самом деле, при решении настоящих задач вы обнаружите, что это очень удобно, поскольку позволяет значительно уменьшить объем вычислений.
Осталось добавить ось z. По традиции, проводим ее перпендикулярно плоскости OXY и направляем вертикально вверх. Получим итоговую картинку:
Запишем теперь координаты точек. Предположим, что все ребра нашей правильной шестигранной призмы равны 1. Итак, координаты нижнего основания:
Координаты верхнего основания сдвинуты на единицу по оси z:
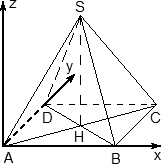
Координаты четырехугольной пирамиды
Пирамида — это вообще очень сурово. Мы разберем только самый простой случай — правильную четырехугольную пирамиду, все ребра которой равны единице. Однако в настоящих задачах C2 длины ребер могут отличаться, поэтому ниже приведена и общая схема вычисления координат.
Итак, правильная четырехугольная пирамида. Это такая же, как у Хеопса, только чуть поменьше. Обозначим ее SABCD, где S — вершина. Введем систему координат: начало в точке A, единичный отрезок AB = 1, ось x направим вдоль AB, ось y — вдоль AD, а ось z — вверх, перпендикулярно плоскости OXY. Для дальнейших вычислений нам потребуется высота SH — вот и построим ее. Получим следующую картинку:
Теперь найдем координаты точек. Для начала рассмотрим плоскость OXY. Здесь все просто: в основании лежит квадрат, его координаты известны. Проблемы возникают с точкой S. Поскольку SH — высота к плоскости OXY, точки S и H отличаются лишь координатой z. Собственно, длина отрезка SH — это и есть координата z для точки S, поскольку H = (0,5; 0,5; 0).
Заметим, что треугольники ABC и ASC равны по трем сторонам (AS = CS = AB = CB = 1, а сторона AC — общая). Следовательно, SH = BH. Но BH — половина диагонали квадрата ABCD, т.е. BH = AB · sin 45°. Получаем координаты всех точек:
Вот и все с координатами пирамиды. Но не с координатами вообще. Мы рассмотрели лишь самые распространенные многогранники, однако этих примеров достаточно, чтобы самостоятельно вычислить координаты любых других фигур. Поэтому можно приступать, собственно, к методам решения конкретных задач C2.
Смотрите также:
- Четырехугольная пирамида в задаче C2
- Метод координат в пространстве
- Сложение и вычитание дробей
- Не пишите единицы измерения в задаче B12
- Как решать простейшие логарифмические уравнения
- Задача B4: транзит нефти


 (подсказка: какие координаты у центра тяжести треугольника?).
(подсказка: какие координаты у центра тяжести треугольника?). определить сможете?
определить сможете? даёт нам точку
даёт нам точку  , или
, или  , и достроение чертежа вправо сделает это весьма наглядным. Значит,
, и достроение чертежа вправо сделает это весьма наглядным. Значит,  , откуда координаты этой точки
, откуда координаты этой точки  .
. , теперь легко найти оставшиеся
, теперь легко найти оставшиеся  .
.