Загрузить PDF
Загрузить PDF
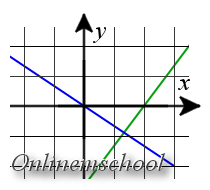
В двумерном пространстве две прямые пересекаются только в одной точке,[1]
задаваемой координатами (х,y). Так как обе прямые проходят через точку их пересечения, то координаты (х,y) должны удовлетворять обоим уравнениям, которые описывают эти прямые. Воспользовавшись некоторыми дополнительными навыками, вы сможете находить точки пересечения парабол и других квадратичных кривых.
-
1
Запишите уравнение каждой прямой, обособив переменную «у» на левой стороне уравнения. Другие члены уравнения должны размещаться на правой стороне уравнения. Возможно, данное вам уравнение вместо «у» будет содержать переменную f(x) или g(x); в этом случае обособьте такую переменную. Для обособления переменной выполните соответствующие математические операции на обеих сторонах уравнения.
-
2
Приравняйте выражения, расположенные с правой стороны каждого уравнения. Наша задача — найти точку пересечения обеих прямых, то есть точку, координаты (х,у) которой удовлетворяют обоим уравнениям. Так как на левой стороне каждого уравнения находится переменная «у», то выражения, расположенные с правой стороны каждого уравнения, можно приравнять. Запишите новое уравнение.
-
3
Найдите значение переменной «х». Новое уравнение содержит только одну переменную «х». Для нахождения «х» обособьте эту переменную на левой стороне уравнения, выполнив соответствующие математические операции на обеих сторонах уравнения. Вы должны получить уравнение вида х = __ (если это невозможно, перейдите в конец этого раздела).
-
4
Используйте найденное значение переменной «х» для вычисления значения переменной «у». Для этого подставьте найденное значение «х» в уравнение (любое) прямой.
-
5
Проверьте ответ. Для этого подставьте значение «х» в другое уравнение прямой и найдите значение «у». Если вы получите разные значение «у», проверьте правильность ваших вычислений.
-
6
Запишите координаты (х,у). Вычислив значения «х» и «у», вы нашли координаты точки пересечения двух прямых. Запишите координаты точки пересечения в виде (х,у).
-
7
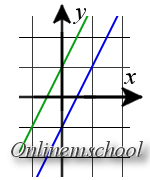
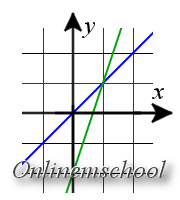
Вычисления в особых случаях. В некоторых случаях значение переменной «х» найти нельзя. Но это не значит, что вы допустили ошибку. Особый случай имеет место при выполнении одного из следующих условий:
Реклама
-
1
Определение квадратичной функции. В квадратичной функции одна или несколько переменных имеют вторую степень (но не выше), например,
или
. Графиками квадратичных функций являются кривые, которые могут не пересекаться или пересекаться в одной или двух точках. В этом разделе мы расскажем вам, как найти точку или точки пересечения квадратичных кривых.
- Если уравнение включает выражение в скобках, раскройте их, чтобы удостовериться, что функция является квадратичной. Например, функция
является квадратичной, так как, раскрыв скобки, вы получите
- Функция, описывающая окружность, включает как
, так и
.[2]
[3]
Если у вас возникли проблемы при решении задач с такой функцией, перейдите в раздел «Советы».
- Если уравнение включает выражение в скобках, раскройте их, чтобы удостовериться, что функция является квадратичной. Например, функция
-
2
Перепишите каждое уравнение, обособив переменную «у» на левой стороне уравнения. Другие члены уравнения должны размещаться на правой стороне уравнения.
-
3
Приравняйте выражения, расположенные с правой стороны каждого уравнения. Так как на левой стороне каждого уравнения находится переменная «у», то выражения, расположенные с правой стороны каждого уравнения, можно приравнять.
-
4
Перенесите все члены полученного уравнения на его левую сторону, а на правой стороне запишите 0. Для этого выполните базовые математические операции. Это позволит вам решить полученное уравнение.
-
5
-
6
Не забудьте про вторую точку пересечения двух графиков. В спешке можно забыть про вторую точку пересечения. Вот как найти координаты «х» двух точек пересечения:
-
7
Графики пересекаются в одной точке или вообще не пересекаются. Такие ситуации имеют место при соблюдении следующих условий:
-
8
Подставьте найденное значение переменной «х» в уравнение (любое) кривой. Так вы найдете значение переменной «у». Если у вас есть два значения переменной «х», проделайте описанный процесс с обоими значениями «х».
-
9
Запишите координаты точки пересечения в виде (х,у). Вычислив значения «х» и «у», вы нашли координаты точки пересечения двух графиков. Если вы определили по два значения «х» и «у», запишите две пары координат, не перепутав соответствующие значения «х» и «у».
Реклама
Советы
- Функция, описывающая окружность, включает как
, так и
. Для нахождения точки (точек) пересечения окружности и прямой вычислите «х», используя линейное уравнение.[4]
Затем подставьте найденное значение «х» в функцию, описывающую окружность, и вы получите простое квадратное уравнение, которое может не иметь решения или иметь одно или два решения. - Окружность и кривая (квадратичная или иная) могут не пересекаться или пересекаться в одной, двух, трех, четырех точках. В этом случае необходимо найти значение x2 (а не «х»), а затем подставить его во вторую функцию. Вычислив «у», вы получите одно или два решения или вообще не получите решений. Теперь подставьте найденное значение «у» в одну из двух функций и найдите значение «х». В этом случае вы получите одно или два решения или вообще не получите решений.
Реклама
Об этой статье
Эту страницу просматривали 94 840 раз.
Была ли эта статья полезной?
Точка пересечения двух прямых на плоскости
Методы решения. Существует два метода решения плоских задач на определение координат точки пересечения прямых:
- графический
- аналитический
Графический метод решения. Используя уравнения, начертить графики прямых и с помощью линейки найти координаты точки пересечения.
Аналитический метод решения. Необходимо объединить уравнения прямых в систему, решение которой, позволит определить точные координаты точки пересечения прямых.
Если система уравнений:
- имеет единственное решение, то прямые пересекаются;
- имеет бесконечное множество решений, то прямые совпадают;
- не имеет решений, то прямые не пересекаются (прямые параллельны между собой)
Пример 1. Найти точку пересечения прямых y = 2x — 1 и y = -3x + 1.
Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:
y = 2x — 1
y = -3x + 1
Вычтем из первого уравнения второе
y — y = 2x — 1 — (-3x + 1)
y = -3x + 1
=>
0 = 5x — 2
y = -3x + 1
Из первого уравнения найдем значение x
5x = 2
y = -3x + 1
=>
x = 25 = 0.4
y = -3x + 1
Подставим значение x во второе уравнение и найдем значение y
x = 0.4
y = -3·(0.4) + 1 = -1.2 + 1 = -0.2
Ответ. Точка пересечения двух прямых имеет координаты (0.4, -0.2)
Пример 2. Найти точку пересечения прямых y = 2x — 1 и x = 2t + 1y = t.
Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:
y = 2x — 1
x = 2t + 1
y = t
В первое уравнение подставим значения x и y из второго и третьего уравнений.
t = 2·(2t + 1) — 1
x = 2t + 1
y = t
=>
t = 4t + 1
x = 2t + 1
y = t
=>
-3t = 1
x = 2t + 1
y = t
=>
t = -13
x = 2t + 1
y = t
Подставим значение t во второе и третье уравнение
t = -13
x = 2·(-13) + 1 = -23 + 1 = 13
y = -13
Ответ. Точка пересечения двух прямых имеет координаты (13, -13)
Пример 3 Найти точку пересечения прямых 2x + 3y = 0 и x — 23 = y4.
Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:
2x + 3y = 0
x — 23 = y4
Из второго уравнения выразим y через x
2x + 3y = 0
y = 4·x — 23
Подставим y в первое уравнение
2x + 3·4·x — 23 = 0
y = 4·x — 23
=>
2x + 4·(x — 2) = 0
y = 4·x — 23
=>
2x + 4x — 8 = 0
y = 4·x — 23
=>
6x = 8
y = 4·x — 23
=>
x = 86 = 43
y = 4·x — 23
=>
x = 86 = 43
y = 4·4/3 — 23 = 4·-2/3 3 = -89
Ответ. Точка пересечения двух прямых имеет координаты (43, -89)
Пример 4. Найти точку пересечения прямых y = 2x — 1 и y = 2x + 1.
Решение: Обе прямые заданы уравнениями с угловым коэффициентом. Так как k1 = k2 = 2, то прямые параллельны. Так как эти прямые не совпадают то точек пересечения нет.
Решим также эту задачу используя систему уравнений:
y = 2x — 1
y = 2x + 1
Вычтем из первого уравнения второе
y — y = 2x — 1 — (2x + 1)
y = -3x + 1
=>
0 = -2
y = -3x + 1
В первом уравнении получили противоречие (0 ≠ -2), значит система не имеет решений — отсутствуют точки пересечения прямых (прямые параллельны).
Ответ. Прямые не пересекаются (прямые параллельны).
Пример 5. Проверить является ли точка N(1, 1) точкой пересечения прямых y = x и y = 3x — 2.
Решение: Подставим координаты точки N в уравнения прямых.
1 = 1
1 = 3·1 — 2 = 1
Ответ. Так как оба уравнения превратились в тождества, то точка N — точка пересечения этих прямых.
Точка пересечения двух прямых в пространстве
Метод решения. Для определение координат точки пересечения прямых в пространстве, необходимо объединить уравнения прямых в систему, решение которой, позволит определить точные координаты точки пересечения прямых.
Если система уравнений:
- имеет единственное решение, то прямые пересекаются;
- имеет бесконечное множество решений, то прямые совпадают;
- не имеет решений, то прямые не пересекаются (прямые параллельны или скрещиваются между собой)
Пример 6. Найти точку пересечения прямых x — 1 = y — 1 = z — 1 и x — 3-2 = 2 — y = z.
Решение: Составим систему уравнений
x — 1 = a
y — 1 = a
z — 1 = a
x — 3-2 = b
2 — y = b
z = b
=>
x = a + 1
y = a + 1
z = a + 1
x — 3-2 = b
2 — y = b
z = b
=>
Подставим значения x, y, z из 1, 2, 3 уравнений в 4, 5, 6 уравнения
x = a + 1
y = a + 1
z = a + 1
a + 1 — 3-2 = b
2 — (a + 1) = b
a + 1 = b
=>
x = a + 1
y = a + 1
z = a + 1
a — 2-2 = b
1 — a = b
a + 1 = b
К шестому уравнению добавим пятое уравнение
x = a + 1
y = a + 1
z = a + 1
a — 2-2 = b
1 — a = b
a + 1 + (1 — a) = b + b
=>
x = a + 1
y = a + 1
z = a + 1
a — 2-2 = b
1 — a = b
b = 1
Подставим значение b в четвертое и пятое уравнения
x = a + 1
y = a + 1
z = a + 1
a — 2-2 = 1
1 — a = 1
b = 1
=>
x = a + 1
y = a + 1
z = a + 1
a — 2 = -2
a = 0
b = 1
=>
x = a + 1
y = a + 1
z = a + 1
a = 0
a = 0
b = 1
=>
x = 0 + 1 = 1
y = 0 + 1 = 1
z = 0 + 1 = 1
a = 0
a = 0
b = 1
Ответ. Прямые пересекаются в точке с координатами (1, 1, 1).
Замечание. Если уравнения прямых заданы параметрически, и в обоих уравнениях параметр задан одной и той же буквой, то при составлении системы в одном из уравнений необходимо заменить букву отвечающую за параметр.
Пример 7. Найти точку пересечения прямых
x = 2t — 3
y = t
z = —t + 2
и
x = t + 1
y = 3t — 2
z = 3
.
Решение: Составим систему уравнений заменив во втором уравнении параметр t на a
x = 2t — 3
y = t
z = —t + 2
x = a + 1
y = 3a — 2
z = 3
Подставим значения x, y, z из 1, 2, 3 уравнений в 4, 5, 6 уравнения
x = 2t — 3
y = t
z = —t + 2
2t — 3 = a + 1
t = 3a — 2
—t + 2 = 3
=>
x = 2t — 3
y = t
z = —t + 2
2t = a + 4
t = 3a — 2
t = -1
=>
Подставим значение t из шестого уравнения в остальные уравнения
x = 2·(-1) — 3
y = (-1)
z = -(-1) + 2
2·(-1) = a + 4
-1 = 3a — 2
t = -1
=>
x = -5
y = -1
z = 3
a = -6
a = 13
t = -1
Ответ. Так как -6 ≠ 13, то прямые не пересекаются.
В данной публикации мы рассмотрим, что такое точка пересечения двух прямых, и как найти ее координаты разными способами. Также разберем пример решения задачи по этой теме.
- Нахождение координат точки пересечения
- Пример задачи
Нахождение координат точки пересечения
Пересекающимися называются прямые, которые имеют одну общую точку.
M – точка пересечения прямых. Она принадлежит им обоим, значит ее координаты одновременно должны удовлетворять обоим их уравнениях.
Для нахождения координат этой точки на плоскости можно использовать два способа:
- графический – чертим графики прямых на координатой плоскости и находим их точку пересечения (не всегда применимо);
- аналитический – более универсальный метод. Мы объединяем уравнения прямых в систему. Затем решаем ее и получаем требуемые координаты. От количества решений зависит то, каким образом ведут себя прямые по отношению друг к другу:
- одно решение – пересекаются;
- множество решений – совпадают;
- нет решений – параллельны, т.е. не пересекаются.
Пример задачи
Найдем координаты точки пересечения прямых y = x + 6 и y = 2x – 8.
Решение
Составим систему уравнений и решим ее:
В первом уравнении выразим x через y:
x = y – 6
Теперь подставим полученное выражение во второе уравнение вместо x:
y = 2 (y – 6) – 8
y = 2y – 12 – 8
y – 2y = -12 – 8
-y = -20
y = 20
Значит, x = 20 – 6 = 14
Таким образом, общая точка пересечения заданных прямых имеет координаты (14, 20).
Не такая тривиальная задача, скажу я вам. Всякий раз, когда возникает необходимость посчитать координату пересечения пары прямых, каждая из которых задана парой точек, снова беру блокнот и вывожу пару формул. И всякий раз – блин, ну это уже когда-то было, опять надо что-то делать с параллельными прямыми, опять появляется пакостная строго вертикальна линия, когда на (x1-x2) никак не разделить и т.д.
Поэтому – в подборку теории и практики, пригодится, сэкономим блокнот, спасем дерево.
Коэффициенты А, B, C
Все помним со школы формулу:
Тоже самое, но с претензией на образование (некоторые индивидуумы утверждают, что существует такая, и только такая, и никакая другая, формулировка):
Те же фаберже, только сбоку.
В теории надо составить и решить систему уравнений для первой и второй линии, где переменными будут X и Y точки пересечения.
Загвоздка в том, что мы не знаем коэффициенты для обеих линий.
В нашем случае известны координаты двух точек, по которым проходит линия. Поэтому мне, как последователю геометрического агностицизма, более привлекательная следующая формула:
Путем несложных операций приходим к следующей записи:
Глядя на вариант в исполнении высшего образования, получаем следующие формулы для нахождения коэффициентов:
Пока все идет отлично, нигде вероятного деления на ноль не встретилось.
Итак, мы можем легко найти два набора коэффициентов для первой и второй прямых. Переходим к системе уравнений.
Система уравнений
Как правило, подобная система уравнений решается путем выражения одной переменной через другую, подстановкой во второе уравнение, получая таким образом уравнение одной переменной. Далее переменная находится, подставляется, решается. Или определяется, что система решения не имеет.
Но нас интересует метод Крамера. Потому что с помощью этого метода можно получить сразу значения для обеих переменных, без дополнительных телодвижений.
Сразу же запишем метод под нашу систему.
Имеем следующую систему:
Определители будут такими:
Исходя из метода, решение выглядит так:
Ага! Вот и возможное деление на ноль, скажете вы. И правильно! В этой, в высшей степени непозволительной ситуации, когда знаменатель равен нулю, решения нет, прямые либо параллельны, либо совпадают (что, впрочем, частный случай параллельности). В коде, естественно, этот момент надо учитывать.
Практика 1
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
//******************************************************* // Нахождение точки пересечения прямых (p1,p2) и (p3,p4) // Результат — факт пересечения //******************************************************* function CrossLines(const p1,p2,p3,p4: TxPoint; var res: TxPoint): Boolean; const Prec = 0.0001; var a1, a2: Extended; b1, b2: Extended; c1, c2: Extended; v: Extended; begin a1 := p2.y — p1.y; a2 := p4.y — p3.y; b1 := p1.x — p2.x; b2 := p3.x — p4.x; v := a1*b2 — a2*b1; Result := (abs(v) > Prec); if Result then begin c1 := p2.x*p1.y — p1.x*p2.y; c2 := p4.x*p3.y — p3.x*p4.y; res.X := —(c1*b2 — c2*b1)/v; res.Y := —(a1*c2 — a2*c1)/v; end; end; |
Частные случаи
- Прямые параллельны: ∆ab = 0
- (A1B2 – B1A2 = 0);
- Прямые совпадают: ∆ab = ∆X = ∆Y = 0
- (A1B2 – B1A2 = 0) И (A1C2 — A2C1 = 0) И (C1B2 -B1C2 = 0);
- Прямые перпендикулярны:
- (A1 A2 + B1 B2 = 0).
Принадлежность точки отрезку
В общем случае, чтобы определить принадлежность точки отрезку, надо установить две вещи:
- Точка принадлежит прямой, проходящей через конечные точки отрезка. Для этого достаточно подставить значение X и Y в уравнение прямой и проверить получившееся равенство. В нашем случае, этот пункт уже выполнен, т.к. точка пересечения априори принадлежит обеим прямым.
- Проверить факт нахождения точки между концами отрезка.
Займемся пунктом 2. Данный факт можно установить двумя способами:
- Логически, т.е. (x1 <= x <= x2) ИЛИ (x1 >= x >= x2). На случай «вертикальности» линии добавить проверку на Y:
- (y1 <= y <= y2) ИЛИ (y1 >= y >= y2).
- Арифметически. Сумма отрезков |x-x1| + |x-x2| должна быть равна длине отрезка |x1-x2|. Аналогично, на случай «вертикальности» , добавить проверку:
- |y-y1| + |y-y2| = |y1-y2|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
//***************************************************** // Проверка факта нахождения точки res между // концами отрезка (p1,p2). // Решение с помощью условных операторов и // коэффициентов A=(y2-y1) B=(x1-x2). // Выступают в качестве параметров, чтобы не тратить // время на их подсчет, т.к. в вызывающей стороне // они уже посчитаны //***************************************************** function CheckCrossPoint(const p1, p2, res: TxPoint; const A,B: Extended): Boolean; begin Result := (((B<0) and (p1.X < res.X) and (p2.X > res.X)) or ((B>0) and (p1.X > res.X) and (p2.X < res.X)) or ((A<0) and (p1.y > res.Y) and (p2.Y < res.Y)) or ((A>0) and (p1.y < res.Y) and (p2.Y > res.Y))); end; //***************************************************** // Проверить факт нахождения точки res между // концами отрезка (p1,p2) // Арифметическое решение без коэффициентов //***************************************************** function CheckCrossPoint(const p1, p2, res: TxPoint): Boolean; begin Result := (abs(p2.x—p1.x)>= abs(p2.x—res.x) + abs(p1.x—res.x)) and (abs(p2.y—p1.y)>= abs(p2.y—res.y) + abs(p1.y—res.y)); end; |
Практика показывает, что арифметический способ быстрее примерно в 3 раза. Когда-то я считал, что операции сравнения самые быстрые. Это давно уже не так.
Задача нахождения принадлежности точки P(x,y) отрезку, заданного двумя точками с координатами P1(x1, y1) и P2(x2, y2) подробно рассмотрена в отдельной статье.
Угол пересечения прямых
Угол пересечения прямых — это угол пересечения направляющих векторов. Т.е., взяв уже знакомые ранее точки p1 и p2, получим направляющий вектор V(p1,p2), и аналогично второй вектор M(p3,p4). В теории мы должны вычислить достаточно «затратную» функцию, с корнями, квадратами, дробями и арккосинусом.
Давайте не будем останавливаться на ней, она долгая, нудная и в нашем случае ненужная. Рассмотрим вектор:
α — угол наклона вектора к оси X, который можно найти, как:
α = arctan (A1 / B1)
Где расстояния:
A1 = (y1 — y2)
B1 = (x2 — x1)
Что-то знакомое? Да это ни что иное, как коэффициенты в уравнении прямой от образованных фанатов. Может они и правы в своем испепеляющем фанатизме…
Одним словом, коэффициенты (расстояния) у нас уже есть по обеим прямым.
Судя по рисунку, угол между векторами, это сумма углов наклона векторов к оси X. Ммм… не совсем так, на самом деле это разность.
По рисунку явно видно, что угол между векторам это γ = (β — α).
В предыдущем примере все правильно, просто знаки углов разные, т.к. находятся по разные стороны от оси X, а формула работает та же.
От теории к практике
Теперь в плане практического применения. Мне нужно точно знать, откуда, куда и в каком направлении этот угол. В теории, углом между прямыми считается наименьший из пары γ и (180-γ). Так вот, нам это не надо. Какой угол получится – такой нам и нужен.
Поэтому, под углом между векторами понимаем угол от вектора V(p1,p2) к вектору M(p3,p4). Если знак угла – отрицательный, понимаем, что он против часовой стрелки, иначе – по часовой стрелке.
Следует заметить, что, зная коэффициенты, для нахождения угла пересечения, координаты уже не нужны. Листинг таков:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
//********************************************************** // Посчитать угол пересечения векторов по коэфф-ам А и B //********************************************************** function CalcCrossAngle(const a1,b1: Extended; const a2,b2: Extended): Extended; var c1, c2: Extended; begin c1 := ArcTan2(a1,b1); c2 := ArcTan2(a2,b2); Result := c2—c1; if Result < —pi then Result := 2*pi + Result; if Result > pi then Result := Result — 2*pi; end; |
Тут ситуация с вертикальной прямой, т.е. когда теоретически происходит деление на ноль, явно не обрабатывается. Она корректно обрабатывается функцией ArcTan2, которая вернет в этом случае и знак, и 90 градусов.
Практика 2
В дополнение к функции нахождения точки пересечения, напишем «продвинутую» функцию, которая находит эту точку, определяет нахождение на каждом из отрезков, и определяет угол между направляющими векторами. Или же определяет, что прямые параллельны/совпадают.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 |
//********************************************************** // Тип пересечения прямых (p1,p2) и (p3,p4) //********************************************************** type TxCrossLineResult = ( xclrEqual = —32// эквивалентны ,xclrParallel = —16// параллельны ,xclrOk = 0 // как минимум пересечение есть ,xclrFirst = 1 // попадает в первый отрезок ,xclrSecond = 2 // попадает во второй отрезок ,xclrBoth = 3 // попадает в оба ,xclrPerpend = 4 // перпендикулярны // можно найти по маске через AND, но для полноты картины ,xclrFirstP = 5 // перпендикулярны и попадает в первый ,xclrSecondP = 6 // перпендикулярны и попадает в второй ,xclrBothP = 7 // перпендикулярны и попадает в оба ); //********************************************************** // Нахождение точки пересечения прямых (p1,p2) и (p3,p4) // Определяет параллельность, совпадение, // перпендикулярность, пересечение. // Определяет, каким отрезкам принадлежит. // Находит угол(рад.) от (p1,p2) к (p3,p4): // отрицательное значение — против часовой // положительное — по часовой //********************************************************** function CrossLines(const p1,p2,p3,p4: TxPoint; var res: TxPoint; var Angle: Extended): TxCrossLineResult; const Prec = 0.0001; var a1, a2: Extended; b1, b2: Extended; c1, c2: Extended; v: Extended; begin Angle := 0; a1 := p2.y — p1.y; a2 := p4.y — p3.y; b1 := p1.x — p2.x; b2 := p3.x — p4.x; c1 := p2.x*p1.y — p1.x*p2.y; c2 := p4.x*p3.y — p3.x*p4.y; v := a1*b2 — a2*b1; if abs(v) > Prec then begin Result := xclrOk; res.X := —(c1*b2 — c2*b1)/v; res.Y := —(a1*c2 — a2*c1)/v; if CheckCrossPoint(p1,p2,res) then Result := TxCrossLineResult(Integer(Result) + Integer(xclrFirst)); if CheckCrossPoint(p3,p4,res) then Result := TxCrossLineResult(Integer(Result) + Integer(xclrSecond)); if (abs(a1*a2 + b1*b2) < Prec) then Result := TxCrossLineResult(Integer(Result) + Integer(xclrPerpend)); Angle := CalcCrossAngle(a1,b1,a2,b2); end else begin Result := xclrParallel; if ((abs(c1*b2 — c2*b1) < Prec) and (abs(a1*c2 — a2*c1) < Prec)) then Result := xclrEqual; end; end; |
Исходники
Небольшие комментарии по интерфейсу.
Скачать (219 Кб): Исходники (Delphi XE 7-10)
Скачать (1.14 Мб): Исполняемый файл
При запуске генерируется случайным образом 4 точки, по две на прямую. Точки и отрезки можно перетаскивать мышкой. Также, слева присутствует панель, на которой можно ввести координаты точек или коэффициенты уравнения прямой. При нажатии «Enter» или когда элемент ввода теряет фокус, происходит перерасчет и перерисовка.
Внизу есть 4 кнопки переключения режимов отображения. Начиная со второй, помимо координат точки пересечений в верхнем левом углу будет отображаться текущий угол пересечения между направляющими векторами.
Если точка пересечений попадает в какой-либо из отрезков, соответствующий заголовок линии отрезка станет жирным. На рисунке это зеленая линия 2.
По умолчанию, рабочее поле системы координат имеет размерность [-10..10], которую можно изменить ползунком в нижнем правом углу.
We will learn how to find the co-ordinates of the point of intersection
of two lines.
Let the equations of two intersecting straight lines be
a(_{1}) x + b(_{1})y + c(_{1}) = 0 ………….. (i) and
a(_{2}) x + b(_{2}) y + c(_{2}) = 0 …….…… (ii)
Suppose the above equations of two intersecting lines intersect at P(x(_{1}), y(_{1})). Then (x(_{1}), y(_{1})) will satisfy both the equations (i) and (ii).
Therefore, a(_{1})x(_{1}) + b(_{1})y(_{1}) + c(_{1}) = 0 and
a(_{2})x(_{1}) + b(_{2})y(_{1}) + c(_{2}) = 0
Solving the above two equations by using the method of
cross-multiplication, we get,
(frac{x_{1}}{b_{1}c_{2} — b_{2}c_{1}} =
frac{y_{1}}{c_{1}a_{2} — c_{2}a_{1}} = frac{1}{a_{1}b_{2} — a_{2}b_{1}})
Therefore, x(_{1}) = (frac{b_{1}c_{2} — b_{2}c_{1}}{a_{1}b_{2}
— a_{2}b_{1}}) and
y(_{1}) = (frac{c_{1}a_{2} — c_{2}a_{1}}{a_{1}b_{2}
— a_{2}b_{1}}), a(_{1})b(_{2}) — a(_{2})b(_{1})
≠ 0
Therefore, the
required co-ordinates of the point of intersection of the lines (i) and (ii)
are
((frac{b_{1}c_{2} — b_{2}c_{1}}{a_{1}b_{2} — a_{2}b_{1}}), ((frac{c_{1}a_{2} — c_{2}a_{1}}{a_{1}b_{2} — a_{2}b_{1}})), a(_{1})b(_{2}) — a(_{2})b(_{1}) ≠ 0
Notes: To find the coordinates of the point of intersection
of two non-parallel lines, we solve the given equations simultaneously and the
values of x and y so obtained determine the coordinates of the point of
intersection.
If a(_{1})b(_{2}) — a(_{2})b(_{1}) = 0 then a(_{1})b(_{2}) = a(_{2})b(_{1})
⇒ (frac{a_{1}}{b_{1}}) = (frac{a_{2}}{b_{2}})
⇒ — (frac{a_{1}}{b_{1}}) = — (frac{a_{2}}{b_{2}}) i.e., the slope of line (i) = the slope
of line
(ii)
Therefore, in this case the straight lines (i) and (ii) are
parallel and hence they do not intersect at any real point.
Solved example to find the co-ordinates of the point of intersection
of two given intersecting straight lines:
Find the coordinates of the point of intersection of the
lines 2x — y + 3 = 0 and x + 2y — 4 = 0.
Solution:
We know that the co-ordinates of the point of intersection
of the lines a(_{1}) x+ b(_{1})y+ c(_{1})
= 0 and a(_{2}) x + b(_{2}) y + c(_{2}) = 0 are
((frac{b_{1}c_{2} — b_{2}c_{1}}{a_{1}b_{2} — a_{2}b_{1}}), ((frac{c_{1}a_{2} — c_{2}a_{1}}{a_{1}b_{2} — a_{2}b_{1}})), a(_{1})b(_{2}) — a(_{2})b(_{1}) ≠ 0
Given equations are
2x — y + 3 = 0 …………………….. (i)
x + 2y — 4 = 0 …………………….. (ii)
Here a(_{1}) = 2, b(_{1}) = -1, c(_{1}) = 3, a(_{2})
= 1, b(_{2}) = 2 and c(_{2}) = -4.
((frac{(-1)cdot (-4) — (2)cdot (3)}{(2)cdot (2) —
(1)cdot (-1)}), (frac{(3)cdot (1) — (-4)cdot (2)}{(2)cdot (2) — (1)cdot
(-1)}))
⇒ ((frac{4 — 6}{4 + 1}), (frac{3 + 8}{4 + 1}))
⇒ ((frac{11}{5}, frac{-2}{5}))
Therefore, the co-ordinates of the point of intersection of
the lines 2x — y + 3 = 0 and x + 2y — 4 = 0 are ((frac{11}{5}, frac{-2}{5})).
● The Straight Line
- Straight Line
- Slope of a Straight Line
- Slope of a Line through Two Given Points
- Collinearity of Three Points
- Equation of a Line Parallel to x-axis
- Equation of a Line Parallel to y-axis
- Slope-intercept Form
- Point-slope Form
- Straight line in Two-point Form
- Straight Line in Intercept Form
- Straight Line in Normal Form
- General Form into Slope-intercept Form
- General Form into Intercept Form
- General Form into Normal Form
- Point of Intersection of Two Lines
- Concurrency of Three Lines
- Angle between Two Straight Lines
- Condition of Parallelism of Lines
- Equation of a Line Parallel to a Line
- Condition of Perpendicularity of Two Lines
- Equation of a Line Perpendicular to a Line
- Identical Straight Lines
- Position of a Point Relative to a Line
- Distance of a Point from a Straight Line
- Equations of the Bisectors of the Angles between Two Straight Lines
- Bisector of the Angle which Contains the Origin
- Straight Line Formulae
- Problems on Straight Lines
- Word Problems on Straight Lines
- Problems on Slope and Intercept
Didn’t find what you were looking for? Or want to know more information
about Math Only Math.
Use this Google Search to find what you need.