Бинарные деревья поиска и рекурсия – это просто
Время на прочтение
8 мин
Количество просмотров 525K
Существует множество книг и статей по данной теме. В этой статье я попробую понятно рассказать самое основное.
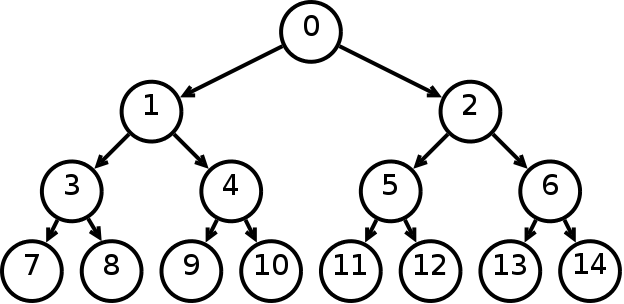
Бинарное дерево — это иерархическая структура данных, в которой каждый узел имеет значение (оно же является в данном случае и ключом) и ссылки на левого и правого потомка. Узел, находящийся на самом верхнем уровне (не являющийся чьим либо потомком) называется корнем. Узлы, не имеющие потомков (оба потомка которых равны NULL) называются листьями.
Рис. 1 Бинарное дерево
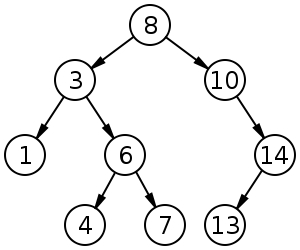
Бинарное дерево поиска — это бинарное дерево, обладающее дополнительными свойствами: значение левого потомка меньше значения родителя, а значение правого потомка больше значения родителя для каждого узла дерева. То есть, данные в бинарном дереве поиска хранятся в отсортированном виде. При каждой операции вставки нового или удаления существующего узла отсортированный порядок дерева сохраняется. При поиске элемента сравнивается искомое значение с корнем. Если искомое больше корня, то поиск продолжается в правом потомке корня, если меньше, то в левом, если равно, то значение найдено и поиск прекращается.
Рис. 2 Бинарное дерево поиска
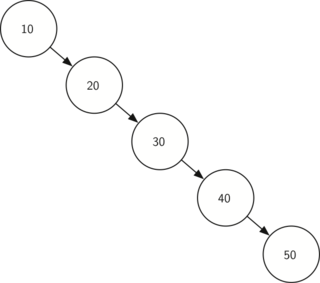
Сбалансированное бинарное дерево поиска — это бинарное дерево поиска с логарифмической высотой. Данное определение скорее идейное, чем строгое. Строгое определение оперирует разницей глубины самого глубокого и самого неглубокого листа (в AVL-деревьях) или отношением глубины самого глубокого и самого неглубокого листа (в красно-черных деревьях). В сбалансированном бинарном дереве поиска операции поиска, вставки и удаления выполняются за логарифмическое время (так как путь к любому листу от корня не более логарифма). В вырожденном случае несбалансированного бинарного дерева поиска, например, когда в пустое дерево вставлялась отсортированная последовательность, дерево превратится в линейный список, и операции поиска, вставки и удаления будут выполняться за линейное время. Поэтому балансировка дерева крайне важна. Технически балансировка осуществляется поворотами частей дерева при вставке нового элемента, если вставка данного элемента нарушила условие сбалансированности.
Рис. 3 Сбалансированное бинарное дерево поиска
Сбалансированное бинарное дерево поиска применяется, когда необходимо осуществлять быстрый поиск элементов, чередующийся со вставками новых элементов и удалениями существующих. В случае, если набор элементов, хранящийся в структуре данных фиксирован и нет новых вставок и удалений, то массив предпочтительнее. Потому что поиск можно осуществлять алгоритмом бинарного поиска за то же логарифмическое время, но отсутствуют дополнительные издержки по хранению и использованию указателей. Например, в С++ ассоциативные контейнеры set и map представляют собой сбалансированное бинарное дерево поиска.
Рис. 4 Экстремально несбалансированное бинарное дерево поиска
Теперь кратко обсудим рекурсию. Рекурсия в программировании – это вызов функцией самой себя с другими аргументами. В принципе, рекурсивная функция может вызывать сама себя и с теми же самыми аргументами, но в этом случае будет бесконечный цикл рекурсии, который закончится переполнением стека. Внутри любой рекурсивной функции должен быть базовый случай, при котором происходит выход из функции, а также вызов или вызовы самой себя с другими аргументами. Аргументы не просто должны быть другими, а должны приближать вызов функции к базовому случаю. Например, вызов внутри рекурсивной функции расчета факториала должен идти с меньшим по значению аргументом, а вызовы внутри рекурсивной функции обхода дерева должны идти с узлами, находящимися дальше от корня, ближе к листьям. Рекурсия может быть не только прямой (вызов непосредственно себя), но и косвенной. Например А вызывает Б, а Б вызывает А. С помощью рекурсии можно эмулировать итеративный цикл, а также работу структуры данных стек (LIFO).
int factorial(int n)
{
if(n <= 1) // Базовый случай
{
return 1;
}
return n * factorial(n - 1); //рекурсивеый вызов с другим аргументом
}
// factorial(1): return 1
// factorial(2): return 2 * factorial(1) (return 2 * 1)
// factorial(3): return 3 * factorial(2) (return 3 * 2 * 1)
// factorial(4): return 4 * factorial(3) (return 4 * 3 * 2 * 1)
// Вычисляет факториал числа n (n должно быть небольшим из-за типа int
// возвращаемого значения. На практике можно сделать long long и вообще
// заменить рекурсию циклом. Если важна скорость рассчетов и не жалко память, то
// можно совсем избавиться от функции и использовать массив с предварительно
// посчитанными факториалами).
void reverseBinary(int n)
{
if (n == 0) // Базовый случай
{
return;
}
cout << n%2;
reverseBinary(n/2); //рекурсивеый вызов с другим аргументом
}
// Печатает бинарное представление числа в обратном порядке
void forvardBinary(int n)
{
if (n == 0) // Базовый случай
{
return;
}
forvardBinary(n/2); //рекурсивеый вызов с другим аргументом
cout << n%2;
}
// Поменяли местами две последние инструкции
// Печатает бинарное представление числа в прямом порядке
// Функция является примером эмуляции стека
void ReverseForvardBinary(int n)
{
if (n == 0) // Базовый случай
{
return;
}
cout << n%2; // печатает в обратном порядке
ReverseForvardBinary(n/2); //рекурсивеый вызов с другим аргументом
cout << n%2; // печатает в прямом порядке
}
// Функция печатает сначала бинарное представление в обратном порядке,
// а затем в прямом порядке
int product(int x, int y)
{
if (y == 0) // Базовый случай
{
return 0;
}
return (x + product(x, y-1)); //рекурсивеый вызов с другим аргументом
}
// Функция вычисляет произведение x * y ( складывает x y раз)
// Функция абсурдна с точки зрения практики,
// приведена для лучшего понимания рекурсии
Кратко обсудим деревья с точки зрения теории графов. Граф – это множество вершин и ребер. Ребро – это связь между двумя вершинами. Количество возможных ребер в графе квадратично зависит от количества вершин (для понимания можно представить турнирную таблицу сыгранных матчей). Дерево – это связный граф без циклов. Связность означает, что из любой вершины в любую другую существует путь по ребрам. Отсутствие циклов означает, что данный путь – единственный. Обход графа – это систематическое посещение всех его вершин по одному разу каждой. Существует два вида обхода графа: 1) поиск в глубину; 2) поиск в ширину.
Поиск в ширину (BFS) идет из начальной вершины, посещает сначала все вершины находящиеся на расстоянии одного ребра от начальной, потом посещает все вершины на расстоянии два ребра от начальной и так далее. Алгоритм поиска в ширину является по своей природе нерекурсивным (итеративным). Для его реализации применяется структура данных очередь (FIFO).
Поиск в глубину (DFS) идет из начальной вершины, посещая еще не посещенные вершины без оглядки на удаленность от начальной вершины. Алгоритм поиска в глубину по своей природе является рекурсивным. Для эмуляции рекурсии в итеративном варианте алгоритма применяется структура данных стек.
С формальной точки зрения можно сделать как рекурсивную, так и итеративную версию как поиска в ширину, так и поиска в глубину. Для обхода в ширину в обоих случаях необходима очередь. Рекурсия в рекурсивной реализации обхода в ширину всего лишь эмулирует цикл. Для обхода в глубину существует рекурсивная реализация без стека, рекурсивная реализация со стеком и итеративная реализация со стеком. Итеративная реализация обхода в глубину без стека невозможна.
Асимптотическая сложность обхода и в ширину и в глубину O(V + E), где V – количество вершин, E – количество ребер. То есть является линейной по количеству вершин и ребер. Записи O(V + E) с содержательной точки зрения эквивалентна запись O(max(V,E)), но последняя не принята. То есть, сложность будет определятся максимальным из двух значений. Несмотря на то, что количество ребер квадратично зависит от количества вершин, мы не можем записать сложность как O(E), так как если граф сильно разреженный, то это будет ошибкой.
DFS применяется в алгоритме нахождения компонентов сильной связности в ориентированном графе. BFS применяется для нахождения кратчайшего пути в графе, в алгоритмах рассылки сообщений по сети, в сборщиках мусора, в программе индексирования – пауке поискового движка. И DFS и BFS применяются в алгоритме поиска минимального покрывающего дерева, при проверке циклов в графе, для проверки двудольности.
Обходу в ширину в графе соответствует обход по уровням бинарного дерева. При данном обходе идет посещение узлов по принципу сверху вниз и слева направо. Обходу в глубину в графе соответствуют три вида обходов бинарного дерева: прямой (pre-order), симметричный (in-order) и обратный (post-order).
Прямой обход идет в следующем порядке: корень, левый потомок, правый потомок. Симметричный — левый потомок, корень, правый потомок. Обратный – левый потомок, правый потомок, корень. В коде рекурсивной функции соответствующего обхода сохраняется соответствующий порядок вызовов (порядок строк кода), где вместо корня идет вызов данной рекурсивной функции.
Если нам дано изображение дерева, и нужно найти его обходы, то может помочь следующая техника (см. рис. 5). Обводим дерево огибающей замкнутой кривой (начинаем идти слева вниз и замыкаем справа вверх). Прямому обходу будет соответствовать порядок, в котором огибающая, двигаясь от корня впервые проходит рядом с узлами слева. Для симметричного обхода порядок, в котором огибающая, двигаясь от корня впервые проходит рядом с узлами снизу. Для обратного обхода порядок, в котором огибающая, двигаясь от корня впервые проходит рядом с узлами справа. В коде рекурсивного вызова прямого обхода идет: вызов, левый, правый. Симметричного – левый, вызов, правый. Обратного – левый правый, вызов.
Рис. 5 Вспомогательный рисунок для обходов
Для бинарных деревьев поиска симметричный обход проходит все узлы в отсортированном порядке. Если мы хотим посетить узлы в обратно отсортированном порядке, то в коде рекурсивной функции симметричного обхода следует поменять местами правого и левого потомка.
struct TreeNode
{
double data; // ключ/данные
TreeNode *left; // указатель на левого потомка
TreeNode *right; // указатель на правого потомка
};
void levelOrderPrint(TreeNode *root) {
if (root == NULL)
{
return;
}
queue<TreeNode *> q; // Создаем очередь
q.push(root); // Вставляем корень в очередь
while (!q.empty() ) // пока очередь не пуста
{
TreeNode* temp = q.front(); // Берем первый элемент в очереди
q.pop(); // Удаляем первый элемент в очереди
cout << temp->data << " "; // Печатаем значение первого элемента в очереди
if ( temp->left != NULL )
q.push(temp->left); // Вставляем в очередь левого потомка
if ( temp->right != NULL )
q.push(temp->right); // Вставляем в очередь правого потомка
}
}
void preorderPrint(TreeNode *root)
{
if (root == NULL) // Базовый случай
{
return;
}
cout << root->data << " ";
preorderPrint(root->left); //рекурсивный вызов левого поддерева
preorderPrint(root->right); //рекурсивный вызов правого поддерева
}
// Функция печатает значения бинарного дерева поиска в прямом порядке.
// Вместо печати первой инструкцией функции может быть любое действие
// с данным узлом
void inorderPrint(TreeNode *root)
{
if (root == NULL) // Базовый случай
{
return;
}
preorderPrint(root->left); //рекурсивный вызов левого поддерева
cout << root->data << " ";
preorderPrint(root->right); //рекурсивный вызов правого поддерева
}
// Функция печатает значения бинарного дерева поиска в симметричном порядке.
// То есть в отсортированном порядке
void postorderPrint(TreeNode *root)
{
if (root == NULL) // Базовый случай
{
return;
}
preorderPrint(root->left); //рекурсивный вызов левого поддерева
preorderPrint(root->right); //рекурсивный вызов правого поддерева
cout << root->data << " ";
}
// Функция печатает значения бинарного дерева поиска в обратном порядке.
// Не путайте обратный и обратноотсортированный (обратный симметричный).
void reverseInorderPrint(TreeNode *root)
{
if (root == NULL) // Базовый случай
{
return;
}
preorderPrint(root->right); //рекурсивный вызов правого поддерева
cout << root->data << " ";
preorderPrint(root->left); //рекурсивный вызов левого поддерева
}
// Функция печатает значения бинарного дерева поиска в обратном симметричном порядке.
// То есть в обратном отсортированном порядке
void iterativePreorder(TreeNode *root)
{
if (root == NULL)
{
return;
}
stack<TreeNode *> s; // Создаем стек
s.push(root); // Вставляем корень в стек
/* Извлекаем из стека один за другим все элементы.
Для каждого извлеченного делаем следующее
1) печатаем его
2) вставляем в стек правого! потомка
(Внимание! стек поменяет порядок выполнения на противоположный!)
3) вставляем в стек левого! потомка */
while (s.empty() == false)
{
// Извлекаем вершину стека и печатаем
TreeNode *temp = s.top();
s.pop();
cout << temp->data << " ";
if (temp->right)
s.push(temp->right); // Вставляем в стек правого потомка
if (temp->left)
s.push(temp->left); // Вставляем в стек левого потомка
}
}
// В симметричном и обратном итеративном обходах просто меняем инструкции
// местами по аналогии с рекурсивными функциями.
Надеюсь Вы не уснули, и статья была полезна. Скоро надеюсь последует продолжение
банкета
статьи.
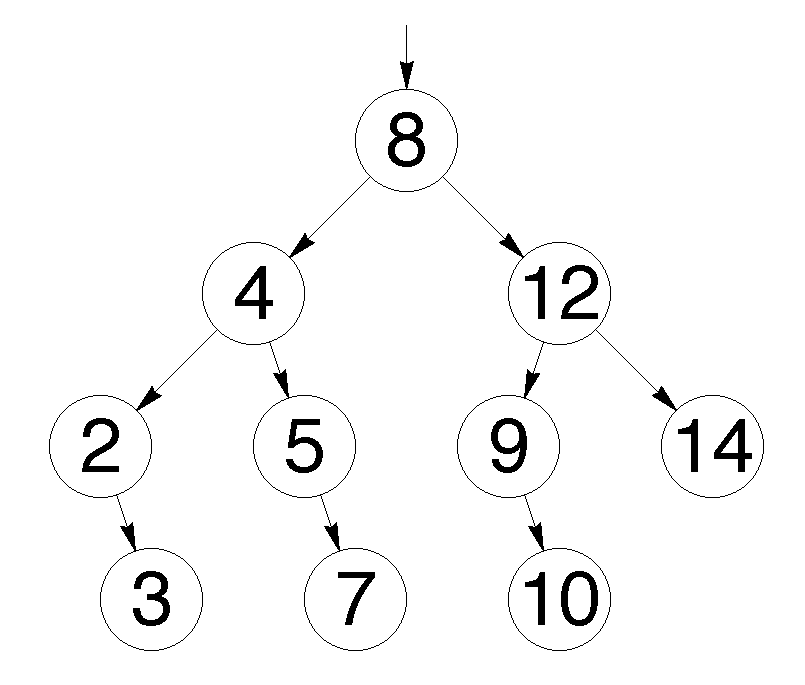
Бинарное дерево поиска из 9 элементов
Бинарное дерево поиска (англ. binary search tree, BST) — структура данных для работы с упорядоченными множествами.
Бинарное дерево поиска обладает следующим свойством: если — узел бинарного дерева с ключом , то все узлы в левом поддереве должны иметь ключи, меньшие , а в правом поддереве большие .
Содержание
- 1 Операции в бинарном дереве поиска
- 1.1 Обход дерева поиска
- 1.2 Поиск элемента
- 1.3 Поиск минимума и максимума
- 1.4 Поиск следующего и предыдущего элемента
- 1.4.1 Реализация с использованием информации о родителе
- 1.4.2 Реализация без использования информации о родителе
- 1.5 Вставка
- 1.5.1 Реализация с использованием информации о родителе
- 1.5.2 Реализация без использования информации о родителе
- 1.6 Удаление
- 1.6.1 Нерекурсивная реализация
- 1.6.2 Рекурсивная реализация
- 2 Задачи о бинарном дереве поиска
- 2.1 Проверка того, что заданное дерево является деревом поиска
- 2.2 Задачи на поиск максимального BST в заданном двоичном дереве
- 2.3 Восстановление дерева по результату обхода preorderTraversal
- 3 См. также
- 4 Источники информации
Операции в бинарном дереве поиска
Для представления бинарного дерева поиска в памяти будем использовать следующую структуру:
struct Node: T key // ключ узла Node left // указатель на левого потомка Node right // указатель на правого потомка Node parent // указатель на предка
Обход дерева поиска
Есть три операции обхода узлов дерева, отличающиеся порядком обхода узлов:
- — обход узлов в отсортированном порядке,
- — обход узлов в порядке: вершина, левое поддерево, правое поддерево,
- — обход узлов в порядке: левое поддерево, правое поддерево, вершина.
func inorderTraversal(x : Node):
if x != null
inorderTraversal(x.left)
print x.key
inorderTraversal(x.right)
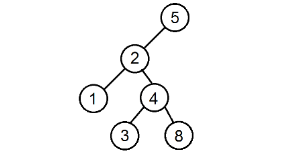
При выполнении данного обхода вершины будут выведены в следующем порядке: 1 3 4 6 7 8 10 13 14.
func preorderTraversal(x : Node)
if x != null
print x.key
preorderTraversal(x.left)
preorderTraversal(x.right)
При выполнении данного обхода вершины будут выведены в следующем порядке: 8 3 1 6 4 7 10 14 13.
func postorderTraversal(x : Node)
if x != null
postorderTraversal(x.left)
postorderTraversal(x.right)
print x.key
При выполнении данного обхода вершины будут выведены в следующем порядке: 1 4 7 6 3 13 14 10 8.
Данные алгоритмы выполняют обход за время , поскольку процедура вызывается ровно два раза для каждого узла дерева.
Поиск элемента
Поиск элемента 4
Для поиска элемента в бинарном дереве поиска можно воспользоваться следующей функцией, которая принимает в качестве параметров корень дерева и искомый ключ. Для каждого узла функция сравнивает значение его ключа с искомым ключом. Если ключи одинаковы, то функция возвращает текущий узел, в противном случае функция вызывается рекурсивно для левого или правого поддерева. Узлы, которые посещает функция образуют нисходящий путь от корня, так что время ее работы , где — высота дерева.
Node search(x : Node, k : T):
if x == null or k == x.key
return x
if k < x.key
return search(x.left, k)
else
return search(x.right, k)
Поиск минимума и максимума
Чтобы найти минимальный элемент в бинарном дереве поиска, необходимо просто следовать указателям от корня дерева, пока не встретится значение . Если у вершины есть левое поддерево, то по свойству бинарного дерева поиска в нем хранятся все элементы с меньшим ключом. Если его нет, значит эта вершина и есть минимальная. Аналогично ищется и максимальный элемент. Для этого нужно следовать правым указателям.
Node minimum(x : Node):
if x.left == null
return x
return minimum(x.left)
Node maximum(x : Node):
if x.right == null
return x
return maximum(x.right)
Данные функции принимают корень поддерева, и возвращают минимальный (максимальный) элемент в поддереве. Обе процедуры выполняются за время .
Поиск следующего и предыдущего элемента
Реализация с использованием информации о родителе
Если у узла есть правое поддерево, то следующий за ним элемент будет минимальным элементом в этом поддереве. Если у него нет правого поддерева, то нужно следовать вверх, пока не встретим узел, который является левым дочерним узлом своего родителя. Поиск предыдущего выполнятся аналогично. Если у узла есть левое поддерево, то предыдущий ему элемент будет максимальным элементом в этом поддереве. Если у него нет левого поддерева, то нужно следовать вверх, пока не встретим узел, который является правым дочерним узлом своего родителя.
Node next(x : Node):
if x.right != null
return minimum(x.right)
y = x.parent
while y != null and x == y.right
x = y
y = y.parent
return y
Node prev(x : Node):
if x.left != null
return maximum(x.left)
y = x.parent
while y != null and x == y.left
x = y
y = y.parent
return y
Обе операции выполняются за время .
Реализация без использования информации о родителе
Рассмотрим поиск следующего элемента для некоторого ключа . Поиск будем начинать с корня дерева, храня текущий узел и узел , последний посещенный узел, ключ которого больше .
Спускаемся вниз по дереву, как в алгоритме поиска узла. Рассмотрим ключ текущего узла . Если , значит следующий за узел находится в правом поддереве (в левом поддереве все ключи меньше ). Если же , то , поэтому может быть следующим для ключа , либо следующий узел содержится в левом поддереве . Перейдем к нужному поддереву и повторим те же самые действия.
Аналогично реализуется операция поиска предыдущего элемента.
Node next(x : T):
Node current = root, successor = null // root — корень дерева
while current != null
if current.key > x
successor = current
current = current.left
else
current = current.right
return successor
Вставка
Операция вставки работает аналогично поиску элемента, только при обнаружении у элемента отсутствия ребенка нужно подвесить на него вставляемый элемент.
Реализация с использованием информации о родителе
func insert(x : Node, z : Node): // x — корень поддерева, z — вставляемый элемент
while x != null
if z.key > x.key
if x.right != null
x = x.right
else
z.parent = x
x.right = z
break
else if z.key < x.key
if x.left != null
x = x.left
else
z.parent = x
x.left = z
break
Реализация без использования информации о родителе
Node insert(x : Node, z : T): // x — корень поддерева, z — вставляемый ключ if x == null return Node(z) // подвесим Node с key = z else if z < x.key x.left = insert(x.left, z) else if z > x.key x.right = insert(x.right, z) return x
Время работы алгоритма для обеих реализаций — .
Удаление
Нерекурсивная реализация
Для удаления узла из бинарного дерева поиска нужно рассмотреть три возможные ситуации. Если у узла нет дочерних узлов, то у его родителя нужно просто заменить указатель на . Если у узла есть только один дочерний узел, то нужно создать новую связь между родителем удаляемого узла и его дочерним узлом. Наконец, если у узла два дочерних узла, то нужно найти следующий за ним элемент (у этого элемента не будет левого потомка), его правого потомка подвесить на место найденного элемента, а удаляемый узел заменить найденным узлом. Таким образом, свойство бинарного дерева поиска не будет нарушено. Данная реализация удаления не увеличивает высоту дерева. Время работы алгоритма — .
| Случай | Иллюстрация |
|---|---|
| Удаление листа | 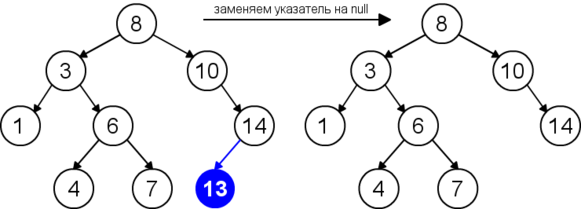
|
| Удаление узла с одним дочерним узлом | 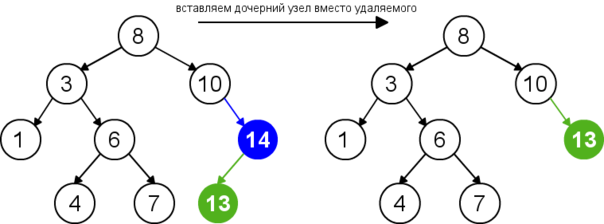
|
| Удаление узла с двумя дочерними узлами | 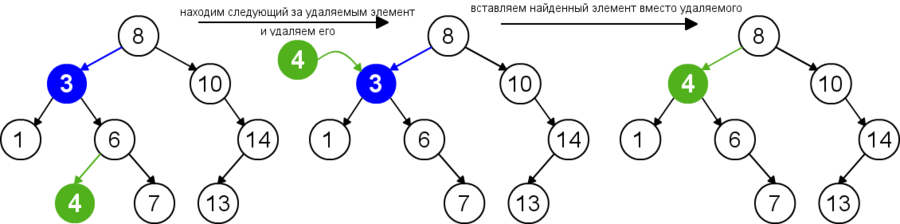
|
func delete(t : Node, v : Node): // — дерево, — удаляемый элемент p = v.parent // предок удаляемого элемента if v.left == null and v.right == null // первый случай: удаляемый элемент - лист if p.left == v p.left = null if p.right == v p.right = null else if v.left == null or v.right == null // второй случай: удаляемый элемент имеет одного потомка if v.left == null if p.left == v p.left = v.right else p.right = v.right v.right.parent = p else if p.left == v p.left = v.left else p.right = v.left v.left.parent = p else // третий случай: удаляемый элемент имеет двух потомков successor = next(v, t) v.key = successor.key if successor.parent.left == successor successor.parent.left = successor.right if successor.right != null successor.right.parent = successor.parent else successor.parent.right = successor.right if successor.right != null successor.right.parent = successor.parent
Рекурсивная реализация
При рекурсивном удалении узла из бинарного дерева нужно рассмотреть три случая: удаляемый элемент находится в левом поддереве текущего поддерева, удаляемый элемент находится в правом поддереве или удаляемый элемент находится в корне. В двух первых случаях нужно рекурсивно удалить элемент из нужного поддерева. Если удаляемый элемент находится в корне текущего поддерева и имеет два дочерних узла, то нужно заменить его минимальным элементом из правого поддерева и рекурсивно удалить этот минимальный элемент из правого поддерева. Иначе, если удаляемый элемент имеет один дочерний узел, нужно заменить его потомком. Время работы алгоритма — .
Рекурсивная функция, возвращающая дерево с удаленным элементом :
Node delete(root : Node, z : T): // корень поддерева, удаляемый ключ
if root == null
return root
if z < root.key
root.left = delete(root.left, z)
else if z > root.key
root.right = delete(root.right, z)
else if root.left != null and root.right != null
root.key = minimum(root.right).key
root.right = delete(root.right, root.key)
else
if root.left != null
root = root.left
else if root.right != null
root = root.right
else
root = null
return root
Задачи о бинарном дереве поиска
Проверка того, что заданное дерево является деревом поиска
| Задача: |
| Определить, является ли заданное двоичное дерево деревом поиска. |
Пример дерева, для которого недостаточно проверки лишь его соседних вершин
Для того чтобы решить эту задачу, применим обход в глубину. Запустим от корня рекурсивную логическую функцию, которая выведет , если дерево является BST и в противном случае. Чтобы дерево не являлось BST, в нём должна быть хотя бы одна вершина, которая не попадает под определение дерева поиска. То есть достаточно найти всего одну такую вершину, чтобы выйти из рекурсии и вернуть значение . Если же, дойдя до листьев, функция не встретит на своём пути такие вершины, она вернёт значение .
Функция принимает на вход исследуемую вершину, а также два значения: и , которые до вызова функции равнялись и соответственно, где — очень большое число, т.е. ни один ключ дерева не превосходит его по модулю. Казалось бы, два последних параметра не нужны. Но без них программа может выдать неверный ответ, так как сравнения только вершины и её детей недостаточно. Необходимо также помнить, в каком поддереве для более старших предков мы находимся. Например, в этом дереве вершина с номером находится левее вершины, в которой лежит , чего не должно быть в дереве поиска, однако после проверки функция бы вернула .
bool isBinarySearchTree(root: Node): // Здесь root — корень заданного двоичного дерева. bool check(v : Node, min: T, max: T): // min и max — минимально и максимально допустимые значения в вершинах поддерева. if v == null return true if v.key <= min or max <= v.key return false return check(v.left, min, v.key) and check(v.right, v.key, max) return check(root, , )
Время работы алгоритма — , где — количество вершин в дереве.
Задачи на поиск максимального BST в заданном двоичном дереве
| Задача: |
| Найти в данном дереве такую вершину, что она будет корнем поддерева поиска с наибольшим количеством вершин. |
Если мы будем приведённым выше способом проверять каждую вершину, мы справимся с задачей за . Но её можно решить за , идя от корня и проверяя все вершины по одному разу, основываясь на следующих фактах:
- Значение в вершине больше максимума в её левом поддереве;
- Значение в вершине меньше минимума в её правом поддереве;
- Левое и правое поддерево являются деревьями поиска.
Введём и , которые будут хранить минимум в левом поддереве вершины и максимум в правом. Тогда мы должны будем проверить, являются ли эти поддеревья деревьями поиска и, если да, лежит ли ключ вершины между этими значениями и . Если вершина является листом, она автоматически становится деревом поиска, а её ключ — минимумом или максимумом для её родителя (в зависимости от расположения вершины). Функция записывает в количество вершин в дереве, если оно является деревом поиска или в противном случае. После выполнения функции ищем за линейное время вершину с наибольшим значением .
int count(root: Node): // root — корень заданного двоичного дерева.
int cnt(v: Node):
if v == null
v.kol = 0
return = 0
if cnt(v.left) != -1 and cnt(v.right) != -1
if v.left == null and v.right == null
v.min = v.key
v.max = v.key
v.kol = 1
return 1
if v.left == null
if v.right.max > v.key
v.min = v.key
v.kol = cnt(v.right) + 1
return v.kol
if v.right == null
if v.left.min < v.key
v.max = v.key
v.kol = cnt(v.left) + 1
return v.kol
if v.left.min < v.key and v.right.max > v.key
v.min = v.left.min
v.max = v.right.max
v.kol = v.left.kol + v.right.kol + 1
v.kol = cnt(v.left) + cnt(v.right) + 1
return v.kol
return -1
return cnt(root)
Алгоритм работает за , так как мы прошлись по дереву два раза за время, равное количеству вершин.
Восстановление дерева по результату обхода preorderTraversal
| Задача: |
| Восстановить дерево по последовательности, выведенной после выполнения процедуры . |
Восстановление дерева поиска по последовательности ключей
Как мы помним, процедура выводит значения в узлах поддерева следующим образом: сначала идёт до упора влево, затем на каком-то моменте делает шаг вправо и снова движется влево. Это продолжается до тех пор, пока не будут выведены все вершины. Полученная последовательность позволит нам однозначно определить расположение всех узлов поддерева. Первая вершина всегда будет в корне. Затем, пока не будут использованы все значения, будем последовательно подвешивать левых сыновей к последней добавленной вершине, пока не найдём номер, нарушающий убывающую последовательность, а для каждого такого номера будем искать вершину без правого потомка, хранящую наибольшее значение, не превосходящее того, которое хотим поставить, и подвешиваем к ней элемент с таким номером в качестве правого сына. Когда мы, желая найти такую вершину, встречаем какую-нибудь другую, уже имеющую правого сына, проходим по ветке вправо. Мы имеем на это право, так как если такая вершина стоит, то процедура обхода в ней уже побывала и поворачивала вправо, поэтому спускаться в другую сторону смысла не имеет. Вершину с максимальным ключом, с которой будем начинать поиск, будем запоминать. Она будет обновляться каждый раз, когда появится новый максимум.
Процедура восстановления дерева работает за .
Разберём алгоритм на примере последовательности .
Будем выделять красным цветом вершины, рассматриваемые на каждом шаге, чёрным жирным — их родителей, курсивом — убывающие подпоследовательности (в случаях, когда мы их рассматриваем) или претендентов на добавление к ним правого ребёнка (когда рассматривается вершина, нарушающая убывающую последовательность).
| Состояние
последовательности |
Действие | Пояснение |
|---|---|---|
| 8 2 1 4 3 5 | Делаем вершину корнем. | Первая вершина всегда будет корнем, так как вывод начинался с него. |
| 8 2 1 4 3 5 | Находим убывающую подпоследовательность. Каждую вершину подвешиваем к последней из взятых ранее в качестве левого сына. | Каждая последующая вершина становится левым сыном предыдущей, так как выводя ключи, мы двигались по дереву поиска влево, пока есть вершины. |
| 8 2 1 4 3 5 | ||
| 8 2 1 4 3 5 | Для вершины, нарушившей убывающую последовательность, ищем максимальное значение, меньшее его. В данном случае оно равно . Затем добавляем вершину. | На моменте вывода следующего номера процедура обратилась уже к какому-то из правых поддеревьев, так как влево идти уже некуда. Значит, нам необходимо найти узел, для которого данная вершина являлась бы правым сыном. Очевидно, что в её родителе не может лежать значение, которое больше её ключа. Но эту вершину нельзя подвесить и к меньшим, иначе нашёлся бы более старший предок, также хранящий какое-то значение, которое меньше, чем в исследуемой. Для этого предка вершина бы попала в левое поддерево. И тогда возникает противоречие с определением дерева поиска. Отсюда следует, что родитель определяется единственным образом — он хранит максимум среди ключей, не превосходящих значения в подвешиваемой вершине, что и требовалось доказать. |
| 8 2 1 4 3 5 | Находим убывающую подпоследовательность. Каждую вершину подвешиваем к последней из взятых ранее в качестве левого сына. | Зайдя в правое поддерево, процедура обхода снова до упора начала двигаться влево, поэтому действуем аналогичным образом. |
| 8 2 1 4 3 5 | Для этой вершины ищем максимальное значение, меньшее его. Затем добавляем вершину. | Здесь процедура снова обратилась к правому поддереву. Рассуждения аналогичны. Ключ родителя этой вершины равен . |
См. также
- Поисковые структуры данных
- Рандомизированное бинарное дерево поиска
- Красно-черное дерево
- АВЛ-дерево
Источники информации
- Википедия — Двоичное дерево поиска
- Wikipedia — Binary search tree
- Кормен, Т., Лейзерсон, Ч., Ривест, Р., Штайн, К. Алгоритмы: построение и анализ = Introduction to Algorithms / Под ред. И. В. Красикова. — 2-е изд. — М.: Вильямс, 2005. — 1296 с. — ISBN 5-8459-0857-4
В этой статье рассмотрим двоичное дерево, как оно строится и варианты обходов.
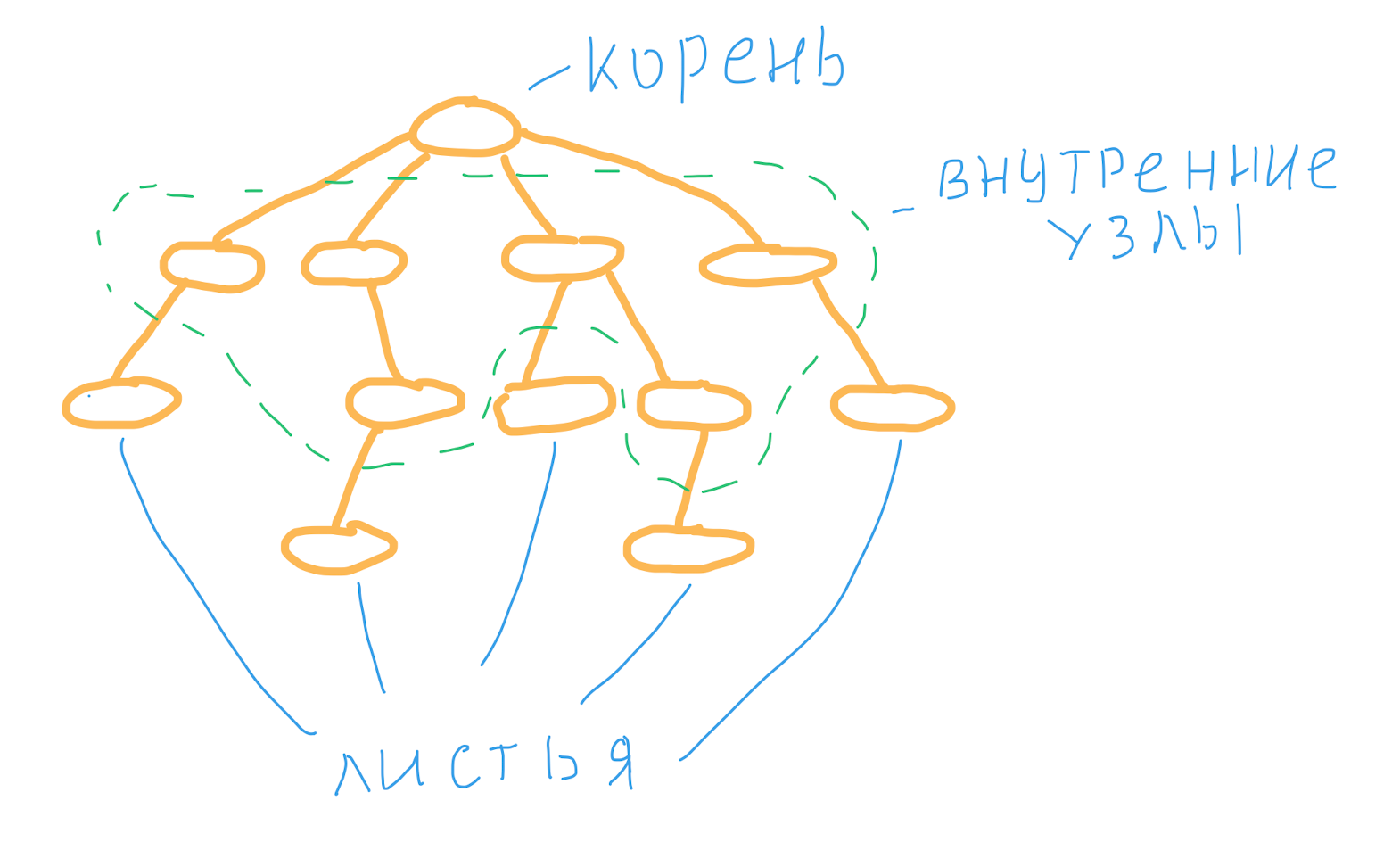
Двоичное дерево в первую очередь дерево. В программировании – структура данных, которая имеет корень и дочерние узлы, без циклических связей. Если рассмотреть отдельно любой узел с дочерними элементами, то получится тоже дерево. Узел называется внутренним, если имеет хотя бы одно поддерево. Cамые нижние элементы, которые не имеют дочерних элементов, называются листами или листовыми узлами.
Дерево обычно рисуется сверху вниз.
В узлах может храниться любая информация, от примитивных типов до объектов. В этой статье, мы рассмотрим реализацию, когда в узле также хранятся ссылки на дочерние элементы. Кроме такого подхода, возможен альтернативный подход для двоичного дерева — хранение в массиве.
Первая особенность двоичного дерева, что любой узел не может иметь более двух детей. Их называют просто — левый и правый потомок, или левое и правое поддерево.
Вторая особенность двоичного дерева, и основное правило его построения, заключается в том что левый потомок меньше текущего узла, а правый потомок больше. Отношение больше/меньше имеет смысл для сравниваемых объектов, например числа, строки, если в дереве содержатся сложные объекты, то для них берётся какая-нибудь процедура сравнения, и она будет отрабатывать при всех операциях работы с деревом.
Создание дерева, вставка
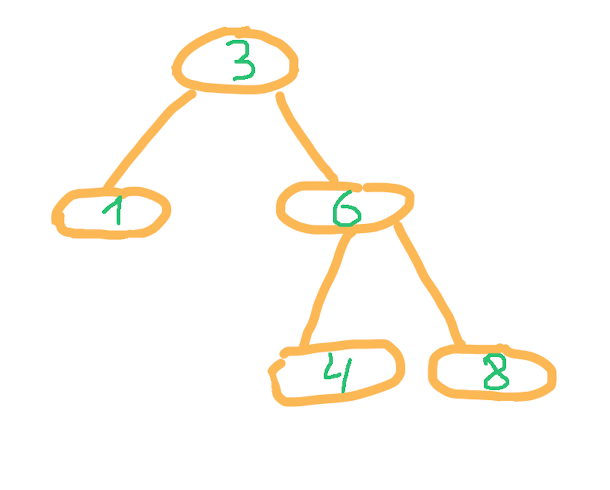
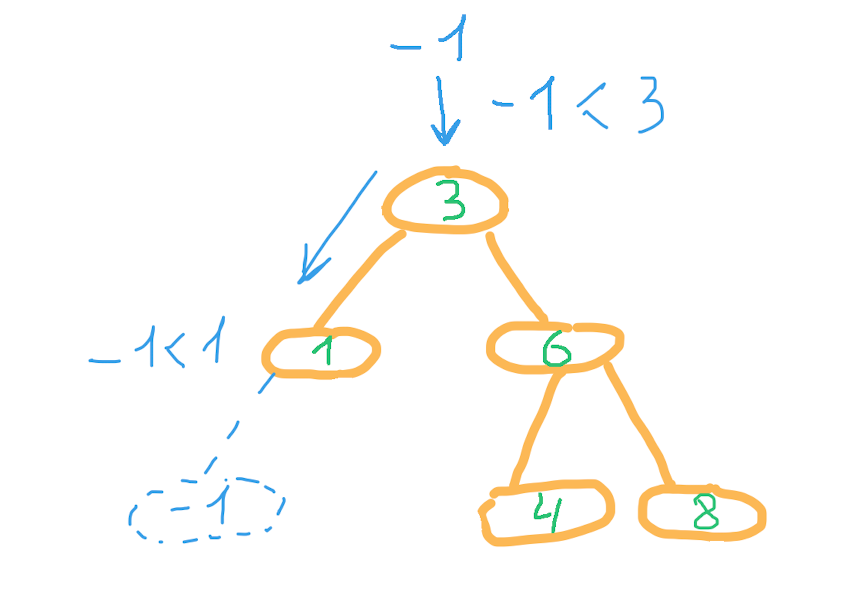
Рассмотрим существующее двоичное дерево. Корень содержит число 3, все узлы в левом поддереве меньше текущего, в правом — больше. Такие же правила действуют для любого рассматриваемого узла и его поддеревьев.
Попробуем вставить в это дерево элемент -1.
Из корня идем в левое поддерево, так как -1 меньше 3. Из узла со значением 1 также идём в левое поддерево. Но в этом узле левое поддерево отсутствует, вставляем в эту позицию элемент, создавая новый узел дерева.
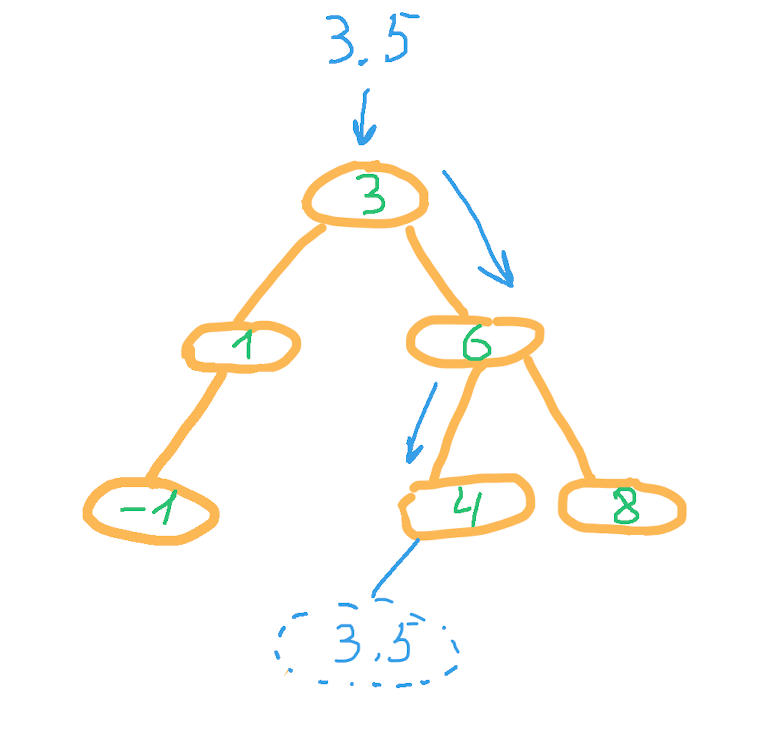
Вставим в получившееся дерево элемент 3.5.
Проходим по дереву, сравнивая на каждом из этапов вставляемое значение с элементом в узле, пока не дойдем до узла, в котором следующий узел для сравнения отсутствует, в эту позицию и вставляем новый узел.
Если дерево не существует, то есть root равен null, то элемент вставляется в корень, после этого проводится вставка по описанному выше алгоритму.
Напишем класс для создания двоичного дерева:
// дополнительный класс для хранения информации узла
class BinaryTreeItem {
constructor(itemValue) {
this.value = itemValue;
this.left = null;
this.right = null;
}
}
const elementExistMessage =
"The element has already in the tree";
class BinaryTree {
// в начале работы дерево пустое, root отсутствует
constructor() {
this.root = null;
}
insertItem(newItem) {
// создание нового узла дерева
const newNode = new BinaryTreeItem(newItem);
// проверка на пустой root, если пустой, то заполняем
// и завершаем работу
if (this.root === null) {
this.root = newNode;
return;
}
// вызов рекурсивного добавления узла
this._insertItem(this.root, newNode);
}
_insertItem(currentNode, newNode) {
// если значение в добавляемом узле
// меньше текущего рассматриваемого узла
if (newNode.value < currentNode.value) {
// если меньше и левое поддерево отсутствует
// то добавляем
if (currentNode.left === null) {
currentNode.left = newNode;
} else {
// если левое поддерево существует,
// то вызываем для этого поддерева
// процедуру добавления нового узла
this._insertItem(currentNode.left, newNode);
}
}
// для правого поддерева алгоритм аналогичен
// работе с левым поддеревом, кроме операции сравнения
if (newNode.value > currentNode.value) {
if (currentNode.right === null) {
currentNode.right = newNode;
} else {
this._insertItem(currentNode.right, newNode);
}
}
// если элемент равен текущему элементу,
// то можно реагировать по разному, например просто
// вывести предупреждение
// возможно стоит добавить проверку на NaN,
// зависит от потребностей пользователей класса
if (newNode.value === currentNode.value) {
console.warn(elementExistMessage);
}
}
}
const binaryTree = new BinaryTree();
binaryTree.insertItem(3);
binaryTree.insertItem(1);
binaryTree.insertItem(6);
binaryTree.insertItem(4);
binaryTree.insertItem(8);
binaryTree.insertItem(-1);
binaryTree.insertItem(3.5);
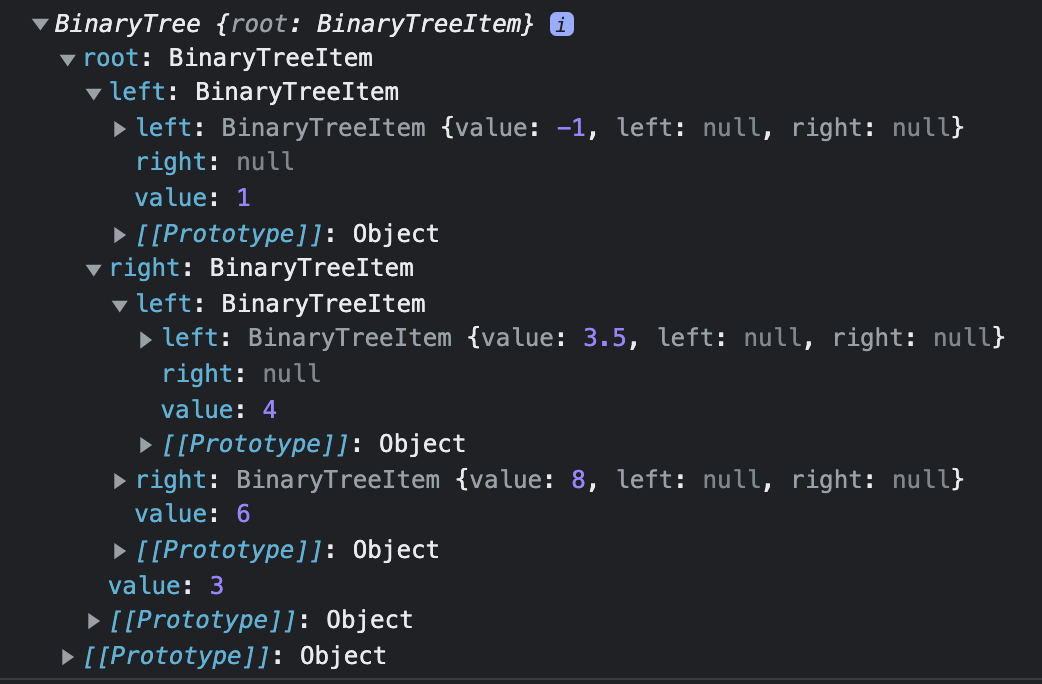
console.log(binaryTree);На скриншоте ниже то, какую информацию хранит в себе binaryTree:
Обход
Рассмотрим несколько алгоритмов обхода/поиска элементов в двоичном дереве.
Мы можем спускаться по дереву, в каждом из узлов есть выбор куда можем пойти в первую очередь и какой из элементов обработать сначала: левое поддерево, корень или право поддерево. Такие варианты обхода называются обходы в глубину (depth first).
Какие возможны варианты обхода (слово поддерево опустим):
- корень, левое, правое (preorder, прямой);
- корень, правое, левое;
- левое, корень, правое (inorder, симметричный, центрированный);
- левое, правое, корень (postorder, обратный);
- правое, корень, левое;
- правое, левое, корень.
Также используется вариант для обхода деревьев по уровням. Уровень в дереве — его удалённость от корня. Сначала обходится корень, после этого узлы первого уровня и так далее. Называется обход в ширину, по уровням, breadth first, BFS — breadth first search или level order traversal.
Выбирается один из этих вариантов, и делается обход, в каждом из узлов применяя выбранную стратегию.
Обычно для обходов в глубину применяется рекурсия. Реализуем один из вариантов, например симметричный: левое поддерево, корень, правое поддерево.
При этом мы обработаем первым самый левый узел, где левое поддерево окажется пустым, но правое может присутствовать. То есть в каждом из узлов будем спускаться ниже и ниже, пока левое поддерево не окажется пустым.
class BinaryTreeItem {
constructor(itemValue) {
this.value = itemValue;
this.left = null;
this.right = null;
}
}
const elementExistMessage =
"The element has already in the tree";
class BinaryTree {
constructor() {
this.root = null;
}
insertItem(newItem) {
// .....
}
inorder(handlerFunction) {
// просто вызываем функцию с другими параметрами,
// добавляя текущий обрабатываемый узел
// в рекурсивные вызов
this._inorderInternal(this.root, handlerFunction);
}
_insertItem(currentNode, newNode) {
// .....
}
_inorderInternal(currentNode, handlerFunction) {
// если узла нет, то его обрабатывать не нужно
if (currentNode === null) return;
// порядок обхода, для каждого из поддеревьев:
// 1. проваливаемся в левое поддерево
// 2. вызываем обрабатывающую функцию
// 3. проваливаемся в правое поддерево
this._inorderInternal(currentNode.left,
handlerFunction);
handlerFunction(currentNode.value);
this._inorderInternal(currentNode.right,
handlerFunction);
}
}
const binaryTree = new BinaryTree();
binaryTree.insertItem(3);
binaryTree.insertItem(1);
binaryTree.insertItem(6);
binaryTree.insertItem(4);
binaryTree.insertItem(8);
binaryTree.insertItem(-1);
binaryTree.insertItem(3.5);
binaryTree.inorder(console.log);
// вызов inorder(console.log) выведет
// -1
// 1
// 3
// 3.5
// 4
// 6
// 8
Для реализации других вариантов обхода просто меняем порядок вызова функций в функции _inorderInternal. И нужно не забыть переименовать функцию, чтобы название соответствовало содержимому.
Рассмотрим inorder алгоритм обхода на примере дерева, созданного в предыдущем блоке кода.
// 1
this._inorderInternal(currentNode.left, handlerFunction);
// 2
handlerFunction(currentNode.value);
// 3
this._inorderInternal(currentNode.right, handlerFunction);
Сначала мы спустимся в самое левое поддерево — узел -1. Зайдем в его левое поддерево, которого нет, первая конструкция выполнится, ничего не сделав внутри функции. Вызовется обработчик handlerFunction, на узле -1. После этого произойдёт попытка войти в правое поддерево, которого нет. Работа функции для узла -1 завершится.
В вызов для узла -1 мы пришли через вызов функции _inorderInternal для левого поддерева узла 1. Вызов для левого поддерева -1 завершился, вызовется обработчик для значения узла 1, после этого — для правого поддерева. Правого поддерева нет, функция для узла 1 заканчивает работу. Выходим в обработчик для корня дерева.
Для корня дерева левое поддерево полностью отработало, происходит переход ко второй строке процедуры обхода — вызов обработчика значения узла. После чего вызов функции для обработчика правого поддерева.
Аналогично продолжая рассуждения, и запоминая на какой строке для определенного узла мы вошли в рекурсивный вызов, можем пройти алгоритм «руками», лучше понимая его работу.
Для обходов в ширину используется дополнительный массив.
class BinaryTreeItem {
constructor(itemValue) {
this.value = itemValue;
this.left = null;
this.right = null;
}
}
const elementExistMessage =
"The element has already in the tree";
class BinaryTree {
constructor() {
this.root = null;
}
insertItem(newItem) {
// .....
}
breadthFirstHandler(handlerFunction) {
if (this.root === null) return;
// массив, в который будем добавлять элементы,
// по мере спускания по дереву
const queue = [this.root];
// используем позицию в массиве для текущего
// обрабатываемого элемента
let queuePosition = 0;
// можем убирать обработанные элементы из очереди
// например функцией shift
// для обработки всегда брать нулевой элемент
// и завершать работу, когда массив пуст
// но shift работает за линейное время, что увеличивает
// скорость работы алгоритма
// while (queue.length > 0) {
// const currentNode = queue.shift();
while (queuePosition < queue.length) {
// текущий обрабатываемый элемент в queuePosition
const currentNode = queue[queuePosition];
handlerFunction(currentNode.value);
// добавляем в список для обработки дочерние узлы
if (currentNode.left !== null) {
queue.push(currentNode.left);
}
if (currentNode.right !== null) {
queue.push(currentNode.right);
}
queuePosition++;
}
}
_insertItem(currentNode, newNode) {
// ......
}
}
const binaryTree = new BinaryTree();
binaryTree.insertItem(3);
binaryTree.insertItem(1);
binaryTree.insertItem(6);
binaryTree.insertItem(4);
binaryTree.insertItem(8);
binaryTree.insertItem(-1);
binaryTree.insertItem(3.5);
binaryTree.breadthFirstHandler(console.log);
// вызов breadthFirstHandler(console.log) выведет
// 3 корень
// 1 узлы первого уровня
// 6
// -1 узлы второго уровня
// 4
// 8
// 3.5 узел третьего уровня
Поиск
Операция поиска — вернуть true или false, в зависимости от того, содержится элемент в дереве или нет. Может быть реализована на основе поиска в глубину или ширину, посмотрим на реализацию на основе алгоритма обхода в глубину.
search(value) {
return this._search(this.root, value);
}
_search(currentNode, value) {
// дополнительные проверки,
// обрабатывающие завершение поиска
// либо проваливание в несуществующий узел
// либо найденной значение
if (currentNode === null) return false;
if (currentNode.value === value) return true;
// this._search проваливаются в дерево
// когда поиск завершен
// то по цепочке рекурсивных вызовов
// будет возвращен результат
if (value < currentNode.value) {
return this._search(currentNode.left, value);
}
if (value > currentNode.value) {
return this._search(currentNode.right, value);
}
}Функция сравнения или получение ключа
До этого мы рассматривали простые данные, для которых определена операция сравнения между ключами. Не всегда возможно реализовать сравнение таким простым образом.
Можно сделать функцию, которая будет получать ключ из данных, которые хранятся в узле.
class BinaryTreeItem {
constructor(itemValue) {
this.value = itemValue;
this.left = null;
this.right = null;
}
}
const elementExistMessage =
"The element has already in the tree";
class BinaryTree {
// параметр при создании дерева -
// функция получения ключа
// ключи должны быть сравнимы
constructor(getKey) {
this.root = null;
this.getKey = getKey;
}
insertItem(newItem) {
const newNode = new BinaryTreeItem(newItem);
if (this.root === null) {
this.root = newNode;
return;
}
this._insertItem(this.root, newNode);
}
breadthFirstHandler(handlerFunction) {
// .....
}
_insertItem(currentNode, newNode) {
// отличие во всех процедурах сравнения
// вместо просто сравнивания value
// перед этим применяем функцию получения ключа
if (this.getKey(newNode.value) <
this.getKey(currentNode.value)) {
if (currentNode.left === null) {
currentNode.left = newNode;
} else {
this._insertItem(currentNode.left, newNode);
}
}
if (this.getKey(newNode.value) >
this.getKey(currentNode.value)) {
if (currentNode.right === null) {
currentNode.right = newNode;
} else {
this._insertItem(currentNode.right, newNode);
}
}
if (this.getKey(newNode.value) ===
this.getKey(currentNode.value)) {
console.warn(elementExistMessage);
}
}
}
const getKey = (element) => element.key;
const binaryTree = new BinaryTree(getKey);
binaryTree.insertItem({ key: 3 });
binaryTree.insertItem({ key: 1 });
binaryTree.insertItem({ key: 6 });
binaryTree.insertItem({ key: 4 });
binaryTree.insertItem({ key: 8 });
binaryTree.insertItem({ key: -1 });
binaryTree.insertItem({ key: 3.5 });
binaryTree.breadthFirstHandler(console.log);Можно передать в конструктор специальную функцию сравнения. Эту функцию можно сделать как обычно делают функции сравнения в программировании, возвращать 0, если ключи равны. Значение больше нуля, если первый переданный объект больше второго, и меньше нуля если меньше. Важно не перепутать когда что возвращается и правильно передать параметры. Например, текущий узел, уже существующий в дереве, первым параметром, а тот, с которым производится текущая операция — вторым.
Для реализации такой возможности потребуется во всех местах сравнения использовать эту функцию
class BinaryTreeItem {
constructor(itemValue) {
this.value = itemValue;
this.left = null;
this.right = null;
}
}
const elementExistMessage =
"The element has already in the tree";
class BinaryTree {
// в конструкторе передаем функцию сравнения
constructor(compareFunction) {
this.root = null;
this.compareFunction = compareFunction;
}
insertItem(newItem) {
const newNode = new BinaryTreeItem(newItem);
if (this.root === null) {
this.root = newNode;
return;
}
this._insertItem(this.root, newNode);
}
breadthFirstHandler(handlerFunction) {
// .....
}
_insertItem(currentNode, newNode) {
// вместо сравнения value
// вызываем функцию сравнения
// и проверяем больше или меньше нуля
// получился результат сравнения
if (this.compareFunction(currentNode.value,
newNode.value) > 0) {
if (currentNode.left === null) {
currentNode.left = newNode;
} else {
this._insertItem(currentNode.left, newNode);
}
}
// текущий узел меньше нового,
// значит новый узел должен быть отправлен
// в правое поддерево
if (this.compareFunction(currentNode.value,
newNode.value) < 0) {
if (currentNode.right === null) {
currentNode.right = newNode;
} else {
this._insertItem(currentNode.right, newNode);
}
}
if (this.compareFunction(currentNode.value,
newNode.value) === 0) {
console.warn(elementExistMessage);
}
}
}
const compare = (object1, object2) => {
return object1.key - object2.key;
};
const binaryTree = new BinaryTree(compare);
binaryTree.insertItem({ key: 3 });
binaryTree.insertItem({ key: 1 });
binaryTree.insertItem({ key: 6 });
binaryTree.insertItem({ key: 4 });
binaryTree.insertItem({ key: 8 });
binaryTree.insertItem({ key: -1 });
binaryTree.insertItem({ key: 3.5 });
binaryTree.breadthFirstHandler(console.log);Заключение
Мы познакомились с концепцией двоичных деревьев и операциями для создания такого типа дерева. Эти операции интуитивно понятны, в следующей статье рассмотрим процедуру удаления и скорость работы двоичного дерева.
Прелюдия
Эта статья посвящена бинарным деревьям поиска. Недавно делал статью про сжатие данных методом Хаффмана. Там я не очень обращал внимание на бинарные деревья, ибо методы поиска, вставки, удаления не были актуальны. Теперь решил написать статью именно про деревья. Пожалуй, начнем.
Дерево — структура данных, состоящая из узлов, соединенных ребрами. Можно сказать, что дерево — частный случай графа. Вот пример дерева:
Это не бинарное дерево поиска! Все под кат!
Терминология
Корень
Корень дерева — это самый верхний его узел. В примере — это узел A. В дереве от корня к любому другому узлу может вести только один путь!
Родители/потомки
Все узлы, кроме корневого, имеют ровно одно ребро, ведущее вверх к другому узлу. Узел, расположенный выше текущего, называется родителем этого узла. Узел, расположенный ниже текущего, и соединенный с ним называется потомком этого узла. Давайте на примере. Возьмем узел B, тогда его родителем будет узел A, а потомками — узлы D, E и F.
Лист
Узел, у которого нет потомков, будет называться листом дерева. В примере листьями будут являться узлы D, E, F, G, I, J, K.
Это основная терминология. Другие понятия будут разобраны далее. Итак, бинарное дерево — дерево, в котором каждый узел будет иметь не более двух потомков. Как вы догадались, дерево из примера не будет являться бинарным, ибо узлы B и H имеют более двух потомков. Вот пример бинарного дерева:
В узлах дерева может находиться любая информация. Двоичное дерево поиска — это двоичное дерево, для которого характерны следующие свойства:
- Оба поддерева — левое и правое — являются двоичными деревьями поиска.
- У всех узлов левого поддерева произвольного узла X значения ключей данных меньше, нежели значение ключа данных самого узла X.
- У всех узлов правого поддерева произвольного узла X значения ключей данных больше либо равны, нежели значение ключа данных самого узла X.
Ключ — какая-либо характеристика узла(например, число). Ключ нужен для того, чтобы можно было найти элемент дерева, которому соответствует этот ключ. Пример бинарного дерева поиска:
Представление дерева
По мере продвижения я буду приводить некоторые(возможно, неполные) куски кода, для того, чтобы улучшить ваше понимание. Полный код будет в конце статьи.
Дерево состоит из узлов. Структура узла:
public class Node {
private int data;
private Node leftChild;
private Node rightChild;
public Node(int newData) {
data = newData;
}
//методы узла
}
Каждый узел имеет двух потомков(вполне возможно, потомки leftChild и/или rightChild будут содержать значение null). Вы, наверное, поняли, что в данном случае число data — ключ узла.
Ключ и информация в узле могут не совпадать! Например, вы могли сделать так:
public class Node {
private int key;
private Data myData;
private Node leftChild;
private Node rightChild;
public Node(int newData) {
data = newData;
}
public Node getLeftChild() {
return leftChild;
}
public Node getRightChild() {
return rightChild;
}
//методы узла
}
class Data {
private String s;
public Data(String s) {
this.s = s;
}
public String getString() {
return s;
}
}
Здесь myData хранит информацию узла дерева. Важно понимать, что узел дерева может хранить любую информацию.
С узлом разобрались, теперь поговорим
о проблемах насущных
о деревьях. Здесь и далее под словом «дерево» буду подразумевать понятие бинарного дерева поиска. Структура бинарного дерева:
public class BinaryTree {
private Node root;
//методы дерева
}
Как поле класса нам понадобится только корень дерева, ибо от корня с помощью методов getLeftChild() и getRightChild() можно добраться до любого узла дерева.
Алгоритмы в дереве
Поиск
Допустим, у вас есть построенное дерево. Как найти элемент с ключом key? Нужно последовательно двигаться от корня вниз по дереву и сравнивать значение key с ключом очередного узла: если key меньше, чем ключ очередного узла, то перейти к левому потомку узла, если больше — к правому, если ключи равны — искомый узел найден! Соответствующий код:
public Node find(int findData) {
Node current = root;
while (current.getData() != findData) {
if (findData < current.getData()) //идем налево
current = current.getLeftChild();
else //идем направо(ситуацию равенства проверяет цикл)
current = current.getRightChild();
if (current == null)//если потомка не существует, значит в дереве нет элемента с ключом findData
return null;
}
return current;
}
Если current становится равным null, значит, перебор достиг конца дерева(на концептуальном уровне вы находитесь в несуществующем месте дерева — потомке листа).
Рассмотрим эффективность алгоритма поиска на сбалансированном дереве(дереве, в котором узлы распределены более-менее равномерно). Тогда эффективность поиска будет O(log(n)), причем логарифм по основанию 2. Смотрите: если в сбалансированном дереве n элементов, то это значит, что будет log(n) по основанию 2 уровней дерева. А в поиске, за один шаг цикла, вы спускаетесь на один уровень.
Вставка
Если вы уловили суть поиска, то понять вставку не составит вам труда. Надо просто спуститься до листа дерева(по правилам спуска, описанным в поиске) и стать его потомком — левым, или правым, в зависимости от ключа. Реализация:
public void insert(int insertData) {
Node current = root;
Node parent;//родитель текущего узла
Node newNode = new Node(insertData);
if (root == null)
root = newNode;
else {
while (true) {
parent = current;
if (insertData < current.getData()) {
current = current.getLeftChild();
if (current == null) {
parent.setLeftChild(newNode);
return;
}
}
else {
current = current.getRightChild();
if (current == null) {
parent.setRightChild(newNode);
return;
}
}
}
}
}
В данном случае надо, помимо текущего узла, хранить информацию о родителе текущего узла. Когда current станет равным null, в переменной parent будет лежать нужный нам лист.
Эффективность вставки, очевидно, будет такой же как и у поиска — O(log(n)).
Удаление
Удаление — самая сложная операция, которую надо будет провести с деревом. Понятно, что сначала надо будет найти элемент, который мы собираемся удалять. Но что потом? Если просто присвоить его ссылке значение null, то мы потерям информацию о поддереве, корнем которого является этот узел. Методы удаления дерева разделяют на три случая.
Первый случай. Удаляемый узел не имеет потомков
Если удаляемый узел не имеет потомков, то это значит, что он является листом. Следовательно, можно просто полям leftChild или rightChild его родителя присвоить значение null. В зависимости от того, является ли удаляемый узел левым или правым потомком своего родителя, переменная isLeftChild будет принимать значение true или false соответственно.
public boolean delete(int deleteData) {
Node current = root;
Node parent = current;
boolean isLeftChild = false;//информация о местоположении удаляемого листа по отношению к его родителю
while (current.getData() != deleteData) {
parent = current;
if (deleteData < current.getData()) {
current = current.getLeftChild();
isLeftChild = true;
} else {
isLeftChild = false;
current = current.getRightChild();
}
if (current == null)
return false;
}
if (current.getLeftChild() == null && current.getRightChild() == null) {//если удаляем лист
if (current == root)//если он корень, то достаточно сделать его равным null
current = null;
else if (isLeftChild)//удалем некорневой лист, являющийся
parent.setLeftChild(null);//левым потомком своего родителя
else
parent.setRightChild(null);//правым потомком своего родителя
}
...
Второй случай. Удаляемый узел имеет одного потомка
Этот случай тоже не очень сложный. Вернемся к нашему примеру. Допустим, надо удалить элемент с ключом 14. Согласитесь, что так как он — правый потомок узла с ключом 10, то любой его потомок(в данном случае правый) будет иметь ключ, больший 10, поэтому можно легко его «вырезать» из дерева, а родителя соединить напрямую с потомком удаляемого узла, т.е. узел с ключом 10 соединить с узлом 13. Аналогичной была бы ситуация, если бы надо было удалить узел, который является левым потомком своего родителя. Подумайте об этом сами — точная аналогия.
Код:
//продолжение метода delete
else if (current.getRightChild() == null) {//Если удаляемый узел имеет левого потомка
if (current == root)//удаляемый узел - корень
root = current.getLeftChild();//сделать корнем его (единственный) левый потомок
else if (isLeftChild)//Если удаляемый узел является
parent.setLeftChild(current.getLeftChild());//левым потомком своего родителя
else
current.setRightChild(current.getLeftChild());//правым потомком своего родителя
} else if (current.getLeftChild() == null) {//Если удаляемый узел имеет правого потомка
if (current == root)//удаляемый узел - корень
root = current.getRightChild();//сделать корнем его (единственный) правый потомок
else if (isLeftChild)//если удаляемый узел является
parent.setLeftChild(current.getRightChild());//левым потомком своего родителя
else
parent.setRightChild(current.getRightChild());//правым потомком своего родителя
}
...
Третий случай. Узел имеет двух потомков
Наиболее сложный случай. Разберем на новом примере.
Поиск преемника
Допустим, надо удалить узел с ключом 25. Кого поставим на его место? Кто-то из его последователей(потомков или потомков потомков) должен стать преемником(тот, кто займет место удаляемого узла).
Как понять, кто должен стать преемником? Интуитивно понятно, что это узел в дереве, ключ которого — следующий по величине от удаляемого узла. Алгоритм заключается в следующем. Надо перейти к его правому потомку(всегда к правому, ибо уже говорилось, что ключ преемника больше ключа удаляемого узла), а затем пройтись по цепочке левых потомков этого правого потомка. В примере мы должны перейти к узлу с ключом 35, а затем пройтись до листа вниз по цепочке его левых потомков — в данном случае, эта цепочка состоит только из узла с ключом 30. Строго говоря, мы ищем наименьший узел в наборе узлов, больших искомого узла.
Код:
public Node getSuccessor(Node deleteNode) {
Node parentSuccessor = deleteNode;//родитель преемника
Node successor = deleteNode;//преемник
Node current = successor.getRightChild();//просто "пробегающий" узел
while (current != null) {
parentSuccessor = successor;
successor = current;
current = current.getLeftChild();
}
//на выходе из цикла имеем преемника и родителя преемника
if (successor != deleteNode.getRightChild()) {//если преемник не совпадает с правым потомком удаляемого узла
parentSuccessor.setLeftChild(successor.getRightChild());//то его родитель забирает себе потомка преемника, чтобы не потерять его
successor.setRightChild(deleteNode.getRightChild());//связываем преемника с правым потомком удаляемого узла
}
return successor;
}
Теперь можем закончить метод delete:
//продолжение метода delete
else {
Node successor = getSuccessor(current);//получить преемника
if (current == root)//если удаляемый элемент - корень дерева
root = successor;//то сделать его преемника корнем
else if (isLeftChild)//если удаляемый элемент является
parent.setLeftChild(successor);//левым потомком своего родителя
else
parent.setRightChild(successor);//правым потомком своего родителя
}
return true;
}
Полный код метода delete:
public boolean delete(int deleteData) {
Node current = root;
Node parent = current;
boolean isLeftChild = false;
while (current.getData() != deleteData) {
parent = current;
if (deleteData < current.getData()) {
current = current.getLeftChild();
isLeftChild = true;
} else {
isLeftChild = false;
current = current.getRightChild();
}
if (current == null)//удаляемый элемент не найден
return false;
}
if (current.getLeftChild() == null && current.getRightChild() == null) {
if (current == root)
current = null;
else if (isLeftChild)
parent.setLeftChild(null);
else
parent.setRightChild(null);
}
else if (current.getRightChild() == null) {
if (current == root)
root = current.getLeftChild();
else if (isLeftChild)
parent.setLeftChild(current.getLeftChild());
else
current.setRightChild(current.getLeftChild());
} else if (current.getLeftChild() == null) {
if (current == root)
root = current.getRightChild();
else if (isLeftChild)
parent.setLeftChild(current.getRightChild());
else
parent.setRightChild(current.getRightChild());
}
else {
Node successor = getSuccessor(current);
if (current == root)
root = successor;
else if (isLeftChild)
parent.setLeftChild(successor);
else
parent.setRightChild(successor);
}
return true;
}
Сложность может быть аппроксимирована к O(log(n)).
Поиск максимума/минимума в дереве
Очевидно, как найти минимальное/максимальное значение в дереве — надо последовательно переходить по цепочке левых/правых элементов дерева соответственно; когда доберетесь до листа, он и будет минимальным/максимальным элементом.
public Node getMinimum(Node startPoint) {
Node current = startPoint;
Node parrent = current;
while (current != null) {
parrent = current;
current = current.getLeftChild();
}
return parrent;
}
public Node getMaximum(Node startPoint) {
Node current = startPoint;
Node parrent = current;
while (current != null) {
parrent = current;
current = current.getRightChild();
}
return parrent;
}
Сложность — O(log(n))
Симметричный обход
Обход — посещение каждого узла дерева с целью сделать с ним какую-то функцию.
Алгоритм рекурсивного симметричного обхода:
- Сделать действие с левым потомком
- Сделать действие с собой
- Сделать действие с правым потомком
Код:
public void inOrder(Node current) {
if (current != null) {
inOrder(current.getLeftChild());
System.out.println(current.getData() + " ");//Здесь может быть все, что угодно
inOrder(current.getRightChild());
}
}
Заключение
Наконец-то! Если я что-то недообъяснил или есть какие-либо замечания, то жду в комментариях. Как обещал, привожу полный код.
Node.java:
public class Node {
private int data;
private Node leftChild;
private Node rightChild;
public Node(int newData) {
data = newData;
}
public void setLeftChild(Node newNode) {
leftChild = newNode;
}
public void setRightChild(Node newNode) {
rightChild = newNode;
}
public Node getLeftChild() {
return leftChild;
}
public Node getRightChild() {
return rightChild;
}
public int getData() {
return data;
}
}
BinaryTree.java:
public class BinaryTree {
private Node root;
public Node find(int findData) {
Node current = root;
while (current.getData() != findData) {
if (findData < current.getData())
current = current.getLeftChild();
else
current = current.getRightChild();
if (current == null)
return null;
}
return current;
}
public void insert(int insertData) {
Node current = root;
Node parrent;
Node newNode = new Node(insertData);
if (root == null)
root = newNode;
else {
while (true) {
parrent = current;
if (insertData < current.getData()) {
current = current.getLeftChild();
if (current == null) {
parrent.setLeftChild(newNode);
return;
}
}
else {
current = current.getRightChild();
if (current == null) {
parrent.setRightChild(newNode);
return;
}
}
}
}
}
public Node getMinimum(Node startPoint) {
Node current = startPoint;
Node parrent = current;
while (current != null) {
parrent = current;
current = current.getLeftChild();
}
return parrent;
}
public Node getMaximum(Node startPoint) {
Node current = startPoint;
Node parrent = current;
while (current != null) {
parrent = current;
current = current.getRightChild();
}
return parrent;
}
public Node getRoot() {
return root;
}
public Node getSuccessor(Node deleteNode) {
Node parrentSuccessor = deleteNode;
Node successor = deleteNode;
Node current = successor.getRightChild();
while (current != null) {
parrentSuccessor = successor;
successor = current;
current = current.getLeftChild();
}
if (successor != deleteNode.getRightChild()) {
parrentSuccessor.setLeftChild(successor.getRightChild());
successor.setRightChild(deleteNode.getRightChild());
}
return successor;
}
public boolean delete(int deleteData) {
Node current = root;
Node parent = current;
boolean isLeftChild = false;
while (current.getData() != deleteData) {
parent = current;
if (deleteData < current.getData()) {
current = current.getLeftChild();
isLeftChild = true;
} else {
isLeftChild = false;
current = current.getRightChild();
}
if (current == null)
return false;
}
if (current.getLeftChild() == null && current.getRightChild() == null) {
if (current == root)
current = null;
else if (isLeftChild)
parent.setLeftChild(null);
else
parent.setRightChild(null);
}
else if (current.getRightChild() == null) {
if (current == root)
root = current.getLeftChild();
else if (isLeftChild)
parent.setLeftChild(current.getLeftChild());
else
current.setRightChild(current.getLeftChild());
} else if (current.getLeftChild() == null) {
if (current == root)
root = current.getRightChild();
else if (isLeftChild)
parent.setLeftChild(current.getRightChild());
else
parent.setRightChild(current.getRightChild());
}
else {
Node successor = getSuccessor(current);
if (current == root)
root = successor;
else if (isLeftChild)
parent.setLeftChild(successor);
else
parent.setRightChild(successor);
}
return true;
}
public void inOrder(Node current) {
if (current != null) {
inOrder(current.getLeftChild());
System.out.println(current.getData() + " ");
inOrder(current.getRightChild());
}
}
}
Main.java:
import java.util.Scanner;
public class Main {
public static void main (String[] args) {
Scanner scanner = new Scanner(System.in);
BinaryTree binaryTree = new BinaryTree();
int operationCommand = 0;
int data = 0;
while (true) {
System.out.println("Input 1 to add element, 2 to delete, 3 to search, 4 to get max, 5 to get min, 0 to exit");
operationCommand = scanner.nextInt();
switch (operationCommand) {
case 0:
scanner.close();
return;
case 1:
System.out.println("Input element");
data = scanner.nextInt();
binaryTree.insert(data);
break;
case 2:
System.out.println("Input element");
data = scanner.nextInt();
binaryTree.delete(data);
break;
case 3:
System.out.println("Input element");
data = scanner.nextInt();
if (binaryTree.find(data) != null)
System.out.println("OK");
else
System.out.println("Not found");
break;
case 4:
System.out.println(binaryTree.getMaximum(binaryTree.getRoot()));
break;
case 5:
System.out.println(binaryTree.getMinimum(binaryTree.getRoot()));
break;
default:
System.out.println("Another key to continue");
break;
}
}
}
}
В этом руководстве вы узнаете, как работает двоичное дерево поиска. Здесь же собраны примеры реализации дерева двоичного поиска на Си, C++, Java и Python.
Дерево двоичного поиска — это структура данных, которая позволяет быстро работать с отсортированном списком чисел.
- Дерево двоичное, потому что у каждого узла не более двух дочерних элементов.
- Дерево поиска, потому что его можно использовать для проверки вхождения числа — за время
O(log(n)).
Чем отличается от обычного двоичного дерева
- Все узлы левого поддерева меньше корневого узла.
- Все узлы правого поддерева больше корневого узла.
- Оба поддерева каждого узла тоже являются деревьями двоичного поиска, т. е. также обладают первыми двумя свойствами.
У правого дерева есть поддерево со значением 2, которое меньше, чем корень 3 — таким дерево двоичного поиска быть не может.
Операции с двоичным деревом поиска
Поиск элемента
Сложность в среднем: O(log n)
Сложность в худшем случае: O(n)
Алгоритм зависит от свойств дерева: у каждого левого поддерева есть значения, которые ниже корня или у каждого правого поддерева есть значения, которые выше корня.
Если значение ниже корня, мы можем точно сказать, что оно находится не в правильном поддереве. Тогда нам нужно искать только в левом поддереве. А если значение выше корня, можно точно сказать, что значения нет в левом поддереве. Тогда ищем только в правом поддереве.
Алгоритм:
If root == NULL
return NULL;
If number == root->data
return root->data;
If number < root->data
return search(root->left)
If number > root->data
return search(root->right)
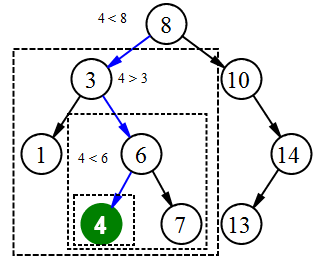
Изобразим это на диаграмме.
• Не нашли 4 → идем по левому поддереву корня 8
• Не нашли 4 → идем по левому поддереву корня 3
• Не нашли 4 → идем по левому поддереву корня 6
• Нашли 4 — ура.
Если мы нашли значение, мы возвращаем его так, чтобы оно распространялось на каждом шаге рекурсии — рассмотрите рисунок ниже.
Как вы могли заметить, мы четыре раза вызывали search(struct node*). Когда мы возвращаем новый узел или NULL, значение возвращается снова и снова, пока search(root) не вернет окончательный результат.
Если мы не нашли значение, значит, мы достигли левого или правого дочернего элемента листового узла, который имеет значение NULL — это значение также рекурсивно распространяется и возвращается.
Вставка элемента
Сложность в среднем: O(log n)
Сложность в худшем случае: ΘO(n)
Операция вставки значения похожа на поиск элемента. Мы также придерживаемся правила: левое поддерево меньше корня, правое поддерево — больше.
Мы продолжаем переходить либо к правому поддереву, либо к левому поддереву в зависимости от значения узла, и когда достигаем точки, в которой левое или правое поддерево имеет значение NULL, помещаем туда новый узел.
Алгоритм:
If node == NULL
return createNode(data)
if (data < node->data)
node->left = insert(node->left, data);
else if (data > node->data)
node->right = insert(node->right, data);
return node;
Алгоритм не такой простой, как может показаться на первый взгляд. Давайте визуализируем процесс.
• 4 < 8 → идем через левого «ребенка» 8.
• 4 > 3 → идем через правого «ребенка» 3.
• 4 < 6 → идем через левого «ребенка» 6.
• Левого «ребенка» у 6 нет → вставляем 4 как левый дочерний элемент 6.
Мы вставили узел в нужное место, но нам всё еще нужно выйти из функции, не повредив при этом остальную часть дерева. Здесь пригодится return node;. В случае с NULL, вновь созданный узел возвращается и присоединяется к родительскому узлу, иначе тот же узел возвращается без каких-либо изменений по мере продвижения вверх, пока мы не вернемся к корню.
Таким образом, когда мы будем двигаться обратно вверх по дереву, связи других узлов не изменятся.
Корень возвращаем в конце — так ничего не сломается.
Удаление элемента
Сложность в среднем: O(log n)
Сложность в худшем случае: O(n)
Всего может быть три случая при удаление элемента из дерева двоичного поиска. Давайте рассмотрим каждый.
Случай I: лист
Первый случай — когда нужно удалить листовой элемент. Просто удаляем узел из дерева.
• Нужно удалить 4.
• Просто удалили узел.
Случай II: есть дочерний элемент
Во втором случае у узла, который мы хотим удалить, есть один дочерний узел. В этом случае действуем так:
- Заменяем удаляемый узел на дочерний узел.
- Удаляем дочерний узел.
• Нужно удалить 6.
• Меняем 6 на 7 и удаляем узел 7.
•Нужный узел удален.
Случай III: два дочерних элемента
Если у узла, который мы хотим удалить, есть два потомка, делаем так:
- Получаем значение inorder-преемника этого узла.
- Заменяем удаляем узел на inorder-преемника.
- Удаляем inorder-преемника.
• Хотим удалить 3.
• Копируем значение inorder-преемника — 4.
• Удаляем inorder-преемника.
Реализация на языках программирования
Python
# Операции с двоичным деревом поиска на Python
# Создаем узел
class Node:
def __init__(self, key):
self.key = key
self.left = None
self.right = None
# Отсортированный (inorder) обход
def inorder(root):
if root is not None:
# Обходим левое поддерево
inorder(root.left)
# Обходим корень
print(str(root.key) + "->", end=' ')
# Обходим правое поддерево
inorder(root.right)
# Вставка элемента
def insert(node, key):
# Возвращаем новый узел, если дерево пустое
if node is None:
return Node(key)
# Идем в нужное место и вставляет узел
if key < node.key:
node.left = insert(node.left, key)
else:
node.right = insert(node.right, key)
return node
# Поиск inorder-преемника
def minValueNode(node):
current = node
# Найдем крайний левый лист — он и будет inorder-преемником
while(current.left is not None):
current = current.left
return current
# Удаление узла
def deleteNode(root, key):
# Возвращаем, если дерево пустое
if root is None:
return root
# Найдем узел, который нужно удалить
if key < root.key:
root.left = deleteNode(root.left, key)
elif(key > root.key):
root.right = deleteNode(root.right, key)
else:
# Если у узла только один дочерний узел или вообще их нет
if root.left is None:
temp = root.right
root = None
return temp
elif root.right is None:
temp = root.left
root = None
return temp
# Если у узла два дочерних узла,
# помещаем центрированного преемника
# на место узла, который нужно удалить
temp = minValueNode(root.right)
root.key = temp.key
# Удаляем inorder-преемниа
root.right = deleteNode(root.right, temp.key)
return root
# Тестим функции
root = None
root = insert(root, 8)
root = insert(root, 3)
root = insert(root, 1)
root = insert(root, 6)
root = insert(root, 7)
root = insert(root, 10)
root = insert(root, 14)
root = insert(root, 4)
print("Отсортированный обход: ", end=' ')
inorder(root)
print("nПосле удаления 10")
root = deleteNode(root, 10)
print("Отсортированный обход: ", end=' ')
inorder(root)Java
// Операции с двоичным деревом поиска на Java
// Создаем узел
class BinarySearchTree {
class Node {
int key;
Node left, right;
public Node(int item) {
key = item;
left = right = null;
}
}
Node root;
BinarySearchTree() {
root = null;
}
void insert(int key) {
root = insertKey(root, key);
}
// Вставляем в дерево элемент
Node insertKey(Node root, int key) {
// Возвращаем новый узел, если дерево пустое
if (root == null) {
root = new Node(key);
return root;
}
// Идем в нужное место и вставляем узел
if (key < root.key)
root.left = insertKey(root.left, key);
else if (key > root.key)
root.right = insertKey(root.right, key);
return root;
}
void inorder() {
inorderRec(root);
}
// Отсортированный (inorder) обход
void inorderRec(Node root) {
if (root != null) {
inorderRec(root.left);
System.out.print(root.key + " -> ");
inorderRec(root.right);
}
}
void deleteKey(int key) {
root = deleteRec(root, key);
}
Node deleteRec(Node root, int key) {
// Возвращаем, если дерево пустое
if (root == null)
return root;
// Ищем узел, который нужно удалить
if (key < root.key)
root.left = deleteRec(root.left, key);
else if (key > root.key)
root.right = deleteRec(root.right, key);
else {
// Если у узла только один дочерний элемент или их вообще нет
if (root.left == null)
return root.right;
else if (root.right == null)
return root.left;
// Если у узла два дочерних элемента
// Помещаем inorder-преемника на место узла, который хотим удалить
root.key = minValue(root.right);
// Удаляем inorder-преемника
root.right = deleteRec(root.right, root.key);
}
return root;
}
// Ищем inorder-преемника
int minValue(Node root) {
int minv = root.key;
while (root.left != null) {
minv = root.left.key;
root = root.left;
}
return minv;
}
// Тестим функции
public static void main(String[] args) {
BinarySearchTree tree = new BinarySearchTree();
tree.insert(8);
tree.insert(3);
tree.insert(1);
tree.insert(6);
tree.insert(7);
tree.insert(10);
tree.insert(14);
tree.insert(4);
System.out.print("Отсортированный обход: ");
tree.inorder();
System.out.println("nnПосле удаления 10");
tree.deleteKey(10);
System.out.print("Отсортированный обход: ");
tree.inorder();
}
}C
// Операции с двоичным деревом поиска на C
#include <stdio.h>
#include <stdlib.h>
struct node {
int key;
struct node *left, *right;
};
// Создаем узел
struct node *newNode(int item) {
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
// Отсортированный (inorder) обход
void inorder(struct node *root) {
if (root != NULL) {
// Обходимо лево
inorder(root->left);
// Обходим корень
printf("%d -> ", root->key);
// Обходимо право
inorder(root->right);
}
}
// Вставка узла
struct node *insert(struct node *node, int key) {
// Возвращаем новый узел, если дерево пустое
if (node == NULL) return newNode(key);
// Проходим в нужное место и вставляем узел
if (key < node->key)
node->left = insert(node->left, key);
else
node->right = insert(node->right, key);
return node;
}
// Поиск inorder-преемника
struct node *minValueNode(struct node *node) {
struct node *current = node;
// Находим крайний левый лист — он и будет inorder-преемником
while (current && current->left != NULL)
current = current->left;
return current;
}
// Удаляем узел
struct node *deleteNode(struct node *root, int key) {
// Возвращаем, если дерево пустое
if (root == NULL) return root;
// Ищем узел, который нужно удалить
if (key < root->key)
root->left = deleteNode(root->left, key);
else if (key > root->key)
root->right = deleteNode(root->right, key);
else {
// Если у узла только один дочерний элемент или их вообще нет
if (root->left == NULL) {
struct node *temp = root->right;
free(root);
return temp;
} else if (root->right == NULL) {
struct node *temp = root->left;
free(root);
return temp;
}
// Если у узла два дочерних элемента
struct node *temp = minValueNode(root->right);
// Помещаем inorder-преемника на место узла, который хотим удалить
root->key = temp->key;
// Удаляем inorder-преемника
root->right = deleteNode(root->right, temp->key);
}
return root;
}
// Тестим функции
int main() {
struct node *root = NULL;
root = insert(root, 8);
root = insert(root, 3);
root = insert(root, 1);
root = insert(root, 6);
root = insert(root, 7);
root = insert(root, 10);
root = insert(root, 14);
root = insert(root, 4);
printf("Отсортированный обход: ");
inorder(root);
printf("nПосле удаления 10n");
root = deleteNode(root, 10);
printf("Отсортированный обход: ");
inorder(root);
}C++
// Операции с двоичным деревом поиска на C++
#include <iostream>
using namespace std;
struct node {
int key;
struct node *left, *right;
};
// Создаем узел
struct node *newNode(int item) {
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
// Отсортированный (inorder) обход
void inorder(struct node *root) {
if (root != NULL) {
// Обходим лево
inorder(root->left);
// Обходим корень
cout << root->key << " -> ";
// Обходим право
inorder(root->right);
}
}
// Вставка узла
struct node *insert(struct node *node, int key) {
// Возвращаем новый узел, если дерево пустое
if (node == NULL) return newNode(key);
// Проходим в нужное место и вставляет узел
if (key < node->key)
node->left = insert(node->left, key);
else
node->right = insert(node->right, key);
return node;
}
// Поис inorder-преемника
struct node *minValueNode(struct node *node) {
struct node *current = node;
// Ищем крайний левый лист — он и будет inorder-преемником
while (current && current->left != NULL)
current = current->left;
return current;
}
// Удаление узла
struct node *deleteNode(struct node *root, int key) {
// Возвращаем, если дерево пустое
if (root == NULL) return root;
// Ищем узел, который хотим удалить
if (key < root->key)
root->left = deleteNode(root->left, key);
else if (key > root->key)
root->right = deleteNode(root->right, key);
else {
// Если у узла один дочерний элемент или их нет
if (root->left == NULL) {
struct node *temp = root->right;
free(root);
return temp;
} else if (root->right == NULL) {
struct node *temp = root->left;
free(root);
return temp;
}
// Если у узла два дочерних элемента
struct node *temp = minValueNode(root->right);
// Помещаем inorder-преемника на место узла, который хотим удалить
root->key = temp->key;
// Удаляем inorder-преемника
root->right = deleteNode(root->right, temp->key);
}
return root;
}
// Тестим функции
int main() {
struct node *root = NULL;
root = insert(root, 8);
root = insert(root, 3);
root = insert(root, 1);
root = insert(root, 6);
root = insert(root, 7);
root = insert(root, 10);
root = insert(root, 14);
root = insert(root, 4);
cout << "Отсортированный обход: ";
inorder(root);
cout << "nПосле удаления 10 10n";
root = deleteNode(root, 10);
cout << "Отсортированный обход: ";
inorder(root);
}Где используется
- При многоуровневой индексации в базе данных.
- Для динамической сортировки.
- Для управления областями виртуальной памяти в ядре Unix.