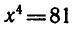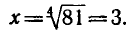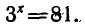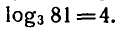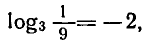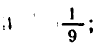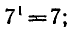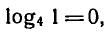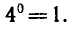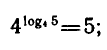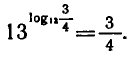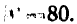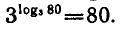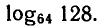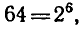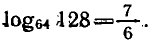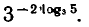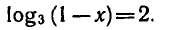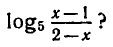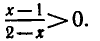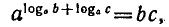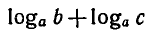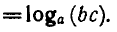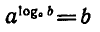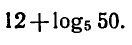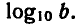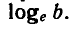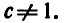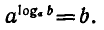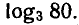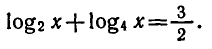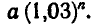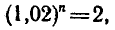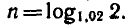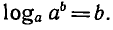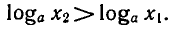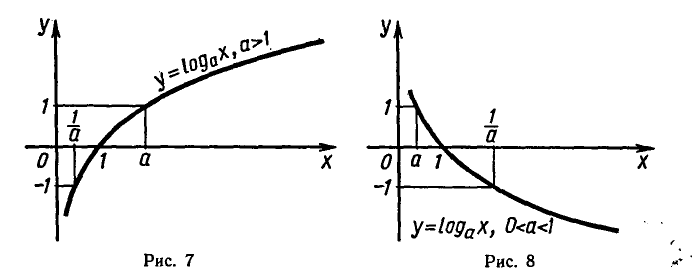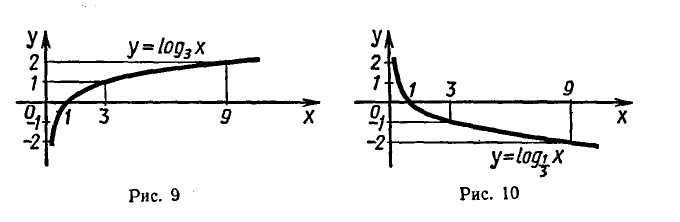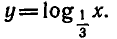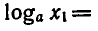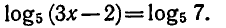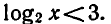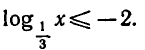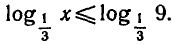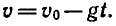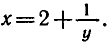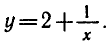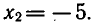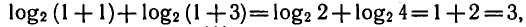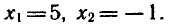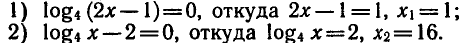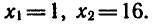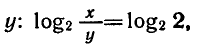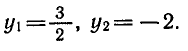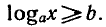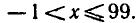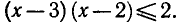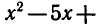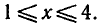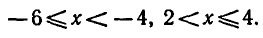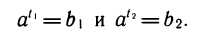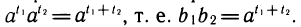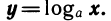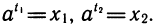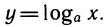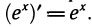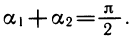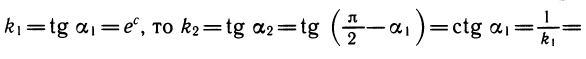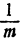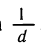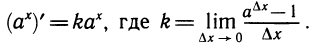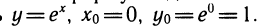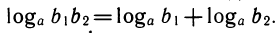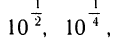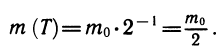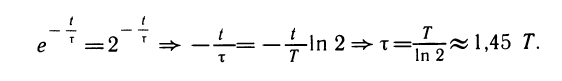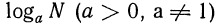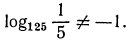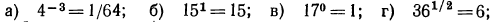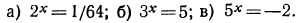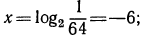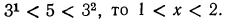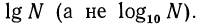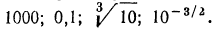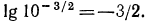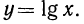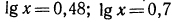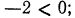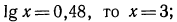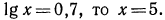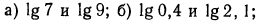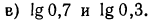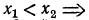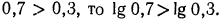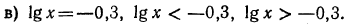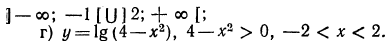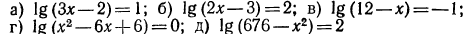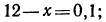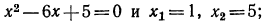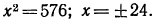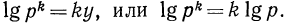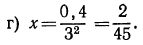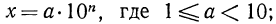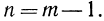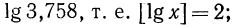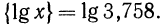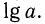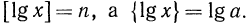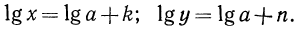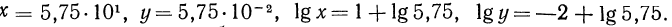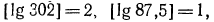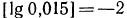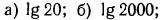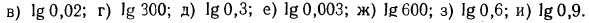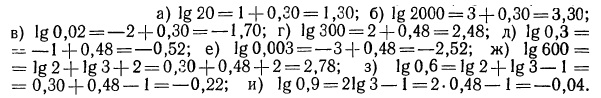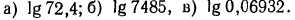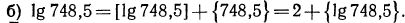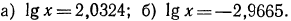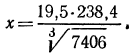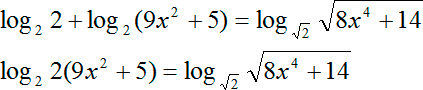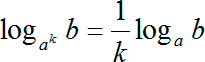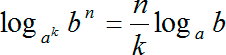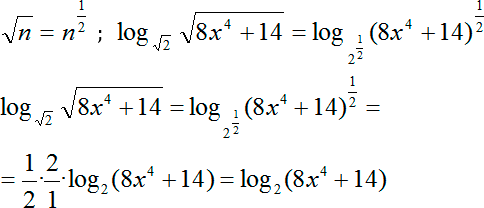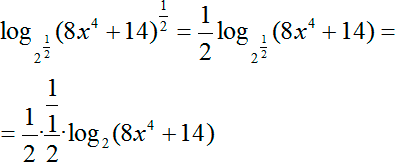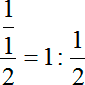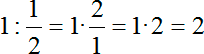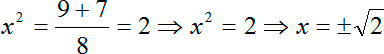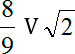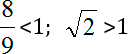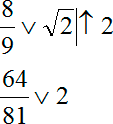Как найти корень если есть логарифм - Исправление недочетов и поиск решений вместе с Examum.ru

Свойства логарифмов
- Десятичные и натуральные логарифмы
- Логарифмическая функция и ее график
- Обратная функция
- Логарифмические уравнения
- Логарифмические неравенства
Свойства логарифмов
- Модуль перехода
Исследование логарифмической функции
- Производная логарифмической функции
Вычисление логарифмов
- Прикладные примеры
Дополнение к логарифмической функции
Логарифмическая функция
- Десятичные логарифмы
- Логарифмирование и потенцирование
- Стандартный вид числа. Характеристика и мантисса
- Вычисления с помощью таблиц логарифмов

Пример:

Найти положительный корень уравнения

( По определению арифметического корня имеем-

Пример:

Решить уравнение

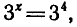
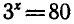
Запишем данное уравнение так: откуда х = 4. В задаче 1 неизвестным является основание степени, а в задаче 2 — показатель степени; Способ решения задачи 2 состоял в том, что левую и правую части уравнения удалось представить в виде степени с одним тем же основанием 3. Но уже, например, уравнение таким способом решить не удается. Однако вы знаете, что это уравнение имеет корень. Чтобы уметь решать такие уравнения, вводите понятие логарифма числа.

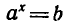
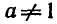
Уравнение , где а > 0 , а , имеет единственный корень. Этот корень называют ло-1
гарифмом числа b по основанию а и обозначают 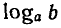. Например
корнем уравнения 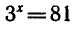является число 4, т. е.

Лаплас Пьер Симон (1749— 1827)— французский математик, физик и астроном, адъюнкт Французской Академии Наук. После Великой Французской революции принимал активное участие в реорганизации системы образования. Важнейшие направления его исследований — математика, небесная механика и математическая физика. Один из создателей теории вероятностей.

Итак, логарифмом положительного числа b по основанию а, где
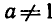
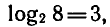
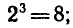
а > 0, , называется показатель степени, и которую надо возвести число а, чтобы получить b .
Например, так как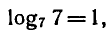

так как так как

так как

Определение логарифма можно кратко записать так:

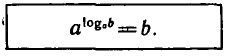
Это равенство справедливо при b > 0, а > 0, 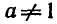. Его обычно
называют основным логарифмическим тождеством.
Например,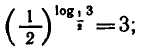

С помощью основного логарифмического тождества можио
показать, например, что 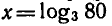является корнем уравнения

В самом деле,

Действие нахождения логарифма числа называют логарифмированием.

Пример:

Вычислить

Обозначим 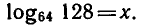По определению логарифма

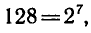
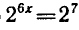
Так как то ,

откуда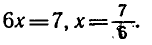
Ответ.

Пример:

Вычислить

Используя свойства степени и основное логарифмическое равенство, находим:

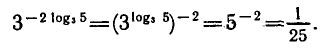
Пример:

Решить уравнение

Но определению логарифма 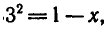откуда х = — 8.

Пример:

При каких значениях х существует

Так как основание логарифма 5 > 0 и 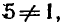то данный логарифм
существует тогда и только тогда, когда

Получено неравенство, находим 1 < х < 2.

Свойства логарифмов

При выполнении преобразований выражений, содержащих логарифмы, при вычислениях и при решении уравнений часто используются различные свойства логарифмов. Рассмотрим основные из них.

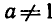
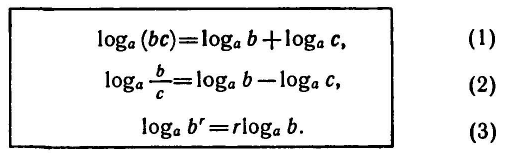
Пусть а>0, , b > 0, с > 0, r —любое действительное число. Тогда справедливы формулы:

По основному логарифмическому тождеству

1) Перемножая равенства (4) и (5), получаем:

откуда по определению логарифма

Формула (1) доказана.

2) Разделив равенства (4) и (5), получим:

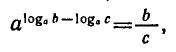
откуда по определению логарифма следует формула (2).
3) Возводя основное логарифмическое тождество
в степень с показателем r, получаем:

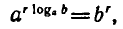
откуда по определению логарифма следует формула (3). •
Приведем примеры применения формул (1) — (3):

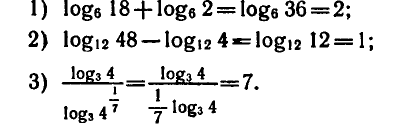
Пример:

Вычислить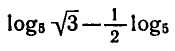
Применяя формулы (1) — (3), находим:

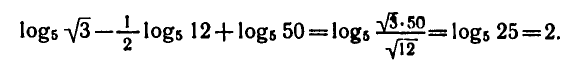
Десятичные и натуральные логарифмы

Для логарифмов чисел составлены специальные таблицы
(таблицы логарифмов). Логарифмы вычисляют также с помощью
микрокалькулятора. И в том и в другом случае находятся только
десятичные или натуральные логарифмы.

Десятичным логарифмом числа называют логарифм этого числа по основанию 10 и пишут lg b вместо

Натуральным логарифмом числа называют логарифм этого числа по основанию e, где е — иррациональное число, приближенно равное 2,7. При этом пишут ln e вместо

Иррациональное число е играет важную роль в математике
и ее приложениях. Число е можно представить как сумму:

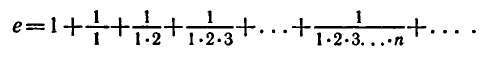
Вычисление числа е на микрокалькуляторе проводится по
программе:

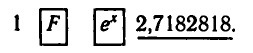
Вычисления на микрокалькуляторе lg b и ln b проводятся
соответственно по программам:

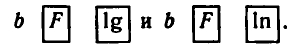
Например, вычисляя lg 13, получаем:

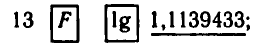
вычисляя ln 13, получаем:

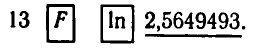
Оказывается, что достаточно знать значения только десятичных или только натуральных логарифмов чисел, чтобы находить
логарифмы чисел по любому основанию. Для этого используется
формула перехода от логарифма по одному основанию к
логарифму по другому основанию:

где b > 0, а > 0 , 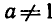, с > 0 ,

Докажем справедливость формулы (1).
Запишем основное логарифмическое тождество
Возьмем от обеих его частей логарифмы по основанию с:

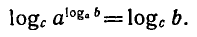
Используя свойство логарифма степени, получаем:

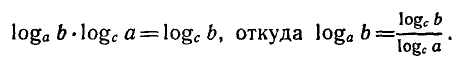
Из формулы (1) при с = 10 и с = е получаются формулы
перехода к десятичным и натуральным логарифмам:

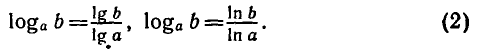
Пример:

С помощью микрокалькулятора МК-54 вычислить

1) С помощью десятичных логарифмов:

2) С помощью натуральных логарифмов:

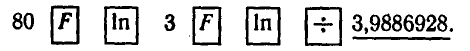
Ответ. ▲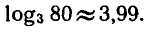

Формула перехода от одного основания логарифма к другому
иногда используется при решении уравнений.

Пример:

Решить уравнение

По формуле перехода

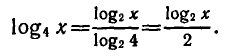
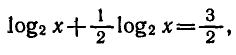
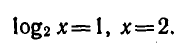
Поэтому уравнение принимает вид откуда ▲

Пример:

Двухпроцентный вклад в Сбербанк, равный
а рублям, через п лет становится равным 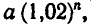а
трехпроцентный вклад становится равным

Через сколько лет каждый из вкладов удвоится?

1) Для первого вклада 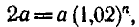откуда

2. Вычисления проведем на МК-54:

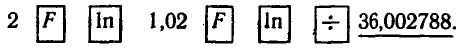
2) Для второго вклада 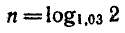и программа вычислений
такова:

Ответ. По первому вкладу приближенно через 36 лет, а
по второму — через 23,5 года.

Логарифмическая функция и ее график

В математике и ее приложениях часто встречается
логарифмическая функция

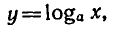
где а — заданное число, а > 0, .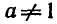
Логарифмическая функция обладает следующими свойствами:
1) Область определения логарифмической функции — множество всех положительных чисел.
Это следует из определения логарифма, так как выражение 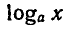; имеет смысл только при x > 0.

2) Множество значений логарифмической функции — множество R всех действительных чисел.
Это следует из того, что для любого действительного числа
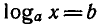
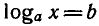
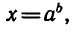
b есть такое положительное число х, что , т. е. уравнение имеет корень. Такой корень существует и равен так как

3) Логарифмическая функция 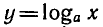является возрастающей на промежутке x > 0, если а > 1 , и убывающей, если
0 < а < 1 .

Пусть а > 1. Докажем, что если 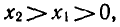то т. е.

Пользуясь основным логарифмическим
тождеством, условие 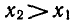можно записать так: Из этого неравенства по свойству степени с основанием a > 1 следует, что

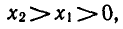
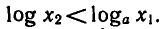
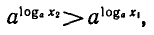
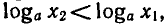
Пусть 0 < a < 1 . Докажем, что если то Записав условие в виде получим так как 0 < а < 1 .

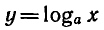
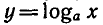
4) Если а > 1, то функция принимает положительные значения при х >1, отрицательные — при 0 < x < ;1. Если 0 < а < 1 , то функция принимает положительные значения при 0 < x < 1, отрицательные — при х > 1.

Это следует из того, что функция 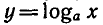принимает
значение, равное нулю, при x = 1 и является возрастающей на промежутке x > 0, если а > 1, и убывающей, если 0 < а < 1 .

Из рассмотренных свойств логарифмической функции 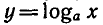следует, что ее график расположен правее оси Оу и имеет вид, указанный на рисунке 7, если а > 1, и на рисунке 8, если 0 < a < 1 .

На рисунке 9 изображен график функции а на рисунке 10 — график функции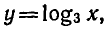

Отметим, что график любой логарифмической функции 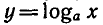проходит через точку ( 1 ; 0). При решении уравнений часто используется следующая теорема:

Теорема:

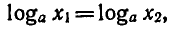
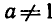
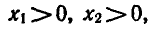
Если где a > 0, , то

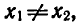
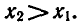
Предположим, что например Если a > 1, то из неравенства следует, что если
0 < а < 1 , то из неравенства следует, что

В обоих случаях получилось противоречие с условием 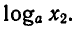Следовательно,

Пример:

Решить уравнение

Используя доказанную теорему, получаем Зх — 2 = 7, откуда Зх = 9,
х = 3.
Пример:

Решить неравенство

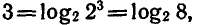
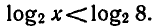
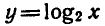
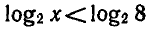
Пользуясь тем, что запишем данное неравенство так: Так как функция определена при x > 0 и возрастает, то неравенство выполняется при х > 0 и x < 8.
Ответ. 0 < х < 8 .

Пример:

Решить неравенство

Запишем данное неравенство так:

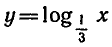
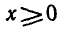
Функция определена при и убывает, поэтому неравенство выполняется при х > 0 и

Ответ.

Обратная функция

Известно, что зависимость скорости v от времени t движения
тела, брошенного вверх с начальной скоростью 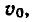выражается
формулой

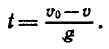
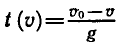
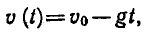
Из этой формулы можно найти обратную зависимость — времени от скорости: Функцию называют обратной к функции а функцию v (t) — обратной к функции t (v ). Отметим, что в этом примере каждому значению t соответствует единственное значение v и, наоборот, каждому значению v соответствует единственное значение t.

Рассмотрим теперь показательную и логарифмическую
функции. Обозначим символом f(х) показательную функцию,
a g (х) — логарифмическую функцию:

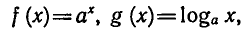
где а — заданное число, а > 0, .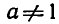

Решим уравнение 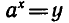относительно х. По определению
логарифма 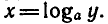Поменяв в этом равенстве местами х и у,
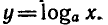
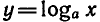
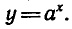
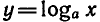
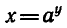
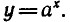
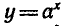
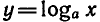
получим логарифмическую функцию Функцию называют обратной к функции Если из равенства найти х, то получим , а поменяв местами х и у — показательную функцию Функцию называют обратной к функции . Поэтому функции f (х) и g (х) называют взаимно обратными.

Вообще если функция y = f(x) задана формулой, то для
нахождения обратной функции нужно решить уравнение
f (x) = у относительно х и затем поменять местами х и у.

Если уравнение f(x)= y имеет более чем один корень, то
функции, обратной к y = f (x), не существует.

Например, функция 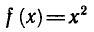не имеет обратной, так как
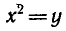
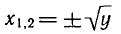
уравнение имеет два корня для любого
у > 0.
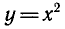
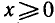
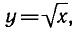
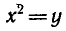
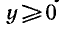
Если функцию рассматривать только на промежутке , то она будет иметь обратную так как уравнение при имеет только один неотрицательный корень.

Пример:

Найти функцию, обратную к функции

Решая это уравнение относительно х, получаем
Заменив х на у и у на х, находим

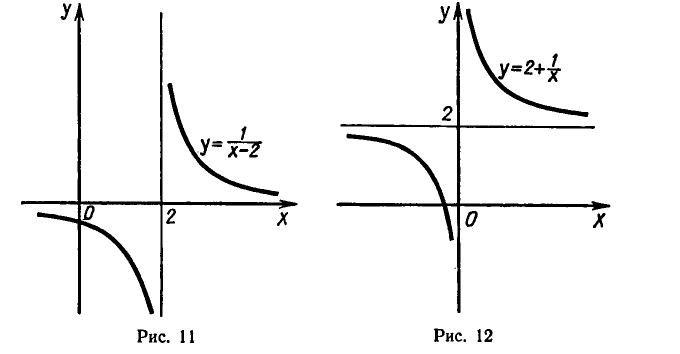
В этой задаче область определения функции 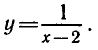есть
множество действительных чисел, не равных 2, а множество ее значений — все действительные числа, не равные 0. График этой
функции изображен на рисунке 11.
Для обратной функции 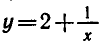область определения —
множество действительных чисел, не равных 0, а множество значений — все действительные числа, не равные 2. График обратной функции изображен на рисунке 12.

Вообще область определения обратной функции совпадает
с множеством значений исходной функции, а множество
значений обратной функции совпадает с областью определения
исходной функции.
Можно показать, что если функция имеет обратную, то
график обратной функции симметричен графику данной
функции относительно прямой у = х.
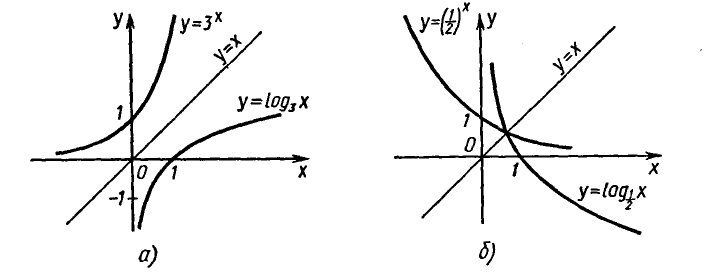
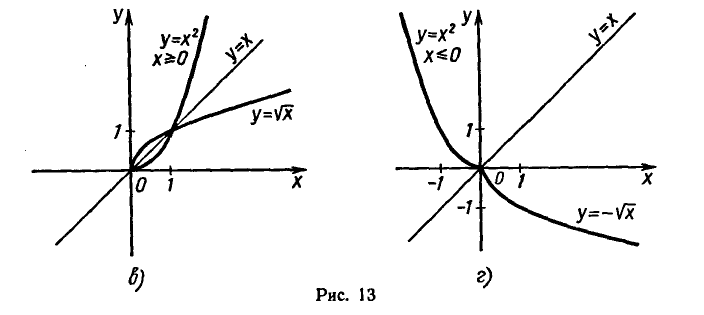
Примеры графиков взаимно обратных функций показаны на
рисунке 13.

Логарифмические уравнения

Пример:

Решить уравнение

( 1 )

Предположим, что х — такое число, при котором равенство ( 1 ) является верным, т. е. х — корень уравнения ( 1 ).
Тогда по свойству логарифма верно равенство

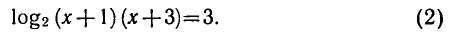
Из этого равенства по определению логарифма получаем:

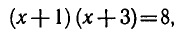
откуда 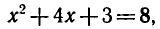т. е.

Последнее равенство верно, если 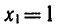или

Итак, предположив, что число х — корень уравнения (1),
мы показали, что х может быть равным или 1, или —5.
Проверим, являются ли эти числа корнями уравнения (1).
Подставляя в левую часть данного уравнения х = 1 , получаем

т. е. х = 1 — корень уравнения ( 1 ).

При х = — 5 числа х + 1 и х + З отрицательны, и поэтому
левая часть уравнения ( 1 ) не имеет смысла, т. е. х = — 5 не
является корнем этого уравнения.
Ответ. х = 1 .

Заметим, что х = — 5 является корнем уравнения (2), так
как

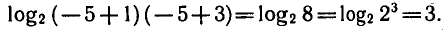
Получилось, что число х = 1 является корнем обоих уравнений
( 1 ) и (2), а число х = — 5 не является корнем уравнения (1 ), но является корнем уравнения (2). Таким образом, при переходе от уравнения (1) к уравнению (2 ) корень х = 1 сохранился и появился посторонний корень х = —5. В этом случае уравнение (2) называют следствием уравнения (1 ).

Если все корни первого уравнения являются корнями второго уравнения, то второе уравнение называется следствием первого уравнения.

Отметим, что в уравнении, которое является следствием
данного, не всегда появляются посторонние корни; важно лишь
то, чтобы корни исходного уравнения не терялись.

В большинстве случаев, как и в задаче 1, уравнения решаются постепенным переходом к более простым уравнениям,
которые являются следствием исходного уравнения. В таких
случаях после нахождения корней необходима их проверка.

Пример:

Решить уравнение

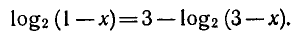
Перенесем логарифм из правой части в левую;

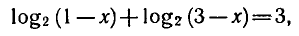
откуда

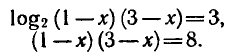
Решая это уравнение, получаем

Число не является корнем исходного уравнения, так
как при x = 5 левая и правая части уравнения теряю т смысл.
Проверка показывает, что число х = — 1 является корнем
исходного уравнения.
Ответ. х = — 1. ▲

Пример:

Решить уравнение

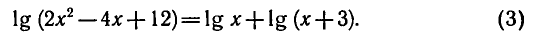
По свойству логарифмов

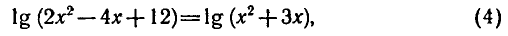
откуда

Проверка показывает, что оба значения x
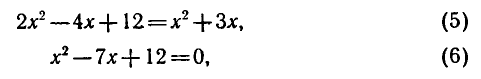
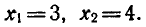
являются корнями исходного уравнения.
Ответ. ▲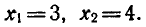

Проверкой можно убедиться в том, что числа 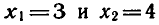являются корнями не только уравнений (6) и (3), но и уравнений
(4) и (5). Все эти уравнения других корней не имеют. Такие
уравнения называют равносильными.

Уравнения, имеющие одно и то же множество корней,
называют равносильными.
В частности, два уравнения, не имеющие корней, являются
равносильными.

Отметим, что любое из двух равносильных уравнений является следствием другого.
Большинство уравнений, с которыми вы встречались в курсе
алгебры, решались с помощью перехода от данного уравнения
к равносильному. Так решались уравнения первой степени с
одним неизвестным, квадратные уравнения, показательные
уравнения.

Напомним, что уравнение заменяется ему равносильным при
следующих преобразованиях:
любой член уравнения можно переносить из одной части
в другую, изменив его знак на противоположный;
обе части уравнения можно умножить или разделить на
одно и то же число, не равное нулю.

Однако не при любом преобразовании уравнение заменяется
на равносильное. Например, при возведении обеих частей
уравнения в квадрат получается уравнение , которое является следствием первого, но не равносильным ему. Поэтому после решения второго уравнения необходимо проверить, являются ли его корни корнями исходного уравнения.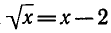

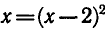
Пример:

Решить уравнение

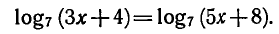
Приравнивая выражения, стоящие под знаком логарифма,
получаем:

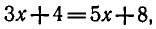
откуда х = — 2. Выполняя проверку, убеждаемся, что при х = — 2
левая и правая части исходного уравнения не имеют смысла.
Ответ. Корней нет.

Здесь посторонний корень появился потому, что при переходе
от равенства логарифмов к равенству чисел не было учтено
требование, чтобы эти числа были положительными.
Рассмотренные примеры логарифмических уравнений
показывают, что при их решении с использованием свойств логарифмов получаются уравнения, которые являются следствиями исходного. Поэтому необходима проверка, которая позволяет
обнаружить посторонние корни. ▲

Пример:

Решить уравнение

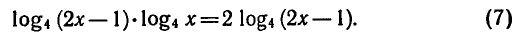
Преобразуем данное уравнение:

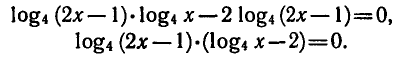
Приравнивая каждый из множителей левой части уравнения
к нулю, получаем:

Проверка показывает, что оба значения х являются корнями
исходного уравнения.
Ответ.

Отметим, что если обе части уравнения (7) разделить на
выражение 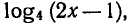то будет потерян корень х = 1.

Вообще при делении обеих частей уравнения на выражение, содержащее неизвестное, может произойти потеря корней.
Поэтому уравнение, обе части которого содержат общий
множитель, решают переносом всех членов в одну часть и
разложением на множители.

При решении уравнений главное не потерять корни, а наличие посторонних корней можно установить проверкой. Поэтому важно следить за тем, чтобы при преобразовании уравнения каждое следующее уравнение было следствием предыдущего.

Пример:

Решить систему уравнений

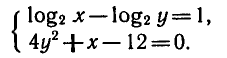
Из первого уравнения выразим х через 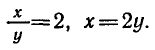Подставив х = 2у во второе уравнение системы,

получим 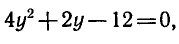откуда

Найдем значения х : 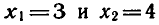Проверкой убеждаемся,
что 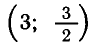— решение системы, а ( — 4; —2) — постороннее
решение.
Ответ.

Логарифмические неравенства

При изучении логарифмической функции рассматривались
неравенства вида 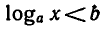и

Приведем примеры решения более сложных логарифмических неравенств. Обычный способ решения таких неравенств заключается в переходе от них к более простому неравенству или системе неравенств, имеющей то же самое множество решений.

Пример:

Решить неравенство

Правая часть данного неравенства имеет смысл при всех значениях x, а левая часть — при x + 1 > 0, т. е. при х > — 1.
Промежуток х > — 1 называют областью определения неравенства (1). Так как логарифмическая функция с основанием
10 возрастающая, то неравенство ( 1 ) при условии x + 1 > 0
выполняется, если 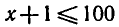(так как 2 = lg 100). Таким
образом, неравенство ( 1 ) равносильно системе неравенств

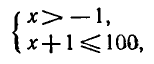
т. е. неравенство ( 1 ) и система (2) имеют одно и то же множество решений. Решая систему (2), находим

Пример:

Решить неравенство

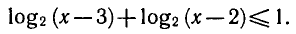
Логарифмическая функция определена при положительных значениях аргумента, поэтому левая часть неравенства имеет смысл при х — 3 > 0 и х — 2 > 0.

Следовательно, областью определения этого неравенства является промежуток х > 3 . По свойствам логарифма неравенство (3)
при х > 3 равносильно неравенству

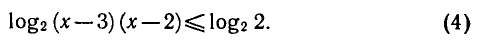
Логарифмическая функция с основанием 2 возрастающая. Поэтому при х > 3 неравенство (4) выполняется, если

Таким образом, исходное неравенство (3) равносильно системе неравенств

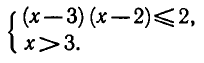
Решая первое неравенство этой системы, получаем 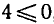откуда

Совмещая этот отрезок с промежутком х > 3 , получаем 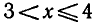(рис. 14).

Пример:

Решить неравенство

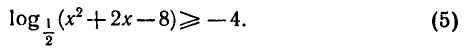
Область определения неравенства находится из условия

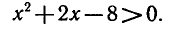
Неравенство (5) можно записать в следующем виде:

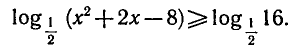
Так как логарифмическая функция с основанием 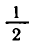является
убывающей, то для всех х из области определения неравенства
получаем:

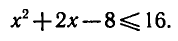
Таким образом, исходное неравенство (5) равносильно системе неравенств

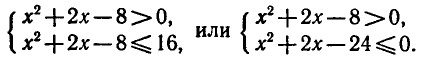
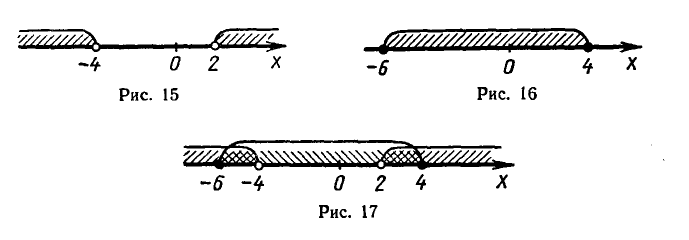
Решая первое квадратное неравенство, получаем х < — 4, х > 2 (рис. 15). Решая второе квадратное неравенство, получаем (рис. 16). Следовательно, оба неравенства систе
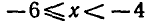
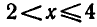
мы выполняются одновременно при и при . (рис. 17).
Ответ.

Определение:

Логарифмом числа а по основанию b называется показатель степени, в которую надо возвести а, чтобы получить число b.

В качестве основания мы будем всегда брать положительное число а, отличное от 1.

В записи b = число а является основанием степени, t — показателем, b — степенью. Число t — это показатель степени, в которую надо возвести основание а, чтобы получить число b. Следовательно, t — это логарифм числа b по основанию а:

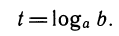
Можно сказать, что формулы = b и t = равносильны, выражают одну и ту же связь между числами a, t и b (при а>0, а ≠ 1, b>0). Число t — произвольно, никаких ограничений на показатель степени не накладывается.

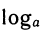
Подставляя в равенство = b запись числа t в виде логарифма, получаем равенство, называемое основным логарифмическим тождеством:

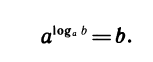
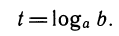
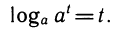
Представляя в равенстве выражение b в виде степени, получим еще одно тождество:

Свойства логарифмов

Теорема:

Верны следующие тождества, выражающие свойства логарифмов:

1), т. е. логарифм произведения равен сумме логарифмов множителей;

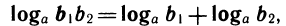
2) т. е. логарифм дроби равен разности логарифмов числителя и знаменателя;

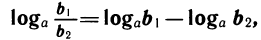
3) т. е. логарифм степени равен показателю степени, умноженному на логарифм основания.

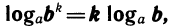
Доказательство:

Свойства логарифмов выводятся из свойств степеней с помощью основного логарифмического тождества, выражающего определение логарифма. Выведем для примера первое свойство.

Обозначим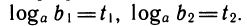 По основному логарифмическому тождеству имеем:

Перемножим эти равенства: 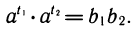По свойству степеней

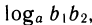
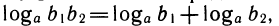
По определению логарифма t1+ t2 = т. е. что и требовалось доказать. Свойства 2 и 3 выведите самостоятельно.

Свойства степеней и логарифмов тесно связаны между собой. Они фактически выражают одно и то же, только один раз мы обращаем внимание на поведение самих степеней, а другой — на поведение показателей:

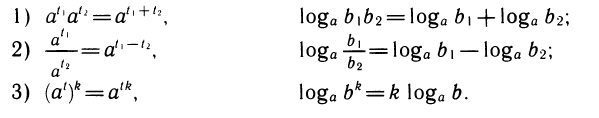
С помощью свойств логарифмов можно логарифмировать выражения, составленные с помощью операций умножения, деления и возведения в степень.
Примеры.

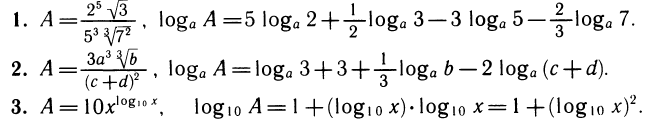
Иногда приходится искать выражение по его логарифму. Такую операцию называют потенцированием.

Примеры:

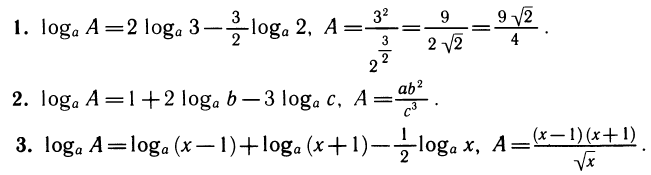
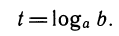
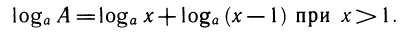
Замечание. Запись имеет смысл лишь при b> 0. Поэтому в тождествах, отражающих свойства логарифмов, все выражения, стоящие под знаком логарифма, будем считать положительными. При логарифмировании буквенных выражений надо их раскладывать на множители так, чтобы все множители были положительны. Например, пусть необходимо прологарифмировать выражение А=х(х — 1). Сделать это можно лишь тогда, когда А >0, т. е. когда либо х<0, либо х> 1. Если х> 1, то оба множителя х и х— 1 положительны и мы можем записать:

Если же х<0, то оба множителя отрицательны и А нужно разложить на множители так: А =( — x)(1 — x), откуда

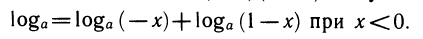
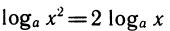
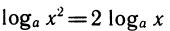
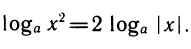
Аналогично при ( —x) при x<0. С помощью модуля это можно записать короче:

Модуль перехода

В вычислениях в качестве основания а часто берется число а=10. В то же время зачастую необходимы вычисления степеней и логарифмов с разными основаниями. Возникает вопрос: как связать между собой степени и логарифмы с разными основаниями?

Пусть дана степень b = . Мы хотим перейти к новому основанию с, т. е. записать число в виде сх при некотором х. Записав равенство и прологарифмировав его по основанию а, получим , откуда Так как = b, = b, то можно с помощью логарифмов записать: , , откуда

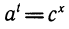
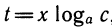
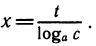
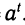
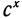
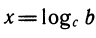
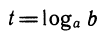
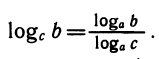
Выведенную формулу называют формулой перехода от одного основания логарифма к другому.

Таким образом, мы видим, что при изменении основания значения логарифмов изменяются пропорционально. Коэффициент пропорциональности 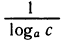называют модулем перехода.

Отметим простые следствия выведенной формулы:

1) (положим в формуле перехода b = а)

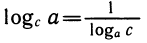
2) (положим в формуле перехода с = аk)

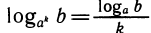
3) (положим в предыдущей формуле k=-l).

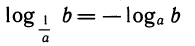
С помощью логарифмов все степени можно привести к одному основанию. Если в качестве основания берется число a =10, то соответствующие логарифмы обозначаются знаком lg и называются десятичными. Можно записать:

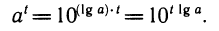
Если в качестве основания берется число е, то соответствующие логарифмы обозначаются знаком ln и называются натуральными:

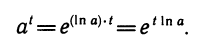
Значения модулей перехода от десятичных логарифмов к натуральным и наоборот таковы:

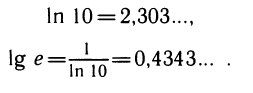
Исследование логарифмической функции

Определение:

Логарифмической функцией называется функция вида

Напомним, что в качестве основания логарифмов выбирается число а> 0, отличное от 1.

Основные свойства логарифмической функции (схема X).

1) Область определения: множество всех положительных чисел, т. е. промежуток (0; + ∞).
2) Монотонность: если а>1, то логарифмическая функция строго возрастает; если 0<а<1, то она строго убывает.
3) Область значений: множество всех вещественных чисел R.

Так как определение логарифмов основано на понятии степени,

то при доказательстве свойств логарифмической функции используют свойства показательной функции.

Свойство 1 в доказательстве не нуждается: оно опирается на определение логарифма числа х, по которому необходимо, чтобы число х было положительным.

Докажем свойство 2. Для этого сначала рассмотрим случай а>1. Возьмем два положительных числа х1 и x2, такие, что x1 <x2, и докажем, что 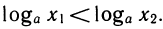Обозначив первое из этих чисел через t1, второе — через t2, по определению логарифма получим

Если бы выполнялось неравенство t1 ≥ t2, то по свойству монотонности показательной функции выполнялось бы неравенство т. е. 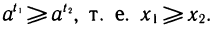Это противоречит условию.

Следовательно, t1<t2, что и требовалось доказать. Случай 0<а<1 рассматривается аналогично.

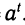
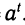
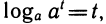
Свойство 3 утверждает, что всякое вещественное число t может быть логарифмом некоторого числа х. Так как степень определена при любом t, то, взяв х =, получим что и требовалось доказать.

Графики логарифмических функций при различных основаниях показаны на рисунке 108.

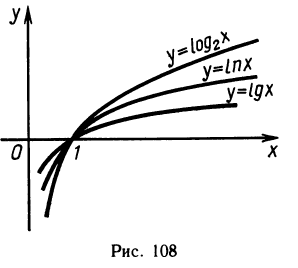
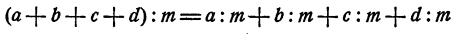
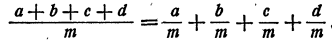
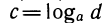
Графики функций симметричны друг другу относительно прямой у = х. Действительно, если точка Р {с; d) лежит на графике функции у = ах, то d = ac. Но тогда и точка Q {d; с) лежит на графике функции

Так как точки Р (с; d) и Q (d; с) симметричны относительно прямой у = х (рис. 109), то симметричны и графики показательной и логарифмической функций.

Вместо логарифмических функций с произвольным основанием удобно рассматривать функции вида у = с ln х. Так как 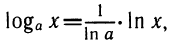то указанные функции исчерпывают все логарифмические функции.

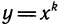
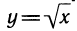
Функция у = ln х растет с ростом х, однако медленнее, чем любая степенная функция вида (k>0), в частности медленнее, чем (схема IX).

Производная логарифмической функции

Рассмотрим две функции у = 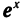и у = ln х. Мы знаем, что их графики симметричны относительно прямой у = х. Это поможет нам найти производную логарифмической функции, зная производную экспоненты. Возьмем точку Р (с; d) на графике экспоненты (т. е. d = ec) и симметричную точку Q (d; с) на графике логарифмической функции (т. е. c = lnd). Касательные к графикам в этих точках тоже будут симметричны (рис. 109). Угловой коэффициент k1 касательной к графику экспоненты равен значению производной функции у = ех при х = с, т. е. k1=ec, так как

Пусть a1 и а2 — углы, образованные проведенными касательными с осью абсцисс. Из рисунка 109 ясно, что

Так как

Таким образом, производная функции у = ln х в точке x = d равна

Можно написать:

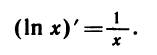
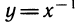
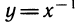
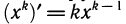
Мы видим, что производная логарифмической функции y = ln х равна степенной функции . Интересно заметить, что функция не получается как производная какой-либо другой степенной функции вида у = схк. Действительно, хотя при любом к, но получить значение к— 1, равное —1, можно лишь при k = 0, а (x°)’ = 0.

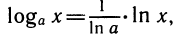
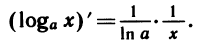
Так как то

По формулам производной показательной функции 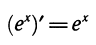и

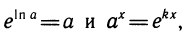
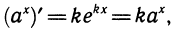
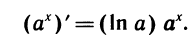
Известно, что ,где k= ln а. Поэтому т. е.

Примеры:

Зная производные экспоненты и логарифма, можно получить приближенные формулы для их вычисления.

Пусть

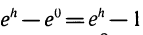
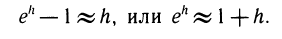
Разность —это приращение у на отрезке [0; h]. Вычислив dy при хо = 0, получим dy = y’ (0) dx. Так как у’ = ех, то у'(0)= 1. Заменив ∆у на dy и подставив dx = h, получим приближенную формулу

Более точная формула для вычисления экспоненты такова:

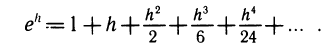
Пусть теперь у =lnх. Выберем дго=1, xо = ln l =0. Положим dx = h и вычислим ln (l+h). Найдем dy при xo=1. Так как

(In то y’ (jc0)= 1 и dy= 1 •dx = h.

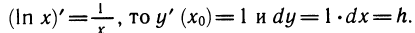
Заменяя ∆y= ln (1+h) — ln l = ln (l+h), получаем приближенную формулу

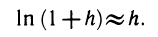
Более точная формула для вычисления логарифма такова:

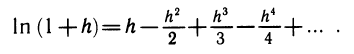
Вычисление логарифмов

Более 300 лет логарифмы использовались для облегчения вычислений. Их основное достоинство — способность сводить умножение к сложению по формуле

Были составлены обширные таблицы логарифмов чисел, с помощью которых можно легко переходить от чисел к их логарифмам и обратно.

Все таблицы логарифмов до 1950 г. являлись перепечаткой или сокращением таблиц Бриггса. Генри Бриггс (1561 —1630) с очень большой точностью (16 знаков после запятой) извлек подряд 57 квадратных корней из 10 и получил значения

Комбинируя эти значения, он получил густую сетку чисел с известными десятичными логарифмами: 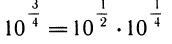и т. п. После этого десятичный логарифм любого числа х из промежутка [1; 10] с хорошей точностью находится округлением до ближайшего известного.

Это огромная работа, и за 300 лет не нашлось никого, кто повторил бы ее. Любопытно, что немного раньше Бриггса таблицу натуральных логарифмов составил Джон Непер (1550—1617).

С появлением ЭВМ ситуация переменилась. Умножение по-прежнему выполняется дольше, чем сложение, но логарифмирование требует еще больше времени. Поиск числа в таблице очень дорогая операция для ЭВМ. Поэтому теперь значение логарифмов как инструмента вычисления резко упало, а с распространением калькуляторов оно сходит на нет. С другой стороны, сами по себе логарифмические зависимости легко обрабатываются и используются при вычислениях на ЭВМ. Например, формула xk = exp(k ln x) служит основным средством возведения в степень (кроме k= l, 2, 3) на всех ЭВМ и на калькуляторах.

На современных ЭВМ (и на калькуляторах) значения In х и 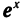вычисляют, пользуясь заранее найденными приближенными формулами. По этим формулам вычисление логарифмов становится довольно простым. Пользователю ЭВМ никогда не приходится думать о вычислении логарифмов: на всех ЭВМ для этого имеются стандартные программы.

Прикладные примеры

Во вводной беседе мы уже говорили о том, что многие процессы описываются с помощью показательных функций. Почему так происходит, это мы обсудим в следующей главе, а сейчас приведем примеры зависимостей, в которых встречаются экспоненты и логарифмы.

Радиоактивный распад. Изменение массы радиоактивного вещества происходит по формуле , где m0 — масса вещества в начальный момент t = 0, m — масса вещества в момент времени t, Т — некоторая константа, смысл которой мы сейчас выясним.

Вычислим значение m при t — Т. Так,

Это означает, что через время Т после начального момента масса радиоактивного вещества уменьшается вдвое. Поэтому число Т называют периодом полураспада. Период полураспада радия равен 1600 лет, урана-238 — 4,5 млрд. лет, цезия-137 —31 год, иода-131 —8 суток.

Закон радиоактивного распада часто записывают в стандартном виде 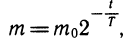. Связь константы т с периодом полураспада нетрудно найти:

2. Рост народонаселения. Изменение количества людей в стране на небольшом отрезке времени с хорошей точностью описывается формулой 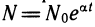, где Nо — число людей при t= 0, N — число людей в момент времени t, а — некоторая константа.

Барометрическая формула. Давление воздуха убывает с высотой (при постоянной температуре) по закону 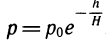где ро — давление на уровне моря (А = 0), р — давление на высоте h, H — некоторая константа, зависящая от температуры. Для температуры 20 °С величина Н ≈ 7,7 км.

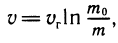
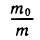
4. Формула Циолковского. Эта формула, связывающая скорость ракеты у с ее массой m, такова: , где vr — скорость вылетающих газов, mо — стартовая масса ракеты. Скорость истечения газа при сгорании топлива vr невелика (в настоящее время она меньше или равна 2 км/с). Логарифм растет очень медленно, и, для того чтобы достичь космической скорости, необходимо сделать большим отношение , т. е. почти всю стартовую массу отдать под топливо.

5. Коэффициент звукоизоляции стен измеряется по формуле 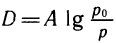где po — давление звука до поглощения, р — давление звука, прошедшего через стену, А — некоторая константа, которая в расчетах принимается равной 20 дБ. Если коэффициент звукоизоляции D равен, например, 20 дБ, то это означает, что =1 и po = 10 p, т. е. стена снижает давление звука в 10 раз (такую звукоизоляцию имеет деревянная дверь).

Дополнение к логарифмической функции

Смотрите также:

Предмет высшая математика

Логарифмическая функция

Определение логарифма: Логарифмом числа N по данному основанию а называется такой показатель степени, в который надо возвести основание а, чтобы получить число N; запись

Примеры:

Таким образом, 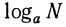это другое название для показателя степени.

Примеры:

1. Проверить справедливость следующих равенств:

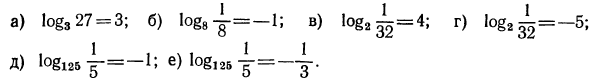
Решение:

следовательно, равенства

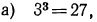
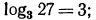
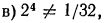
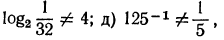
б), г), е) верны; следовательно, следовательно,

2.Следующие равенства переписать в виде логарифмических равенств:

Решение:

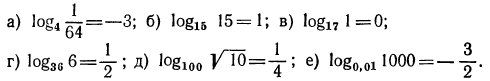
Указать, какие из нижеследующих уравнений имеют решение. Запишите это решение с помощью логарифма:

Решение:

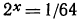
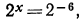
а) Уравнение можно переписать в вид откуда х = —6, или

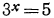
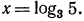
б) Уравнение также имеет решение Так как

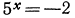
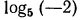
в) Уравнение не имеет решения (показательная функция не может принимать отрицательных значений). Таким образом, выражение не имеет смысла.

Десятичные логарифмы

Если основанием логарифмов служит число 10, то такие логарифмы называются десятичными. Десятичный логарифм числа N принято обозначать

Примеры:

Найти десятичные логарифмы следующих чисел:

Решение:

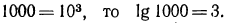
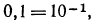
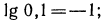
Так как Аналогично: поэтому наконец,

2.Решить следующие уравнения:

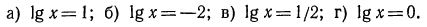
Решение:

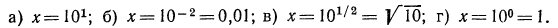
Функция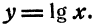

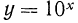
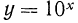
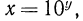
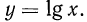
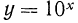
Функция является монотонно возрастающей, поэтому у нее есть обратная функция. Для того чтобы найти эту обратную функцию, поменяем в равенстве переменные х и у местами. Получим откуда Этой формулой задается функция, обратная показательной функции Как отмечалось выше (см. стр. 118), графики взаимно обратных функций симметричны относительно прямой у = х—биссектрисы первого и третьего координатных углов (рис. 88). Отметим основные свойства функции

1.Областью определения функции является множество всех положительных чисел.

2.Областью значений функции является множество всех действительных чисел.

Справедливость этих двух свойств вытекает из того факта, что функции 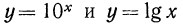являются взаимно обратными и, следовательно, область определения и множество значений у них меняются местами.

3.Функция 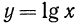является монотонно возрастающей (большему числу соответствует больший логарифм).

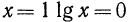
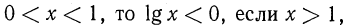
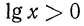
4.При (график пересекает ось абсцисс в точке (1; 0)); если то (рис. 88).

Примеры:

1. На рис. 89 изображен график функции 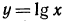в случае, когда масштаб по оси Оу в 10 раз крупнее масштаба по оси Ох. Воспользовавшись этим графиком:

а) найти 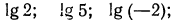б) найти х, если

Решение:

не существует, так как

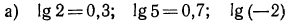
б) если

Если

2.Сравнить значения выражений:

Решение:

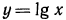
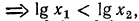
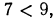
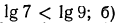
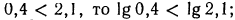
а) Функция возрастающая, значит, так как то, следовательно, б) так как в) так как

3.Решить уравнения и неравенства:

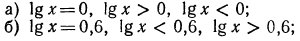
Решение:

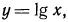
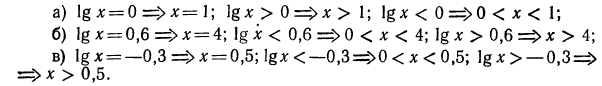
Воспользовавшись изображенным на рис. 89 графиком функции получим следующие результаты:

4.Найти область определения функции:

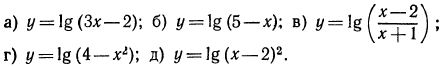
Решение:

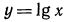
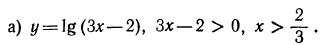
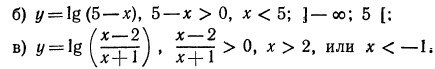
При решении этих примеров надо помнить о том, что область определения функции есть множество положительных чисел.

Таким образом областью определения служит множество

Область определения —объединение двух множеств

Область определения —множество

Выражение, стоящее под знаком логарифма, положительно при всех значениях х, кроме х = 2 (при котором оно обращается в ноль), а поэтому область определения этой функции есть множество

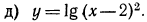
5.Решить уравнения:

Решение:

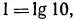
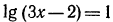
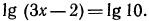
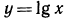
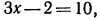
а) Так как то уравнение можно переписать в виде Далее из свойства монотонности функции вытекает, что эта функция каждое значение принимает только один раз. Следовательно, откуда х = 4.

Аналогично решаются и остальные уравнения;

т.е. данное уравнение может быть записано в виде откуда

поэтому откуда

поэтому откуда или

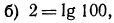
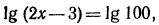
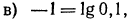
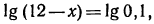
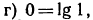
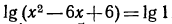
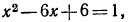
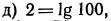
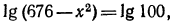
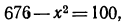
Логарифмирование и потенцирование

Применение логарифмов позволяет во многих случаях значительно упростить вычисления. Чтобы убедиться в этом, прежде всего выясним, как находятся логарифмы произведения, частного, степени и корня.

Теорема:

Логарифм произведения любых двух положительных чисел равен сумме логарифмов множителей, т. е.

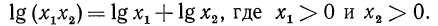
Доказательство:

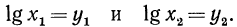
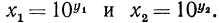
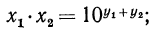
Пусть Тогда по определению логарифма Перемножив эти равенства почленно, получим

значит,

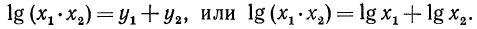
Предлагаем читателю самому доказать, что установленное свойство справедливо для любого числа положительных множителей.

Теорема:

Логарифм степени с положительным основанием равен произведению показателя степени и логарифма ее основания, т. е.

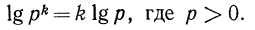
Доказательство:

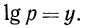
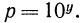
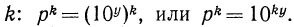
Пусть Тогда по определению логарифма Возведем обе части этого равенства в степень Следовательно,

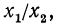
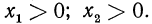
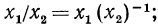
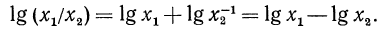
Покажем, что знания этих теорем достаточно для нахождения логарифмов дроби и корня. Действительно, пусть дано выражение где Это выражение можно переписать в виде тогда

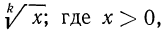
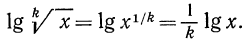
Пусть теперь дано выражение тогда Таким образом, если некоторое выражение составлено из положительных чисел с помощью операций умножения, деления, возведения в степень и извлечения корня, то его логарифм можно выразить через логарифмы входящих в него чисел. Такое преобразование называется логарифмированием. Действие, обратное логарифмированию, называется потенцированием.

Примеры:

1. Найти приближенные значения следующих логарифмов: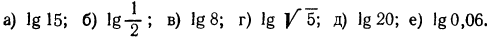

Решение:

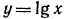
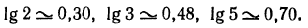
Прежде всего, воспользовавшись графиком функции (см. рис. 89), выпишем приближенные значения следующих логарифмов:

Теперь имеем:

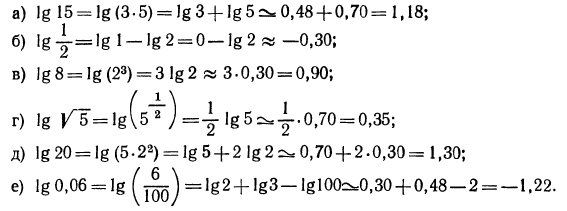
2.Прологарифмировать следующие выражения (буквами обозначены положительные числа):

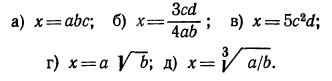
Решение:

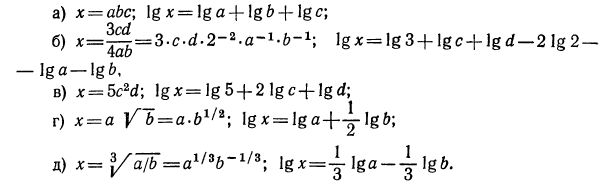
3.Решить уравнения:

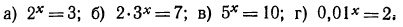
Решение:

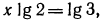
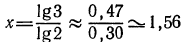
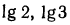
а) Прологарифмировав обе части данного равенства, получим откуда (значения найдены графически с помощью рис. 89);

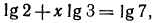
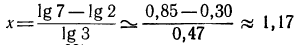
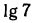
б) в результате логарифмирования имеем равенство откуда (значение найдено с помощью рис. 89);

4.Найти x, если:

Решение:

5.Решить уравнения:

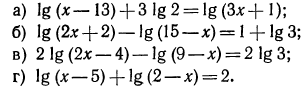
Решение:

а) Потенцируя обе части равенства, получаем уравнение

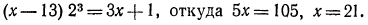
Сделаем проверку. Подставив в уравнение найденное решение х = 21, получим:

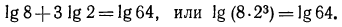
Таким образом, корень данного уравнения x=21;

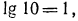
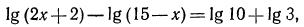
б) прежде чем потенцировать, заметим, что и перепишем уравнение в виде

откуда

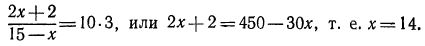
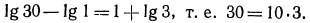
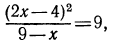
Сделаем проверку: Итак, х= 14 —корень уравнения; в) потенцируя, получаем

откуда

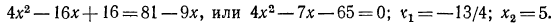
Сделаем проверку. Корень является посторонним, так как при этом значении x выражение 2х—4 будет отрицательным, а, как мы знаем, область определения логарифмической функции есть множество положительных чисел.

Корень x = 5, как легко видеть, удовлетворяет уравнению (Проверьте сами!);

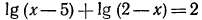
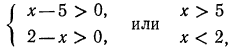
г) уравнение не имеет корней, так как искомое значение х должно удовлетворять системе неравенств

а эта система противоречива и решения не имеет.

Стандартный вид числа. Характеристика и мантисса

Любое положительное число х можно записать в так называемом стандартном виде: 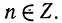Число n называется порядком числа х.

Примеры:

Записать следующие числа в стандартном виде и указать их порядок: а) 273; б) 51,83; в) 0,8912; г) 400012; д) 0,00051; е) 1,002.

Решение:

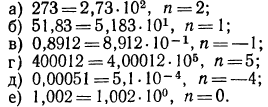
Легко видеть, что если то порядок числа неотрицателен, причем трехзначное число, например 273, имеет порядок 2; а число, содержащее две цифры в целой части, например 51,83, имеет порядок n= 1; наконец, число, содержащее одну цифру в целой части, имеет порядок n= 0. Можно сделать следующий вывод: если число содержит в целой части m цифр, то его порядок будет

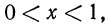
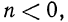
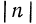
Если же число то его порядок отрицателен, причем равен числу нулей в x: до первой значащей цифры, включая ноль целых. Так, если x: = 0,8912, то n = —1; если х = 0,00051, то n = —4.

Пример:

Не переходя к стандартному виду записи, найти порядок чисел: а) х = 373,25; б) x: = 0,00085.

Решение:

а) Число 373,25 больше единицы и содержит в целой части три цифры. Следовательно, его порядок n= 2;

б) число 0,00085 меньше единицы и содержит четыре нуля до первой значащей цифры. Следовательно, n =—4.

Пусть х=375,8. Запишем это число в стандартном виде и найдем его логарифм:

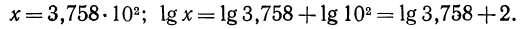
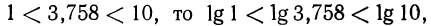
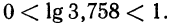
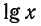
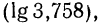
Так как т. е. Таким образом, представлен в виде суммы целого числа 2 и положительного числа, меньшего единицы т. е. в виде суммы его целой и дробной частей. Целая часть логарифма числа х равна порядку этого числа, а дробная часть равна

Целая часть логарифма числа называется его характеристикой, а дробная часть — мантиссой.

Теорема:

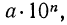
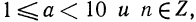
Характеристика логарифма числа где равна порядку этого числа, т. е. n, а мантисса равна

Доказательство:

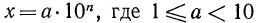
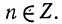
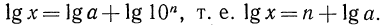
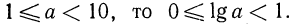
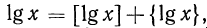
Пусть и Тогда Так как Следовательно, причем

Следствие:

Логарифмы чисел, отличающихся друг от друга только порядком, имеют одну и ту же мантиссу.

Доказательство:

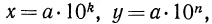
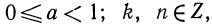
Пусть где тогда

Таким образом,

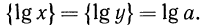
Например, пусть 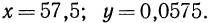Запишем эти числа в стандартном виде и найдем их логарифмы:

Таким образом, доказанное следствие можно сформулировать иначе: мантисса логарифма числа не зависит от положения запятой в числе.

Примеры:

1. Найти характеристику логарифма числа а) 302;б) 87,5; в) 0,015.

Решение:

Как было доказано Выше, характеристика логарифма числа равна его порядку, а поэтому

2.Зная, что 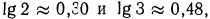найти:

Решение:

Вычисления с помощью таблиц логарифмов

Как известно, характеристика логарифма числа легко находится устно (она равна порядку числа). Значения мантисс приведены в таблице «Четырехзначных математических таблиц» В. М. Брадиса. Приведем часть этой таблицы и укажем как ею пользоваться.

Примеры:

1. Найти логарифмы следующих чисел:

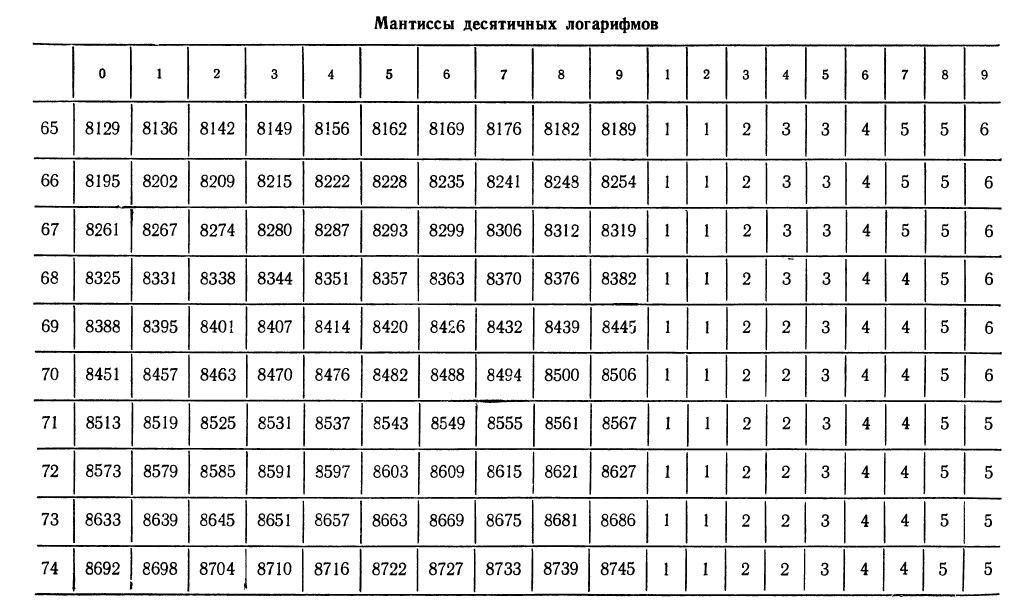
Решение:

а) Характеристика равна 1, так как Мантиссу найдем на пересечении строки с меткой «72» и столбца с меткой «4». Получаем число 8597. Значит, мантисса равна (приблизительно) 0,8597. Отсюда:

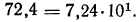
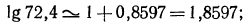
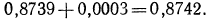
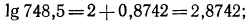
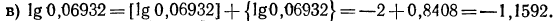
Для отыскания мантиссы мы, прочитав число 8739 на пересечении строки с меткой «74» и столбца с меткой «8», прибавим к этому числу поправку на четвертую цифру. Эта поправка расположена в правой части таблицы на пересечении той же строки и столбца поправок с меткой «5». Поправка равна 3, следовательно, мантисса равна Таким образом,

Для решения обратной задачи —нахождения числа по его логарифму пользуются таблицей, с которой мы уже знакомы (см. стр. 198)4

2.Найти x:, если:

Решение:

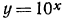
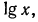
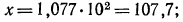
а) По таблице значений функции найдем число 1,077, соответствующее мантиссе равной 0,0324. Так как характеристика логарифма равна 2, то

б) представим данный логарифм в виде суммы характеристики и мантиссы:

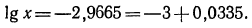
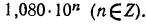
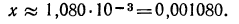
Мантиссу 0,0335 имеет любое число вида Характеристика равна —3, поэтому

В заключение приведем пример вычисления с помощью таблиц логарифмов.

3.Вычислить значение х, если

Решение:

Логарифмируя, имеем:

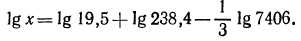
По таблице логарифмов найдем:

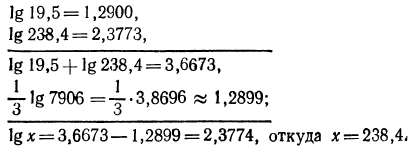
Решение:

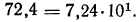
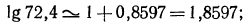
Решение заданий и задач по предметам:

Математика
Высшая математика
Математический анализ
Линейная алгебра

Дополнительные лекции по высшей математике:

Тождественные преобразования алгебраических выражений
Функции и графики
Преобразования графиков функций
Квадратная функция и её графики
Алгебраические неравенства
Неравенства
Неравенства с переменными
Прогрессии в математике
Арифметическая прогрессия
Геометрическая прогрессия
Показатели в математике
Логарифмы в математике
Исследование уравнений
Уравнения высших степеней
Уравнения высших степеней с одним неизвестным
Комплексные числа
Непрерывная дробь (цепная дробь)
Алгебраические уравнения
Неопределенные уравнения
Соединения
Бином Ньютона
Число е
Непрерывные дроби
Функция
Исследование функций
Предел
Интеграл
Двойной интеграл
Тройной интеграл
Интегрирование
Неопределённый интеграл
Определенный интеграл
Криволинейные интегралы
Поверхностные интегралы
Несобственные интегралы
Кратные интегралы
Интегралы, зависящие от параметра
Квадратный трехчлен
Производная
Применение производной к исследованию функций
Приложения производной
Дифференциал функции
Дифференцирование в математике
Формулы и правила дифференцирования
Дифференциальное исчисление
Дифференциальные уравнения
Дифференциальные уравнения первого порядка
Дифференциальные уравнения высших порядков
Дифференциальные уравнения в частных производных
Тригонометрические функции
Тригонометрические уравнения и неравенства
Показательная функция
Показательные уравнения
Обобщенная степень
Взаимно обратные функции
Уравнения и неравенства
Положительные и отрицательные числа
Алгебраические выражения
Иррациональные алгебраические выражения
Преобразование алгебраических выражений
Преобразование дробных алгебраических выражений
Разложение многочленов на множители
Многочлены от одного переменного
Алгебраические дроби
Пропорции
Уравнения
Системы уравнений
Системы уравнений высших степеней
Системы алгебраических уравнений
Системы линейных уравнений
Системы дифференциальных уравнений
Арифметический квадратный корень
Квадратные и кубические корни
Извлечение квадратного корня
Рациональные числа
Иррациональные числа
Арифметический корень
Квадратные уравнения
Иррациональные уравнения
Последовательность
Ряды сходящиеся и расходящиеся
Тригонометрические функции произвольного угла
Тригонометрические формулы
Обратные тригонометрические функции
Теорема Безу
Математическая индукция
Показатель степени
Показательные функции и логарифмы
Множество
Множество действительных чисел
Числовые множества
Преобразование рациональных выражений
Преобразование иррациональных выражений
Геометрия
Действительные числа
Степени и корни
Степень с рациональным показателем
Тригонометрические функции угла
Тригонометрические функции числового аргумента
Тригонометрические выражения и их преобразования
Преобразование тригонометрических выражений
Комбинаторика
Вычислительная математика
Прямая линия на плоскости и ее уравнения
Прямая и плоскость
Линии и уравнения
Прямая линия
Уравнения прямой и плоскости в пространстве
Кривые второго порядка
Кривые и поверхности второго порядка
Числовые ряды
Степенные ряды
Ряды Фурье
Преобразование Фурье
Функциональные ряды
Функции многих переменных
Метод координат
Гармонический анализ
Вещественные числа
Предел последовательности
Аналитическая геометрия
Аналитическая геометрия на плоскости
Аналитическая геометрия в пространстве
Функции одной переменной
Высшая алгебра
Векторная алгебра
Векторный анализ
Векторы
Скалярное произведение векторов
Векторное произведение векторов
Смешанное произведение векторов
Операции над векторами
Непрерывность функций
Предел и непрерывность функций нескольких переменных
Предел и непрерывность функции одной переменной
Производные и дифференциалы функции одной переменной
Частные производные и дифференцируемость функций нескольких переменных
Дифференциальное исчисление функции одной переменной
Матрицы
Линейные и евклидовы пространства
Линейные отображения
Дифференциальные теоремы о среднем
Теория устойчивости дифференциальных уравнений
Функции комплексного переменного
Преобразование Лапласа
Теории поля
Операционное исчисление
Системы координат
Рациональная функция
Интегральное исчисление
Интегральное исчисление функций одной переменной
Дифференциальное исчисление функций нескольких переменных
Отношение в математике
Математическая логика
Графы в математике
Линейные пространства
Первообразная и неопределенный интеграл
Линейная функция
Выпуклые множества точек
Система координат

Источник

На чтение 1 мин. Просмотров 1.9k.

Найти корень логарифмического уравнения непросто — сначала, возможно, потребуется упрощение уравнения, применение известных свойств логарифма. Цель — сделать так, чтобы и слева, и справа от равенства был логарифм по одинаковому основанию.

Найдите корень уравнения .

Решение:

Представим 2 в виде логарифма, используя свойство , где -любое положительное число () и .

Получим:

Уравнение примет вид:

Здесь мы упростили , использовав свойство логарифмов:

Слева логарифм по основанию 4 и справа логарифм по основанию 4, значит, будут равны и числа под знаком логарифма:

Решим полученное уравнение:

Так как число под знаком логарифма не может быть отрицательным, проверим и .

Проверка:

Уравнение решено верно.

Ответ: -0,9.

( 3 оценки, среднее 5 из 5 )

Источник

18 февраля 2014

В этом видеоуроке мы рассмотрим решение довольно серьезного логарифмического уравнения, в котором не просто требуется найти корни, но и отобрать те из них, которые лежат на заданном отрезке.

Задача C1. Решите уравнение. Найдите все корни этого уравнения, принадлежащие промежутку.

Замечание по поводу логарифмический уравнений

Перед тем как переходить непосредственно к уравнению, хочу поделиться небольшой исторической справкой. Дело в том, что ЕГЭ по математике в том виде, котором нам предстоит его сдавать, существует в России уже не первый год. И то уравнение, которое вы сейчас видите на своих экранах, появилось в контрольно-измерительных материалах уже давно.

Однако из года в год ко мне приходят ученики которые пытаются решать вот такие, прямо скажем, непростые уравнения, но при этом не могут понять: с чего им вообще начинать и как подступиться к логарифмам? Такая проблема может возникнуть даже у сильных, хорошо подготовленных учеников.

В результате многие начинают опасаться этой темы, а то и вовсе считать себя тупыми. Так вот, запомните: если у вас не получается решить такое уравнение, это совершенно не значит, что вы — тупые. Потому что, например, вот с таким уравнением вы справитесь практически устно:

log₂ x = 4

А если это не так, вы сейчас не читали бы этот текст, поскольку были заняты более простыми и приземленными задачами. Конечно, кто-то сейчас возразит: «А какое отношение это простейшее уравнение имеет к нашей здоровой конструкции?» Отвечаю: любое логарифмическое уравнение, каким бы сложным оно ни было, в итоге сводится вот к таким простейшим, устно решаемым конструкциям.

Разумеется, переходить от сложных логарифмических уравнений к более простым нужно не с помощью подбора или танцев с бубном, а по четким, давно определенным правилам, которые так и называются — правила преобразования логарифмических выражений. Зная их, вы без труда разберетесь даже с самыми навороченными уравнениями в ЕГЭ по математике.

И именно об этих правилах мы будем говорить в сегодняшнем уроке. Поехали!

Решение логарифмического уравнения в задаче C1

Итак, решаем уравнение:

В первую очередь, когда речь заходит о логарифмических уравнениях, вспоминаем основную тактику — если можно выразиться, основное правило решения логарифмических уравнений. Заключается оно в следующем:

Теорема о канонической форме. Любое логарифмическое уравнение, что бы в него не входило, какие бы логарифмы, по какому бы основанию, и что бы в себе не cодержали, обязательно нужно привести к уравнению вида:

log_a f (x) = log_a g(x)

Если мы посмотрим на наше уравнение, то заметим сразу две проблемы:

Слева у нас стоит сумма двух чисел, одно из которых вообще не является логарифмом.
Справа стоит вполне себе логарифм, однако в его основании стоит корень. А у логарифма слева — просто 2, т.е. основания логарифмов слева и справа различаются.

Итак, мы составили этакий список проблем, которые отделяют наше уравнение от того канонического уравнения, к которому нужно привести любое логарифмическое уравнение в процессе решения. Таким образом, решение нашего уравнения на данном этапе сводится к тому, чтобы устранить описанные выше две проблемы.

Любое логарифмическое уравнение решается быстро и легко, если свести его к канонической форме.

Сумма логарифмов и логарифм произведения

Давайте действовать по порядку. Сначала разберемся с конструкцией, которая стоит слева. Что мы можем сказать про сумму двух логарифмов? Давайте вспомним замечательную формулу:

log_a f (x) + log_a g(x) = log_a f (x) · g(x)

Но стоить учесть, что в нашем случае первое слагаемо вообще не является логарифмом. Значит, нужно представить единицу в виде логарифма по основанию 2 (именно 2, потому что слева стоит логарифм по основанию 2). Как это сделать? Опять вспоминаем замечательную формулу:

a = log_b b^a

Здесь нужно понимать: когда мы говорим «Любое основание b», то подразумеваем, что b все-таки не может быть произвольным числом. Если мы вставляем какое-то число в логарифм, на него сразу накладываются определенные ограничения, а именно: основание логарифма должно быть больше 0 и не должно быть равно 1. Иначе логарифм просто не имеет смысла. Запишем это:

0 < b ≠ 1

Давайте посмотрим, что происходит в нашем случае:

1 = log₂ 2¹ = log₂ 2

Теперь перепишем все наше уравнение с учетом этого факта. И сразу же применяем другое правило: сумма логарифмов равна логарифму произведения аргументов. В итоге получим:

Мы получили новое уравнение. Как видим, оно уже гораздо ближе к тому каноническому равнению, к которому мы стремимся. Но есть одна проблема, мы записали ее в виде второго пункта: у наших логарифмов, которые стоят слева и справа, разные основания. Переходим к следующему шагу.

Правила вынесения степеней из логарифма

Итак у логарифма, который стоит слева, основание просто 2, а у логарифма, который стоит справа, в основании присутствует корень. Но и это не является проблемой, если вспомнить, что из оснований из аргументов логарифма можно выносить в степень. Давайте запишем одно из этих правил:

log_a bⁿ = n · log_a b

Переведя на человеческий язык: можно выносить степень из основания логарифма и ставить ее спереди в качестве множителя. Число n «мигрировало» из логарифма наружу и стало коэффициентом спереди.

С тем же успехом мы можем вынести степень из основания логарифма. Выглядеть это будет так:

Другими словами, если вынести степень из аргумента логарифма, эта степень также пишется в качестве множителя перед логарифмом, но уже не в виде числа, а в виде обратного числа 1/k.

Однако и это еще не все! Мы можем объединить две данные формулы и почить следующую формулу:

Когда степень стоит и в основании, и в аргументе логарифма, мы можем сэкономить время и упростить вычисления, если сразу же вынести степени и из основания, и из аргумента. При этом то, что стояло в аргументе (в нашем случае это коэффициент n), окажется в числителе. А то, что было степенью у основания, a^k, отправится в знаменатель.

И именно эти формулы мы сейчас будем применять для того, чтобы свести наши логарифмы к одному и тому же основанию.

Вынесение степени из основания логарифма

Прежде всего, выберем более-менее красивое основание. Очевидно, что с двойкой в основании намного приятней работать, чем с корнем. Таким образом, давайте попробуем привести второй логарифм к основанию 2. Давайте выпишем этот логарифм отдельно:

Что мы можем здесь сделать? Вспомним формулу степени с рациональным показателем. Другими словами, мы можем записать в корни в качестве степени с рациональным показателем. А затем выносим степень 1/2 и из аргумента, и из основания логарифма. Сокращаем двойки в коэффициентах в числителе и знаменателе, стоящих перед логарифмом:

Наконец, перепишем исходное уравнение с учетом новых коэффициентов:

log₂ 2(9x² + 5) = log₂ (8x⁴ + 14)

Мы получили каноническое логарифмическое уравнение. И слева, и справа у нас стоит логарифм по одному и тому же основанию 2. Помимо этих логарифмов никаких коэффициентов, никаких слагаемых ни слева, ни справа нет.

Следственно, мы можем избавиться от знака логарифма. Разумеется, с учетом области определения. Но прежде, чем это сделать, давайте вернемся назад и сделаем небольшое уточнение по поводу дробей.

Деление дроби на дробь: дополнительные соображения

Далеко не всем ученикам понятно, откуда берутся и куда деваются множители перед правым логарифмом. Запишем еще раз:

Давайте разберемся, что такое дробь. Запишем:

А теперь вспоминаем правило деления дробей: чтобы разделить на 1/2 нужно умножить на перевернутую дробь:

Разумеется, для удобства дальнейших вычислений мы можем записать двойку как 2/1 — и именно это мы наблюдаем в качестве второго коэффициента в процессе решения.

Надеюсь, теперь всем понятно, откуда берется второй коэффициент, поэтому переходим непосредственно к решению нашего канонического логарифмического уравнения.

Избавление от знака логарифма

Напоминаю, что сейчас мы можем избавиться от логарифмов и оставить следующее выражение:

2(9x² + 5) = 8x⁴ + 14

Давайте раскроем скобки слева. Получим:

18x² + 10 = 8x⁴ + 14

Перенесем все из левой части в правую:

8x⁴ + 14 − 18x² − 10 = 0

Приведем подобные и получим:

8x⁴ − 18x² + 4 = 0

Можем разделить обе части этого уравнения на 2, чтобы упростить коэффициенты, и получим:

4x⁴ − 9x² + 2 = 0

Перед нами обычное биквадратное уравнение, и его корни легко считаются через дискриминант. Итак, запишем дискриминант:

D = 81 − 4 · 4 · 2 = 81 − 32 = 49

Прекрасно, Дискриминант «красивый», корень из него равен 7. Все, считаем сами иксы. Но в данном случае корни получатся не x, а x², потому что у нас биквадратное уравнение. Итак, наши варианты:

Обратите внимание: мы извлекали корни, поэтому ответов будет два, т.к. квадрат — функция четная. И если мы напишем лишь корень из двух, то второй корень мы просто потеряем.

Теперь расписываем второй корень нашего биквадратного уравнения:

Опять же, мы извлекаем арифметический квадратный корень из обеих частей нашего уравнения и получаем два корня. Однако помните:

Недостаточно просто приравнять аргументы логарифмов в канонической форме. Помните об области определения!

Итого мы получили четыре корня. Все они действительно являются решениями нашего исходного уравнения. Взгляните: в нашем исходном логарифмическом уравнении внутри логарифмов стоит либо 9x² + 5 (эта функция всегда положительна), либо 8x⁴ + 14 — она тоже всегда положительна. Следовательно, область определения логарифмов выполняется в любом случае, какой бы корень мы не получили, а это значит, что все четыре корня являются решениями нашего уравнения.

Прекрасно, теперь переходим ко второй части задачи.

Отбор корней логарифмического уравнения на отрезке

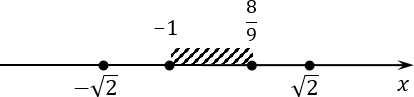
Отбираем из наших четырех корней те, которые лежат на отрезке [−1; 8/9]. Возвращаемся к нашим корням, и сейчас будем выполнять их отбор. Для начала предлагаю начертить координатную ось и отметить на ней концы отрезка:

Обе точки будут закрашенные. Т.е. по условию задачи нас интересует заштрихованный отрезок. Теперь давайте разбираться с корнями.

Иррациональные корни

Начнем с иррациональных корней. Заметим, что 8/9 < 9/9 = 1. С другой стороны, корень из двух явно больше единицы. Следовательно, наши корни будут находиться на отрезке в таком положении:

Из этого следует, что корень из двух не попадает в интересующий нас отрезок. Аналогично мы получим и с отрицательным корнем: он меньше, чем −1, т. е. лежит левее интересующего нас отрезка.

Рациональные корни

Остается два корня: x = 1/2 и x = −1/2. Давайте заметим, что левый конец отрезка (−1) — отрицательный, а правый (8/9) — положительный. Следовательно, где-то между этими концами лежит число 0. Корень x = −1/2 будет находиться между −1 и 0, т.е. попадет в окончательный ответ. Аналогично поступаем с корнем x = 1/2. Этот корень также лежит на рассматриваемом отрезке.

Убедиться, что число 8/9 больше, чем 1/2, можно очень просто. Давайте вычтем эти числа друг из друга:

Получили дробь 7/18 > 0, а это по определению означает, что 8/9 > 1/2.

Давайте отметим подходящие корни на оси координат:

Окончательным ответом будут два корня: 1/2 и −1/2.

Сравнение иррациональный чисел: универсальный алгоритм

В заключении хотел бы еще раз вернуться к иррациональным числам. На их примере мы сейчас посмотрим, как сравнивать рациональные и иррациональные величины в математике. Для начала по между ними вот такую галочку V — знак «больше» или «меньше», но мы пока не знаем, в какую сторону он направлен. Запишем:

Зачем вообще нужны какие-то алгоритмы сравнения? Дело в том, что в данной задаче нам очень повезло: в процессе решения возникло разделяющее число 1, про которое мы точно можем сказать:

Однако далеко не всегда вы с ходу увидите такое число. Поэтому давайте попробуем сравнить наши числа «в лоб», напрямую.

Как это делается? Делаем то же самое, что и с обычными неравенствами:

Сначала, если бы у нас где-то были отрицательные коэффициенты, то мы умножили бы обе части неравенства на −1. Разумеется, поменяв при этом знак. Вот такая галочка V изменилась бы на такую — Λ.
Но в нашем случае обе стороны уже положительны, поэтому ничего менять не надо. Что действительно нужно, так это возвести обе части в квадрат, чтобы избавится от радикала.

Если при сравнении иррациональных чисел не удается с ходу подобрать разделяющий элемент, рекомендую выполнять такое сравнение «в лоб» — расписывая как обычное неравенство.

При решении это оформляется вот таким образом:

Теперь это все легко сравнивается. Дело в том, что 64/81 < 81/81 = 1 < 2. На основании той цепочки преобразований мы заключаем, что 64/81 < 2 и, следовательно, корень больше 8/9.

Все, мы получили строгое доказательство, что все числа отмечены на числовой прямой х правильно и именно в той последовательности, в которой они должны быть на самом деле. Вот к такому решению никто не придерется, поэтому запомните: если вы сразу не видите разделяющее число (в нашем случае это 1), то смело выписывайте приведенную выше конструкцию, умножайте, возводите в квадрат — и в итоге вы получите красивое неравенство. Из этого неравенства точно будет понятно, какое число больше, а какое — меньше.

Возвращаясь к нашей задаче, хотелось бы еще раз обратить ваше внимание на то, что мы делали в самом начале при решении нашего уравнения. А именно: мы внимательно посмотрели на наше исходное логарифмическое уравнение и попытались свести его к каноническому логарифмическому уравнению. Где слева и справа стоят только логарифмы — без всяких дополнительных слагаемых, коэффициентов спереди и т. д. Нам нужны не два логарифма по основанию a или b, именно логарифм, равный другому логарифму.

Кроме того, основания логарифмов также должны быть равны. При этом если уравнение составлено грамотно, то с помощью элементарных логарифмических преобразований (сумма логарифмов, преобразование числа в логарифм и т.д.) мы сведем это уравнение именно к каноническому.

Поэтому впредь, когда вы видите логарифмическое равнение, которое не решается сразу «в лоб», не стоит теряться или пробовать подобрать ответ. Достаточно выполнить следующие шаги:

Привести все свободные элементы к логарифму;
Затем эти логарифмы сложить;
В полученной конструкции все логарифмы привести к одному и тому же основанию.

В результате вы получите простое уравнение, которое решается элементарными средствами алгебры из материалов 8—9 класса. В общем, заходите на мой сайт, тренируйтесь решать логарифмы, решайте логарифмические уравнения как я, решайте их лучше меня. А у меня на этом все. С Вами был Павел Бердов. До новых встреч!

Смотрите также:

Задача C1: логарифмы и тригонометрия в одном уравнении
Задача C1: еще одно показательное уравнение
Тест к уроку «Что такое логарифм» (средний)
Решение задач B12: №448—455
Как решать задачу 18: графический подход
Задача B15: частный случай при работе с квадратичной функцией

Источник

Как решать логарифмические уравнения – подробный разбор

Опубликовано 12.01.2018

Чтобы ответить на вопрос как решать логарифмические уравнения давайте вспомним, что такое логарифм. Логарифм – это показатель степени, в которую нужно возвести основание логарифма, чтобы получить число.

Например,

или число 3 (показатель степени) мы можем записать так $log_2{8}$ , таким образом $log_2{8} =3$

Основание логарифма всегда положительное число, не равное 1. Число под знаком логарифма – строго больше нуля.

Теперь переходим непосредственно к вопросу – как решать логарифмические уравнения из профильного и из базового ЕГЭ.

Пример 1 Найдите корень уравнения.

$log_2{(7-x)}=5$

согласно определению логарифма:

Все неизвестные переносим в левую часть уравнения (слева от =), а известные – переносим в правую сторону.

Получим:

Делаем проверку:

$log_2{(7-(-25))}=5$

$log_2{32}=5$

Ответ:

Пример 2. Найдите корень уравнения.

$log_7{(9-x)}=3log_7{3}$

Здесь для решения данного логарифмического уравнения будем использовать свойство логарифма:

$mlog_a{b}=log_a{b^m}$

То есть внесем число 3 справа под знак логарифма.

$log_7{(9-x)}=log_7{3^3}$

или

$log_7{(9-x)}=log_7{27}$

Если показатели степени равны, основания степени равны, то равны числа, получаемые в результате, то есть получим

Делаем проверку: $log_7{(9+18)}=log_7{27}$

Получаем: $log_7{27}=log_7{27}$

Ответ:

Пример 3. Найдите корень уравнения

$log_4{(2-x)}=log_{16}{25}$

Используем следующее свойство логарифма:

$log_{a^n}{b}=frac{1}{n}log_a{b}=log_a{b^{frac{1}{n}}}$

Тогда получим:

$log_4{(2-x)}=log_4{25^{frac{1}{2}}}$

$log_4{(2-x)}=log_4{5}$

Делаем проверку:

$log_4{(2-(-3))}=log_{16}{25}$

$log_4{5}=log_4{5}$

Ответ:

Пример 4. Найдите корень уравнения.

$log_2{(4-x)}=8$

Используя определение логарифма, получим:

Проверим: $log_2{(4-(-252))}=8$

$log_2{256}=8$

Ответ: .

Таким образом, теперь вы можете составить четкую инструкцию, как решать логарифмические уравнения. Она заключается в следующих шагах:

Сделать справа и слева от знака равенства (=) логарифмы по одному основанию, избавившись от коэффициентов перед логарифмами, используя свойства логарифмов.
Избавляемся от логарифмов, используя правило потенцирования. Остаются только числа, которые были под знаком логарифма.
Решаем получившееся обычное уравнение – как найти корень уравнения смотрите здесь.
Делаем проверку
Записываем ответ.

( 4 оценки, среднее 5 из 5 )

Источник

Захотел тут порешать задачки по математике, просто для удовольствия, чтобы мозги не ржавели… И понял, что уже поздно — заржавели.

Не врублюсь, как следует решать вот эту задачу. Нужно вычислить:

$sqrt{log^2_2{3} + 1 - log_2{9}} - log_2{Big(12sqrt{2}Big)}$

Известен ответ, который должен получиться:

$-dfrac{7}{2}$

И это действительно так — я проверял на калькуляторе. Но вот как прийти к этому ответу — не имею ни малейшего представления.

Кое-что я, конечно, попытался сделать, в меру своих убогих умственных способностей:

$noindent $sqrt{log^2_2{3} + 1 - log_2{9}} - log_2{Big(12sqrt{2}Big)} = \\ = sqrt{log_2{3} cdot log_2{3} + log_2{2} - log_2{9}} - (log_2{12} + log_2{sqrt{2}}) = \\ = sqrt{log_2{3^{log_2{3}}} + log_2{dfrac{2}{9}}} - log_2{12} - dfrac{1}{2} = \\ = sqrt{log_2{Big(dfrac{2 cdot 3^{log_2{3}}}{9}}Big)} - (log_2{3} + log_2{4}) - dfrac{1}{2} = \\ = sqrt{log_2{Big(dfrac{2 cdot 3^{log_2{3}}}{3^2}}Big)} - log_2{3} - 2 - dfrac{1}{2} = \\ = sqrt{log_2{Big(2 cdot 3^{log_2{3} - 2}}Big)} - log_2{3} - dfrac{5}{2} = \\ = sqrt{log_2{Big(3^{log_3{2}} cdot 3^{log_2{3} - 2}}Big)} - log_2{3} - dfrac{5}{2} = \\ = sqrt{log_2{Big(3^{log_3{2} + log_2{3} - 2}}Big)} - log_2{3} - dfrac{5}{2} = \\ = sqrt{log_2{Big(Big(2^{log_2{3}}Big)^{log_3{2} + log_2{3} - 2}}Big)} - log_2{3} - dfrac{5}{2} = \\ = sqrt{log_2{Big(2^{log_2{3} cdot ({log_3{2} + log_2{3} - 2}})}Big)} - log_2{3} - dfrac{5}{2} = \\ = sqrt{log_2{3} cdot ({log_3{2} + log_2{3} - 2})} - log_2{3} - dfrac{5}{2} = \\ = sqrt{log_2{3} cdot log_3{2} + log^2_2{3} - 2 log_2{3}} - log_2{3} - dfrac{5}{2} = \\ = sqrt{1 + log_2{3} cdot (log_2{3} - 2)} - log_2{3} - dfrac{5}{2} = \\ = sqrt{log_2{2} + log_2{3^{log_2{3} - 2}}} - log_2{3} - dfrac{5}{2} = \\ = sqrt{log_2{Big(2 cdot 3^{log_2{3} - 2}Big)}} - log_2{3} - dfrac{5}{2} $$

Как вы можете видеть, в итоге мы просто сделали круг и вернулись к тому, что уже было ранее, в шестой сверху строке. Сусанин одобряет.

Из плюсов: я могу быть уверен, что нигде не ошибся в расчётах. Из минусов: все эти трепыхания ни к чему не привели! Я ходил по кругу! И так каждый раз. Как бы я ни пытался преобразовать это подкоренное выражение, рано или поздно я возвращаюсь к тому, что уже было!

(Оффтоп)

Понятия не имею, куда двигаться дальше. Я просто не знаю, что делать с квадратным корнем из логарифма, как его можно преобразовать?.. Похоже, я не знаю какого-то простого правила для действий с логарифмами, поэтому и не могу найти выхода.

Пытался гуглить по запросам «квадратный корень из логарифма»

и «square root of logarithm»

, но находится только логарифм квадратного корня, который мне и так известен.

Источник