Прежде чем разбираться, как решать квадратное неравенство,
давайте рассмотрим, какое неравенство называют квадратным.
Запомните!
Неравенство называют квадратным, если старшая (наибольшая) степень неизвестного «x»
равна двум.
Потренируемся определять тип неравенства на примерах.
| Неравенство | Тип |
|---|---|
| x − 7 < 0 | линейное |
| x2 + 5x ≥ 0 | квадратное |
| 2x − 7 > 5 | линейное |
| x2 + x − 12 ≤ 0 | квадратное |
Как решить квадратное неравенство
В предыдущих уроках мы разбирали, как решать
линейные неравенства.
Но в отличие от линейных неравенств квадратные решаются совсем иным образом.
Важно!
Решать квадратное неравенство таким же образом как и линейное нельзя!
Для решения квадратного неравенства используется специальный способ, который называется методом интервалов.
Что такое метод интервалов
Методом интервалов называют специальный способ решения квадратных неравенств. Ниже мы объясним, как использовать
этот метод и почему он получил такое название.
Запомните!
Чтобы решить квадратное неравенство методом интервалов нужно:
- перенести все члены неравенства в левую часть, так чтобы в правой остался только ноль;
- сделать так, чтобы при неизвестном «x2» стоял положительный коэффициент;
- приравнять левую часть неравенства к нулю и решить полученное квадратное уравнение;
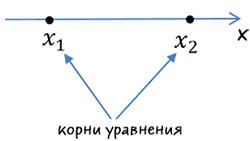
- полученные корни уравнения разместить на числовой оси в порядке возрастания;
- нарисовать «арки» для интервалов. Справа налево,
начиная с «+», проставить чередуя знаки «+»
и «−»; - выбрать необходимые интервалы и записать их в ответ.
Мы понимаем, что правила, описанные выше, трудно воспринимать только в теории, поэтому сразу рассмотрим пример решения
квадратного неравенства по алгоритму выше.
Требуется решить квадратное неравенство.
x2 + x − 12 < 0
Итак, согласно п.1 мы должны перенести
все члены неравенства в левую часть, так чтобы в правой остался только ноль.
В заданном неравенстве
«x2 + x − 12 < 0» ничего дополнительно делать не требуется,
так как в правой части и так уже стоит ноль.
Переходим к п.2. Необходимо сделать так, чтобы перед «x2»
стоял положительный коэффициент. В неравенстве
«x2 + x − 12 < 0»
при «x2» стоит положительный коэффициент «1»,
значит, снова нам ничего делать не требуется.
Согласно п.3 приравняем левую часть неравенства к нулю и решим полученное квадратное уравнение.
x2 + x − 12 = 0
x1;2 =
| −1 ± √12 − 4 · 1 · (−12) |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
|
x1 = |
x2 = |
|
x1 = |
x2 = |
|
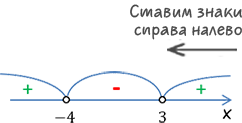
x1 = −4 |
x2 = 3 |
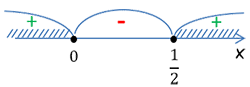
Теперь по п.4 отметим полученные корни на числовой оси в порядке возрастания.
Помните, что, исходя их того, какое перед нами неравенство (строгое или нестрогое) мы отмечаем точки на числовой оси
разным образом.
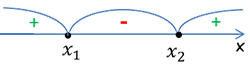
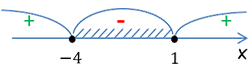
Теперь, как сказано в п.5, нарисуем «арки» над интервалами между отмеченными точками.
Проставим знаки внутри интервалов.
Справа налево чередуя, начиная с «+», отметим знаки.
Нам осталось только выполнить пункт 6, то есть выбрать нужные интервалы и записать их в ответ.
Вернемся к нашему неравенству.
Так как в нашем неравенстве
«x2 + x − 12 < 0»,
значит, нам требуются отрицательные интервалы.
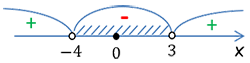
Заштрихуем все отрицательные области на числовой оси и выпишем их в ответ.
Отрицательным интервалом оказался лишь один, который находится между числами
«−4» и «3», поэтому
запишем его в ответ в виде двойного неравенства
−4 < x < 3.
Запишем полученный ответ квадратного неравенства.
Ответ: −4 < x < 3
Именно из-за того, что при решении квадратного неравенства мы рассматриваем интервалы между числами,
метод интервалов и получил свое название.
После получения ответа имеет смысл сделать его проверку, чтобы убедиться в правильности решения.
Выберем любое число, которое находится в заштрихованной области полученного ответа −4 < x < 3
и подставим его вместо «x» в исходное неравенство.
Если мы получим верное неравенство,
значит мы нашли ответ квадратного неравенства верно.
Возьмем, например, из интервала число «0». Подставим его в исходное неравенство
«x2 + x − 12 < 0».
x2 + x − 12 < 0
02 + 0 − 12 < 0
−12 < 0
(верно)
Мы получили верное неравенство при подстановке числа из области решений, значит ответ найден правильно.
Краткая запись решения методом интервалов
Сокращенно запись решения квадратного неравенства
«x2 + x − 12 < 0»
методом интервалов будет выглядеть так:
x2 + x − 12 < 0
x2 + x − 12 = 0
x1;2 =
| −1 ± √12 − 4 · 1 · (−12) |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
|
x1 = |
x2 = |
|
x1 = |
x2 = |
|
x1 = −4 |
x2 = 3 |
Ответ: −4 < x < 3
Другие примеры решения квадратных неравенств
Рассмотрим решение других примеров квадратных неравенств. Требуется решить квадратное неравенство:
2x2 − x ≥ 0
В правой части неравенство уже стоит ноль. При «x2»
стоит «2» (положительный коэффициент), значит можно сразу переходить
к поиску корней.
2x2 − x ≥ 0
2x2 − x = 0
x1;2 =
| −(−1) ± √(−12) − 4 · 2 · 0 |
| 2 · 2 |
x1;2 =
x1;2 =
| x1 = |
x2 = |
| x1 = |
x2 = |
| x1 = |
x2 = 0 |
Ответ: x ≤ 0; x ≥
Рассмотрим пример, где перед «x2» в квадратном неравенстве стоит
отрицательный коэффициент.
−x2 − 3x + 4 ≥ 0
По п.2 общих правил решения методом интервалов нам нужно сделать так, чтобы
перед «x2» стоял положительный
коэффициент. Для этого умножим все неравенство на «−1».
−x2 − 3x + 4 ≥ 0 | ·(−1)
x2 + 3x − 4 ≤ 0
Можно переходить к п.4 и п.5. Приравняем левую часть неравенства к нулю и решим полученное квадратное уравнение.
Затем расположим полученные корни на числовой оси и проведем между ними «арки».
x2 + 3x − 4 ≤ 0
x2 + 3x − 4 = 0
x1;2 =
| −3 ± √32 − 4 · 1 · (−4) |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
|
x2 = |
x1 = |
|
x2 = |
x1 = |
| x2 = −4 | x1 = 1 |
Важно!
При определении того какие интервалы нам нужно брать в ответ, исходить нужно из самого последнего изменения неравенства
перед нахождением его корней.
В нашем случае самая последняя версия неравенства перед поиском корней уравнения это
«x2 + 3x − 4 ≤ 0».
Значит для ответа нужно выбирать интервалы со знаком «−».
Ответ: −4 ≤ x ≤ 1
К сожалению, при решении квадратного неравенства не всегда получаются два корня и все идет по общему плану выше.
Возможны случаи, когда получается один корень или даже ни одного корня.
Как решить квадратные неравенства в таких случаях, мы разберем в следующем уроке
«Квадратные неравенства
с одним корнем или без корней».
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
5 апреля 2019 в 8:15
Gulnara Muslimova
Профиль
Благодарили: 0
Сообщений: 1
Gulnara Muslimova
Профиль
Благодарили: 0
Сообщений: 1
Помогите решить неравенство (желательно подробно и с пояснениями):
(x2+3x+3)x^2 -1<(8x-3)x^2 -1
0
Спасибо
Ответить
6 апреля 2019 в 16:12
Ответ для Gulnara Muslimova
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Логарифмируем
ac < bc <=> c·ln(a/b) < 0
и метод интервалов.
0
Спасибо
Ответить
15 сентября 2018 в 22:11
Vlad Lukashenok
Профиль
Благодарили: 0
Сообщений: 1
Vlad Lukashenok
Профиль
Благодарили: 0
Сообщений: 1
Решите неравенство:
x · sin2(πx)>=0
0
Спасибо
Ответить
17 сентября 2018 в 23:05
Ответ для Vlad Lukashenok
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
x = k ∈ Ζ; x > 0.
0
Спасибо
Ответить
Квадратные неравенства – это неравенства вида: a x 2 + b x + c > 0 a x 2 + b x + c ≥ 0 a x 2 + b x + c < 0 a x 2 + b x + c ≤ 0 где a, b, c – некоторые числа, причем a ≠ 0, x – переменная.
Существует универсальный метод решения неравенств степени выше первой (квадратных, кубических, биквадратных и т.д.) – метод интервалов. Если его один раз как следует осмыслить, то проблем с решением любых неравенств не возникнет.
Для того, чтобы применять метод интервалов для решения квадратных неравенств, надо уметь хорошо решать квадратные уравнения.
Алгоритм решения квадратного неравенства методом интервалов
- Решить уравнение a x 2 + b x + c = 0 и найти корни x 1 и x 2 .
- Отметить на числовой прямой корни трехчлена.
Если знак неравенства строгий > , < , точки будут выколотые.
Если знак неравенства нестрогий ≥ , ≤ , точки будут жирные (заштрихованный).
- Расставить знаки на интервалах. Для этого надо выбрать точку из любого промежутка (в примере взята точка A) и подставить её значение в выражение a x 2 + b x + c вместо x.
Если получилось положительное число, знак на интервале плюс. На остальных интервалах знаки будут чередоваться.
Точки выколотые, если знак неравенства строгий.
Точки жирные, если знак неравенства нестрогий.
Если получилось отрицательное число, знак на интервале минус. На остальных интервалах знаки будут чередоваться.
Точки выколотые, если знак неравенства строгий.
Точки жирные, если знак неравенства нестрогий.
- Выбрать подходящие интервалы (или интервал).
Если знак неравенства > или ≥ в ответ выбираем интервалы со знаком +.
Если знак неравенства < или ≤ в ответ выбираем интервалы со знаком -.
- Записать ответ.
Примеры решения квадратных неравенств:
№1. Решить неравенство x 2 ≥ x + 12.
№2. Решить неравенство − 3 x − 2 ≥ x 2 .
№3. Решить неравенство 4 < x 2 + 3 x .
№4. Решить неравенство x 2 − 5 x < 6.
№5. Решить неравенство x 2 < 4.
№6. Решить неравенство x 2 + x ≥ 0.
Квадратные неравенства — коротко о главном
Квадратичная функция–это функция вида: ( displaystyle fleft( x right)=a{{x}^{2}}+bx+c=0), ( displaystyle ane 0)
График квадратичной функции – парабола. Её ветви направлены вверх, если ( displaystyle a>0), и вниз, если ( displaystyle a<0):
Если требуется найти числовой промежуток, на котором квадратный трёхчлен больше нуля, то это числовой промежуток, где парабола лежит выше оси ( Ox).
Если требуется найти числовой промежуток, на котором квадратный трёхчлен меньше нуля, то это числовой промежуток, где парабола лежит ниже оси ( Ox).
Виды квадратных неравенств
Все квадратные неравенства сводятся к следующим четырём видам:
( displaystyle left. begin{array}{l}a{{x}^{2}}+bx+c ge 0\a{{x}^{2}}+bx+c>0\a{{x}^{2}}+bx+cle 0\a{{x}^{2}}+bx+c<0end{array} rightrangle ane 0)
Алгоритм решения квадратных неравенств:
1) Запишем соответствующее неравенству квадратное уравнение (просто меняем знак неравенства ( >,text{ }<,text{ }ge ,text{ }le ) на знак равенства «( displaystyle=)»).
Пример:
( 2{{x}^{2}}+x-3ge 0)
( 2{{x}^{2}}+x-3=0)
2) Найдём корни этого уравнения:
( {{x}_{1}}=-frac{3}{2};text{ }{{x}_{2}}=1)
3) Отметим корни на оси ( Ox) и схематично покажем ориентацию ветвей параболы («вверх» или «вниз»)
4) Расставим на оси знаки, соответствующие знаку квадратичной функции: там где парабола выше оси, ставим «( +)», а там где ниже – «( —)».
5) Выписываем интервал(ы), соответствующий(ие) «( +)» или «( —)», в зависимости от знака неравенства. Если неравенство нестрогое, корни входят в интервал, если строгое — не входят.
( xin left( -infty ;-frac{3}{2} right]cup left[ 1;+infty right))
А теперь еще раз тоже самое но более сжато (то есть на языке математики)
Прежде чем говорить о теме «квадратные неравенства», вспомним что такое квадратичная функция и что из себя представляет её график.
Квадратичная функция – это функция вида ( fleft( x right)=a{{x}^{2}}+bx+c=0), ( ane 0)
Другими словами, это многочлен второй степени.
График квадратичной функции – парабола (помнишь, что это такое?)
- если ( a>0), то ветви параболы направлены вверх;
- если ( a<0), то ветви параболы направлены вниз.
Если парабола не пересекает ось Х и ее ветви направлены вверх, функция при всех значениях Х принимает лишь положительные значения.
Если парабола не пересекает ось Х и ее ветви направлены вниз – лишь отрицательные.
В случае, когда у уравнения (( 1)) ровно один корень (например, если дискриминант равен нулю), это значит, что график касается оси ( Ox):
Тогда, аналогично предыдущему случаю, при ( a>0) функция неотрицательна ( left( f(x) ge 0 right)) при всех ( x), а при ( a<0) – неположительна ( left( f(x) le 0 right)).
Так вот, мы ведь недавно уже научились определять, где квадратичная функция больше нуля, а где – меньше:
Если квадратное неравенство нестрогое, то корни входят в числовой промежуток, если строгое — не входят.
Если корень только один, – ничего страшного, будет везде один и тот же знак. Если корней нет, всё зависит только от коэффициента ( a): если ( a>0), то всё выражение больше 0, и наоборот.
Ну что, уловил? Тогда давай смотреть примеры!
В данной публикации мы рассмотрим, что такое квадратное неравенство, и как оно решается методом интервалов в зависимости от количества корней. Также разберем практические примеры по этой теме.
- Определение квадратного неравенства
-
Решение квадратных неравенств
- С двумя корнями
- С одним корнем
- Без корней
Определение квадратного неравенства
Если старшая степень неизвестной переменной (чаще всего это x) равняется двум, то неравенство называется квадратным.
Например:
- x2 – 3x + 4 > 0
- 2x2 + 7x – 5 < 0
- x2 + 12x + 2 ≥ 0
- 3x2 – 4 ≤ 0
Решение квадратных неравенств
С двумя корнями
Квадратные уравнения решаются с помощью так называемого метода интервалов, принцип которого заключается в следующем:
1. Все элементы неравенства собираем в левой части, в правой должен остаться только ноль. Помним, что при переносе элемента из одной части в другую его знак меняется на противоположный.
2. Если перед неизвестной переменной во второй степени стоит отрицательный коэффициент, умножаем все элементы неравенства на число -1, изменив знак сравнения на противоположный.
3. Заменив знак сравнения на “равно” решаем полученное квадратное уравнение.
4. Найденные корни отмечаем на числовой оси.
При этом, если знак сравнения строгий (“больше” или “меньше”), то отметкой обычно является незакрашенный внутри кружок, если нестрогий (“больше или равно”, “меньше или равно”) – закрашенный.
5. Рисуем интервалы, и справа-налево присваиваем им знаки “плюс” и “минус” (начинаем с “+”, затем чередуем).
6. Если в неравенстве стоят знаки “>“ или “≥“, нам нужны положительные интервалы, если “<“ или “≤“ – отрицательные.
Пример 1
Решим квадратное неравенство x2 + 4x > -3.
Решение:
1. Т.к. правая часть должны быть нулевой, перенесем число -3 в левую, заменив его знак на “плюс”:
x2 + 4x + 3 > 0
2. Теперь найдем корни квадратного уравнения x2 + 4x + 3 = 0.
Мы подробно рассматривали данный вопрос в отдельной публикации, поэтому здесь отдельно на этом останавливаться не будем.
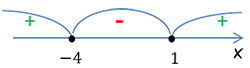
Итак, корни заданного уравнения: x1 = -1, x2 = -3. Отмечаем их на числовой оси (незакрашенные кружки, т.к. неравенство является строгим).
Рисуем интервалы, отметив знаками “плюс” и “минус”.
Нам нужные только положительные области, т.к. в неравенстве стоит знак “больше”.
Таким образом, решение неравенства следующее:
x > -1 и x < -3.
Примечание: если бы в рассматриваемом нами неравенстве стояли другие знаки, область решения была бы следующей:
- знак “<“, тогда -3 < x < -1
- знак “≥”, тогда x ≥ -1 и x ≤ -3
- знак “≤”, тогда -3 ≤ x ≤ -1
С одним корнем
Квадратные уравнения не всегда имеют два корня, иногда он может быть один.
Пример 2
Давайте решим x2 – 4x + 4 < 0.
Решение:
Корень у соответствующего квадратного уравнения всего один: x1 = x2 = 2, т.е. его значение повторяется дважды.
Отмечаем точку в виде незаполненного кружка на числовой оси и рисуем два исходящих от нее интервала.
Теперь нужно присвоить знаки интервалам, и здесь эта процедура отличается от описанного выше (когда у уравнения два корня): если значение корня в уравнении повторяется четное количество раз, то при смене интервалов знак не меняется. Проставляем их, также, справа-налево, начав с “плюса”.
В нашем случае значение повторяется два раза, т.е. получаем:
Нам нужны только отрицательные интервалы, а их здесь нет. К тому же, неравенство строгое. Следовательно, решений у него нет.
Примечание: если бы этом неравенстве стояли другие знаки, область решения была бы следующей:
- знак “>”, тогда x > 2 и x < 2
- знак “≥”, тогда x ≥ 2 и x ≤ 2, т.е. все действительные числа.
- знак “≤”, единственное решение – это x = 2
Без корней
В некоторых случаях квадратные уравнения могут и вовсе не иметь действительных корней.
В этом случае у соответствующее неравенства, также, не будет действительных решений. Это и будет ответом.
Пример 3
x2 + 3x + 5 > 0
Решение:
Уравнение не имеет корней, следовательно, у неравенства нет действительных решений.