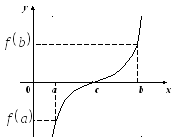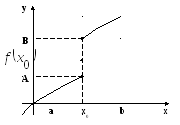Как найти корень непрерывной функции - Исправление недочетов и поиск решений вместе с Examum.ru

Алгоритмы поиска корней непрерывных функций

В математике и вычисляя, алгоритм поиска корня является алгоритмом для поиска нулей, также называемых «корнями», непрерывных функций. Ноль функции f, от действительных чисел до действительных чисел или от комплексных чисел до комплексных чисел, является числом x таким, что f ( x) = 0. Поскольку, как правило, нули функции не могут быть точно вычислены или выражены в закрытой форме, алгоритмы поиска корня обеспечивают приближение к нулям, выраженное либо как с плавающей запятой числа или как небольшие изолирующие интервалы, или диски для комплексных корней (интервал или вывод диска эквивалентен приблизительному выводу вместе с границей ошибки).

Решение уравнения f (x) = g (x) аналогично нахождению корней функции h (x) = f (x) — g (x). Таким образом, алгоритмы поиска корней позволяют решить любое уравнение, заданное непрерывными функциями. Однако большинство алгоритмов поиска корней не гарантируют, что они найдут все корни; в частности, если такой алгоритм не находит корня, это не означает, что корня не существует.

Большинство численных методов поиска корня используют итерацию, создавая последовательность чисел, которые, надеюсь, сходятся к корню как предел. Для них требуется одно или несколько начальных предположений о корне в качестве начальных значений, затем каждая итерация алгоритма дает более точное приближение к корню. Поскольку в какой-то момент итерация должна быть остановлена, эти методы дают приближение к корню, а не точное решение. Многие методы вычисляют последующие значения, оценивая вспомогательную функцию для предыдущих значений. Таким образом, предел представляет собой фиксированную точку вспомогательной функции, которая выбрана для того, чтобы корни исходного уравнения были фиксированными точками, и для быстрого схода с этими фиксированными точками.

Поведение общих алгоритмов поиска корней изучается в численном анализе. Однако для многочленов поиск корней обычно относится к компьютерной алгебре, поскольку алгебраические свойства многочленов являются фундаментальными для наиболее эффективных алгоритмов. Эффективность алгоритма может сильно зависеть от характеристик данных функций. Например, многие алгоритмы используют производную входной функции, в то время как другие работают с каждой непрерывной функцией. В общем, численные алгоритмы не гарантируют нахождение всех корней функции, поэтому невозможность найти корень не доказывает, что корня нет. Однако для многочленов существуют определенные алгоритмы, которые используют алгебраические свойства для подтверждения того, что корень не пропущен, и поиска корней в отдельных интервалах (или дисков для сложных корней), которые малы достаточно, чтобы обеспечить сходимость численных методов (обычно метод Ньютона ) к уникальному корню, расположенному таким образом.

Содержание

1 Методы брекетинга
- 1.1 Метод деления пополам
- 1.2 Ложное положение (regula falsi)
2 Интерполяция
3 Итерационные методы
- 3.1 Метод Ньютона (и аналогичные методы, основанные на производных)
- 3.2 Метод секущих
- 3.3 Метод Стеффенсена
- 3.4 Обратная интерполяция
4 Комбинации методов
- 4.1 Метод Брента
5 Корни многочленов
- 5.1 Нахождение одного корня
- 5.2 Поиск корней в парах
- 5.3 Поиск всех корней одновременно
- 5.4 Методы исключения и включения
- 5.5 Изоляция действительного корня
- 5.6 Поиск нескольких корней многочленов
6 См. Также
7 Ссылки

Методы скобок

Методы скобок определяют последовательно меньшие интервалы (скобки), содержащие корень. Когда интервал достаточно мал, значит, корень найден. Обычно они используют теорему о промежуточном значении, которая утверждает, что если непрерывная функция имеет значения противоположных знаков в конечных точках интервала, то функция имеет по крайней мере один корень в интервале. Следовательно, они требуют начинать с интервала, так что функция принимает противоположные знаки в конечных точках интервала. Однако в случае многочленов существуют другие методы (правило знаков Декарта, теорема Будана и теорема Штурма ) для получения информация о количестве корней в интервале. Они приводят к эффективным алгоритмам изоляции действительных корней многочленов, которые обеспечивают нахождение всех действительных корней с гарантированной точностью.

Метод деления пополам

Простейшим алгоритмом поиска корня является метод деления пополам. Пусть f — непрерывная функция, для которой известен интервал [a, b] такой, что f (a) и f (b) имеют противоположные знаки (скобка). Пусть c = (a + b) / 2 — середина интервала (середина или точка, которая делит интервал пополам). Тогда либо f (a) и f (c), либо f (c) и f (b) имеют противоположные знаки, и один разделил размер интервала на два. Хотя метод деления пополам является надежным, он дает один и только один бит точности с каждой итерацией. Другие методы, при соответствующих условиях, могут быстрее повысить точность.

Ложное положение (regula falsi)

Метод ложного положения, также называемый методом regula falsi, аналогичен методу деления пополам, но вместо использования середины поиска пополам интервала он использует x-точку пересечения линии, которая соединяет построенные значения функции в конечных точках интервала, то есть

c = af (b) — bf (a) f (b) — f (а). { displaystyle c = { frac {af (b) -bf (a)} {f (b) -f (a)}}.} ${ displaystyle c = { frac {af (b) -bf (a)} {f (b) -f (a)}}.}$

Ложное положение аналогично методу секущей, за исключением того, что вместо сохранения двух последних точек он сохраняет по одной точке по обе стороны от корня. Метод ложного положения может быть быстрее, чем метод деления пополам, и никогда не будет расходиться, как метод секущей; однако он может не сойтись в некоторых наивных реализациях из-за ошибок округления, которые могут привести к неправильному знаку для f (c); обычно это может происходить, если скорость изменения f велика в окрестности корня.

Метод Риддерса — вариант метода ложного положения, который использует значение функции в середине интервала для получения функции с тем же корнем, к которой применяется метод ложного положения. Это дает более быструю сходимость с аналогичной надежностью.

Интерполяция

Многие процессы поиска корней работают с помощью интерполяции. Это заключается в использовании последних вычисленных приближенных значений корня для аппроксимации функции полиномом низкой степени, который принимает те же значения в этих приближенных корнях. Затем вычисляется корень полинома и используется как новое приближенное значение корня функции, и процесс повторяется.

Два значения позволяют интерполировать функцию полиномом первой степени (то есть аппроксимировать график функции линией). Это основа метода секущих. Три значения определяют квадратичную функцию, которая аппроксимирует график функции параболой . Это метод Мюллера..

Regula falsi — это также метод интерполяции, который отличается от метода секущей за счет использования для интерполяции по линии двух точек, которые не обязательно являются двумя последними вычисленными точками.

Итерационные методы

Хотя все алгоритмы поиска корней выполняются с помощью итерации, итеративный метод поиска корней обычно использует определенный тип итерации, состоящий из определения вспомогательной функции, которая применяется к последним вычисленным приближениям корня для получения нового приближения. Итерация останавливается, когда фиксированная точка (от до желаемая точность) вспомогательной функции достигается, то есть когда новое вычисленное значение достаточно близко к предыдущим.

Метод Ньютона (и аналогичные методы, основанные на производной)

Метод Ньютона предполагает, что функция f имеет непрерывную производную. Метод Ньютона может не сходиться, если начат слишком далеко от корня. Однако когда он сходится, он быстрее, чем метод деления пополам, и обычно является квадратичным. Метод Ньютона важен еще и потому, что он легко обобщается на многомерные проблемы. Ньютоноподобные методы с более высокими порядками сходимости — это методы Хаусхолдера. Первым после метода Ньютона является метод Галлея с кубическим порядком сходимости.

Метод секущих

Заменяя производную в методе Ньютона на конечную разность, мы получаем метод секанса. Этот метод не требует вычисления (или наличия) производной, но цена сходимости медленнее (порядок равен примерно 1,6 (золотое сечение )). Обобщением метода секущих в более высоких измерениях является метод Бройдена.

метод Стеффенсена

Если мы используем полиномиальную аппроксимацию для удаления квадратичной части конечной разности, используемой в методе секанса, чтобы она лучше аппроксимирует производную, мы получаем метод Стеффенсена, который имеет квадратичную сходимость и поведение которого (как хорошее, так и плохое) по существу совпадает с методом Ньютона, но не требует производной.

Обратная интерполяция

Появления комплексных значений в методах интерполяции можно избежать путем интерполяции обратного f, что приводит к обратной квадратичной интерполяции метод. Опять же, сходимость асимптотически быстрее, чем метод секущей, но обратная квадратичная интерполяция часто ведет себя плохо, когда итерации не близки к корню.

Комбинации методов

Метод Брента

Метод Брента представляет собой комбинацию метода деления пополам, метода секущей и обратной квадратичной интерполяции. На каждой итерации метод Брента решает, какой из этих трех методов с наибольшей вероятностью будет работать лучше, и продолжает выполнение шага в соответствии с этим методом. Это дает надежный и быстрый метод, который поэтому пользуется большой популярностью.

Корни многочленов

Нахождение корней многочлена — давняя проблема, которая на протяжении всей истории была объектом многих исследований. Свидетельством этого является то, что до 19 века алгебра по существу означала теорию полиномиальных уравнений.

Найти корень линейного многочлена (первая степень) легко и нужно только одно деление. Для квадратичных многочленов (степень два) квадратная формула дает решение, но ее численная оценка может потребовать некоторой осторожности для обеспечения числовой стабильности. Для степеней третьей и четвертой существуют решения в замкнутой форме в терминах радикалов, которые, как правило, неудобны для числовой оценки, так как являются слишком сложными и включают вычисление нескольких корней n-й степени вычисление которого не проще, чем прямое вычисление корней многочлена (например, выражение вещественных корней кубического многочлена может включать нереальные кубические корни ). Для многочленов пятой степени и выше теорема Абеля – Руффини утверждает, что, как правило, не существует радикального выражения корней.

Итак, за исключением очень низких степеней, поиск корней многочленов заключается в нахождении приближений корней. По основной теореме алгебры известно, что многочлен степени n имеет не более n действительных или комплексных корней, и это число достигается почти для всех многочленов.

Отсюда следует, что задачу нахождения корня для многочленов можно разделить на три разные подзадачи;

Нахождение одного корня
Нахождение всех корней
Нахождение корней в определенной области комплексной плоскости, как правило, настоящие корни или действительные корни в заданном интервале (например, когда корни представляют физическую величину, интересны только действительные положительные).

Для поиска одного корня, метод Ньютона и другие общие итерационные методы обычно работают хорошо.

Самый старый метод поиска всех корней — это, когда корень r был найден, разделить многочлен на x — r и итеративно перезапустить поиск корня частного многочлена. Однако, за исключением низких степеней, это не работает из-за числовой нестабильности : многочлен Уилкинсона показывает, что очень небольшое изменение одного коэффициента может резко изменить не только значение корни, но также и их природа (реальная или сложная). Кроме того, даже с хорошим приближением, когда кто-то оценивает многочлен с приближенным корнем, он может получить результат, который далеко не будет близким к нулю. Например, если полином степени 20 (степень многочлена Уилкинсона) имеет корень, близкий к 10, производная полинома в корне может иметь порядок 10 20; { displaystyle 10 ^ {20};} ${ displaystyle 10 ^ {20};}$ это означает, что ошибка 10–10 { displaystyle 10 ^ {- 10}} $10 ^ {{- 10}}$ в значении корня может дать значение полинома в приближенном корне, которое имеет порядок 10 10. { displaystyle 10 ^ {10}.} ${ displaystyle 10 ^ {10}.}$

Чтобы избежать этих проблем, были разработаны методы, которые вычисляют все корни одновременно с любой желаемой точностью. В настоящее время наиболее эффективным методом является метод Аберта. Бесплатная реализация доступна под названием MPSolve. Это эталонная реализация, которая может регулярно находить корни многочленов степени более 1000 с более чем 1000 значащими десятичными знаками.

Методы вычисления всех корней могут использоваться для вычисления действительных корней. Однако может быть сложно решить, является ли корень с небольшой мнимой частью реальным или нет. Более того, поскольку количество реальных корней в среднем является логарифмом степени, вычисление нереальных корней является пустой тратой компьютерных ресурсов, когда кто-то интересуется реальными корнями.

Самый старый метод вычисления количества действительных корней и количества корней в интервале является результатом теоремы Штурма, но методы, основанные на правиле знаков Декарта и его расширения — теоремы Будана и Винсента — обычно более эффективны. Для нахождения корней все действуют путем уменьшения размера интервалов, в которых ищутся корни, до получения интервалов, содержащих ноль или один корень. Затем интервалы, содержащие один корень, могут быть дополнительно сокращены для получения квадратичной сходимости метода Ньютона к изолированным корням. Основные системы компьютерной алгебры (Maple, Mathematica, SageMath, PARI / GP ) имеют каждый вариант этого метода в качестве алгоритма по умолчанию для действительных корней многочлена.

Нахождение одного корня

Наиболее широко используемым методом вычисления корня является метод Ньютона, который состоит из итераций вычисления

xn + 1 = xn — е (xn) f ′ (xn), { displaystyle x_ {n + 1} = x_ {n} — { frac {f (x_ {n})} {f ‘(x_ {n})}},} ${displaystyle x_{n+1}=x_{n}-{frac {f(x_{n})}{f'(x_{n})}},}$

, начиная с правильно выбранного значения x 0. { displaystyle x_ {0}.} $x_ {0}.$ Если f является многочленом, вычисления выполняются быстрее при использовании правила Хорнера для вычисления многочлена и его производной.

Сходимость обычно квадратичная, она может сходиться очень медленно или даже не сходиться вообще. В частности, если многочлен не имеет действительного корня и x 0 { displaystyle x_ {0}} $x_ {0}$ реально, то метод Ньютона не может сходиться. Однако, если у многочлена есть действительный корень, который больше, чем больший действительный корень его производной, то метод Ньютона квадратично сходится к этому наибольшему корню, если x 0 { displaystyle x_ {0}} $x_ {0}$ больше, чем этот больший корень (есть простые способы вычисления верхней границы корней, см. Свойства полиномиальных корней ). Это отправная точка метода Хорнера для вычисления корней.

Когда был найден один корень r, можно использовать евклидово деление для удаления множителя x — r из полинома. Вычисление корня из полученного частного и повторение процесса в принципе обеспечивают способ вычисления всех корней. Однако эта итерационная схема численно нестабильна; ошибки аппроксимации накапливаются во время последовательных факторизаций, так что последние корни определяются с помощью полинома, который сильно отличается от множителя исходного полинома. Чтобы уменьшить эту ошибку, для каждого найденного корня можно перезапустить метод Ньютона с исходным полиномом и этим приблизительным корнем в качестве начального значения.

Однако нет гарантии, что это позволит найти все корни. Фактически, проблема нахождения корней многочлена по его коэффициентам в целом очень плохо обусловлена . Это иллюстрируется многочленом Уилкинсона : корни этого многочлена степени 20 — это 20 первых положительных целых чисел; изменение последнего бита 32-битного представления одного из его коэффициентов (равного –210) дает полином только с 10 действительными корнями и 10 комплексными корнями с мнимой частью больше 0,6.

Тесно связаны с методом Ньютона методом Галлея и методом Лагерра. Оба используют полином и его два первых вывода для итерационного процесса, который имеет кубическую сходимость. Объединяя два последовательных шага этих методов в один тест, мы получаем коэффициент сходимости , равный 9, за счет 6 полиномиальных вычислений (с правилом Хорнера). С другой стороны, объединение трех шагов метода Ньютона дает скорость сходимости 8 за счет того же количества полиномиальных вычислений. Это дает небольшое преимущество этим методам (менее ясно для метода Лагерра, поскольку квадратный корень должен вычисляться на каждом шаге).

При применении этих методов к многочленам с действительными коэффициентами и действительными начальными точками методы Ньютона и Галлея остаются внутри линии действительных чисел. Чтобы найти сложные корни, нужно выбрать сложные отправные точки. Напротив, метод Лагерра с квадратным корнем в оценке сам по себе оставляет действительную ось.

Другой класс методов основан на преобразовании задачи поиска корней полинома в задачу поиска собственных значений сопутствующей матрицы полинома. В принципе, можно использовать любой алгоритм собственных значений , чтобы найти корни полинома. Однако из соображений эффективности предпочтение отдается методам, использующим структуру матрицы, т.е. которые могут быть реализованы в безматричной форме. Среди этих методов — метод степени , применение которого для транспонирования сопутствующей матрицы является классическим методом нахождения корня из наибольшего модуля. Метод обратной мощности со сдвигами, который сначала находит какой-то наименьший корень, — это то, что управляет сложным (cpoly) вариантом алгоритма Дженкинса – Трауба и придает ему численную стабильность. Кроме того, он нечувствителен к множественным корням и имеет быструю сходимость с порядком 1 + φ ≈ 2.6 { displaystyle 1+ varphi приблизительно 2.6}(где φ { displaystyle varphi } varphi — это золотое сечение ) даже при наличии кластерных корней. Эта быстрая сходимость требует трех вычислений полинома на шаг, что приводит к невязке O (| f (x) |), что является более медленной сходимостью, чем с тремя шагами метода Ньютона.

Поиск корней в парах

Если данный полином имеет только действительные коэффициенты, можно избежать вычислений с комплексными числами. Для этого нужно найти квадратичные множители для пар сопряженных комплексных корней. Применение многомерного метода Ньютона к этой задаче приводит к методу Бэрстоу.

Реальный вариант алгоритма Дженкинса – Трауба является усовершенствованием этого метода.

Поиск всех корней одновременно

Простой Дюран-Кернер и немного более сложный метод Аберта одновременно находят все корни, используя только простые комплексное число арифметика. Ускоренные алгоритмы для многоточечной оценки и интерполяции, подобные быстрому преобразованию Фурье, могут помочь ускорить их для больших степеней полинома. Желательно выбирать асимметричный, но равномерно распределенный набор начальных точек. Реализация этого метода в бесплатном программном обеспечении MPSolve является эталоном его эффективности и точности.

Другой метод с этим стилем — это метод Данделина – Греффе (иногда также приписываемый Лобачевскому ), который использует полиномиальные преобразования для многократного и неявно возводить корни в квадрат. Это значительно увеличивает отклонения в корнях. Применяя формулы Виэта, можно получить простые приближения для модуля корней и, с некоторыми дополнительными усилиями, для самих корней.

Методы исключения и включения

Существует несколько быстрых тестов, которые определяют, не содержит ли сегмент реальной линии или область комплексной плоскости корней. Ограничивая модуль корней и рекурсивно разделяя начальную область, указанную этими границами, можно выделить небольшие области, которые могут содержать корни, а затем применить другие методы для их точного определения.

Все эти методы включают нахождение коэффициентов сдвинутых и масштабированных версий полинома. Для больших степеней становятся возможными ускоренные методы на основе БПФ.

Реальные корни см. В следующих разделах.

Алгоритм Лемера – Шура использует тест Шура – Кона для кругов; в качестве варианта алгоритм глобального деления пополам Уилфа использует вычисление числа витков для прямоугольных областей в комплексной плоскости.

В методе разбиения круга используются полиномиальные преобразования на основе БПФ для поиска факторов большой степени, соответствующих кластерам корней. Точность факторизации максимизируется с помощью итерации типа Ньютона. Этот метод полезен для поиска корней многочленов высокой степени с произвольной точностью; в этой настройке он имеет почти оптимальную сложность.

Изоляция действительного корня

Нахождение действительных корней многочлена с действительными коэффициентами — проблема, которой уделялось много внимания с начала 19 века, и до сих пор является активной областью исследований. Большинство алгоритмов поиска корней могут найти некоторые настоящие корни, но не могут подтвердить, что нашли все корни. Методы поиска всех сложных корней, такие как метод Аберта, могут предоставить реальные корни. Однако из-за числовой нестабильности многочленов (см. многочлен Уилкинсона ) им может потребоваться арифметика произвольной точности для определения того, какие корни являются действительными. Более того, они вычисляют все комплексные корни, хотя лишь немногие из них настоящие.

Отсюда следует, что стандартный способ вычисления действительных корней заключается в вычислении первых непересекающихся интервалов, называемых изолирующими интервалами, так что каждый из них содержит ровно один действительный корень, а вместе они содержат все корни. Это вычисление называется изоляцией реального корня. Имея разделительный интервал, можно использовать быстрые численные методы, такие как метод Ньютона для повышения точности результата.

Самый старый полный алгоритм изоляции действительного корня является результатом теоремы Штурма. Однако он оказывается намного менее эффективным, чем методы, основанные на правиле знаков Декарта и теореме Винсента. Эти методы делятся на два основных класса: один использует непрерывные дроби, а другой — деление пополам. Оба метода были значительно усовершенствованы с начала 21 века. Благодаря этим усовершенствованиям они достигают вычислительной сложности, которая аналогична сложности лучших алгоритмов для вычисления всех корней (даже если все корни действительны).

Эти алгоритмы реализованы и доступны в Mathematica (метод непрерывных дробей) и Maple (метод деления пополам). Обе реализации могут регулярно находить действительные корни многочленов степени выше 1000.

Нахождение множественных корней многочленов

Большинство алгоритмов поиска корней плохо себя ведут при множественных корнях или очень близких корнях. Однако для многочленов, коэффициенты которых точно заданы как целые числа или рациональные числа, существует эффективный метод разложения их на множители, которые имеют только простые корни и коэффициенты которых также точно заданы. Этот метод, называемый факторизация без квадратов, основан на том, что кратные корни многочлена являются корнями наибольшего общего делителя многочлена и его производной..

Факторизация многочлена p без квадратов является факторизацией p = p 1 p 2 2 ⋯ pkk { displaystyle p = p_ {1} p_ {2} ^ {2} cdots p_ {k} ^ {k}} $p = p_ {1} p_ {2} ^ {2} cdots p_ {k} ^ {k}$ , где каждый pi { displaystyle p_ {i}} $p_{i}$ равен 1 или многочлену без нескольких корней и двум различным pi { displaystyle p_ {i}} $p_{i}$ не имеют общего корня.

Эффективным методом вычисления этой факторизации является алгоритм Юна.

См. Также

Список алгоритмов поиска корня
метод Бройдена — квазиньютоновский метод поиска корня для многопараметрический случай
Криптографически безопасный генератор псевдослучайных чисел — Тип функций, неразрешимых с помощью алгоритмов поиска корней
Научная библиотека GNU
Метод Греффе — Алгоритм нахождения полиномиальных корней
Лилля метод — Графический метод для вещественных корней многочлена
MPSolve — Программное обеспечение для приближения корней многочлена с произвольно высокой точностью
Кратность (математика) — Количество раз, когда объект необходимо учитывать для выполнения общей формулы
алгоритм n-го корня
Система полиномиальных уравнений — Алгоритмы нахождения корней для общих корней нескольких многомерных многочленов
Теорема Канторовича — Начальные условия, обеспечивающие сходимость метода Ньютона

Литература

Источник

Пусть
и.
Тогдатакое, что.

Доказательство.
Пусть
,.
Разделим отрезокпополам:

если
,
то;
если
,
то обозначим,;
если
,
то обозначим,.

Заметим,
что длина отрезка
в два раза меньше длины отрезка.

Разделим
теперь отрезок
пополам и повторим предыдущие рассуждения.
То есть, если в точке деления функция
обращается в ноль, то нужная точка уже
найдена. В противном случае выберем тот
из получившихся отрезков, в концах
которого функция принимает значения
разных знаков. Обозначим этот отрезоки заметим, чтои.

Продолжим
этот процесс. Если
,
то.

Если мы
не встретим нуль функции на каком-то
шаге, то получим последовательность
вложенных отрезков
,
длины которых.
Значит, согласнолемме
Коши-Кантора о вложенных
отрезках существует точка
.

Докажем,
что
.
Так как последовательностьи ограничена,.
Так как последовательностьи ограничена,.
Для каждого,
следовательно,.

Функция
непрерывна в точке,
поэтому

,
.

,
(1)

.(2)

Из (1) и (2) вытекает,
что.Теорема доказана.

Следствие
(теорема
о прохождении непрерывной на отрезке
функции через любое промежуточное
значение).

Пусть
и.
Тогда для любого числа,
заключенного междуи,
существует такое,
что
.

Доказательство.
Рассмотрим функцию
.
Функциянепрерывна наи.
Согласно теореме Больцано-Коши о нуле
непрерывной функции,
то есть.
Теорема доказана.

Следствие.
Если функция непрерывна на
,
то

,
(3)

где
,.

Доказательство.
Для каждого
,
поэтому

.
(4) По теореме Вейерштрасса,.

Пусть
(если).
Имеем:,.
По теореме Больцано-Коши о промежуточных
значениях.
То есть мы доказали, что функцияпринимает все
значения от
до,
следовательно,

.
(5)

Из (4) и (5) вытекает
(3).

Другая формулировка
следствия:

Если
,
то.

7.4 Обратная функция. Теорема о существовании и непрерывности обратной функции

Лемма.
Функция
,
монотонная на,
непрерывна на нем тогда только тогда,
когда,.

Доказательство.
Необходимость. Согласно следствию из
теоремы Больцано-Коши о промежуточных
значениях
.

Пусть функция
возрастает на.
Тогда,
следовательно,,.

Достаточность.
Пусть функция
монотонно возрастает наи.
Покажем, что функциянепрерывна на.
Доказательство проведем от противного.
Предположим, что функцияразрывна и пусть— точка разрыва (первого рода!). Возможны
три случая:

1);
2);
3).

1) Если
,
то, так как функциявозрастает, то,,,
причем(в силу монотонности функции)

Выберем такое
число
,
что

(6)

Так как
,,
то.
Если,
то,
что противоречит (6).

Так как
,
то.
Поэтому, если,
то,
то есть,
что опять противоречит выбору.
Таким образом, точкане может быть точкой разрыва функции.

2) Доказывается
аналогично.

3)
.
Пусть,.

Так как
,
то

,
(7)

а так как
– точка разрыва (первого рода), то(одно из неравенств в (7) является
строгим).

Выберем
()
так, что.
(8) Так как,
то.
Имеем.
Поэтому.
Если,
то,
что противоречит (8). Так как,
то.
Если,
то,
что противоречит (8).

Если
,
то,
что также противоречит выбору числа.

Таким образом,
точка
не может быть точкой разрыва функции.

Лемма доказана.

Пусть
биективное отображение. В таком случае
функцияобратима. Справедлива

Теорема
о существовании и непрерывности обратной
функции

ТЕОРЕМА.
Пусть функция
строго возрастает (убывает) и непрерывна
на.
Тогда:

;
обратима;

C)
обратная функция
непрерывна и строго возрастает (убывает)
на.

Доказательство.

А)
Смотри лемму.

B)
Отображение

биективно (
или
)
и, значит, обратимо.(Смотри
Обратное отображение (Лекция №4)).

С) Пусть
строго возрастает на.
Покажем, чтострого возрастает на.
Пусть,.
Тогда,.
Для.
В самом деле, если,
то есть;
если,
то есть.
Поэтому.

Так как
строго возрастает наи,
то по лемменепрерывна на.
Теорема доказана.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

СВОЙСТВА ФУНКЦИЙ, НЕПРЕРЫВНЫХ НА ОТРЕЗКЕ

Рассмотрим некоторые
свойства функций непрерывных на отрезке. Эти свойства приведём без
доказательства.

Функцию y = f(x)

называют непрерывной на отрезке
[a
, b
], если она непрерывна во
всех внутренних точках этого отрезка, а на его концах, т.е. в точках a
и b
, непрерывна соответственно
справа и слева.

Теорема 1.
Функция, непрерывная на отрезке [a
, b
], хотя бы в одной точке этого
отрезка принимает наибольшее значение и хотя бы в одной – наименьшее.

Теорема утверждает, что если
функция y = f(x)
непрерывна
на отрезке [a
, b
], то найдётся хотя бы одна
точка x 1
Î
[a
, b
] такая, что значение
функции f(x)
в
этой точке будет самым большим из всех ее значений на этом отрезке: f(x 1) ≥ f(x)
.
Аналогично найдётся такая точка x 2
, в которой значение функции
будет самым маленьким из всех значений на отрезке: f(x 1) ≤ f(x)
.

Ясно, что таких
точек может быть и несколько, например, на рисунке показано, что функция f(x)

принимает наименьшее значение в двух точках x 2
и x
2 «.

Замечание
. Утверждение теоремы можно
стать неверным, если рассмотреть значение функции на интервале (a
, b
). Действительно, если
рассмотреть функцию y = x
на (0, 2), то она
непрерывна на этом интервале, но не достигает в нём ни наибольшего, ни
наименьшего значений: она достигает этих значений на концах интервала, но концы
не принадлежат нашей области.

Также теорема перестаёт
быть верной для разрывных функций. Приведите пример.

Следствие.
Если функция f(x)

непрерывна на [a
, b
], то она ограничена на этом
отрезке.

Теорема 2.
Пусть функция y = f(x)

непрерывна на отрезке [a
, b
] и на концах этого отрезка
принимает значения разных знаков, тогда внутри отрезка
найдется, по крайней мере, одна точка x = C
, в которой функция
обращается в ноль: f(C)
= 0, где a < C< b

Эта теорема имеет простой
геометрический смысл: если точки графика непрерывной функции y = f(x)
,
соответствующие концам отрезка [a
, b
] лежат по разные стороны от
оси Ox
, то этот график хотя бы в
одной точке отрезка пересекает ось Ox
.
Разрывные функции этим свойством могут не обладать.

Эта теорема допускает
следующее обобщение.

Теорема 3 (теорема о промежуточных значениях).
Пусть функцияy = f(x)

непрерывна на отрезке [a
, b
] и f(a) = A
, f(b) = B
. Тогда для любого числа C
, заключённого между A
и B
, найдётся внутри этого
отрезка такая точка C
Î [a
, b
], что f(c) = C
.

Эта теорема геометрически
очевидна. Рассмотрим график функции y = f(x)
.
Пусть f(a) = A
, f(b) = B
. Тогда любая прямая y = C
, где C
– любое число, заключённое
между A
и B
, пересечёт график функции,
по крайней мере, в одной точке. Абсцисса точки пересечения и будет тем
значением x = C
, при котором f(c) = C
.

Таким образом, непрерывная функция, переходя от одного своего значения к
другому, обязательно проходит через все промежуточные значения. В частности:

Следствие.
Если функция y = f(x)

непрерывна на некотором интервале и принимает наибольшее и наименьшее значения,
то на этом интервале она принимает, по крайней мере, один раз любое значение,
заключённое между её наименьшим и наибольшим значениями.

ПРОИЗВОДНАЯ И ЕЕ ПРИЛОЖЕНИЯ. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ

Пусть имеем
некоторую функцию y=f(x),

определенную на некотором промежутке. Для каждого значения аргумента x
из этого промежутка функция y=f(x)
имеет
определенное значение.

Рассмотрим два значения аргумента: исходное x
0 и новое x
.

Разность x– x
0 называется приращением аргумента x
в точке x
0 и обозначается Δx
. Таким образом, Δx = x – x
0 (приращение аргумента может
быть как положительным, так и отрицательным). Из этого равенства следует, что x=x
0 +Δx
, т.е. первоначальное значение переменной получило некоторое приращение.
Тогда, если в точке x
0 значение функции было f(x
0 ),

то в новой точке x
функция будет принимать
значение f(x) = f(x
0 +Δx)
.

Разность y – y
0 = f(x) – f(x
0 )
называется
приращением функции
y = f(x)
в
точке x
0 и обозначается символом Δy
. Таким образом,

Δy = f(x) – f(x
0 ) =
f(x
0 +Δx) — f(x
0 )
.

(1)

Обычно исходное
значение аргумента x
0 считается фиксированным, а новое
значение x
– переменным. Тогда y
0 = f(x
0 )
оказывается
постоянной, а y = f(x)
–
переменной. Приращения Δy
и Δx
также будут переменными и формула
(1) показывает, что Dy
является функцией переменной Δx
.

Составим
отношение приращения функции к приращению аргумента

Найдем предел этого
отношения при Δx
→0. Если этот предел
существует, то его называют производной данной функции f(x)
в
точке x
0 и обозначают f
«(x
0).
Итак,

Производной
данной функции y = f(x)
в
точке x
0 называется предел отношения
приращения функции Δy
к приращению аргумента Δx
, когда последнее произвольным образом
стремится к нулю.

Заметим, что для
одной и той же функции производная в различных точках x
может принимать различные
значения, т.е. производную можно рассматривать как функцию аргумента x
. Эта функция обозначается f
«(x
)

Производная
обозначается символами f
«(x),y
«, . Конкретное значение производной при x = a
обозначается f
«(a
) или
y
«| x=a
.

Операция
нахождения производной от функции f(x)
называется
дифференцированием этой функции.

Для непосредственного
нахождения производной по определению можно применить следующее практическое правило
:

Примеры.

МЕХАНИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ

Из физики известно,
что закон равномерного движения имеет вид s = v·t
, где s
– путь, пройденный к
моменту времени t
, v
– скорость равномерного движения.

Однако, т.к.
большинство движений происходящих в природе, неравномерно, то в общем случае
скорость, а, следовательно, и расстояние s
будет зависеть от времени t
,
т.е. будет функцией времени.

Итак, пусть
материальная точка движется по прямой в одном
направлении по закону s=s(t).

Отметим
некоторый момент времени t
0 . К этому моменту точка
прошла путь s=s(t
0 ).
Определим
скорость v
материальной точки в момент времени t
0 .

Для этого
рассмотрим какой-нибудь другой момент времени t
0 +
Δt
. Ему соответствует
пройденный путь s=s(t
0 +
Δt
). Тогда за промежуток
времени Δt
точка прошла путь Δs=s(t
0 +
Δt)
–s(t).

Рассмотрим
отношение . Оно называется средней скоростью в промежутке времени Δt
. Средняя скорость не может
точно охарактеризовать быстроту перемещения точки в момент t
0 (т.к. движение
неравномерно). Для того, чтобы точнее выразить эту
истинную скорость с помощью средней скорости, нужно взять меньший промежуток
времени Δt
.

Итак, скоростью
движения в данный момент времени t
0 (мгновенной скоростью)
называется предел средней скорости в промежутке от t
0 до t
0 +Δt
, когда Δt
→0:

т.е. скорость
неравномерного движения
это производная от пройденного пути по времени.

ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ

Введем
сначала определение касательной к кривой в данной точке.

Пусть имеем
кривую и на ней фиксированную точку М 0
(см. рисунок).Рассмотрим другую точку М
этой кривой и проведем секущую M 0 M
. Если точка М
начинает перемещаться по кривой, а
точка М 0

остается неподвижной, то секущая меняет свое положение. Если при неограниченном
приближении точки М
по кривой к точке
М 0

с любой стороны секущая стремится занять положение определенной прямой М 0 Т
, то прямая М 0 Т
называется касательной к
кривой в данной точке М 0
.

Т.о., касательной
к кривой в данной точке М 0

называется предельное положение секущей М 0 М
,
когда точка М
стремится вдоль кривой
к точке М 0
.

Рассмотрим теперь непрерывную функцию y=f(x)
и
соответствующую этой функции кривую. При некотором значении х
0
функция принимает значение y 0 =f(x 0).
Этим значениям x
0 и y
0 на кривой соответствует
точка М 0 (x 0 ; y 0).
Дадим аргументу x 0
приращение Δх
.
Новому значению аргумента соответствует наращенное значение функции y
0 +Δ y=f(x
0 –Δx)
.
Получаем точку М(x 0
+Δx
; y 0
+Δy).

Проведем секущую М 0 М
и
обозначим через φ угол, образованный секущей
с положительным направлением оси Ox
. Составим
отношение и заметим, что .

Если теперь Δx
→0, то в силу непрерывности
функции Δу
→0, и поэтому точка М
, перемещаясь по кривой, неограниченно
приближается к точке М 0
.
Тогда секущая М 0 М
будет
стремиться занять положение касательной к кривой в точке М 0
, а угол φ→α при Δx
→0, где через α обозначили угол между
касательной и положительным направлением оси Ox
. Поскольку функция tg φ непрерывно зависит от φ при φ≠π/2 то при φ→α tg φ → tg α и, следовательно, угловой
коэффициент касательной будет:

т.е. f «(x)
= tg α .

Т.о.,
геометрически у «(x 0)
представляет угловой
коэффициент касательной к графику этой функции в точке x 0
, т.е. при данном значении аргумента x
, производная равна
тангенсуугла, образованного касательной
к графику функции f(x)
в
соответствующей точке М 0
(x; y)
с
положительным направлением оси Ox.

Пример.
Найти
угловой коэффициент касательной к кривой у
= х
2 в точке М
(-1; 1).

Ранее мы уже
видели, что (x
2)» = 2х
. Но угловой коэффициент касательной к кривой есть tg α = y
«| x=-1
= – 2.

ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИЙ. НЕПРЕРЫВНОСТЬ ДИФФЕРЕНЦИРУЕМОЙ ФУНКЦИИ

Функция y=f(x)
называется
дифференцируемой
в некоторой точке x
0 , если она имеет в этой точке определенную
производную, т.е. если предел отношения существует и конечен.

Если функция
дифференцируема в каждой точке некоторого отрезка [а
; b
] или интервала (а
; b
), то говорят, что она дифференцируема
на отрезке [а
; b
] или соответственно в
интервале (а
; b
).

Справедлива следующая
теорема, устанавливающая связь между дифференцируемыми и непрерывными
функциями.

Теорема.
Если функция y=f(x)
дифференцируема в некоторой точке x 0
,
то она в этой точке непрерывна.

Таким образом,из дифференцируемости функции следует ее непрерывность.

Доказательство
. Если
, то

где α
бесконечно малая величина, т.е. величина, стремящаяся к нулю при Δx
→0.
Но тогда

Δy
=f
«(x 0
)
Δx
+αΔx
=> Δy
→0
при Δx
→0, т.е f(x) – f(x 0)
→0
при x
→x
0 , а это и означает, что функция f(x)
непрерывна в точке x
0 . Что и требовалось доказать.

Таким образом, в точках
разрыва функция не может иметь производной. Обратное утверждение неверно:
существуют непрерывные функции, которые в некоторых точках не являются
дифференцируемыми (т.е. не имеют в этих точках производной).

Рассмотрим на рисунке точки а, b, c.

В точке a
при Δx
→0 отношение не имеет предела (т.к.
односторонние пределы различны при Δx
→0–0 и Δx
→0+0).
В точке A
графика нет определенной
касательной, но есть две различные односторонние касательные с угловыми коэффициентами
к
1
и к
2 . Такой тип точек
называют угловыми точками.

В точке b
при Δx
→0 отношение является знакопостоянной бесконечно большой величиной . Функция имеет бесконечную производную. В этой точке
график имеет вертикальную касательную. Тип точки – «точка перегиба» cвертикальной
касательной.

В точке c
односторонние производные являются бесконечно большими
величинами разных знаков. В этой точке график имеет две слившиесявертикальные касательные. Тип – «точка
возврата» с вертикальной касательной – частный случай угловой точки.

Непрерывность элементарных функций

Теоремы о непрерывности функций следуют непосредственно из соответствующих теорем о пределах.

Теорема.
Сумма, произведение и частное двух непрерывных функций есть функция непрерывная (для частного за исключением тех значений аргумента, в которых делитель равен нулю).

Теорема.
Пусть функции u
= φ
(x
) непрерывна в точке х
0 , а функция y
= f
(u
) непрерывна в точке u
0 = φ
(х
0). Тогда сложная функция f
(φ
(x
)) состоящая из непрерывных функций, непрерывна в точке x
0 .

Теорема.
Если функция у
= f
(х
) непрерывна и строго монотонна на [а
; b
] оси Ох
, то обратная функция у
= φ
(х
) также непрерывна и монотонна на соответствующем отрезке [c
;d
] оси Оу
(без доказательства).

Непрерывные на отрезке функции имеют ряд важных свойств. Сформулируем их в виде теорем, не приводя доказательств.

Теорема (Вейерштрасса)
. Если функция непрерывна на отрезке, то она достигает на этом отрезке своего наибольшего и наименьшего значений.

Изображенная на рисунке 5 функция у
= f
(x
) непрерывна на отрезке [а
; b
], принимает свое наибольшее значение М
в точке x
1 , а наименьшее m —
в точке х
2 . Для любого х
[а
; b
] имеет место неравенство m
≤ f
(x
) ≤ М
.

Следствие.
Если функция непрерывна на отрезке, то она ограничена на этом отрезке.

Теорема (Больцано — Коши).
Если функция у
= f
(x
) непрерывна на отрезке [a
; b
] и принимает на его концах неравные значения f
(a
) = A
и f
(b
) = =В
, то на этом отрезке она принимает и все промежуточные значения между А
и В
.

Геометрически теорема очевидна (см. рис. 6).

Для любого числа С
, заключенного между А
и В
, найдется точка с
внутри этого отрезка такая, что f
(с
) = С
. Прямая у
= С
пересечет график функции по крайней мере в одной точке.

Следствие.
Если функция у
= f
(x
) непрерывна на отрезке [а
; b
] и на его концах принимает значения разных знаков, то внутри отрезка [а
; b
] найдется хотя бы одна точка с
, в которой данная функция f
(x
) обращается в нуль: f
(с
) = 0.

Геометрический смысл теоремы: если график непрерывной функции переходит с одной стороны оси Ох
на другую, то он пересекает ось Ox
(см. рис. 7).

Рис. 7.

Определение
3
.
3

Пусть —
некоторая функция, —
её область определения и —
некоторый (открытый) интервал (может
быть, с и/или ) 7
.
Назовём функцию непрерывной
на интервале
,
если непрерывна
в любой точке ,
то есть для любого существует (в
сокращённой записи:

Пусть
теперь —
(замкнутый) отрезок в .
Назовём функцию непрерывной
на отрезке
,
если непрерывна
на интервале ,
непрерывна справа в точке и
непрерывна слева в точке ,
то есть

Пример
3
.
13

Рассмотрим функцию (функция
Хевисайда
) на
отрезке , .
Тогда непрерывна
на отрезке (несмотря
на то, что в точке она
имеет разрыв первого рода).

Рис.3.15.График
функции Хевисайда

Аналогичное
определение можно дать и для полуинтервалов
вида и ,
включая случаи и .
Однако можно обобщить данное определение
на случай произвольного подмножества следующим
образом. Введём сначала
понятие индуцированной
на базы:
пусть —
база, все окончания которой
имеют непустые пересечения с .
Обозначим через и
рассмотрим множество всех .
Нетрудно тогда проверить, что
множество будет
базой. Тем самым для определены
базы , и ,
где , и —
базы непроколотых двусторонних
(соответственно левых, правых) окрестностей
точки (их
определение см. в начале текущей главы).

Определение
3
.
4

Назовём функцию непрерывной
на множестве
,
если

Нетрудно
видеть, что тогда при и
при это
определение совпадает с теми, что были
выше даны специально для интервала и
отрезка.

Напомним,
что все элементарные функции непрерывны
во всех точках своих областей определения
и, следовательно, непрерывны на любых
интервалах и отрезках, лежащих в их
областях определения.

Поскольку
непрерывность на интервале и отрезке
определяется поточечно, имеет место
теорема, которая является непосредственным
следствием теоремы
3.1:

Теорема
3
.
5
Пусть

и

—
функции и

—
интервал или отрезок, лежащий в

.
Пусть

и

непрерывны
на

.
Тогда функции
,
,
непpеpывны
на

.
Если вдобавок

пpи
всех

,
то функция

также
непpеpывна на

.

Из
этой теоpемы вытекает следующее
утвеpждение, точно так же, как из
теоpемы 3.1 —
пpедложение 3.3:

Предложение
3
.
4
Множество

всех
функций, непpеpывных на интеpвале или
отpезке

—
это линейное пpостpанство:

Более
сложное свойство непрерывной функции
выражает следующая теорема.

Теорема
3
.
6
(о
корне непрерывной функции) Пусть
функция

непрерывна
на отрезке

,
причём

и

—
числа разных знаков. (Будем для
определённости считать, что

,
а

.)
Тогда существует хотя бы одно такое
значение

,
что

(то
есть существует хотя бы один
корень

уравнения

).

Доказательство
.
Рассмотрим середину отрезка .
Тогда либо ,
либо ,
либо .
В первом случае корень найден: это .
В остальных двух случаях рассмотрим ту
часть отрезка, на концах которой
функция принимает
значения разных знаков: в
случае или в
случае .
Выбранную половину отрезка обозначим
через и
применим к ней ту же процедуру: разделим
на две половины и ,
где ,
и найдём .
В случае корень
найден; в случае рассматриваем
далее отрезок ,
в случае —
отрезок и
т. д.

Рис.3.16.Последовательные
деления отрезка пополам

Получаем,
что либо на некотором шаге будет найден
корень ,
либо будет построена система вложенных
отрезков

в
которой каждый следующий отрезок вдвое
короче предыдущего. Последовательность —
неубывающая и ограниченная сверху
(например, числом );
следовательно (по теореме
2.13),
она имеет предел .
Последовательность —
невозрастающая и ограниченная снизу
(например, числом );
значит, существует предел .
Поскольку длины отрезков образуют
убывающую геометрическую прогрессию
(со знаменателем ),
то они стремятся к 0, и ,
то есть .
Положим теперь .
Тогда

поскольку
функция непрерывна.
Однако, по построению
последовательностей и , и ,
так что, по теореме о переходе к пределу
в неравенстве (теорема 2.7), и ,
то есть и .
Значит, ,
и —
корень уравнения .

Пример
3
.
14

Рассмотрим функцию на
отрезке .
Поскольку и —
числа разных знаков, то функция обращается
в 0 в некоторой точке интервала .
Это означает, что уравнение имеет
корень .

Рис.3.17.Графическое
представление корня уравнения

Доказанная теорема фактически
даёт нам способ нахождения корня ,
хотя бы приближённого, с любой заданной
наперёд степенью точности. Это —
метод деления отрезка пополам, описанный
при доказательстве теоремы. Более
подробно с этим и другими, более
эффективными, способами приближённого
нахождения корня мы познакомимся ниже,
после того, как изучим понятие и свойства
производной.

Заметим, что теорема не
утверждает, что если её условия выполнены,
то корень —
единственный. Как показывает следующий
рисунок, корней может быть и больше
одного (на рисунке их 3).

Рис.3.18.Несколько
корней функции, принимающей значения
разных знаков в концах отрезка

Однако, если функция монотонно
возрастает или монотонно убывает на
отрезке, в концах которого принимает
значения разных знаков, то корень —
единственный, так как строго монотонная
функция каждое своё значение принимает
ровно в одной точке, в том числе и значение
0.

Рис.3.19.Монотонная
функция не может иметь более одного
корня

Непосредственным
следствием теоремы о корне непрерывной
функции является следующая теорема,
которая и сама по себе имеет очень важное
значение в математическом анализе.

Теорема
3
.
7
(о
промежуточном значении непрерывной
функции) Пусть
функция

непрерывна
на отрезке

и

(будем
для определённости считать, что

).
Пусть

—
некоторое число, лежащее между

и

.
Тогда существует такая точка

,
что

.

Рис.3.20.Непрерывная
функция принимает любое промежуточное
значение

Доказательство
.
Рассмотрим вспомогательную функцию ,
где .
Тогда и .
Функция ,
очевидно, непрерывна, и по предыдущей
теореме существует такая точка ,
что .
Но это равенство означает, что .

Заметим,
что если функция не является непрерывной,
то она может принимать не все промежуточные
значения. Например, функция
Хевисайда (см. пример
3.13) принимает
значения , ,
но нигде, в том числе и на интервале ,
не принимает, скажем, промежуточного
значения .
Дело в том, что функция Хевисайда имеет
разрыв в точке ,
лежащей как раз в интервале .

Для
дальнейшего изучения свойств функций,
непрерывных на отрезке, нам понадобится
следующее тонкое свойство системы
вещественных чисел (мы уже упоминали
его в главе 2 в связи с теоремой о пределе
монотонно возрастающей ограниченной
функции): для любого ограниченного снизу
множества (то
есть такого, что при
всех и
некотором ;
число называется нижней
гранью
множества )
имеется точная
нижняя грань
,
то есть наибольшее из чисел ,
таких что при
всех .
Аналогично, если множество ограничено
сверху, то оно имеет точную
верхнюю грань
:
это наименьшая из верхних
граней
(для
которых при
всех ).

Рис.3.21.Нижняя
и верхняя грани ограниченного множества

Если ,
то существует невозрастающая
последовательность точек ,
которая стремится к .
Точно так же если ,
то существует неубывающая последовательность
точек ,
которая стремится к .

Если
точка принадлежит
множеству ,
то является
наименьшим элементом этого множества: ;
аналогично, если ,
то .

Кроме
того, для дальнейшего нам понадобится
следующая

Лемма
3
.
1
Пусть

—
непрерывная функция на отрезке

,
и множество

тех
точек

,
в которых

(или

,
или

)
не пусто. Тогда в множестве

имеется
наименьшее значение

,
такое что

при
всех

.

Рис.3.22.Наименьший
аргумент, при котором функция принимает
заданное значение

Доказательство
.
Поскольку —
ограниченное множество (это часть
отрезка ),
то оно имеет точную нижнюю грань .
Тогда существует невозрастающая
последовательность , ,
такая что при .
При этом ,
по определению множества .
Поэтому, переходя к пределу, получаем,
с одной стороны,

а
с другой стороны, вследствие непрерывности
функции ,

Значит, ,
так что точка принадлежит
множеству и .

В
случае, когда множество задано
неравенством ,
мы имеем при
всех и
по теореме о переходе к пределу в
неравенстве получаем

откуда ,
что означает, что и .
Точно так же в случае неравенства переход
к пределу в неравенстве даёт

откуда , и .

Теорема
3
.
8
(об
ограниченности непрерывной функции)
Пусть
функция

непрерывна
на отрезке

.
Тогда

ограничена
на

,
то есть существует такая постоянная

,
что

при
всех

.

Рис.3.23.Непрерывная
на отрезке функция ограничена

Доказательство
.
Предположим обратное: пусть не
ограничена, например, сверху. Тогда все
множества , , ,
не пусты. По предыдущей лемме в каждом
из этих множеств имеется
наименьшее значение , .
Покажем, что

Действительно, .
Если какая-либо точка из ,
например ,
лежит между и ,
то

то
есть —
промежуточное значение между и .
Значит, по теореме о промежуточном
значении непрерывной функции, существует
точка ,
такая что ,
и .
Но ,
вопреки предположению о том, что —
наименьшее значение из множества .
Отсюда следует, что при
всех .

Точно
так же далее доказывается, что при
всех , при
всех ,
и т. д. Итак, —
возрастающая последовательность,
ограниченная сверху числом .
Поэтому существует .
Из непрерывности функции следует,
что существует ,
но при ,
так что предела не существует. Полученное
противоречие доказывает, что
функция ограничена
сверху.

Аналогично
доказывается, что ограничена
снизу, откуда следует утверждение
теоремы.

Очевидно,
что ослабить условия теоремы нельзя:
если функция не является непрерывной,
то она не обязана быть ограниченной на
отрезке (приведём в качестве примера
функцию

на
отрезке .
Эта функция не ограничена на отрезке,
так как при имеет
точку разрыва второго рода, такую
что при .
Также нельзя заменить в условии теоремы
отрезок интервалом или полуинтервалом:
в качестве примера рассмотрим ту же
функцию на
полуинтервале .
Функция непрерывна на этом полуинтервале,
но неограничена, вследствие того
что при .

Поиск
наилучших постоянных, которыми можно
ограничить функцию сверху и снизу на
заданном отрезке, естественным образом
приводит нас к задаче об отыскании
минимума и максимума непрерывной функции
на этом отрезке. Возможность решения
этой задачи описывается следующей
теоремой.

Теорема
3
.
9
(о
достижении экстремума непрерывной
функцией) Пусть
функция

непрерывна
на отрезке

.
Тогда существует точка

,
такая что

при
всех

(то
есть

—
точка минимума:
),
и существует точка

,
такая что
при
всех

(то
есть

—
точка максимума:
).
Иными словами, минимальное и
максимальное
8

значения
непрерывной функции на отрезке существуют
и достигаются в некоторых точках

и

этого
отрезка.

Рис.3.24.Непрерывная
на отрезке функция достигает максимума
и минимума

Доказательство
.
Так как по предыдущей теореме
функция ограничена
на сверху,
то существует точная верхняя грань
значений функции на —
число .
Тем самым, множества , ,…, ,…,
не пусты, и по предыдущей лемме в них
есть наименьшие значения : , .
Эти не
убывают (доказывается это утверждение
точно так же, как в предыдущей теореме):

и
ограничены сверху числом .
Поэтому, по теореме о пределе монотонной
ограниченной последовательности,
существует предел Так
как ,
то и

по
теореме о переходе к пределу в неравенстве,
то есть .
Но при всех ,
и в том числе .
Отсюда получается, что ,
то есть максимум функции достигается
в точке .

Аналогично
доказывается существование точки
минимума.

В
этой теореме, как и в предыдущей, нельзя
ослабить условия: если функция не
является непрерывной, то она может не
достигать своего максимального или
минимального значения на отрезке, даже
будучи ограниченной. Для примера возьмём
функцию

на
отрезке .
Эта функция ограничена на отрезке
(очевидно, что )
и ,
однако значение 1 она не принимает
ни в одной точке отрезка (заметим, что ,
а не 1). Дело в том, что эта функция имеет
разрыв первого рода в точке ,
так что при предел не
равен значению функции в точке 0.
Далее, непрерывная функция, заданная
на интервале или другом множестве, не
являющемся замкнутым отрезком (на
полуинтервале, полуоси) также может не
принимать экстремального значения. В
качестве примера рассмотрим функцию на
интервале .
Очевидно, что функция непрерывна и
что и ,
однако ни значения 0, ни значения 1
функция не принимает ни в какой точке
интервала .
Рассмотрим также функцию на
полуоси .
Эта функция непрерывна на ,
возрастает, принимает своё минимальное
значение 0 в точке ,
но не принимает ни в какой точке
максимального значения (хотя ограничена
сверху числом и

Определение

Пусть функция `y=f(x)` определена на некотором интервале, содержащем точку `ainR`. Точка `a` называется точкой локального максимума
функции `f`, если существует `epsilon` — окрестность точки `a` что для любого `x!=a` из этой окрестности `f(x)

Если выполнено неравенство `f(x)>f(a)`, то `a` называется точкой локального минимума
функции `f`.

Точки локального максимума и локального минимума называют точками локального экстремума.

Теорема 5.1 (Ферма)

Если точка `a` является точкой локального экстремума функции `y=f(x)` и функция `f` имеет производную в этой точке, то `f^»(a)=0`.

Физический смысл: при одномерном движении с возвращением в точке максимального удаления должна быть остановка. Геометрический смысл: касательная в точке локального экстремума горизонтальна.

Замечание.

Из теоремы Ферма следует, что если функция имеет экстремум в точке `a`, то в этой точке производная функции либо равна нулю, либо не существует. Например, функция `y=|x|` имеет минимум в точке `x=0`, а производная в этой точке не существует (см. пример 4.2). Точки, в которых функция определена, а производная равна нулю или не существует, будем называть критическими
.

Итак, если у функции имеются точки экстремума, то они лежат среди критических точек (критические точки «подозрительны» на экстремум). Для формулировки условий, обеспечивающих наличие экстремума в критической точке, нам потребуется следующее понятие.

Напомним, что под промежутком понимается интервал (конечный или бесконечный), полуинтервал или отрезок числовой прямой.

Определение

Пусть функция `y=f(x)` определена на промежутке `I`.

1) Функция `y=f(x)` возрастает

2) Функция `y=f(x)` убывает
на `I`, если для любых `x,yinI`, `xf(y)`.

Если функция возрастает или убывает на `I`, то говорят, что функция монотонна
на промежутке `I`.

Условия монотонности
. Пусть функция `y=f(x)` определена на промежутке `I` с концами `a`, `b`, дифференцируема на `(a, b)` и непрерывна в концах, если они принадлежат `I`. Тогда

1) если `f^»(x)>0` на `(a, b)`, то функция возрастает на `I`;

2) если `f^»(x)<0` на `(a, b)`, то функция убывает на `I`.

Условия экстремума
. Пусть функция `y=f(x)` определена на интервале `(ab)`, непрерывна в точке `x_0 in(a, b)` и дифференцируема на `(a,x_0) uu (x_0,b)`. Тогда

1) если `f^»(x)>0` на `(a;x_0)` и `f^»(x)<0` на `(x_0;b)`, то `x_0` — точка локального максимума функции `f`;

2) если `f^»(x)<0` на `(a;x_0)` и `f^»(x)>0` на `(x_0;b)`, то `x_0` — точка локального минимума функции `f`.

Пример 5.1

Исследовать функцию `y=x^3-3x` на монотонность и экстремумы на области определения.

Данная функция определена на `R` и дифференцируема в каждой точке (см. следствие теоремы 4.2), причём `y^»=3(x^2-1)`. Так как `y^»<0` при `x in(-1,1)`; `y^»>0` при `x in(-oo,-1)uu(1,+oo)`, то функция возрастает на лучах `(-oo,-1]` и «. По условию экстремума `x=-1` — точка локального максимума, а `x=1` — точка локального минимума. Так как `y^»=0` только в точках `x=1` и `x=-1`, то по теореме Ферма других точек экстремума у функции нет.

Рассмотрим важный класс задач, в которых используется понятие производной — задачи нахождения наибольшего и наименьшего значения функции на отрезке.

Пример 5.2

Найти наибольшее и наименьшее значение функции `y=x^3-3x` на отрезке: а) `[-2;0]`; б) «.

а) Из примера 5.1 следует, что функция возрастает на `(-oo,-1]` и убывает на `[-1,1]`. Так что `y(-1)>=y(x)` при всех `x in[-2;0]` и `y_»наиб»=y(-1)=2` — наибольшее значение функции на отрезке `[-2;0]`. Чтобы найти наименьшее значение, нужно сравнить значения функции на концах отрезка. Поскольку `y(-2)=-2`, а `y(0)=0`, то `y_»наим»=-2` — наименьшее значение функции на отрезке `[-2;0]`.

б) Так как на луче «, поэтому `y_»наим»=y(1)=-2`, `y_»наиб»=y(3)=18`.

Замечание

Отметим, что непрерывная на отрезке функция всегда имеет наибольшее и наименьшее значение.

Пример 5.3

Найти наибольшее и наименьшее значение функции `y=x^3-12|x+1|` на отрезке `[-4;3]`.

Отметим, что функция непрерывна на всей числовой прямой. Обозначим `f_1(x)=x^3+12(x+1)`, `f_2(x)=x^3-12(x+1)`. Тогда `y=f_1(x)` при `-4<=x<=-1` и `y=f_2(x)` при `-1<=x<=3`. Находим `f_1^»(x)=3x^2+12`, `f_2^»(x)=3x^2-12`. Уравнение `f_1^»(x)=0` не имеет действительных корней, а уравнение `f_2^»(x)=0` имеет два действительных корня `x_1=-2`, `x_2=2`, из которых интервалу `(-1;3)` принадлежит только точка `x_2`. В точке `x=-1` функция определена, но не имеет производной (можно, например, провести рассуждения, аналогичные рассуждениям примера 4.2). Итак, имеется две критические точки: `x=-1` и `x=2`. Производная `y^»(x)=f_1^»(x)>0` на `(-4;-1)`, `y^»(x)=f_2^»(x)<0` на `(-1;2)` и `y^»(x)=f_2^»(x)>0` на `(2;3)`. Запишем все исследования в таблице:

`y_»наиб»=-1`; `y_»наим»=-100`.

Непрерывность функции на отрезке.

Наряду с непрерывностью функции в точке рассматривают ее непрерывность на разных промежутках.

Функция f (x) называется непрерывной на интервале (a , b), если она непрерывна в каждой точке этого интервала.

Функция f (x) называется непрерывной на отрезке [ a , b ], если она непрерывна на интервале (a , b), непрерывна справа в точке a и непрерывна слева в точке b .

Функция
называется
непрерывной на отрезке
, если она является непрерывной в интервале
, непрерывной справа в точке
, то есть
и непрерывной слева в точке
, то есть
.

Замечание.
Функция, непрерывная на отрезке [ a , b ] может быть разрывной в точках a и b (рис. 1)

Множество функций, непрерывных на отрезке [ a , b ] обозначается символом C [ a , b ].

Основные теоремы о функциях, непрерывных на отрезке.

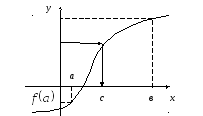
Теорема 1
( об ограниченности непрерывной функции ).
Если функция f (x) непрерывна на отрезке [ a , b ], то она ограничена на этом отрезке, т.е. существует такое число C > 0, что »
x О
[ a , b ] выполняется неравенство | f (x)| ≤ C .

Теорема 2
(Вейерштрасс). Если функция f (x) непрерывна на отрезке [ a , b ], то она достигает на этом отрезке своего наибольшего значения M и наименьшего значения m , т.е. существуют точки α , β О
[ a , b ] такие, что m = f (α) ≤ f (x) ≤ f (β) = M для всех x О
[ a , b ] (рис.2).

Наибольшее значение M обозначается символом max x О
[ a , b ]
f (x), а наименьшее значение m — символом min x О
[ a , b ]
f (x).
Теорема 3
(о существовании нуля). Если функция f (x) непрерывна на отрезке [ a , b ] и на концах отрезка принимает ненулевые значения разных знаков, то на интервале (a , b) найдется по крайней мере одна точка ξ в которой f (ξ) = 0.

Геометрический смысл теоремы состоит в том, что график функции, удовлетворяющей условиям теоремы, обязательно пересечет ось OX
(рис.3).

Замечание.
На этой теореме основан метод приближенного решения уравнения

называемый методом бисекции (дихотомии) , или методом половинного деления.

Теорема 4
(Больцано–Коши). Если функция f (x) непрерывна на отрезке [ a , b ], то она принимает на (a , b) все промежуточные значения между f (a) и f (b).

Cуществование непрерывной обратной функции
Пусть функция y = f (x) определена, строго монотонна и непрерывна на отрезке [ a , b ]. Тогда на отрезке [ α , β ] (α = f (a), β = f (b)) cуществует обратная функция x = g (y), также строго монотонная и непрерывная на отрезке (α , β).

Источник