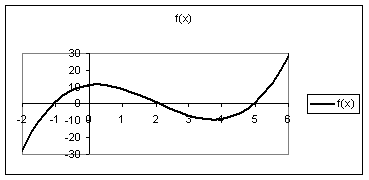
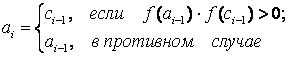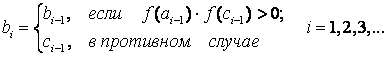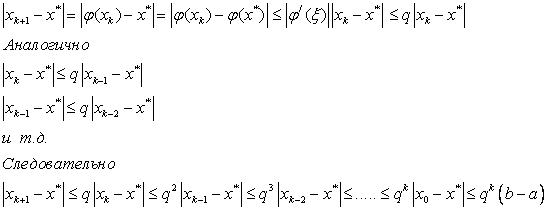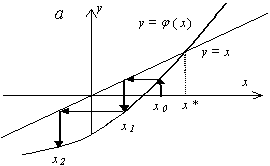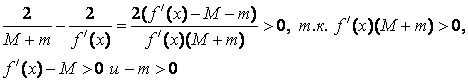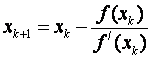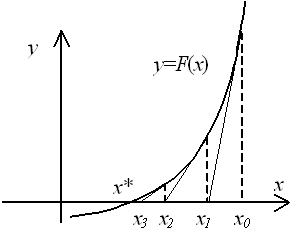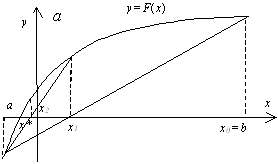Корень нелинейной функции
Синтаксис
Описание
пример
x = fzero(fun,x0)x где fun(x) = 0. Это решение состоит в том где fun(x) изменяет знак — fzero не может найти корень функции, такой как x^2.
пример
x = fzero(fun,x0,options)options изменить процесс решения.
пример
x = fzero(problem)problem.
пример
[ возвращает x,fval,exitflag,output]
= fzero(___)fun(x) в fval выведите, exitflag кодирование причины fzero остановленный, и структура output, содержащая информацию о процессе решения.
Примеры
свернуть все
Корень, начинающий с одной точки
Вычислить π путем нахождения нуля синусоидальной функции около 3.
fun = @sin; % function x0 = 3; % initial point x = fzero(fun,x0)
Корень, начинающий с интервала
Найдите нуль косинуса между 1 и 2.
fun = @cos; % function x0 = [1 2]; % initial interval x = fzero(fun,x0)
Обратите внимание на то, что cos(1) и cos(2) отличайтесь по знаку.
Корень функции, определяемой файлом
Найдите нуль функционального f (x) = x3 – 2x – 5.
Во-первых, запишите файл под названием f.m.
function y = f(x)
y = x.^3-2*x-5;
Сохраните f.m на вашем MATLAB® path.
Найдите нуль f (x) около 2.
fun = @f; % function x0 = 2; % initial point z = fzero(fun,x0)
Начиная с f(x) полином, можно найти тот же действительный нуль и комплексно-сопряженную пару нулей, с помощью roots команда.
ans = 2.0946 -1.0473 + 1.1359i -1.0473 - 1.1359i
Корень функции с дополнительным параметром
Найдите корень функции, которая имеет дополнительный параметр.
myfun = @(x,c) cos(c*x); % parameterized function c = 2; % parameter fun = @(x) myfun(x,c); % function of x alone x = fzero(fun,0.1)
Опции не по умолчанию
Постройте процесс решения путем установки некоторых функций построения графика.
Задайте функциональную и начальную точку.
fun = @(x)sin(cosh(x)); x0 = 1;
Исследуйте процесс решения путем установки опций, которые включают функции построения графика.
options = optimset('PlotFcns',{@optimplotx,@optimplotfval});
Запустите fzero включая options.
x = fzero(fun,x0,options)
Решение проблемной структуры
Решите задачу, которая описана структурой задачи.
Задайте структуру, которая кодирует находящую корень проблему.
problem.objective = @(x)sin(cosh(x)); problem.x0 = 1; problem.solver = 'fzero'; % a required part of the structure problem.options = optimset(@fzero); % default options
Решите задачу.
Больше информации из решения
Найдите точку где exp(-exp(-x)) = x, и отобразите информацию о процессе решения.
fun = @(x) exp(-exp(-x)) - x; % function x0 = [0 1]; % initial interval options = optimset('Display','iter'); % show iterations [x fval exitflag output] = fzero(fun,x0,options)
Func-count x f(x) Procedure
2 1 -0.307799 initial
3 0.544459 0.0153522 interpolation
4 0.566101 0.00070708 interpolation
5 0.567143 -1.40255e-08 interpolation
6 0.567143 1.50013e-12 interpolation
7 0.567143 0 interpolation
Zero found in the interval [0, 1]
output = struct with fields:
intervaliterations: 0
iterations: 5
funcCount: 7
algorithm: 'bisection, interpolation'
message: 'Zero found in the interval [0, 1]'
fval = 0 средних значений fun(x) = 0, как желаемый.
Входные параметры
свернуть все
fun — Функция, чтобы решить
указатель на функцию | имя функции
Функция, чтобы решить в виде указателя на скалярную функцию или имя такой функции. fun принимает скалярный x и возвращает скалярный fun(x).
fzero решает fun(x) = 0. Решить уравнение fun(x) = c(x), вместо этого решите fun2(x) = fun(x) - c(x) = 0.
Чтобы включать дополнительные параметры в вашу функцию, смотрите Корень в качестве примера Функции Дополнительным Параметром и разделом Passing Extra Parameters.
Пример: 'sin'
Пример: @myFunction
Пример: @(x)(x-a)^5 - 3*x + a - 1
Типы данных: char | function_handle | string
x0 — Начальное значение
скаляр | вектор с 2 элементами
Начальное значение в виде действительного скаляра или вектора действительных чисел с 2 элементами.
-
Скаляр —
fzeroначинается вx0и попытки определить местоположение точкиx1гдеfun(x1)имеет противоположный знакfun(x0). Затемfzeroитеративно уменьшает интервал гдеfunизменяет знак, чтобы достигнуть решения. -
Вектор с 2 элементами —
fzeroпроверки, чтоfun(x0(1))иfun(x0(2))имейте противоположные знаки и ошибки, если они не делают. Это затем итеративно уменьшает интервал гдеfunизменяет знак, чтобы достигнуть решения. Интервалx0mustBeFinite; это не может содержать ±Inf.
Совет
Вызов fzero с интервалом (x0 с двумя элементами), часто быстрее, чем вызов его со скалярным x0.
Пример 3
Пример: [2,17]
Типы данных: double
options — Опции для процесса решения
структура, обычно созданное использование optimset
Опции для процесса решения в виде структуры. Создайте или измените options использование структуры optimsetfzero использование они options поля структуры.
|
|
Level of display (см. Итеративное Отображение):
|
|
|
Проверяйте, допустимы ли значения целевой функции.
|
|
|
Задайте одну или несколько пользовательских функций, которые оптимизационная функция вызывает на каждой итерации, или как указатель на функцию или как cell-массив указателей на функцию. Значение по умолчанию не ни один ( |
|
|
Постройте различные показатели прогресса, в то время как алгоритм выполняется. Выберите из предопределенных графиков или запишите свое собственное. Передайте указатель на функцию или cell-массив указателей на функцию. Значение по умолчанию не ни один (
Пользовательские функции построения графика используют тот же синтаксис в качестве выходных функций. Смотрите Выходные функции для Optimization Toolbox™ и Синтаксис Функции построения графика и Выходную функцию. |
|
|
Допуск завершения на |
Пример: options = optimset('FunValCheck','on')
Типы данных: struct
problem — Находящая корень проблема
структура
Находящая корень проблема в виде структуры со всеми следующими полями.
|
|
Целевая функция |
|
|
Начальная точка для x, скалярный или 2D вектор |
|
|
'fzero' |
|
|
Структура опций, обычно созданное использование optimset |
Типы данных: struct
Выходные аргументы
свернуть все
x — Местоположение корня или изменения знака
действительный скаляр
Местоположение корня или изменения знака, возвращенного как скаляр.
fval — Значение функции в x
действительный скаляр
Значение функции в x, возвращенный как скаляр.
exitflag — Целое число, кодирующее выходное условие
целое число
Целое число, кодирующее выходное условие, означая причину fzero остановленный его итерации.
|
1 |
Функция сходилась к решению |
|
-1 |
Алгоритм был отключен выходной функцией или функцией построения графика. |
|
-3 |
|
-4 |
Со значением комплексной функции столкнулись при поиске интервала, содержащего изменение знака. |
-5 |
Алгоритм может сходиться к особой точке. |
-6 |
|
output — Информация о находящем корень процессе
структура
Информация о находящем корень процессе, возвращенном как структура. Поля структуры:
intervaliterations |
Количество проделанных итераций, чтобы найти интервал, содержащий корень |
iterations |
Количество находящих нуль итераций |
funcCount |
Количество вычислений функции |
algorithm |
|
message |
Выходное сообщение |
Алгоритмы
fzero команда является файлом функции. Алгоритм, созданный Т. Деккером, использует комбинацию деления пополам, секанса и обратных квадратичных методов интерполяции. Алгол 60 версий, с некоторыми улучшениями, дан в [1]. Версия Фортрана, на который fzero базируется, находится в [2].
Альтернативная функциональность
Приложение
Оптимизировать задача Live Editor обеспечивает визуальный интерфейс для fzero.
Ссылки
[1] Брент, R., алгоритмы для минимизации без производных, Prentice Hall, 1973.
[2] Форсайт, G. E. М. А. Малкольм, и К. Б. Молер, компьютерные методы для математических вычислений, Prentice Hall, 1976.
Расширенные возможности
Генерация кода C/C++
Генерация кода C и C++ с помощью MATLAB® Coder™.
Для генерации кода C/C++:
-
funвходной параметр должен быть указателем на функцию, и не структурой или вектором символов. -
fzeroигнорирует все опции за исключениемTolXиFunValCheck. -
fzeroне поддерживает четвертый выходной аргумент, структуру output.
Представлено до R2006a
№70 Анализ переходных процессов в цепи R, L, C.
Переходные процессы в цепи R, L, C описываются дифференциальным уравнением 2-го порядка. Установившиеся составляющие токов и напряжений определяются видом источника энергии и определяются известными методами расчета установившихся режимов. Наибольший теоретический интерес представляют свободные составляющие, так как характер свободного процесса оказывается существенно различным в зависимости от того, являются ли корни характеристического уравнения вещественными или комплексными сопряженными.
Проанализируем переходной процесс в цепи R, L, C при включении ее к источнику постоянной ЭДС (рис. 70.1).
Общий вид решения для тока: i(t)=iy(t)+iсв(t)=Iy+A1ep2t+A2ep2t
Установившаяся составляющая: Iy=0
Характеристическое уравнение и его корни:
Независимые начальные условия: i(0)=0; uc(0)=0.
Зависимое начальное условие:
Постоянные интегрирования определяется из соместного решения системы уравнений:
Окончательное решение для тока:
Исследуем вид функции i(t) при различных значениях корней характеристического уравнения.
а) Корни характеристического уравнения вещественные, не равны друг другу.
Это имеет место при условии:

При изменении t от 0 до ∞ отдельные функции ep1t и ep2t убывают по экспоненциальному закону от 1 до 0, причем вторая из них убывает быстрее, при этом их разность ep1t — ep2t ≥ 0. Из этого следует вывод, что искомая функция тока i(t) в крайних точках при t = 0 и при t = ∞ равна нулю, а в промежутке времени 0
4.4. Переходные процессы в RLC-цепях
4.4. Переходные процессы в RLC-цепях
Рассмотрим переходные процессы в RLC-цепях на примере цепи последовательного колебательного контура рис. 4.3,а, потери в котором будем учитывать путем включения в цепь резистораR.
Рис.4.3. RLC-цепь (а) и переходные процессы в ней (б) и (в).
Переходные процессы в последовательном колебательном контуре при нулевых начальных условиях. Установим ключ К в положение 1, и подключим входное воздействие к контуру. Под действием подключенного источника u в контуре потечет ток i, который создаст напряжения uR, uL, uC .
На основании второго закона Кирхгофа для этого контура можно записать следующее уравнение

Учитывая, что 

Общее решение уравнения (4.34) будем искать в виде суммы свободной uС св и принужденной uС пр составляющих:

Свободная составляющая определяется решением однородного дифференциального уравнения, которое получается из (4.34) при u = 0

Решение (4.36) зависит от корней характеристического уравнения, которое получается из (4.36) и имеет вид

Корни этого уравнения определяются только параметрами цепи R, L ,C и равны

где α = R/2L – коэффициент затухания контура;

Из (4.38) видно, что корни р1 и р2 зависят от характеристического сопротивления контура 
при R > 2ρ вещественными и различными;
при R 2ρ свободная составляющая будет равна:

Пусть входное воздействие u = U = const, тогда принужденная составляющая uпр = U. Учитывая выражение (4.39) и что uпр = U выражение (4.35) примет вид:

Зная uС находим ток в контуре

Для определения постоянных интегрирования А1 и А2 запишем начальные условия для uC и i при t = 0:

Решая систему уравнений (4.42) получаем:


Подставляя А1 и А2 в уравнения (4.40) и (4.41) и учитывая, что в соответствии с (4.38) p1 p2=1/LC будем иметь:


Так как 

Графики изменения uС, i, uL в последовательном колебательном контуре при условии R > 2ρ приведены на рис. 4.3,б).
Моменты времени t1 и t2 определяются соответственно из условий



Анализ графиков, описываемых выражениями (4.43 – 4.45) показывает, что при R > 2ρ (при больших потерях) в контуре происходят апериодические процессы.
Рассмотрим процессы в контуре при R 2ρ, то корни р1 и р2 в (4.38) будут вещественны и различны и решение уравнения (4.36) будет иметь вид

Напряжение uC создает ток в цепи

Для определения постоянных интегрирования А1 и А2 положим t = 0 и учтем, что на момент коммутации uC = U, i = 0, тогда из (4.54) и (4.55) получим

Решая систему уравнений (4.56) находим


Подставляя А1 и А2 в (4.54) и (4.55) получаем уравнения для напряжения uC и тока i в цепи контура


Из выражений (4.57) и (4.58) видно, что при отключении входного воздействия от цепи контура, который имеет большое затухание (R > 2ρ) происходит апериодический разряд емкости С. Запасенная до отключения входного воздействия энергия в емкости WС = CU2/2 расходуется на покрытие тепловых потерь в резисторе R и создания магнитного поля в индуктивности L. Затем энергия электрического поля емкости WС и магнитная энергия индуктивности WL расходуется в резисторе R.
Найдем закон изменения напряжения uC и тока i в цепи, когда контур обладает малыми потерями, т.е. при условии R
Как найти корни характеристического уравнения rlc цепь
Характеристическое уравнение составляется для цепи после коммутации. Оно может быть получено следующими способами:
- непосредственно на основе дифференциального уравнения вида (2) (см. лекцию №24), т.е. путем исключения из системы уравнений, описывающих электромагнитное состояние цепи на основании первого и второго законов Кирхгофа, всех неизвестных величин, кроме одной, относительно которой и записывается уравнение (2);
- путем использования выражения для входного сопротивления цепи на синусоидальном токе;
- на основе выражения главного определителя.
Согласно первому способу в предыдущей лекции было получено дифференциальное уравнение относительно напряжения 
Следует отметить, что, поскольку линейная цепь охвачена единым переходным процессом, корни характеристического уравнения являются общими для всех свободных составляющих напряжений и токов ветвей схемы, параметры которых входят в характеристическое уравнение. Поэтому по первому способу составления характеристического уравнения в качестве переменной, относительно которой оно записывается, может быть выбрана любая.
Применение второго и третьего способов составления характеристического уравнения рассмотрим на примере цепи рис. 1.
Составление характеристического уравнения по методу входного сопротивления заключается в следующем:
записывается входное сопротивление цепи на переменном токе;
j w заменяется на оператор р;
полученное выражение 
совпадает с характеристическим.
Следует подчеркнуть, что входное сопротивление может быть записано относительно места разрыва любой ветви схемы. При этом активный двухполюсник заменяется пассивным по аналогии с методом эквивалентного генератора. Данный способ составления характеристического уравнения предполагает отсутствие в схеме магнитосвязанных ветвей; при наличии таковых необходимо осуществить их предварительное развязывание.
Для цепи на рис. 1 относительно зажимов источника

Заменив j w на р и приравняв полученное выражение к нулю, запишем
 . . |
(1) |
При составлении характеристического уравнения на основе выражения главного определителя число алгебраических уравнений, на базе которых он записывается, равно числу неизвестных свободных составляющих токов. Алгебраизация исходной системы интегро-дифференциальных уравнений, составленных, например, на основании законов Кирхгофа или по методу контурных токов, осуществляется заменой символов дифференцирования и интегрирования соответственно на умножение и деление на оператор р. Характеристическое уравнение получается путем приравнивания записанного определителя к нулю. Поскольку выражение для главного определителя не зависит от правых частей системы неоднородных уравнений, его составление можно производить на основе системы уравнений, записанных для полных токов.
Для цепи на рис. 1 алгебраизованная система уравнений на основе метода контурных токов имеет вид
Отсюда выражение для главного определителя этой системы

Приравняв D к нулю, получим результат, аналогичный (1).
Общая методика расчета переходных процессов классическим методом
В общем случае методика расчета переходных процессов классическим методом включает следующие этапы:
- Запись выражения для искомой переменной в виде
.
(2) - Нахождение принужденной составляющей общего решения на основании расчета установившегося режима послекоммутационной цепи.
- Составление характеристического уравнения и определение его корней (для цепей, описываемых дифференциальными уравнениями первого порядка, вместо корней можно находить постоянную времени t — см. лекцию №26). Запись выражения свободной составляющей в форме, определяемой типом найденных корней.
- Подстановка полученных выражений принужденной и свободной составляющих в соотношение (2).
- Определение начальных условий и на их основе – постоянных интегрирования.
Примеры расчета переходных процессов классическим методом
1. Переходные процессы в R-L цепи при ее подключении к источнику напряжения
Такие процессы имеют место, например, при подключении к источнику питания электромагнитов, трансформаторов, электрических двигателей и т.п.
Рассмотрим два случая:
а)
б) 
Согласно рассмотренной методике для тока в цепи на рис. 2 можно записать
 . . |
(3) |
Тогда для первого случая принужденная составляющая тока
 . . |
(4) |

откуда 

 . . |
(5) |
Подставляя (4) и (5) в соотношение (3), запишем

В соответствии с первым законом коммутации 

откуда 
Таким образом, ток в цепи в переходном процессе описывается уравнением

а напряжение на катушке индуктивности – выражением

Качественный вид кривых 

При втором типе источника принужденная составляющая рассчитывается с использованием символического метода:

где 

Выражение свободной составляющей не зависит от типа источника напряжения. Следовательно,

Поскольку 

Таким образом, окончательно получаем
 . . |
(6) |
Анализ полученного выражения (6) показывает:
- При начальной фазе напряжения
постоянная интегрирования А=0. Таким образом, в этом случае коммутация не повлечет за собой переходного процесса, и в цепи сразу возникнет установившийся режим.
- При
свободная составляющая максимальна по модулю. В этом случае ток переходного процесса достигает своей наибольшей величины.
Если 





Таким образом, для линейной цепи максимальное значение тока переходного режима не может превышать удвоенной амплитуды принужденного тока: 
Аналогично для линейной цепи с конденсатором: если в момент коммутации принужденное напряжение равно своему амплитудному значению и постоянная времени 


2. Переходные процессы при отключении катушки индуктивности от источника питания
При размыкании ключа в цепи на рис. 5 принужденная составляющая тока через катушку индуктивности 

откуда 

В соответствии с первым законом коммутации

Таким образом, выражение для тока в переходном режиме
и напряжение на катушке индуктивности
 . . |
(7) |
Анализ (7) показывает, что при размыкании цепей, содержащих индуктивные элементы, могут возникать большие перенапряжения, которые без принятия специальных мер могут вывести аппаратуру из строя. Действительно, при 

3. Заряд и разряд конденсатора
При переводе ключа в положение 1 (см. рис. 6) начинается процесс заряда конденсатора:

Принужденная составляющая напряжения на конденсаторе 
Из характеристического уравнения
определяется корень 


При t=0 напряжение на конденсаторе равно 



Соответственно для зарядного тока можно записать

В зависимости от величины 




При разряде конденсатора на резистор 


Тогда, принимая, что к моменту коммутации конденсатор был заряжен до напряжения 


Соответственно разрядный ток
 . . |
(8) |
Как видно из (8), во избежание значительных бросков разрядного тока величина 
В заключение отметим, что процессы заряда и разряда конденсатора используются в генераторах пилообразного напряжения, широко применяемых в автоматике. Для этого ключ в схеме на рис. 6 заменяется на электронный.
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.
- Составить характеристическое уравнение для цепи на рис. 1, используя выражение входного сопротивления относительно места разрыва ветви с резистором
.
- Может ли в одной части линейной цепи протекать колебательный переходный процесс, а в другой – апериодический?
- Для чего в схеме на рис. 5 служит цепочка, состоящая из диода и резистора R?
- Почему можно разрывать ветвь с конденсатором и нельзя – ветвь с индуктивным элементом?
- Почему корни характеристического уравнения не зависят от того, относительно какой переменной было записано дифференциальное уравнение?
- Для цепи на рис. 8 составить характеристическое уравнение и определить, при каких значениях
переходный процесс в ней будет носить апериодический характер, если
.
Ответ: 
Определить 




Ответ: 
источники:
http://support17.com/rtcs-lecture-27/
http://toehelp.ru/theory/toe/lecture25/lecture25.html
Численные методы решения нелинейных уравнений
Корни нелинейных уравнений
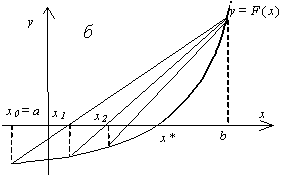
Пусть дано нелинейное уравнение
где — функция, определенная и непрерывная на некотором промежутке. В некоторых случаях на функцию
могут быть наложены дополнительные ограничения, например, непрерывность первой и второй производных, что специально оговаривается. Функция
может быть задана в виде алгебраического многочлена или трансцендентной функции (тогда ей соответствует алгебраическое или трансцендентное уравнение).
Требуется найти корни нелинейного уравнения (3.1), т.е. числа которые путем подстановки их в (3.1) превращают уравнение в верное числовое равенство. Числа
называются также нулями функции
.
На практике часто бывает выгодно уравнение (3.1) заменить равносильным ему уравнением (уравнения равносильны, если имеют одинаковые корни):
(3.2)
где функции — более простые, чем функция
. Тогда при задании уравнения в виде (3.1) нулями функции
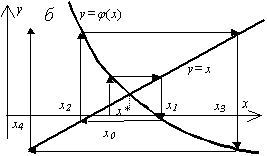
являются точки пересечения
с осью
(рис. 3.1,д), а при задании в виде (3.2) — абсциссы точек пересечения функций
и
(рис. 3.1,б).
Замечания
1. Если — алгебраический многочлен, то уравнение (3.1) называется также алгебраическим n-й степени:
(3.3)
где — действительные числа, коэффициенты уравнения.
2. На практике встречаются задачи нахождения корней уравнения , левая часть которого задана сеточной функцией
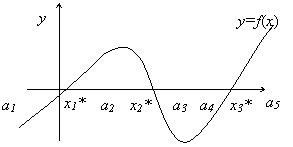
(рис. 3.2).
Число есть корень уравнения (3.1) кратности
, если при
вместе с функцией
обращаются в нуль ее производные до (k-1)-го порядка включительно, т.е.
, а
. Корень кратности к = 1 называется простым. На рис 3.1,с простыми корнями являются
, a корни
— кратные.
В соответствии с классическим результатом Галуа алгебраическое уравнение (3.1) при не имеет решения в замкнутом (формульном) виде. Сеточные уравнения вообще не имеют формульных решений. Поэтому корни алгебраических
, трансцендентных и сеточных уравнений, как правило, определяются приближенно с заданной точностью.
Решение осуществляется в два этапа:
Первый этап. Находятся отрезки , внутри каждого из которых содержится один простой или кратный корень
(см. рис. 3.1). Этот этап называется процедурой отделения корней. По сути на нем осуществляется грубое нахождение корней
.
Второй этап. Грубое значение каждого корня уточняется до заданной точности одним из численных методов, в которых реализуются последовательные приближения. Порядок (скорость) сходимости метода определяется так же, как в методе простых итераций.
Отделение корней уравнения
Для отделения действительных корней полезно определять заранее число корней, а также верхнюю и нижнюю границы их расположения. Для этого используется ряд теорем.
Теорема 3.1 (о числе корней алгебраического уравнения (3.3)). Алгебраическое уравнение (3.3) n-й степени имеет ровно корней, действительных или комплексных, при условии, что каждый корень считается столько раз, какова его кратность.
Теорема 3.2 (о свойстве парной сопряженности комплексных корней уравнения (3.3)). Если — корень алгебраического уравнения (3.3) кратности
, то число
также является корнем той же кратности.
Следствие. Алгебраическое уравнение нечетной степени имеет по крайней мере один действительный корень.
Теорема 3.3 (об оценке модулей корней уравнения (3.3)). Пусть
где — коэффициенты уравнения
. Тогда модули всех корней
уравнения удовлетворяют неравенству
(3.4)
т.е. корни уравнения расположены в кольце.
Следствие. Числа и
являются соответственно нижней и верхней границами положительных корней алгебраического уравнения:
. Аналогично числа
и
служат нижней и верхней границами отрицательных корней уравнения:
.
Приведем полезные теоремы, используемые для более точного установления границ действительных корней алгебраических уравнений.
Теорема 3.4 (теорема Лагранжа о верхней границе положительных корней уравнения (3.3)). Пусть и
— первый отрицательный коэффициент в последовательности
— наибольшая из абсолютных величин отрицательных коэффициентов. Тогда за верхнюю границу положительных корней уравнения (3.3) может быть принято число
(3.5)
Теорема 3.5 (о нижних и верхних границах положительных и отрицательных корней алгебраического уравнения). Пусть — верхняя граница положительных корней уравнения
,
— верхняя граница положительных корней уравнения
,
— верхняя граница положительных корней уравнения
,
— верхняя граница положительных корней уравнения
.
Тогда положительные корни и отрицательные корни
уравнения (3.3) удовлетворяют неравенствам
(3.6)
Теорема 3.6 (теорема Декарта о количестве действительных корней алгебраических уравнений). Число положительных корней (с учетом их кратностей) алгебраического уравнения
равно числу перемен знаков в последовательности коэффициентов
(коэффициенты, равные нулю, не учитываются) многочлена
или меньше этого числа на четное число. Число
отрицательных корней (с учетом их кратностей) алгебраического уравнения
равно числу перемен знаков в последовательности
многочлена
или меньше этого числа на четное число.
Теорема 3.7 (теорема Гюа о необходимом условии действительности всех корней алгебраического уравнения). Если алгебраическое уравнение (3.3) имеет все действительные корни, то квадрат каждого некрайнего коэффициента больше произведения двух его соседних коэффициентов.
Следствие. Если при каком-нибудь выполнено неравенство
, то уравнение (3.3) имеет по крайней мере одну пару комплексных корней.
Для отделения корней применяется следующая теорема.
Теорема 3.8. Если функция , определяющая уравнение
, на концах отрезка
принимает значения разных знаков, т.е.
, то на этом отрезке содержится по крайней мере один корень уравнения. Если же
непрерывна и дифференцируема и ее первая производная сохраняет знак внутри отрезка
, то на
находится только один корень уравнения.
Способы отделения корней
В вычислительной практике обычно используются следующие способы отделения корней:
1) средствами машинной графики: функция представляется на дисплее и приближенно определяются отрезки, которым принадлежат точки
;
2) средствами математического анализа с помощью исследования функций и построения графиков (см. рис. 3.1,д);
3) формированием простых функций и
таких, что получается равносильное уравнение в виде (3.2), и дальнейшим построением графиков этих функций (см. рис. 3.1,б).
▼ Примеры 3.1-3.3
Пример 3.1. Определить число положительных и отрицательных корней, а также их границы для уравнения
Решение
В данной задаче . Согласно теореме 3.1 уравнение имеет пять корней. Поскольку
, то по следствию из теоремы 3.2 уравнение имеет по крайней мере один действительный корень.
Оценим модули корней по теореме 3.3. Так как
то или
, т.е. все корни лежат внутри данного кольца. По следствию из теоремы 3.3 это означает, что положительные корни удовлетворяют неравенству
, а отрицательные — неравенству
.
Применим теоремы 3.4 и 3.5 для уточнения приведенных результатов. Найдем верхнюю границу положительных корней. Так как — первый отрицательный коэффициент в последовательности
, то
, а
— наибольшая из абсолютных величин отрицательных коэффициентов. Следовательно,
.
Найдем нижнюю границу положительных корней. Составим уравнение:
или (старший коэффициент должен быть положительным). Для этого уравнения
, поэтому
. Отсюда
.
Уточним границы отрицательных корней. Составим уравнение:
или
.
Для этого уравнения , поэтому
. Составим уравнение
или . Для этого уравнения
, поэтому
. Отсюда находим:
. Заметим, что данный результат совпадает с полученным ранее.
Исследуем структуру корней уравнения. Так как квадрат каждого некрайнего коэффициента больше произведения двух его соседних коэффициентов, то по теореме 3.7 необходимое условие действительности всех корней уравнения выполняется.
На основе теоремы 3.6 определим число положительных и отрицательных корней. Выписываем коэффициенты многочлена . Так как число перемен знака
, то число положительных корней равно трем или меньше на четное число, т.е. равно 1. Далее выписываем коэффициенты многочлена
. Так как число перемен знаков
, то число отрицательных корней равно двум или меньше на четное число, т.е. их вообще нет.
Пример 3.2. Отделить корни кубического уравнения .
Решение
Согласно теореме 3.1 уравнение имеет три корня, среди которых по крайней мере один действительный (следствие из теоремы 3.2, поскольку это уравнение нечетной степени).
Оценим модули корней уравнения по теореме 3.3. Так как
, то
или
.
Отсюда и
.
Определим число положительных и отрицательных корней. Выписываем коэффициенты многочлена . Так как число перемен знака
(нулевой коэффициент не учитывается), то число положительных корней равно двум или меньше на четное число, т.е. они отсутствуют. Далее выписываем коэффициенты многочлена
. Так как число перемен знака
(нулевой коэффициент не учитывается), то число отрицательных корней равно единице.
Отделим корни третьим способом. Для этого преобразуем уравнение к равносильному виду (3.2): и найдем точки пересечения фафиков
и
(рис. 3.3).
Очевидно, корень уравнения .
Пример 3.3. Отделить корни уравнения третьего порядка .
Решение
Метод половинного деления
Пусть дано уравнение и отделен простой корень
, т.е. найден такой отрезок
, что
и на концах отрезка функция имеет значения, противоположные по знаку
. Отрезок
называется начальным интервалом неопределенности, потому что известно, что корень ему принадлежит, но его местоположение с требуемой точностью не определено.
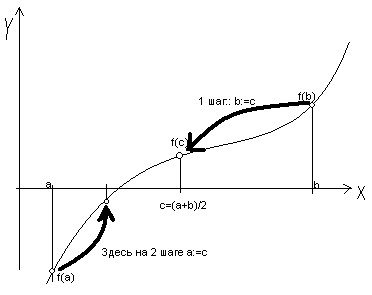
Процедура уточнения положения корня заключается в построении последовательности вложенных друг в друга отрезков, каждый из которых содержит корень уравнения. Для этого находится середина текущего интервала неопределенности , и в качестве следующего интервала неопределенности из двух возможных выбирается тот, на концах которого функция
имеет разные знаки (рис. 3.5).
Процесс завершается, когда длина текущего интервала неопределенности становится меньше заданной величины , задающей точность нахождения корня. В качестве приближенного значения корня берется середина последнего интервала неопределенности.
Алгоритм метода половинного деления
1. Найти начальный интервал неопределенности одним из методов отделения корней, задать малое положительное число
. Положить
.
2. Найти середину текущего интервала неопределенности: .
3. Если , то положить
, а если
, то принять
. В результате находится текущий интервал неопределенности
.
4. Если , то процесс завершить:
. Приближенное значение корня можно найти по формуле
.
Если , положить
и перейти к п.2.
Замечания
1. Метод имеет линейную, но безусловную сходимость, и его погрешность за каждую итерацию уменьшается в два раза:
Из последнего соотношения можно оценить число итераций для достижения заданной точности
Отсюда видно, что, например, для достижения точности при
необходимо выполнить примерно десять итераций.
2. К достоинствам метода следует отнести то, что он позволяет найти простой корень уравнения любых непрерывных функций
при любых значениях
таких, что
. Недостатки метода — он не обобщается на системы нелинейных уравнений и не может использоваться для нахождения корней четной кратности.
▼ Примеры 3.4-3.6
Пример 3.4. Найти корень уравнения методом половинного деления с точностью
и
.
Решение
Пример 3.5. Найти корень уравнения методом половинного деления с точностью
.
Решение
В примере 3.3 были отделены корни уравнения. Уточним корень, лежащий на отрезке . Результаты расчетов поместим в табл. 3.2.
В результате найден интервал и приближенное значение корня
.
Пример 3.6. Отделить корни трансцендентного уравнения и найти один из корней с точностью
.
Решение
1. Можно отделить корни уравнения, преобразовав его к равносильному виду и определив абсциссу точек пересечения графиков функций
и
. При этом
.
2. Уточним корень. Результаты расчетов приведем в табл. 3.3.
Вычисления показывают, что .
Поэтому .
Метод хорд
Этот метод при тех же предположениях обеспечивает более быстрое нахождение корня, чем метод половинного деления. Для этого отрезок делится не пополам, а в отношении
.
Геометрически метод хорд эквивалентен замене кривой хордой, проходящей через точки
и
(рис. 3.6).
Уравнение хорды имеет вид
. Полагая
и
, получаем
Предположим, что вторая производная сохраняет постоянный знак, и рассмотрим два случая:
(рис. 3.7,д) и
(рис. 3.7,б). Случай
сводится к рассматриваемому, если уравнение записать в форме:
. Первому случаю (см. рис. 3.7,д) соответствует формула (3.7), а второму случаю (3.8) (см. рис. 3.7,б):
(3.7)
(3.8)
В первом случае остается неподвижным конец , а во втором случае конец
.
Замечание. Для выявления неподвижного конца используется условие , где
или
. Если неподвижен конец
, применяется формула (3.7), а если конец
, — формула (3.8).
Пример 3.7. Найти корень уравнения методом хорд с точностью
.
Решение
Рассмотрим задачу нахождения корня на отрезке (см. пример 3.2). Так как
, a
на отрезке
, то
и, следовательно, имеем второй случай (см. рис. 3.7,б).
Положим . Тогда по формуле (3.8) получаем
Так как , то положим
и продолжим процесс:
Так как , то положим
и продолжим процесс:
Поскольку , положим
Так как , положим
Поскольку , положим
Так как , положим
Поскольку , положим
Так как , то корень уравнения
. Из анализа поведения
следует, что сходимость метода хорд линейная, однако более быстрая, чем сходимость метода половинного деления.
Метод простых итераций
Пусть известно, что корень уравнения
лежит на отрезке
.
Методика решения задачи
1. Уравнение равносильным преобразованием привести к виду
. Это преобразование может быть осуществлено различными путями, но для сходимости нужно обеспечить выполнение условия
(
— некоторая константа). При этом задача сводится к нахождению абсциссы точки пересечения прямой
и кривой
(рис. 3.8).
2. Задать начальное приближение и малое положительное число
. Положить
.
3. Вычислить следующее приближение:
(3.9)
4. Если , итерации завершаются и
. Если
, положить
и перейти к п.3.
Замечание. В качестве условия завершения итераций при известном значении может быть использовано неравенство
Проблемы сходимости и единственности численного решения, являющиеся главными при использовании этого метода, решаются и исследуются с помощью понятия о сжимающем отображении и теоремы о достаточном условии сходимости метода.
Отображение (функция) называется сжимающим в области
с коэффициентом
, если для любых двух
из
выполнено неравенство
(3.10)
Теорема 3.9 (о сходимости метода простых итераций и единственности получаемого численного решения)
Пусть выполнены условия:
1. Нелинейное уравнение имеет решение
.
2. Отображение является сжимающим в области
с некоторым коэффициентом
.
Тогда:
а) решение является единственным решением в области
;
б) последовательность , определяемая по отображению на основе итерационного процесса, сходится к решению
со скоростью геометрической прогрессии, т.е. при выборе
из условия
, где
— некоторое малое число, справедливо неравенство
Теорема 3.9 утверждает, что при выполнении условий 1,2 существует окрестность такая, что если взять
в этой окрестности и вычислять
по формуле (3.9), то в результате с любой наперед заданной точностью можно вычислить
, соответствующее искомому (единственному) корню. Но так как эта окрестность неизвестна, то можно взять произвольное
. Если при этом вычисляется последовательность
, сходящаяся к некоторому значению
, то в силу теоремы
. Если сходимость отсутствует, то надо взять другое
и повторить расчет.
Теорема 3.10 (о достаточном условии сходимости метода простых итераций). Пусть выполнены условия:
1. Функция имеет производные для всех
.
2. Существует число , такое, что
для всех
.
Тогда отображение является сжимающим в
с коэффициентом сжатия х и последовательность
, определяемая на основе итерационного процесса, сходится к решению
, то есть
при
.
▼ Доказательство
В силу условия 1 справедлива теорема Лагранжа о конечных приращениях:
для
,
где — точка, лежащая между
и
. Но тогда с учетом условия 2 и замены
ее мажорантой
получим
т.е. отображение — сжимающее, и, таким образом, последовательность
сходится к некоторому
. Но тогда в силу непрерывности
в
имеет место равенство
.
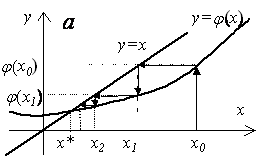
Геометрическая интерпретация процесса сходимости и расходимости в зависимости от выполнения или невыполнения достаточного условия сходимости представлена на рис. 3.9.
Из рис. 3.9 видно, что при и при
(см.рис. 3.9,д,б) итерационные последовательности
сходятся к
. Причем в первом случае реализуется односторонняя (монотонная) сходимость, а во втором — двусторонняя (немонотонная). При
(см.рис. 3.9,в,г) процесс расходится несмотря на то, что точка
очень близка к
. Процессы на рис. 3.9,а,б соответствуют сжимающему отображению.
Преобразование уравнения к равносильному виду
может быть выполнено неоднозначно. Рассмотрим универсальные практические приемы равносильного преобразования
, дающие сжимающие отображения.
1. Можно заменить уравнение на равносильное
, где
. Тогда, принимая правую часть этого уравнения за
и раскрывая
, получаем условие
(3.11)
Таким образом, можно найти константу на отрезке
так, чтобы удовлетворялись неравенства (3.11). При этом надо стремиться получить такую постоянную
, которая бы больше отличалась от нуля, и тогда будет реализовы-ваться более быстрая сходимость.
Можно показать, что абсолютная погрешность метода оценивается по формуле (эта оценка выражается через два последовательных приближения)
(3.12)
или по формуле (эта оценка выражается через два приближения и
)
(3.13)
Из оценки следует условие выхода из итерационного процесса. Если значение неизвестно, то выход осуществляется по условию
2. Уравнение заменяется равносильным (где знак в правой части выбирается из условия
):
при
,
3. Можно выразить из уравнения
так, чтобы для полученного уравнения
выполнялось условие сходимости
в окрестности искомого корня.
Замечание к доказательству. Выполнение условия не гарантирует близости к точному решению (на рис. 3.10 достигается область, где условие окончания выполняется, но корень
расположен достаточно далеко от этой области).
▼ Примеры 3.8-3.10
Пример 3.8. Методом простых итераций с точностью уточнить корень трансцендентного уравнения
, причем искомый корень
.
Решение
Пример 3.9. Найти решение уравнения методом простых итераций с точностью
и
.
Решение
Пример 3.10. Найти корни уравнения методом простых итераций с точностью
.
Решение
1. Преобразуем уравнение к виду .
В примере 3.3 была выполнена операция отделения корней и получены отрезки .
Можно показать, что на отрезках функция
удовлетворяет условию
.
На отрезке используем другой вид уравнения:
. Также легко проверить, что функция
удовлетворяет достаточному условию сходимости на отрезке
.
2. В качестве начальных приближений выберем:
– точку на отрезке
;
– точку на отрезке
;
– точку на отрезке
;.
В поставленной задаче .
3,4. Выполним расчеты по формуле
с начальными значениями и
и по формуле
с начальным значением .
Результаты расчетов занесены в табл. 3.6–3.8.
В результате получены приближенные значения корней:
Обратим внимание на сильное различие в числе итераций, потребовавшихся для нахождения корней (табл. 3.6) и
(табл. 3.7), с помощью одной и той же формулы. Заметим, что в окрестности корня
значения модуля производной функции
равны:
С другой стороны, в окрестности корня имеем:
Анализ результатов показывает, что чем меньше значения модуля производной , тем быстрее сходимость.
Метод Ньютона для решения нелинейных уравнений
Метод Ньютона (метод касательных, или метод линеаризации) является одним из наиболее популярных численных методов. Он быстро сходится (имеет квадратичную сходимость) и допускает различные модификации, приспособленные для решения векторных задач и сеточных уравнений. Однако этот метод эффективен при весьма жестких ограничениях на характер функции
1) существование второй производной функции на множестве
;
2) удовлетворение первой производной условию для всех
;
3) знакопостоянство для всех
.
Поэтому его желательно использовать совместно с другими методами, например методом половинного деления, чтобы достигнуть диапазона , где указанные условия начинают выполняться.
Геометрическая интерпретация метода Ньютона состоит в следующем. Задается начальное приближение . Далее проводится касательная к кривой
в точке
(рис. 3.11), т.е. кривая заменяется прямой линией. В качестве следующего приближения выбирается точка пересечения этой касательной с осью абсцисс. Процесс построения касательных и нахождения точек пересечения с осью абсцисс повторяется до тех пор, пока приращение не станет меньше заданной величины
.
Получим расчетную формулу метода Ньютона. Вместо участка кривой (точка
соответствует
) возьмем участок
— касательную, проведенную в точке
). Для этого отрезка справедливо конечное соотношение:
где — угол наклона касательной в точке
к оси абсцисс. Разрешая это соотношение относительно
, получаем
. Повторяя процесс, находим общую формулу:
(3.14)
Подчеркнем, что если отбросить итерационный индекс, то (3.14) записывается в виде нелинейного уравнения
(3.15)
которое, однако, на не равносильно исходному, а является таковым только в одной точке при
. Поэтому данный метод не служит разновидностью метода простых итераций.
Применим теперь для вывода формулы (3.14) метод линеаризации. Положим, что итерационный процесс имеет вид
(3.16)
где — поправка к k-му приближению, которую необходимо найти. Предполагая, что
имеет непрерывную вторую производную, разложим
по формуле Тейлора относительно точки
где . Учитывая, что
(это соответствует нахождению точки пересечения с осью абсцисс), и оставляя только линейную (относительно
) часть разложения (отсюда и название — метод линеаризации), записываем линейное относительно
уравнение
Отсюда выражается поправка . Подставляя
в (3.16), получаем (3.14).
Теорема 3.11 (о достаточных условиях сходимости метода Ньютона). Пусть выполняются следующие условия:
1. Функция определена и дважды дифференцируема на
.
2. Отрезку принадлежит только один простой корень
, так что
.
3. Производные на
сохраняют знак, и
.
4. Начальное приближение удовлетворяет неравенству
(знаки функций
и
в точке
совпадают).
Тогда с помощью метода Ньютона (3.14) можно вычислить корень уравнения с любой точностью.
Замечания
1. Метод Ньютона характеризуется вторым порядком сходимости вблизи корня и первым порядком — вдали от него. Данную оценку проверяем для двух случаев, когда находится далеко от корня
(это возможно на первых итерациях) и когда
располагается вблизи
.
Первый случай. Пусть отрезок не мал. Тогда на основе теоремы Лагранжа получим (где
)
(3.17)
Преобразуем с использованием (3.17) итерационную формулу (3.14) (где ):
В силу монотонности последовательности имеем
Таким образом, вдали от корня получаем линейную сходимость
, где
.
Второй случай. Пусть теперь отрезок мал, т.е. итерации выполняются вблизи корня. Тогда, полагая, что указанные выше предположения 1–4 теоремы 3.10 выполнены, разложим функцию
в окрестности корня
относительно точки
, учитывая члены до второго порядка. Получим
где (
— малая величина). Из данного соотношения выражаем
Но первые два слагаемых в правой части в соответствии с (3.14) равны . Тогда будем иметь
Из последнего соотношения следует оценка погрешности (k+1)-го приближения через погрешность k-го приближения:
(3.18)
где принято . Оценка (3.18) свидетельствует о квадратичной сходимости метода касательных вблизи корня. С вычислительной точки зрения это означает, что на каждом приближении количество верных цифр результата удваивается.
2. Для нахождения комплексных корней уравнения можно также использовать (3.14) в форме (где
— комплексная переменная)
Метод Ньютона может применяться не только для нахождения простых корней, но для определения кратных корней, т.е. когда на отрезке содержащем корень, не выполняется условие
(условие 2 теоремы 3.11). Наряду с теоремой 3.11 удобно также пользоваться следующей теоремой.
Достаточные условия сходимости метода Ньютона
Теорема 3.12 (достаточные условия сходимости метода Ньютона). Пусть:
а) дана функция , где
— открытый интервал, и
;
б) для некоторого выполняется условие
при всех
из
.
Если уравнение имеет решение
, то существует некоторое
, такое, что если
, то последовательность
, задаваемая формулой (3.14), существует и сходится к
. Более того, справедлива оценка
Здесь обозначение означает, что функция
непрерывна по Липшицу с константой
на множестве
, то есть
для любых
из
.
Замечания
1. Требование теоремы 3.12, чтобы производная имела ненулевую нижнюю границу в
, определяет, что значение
должно быть ненулевым для квадратичной сходимости метода Ньютона. Если же
, то
является кратным корнем, а метод Ньютона сходится лишь линейно.
2. Выполнение условий теоремы 3.12 гарантирует сходимость метода Ньютона только из «хорошего» начального приближения .
3. Метод Ньютона является локально сходящимся, так как он сходится с определенной скоростью к истинному решению при условии, что стартует в достаточной близости от этого решения.
Методика решения задачи
1. Задать начальное приближение так, чтобы выполнялось неравенство
, а также малое положительное число
. Положить
.
2. Вычислить по формуле
.
3. Если , процесс завершить и положить
.
Если , положить
и перейти к п.2.
▼ Примеры 3.11-3.14
Пример 3.11. Методом Ньютона с точностью уточнить корень трансцендентного уравнения
, причем искомый корень
.
Решение
Можно проверить, что на множестве удовлетворяются условия 1, 2, 3 теоремы 3.11, обеспечивающие сходимость метода касательных.
1. Зададим начальное приближение из условия 4. Так как для справедливо
на множестве
, то
, поэтому
.
2,3. Результаты расчетов по формуле (3.14) помещены в табл. 3.9.
Из табл. 3.9 можно сделать следующие выводы:
1. Для достижения заданной точности, проверяемой по модулю разности , потребовалось выполнить три приближения. Если же выход организовать по условию
, то достаточно двух приближений.
2. Вблизи корня количество верных цифр в результатах
удваивается, так что все цифры в
являются верными, тогда как в
верными являются первые три цифры после запятой.
3. Скорость сходимости метода Ньютона выше скорости сходимости метода простых итераций (та же точность была достигнута за пять итераций).
Пример 3.12. Методом Ньютона найти корень уравнения .
Решение
Пример 3.13. Найти корни уравнения методом Ньютона с точностью
.
Решение
Процедура отделения корней была выполнена в примере 3.3. В качестве отрезков , которым принадлежат корни уравнения, выберем
.
Так как , то есть
, производные
сохраняют знак при
, то условия сходимости выполняются.
Так как , то есть
, и производные
сохраняют знак при
, то условия сходимости на этом отрезке тоже выполняются.
Так как , то есть
, и производные
сохраняют знак при
, то условия сходимости выполняются.
1. Зададим начальные приближения: на отрезке выберем
, так как
; на отрезке
выберем
, так как
; аналогично на отрезке
выберем
. В поставленной задаче
.
2,3. Результаты расчетов по формуле (3.14) приведены в табл. 3.11–3.13.
В результате получены приближенные значения корней:
Пример 3.14. Найти корень уравнения методом Ньютона с точностью
.
Решение
Очевидно, уравнение имеет один кратный корень . Согласно замечанию к теореме 3.12 применение метода Ньютона для решения поставленной задачи сопровождается линейной сходимостью (табл. 3.14).
Полученное приближенное решение .
Метод касательных
Метод касательных, являясь весьма эффективным средством численного анализа, к сожалению, имеет достаточно жесткие ограничения. Действительно, он не может применяться для сеточных уравнений (см. рис. 3.2); при нарушении знакопостоянства производных (рис. 3.12); при существовании неограниченных вторых производных и др. Так, если даже условие знакопостоянства нарушено вдали от корня, где выбрано , а вблизи корня выполняется, то все равно метод касательных неприменим (см. рис. 3.12), если не произвести сужения начального отрезка.
Кроме того, если функция очень сложная, то будет сложной и ее производная, и поэтому на каждой итерации приходится рассчитывать две функции, что снижает эффективность метода касательных.
В силу этого в ряде случаев могут оказаться более предпочтительными модификации метода касательных. Рассмотрим три из них.
Упрощенный метод Ньютона. Методика его применения совпадает с изложенной ранее, но вместо формулы (3.14) используется
Отличие от метода Ньютона заключается в том, что производная функции подсчитывается только в точке начального приближения, а на последующих итерациях не уточняется. Процесс последовательных приближений отражен на рис. 3.13. Первая итерация совпадает с первой итерацией метода Ньютона. На последующих итерациях соответствующие отрезки параллельны касательной, проведенной в начальной точке.
Для этой модификации снимаются некоторые ограничения метода касательных, например условие знакопостоянства производных. Сходимость упрощенного метода Ньютона линейная.
Пример 3.15. Найти корень уравнения упрощенным методом Ньютона.
Решение
Корень уравнения отделен в примере 3.2: .
1. Выберем начальное приближение и зададим
и
.
2,3. Выполним расчеты по формуле (3.19):
Результаты расчетов приведены в табл. 3.15.
При получено решение
, а при
— решение
. Очевидно, по сравнению с методом Ньютона сходимость замедляется (см. пример 3.12).
Метод Ньютона-Бройдена
Этот метод позволяет увеличить скорость сходимости последовательных приближений благодаря использованию формулы
(3.20)
где — число, которое выбирается на каждой итерации так, чтобы уменьшить значение
по сравнению с
. При
метод Ньютона-Бройдена совпадает с методом Ньютона.
Как правило, при плохой сходимости или ее отсутствии полагают (рис. 3.14,д), а при хорошей сходимости для
полагают
(это ускоряет сходимость (рис. 3.14,б)).
На рис. 3.14 прямоугольниками отмечены точки , полученные при
, — поправка, соответствующая методу Ньютона, а точки
получены по методу Ньютона-Бройдена.
Метод секущих
В этом методе производная функции подсчитывается с помощью конечно-разностных соотношений:
– в точке используется формула
, где
— малая положительная величина;
– в точках , используется формула
.
Вычисленное значение определяет тангенс угла наклона секущей (рис. 3.15).
Методика применения метода секущих совпадает с описанной ранее, но вместо (3.14) используется формула
(3.21)
Замечания
1. Метод секущих является более экономичным по сравнению с методом Ньютона по количеству функций, подлежащих расчету: на каждой итерации в методе секущих необходимо рассчитать только значение , так как величина
уже подсчитана на предыдущей итерации.
2. Метод секущих может применяться и для решения сеточных уравнений. Для сеточной функции производные в методе секущих определяются так же, но для определения в промежуточных точках осуществляется аппроксимация (как правило, интерполяция) функции
(рис. 3.16). На этом рисунке штриховой линией показана аппроксимационная кривая.
3. Для всех описанных модификаций скорость сходимости по сравнению с методом касательных снижается:
. Однако для некоторых из них (метод секущих) значение
и может достигать
.
Пример 3.16. Методом секущих найти корень уравнения с точностью
.
Решение
1. Зададим начальное приближение (см. пример 3.12).
2. Для вычисления зададим
. Тогда
Отсюда .
Дальнейшие расчеты выполняются по формуле (3.21):
Результаты расчетов приведены в табл. 3.16.
Очевидно, метод сходится чуть хуже метода Ньютона (см. пример 3.12), однако скорость сходимости выше линейной.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Пусть имеется уравнение вида
f(x)= 0
где f(x) — заданная алгебраическая или трансцендентная функция.
Решить уравнение — значит найти все его корни, то есть те значения x, которые обращают уравнение в тождество.
Если уравнение достаточно сложно, то задача точного определения корней является в некоторых случаях нерешаемой. Поэтому ставится задача найти такое приближенное значение корня xПP, которое отличается от точного значения корня x* на величину, по модулю не превышающую указанной точности (малой положительной величины) ε, то есть
│x* – xпр │< ε
Величину ε также называют допустимой ошибкой, которую можно задать по своему усмотрению.
Этапы приближенного решения нелинейных уравнений
Приближенное решение уравнения состоит из двух этапов:
- Отделение корней, то есть нахождение интервалов из области определения функции f(x), в каждом из которых содержится только один корень уравнения f(x)=0.
- Уточнение корней до заданной точности.
Отделение корней
Отделение корней можно проводить графически и аналитически.
Для того чтобы графически отделить корни уравнения, необходимо построить график функции f(x). Абсциссы точек его пересечения с осью Ox являются действительными корнями уравнения.
Для примера рассмотрим задачу решения уравнения
где угол x задан в градусах. Указанное уравнение можно переписать в виде
Для графического отсечения корней достаточно построить график функции
Из рисунка видно, что корень уравнения лежит в промежутке x∈(6;8).
Аналитическое отделение корней
Аналитическое отделение корней основано на следующих теоремах.
Теорема 1. Если непрерывная функция f(x) принимает на концах отрезка [a; b] значения разных знаков, т.е.
то на этом отрезке содержится по крайней мере один корень уравнения.
Теорема 2. Если непрерывная на отрезке [a; b] функция f(x) принимает на концах отрезка значения разных знаков, а производная f'(x) сохраняет знак внутри указанного отрезка, то внутри отрезка существует единственный корень уравнения f(x) = 0.
Уточнение корней
Для уточнения корней может использоваться один из следующих методов:
- Метод последовательных приближений (метод итераций)
- Метод Ньютона (метод касательных)
- Метод секущих (метод хорд)
- Метод половинного деления (метод дихотомии)
Метод последовательных приближений (метод итераций)
Метод итерации — численный метод решения математических задач, используемый для приближённого решения алгебраических уравнений и систем. Суть метода заключается в нахождении по приближённому значению величины следующего приближения (являющегося более точным). Метод позволяет получить решение с заданной точностью в виде предела последовательности итераций. Характер сходимости и сам факт сходимости метода зависит от выбора начального приближения решения.
Функциональное уравнение может быть записано в виде
Функцию f(x) называют сжимающим отображением.
Последовательность чисел x0, x1 ,…, xn называется итерационной, если для любого номера n>0 элемент xn выражается через элемент xn-1 по рекуррентной формуле
а в качестве x0 взято любое число из области задания функции f(x).
Реализация на C++ для рассмотренного выше примера
Уравнение может быть записано в форме
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#define _USE_MATH_DEFINES
#include <iostream>
#include <cmath>
using namespace std;
double find(double x, double eps)
{
double rez; int iter = 0;
cout << «x0= » << x << » «;
do {
rez = x;
x = 1 / (sin(M_PI*x / 180));
iter++;
} while (fabs(rez — x) > eps && iter<20000);
cout << iter << » iterations» << endl;
return x;
}
int main()
{
cout << find(7, 0.00001);
cin.get();
return 0;
}
Результат выполнения

Метод Ньютона (метод касательных)
Если известно начальное приближение x0 корня уравнения f(x)=0, то последовательные приближения находят по формуле
Графическая интерпретация метода касательных имеет вид
Реализация на C++
Для заданного уравнения
производная будет иметь вид 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#define _USE_MATH_DEFINES
#include <iostream>
#include <cmath>
using namespace std;
double find(double x, double eps)
{
double f, df; int iter = 0;
cout << «x0= » << x << » «;
do {
f = sin(M_PI*x / 180) — 1 / x;
df = M_PI / 180 * cos(M_PI*x / 180) + 1 / (x*x);
x = x — f / df;
iter++;
} while (fabs(f) > eps && iter<20000);
cout << iter << » iterations» << endl;
return x;
}
int main()
{
cout << find(1, 0.00001);
cin.get(); return 0;
}
Результат выполнения

Метод секущих (метод хорд)
Если x0, x1 — приближенные значения корня уравнения f(x) = 0 и выполняется условие
то последующие приближения находят по формуле
Методом хорд называют также метод, при котором один из концов отрезка закреплен, т.е. вычисление приближения корня уравнения f(x) = 0 производят по формулам:
Геометрическая интерпретация метода хорд:
Реализация на C++
В отличие от двух рассмотренных выше методов, метод хорд предполагает наличие двух начальных приближений, представляющих собой концы отрезка, внутри которого располагается искомый корень.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#define _USE_MATH_DEFINES
#include <iostream>
#include <cmath>
using namespace std;
double find(double x0, double x1, double eps)
{
double rez = x1, f0, f;
int iter = 0;
cout << «x0= » << x0 << » x1= » << x1 << » «;
do {
f = sin(M_PI*rez / 180) — 1 / rez;
f0 = sin(M_PI*x0 / 180) — 1 / x0;
rez = rez — f / (f — f0)*(rez — x0);
iter++;
} while (fabs(f) > eps && iter<20000);
cout << iter << » iterations» << endl;
return rez;
}
int main()
{
cout << find(1.0, 10.0, 0.000001);
cin.get(); return 0;
}
Результат выполнения

Метод половинного деления (метод дихотомии)
Если x0, x1 — приближенные значения корня уравнения f(x) = 0 и выполняется условие
то последующие приближения находятся по формуле
и вычисляется f(xi). Если f(xi)=0, то корень найден. В противном случае из отрезков выбирается тот, на концах которого f(x) принимает значения разных знаков, и проделывается аналогичная операция. Процесс продолжается до получения требуемой точности.
Геометрическая интерпретация метода дихотомии
Реализация на C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#define _USE_MATH_DEFINES
#include <iostream>
#include <cmath>
using namespace std;
double func(double x)
{
return (sin(M_PI*x / 180) — 1 / x);
}
double find(double x0, double x1, double eps)
{
double left = x0, right = x1, x, fl, fr, f;
int iter = 0;
cout << «x0= » << x0 << » x1= » << x1 << » «;
do {
x = (left + right) / 2;
f = func(x);
if (f > 0) right = x;
else left = x;
iter++;
} while (fabs(f) > eps && iter<20000);
cout << iter << » iterations» << endl;
return x;
}
int main()
{
cout << find(1.0, 10.0, 0.000001);
cin.get(); return 0;
}
Результат выполнения
Для численного поиска решения также можно использовать генетические алгоритмы.
Назад: Алгоритмизация
1. Приближенное решение нелинейных алгебраических уравнений
Метод деления отрезка пополам (дихотомии)
Метод простой итерации
Метод Ньютона (метод касательных)
Метод хорд
Постановка задачи
Дано
нелинейное алгебраическое уравнение
f(x)=0 (1)
Нелинейность уравнения означает,
что график функции не есть прямая линия, т.е. в f(x) входит x в
некоторой степени или под знаком функции.
Решить
уравнение – это найти такое x* ∈ R: f(x*)=0. Значение x*
называют корнем уравнения. Нелинейное уравнение может иметь
несколько корней. Геометрическая интерпретация корней уравнения представлена на
рис. 1. Корнями уравнения (1) являются точки x1*, x2*,
x3*, в которых функция f(x) пересекает ось x.
нелинейного уравнения (1) можно разделить на точные
(аналитические) и приближенные (итерационные). В точных методах
корень представляется некоторой алгебраической формулой. Например, решение
квадратных уравнений, некоторых тригонометрических уравнений и т. д.
В приближенных
методах процесс нахождения решения, вообще говоря, бесконечен. Решение
получается в виде бесконечной последовательности {xn},
такой, что . По
определению предела, для любого (сколь угодно малого) ε,
найдется такое N, что при n>N,
|xn – x*|<
ε. Члены этой последовательности xn называются последовательными приближениями
к решению, или итерациями. Наперёд заданное число
ε называют точностью метода, а N – это количество
итераций, которое необходимо выполнить, чтобы получить решение с точностью ε.
Существует
различные методы нахождения приближенного решения, т.е. способы построения
последовательности итераций {xn}, однако все они имеют общие
этапы, изображенные на рисунке.
Наиболее часто используется следующий критерий остановки итерационного
процесса: |xn+1–xn|<ε, т.е. разница между соседними итерациями
становится малой. Также для окончания итерационного процесса используется условие
|f(xn)|<ε , где f(xn)
– невязка метода.
Прежде чем использовать приближенный метод, уравнение надо исследовать
его на наличие корней и уточнить, где эти корни находятся, т.е. найти
интервалы изоляции корней. Интервалом изоляции корня
называется отрезок, на котором корень уравнения существует и единственен.
Необходимое условие существования корня уравнения
на отрезке [a,b]: Пусть
f(x) непрерывна и f(a)f(b)<0
(т.е., на концах интервала функция имеет разные знаки). Тогда внутри отрезка [a, b]
существует хотя бы один корень уравнения f(x)=0.
Достаточное
условие единственности корня на отрезке [a,b]:
Корень будет
единственным, если f(a)f(b)<0 и
f /(x) не меняет знак на
отрезке [a, b], т.е. f(x) –
монотонная функция, в этом случае отрезок [a,b]
будет интервалом изоляции.
Если корней несколько, то для каждого нужно найти интервал изоляции.
Существуют различные способы исследования функции: аналитический,
табличный, графический.
Аналитический способ состоит в нахождении экстремумов
функции f(x),
исследование ее поведения при и нахождение участков возрастания и убывания
функции.
Графический способ – это построение графика функции f(x) и определение числа
корней по количеству пересечений графика с осью x.
Табличный способ – это построение таблицы,
состоящей из столбца аргумента x и столбца
значений функции f(x).
О наличии корней свидетельствуют перемены знака функции. Чтобы не произошла потеря
корней, шаг изменения аргумента должен быть достаточно мелким, а интервал
изменения достаточно широким.
Пример.
Решить
уравнение x3‑ 6x2+3x+11=0, т.е. f(x)= x3‑ 6x2+3x+11.
Найдем
производную f/(x)=3x2-12x+3.
Найдем нули
производной f/(x)=3x2-12x+3=0; D=144-4*3*3=108;
X1== 0.268;
X2== 3.732;
Так как f/()>0, то f/(x)>0 при
, f/(x)<0 при
и f/(x)>0 при
. Кроме того, f(
)=
<0, f(
)=
интервале
возрастает от до f(x1)= 3x12-12x1+3=11.39;
на интервале —
убывает до f(x2)= 3x22-12x2+3=-9.39 и на интервале 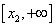
, т.е. уравнение
имеет три корня.
Найдем интервалы изоляции для каждого из корней.
Рассмотрим для первого корня отрезок [-2, -1]:
f(-2)= -27<0, f(-1)= 1>0, f/(x)>0 при т.е. этот отрезок является интервалом изоляции
корня.
Рассмотрим для второго корня отрезок [1, 3]:
f(1)= 9>0, f(3)= -7<0, f/(x)<0 при т.е. этот отрезок является интервалом
изоляции корня.
Рассмотрим для третьего корня отрезок [4, 5]:
f(4)= -9<0, f(5)=1>0, f/(x)>0 при т.е. этот отрезок является интервалом
изоляции корня.
Табличный
способ:
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
f(x) |
-79 |
-27 |
1 |
11 |
9 |
1 |
-7 |
-9 |
1 |
29 |
81 |
Графический
способ
Приближенные (Итерационные) методы.
Пусть интервалы изоляции
корней известны. Познакомимся с несколькими итерационными методами,
позволяющими найти корень на известном интервале изоляции [a, b].
Метод деления отрезка пополам (дихотомии)
Идея метода:
Найдем середину отрезка [a, b]:
c=(a+b)/2. Корень остался на одной из частей:
[a, c] или [c, b]. Если f(a) * f(с)<0,
то корень попал на отрезок [a, c], тогда деление отрезка можно повторить, приняв в
качестве нового правого конца точку c, т.е. b=c. В противном
случае корень попал на половину [c, b], и необходимо изменить значение левого конца
отрезка: a=c. Поскольку корень всегда заключен внутри отрезка,
итерационный процесс можно останавливать, если длина отрезка станет меньше
заданной точности: |b – a|< ε
Найдем первый корень уравнения f(x)=x3 —
6x2+3x+11=0 с точностью
Вычисления оформляются в виде
таблицы
|
k |
a |
b |
c |
f(a) |
f(c) |
|b-a| |
|
0 |
-2 |
-1 |
-1.5 |
-27 |
-10.375 |
1 |
|
1 |
-1.5 |
-1 |
-1.25 |
-10.375 |
-4.07813 |
0.5 |
|
2 |
-1.25 |
-1 |
-1.125 |
-4.07813 |
-1.39258 |
0.25 |
|
3 |
-1.125 |
-1 |
-1.0625 |
-1.39258 |
-0.1604 |
0.125 |
|
4 |
-1.0625 |
-1 |
-1.03125 |
-0.1604 |
0.42868 |
0.0625 |
|
5 |
-1.0625 |
-1.03125 |
-1.04688 |
-0.1604 |
0.136372 |
0.03125 |
|
6 |
………. |
|||||
|
7 |
||||||
|
8 |
||||||
|
9 |
||||||
|
10 |
-1.05469 |
-1.05371 |
-1.0542 |
-0.01146 |
-0.00218 |
0.000977 |
где a0 , b0 — начальные границы
интервала изоляции корня;
В результате
расчета приближенное значение первого корня: при точности
и х=-1.0542 при точности
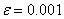
Графическая иллюстрация метода:
Этот пример в Excel: dich.xls (20 Кб)
Метод простой итерации
С помощью эквивалентных преобразований приведем исходное уравнение f(x) к виду, удобному для применения
метода простой итерации: x=φ(x).
Выберем начальное приближение x0∈[a, b]. Следующие
итерации находим по формуле: xk+1=φ(xk),
т.е. x1=φ(x0),
x2=φ(x1)
и т.д.. Итерационный процесс заканчивается, если |xk+1–xk|<ε. Представить
исходное уравнение в эквивалентном виде x=φ(x)
можно бесконечным числом способов. Из всевозможных таких представлений выбирают
тот, который дает сходящуюся к корню последовательность вычислений. Очевидно,
что .
Достаточное условие сходимости: пусть φ(x)
имеет производную на отрезке
[a,b], 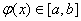
для всех x из отрезка
[a,b], тогда итерационный
процесс сходится к корню уравнения т.е. .
Доказательство
следует из следующих оценок:
Первое неравенство следует из теоремы Лагранжа о среднем и того, что .
Остальные по
инерции.
Так как .
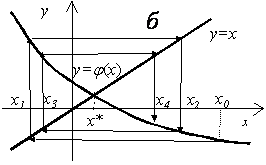
Геометрический смысл метода простой итерации.
|
|
|
|
|
|
|
Сходящийся метод |
|
|
|
|
|
|
|
Расходящийся |
В качестве
начального приближения обычно берут середину отрезка [a,b]: .
На практике часто в качестве берут функцию
, где с – некоторая постоянная.
Постоянную c выбирают таким образом, чтобы для всех x∈[a, b].
При таком выборе функции метод простой итерации называют методом
релаксации.
Получим
условия на выбор с:
Таким образом, если f/(x)<0, то 2/f/(x)<c<0. Если же f/(x)>0, то 2/f/(x)>c>0.
Видно, что знак у с совпадает со знаком f/(x).
Часто с берут в виде: .
Убедимся, что
такое c удовлетворяет условию сходимости:
Пусть f/(x)>0. Тогда M>0 и m>0 -> c>0 и
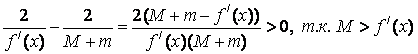
Пусть f/(x)<0. Тогда M<0 и m<0-> c<0 и
Следовательно,
2/f/(x)<c<0.
Найдем, второй корень нашего исходного уравнения x3‑
6x2+3x+11=0, который лежит на интервале [1, 3] с точностью .
Сначала
найдем функцию .
В нашем случае f(x)= x3‑
6x2+3x+11.
Для нахождения c необходимо найти максимальное
и минимальное значения f/(x)
на отрезке [1, 3]. Для этого необходимо найти значения f/(x) на концах интервала и в точках, где f//(x)=0, т.е. в точках экстремума, если такие точки для
рассматриваемого интервала существуют. И выбрать среди этих значений f/(x) максимальное и
минимальное значения.
f/(1)=3x2-12x+3=-6, f/(3)=-6, f//(x)=6x-12=0
при x=2 , f/(2)=-8.
Следовательно,
Таким
образом, .
Вычисления
оформим в виде таблицы:
|
k |
x |
|xk+1-xk| |
|f(xk)| |
|
0 |
2 |
— |
1 |
|
1 |
2.142857 |
0.142857 |
0.282799 |
|
2 |
2.102457 |
0.0404 |
0.07896 |
|
3 |
2.113737 |
0.01128 |
0.022164 |
|
4 |
2.110571 |
0.003166 |
0.006213 |
|
5 |
2.111459 |
0.000888 |
0.001742 |
|
6 |
2.11121 |
0.000249 |
0.000489 |
Здесь x0=(1+3)/2=2, ,
и т.д.
Условием
окончания итерационного процесса является условие: |xk+1–xk|<ε или |f(xk)|<ε.
Метод Ньютона (метод касательных)
Напомним, что
мы решаем уравнение f(x)=0.
Метод
определяется формулой
Геометрическая интерпретация такова:
участок кривой y=f(x) при 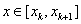
, или
, если
, заменяется отрезком касательной, проведённой
из точки xk.
Уравнение касательной имеет вид . Найдем точку пересечения, которую обозначим xk+1, касательной с осью y=0:
.
Откуда .
Можно
показать, что |xk+1– x*| < q * |xk – x*|2,
т.е. метод сходится со вторым порядком.
Метод Ньютона можно трактовать как метод простой итерации при .
Замечание. Если известен интервал изоляции корня уравнения, в котором f//(x) не меняет знак, то
в качестве начального приближения берут тот конец интервала изоляции, для
которого знаки f(x) и f//(x) совпадают.
Найдем, третий корень методом Ньютона нашего исходного уравнения x3‑
6x2+3x+11=0, который лежит на интервале [4, 5] с точностью . Сначала убедимся, что f//(x) не меняет знака на
этом отрезке.
f//(x)=6x-12.
f//(x)>0 при x>2, т.е. f//(x)>0 на интервале [4,5]. Так как f(5)=1>0,
то x0=5.
Вычисления
оформим в виде таблицы:
|
k |
xk |
|xk+1-xk| |
f(xk) |
f/(xk) |
|
0 |
5 |
— |
1 |
18 |
|
1 |
4.944444 |
0.055556 |
0.027606 |
17.00926 |
|
2 |
4.942821 |
0.001623 |
2.33E-05 |
16.98059 |
|
3 |
4.94282 |
1.37E-06 |
1.66E-11 |
16.98057 |
Здесь f(xk)=xk3‑ 6xk2+3xk+11, f/(xk)=3xk-12xk+3, .
В качестве корня можно взять
значение: x=4.943. Видно, что процесс сошелся уже на
второй итерации.
Для сравнения найдем
первый корень нашего уравнения x3‑ 6x2+3x+11=0 на
отрезке [-2,-1] методом Ньютона:
Так как f//(x)=6x-12,
то f//(x)<0 на
интервале [-2,-1], а так как f(-2)=-27>0, то x0=-2.
|
k |
xk |
|xk+1-xk| |
f(xk) |
f/(xk) |
|
0 |
-2 |
-27 |
39 |
|
|
1 |
-1.30769 |
0.692308 |
-5.41966 |
23.82249 |
|
2 |
-1.08019 |
0.227502 |
-0.50182 |
19.46272 |
|
3 |
-1.05441 |
0.025783 |
-0.00613 |
18.9882 |
|
4 |
-1.05408 |
0.000323 |
-9.5E-07 |
18.98229 |
|
5 |
-1.05408 |
5.02E-08 |
-2.3E-14 |
18.98229 |
Напомним, что методом дихотомии
мы достигли данной точности 0.001 на 10-ой итерации.
Вычислим второй корень нашего
уравнения на отрезке [1,3]. Заметим, что f//(x)=6x-12 меняет знак на отрезке при
х=2. Уменьшим интервал изоляции так, чтобы f//(x) не меняла знака. Рассмотрим интервал [2.1; 3]. f//(2.1)=6*2.1-12=0.6>0 b f(2.1)=0.101>0.
Следовательно, x0=2.1.
|
k |
xk |
|xk+1-xk| |
f(xk) |
f/(xk) |
|
0 |
2.1 |
0.101 |
-8.97 |
|
|
1 |
2.11126 |
0.01126 |
3.95E-05 |
-8.96286 |
|
2 |
2.111264 |
4.4E-06 |
6.47E-12 |
-8.96286 |
|
3 |
2.111264 |
7.22E-13 |
0 |
-8.96286 |
Если сравнивать с методом
простой итерации, то значение этого корня мы получили за две итерации вместо
шести.
Эти примеры показывают, что
метод Ньютона является более быстросходящимся. Но для его использования
необходимо брать начальное приближение достаточно близким к корню.
Упрощенный
метод Ньютона. Эта модификация метода Ньютона используется, если
производная f /(x) представляет
собой сложную функцию, и для ее вычисления на каждой итерации используется
много времени. Зададим x0 – начальное
приближение и вычислим производную z=f /(x0). На следующих итерациях
используется вычисленное значение производной: . Это упрощение
несколько замедляет процесс сходимости к решению, однако сокращает время
каждого итерационного цикла.
Метод хорд
В этом методе
кривая f(x) заменяется прямой линией – хордой, стягивающей точки (a, f(a)) и (b,
f(b)). В зависимости от знака выражения f(a) f //(a)
метод хорд имеет два варианта, изображенных на рис. 2 а, б.
|
|
|
|
Рис. 2. Метод хорд |
Пусть f(a)f //(a)>0 (рис. 2 а). Тогда x0=b,
точка a будет оставаться неподвижной. Следующее приближение x1
находим как точку пересечения хорды, соединяющей точки (a, f(a)) и (x0, f(x0))
с осью x. Уравнение хорды: . Тогда точка пересечения
хорды с осью x: .
Пусть теперь f(a)f //(a)<0 (рис. 2). Тогда x0=a,
точка b неподвижна. Проведем хорду, соединяющую точки (b, f(b)) и (x0, f(x0)):. Вычисляем точку пересечения
хорды с осью x: .
На следующей
итерации в качестве x0 надо взять вычисленное значение x1.
Таким образом,
имеем следующую последовательность вычислений:
Если f(a) f //(a)>0, то x0=b и .
Если же f(a) f //(a)<0, то x0=a и .
Окончание
итерационного цикла в этом методе происходит по условию малости невязки
уравнения: |f(x1)| < ε или .
Задание. Найти первый и третий
корень уравнения x3‑ 6x2+3x+11=0 методом хорд.
Для первого
корня a=-2, b=-1. , тогда расчет ведется по
первым формулам: x0=b
и .
|
k |
xk |
|xk+1-xk| |
f(xk) |
|
0 |
-1 |
1 |
|
|
1 |
-1.03571 |
0.035714 |
0.345618 |
|
2 |
-1.0479 |
0.012187 |
0.117007 |
|
3 |
-1.05201 |
0.004108 |
0.039334 |
|
4 |
-1.05339 |
0.001379 |
0.013192 |
|
5 |
-1.05385 |
0.000462 |
0.004421 |
Для последнего корня: a=4, b=5, 
формулам: x0=a и .
|
k |
xk |
|xk+1-xk| |
f(xk) |
|
0 |
4 |
-9 |
|
|
1 |
4.9 |
0.9 |
-0.711 |
|
2 |
4.941555 |
0.041555 |
-0.02147 |
|
3 |
4.942783 |
0.001229 |
-0.00062 |
|
4 |
4.942819 |
3.57E-05 |
-1.8E-05 |





















 .
.


 постоянная интегрирования А=0. Таким образом, в этом случае коммутация не повлечет за собой переходного процесса, и в цепи сразу возникнет установившийся режим.
постоянная интегрирования А=0. Таким образом, в этом случае коммутация не повлечет за собой переходного процесса, и в цепи сразу возникнет установившийся режим. свободная составляющая максимальна по модулю. В этом случае ток переходного процесса достигает своей наибольшей величины.
свободная составляющая максимальна по модулю. В этом случае ток переходного процесса достигает своей наибольшей величины.





 .
. переходный процесс в ней будет носить апериодический характер, если
переходный процесс в ней будет носить апериодический характер, если  .
.