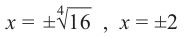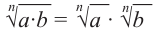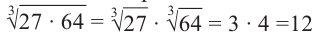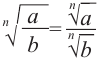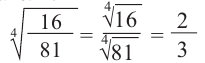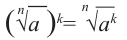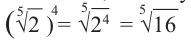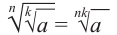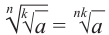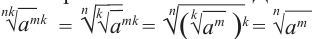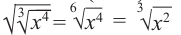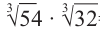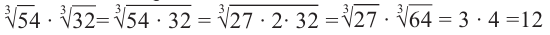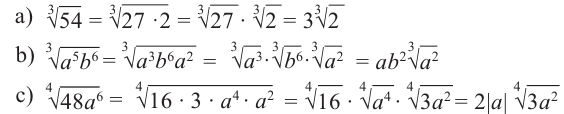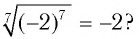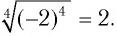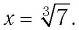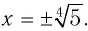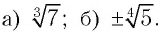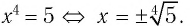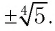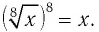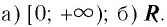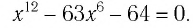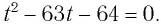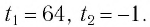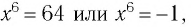Как извлечь корень 6-ой степени из числа?
Корень 6-ой степени обозначается знаком — 6√
6√y=x (корень 6-ой степени из числа y, равен х)
x6= y (в свою очередь при возведении x в 6-ую степень, получим искомое число y)
Что такое корень n-й степени из действительного числа
Чтобы научиться работать с корнями степени (n), необходимо знать, что такое арифметический КВАДРАТНЫЙ корень и его свойства.
Корнем n-й степени ((n=2, 3, 4, 5, 6… )) некоторого числа (a) называют такое неотрицательное число (b), которое при возведении в степень (n in N) дает (a). Корень n-ой степени обозначается при помощи знака радикала (sqrt[n]{a}):
$$ sqrt[n]{a}=b; $$
$$ b^{n}=underbrace{b*b*b*…*b}_{n ; раз}=a. $$
Число (n in N) при этом называют показателем корня, а число (a) подкоренным выражением.
Если (n=2), то перед вами корень 2-й степени или, другими словами, обычный арифметический квадратный корень, который все проходили в 8-м классе.
Если (n=3), то это корень 3-й степени, (sqrt[3]{a}). Его обычно называют кубическим корнем. Чтобы его вычислить, нужно найти такое число, которое умноженное на само себя три раза, даст подкоренное выражение.
Если (n=4), то корень 4-й степени, (sqrt[4]{a}) и т.д.
Операция извлечения корня n-й степени является обратной к операции возведения в n-ю степень. Для того, чтобы вычислить корень n-й степени от (a), нужно сообразить какое число в степени (n) будет давать (a).
Пример 1
$$ sqrt[3]{27}=3 $$
Кубический корень из числа 27 равняется 3. Действительно, если число 3 возвести в 3-ю степень, то мы получим 27.
Пример 2
$$ sqrt[4]{16}=2 $$
Корень 4-й степени из 16-и равен 2. Двойка в 4-й степени равна 16.
Пример 3
$$ sqrt[n]{0}=0 $$
Если извлечь корень n-й степени из 0, всегда будет 0.
Пример 4
$$ sqrt[n]{1}=1 $$
Если извлечь корень n-й степени из 1, всегда будет 1.
Пример 5
$$ sqrt[3]{19}= ? $$
Мы не можем в уме подобрать такое число, которое при возведении в 3-ю степень даст 19. Если посчитать на калькуляторе, то получим (2,668…) – иррациональное число с бесконечным количеством знаков после запятой.
Обычно, в математике, когда у вас получается иррациональное число, корень не считают и оставляют так как есть (sqrt[3]{19}).
Что же делать, если под рукой нет калькулятора, а нужно оценить, чему равен такой корень. В этом случае нужно подобрать справа и слева ближайшие числа, корень из которых посчитать можно:
$$ sqrt[3]{8} le sqrt[3]{19} le sqrt[3]{27} $$
$$ 2 le sqrt[3]{19} le 3 $$
Получается, что наш корень лежит между числами 2 и 3.
Пример 6
Оценить значение (sqrt[4]{15}= ?)
$$ sqrt[4]{1} le sqrt[4]{15} le sqrt[4]{16}; $$
$$ 1 le sqrt[4]{15} le 2; $$
Корень четной и нечетной степеней
Надо четко различать правила работы c четными и нечетными степенями. Дело в том, что корень четной степени можно взять только из неотрицательного числа. Из отрицательных чисел корень четной степени не существует.
Корень нечетной степени можно посчитать из любых действительных чисел. Иногда в школьной программе встречаются задания, в которых требуется определить имеет ли смысл выражение:
Пример 7
$$ sqrt[3]{-27}=-3 $$
Данное выражение имеет смысл, так как корень нечетной степени можно посчитать из любого числа, даже отрицательного. Напоминаю, что извлечь корень 3-й степени, значит найти такое число, которое при возведении в 3-ю степень даст покоренное выражение. Если ((-3)) умножить на само себя три раза, то мы получим покоренное выражение (-27=(-3)*(-3)*(-3)).
Пример 8
$$ sqrt[4]{-27} $$
Так как корень четной степени, а под корнем стоит отрицательное число, то выражение не имеет смысла. Невозможно найти число, которое при умножении на само себя четыре раза, даст отрицательное значение.
Из-под знака нечетного показателя корня можно выносить минус. Это упрощает процесс подсчета.
$$sqrt[5]{-32}=-sqrt[5]{32}=-2;$$
Свойства корня n-й степени
Пусть есть два числа a и b, для них будут выполняться следующие свойства:
$$ (sqrt[n]{a})^n=a $$
$$ sqrt[n]{a^n}=a $$
$$ sqrt[n]{a*b}=sqrt[n]{a}*sqrt[n]{b} $$
$$ sqrt[n]{frac{a}{b}}=frac{sqrt[n]{a}}{sqrt[n]{b}}, b neq 0 $$
$$ (sqrt[n]{a})^k=sqrt[n]{a^k} $$
$$sqrt[n] {sqrt[k]{a}}=sqrt[n*k]{a} $$
$$ sqrt[n*p]{a^{k*p}}=sqrt[n]{a^k} $$
При использовании вышеперечисленных свойств важно помнить: корень четной степени не существует из отрицательных чисел, и сам корень четной степени всегда положителен. Надо быть внимательным и следить, чтобы в ходе преобразований эти ограничения не нарушались.
Рассмотрим примеры на свойства корня степени (n).
Пример 9
$$(sqrt[5]{7})^5=7;$$
При возведении корня с показателем (n) в степень (n) остается просто подкоренное выражение, так как возведение в степень и извлечение корня это взаимно обратные операции.
Обратите внимание, что неважно, где стоит степень — над корнем или под корнем, результат будет одинаковым.
$$sqrt[5]{7^5}=7$$
Из рассмотренного выше примера следует свойство ((sqrt[n]{a})^k=sqrt[n]{a^k}). Не имеет значения, извлекаете ли вы сначала корень, а потом возводите в степень, или наоборот, сначала возводите в степень подкоренное выражение, и только потом извлекаете корень.
Пример 10
$$sqrt[3]{8^2}=(sqrt[3]{8})^2=2^{2}=4;$$
$$sqrt[3]{8^2}=sqrt[3]{64}=4;$$
Получается одно и тоже.
Более того, показатель корня и степень подкоренного выражения можно домножить на одно и тоже число (p), результат от этого не изменится. Может пригодиться в различных преобразованиях и при сравнении корней между собой.
$$ sqrt[n]{a^k}=sqrt[n*p]{a^{k*p}};$$
Пример 11
$$ sqrt[3]{10^2}=sqrt[3*2]{10^{2*2}}=sqrt[6]{10^{4}}=sqrt[6]{1000};$$
Эту же формулу можно использовать наоборот:
$$ sqrt[n*p]{a^{k*p}}=sqrt[n]{a^k} $$
То есть можно сокращать показатель корня и степень подкоренного выражения, что существенно упрощает вычисления в некоторых случаях.
Пример 12
$$ sqrt[6]{16}=sqrt[6]{2^4}=sqrt[3]{2^2}=sqrt[3]{4};$$
Рассмотрим применение формул корня от произведения и частного, без которых невозможно решить ни один приличный пример.
Корень степени (n) от произведения равен произведению корней степени (n) от этих множителей.
$$ sqrt[n]{a*b}=sqrt[n]{a}*sqrt[n]{b} $$
И аналогично корень степени (n) от частного равен частному корней n-й степени.
$$ sqrt[n]{frac{a}{b}}=frac{sqrt[n]{a}}{sqrt[n]{b}}, b neq 0 $$
Пример 13
$$sqrt[3]{125*8}=sqrt[3]{125}*sqrt[3]{8}=5*2=10;$$
$$sqrt[3]{-frac{27}{8}}=frac{-sqrt[3]{27}}{sqrt[3]{8}}=frac{-3}{2};$$
Формулы справедливы не только для двух множителей:
Пример 14
$$sqrt[3]{125*8*27}=sqrt[3]{125}*sqrt[3]{8}*sqrt{27}=5*2*3=30;$$
Пример 15
$$sqrt[4]{frac{16*81}{625}}=frac{sqrt[4]{16*81}}{sqrt[4]{625}}=frac{sqrt[4]{16}*sqrt[4]{81}}{sqrt[4]{625}}=frac{2*3}{5}=frac{6}{5};$$
Обратите внимание! Формулы произведения и частного корней справедливы только для корней с одинаковыми показателями. Нельзя перемножить корни с разными показателями.
$$sqrt[3]{6}*sqrt[4]{7}=?$$
Ничего здесь сделать мы не можем!
И следите за отрицательными числами при использовании корней четной степени. Произведение двух отрицательных чисел может существовать под одним корнем, так как они при умножении дают знак плюс. Но разбивать такое произведение на два корня четной степени ни в коем случае нельзя: выражение теряет всякий смысл.
$$sqrt[4]{-15*(-7)} neq sqrt[4]{-15}*sqrt[4]{-7};$$
$$sqrt[4]{-15*(-7)} = sqrt[4]{15*7}=sqrt[4]{15}*sqrt[4]{7};$$
Корни и степени
-
Степень с натуральным показателем
-
Степень с целым показателем
-
Кубический корень
-
Корень -ной степени
-
Сравнение арифметических корней
-
Как избавиться от иррациональности в знаменателе
-
Как упрощать иррациональные выражения, пользуясь формулами сокращенного умножения
Степенью называется выражение вида .
Здесь — основание степени,
— показатель степени.
к оглавлению ▴
Степень с натуральным показателем
Проще всего определяется степень с натуральным (то есть целым положительным) показателем.
По определению, .
Выражения «возвести в квадрат» и «возвести в куб» нам давно знакомы.
Возвести число в квадрат — значит умножить его само на себя.
.
Возвести число в куб — значит умножить его само на себя три раза.
.
Возвести число в натуральную степень — значит умножить его само на себя
раз:
к оглавлению ▴
Степень с целым показателем
Показатель степени может быть не только натуральным (то есть целым положительным), но и равным нулю, а также целым отрицательным.
По определению,
.
Это верно для . Выражение 00 не определено.
Определим также, что такое степень с целым отрицательным показателем.
Конечно, все это верно для , поскольку на ноль делить нельзя.
Например,
Заметим, что при возведении в минус первую степень дробь переворачивается.
Показатель степени может быть не только целым, но и дробным, то есть рациональным числом. В статье «Числовые множества» мы говорили, что такое рациональные числа. Это числа, которые можно записать в виде дроби , где
— целое,
— натуральное.
Здесь нам понадобится новое понятие — корень -степени. Корни и степени — две взаимосвязанные темы. Начнем с уже знакомого вам арифметического квадратного корня.
Определение.
Арифметический квадратный корень из числа — это такое неотрицательное число, квадрат которого равен
.
Согласно определению,
В школьной математике мы извлекаем корень только из неотрицательных чисел. Выражение для нас сейчас имеет смысл только при
.
Выражение всегда неотрицательно, т.е.
. Например,
.
Свойства арифметического квадратного корня:
Запомним важное правило:
По определению, 
к оглавлению ▴
Кубический корень
Аналогично, кубический корень из — это такое число, которое при возведении в третью степень дает число
.
Например, , так как
;
, так как
;
, так как
.
Обратите внимание, что корень третьей степени можно извлекать как из положительных, так и из отрицательных чисел.
Теперь мы можем дать определение корня -ной степени для любого целого
.
к оглавлению ▴
Корень  -ной степени
-ной степени
Корень -ной степени из числа
— это такое число, при возведении которого в
-ную степень получается число
.
Например,
Заметим, что корень третьей, пятой, девятой — словом, любой нечетной степени, — можно извлекать как из положительных, так и из отрицательных чисел.
Квадратный корень, а также корень четвертой, десятой, в общем, любой четной степени можно извлекать только из неотрицательных чисел.
Итак, — такое число, что
. Оказывается, корни можно записывать в виде степеней с рациональным показателем. Это удобно.
По определению,
в общем случае .
Сразу договоримся, что основание степени больше 0.
Например,
Выражение по определению равно
.
При этом также выполняется условие, что больше 0.
Например,
Запомним правила действий со степенями:
— при перемножении степеней показатели складываются;
— при делении степени на степень показатели вычитаются;
— при возведении степени в степень показатели перемножаются;
Покажем, как применяются эти формулы в заданиях ЕГЭ по математике:
1.
Внесли все под общий корень, разложили на множители, сократили дробь и извлекли корень.
2.
3.
Здесь мы записали корни в виде степеней и использовали формулы действий со степенями.
4. Найдите значение выражения при
Решение:
При получим
Ответ: -0,5.
5. Найдите значение выражения при
Решение:
При a = 12 получим
Мы воспользовались свойствами степеней.
Ответ: 144.
6. Найдите значение выражения при b = — 5.
Решение:
При b = — 5 получим:
Ответ: -125.
7. Расположите в порядке возрастания:
Решение:
Запишем выражения как степени с положительным показателем и сравним.
Так как
то
Так как
то
Сравним и
для этого оценим их разность:
значит
Получим : поэтому
Ответ:
8. Представьте выражение в виде степени:
Решение:
Вынесем за скобку степень с меньшим показателем:
Ответ:
9. Упростите выражение:
Решение:
Приведем основания 6 и 12 к основаниям 2 и 3:
(выполним деление степеней с одинаковыми основаниями)
Ответ: 0,25.
10. Чему равно значение выражения при
?
Решение:
При получим
Ответ: 9.
к оглавлению ▴
Сравнение арифметических корней
11. Какое из чисел больше: или
?
Решение:
Возведем в квадрат оба числа (числа положительные):
Найдем разность полученных результатов:
так как
Значит, первое число больше второго.
Ответ:
к оглавлению ▴
Как избавиться от иррациональности в знаменателе
Если дана дробь вида то нужно умножить числитель и знаменатель дроби на
:
Тогда знаменатель станет рациональным.
Если дана дробь вида или
то нужно умножить числитель и знаменатель дроби на сопряженное выражение, чтобы получить в знаменателе разность квадратов.
Сопряженные выражения — это выражения, отличающиеся только знаками. Например,
и
и
— сопряженные выражения.
Пример:
12. Вот несколько примеров — как избавиться от иррациональности в знаменателе:
Пример 1.
Пример 2.
Пример 3.
Пример 4.
Совет. Если в знаменателе дана сумма двух корней, то в разности первым числом пишите то, которое больше, и тогда разность квадратов корней будет положительным числом.
Пример 5.
13. Сравните и
1)
2) Сравним и 14.
то и
а значит,
Ответ: меньше.
к оглавлению ▴
Как упрощать иррациональные выражения, пользуясь формулами сокращенного умножения
Покажем несколько примеров.
14. Упростите: выражения:
Пример 5.
т.к.
Пример 6.
Пример 7.
так как
Следующие несколько задач решаются с помощью формулы:
Решение:
Получим уравнение
Ответ:
19. Вычислите значение выражения:
Решение:
Ответ: 1.
20. Вычислите значение выражения:
Решение:
Ответ: 1.
21. Вычислите значение выражения: если
Решение.
Если то
следовательно
Ответ: — 1.
22. Вычислите:
Решение:
Ответ: 1.
Рассмотрим уравнение вида где
Это равенство выполняется, только если
Подробно об таких уравнениях — в статье «Показательные уравнения».
При решении уравнений такого вида мы пользуемся монотонностью показательной функции.
23. Решите уравнение:
а)
б)
в)
Решение.
23. Решите уравнение:
Решение:
тогда
Ответ: -1.
24. Решите уравнение:
Решение:
Ответ: 4.
25. Решите уравнение:
Решение:
Значит,
Ответ: -0,2.
Если вы хотите разобрать большее количество примеров — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Корни и степени» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Содержание:
Перейдем к изучению корней степени п для произвольного натурального числа
Определение:
Пусть 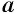
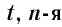
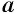
Таким образом, утверждение «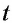
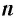
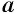
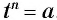
Корень 3-й степени называется также кубическим.
Например, кубический корень из числа 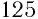
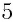

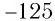
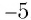
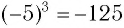
Корень 7-й степени из числа 128 — это число 2, так как 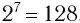
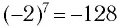
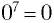
Во множестве действительных чисел существует единственный корень нечетной степени п из любого числа 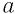
Например, 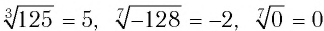
Утверждение о существовании корня нечетной степени из любого числа мы принимаем без доказательства. Согласно определению, когда п нечетное, то при любом значении а верно равенство
Например,
Заметим, что 0 — это единственное число, 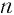
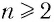
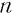
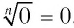
Примерами корней четной степени могут служить квадратные корни: -7 и 7 — квадратные корни из 49, а -15 и 15 — из 225. Рассмотрим еще несколько примеров. Корни 4-й степени из числа 81 — это числа 3 и -3, так как 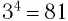
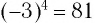
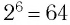
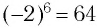
Во множестве действительных чисел существует ровно два корня четной степени п из любого положительного числа а, их модули равны, а знаки противоположны. Положительный корень обозначается
Например,
Утверждение о существовании корня четной степени из любого положительного числа мы принимаем без доказательства. Согласно определению, когда 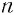
Например, 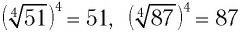
Не существует такого числа, 4-я степень которого равна -81. Поэтому корня 4-й степени из числа -81 не существует. И вообще, поскольку не существует такого числа, четная степень которого была бы отрицательной, то не существует корня четной степени из отрицательного числа.
Определение:
Неотрицательный корень 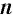
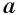
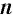
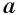
При четном 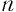
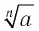
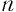
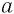
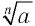
Выражение, стоящее под знаком корня, называется подкоренным выражением.
Извлечь корень 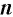
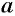
Так как корня четной степени из отрицательного числа не существует, то выражение 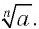
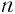
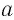
Например, не имеют смысла выражения
Как мы установили, при любом значении 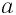
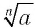
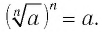
Поэтому равенство (1) является тождеством.
В конце XV в. бакалавр Парижского университета Н. Шюке внес усовершенствования в алгебраическую символику. В частности, знаком корня служил символ 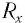
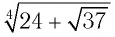
Знак корня 
Знак 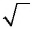
Определение корня n-й степени
Корнем 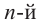
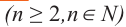
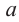
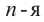
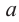
Например, корнем 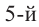
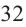
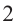
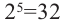
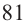
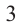
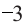
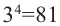
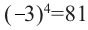
Если 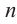
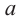
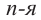
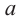
Если 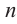
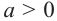
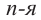
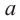
Если 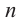
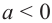
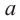
Арифметическим корнем 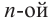
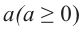
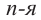
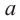
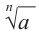
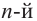
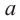
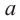
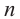
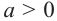
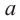
Корень нечетной степени из отрицательного числа можно выразить через арифметический корень той же степени. Например,
Если 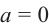
Если 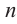
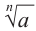
Если 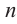
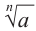
При всех значениях имеющего смысл выражения 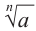
Если 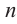
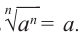
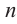
Пример 1:
Если 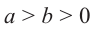
Пример 2:
Примеры:
- Уравнение с нечетной степенью
имеет единственный действительный корень:
- Уравнение
не имеет действительных корней, т.к. степень с четным показателем не равна отрицательному числу.
- Уравнение
имеет два действительных корня:
Корень n-й степени и его свойства
Свойство 1.
Если 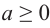
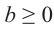
Корень 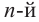
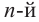
Пример:
Свойство 2.
Если 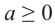
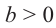
Корень из дроби 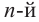
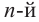
Пример:
Свойство 3.
Если 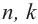
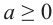
Пример:
Свойство 4.
Если 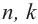
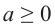
Действительно, при 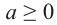
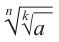
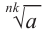
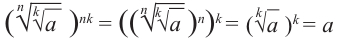
Пример:
Свойство 5.
Если 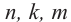
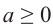
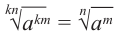
Пример:
Пример: Вычислите значение выражения
- Заказать решение задач по высшей математике
Вынесение множителя из-под знака контроля
Примеры:
Примеры с решением
Пример №1
Верно ли, что:
а)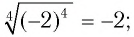
Решение:
а) По определению арифметический корень 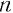
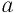
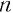

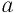
Поскольку 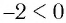
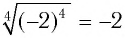
б) По определению корень 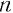
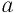
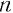
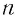
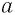
Поскольку 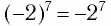
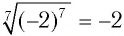
Пример №2
Решить уравнение:
Решение:
а) Решением этого уравнения является такое значение 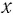
б) Решением этого уравнения является такое значение х, 4-я степень которого равна 5, т. е. (по определению) 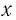
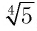
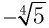
Ответ:
В тетради решение уравнения б) (аналогично и а)) можно записать так:
Решение:
Ответ:
Пример №3
Решить уравнение:
Решение:
а) Число 8 — четное, значит, данное равенство является тождеством при 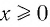
б) Число 13 — нечетное, значит, данное равенство является тождеством при любом значении 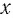
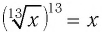
Ответ:
Пример №4
Решить уравнение:
Решение:
Обозначим 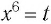
Корни этого уравнения
Таким образом, имеем
откуда 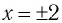
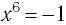
Ответ:
- Тождества с корнями, содержащие одну переменную
- Действия с корнями нечетной степени
- Действия с корнями четной степени
- Бесконечно убывающая геометрическая прогрессия
- Показательные уравнения и неравенства
- Логарифмические уравнения и неравенства
- Степенная функция — определение и вычисление
- Степень с целым показателем

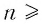
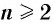
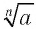
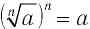
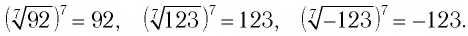
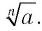
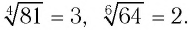
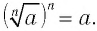
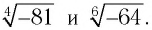
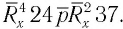
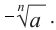
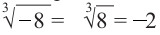
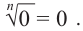
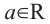
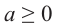
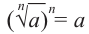
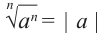

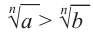
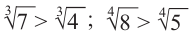
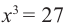 имеет единственный действительный корень:
имеет единственный действительный корень: 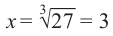
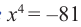 не имеет действительных корней, т.к. степень с четным показателем не равна отрицательному числу.
не имеет действительных корней, т.к. степень с четным показателем не равна отрицательному числу.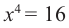 имеет два действительных корня:
имеет два действительных корня: