Основными уравнениями школьной алгебры являются линейные и квадратные. Все остальные уравнения путём различных тождественных преобразований или путём соответствующей подстановки сводятся к ним.
Линейные уравнения
Линейные уравнения ах = b, где а ≠ 0; x=b/a.
Пример 1. Решите уравнение – х + 5,18 = 11,58.
Решение:
– х + 5,18 = 11,58;
– х = – 5,18 + 11,58;
– х = 6,4;
х = – 6,4.
Ответ: – 6,4.
Пример 2. Решите уравнение 3 – 5(х + 1) = 6 – 4х.
Решение:
3 – 5(х + 1) = 6 – 4х;
3 – 5х – 5 = 6 – 4х;
– 5х + 4х = 5 – 3+6;
– х = 8;
х = – 8.
Ответ: – 8.
Пример 3. Решите уравнение 
Решение:

2х + 3(х – 1) = 12; 2х + 3х – 3 =12; 5х = 12 + 3; 5х = 15; х = 3.
Ответ: 3.
Пример 4. Решите систему 
Решение:
Из уравнения 3х – у = 2 найдём у = 3х – 2 и подставим в уравнение 2х + 3у = 5.
Получим: 2х + 9х – 6 = 5; 11х = 11; х = 1.
Следовательно, у = 3∙1 – 2; у = 1.
Ответ: (1; 1).
Замечание.
Если неизвестные системы х и у, то ответ можно записать в виде координаты точки.
Квадратные уравнения
Квадратные уравнения ax2 + bx + c = 0, где а ≠ 0.
D = b2 – 4ac;

нет решения при D < 0.
При решении квадратных уравнений полезно помнить формулу чётного коэффициента, т.е. случай, когда b = 2k или k =b/2:

х2 + px + q = 0 – приведённое квадратное уравнение. Для него справедлива теорема Виета:
где х1 и х2 – корни уравнения.
Пример 5. Решите уравнение 3у + у2 = у.
Решение:
3у + у2 = у – неполное квадратное уравнение; у2 + 3у – у = 0;
у2 + 2у =0; у∙(у + 2) = 0.
Помните! Произведение равно нулю, когда хотя бы один из сомножителей равен нулю, но второй при этом имеет смысл.
y1 = 0, или у + 2 = 0;
у2 = – 2.
Ответ: – 2; 0.
Пример 6. Решите уравнение 18 – х2 = 14.
Решение:
18 – х2 = 14 – неполное квадратное уравнение; – х2 = 14 – 18;
– х2 = – 4; х2 =4; х = ± 2.
Ответ: ± 2.
Пример 7. Решите уравнение х2 + 6х – 3 = 2х3.
Решение:
х2 + 6х – 3 = 2х3 – уравнение 3-ей степени. Оно решается разложением на множители: х2 – 2х3 + 6х – 3 = 0;
– х2(2х – 1 ) + 3(2х – 1) = 0;
(2х – 1)(3 – х2) = 0;
2х – 1 = 0 или 3 – х2 =0;
х1 = 0,5; х2,3 =
Ответ: 0,5; 
Пример 8. Решите уравнение (х2 – 5х)2 – 30 (х2 – 5х) – 216 = 0.
Решение:
(х2 – 5х)2 – 30 (х2 – 5х) – 216 = 0 – биквадратное уравнение. Такое уравнение решается методом подстановки.
Метод подстановки позволяет перейти к уравнению, равносильному данному.
Пусть х2 – 5х = t. Тогда уравнение примет вид t2 – 30t – 216 = 0;
x2 – 5х = – 6 или х2 – 5х = 36;
х2 – 5х + 6 = 0 или х2 – 5х – 36 =0.
По теореме Виета:
х1 = 2, х2 = 3, х3 = – 4, х4 =9.
Ответ: – 4, 2, 3, 9.
Пример 9. Вычислить наибольший корень уравнения х4 – 7х3 + 14х2 – 7х + 1 = 0.
Решение:
х4 – 7х3 + 14х2 – 7х + 1 = 0 │: х2 (х ≠ 0)
t2 – 2 – 7t + 14 = 0;
t2 – 7t + 12 = 0;
t1 =3; t2 = 4.
х2 – 3х + 1 = 0 или х2 – 4х + 1 = 0;
D = 9 – 4 = 5, D = 16 – 4 = 12
x1 и х3 – меньшие корни. Остаётся сравнить х2 и х4.
– больший корень.
Ответ:
Пример 10. Найти все целые решения системы уравнений
Решение:
Решаем уравнение 2(х + у)2 + (х + у) = 21.
Пусть х + у = t. Тогда получим 2t2 + t – 21 = 0; t1 =-7/2 ; t2 = 3.
x + у = -7/2 не удовлетворяет условию задачи, так как хотя бы одно из слагаемых в данной сумме будет нецелым числом.
x + у = 3 – удовлетворяет условию.
Решением системы будут (1; 2) или (2; 1).
Ответ: (1; 2), (2; 1).
Рациональные уравнения
Уравнение, содержащее неизвестную в знаменателе, называют рациональным.
При решении рационального уравнения необходимо исключать те значения неизвестного, при которых знаменатель обращается в нуль.
Пример 11. Решить уравнение

Решение:
Область определения уравнения х – 2 ≠ 0. В данном случае левую часть уравнения можно сократить на ( ).
По т. Виета х1 = 1, х2 = 3.
Ответ: 1; 3.
Пример 12. Решить уравнение
Решение:
Ответ: 2.
Пример 13. Решить уравнение
Решение:
Так как x2+5 быть равным нулю не может, то данное уравнение будет равносильно уравнению 3(x2+5)2-23(x2+5)-8=0, которое решается методом подстановки. Пусть x2+5=t .
Имеем 3t2-23t-8=0; t1=-1/3; t2=8.
x2+5≠-1/3. Остаётся x2+5=8; x2=3; x=
Ответ: 
Пример 14. Решить систему
Решение:
Полученное решение системы удовлетворяет области определения.
Ответ: х = 2; у = 4.
Иррациональные уравнения
Уравнение, содержащее неизвестную под знаком корня n-ой степени, называется иррациональным.
Иррациональное уравнение чаще всего решается путём возведения в степень, которую имеет корень, содержащий неизвестную, или заменой неизвестной. Не следует забывать, что в степень возводятся обе части уравнения.
При возведении в нечётную степень обеих частей уравнения, получаем уравнение, равносильное исходному.
Новое уравнение, получившееся после возведения в чётную степень обеих частей, не всегда равносильно исходному уравнению, поэтому необходимо либо выполнить проверку полученных значений неизвестного путём подстановки в исходное уравнение, либо отбросить корни, не принадлежащие области определения уравнения.
Пример 15. Решить уравнение 
Решение:
Область определения: х + 1 ≥ 0.
x2 – 4 = 0 или х + 1 = 0;
х1 = – 2 , х3 = – 1.
х2 = 2,
х1 = – 2 не принадлежит области определения.
Ответ: – 1; 2
Пример 16. Решить уравнение .
Решение:
Данное уравнение решается возведением в квадрат левой и правой частей, и, так как в правой части уравнения содержится переменная, мы получим уравнение не равносильное исходному.
15 – 3х = х2 + 2х + 1; х2 + 5х – 14 = 0; х1 = – 7, х2 = 2.
Проверка. При х1 = – 7, 
При х2 = 2, 
Ответ: 3.
Пример 17. Решить систему
Решение:
В данном случае не требуется ни проверка, ни нахождение области определения, поскольку правые части обоих уравнений и до возведений в квадрат, и после – заведомо положительны.
Ответ: (29; 20).
Уравнения, содержащие знак модуля
Пример 18. Решите уравнение 
Решение:
х + 5 = 3 или х + 5 = – 3. Откуда х1 = – 2 или х2 = – 8.
Ответ: – 2; – 8.
Пример 19. Решите уравнение 
Решение:
Данное уравнение будем рассматривать на двух числовых промежутках:
Значение –1/2 назовём пограничным, т.е. при х = –1/2, 2х – 1 = 0.
При 
При 
Помните!
Пограничное значение смены знака необходимо включить хотя бы в один из интервалов.
Ответ: -4/3; 2.
Пример 20. Решите уравнение 
Решение:
Двучлен х – 3 меняет свой знак при переходе через х = 3, а х + 1 – при х = – 1. Данное уравнение будем рассматривать на трёх числовых промежутках:
1)

2) 

3) 

Ответ: – 1.
Пример 21. Решить систему
Решение:
Ответ: (3; – 1), (1; – 3).
Уравнения с параметром
Пример 22. При каком значении а уравнение х(2 – а) – х = 5 + х не имеет решений?
Решение:
Выразим х через а. 2х – ах – х – х = 5; – ах = 5; х = –5/a .
При а = 0 х не определён.
Подставим а = 0 в исходное уравнение: х(2 – 0) – х = 5 + х; 2х – 2х = 5; 0 ≠ 5, следовательно, при а =0 данное уравнение не имеет решения.
Ответ: при а = 0.
Пример 23. Корни х1 и х2 уравнения х2 + х + а = 0 обладают свойством x12+x22=5 . Найти а.
Решение:
Уравнение х2 + х + а = 0 – приведённое квадратное. По теореме Виета х1 + х2 = – 1, х1 ∙ х2 = а. Т.к. x12+x22=5, то х1 – х2 = – 5.
Имеем х1 = – 3; х2 = 2, следовательно, а = (– 3)∙2= – 6.
Ответ: а = – 6.
Пример 24. При каких значениях параметра n уравнение (n-2)x2-2nx+n+3=0 имеет корни разных знаков.
Решение:
n – 2 ≠ 0. В противном случае – нет квадратного уравнения.
Приведём исходное уравнение (путём почленного деления обеих частей равенства на n – 2) к приведённому:
Чтобы уравнение имело корни разных знаков, необходимо и достаточно выполнение двух условий одновременно:
1) D/4 > 0 (по формуле чётного коэффициента);
2) x1 ∙ x2 < 0 (по теореме Виета):
Ответ: 
Показательные уравнения и системы уравнений
Пример 25. Решите уравнение 62-x=63-2x.
Решение:
62-x=63-2x; 2 – х = 3 – 2х; х = 1.
Ответ: 1.
Пример 26. Решите уравнение 
Решение:

Ответ: – 2.
Пример 27. Решите уравнение 
Решение:
Ответ: 2.
Пример 28. Решите уравнение .
Решение:
При подстановке полученных значений х1 = 1 и х2 = 10 уравнение 
Ответ: 1, 10.
Пример 29. Укажите промежуток, на котором лежит корень уравнения
Решение:
Применим свойство степени и выделим в левой части уравнения множитель 3х:
Корень уравнения – число 0 – принадлежит промежутку 
Ответ: 1).
Логарифмические уравнения
Пример 30. Укажите отрицательный корень уравнения log5(x2-7x-35)=2.
Решение:
По определению логарифма получаем
Ответ: – 5.
Пример 31. Решите уравнение log3x+log3(3x-2)=log35.
Решение:
Область допустимых значений
В левой части уравнения на основании 3-го свойства получаем log3(x(3x-2))=log35; x(3x-2)=5; 3x2-2x-5=0; x1=5/3; x2=–1. –1 — не принадлежит области допустимых значений, т.е. не является корнем.
5/3 — принадлежит области допустимых значений, т.е. является корнем.
Ответ: 5/3.
Пример 32. Укажите целое решение уравнения
Решение:
Так как правая часть уравнения есть показательная функция, то 
Прологарифмируем обе части уравнения по основанию x2:
К правой части уравнения применим 5-е свойство логарифмов:
К обеим частям уравнения применим 7-е свойство логарифмов:
К обеим частям уравнения применим 4-е свойство логарифмов, сгруппируем и разложим на множители, получим:
(1-logx4)(1+logx4-logx3)=0
1-logx4=0 или 1+logx4-logx3=0
Из первого уравнения получаем х = 4, из второго х = 3/4.
Все найденные значения неизвестного входят в область допустимых значений уравнения, т.е. являются его корнями. Выбираем только целое — 4.
Ответ: 4.
Задачи для самостоятельного решения
Базовый уровень
Линейные уравнения и системы уравнений
1) Решите уравнение 3x=75
2) Решите уравнение 
3) Решите уравнение
4) Решите уравнение 
5) Решите уравнение 
6) Решите систему уравнений
7) Решить систему уравнений


Квадратные уравнения и системы уравнений
9) Решите уравнение х + х2=0.
10) Укажите меньший корень уравнения (2х – 1)(х+3) = 0.
11) Решить систему уравнений
Рациональные уравнения и системы уравнений
12) Решите уравнение 
13) Решите уравнение 
14) Сколько корней имеет уравнение 
Иррациональные уравнения и системы уравнений
15) Решите уравнение 
16) Решите уравнение 
17) Решите уравнение 
18) Решите уравнение 
19) Решите систему уравнений 
20) Решите систему уравнений 
21) Пусть (х0; у0) решение системы уравнений 
22) Решите систему уравнений 
Показательные уравнения и системы уравнений
23) Решите уравнение 52x-3=5 .
24) Решите уравнение 23х+1 = 4.
25) Решите уравнение 9x-5∙3x+1+54=0 .
26) Укажите отрицательный корень уравнения 23x+1-22x=2x+1-1.
27) Решите уравнение 3x+2-3x=72 .
28) Решите уравнение 
29) Решите уравнение 9x-75∙3x-1-54=0.
30) Решите уравнение 
31) Решите уравнение 
Логарифмические уравнения
32) Решите уравнение log2x=5.
33) Решите уравнение 
34) Решите уравнение 3log0.2x=log0.2x4-1 .
35) Решите уравнение 
36) Решите уравнение 
37) Решите уравнение lg(3+2lg(1+x))=0.
38) Решите уравнение log2(54-x3)=3log2x.
Уравнения и системы уравнений, содержащие модуль
39) Найдите наибольший корень уравнения |5-4x|=1.
40) Решите уравнение 2x+|x-13|=8.
41) Решить уравнение |x+1|-8x=|x-5|+4.
42) Решите систему уравнений 
Повышенный уровень
Уравнения с параметром
43) При каких значениях k уравнение x2 + kx + 9 =0 имеет корни?
44) Найти все значения а, при каждом из которых уравнение |2x+3|+|2x-3|=ax+6 имеет один корень.
Сложные уравнения
45) Решите уравнение log3|x+1|=1 .
46) Укажите наибольший корень уравнения
47) Решите уравнение
48) Пусть – решение системы 
49) Укажите целый корень уравнения xlog2x+4=32 .
50) Решите уравнение x2log3x=81x2 и укажите произведение его корней.
51) Решите уравнение lg(x+2)=lg(5x+1)-lg(4-2x).
52) Найдите сумму корней уравнения logx(5x-4)=2.
53) Сколько корней имеет уравнение ln(x2+2x-3)=ln(x-3)?
54) Решите уравнение log7(x-7)-1=log7(5x-1).
55) Укажите все пары (х, у) положительных чисел х и у, удовлетворяющих системе
56) Решите уравнение 
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Натуральные числа и действия над ними
- Уравнения
Уравнение — это равенство, содержащее букву, значение которой надо найти. Например: 


Корень уравнения — это число, которое при подстановке вместо буквы обращает уравнение в верное числовое равенство.
Корень уравнения — это решение уравнения. Уравнение может иметь один и более корней или не иметь их вообще. Тогда говорят, что решить уравнение — значит найти все его корни или показать, что их нет вообще.
Для решения уравнений используют правило нахождения неизвестного:
1) слагаемого: чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.
Решим уравнение 


Ответ: 
2) уменьшаемого: чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
Решим уравнение 


Ответ: 
3) вычитаемого: чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
Решим уравнение 135 — 


Ответ: 
4) множителя: чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
Решим уравнение 
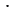


Ответ: 
5) делимого: чтобы найти неизвестное делимое, надо частное умножить на делитель.
Решим уравнение 

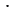

Ответ: 
6) делителя: чтобы найти неизвестный делитель, надо делимое разделить на частное.
Решим уравнение 184 : 


Ответ: 
При решении уравнений проводится проверка решения, для этого найденный корень (или корни) подставляются в уравнение вместо переменной. Если числовое равенство получается верным, то решение найдено верно. При оформлении решения проверка записывается под чертой после решения, а затем пишется ответ, при этом каждое действие записывается на новой строке (т.е. одна строка один знак равенства).
Например, решим уравнение 


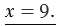
9 + 36 = 45;
45 = 45 — верно.
Ответ: 
Советуем посмотреть:
Понятие о натуральном числе
Сложение натуральных чисел
Вычитание натуральных чисел
Умножение натуральных чисел
Деление натуральных чисел
Порядок выполнения действий
Степень числа. Квадрат и куб числа
Меньше или больше
Меньше или больше на сколько? во сколько раз?
Формулы
Натуральные числа и действия над ними
Правило встречается в следующих упражнениях:
5 класс
Задание 487,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 512,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 569,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 622,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1528,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1664,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1752,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 491,
Мерзляк, Полонский, Якир, Учебник
Номер 1039,
Мерзляк, Полонский, Якир, Учебник
Номер 1088,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 282,
Мерзляк, Полонский, Якир, Учебник
Номер 991,
Мерзляк, Полонский, Якир, Учебник
Номер 997,
Мерзляк, Полонский, Якир, Учебник
Номер 1144,
Мерзляк, Полонский, Якир, Учебник
Номер 1187,
Мерзляк, Полонский, Якир, Учебник
Номер 1210,
Мерзляк, Полонский, Якир, Учебник
Задание 482,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 610,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 886,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1092,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 42,
Мерзляк, Полонский, Якир, Учебник
Номер 45,
Мерзляк, Полонский, Якир, Учебник
Номер 72,
Мерзляк, Полонский, Якир, Учебник
Номер 350,
Мерзляк, Полонский, Якир, Учебник
Номер 427,
Мерзляк, Полонский, Якир, Учебник
Номер 431,
Мерзляк, Полонский, Якир, Учебник
Номер 590,
Мерзляк, Полонский, Якир, Учебник
Номер 1152,
Мерзляк, Полонский, Якир, Учебник
Номер 10,
Мерзляк, Полонский, Якир, Учебник
Номер 11,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 58,
Мерзляк, Полонский, Якир, Учебник
Номер 171,
Мерзляк, Полонский, Якир, Учебник
Номер 175,
Мерзляк, Полонский, Якир, Учебник
Номер 311,
Мерзляк, Полонский, Якир, Учебник
Номер 345,
Мерзляк, Полонский, Якир, Учебник
Номер 353,
Мерзляк, Полонский, Якир, Учебник
Номер 11,
Мерзляк, Полонский, Якир, Учебник
Номер 404,
Мерзляк, Полонский, Якир, Учебник
Номер 405,
Мерзляк, Полонский, Якир, Учебник
Номер 429,
Мерзляк, Полонский, Якир, Учебник
Основные понятия уравнения
Определение
Уравнением называют равенство, в котором одна из переменных неизвестна, и её нужно найти. Значение этой неизвестной должно быть таким, чтобы равенство было верным.
К примеру: 3+4=7 это числовое равенство, при вычислении которого с левой стороны получается 7=7.
Уравнением же будет называться следующее равенство: 3+х=7, поскольку есть неизвестная переменная х, её значение можно найти.
Из этого уравнения следует, что переменная х=4, только при таком его значении равенство 3+х=7, будет верным.
Неизвестные переменные принято писать в виде маленьких латинских букв, можно любыми, но чаще используют x,y,z.
Получается, чтобы равенство сделать уравнением необходимо, чтобы в нем была буква, значение которой неизвестно.
Как мы понимаем существует множество примеров уравнений с разными арифметическими действиями.
Пример: х + 5 = 1= 9; z — 2 = 7; 9 * y = 18, 6 : f = 2
Помимо этого существуют уравнения со скобками. К таким уравнениям относится 8 : (х — 4) = 2 * (8 — х), неизвестных может быть несколько, они могут быть, как слева уравнения, так и справа или в обеих частях.
Помимо таких простых уравнений они могут быть с корнями, логарифмами, степенями и тд.
Уравнение может содержать несколько переменными, тогда их принято называть, соответственно уравнениями с двумя, тремя и более переменными.
Пример:
3 * а = 15 : х — уравнение с двумя переменными:
8 — а = 5 * х — z — уравнение с тремя переменными.
Корень уравнения
Мы часто слышим фразу на уроках математики, «найдите корень уравнения», давайте разберёмся, что же это значит.
Пример:
В примере 3+х=7, можно представить вместо буквы число, и уравнение тогда станет равенством, оно может быть либо верным, либо неверным, если поставить х=3, то первичное равенство примет вид 3+3 = 7 и станет неверным, а если х= 4 то равенство 3+4=7 будет верным, а значит х = 4 будет называться корнем или по другому решением уравнения 3+х=7.
Определение.
Отсюда можно выделить следующее определение: корень уравнения — это такое значение неизвестной переменной, при котором числовое равенство будет верным.
Стоит отметить, что корней может быть несколько или не быть вовсе.
Рассмотрим подробнее пример который не будет иметь корней. Таким примером станет 0 * х = 7, сколько бы чисел мы сюда не подставляли равенство не будет верным, так как умножая на ноль будет ноль, а не 7.
Но существуют и уравнения с множественным числом корней, к примеру, х — 3 = 6, в таком уравнении только один корень 9, а в уравнении квадратного вида х2 = 16, два корня 4 и -4, можно привести пример и с тремя корнями х * (х — 1) * (х — 2) = 0, в данном случае три решения ноль, два и один.
Для того чтобы верно записать результат уравнения мы пишем так:
- Если корня нет, пишем уравнение корней не имеет;
- Если есть и их несколько, они либо прописываются через запятые, либо в фигурных скобках, например, так: {-2, 3, 5};
- Еще одним вариантом написания корней, считается запись в виде простого равенства, к примеру неизвестная х а корни 3,5 тогда результат прописывается так: х=3, х=5.
- или прибавляя индекс снизух1 =3 , х2 = 5. данным способом указывается номер корня;
- Если решений уравнения бесконечное множество, то запись будет либо в виде числового промежутка от и до, или общепринятыми обозначениями. множество натуральных чисел N, целых – Z, действительных — R.
Стоит отметить, что если уравнение имеет два и более корней, то чаще употребляется понятие решение уравнения. Рассмотрим определение уравнения с несколькими переменными.
Решение уравнения с двумя и более переменными, означает, что эти несколько значений превращают уравнение в верное равенство.
Примеры:
Представим, что мы имеем следующее уравнение х + а = 5, такое уравнение имеет две переменные. Если мы поставим вместо них числа 3 и 6 то равенство не будет верным, соответственно и данные числа не являются решением для данного примера. А если взять числа 2 и 3 то равенство превратится в верное, а числа 2 и 3 будут решением уравнения. Представленные уравнения с несколькими переменными, тоже могут или не иметь корня вообще или наоборот иметь множество решений.
Правила нахождения корней
Таких правил существует несколько рассмотрим их ниже.
Пример 1
Допустим мы имеем уравнение 4 + х = 10, чтобы найти корень уравнения или значение х в данном случае необходимо найти неизвестное слагаемое, для этого есть следующее правило или формула. Для нахождения неизвестного слагаемого, нужно из суммы вычесть известное значение.
Решение:
х = 10 — 4
х = 6
Чтобы проверить является ли 6 решением, мы ставим его на место неизвестной переменной х в исходное уравнение, получаем следующее равенство 4 + 6 = 10, такое равенство является верным, что означает число корня уравнения, равно 6.
Пример 2
Возьмём уравнение вида х — 5 = 3, в данном примере х это неизвестное уменьшаемое, для того чтобы его найти необходимо следовать следующему правилу:
Для нахождения уменьшаемого необходимо сложить разность и вычитаемое.
Решение:
х = 3 + 5
х = 8
Проверяем правильность нахождения корня уравнения, подставляем, вместо переменной неизвестной, найденное число 8, получаем равенство 8 — 5 = 3, так как оно верное, то и корень уравнения найден правильно.
Пример 3
Берём уравнение, в котором неизвестное х будет вычитаемое к примеру: 8 — х = 4. для того чтобы найти х необходимо воспользоваться правилом:
Для нахождения вычитаемого, нужно из уменьшаемого вычесть разность.
Решение:
х = 8 — 4
х = 4
Проверяем правильность нахождения корня уравнения, для этого полученное значение ставим вместо неизвестного вычитаемого в исходный пример, и получаем следующее равенство 8 — 4 = 4, равенство верно, значит и корень найден правильно.
Нет времени решать самому?
Наши эксперты помогут!
Пример 4
Возьмём уравнение вида х * 3 = 9, в данном уравнении неизвестна переменная х, является множимым. Для того, чтобы найти корень такого уравнения необходимо использовать следующее правило.
Для нахождения неизвестного множимого, нужно произведение разделить на множитель.
Решение:
х = 9 : 3
х = 3
Для проверки подставим найденное значение х в исходное уравнение, получим равенство 3 * 3 =9, так как равенство является верным, то и решение уравнения верное.
Такое же правило действует и для множителя, чтобы его найти необходимо произведение разделить на множимое.
Пример 5
Возьмём уравнение следующего вида: х : 2 = 10 , в данном уравнении х- это неизвестное делимое, 2 — делитель, а 10 — частное. Для нахождения неизвестного значения х, воспользуемся правилом:
Чтобы найти делимое, необходимо частное умножить на делитель.
Решение:
х = 10 * 2
х = 20
Проверим, вместо неизвестного х, поставим его значение 20, получим следующее равенство 20: 2 = 10. Равенство верное, значит и решение было верным.
Пример 6
Теперь рассмотрим пример с делителем.
Возьмём уравнение 22: х = 11, где х неизвестный делитель. Для того чтобы его найти существует правило:
При нахождении неизвестного делителя нужно делимое разделить на частное.
Решение:
х = 22 : 11
х = 2
Проверяем, 2 ставим на место неизвестного х в исходное уравнение, получаем равенство 22 : 2 = 11. Так как равенство верно, то мы нашли верный корень уравнения.
Пример применения правил в более сложном уравнении: 2х — 5 =5
Решение:
2х = 5 + 5
2х = 10
х = 10 : 2
х = 5
Проверяем, для этого полученное значение х = 5, ставим в исходное уравнение, получаем равенство 2 * 5 — 5 = 5, так как равенство верно, корень найден правильно.
Квадратные уравнения
Существует также уравнения квадратного вида, например: 2х2 = 32, для того, чтобы найти неизвестное или корень квадратного уравнения, в таком уравнении необходимо:
Решение:
х2 = 32 : 2
х2 = 16
х = √16
х = 4
Проверим, для этого полученное значение подставим в исходное уравнение, и получим равенство 242 = 32. так как равенство верное, то и решение уравнения верно.
Как мы видим нахождение корня уравнения не такой сложный процесс, главное запомнить правила. Стоит отметить, что помимо решения различного вида задач, уравнения применяются в других различных науках. Применение уравнений можно найти в экономике, в физике, химии, биологии и других. При их помощи можно вычислить и описать процессы, происходящие вокруг нас.
Калькулятор квадратных корней
Это уравнение вида ax2+bx+c=0ax^2 + bx + c = 0,
где aa – коэффициент перед x2x^2,
bb – коэффициент перед xx,
cc – свободное число.
Существуют разные способы нахождения корней квадратного уравнения. Пожалуй, самый основной и распространенный способ – через вычисление дискриминанта. В этом случае он рассчитывается по формуле:
D=b2–4acD = b^2 – 4ac
Если второй коэффициент уравнения четный, можно решать уравнение через kk, тогда будет другая формула дискриминанта:
D1=k2–acD_1 = k^2 – ac
Если первый коэффициент уравнения равен 1, то можно воспользоваться теоремой Виета, которая имеет 2 условия:
x1+x2=−bx_1 + x_2 = -b
x1⋅x2=cx_1 cdot x_2 = c
Но если мы захотим решить уравнение основным способом, ошибки не будет. Нахождение корней уравнения через дискриминант – универсальный способ, а остальные введены для удобства вычислений.
Задача 1
Решим уравнение: 3×2+7x−6=0.3x^2 + 7x — 6 = 0.
Обозначим коэффициенты:
a=3a = 3,
b=7b = 7,
c=−6c = -6
Далее находим дискриминант по формуле:
D=b2–4acD = b^2 – 4ac
D=72–4∗3∗(−6)=49+72=121=112D = 7^2 – 4 * 3 * (-6) = 49 + 72 = 121 = {11}^2
D>0D > 0 – значит, уравнение имеет 2 корня.
Находим корни уравнения по следующим формулам:
x1=(−b+√D)/2ax_1 = (-b + √D) / 2a
x2=(−b−√D)/2ax_2 = (-b — √D) / 2a
Подставляем численные значения:
x1=(−7+11)/2∗3=4/6=23x_1 = (-7 + 11) / 2*3 = 4 / 6 = frac{2}{3}
x2=(−7–11)/2∗3=−18/6=−3x_2 = (-7 – 11) / 2*3 = -18 / 6 = -3
Ответ: x1=23x_1 = frac{2}{3}, x2=−3x_2 = -3.
Задача 2
Решим уравнение: −x2+7x+8=0.-x^2 + 7x + 8 = 0.
Обозначим коэффициенты:
a=−1a = -1,
b=7b = 7,
c=8.c = 8.
Далее находим дискриминант по формуле:
D=b2–4acD = b^2 – 4ac
D=72–4⋅(−1)⋅8=49+32=81=92D = 7^2 – 4 cdot (-1) cdot 8 = 49 + 32 = 81 = 9^2
D>0D > 0 – значит, уравнение имеет 2 корня.
Находим корни уравнения по следующим формулам:
x1=(−b+√D)/2ax_1 = (-b + √D) / 2a
x2=(−b−√D)/2ax_2 = (-b — √D) / 2a
Подставляем численные значения:
x1=(−7+9)/2∗(−1)=2/(−2)=−1x_1 = (-7 + 9) / 2 * (-1) = 2 / (-2) = -1
x2=(−7–9)/2∗(−1)=−16/(−2)=8x_2 = (-7 – 9) / 2 * (-1) = -16 / (-2) = 8
Ответ: x1=−1x_1 = -1, x2=8x_2 = 8.
Задача 3
Решим уравнение: 4×2+4x+1=0.4x^2 + 4x + 1 = 0.
Обозначим коэффициенты:
a=4a = 4,
b=4b = 4,
c=1.c = 1.
Далее находим дискриминант по формуле: D=b2–4acD = b^2 – 4ac
D=42–4⋅4⋅1=16–16=0D = 4^2 – 4 cdot 4 cdot 1 = 16 – 16 = 0
D=0D = 0 – значит, уравнение имеет 1 корень.
Находим корень уравнения по следующей формуле: x=−b/2ax = -b / 2a
Подставляем численные значения:
x=−4/2⋅4=−4/8=−1/2=−0,5x = -4 / 2 cdot 4 = -4 / 8 = -1 / 2 = -0,5
Ответ: x=−0,5.x = -0,5.
Задача 4
Решим уравнение: 2×2+x+1=0.2x^2 + x + 1 = 0.
Обозначим коэффициенты:
a=2a = 2,
b=1b = 1,
c=1.c = 1.
Далее находим дискриминант по формуле: D=b2–4acD = b^2 – 4ac
D=12–4∗2∗1=1–8=−7D = 1^2 – 4 * 2 * 1 = 1 – 8 = -7
D<0D < 0 – значит, уравнение корней не имеет.
Ответ: корней нет.
Решение квадратного уравнения через k
Если у квадратного уравнения коэффициент bb четный, то можно решать уравнение через kk, при этом k=12bk = frac{1}{2} b.
Задача 5
Решим уравнение: −x2+2x+8=0.-x^2 + 2x + 8 = 0.
Обозначим коэффициенты:
a=−1a = -1,
b=2b = 2,
c=8c = 8
bb – четное.
k=12b=1k = frac {1}{2} b = 1.
Далее находим дискриминант по формуле: D1=k2–acD_1 = k^2 – ac
D1=12–(−1)∗8=1+8=9=32D_1 = 1^2 – (-1) * 8 = 1 + 8 = 9 = 3^2
D1>0D_1 > 0 – значит, уравнение имеет 2 корня.
Находим корни уравнения по следующим формулам:
x1=(−k+D1)/ax_1 = (-k + {sqrt D}_1) / a
x2=(−k−D1)/ax_2 = (-k — {sqrt D}_1) / a
Подставляем численные значения:
x1=(−1+3)/(−1)=2/(−1)=−2x_1 = (-1 + 3) / (-1) = 2 / (-1) = -2
x2=(−1–3)/(−1)=−4/(−1)=4x_2 = (-1 – 3) / (-1) = -4 / (-1) = 4
Ответ: x_1 = -2, x_2 = 4.
Задача 6
Решим уравнение: 9×2–6x+1=0.9x^2 – 6x + 1 = 0.
Обозначим коэффициенты:
a=9a = 9,
b=−6b = -6,
c=1c = 1
bb – четное.
K=12b=−3.K = frac{1}{2} b = -3.
Далее находим дискриминант по формуле: D1=k2–acD_1 = k^2 – ac
D1=(−3)2–9∗1=9–9=0D_1 = {(-3)}^2 – 9 * 1 = 9 – 9 = 0
D1=0D_1 = 0 – значит, уравнение имеет 1 корень.
Находим корень уравнения по следующей формуле: x=−k/ax = -k / a
Подставляем численные значения:
x=3/9=13x = 3 / 9 = frac{1}{3}
Ответ: x=13.x = frac{1}{3}.
Нахождение корней уравнения по теореме Виета
Если в квадратном уравнении a=1a = 1, то можно найти корни уравнения по теореме Виета.
Задача 7
Найдем корни уравнения: x2+3x+2=0.x^2 + 3x + 2 = 0.
Обозначим коэффициенты:
a=1a = 1,
b=3b = 3,
c=2c = 2.
Запишем 2 условия теоремы Виета:
x1+x2=−bx_1 + x_2 = -b
x1∗x2=cx_1 * x_2 = c
Теперь методом подбора найдем 2 числа, которые будут соответствовать этим условиям. Вероятно, это числа -2 и -1.
Значит, корни уравнения равны:
x1=−2x_1 = -2
x2=−1x_2 = -1
Ответ: x1=−2x_1 = -2, x2=−1x_2 = -1.
Задача 8
Найдем корни уравнения: x2–5x+6=0.x^2 – 5x +6 = 0.
Обозначим коэффициенты:
a=1a = 1,
b=−5b = -5,
c=6c = 6
Запишем 2 условия теоремы Виета:
x1+x2=−bx_1 + x_2 = -b
x1∗x2=cx_1 * x_2 = c
Теперь методом подбора найдем 2 числа, которые будут соответствовать этим условиям. Вероятно, это числа 2 и 3.
Значит, корни уравнения равны:
x1=2x_1 = 2
x2=3x_2 = 3
Ответ: x1=2x_1 = 2, x2=3.x_2 = 3.






































