Как найти корень уравнения 6 класс модуль

Уравнения с модулем в 6 классе сводятся к простейшим уравнениям, решение которых опирается на определение модуля. Рассмотрим некоторые из таких уравнений.

Начнем с такого вида:

   

Решаем это уравнение как линейное: неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:

   

Теперь обе части уравнения делим на число, стоящее перед модулем икса:

   

Получили простейшее уравнение с модулем.

Примеры:

   

   

   

   

Ответ: 9;-9.

   

   

   

   

Ответ: 4; -4.

   

   

   

   

Данное уравнение не имеет решений, так как модуль не может быть отрицательным числом.

Ответ: нет решений.

Также в 6 классе встречаются уравнения с модулем вида

   

Это уравнение — почти простейшее уравнение с модулем, соответственно, решаем его аналогично:

   

   

   

Примеры:

   

Каждое из полученных уравнений — линейное. Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:

   

   

   

Ответ:2; -0,8.

   

   

   

Ответ:3.

   

Более сложные уравнения с модулем в 6 классе представляют собой сочетание обоих видов.

Примеры:

   

Сначала рассмотрим это уравнение как линейное (все выражение, стоящее под знаком модуля, считаем одним неизвестным):

   

   

Данное уравнение решим как простейшее уравнение с модулем:

   

   

   

   

Ответ: 2; -4/7.

   

   

   

   

   

   

   

Ответ: 2,5; -3,5.

Наиболее часто возникают ошибки при решении уранений с модулем. Давайте разберем решение простейших уравнений с модулем. Чтобы решить уранения с модулем, надо знать определение модуля. Модуль обозначает абсолютное значение числа и записывается вертикальными черточками:

(|a|) — читается как модуль числа (a).

Определение модуля:

Пример 2. Решите (|x|=0)

Решение: 

(|x|=0)

(x = 0)

Уравнение имеет один корень

Ответ: (x = 0).

Одна из самых сложных тем для учащихся  – это решение уравнений, содержащих переменную под знаком модуля. Давайте разберемся для начала с чем же это связано? Почему, например, квадратные уравнения большинство детей щелкает как орешки, а с таким далеко не самым сложным понятием как модуль имеет столько проблем?

На мой взгляд, все эти сложности связаны с отсутствием четко сформулированных правил для решения уравнений с модулем. Так, решая квадратное уравнение, ученик точно знает, что ему нужно сначала применять формулу дискриминанта, а затем формулы корней квадратного уравнения. А что делать, если в уравнении встретился модуль? Постараемся четко описать необходимый план действий на случай, когда уравнение содержит неизвестную под знаком модуля. К каждому случаю приведем несколько примеров.

Но для начала вспомним определение модуля. Итак,  модулем числа a называется само это число, если a неотрицательно и  -a, если  число a меньше нуля. Записать это можно так:

|a| = a, если a ≥ 0 и |a| = -a, если a < 0

Говоря о геометрическом смысле модуля, следует помнить, что каждому действительному числу соответствует определенная точка на числовой оси – ее  к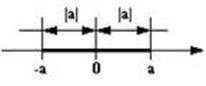оордината. Так вот, модулем или абсолютной величиной числа называется расстояние от этой точки до начала отсчета числовой оси. Расстояние всегда задается положительным числом. Таким образом, модуль любого отрицательного числа есть число положительное. Кстати, даже на этом этапе многие ученики начинают путаться. В модуле может стоять какое угодно число, а вот результат применения модуля всегда число положительное.

Теперь перейдем непосредственно к решению уравнений.

1. Рассмотрим уравнение вида |x| = с, где с – действительное число. Это уравнение можно решить с помощью определения модуля.

Все действительные числа разобьем на три группы: те, что больше нуля, те, что меньше нуля, и третья группа – это число 0. Запишем решение в виде схемы:

                             {±c, если с > 0

 Если |x| = c, то x = {0, если с = 0

                             {нет корней, если с < 0

Примеры:

1) |x| = 5, т.к. 5 > 0, то x = ±5;

2) |x| = -5, т.к. -5 < 0, то уравнение не имеет корней;

3) |x| = 0, то x = 0.

2. Уравнение вида |f(x)| = b, где b > 0. Для решения данного уравнения необходимо избавиться от модуля. Делаем это так: f(x) = b или f(x) = -b. Теперь необходимо решить отдельно каждое из полученных уравнений. Если в исходном уравнении b< 0, решений не будет.

Примеры:

1) |x + 2| = 4, т.к. 4 > 0, то

x + 2 = 4 или x + 2 = -4

x = 2             x = -6

2) |x² – 5| = 11, т.к. 11 > 0, то

x² – 5 = 11 или x² – 5 = -11

x² = 16            x² = -6

x = ± 4             нет корней

3) |x² – 5x| = -8 , т.к. -8 < 0, то уравнение не имеет корней.

3. Уравнение вида |f(x)| = g(x). По смыслу модуля такое уравнение будет иметь решения, если его правая часть больше или равна нулю, т.е. g(x) ≥ 0. Тогда будем иметь:

f(x) = g(x) или f(x) = -g(x).

Примеры:

1) |2x – 1| = 5x – 10. Данное уравнение будет иметь корни, если 5x – 10 ≥ 0. Именно с этого и начинают решение таких уравнений.

1. О.Д.З. 5x – 10 ≥ 0

              5x ≥ 10  

               x ≥ 2.  

2. Решение:

2x – 1 = 5x – 10 или 2x – 1 = -(5x – 10)

3x = 9                     7x = 11

x = 3                       x = 11/7

3. Объединяем О.Д.З. и решение, получаем:

Корень x = 11/7 не подходит по О.Д.З., он меньше 2, а x = 3 этому условию удовлетворяет.

Ответ: x = 3  

2) |x – 1| = 1 – x².

1. О.Д.З. 1 – x² ≥ 0. Решим методом интервалов данное неравенство:

             (1 – x)(1 + x) ≥ 0

             -1 ≤ x ≤ 1  

2. Решение:

x – 1 = 1 – x²      или   x – 1 = -(1 – x²)

x² + x – 2 = 0            x² – x = 0

x = -2 или x = 1         x = 0 или x = 1

3. Объединяем решение и О.Д.З.:

Подходят только корни x = 1 и x = 0.

Ответ: x = 0, x = 1. 

4. Уравнение вида |f(x)| = |g(x)|. Такое уравнение равносильно двум следующим уравнениям f(x) = g(x) или f(x) = -g(x).

Пример:

1) |x² – 5x + 7| = |2x – 5|. Данное уравнение равносильно двум следующим:

x² – 5x + 7  = 2x – 5 или x² – 5x +7  = -2x + 5   

x² – 7x + 12  = 0            x² – 3x + 2  = 0

x = 3 или x = 4             x = 2 или x = 1  

Ответ: x = 1, x = 2, x = 3, x = 4.

5. Уравнения, решаемые методом подстановки (замены переменной). Данный метод решения проще всего объяснить на конкретном примере. Так, пусть дано квадратное уравнение с модулем:

 x² – 6|x| + 5 = 0. По свойству модуля x² = |x|², поэтому уравнение можно переписать  так:

|x|² – 6|x| + 5 = 0. Сделаем замену |x| = t ≥ 0, тогда будем иметь:

t² – 6t + 5 = 0. Решая данное уравнение, получаем, что t = 1 или t = 5. Вернемся к замене:

|x| = 1 или |x| = 5

x = ±1        x = ± 5

Ответ: x = -5, x = -1, x = 1, x = 5. 

Рассмотрим еще один пример:

x² + |x| – 2 = 0. По свойству модуля  x² = |x|², поэтому

|x|² + |x| – 2 = 0. Сделаем замену |x| = t ≥ 0, тогда:

t² + t – 2 = 0. Решая данное уравнение, получаем, t = -2 или t = 1. Вернемся к замене:

|x| = -2   или |x| = 1

Нет корней     x = ± 1

Ответ: x = -1, x = 1.

6. Еще один вид уравнений – уравнения со «сложным» модулем. К таким уравнениям относятся уравнения, в которых есть «модули в модуле». Уравнения данного вида можно решать, применяя свойства модуля.

Примеры:

1) |3 – |x|| = 4. Будем действовать так же, как и в уравнениях второго типа. Т.к. 4 > 0, то получим два уравнения:

3 – |x| = 4 или  3 – |x| = -4.

Теперь выразим в каждом уравнении модуль х, тогда |x| = -1 или |x| = 7.

Решаем каждое из полученных уравнений. В первом уравнении нет корней, т.к. -1 < 0, а во втором x = ±7.

Ответ x = -7, x = 7.

2) |3 + |x + 1|| = 5. Решаем это уравнение аналогичным образом:

3 + |x + 1| = 5      или     3 + |x + 1| = -5

|x + 1| = 2                       |x + 1| = -8

x + 1 = 2 или x + 1 = -2.   Нет корней.

x = 1            x = -3

Ответ: x = -3, x = 1.

Существует еще и универсальный метод решения уравнений с модулем. Это метод интервалов. Но мы его рассмотрим в дальнейшем.

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Тип урока: урок постановки учебной задачи.

Цели урока:

• обучение решению уравнений со знаком модуля на
  основе применения свойств уравнений;
• развитие навыков теоретического мышления с
  применением навыков элементарных операций с
  модулем и определения модуля;
• воспитание внимания и умения анализировать
  полученное решение, участвовать в диалоге с
  товарищами, учителем.

ХОД УРОКА

I. Повторение пройденного

Внимательно рассмотрите предложенные
уравнения:

1) | х | = х + 5;
2) | х | = – 3х + 5;
3) | х – 3 | = 2;
4) | 2х – 5 | = х – 1;
5) = х
– 1;
6)  | 2х – 5 | = 2 – х;
7)  | х + 2 | = 2(3 – х);
  | 3х – 5 | = | 5 – 2х | ;
9)  | х – 2 | = 3 | 3 – х | ;
10) |  | х – 1 |  – 1 | = 2.

Задание 1. Распределите данные
уравнения по группам.

Учащиеся сначала выделили две группы. В
первую группу вошли уравнения 1) –3), 5) –7). Ко
второй группе были отнесены уравнения и 9).
Затем учащиеся заметили уравнение 10), содержащее
знак модуля два раза. Окончательно было выделено
три группы: 1-я группа – модуль содержится в левой
части уравнения; 2-я группа – модуль содержится в
обеих частях уравнения; 3-я группа – в уравнении
содержится двойной модуль.

Учитель. Какую главную задачу мы должны
будем решить сегодня на уроке?

Учащиеся. Мы должны научиться решать
уравнения.

Учитель. Да. Но посмотрите еще раз на все эти
уравнения и выделите их общую особенность.

Учащиеся. Все они содержат модуль.

Учитель. Как точнее сформулировать задачу
нашего урока?

Учащиеся. Применять определение модуля при
решении данных уравнений.

Учитель. Действительно, эту задачу мы и
должны решить на уроке. По-другому ее можно
сформулировать так: “Как решать уравнения с
модулем?” Какие понятия, определения могут быть
полезны при решении этой задачи?

Учащиеся.

1. Что такое модуль?
2. Определение модуля.

Учитель. Вспомним, что такое модуль.

Учащиеся. По определению:

| а | =

если а > 0 если а < 0

Учитель. Что помогло вам так быстро
воспроизвести это понятие?

Учащиеся. Опорный конспект.

Учитель. Обратитесь еще раз к опорному
конспекту и приведите свои примеры.

Учащиеся. |10 | = 10; | – 20 | = 20; | 0 | = 0; | – 100 | = 100.

Задание 2. Вычислите | а |, если: а
= 3; а = – 5. Определите, какие из предложенных
решений верные.

1) | а | = а, если, поэтому | 3 | = 3, так как 3 > 0 (число
положительное).

2) | а | =, если а < 0, поэтому | – 5 | = – 5,
так как – 5 < 0 (число отрицательное).

Учащиеся. Решение 1) – правильное, решение 2)
– нет.

Учитель. Запишите решение 2) правильно.

Учащиеся записывают: | а | = – а,
еслиа < 0, поэтому | –5 | = – (– 5), так как
число – 5 – отрицательное.

Задание 3. Преобразуйте любое из данных
выражений к такому виду, чтобы в записи
аналитического выражения не использовались
знаки модулей.

а) | х – 3 |;
б) 2| х + 4 | + Зх;
в) | х – 1 | + | х – 2 |.

Большинство учащихся выбрали выражение б),
выражение в) – чуть меньше, а выражение а) –
единицы. Таким образом, учащиеся самостоятельно
распределились на три группы. Были предложены
следующие решения:

б) Если 2х + 4 0, то есть х – 2, то | 2х + 4 | = 2х + 4 и мы получаем:
| 2х + 4 | + 3х = 2х + 4 + 3х = 5х + 4.

Если 2х + 4 < 0, то есть х < –2, то | 2х
+ 4 | = – (2х + 4) и мы получаем: | 2х + 4 | + 3х
= – (2х + 4) +3х = –2х – 4 + Зх = х
– 4.

Итак, по определению:

| 2х + 4 | + 3х =

если х > – 2 если х < – 2

в) Самостоятельно задание учащиеся выполнить
не смогли, потребовалась помощь учителя.

Если х < 1, то х – 1 < 0, х – 2 < 0,
значит, | х – 1 | = – (х – 1), | х – 2 | = –
(х – 2), поэтому | х – 1 | + | х – 2 | = – (х
– 1) – (х – 2) = 3 – 2х.

Если 1 х <
2, то (х – 1) 0,
(х – 2) < 0, значит | х – 1| = х – 1, | х
– 2 | = – (х – 2), поэтому | х – 1| + | х –
2 | = (х – 1) – (х – 2) = 1.

Если х 2, то
(х – 1) > 0, значит | х – 1 | = х – 1, | х
– 2 | = х – 2, поэтому | х – 1 | + | х – 2 |
= х – 1 +  х – 2 = 2х – 3.

| х – 1 | + | х – 2 | =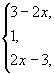

если х < 1 если 1 < х < 2 если х > 2

а) Если х – 3 0, то есть х 3, то | х – 3 | = х – 3;

если х – 3 < 0, то есть х < 3, то | х
– 3 | = (х – 3) = 3 – х.

| х – 3 | =

если х < 3 если х < 3

Учитель. Итак, повторяя, мы вспомнили,
что модуль – это расстояние. Объясним это с
помощью рисунков: | а – 0 | = | а | –
расстояние на координатной прямой точки а от
начала координат.

Учитель. Что такое | а – b | с
точки зрения расстояния? | a – b | – это
расстояние между точками а и b на
координатной прямой.

Задание 4. Решите уравнение | х | = 5.

Учитель. Что нужно найти?

Учащиеся. Все значения x такие,
что соответствующие точки х на координатной
прямой удалены от начала координат на расстояние
5.

Учитель. Изобразите это на
координатной прямой. Сколько получили точек?

Учащиеся. Две.

Учитель. Назовите их.

Учащиеся. 5 и – 5. (Отмечают их на
координатной прямой.)

Учитель. Сколько корней имеет это
уравнение?

Учащиеся. Два.

Учитель. Назовите их.

Учащиеся. 5 и – 5.

Учитель. Запишем решение этого
уравнения.

| x | = 5,
x₁ = 5,
x₂ = –5.

Ответ: 5, –5.

Примечание. При решении
уравнений 1) – 10) обычно составляют систему,
содержащую уравнение, требующее решения, и
неравенство, учитывающее определение модуля. В
6-м классе учащиеся еще не изучают решение
числовых неравенств, поэтому мы вынуждены решать
не систему, а уравнение, опираясь на определение
модуля, и в конце делать проверку, чтобы удалить
значения переменной, не являющиеся корнями
уравнения.

Задание 5. Решите уравнение | х – 3 |
= 2.

Учитель. Что нужно найти?

Учащиеся. Отметить расстояние от
точки 3 влево и вправо на 2 единицы.

Учитель. Сколько точек получилось?

Учащиеся. Две.

Учитель. Изобразите это на
координатной прямой.

Учащиеся изображают схематически.

Учитель. Найдите значения отмеченных
точек при перемещении вправо и влево. Какие
координаты отмеченных точек мы получим?

Учащиеся. 5 и 1.

Учитель. Что это за числа?

Учащиеся. Корни данного уравнения.

Учитель. Запишем решение данного
уравнения.

| х – 3 | = 2.

Решение.

х – 3 = 2, х = 2 + 3, х = 5;

х – 3 = – 2, х = –2 + 3, х = 1.

Ответ: 5, 1.

Задание 6. Решите уравнение | 2х – 5 | =
2 – х. (Решение выполнить самостоятельно.)

Решение.

2х – 5 = 2 – х, 2х + х = 2 + 5, Зх
= 7, х = 2;

2х – 5 = – (2 – х), 2х – 5 = –2 – х,

2х – х = – 2 + 5, х = 3.

Проверка: | 2 · 2 – 5 | = 2 – 2; | 2 · 2 – 5 | = – ; | 2 · 3 – 5 | = 2 – 3, | 2 · 3 – 5 | = –
1.

В обоих случаях значение модуля оказывается
меньше нуля, что противоречит свойству модуля.
Значит, х = 2 и х = 3 не являются корнями исходного
уравнения.

Ответ: нет решений.

II. Самостоятельная работа

Решите по выбору одно из следующих уравнений.

1. | х – 2 | = 1.

2. | – | = х –
1.

3. | х – 2 | = 3 | 3 – х |.

Критерии оценок:

• оценка “3” – уравнение 1;
• оценка “4” – уравнение 2;
• оценка “5” – уравнение 3.

Перед самостоятельной работой решаем
уравнение^

| Зх – 5 | – | б – 2х |.

Решение.

Зх – 5 = 5 – 2х, – (Зх – 5) = – (5 – 2х),

Зх + 2х = 5 + 5, х = 2;

Зх – 5 = – (5 – 2х), – (Зх – 5) = 5 – 2х,

Зх – 2х = – 5 + 5, х = 0.

Ответ: 0, 2.

Учитель. Сколько корней может иметь
уравнение?

Учащиеся. Один, два или не иметь
корней.

Учитель. Вы забыли еще один случай.
Вспомните решение уравнения | 2х – 5 | = 2 – х.
Сколько корней мы получили?

Учащиеся. Нуль.

Учитель. Какой мы записали ответ?

Учащиеся. Уравнение не имеет решения.

Учитель. Уравнение | | х – 1 | – 1 | = 2
мы решим на следующем уроке.

III. Задание на дом

Решите уравнения: 1), 4) и 7).

IV. Рефлексия

При помощи шкалы ответьте на вопросы: кто может
решить уравнение самостоятельно; кому нужна
помощь; кто не сможет совсем решить уравнение?

• Могу решить уравнение самостоятельно (1-я
  группа)
• Нужна помощь (2-я группа)
• Совсем не могут этого сделать (3-я группа)

V. Итог урока

2-й группе оказывается помощь товарищами
(консультантами); 3-й группе – учителем.

Следующий урок начинается с решения уравнения |
| х – 1 | – 1 | = 2.

Решение.

| х – 1 | – 1 = 2, | х – 1 | = 3;

тогда

х – 1 = 3, х = 4; х – 1 = – 3, х = – 2.

| х – 1 | – 1 = – 2, | х – 1 | = – 1;

тогда нет решения, так как модуль (расстояние) –
неотрицательное число.

Проверка:

| | 4 – 1 | – 1 = 2, | | 3 | – 1| = 2, | 3 – 1 | = 2, | 2 | = 2, 2 = 2 –
верно;

| | — 2 – 1 | – 1| = 2, | | –3 | – 1 | = 2, | 3 – 1 | = 2, | 2 | = 2, 2 = 2 –
верно.

Ответ: – 2, 4.

Вопросы при решении уравнения.

1. Чем данное уравнение отличается от
предыдущих? (Двойным модулем.)

2. Сколько сначала составим уравнений? (Два.)

3. Какие могут получиться уравнения? (| х – 1 | –
2 = 2, | х – 1 | = 3; | х – 1 | – 1 = –2, | х – 1 | = –1.)

4. Что можно сказать об уравнении | х – 1 | = –1? (Нет
решений, так как модуль (расстояние) –
неотрицательное число.)

План урока:

Модуль числа

Решение уравнений с модулем

Уравнения с параметрами

Модуль числа

Напомним, что такое модуль числа. Так называют значение числа, взятое без учета его знака. То есть модуль чисел 9 и (– 9) одинаков и равен 9. Для обозначения модуля применяют специальные прямоугольные скобки:

|9| = |– 9| = 9

|674| = |– 674| = 674

|2,536| = |– 2,536| = 2,536

Грубо говоря, операция нахождения модуля сводится к отбрасыванию у числа знака «минус», если он у него есть. Вообще, если число х неотрицательно, то его модуль |х| = х. Если же число отрицательно, то его модуль имеет противоположное значение: |х| = х. Математически это можно записать так:

Именно такое определение обычно и применяется в математике.

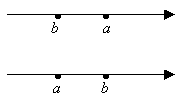
Модуль играет важную роль в математике. Дело в том, с его помощью удобно записывать расстояние между двумя точками на координатной прямой. Пусть на ней отмечены точки a и b. Расстояние между ними равно |a – b|, причем неважно, какое из этих чисел больше, а какое меньше:

Также модуль возникает при извлечении квадратного корня из четной степени числа:

В частности, если n = 1, получим формулу:

Для того чтобы получить график функции у = |x|, сначала надо построить график функции без учета знака модуля:

Далее следует выполнить преобразование. Те точки графика, которые располагаются выше оси Ох, остаются на своем месте. В данном случае это та часть графика, которая находится в I четверти. Те же точки, которые располагаются ниже оси Ох, должны быть симметрично (относительно этой самой оси Ох) отображены. В результате они окажутся выше оси Ох:

В результате получилась «галочка».

Пример. Постройте график ф-ции у = |х² – 4х + 3|

Решение. Для построения графика функции, содержащей модуль, сначала надо построить график для «подмодульного» выражения. Поэтому построим график у = х² – 4х + 3. Это квадратичная ф-ция, ее график – это парабола:

Часть графика, в промежутке от 1 до 3, находится ниже оси Ох. Чтобы построить ф-цию у = |х² – 4х + 3|, надо перевернуть эту часть графика:

Решение уравнений с модулем

Изучим простейший случай уравнения, содержащего модуль, когда вся его слева записано выр-ние в модульных скобках, а справа находится число. То есть уравнение имеет вид

|у(х)| = b

где b – какое-то число, а у(х) – произвольная ф-ция.

Если b< 0, то ур-ние корней не имеет, ведь модуль не может быть отрицательным.

Пример. Найдите корни ур-ния

|125x¹⁰ + 97x⁴– 12,56х³ + 52х² + 1001х – 1234| = – 15

Решение: Справа стоит отрицательное число. Однако модуль не может быть меньше нуля. Это значит, что у ур-ния отсутствуют корни.

Ответ: корни отсутствуют.

Если b = 0, то мы получим какое-то произвольное ур-ние у(х) = 0, у которого могут быть корни. Проще говоря, модульные скобки в таком случае можно просто убрать.

Пример. Решите ур-ние

|13х – 52| = 0

Решение.

Ясно, что подмодульное выр-ние равно нулю:

13х – 52 = 0

13х = 52

х = 4

Ответ: 4.

Наиболее интересен случай, когда b> 0, то есть в правой части стоит положительное число. Ясно, что тогда под модулем находится либо само это число b, либо противоположное ему число – b:

|b| = b

|– b| = b

То есть мы получаем два различных ур-ния: у(х) = bи у(х) = – b.

Пример. Решите ур-ние

|х| = 10

Решение. В правой части – положительное число, поэтому либо х = – 10, либо х = 10.

Ответ: 10; (– 10).

Пример. Решите ур-ние

|10х + 5| = 7

Решение. Исходное ур-ние разбивается на два других ур-ния:

10х + 5 = 7 или 10х + 5 = – 7

10х = 2 или 10х = – 12

х = 0,2 или х = – 1,2

Ответ: 0,2; (– 1,2).

Пример. Найдите корни ур-ния

|x²– 2х – 4| = 4

Решение. Снова заменим исходное равенство на два других:

x²– 2х – 4 = 4 или x²– 2х – 4 = – 4

Имеем два квадратных ур-ния. Решим каждое из них:

x²– 2х – 4 = 4

x²– 2х – 8 = 0

D = b²– 4ас = (– 2)² – 4•1•(– = 4 + 32 = 36

х₁ = (2 – 6)/2 = – 2

х₂ = (2 + 6)/2 = 4

Нашли корни (– 2) и 4. Решаем второе ур-ние:

x²– 2х – 4 = – 4

x²– 2х = 0

х(х – 2) = 0

х = 0 или х – 2 = 0

х = 0 или х = 2

Получили ещё два корня: 0 и 2.

Ответ: – 2, 4, 0, 2

Встречаются случаи, когда в уравнении, содержащем знак модуля, под ним находятся обе части равенства:

|у(х)| = |g(x)|

Здесь возможны два варианта. Либо подмодульные выр-ния равны друг другу (у(х) = g(x)), либо у них противоположные значения (у(х) = – g(x)). То есть снова надо решить два ур-ния.

Пример. Решите ур-ние

|x² + 2x– 1| = |х + 1|

Решение. Выр-ния справа и слева (без знака модуля) либо равны, либо противоположны. Можно составить два ур-ния:

x² + 2x– 1 = х + 1 или x² + 2x– 1 = – (х + 1)

х² + х – 2 = 0 или х² + 3х = 0

Решим 1-ое ур-ние:

х² + х – 2 = 0

D = b²– 4ас = 1² – 4•1•(– 2) = 1 + 8 = 9

х₁ = (1 – 3)/2 = – 1

х₂ = (1 + 3)/2 = 2

Теперь переходим ко 2-омуур-нию:

х² + 3х = 0

х(х + 3) = 0

х = 0 или х + 3 = 0

х = 0 или х = – 3

Всего удалось найти 4 корня: (– 1), (– 2), 2 и 0.

Ответ:(– 1), (– 2), 2, 0.

Возможен случай, когда в левой части равенства находится модуль выр-ния, а в правой – обычное выражение, без модуля. Такое ур-ние имеет вид |у(х)| = g(x). Здесь также возможны два варианта: у(х) = g(x) или у(х) = – g(x). Однако следует учитывать ещё один факт. Модуль не может быть отрицательным, а потому должно выполняться нер-во g(x)⩾ 0. Но это неравенство не надо решать. Достаточно просто подставить в него все полученные корни и проверить, справедливо ли нер-во.

Пример. Найдите решение уравнения, содержащего модуль:

|х² + 3,5х – 20| = 4,5х

Решение. Рассмотрим два отдельных равенства:

х² + 3,5х – 20 = 4,5х илих² + 3,5х – 20 = – 4,5х

х² – х – 20 = 0 или х² + 8х – 20 = 0

Решим каждое из полученных квадратных ур-ний.

х² – х – 20 = 0

D = b²– 4ас = 1² – 4•1•(– 20) = 1 + 80 = 81

х₁ = (1 – 9)/2 = – 4

х₂ = (1 + 9)/2 = 5

х² + 8х – 20 = 0

D = b²– 4ас = 8² – 4•1•(– 20) = 64 + 80 = 144

х₃ = (– 8 – 12)/2 = – 10

х₄ = (– 8 + 12)/2 = 2

Итак, получили 4 корня: (– 4), 5, (– 10) и 2. Однако правая часть исходного ур-ния, 4,5x, не может быть отрицательной, ведь модуль числа – это всегда неотрицательная величина:

4,5х ≥ 0

Для х = – 4 и х = – 10 это условие не выполняется, поэтому эти корни должны быть исключены.

Ответ: 2 и 5

Мы рассмотрели три случая, когда ур-ние имеет вид:

1. у(х) = b (b– это некоторая константа)
2. |у(х)| = |g(x)|
3. |у(х)| = g(x)

Однако порою ур-ние не удается свести ни к одному из этих видов. Тогда для решения уравнений и неравенств, содержащих модуль, следует рассматривать их на отдельных интервалах, где подмодульные выр-ния не изменяют свой знак.

Пример. Найдите корни ур-ния

|x + 1| + |x– 4| = 6

Решение. Выр-ния х + 1 и х – 4 меняют знак при переходе через точки (– 1) и 4:

Если отметить обе точки на прямой, то они образуют на ней 3 интервала:

Исследуем ур-ние на каждом из полученных промежутков.

Так как при х <– 1 оба подмодульные выр-ния отрицательны, то можно записать, что

|x + 1| = – (х + 1) = – х – 1

|x– 4| = – (х – 4) = – х + 4

Тогда ур-ние примет вид

|x + 1| + |x– 4| = 6

– х – 1 – х + 4 = 6

–2х = 3

х = – 1,5

Это значение удовлетворяет условию х <– 1, поэтому корень верный.

Далее изучим случай, когда х∊[– 1; 4). Здесь отрицательно только выражение x– 4, поэтому модули заменяются так:

|x + 1| = х + 1

|x– 4| = – (х – 4) = – х + 4

Ур-ние примет вид:

|x + 1| + |x– 4| = 6

x + 1 – x+ 4 = 6

5 = 6

Получили неверное тождество. Получается, что на промежутке [– 1; 4) корней нет.

При х ≥4 выр-ния х – 4 и х + 1 положительны, поэтому

|x + 1| = х + 1

|x– 4| = х – 4

Исходное ур-ние будет выглядеть так

|x + 1| + |x– 4| = 6

х + 1 + х – 4 = 6

2х = 9

х = 4,5

Найденный корень удовлетворяет условию х ≥4, поэтому он также должен быть включен в ответ.

Уравнения с параметрами

Изучим ур-ния:

5х = 10

5х = 15

5х = 20

Для решения каждого из них надо число справа поделить на 5 (множитель перед х). В итоге получаем значения х, равные 2, 3 и 4.

Теперь обозначим число в правой части буквой, например, как v. Тогда все эти ур-ния будут выглядеть одинаково:

5х = v

Решением таких ур-ний будет дробь v/5.

Надо понимать разный смысл, который мы вкладываем при этом в буквы х и v. Через х мы обозначили переменную, то есть ту величину, значение которой необходимо найти. Под буквой v подразумевалась заранее известная величина, то есть константа, которая известна заранее в каждом конкретном ур-нии. Такую величину называют параметром, а ур-ние 5х = v называют уравнением с параметром.

Изучая уравнение с параметром, мы рассматриваем не одно конкретное ур-ние, а сразу целую группу, или семейство ур-ний. Например, все ур-ния первой степени можно описать в виде

ах + b= 0

где х – это переменная величина, а числа а, b– это параметры. Для описания квадратного ур-ния в общем виде необходимы уже три параметра (а, b и с):

ах² + bx + c = 0

Параметры встречаются не только при описании ур-ний, но и, например, при рассмотрении функций. Так, линейная функция задается формулой у = kx + b. Здесь числа k и b являются параметрами. Так как ур-ние у = kx + b задает на плоскости прямую линию, то величины k и b порою называют параметрами уравнения прямой.

Если при решении обычного ур-ния мы определяем значение его корней в виде конкретных чисел, то при решении ур-ний с параметром находят формулу, позволяющую при заданном значении параметра вычислить значение корня.

Пример. Решите ур-ние

х² – 2ах = 0

и найдите его корни при значении параметра а, равном 3.

Решение. Вынесем множитель х за скобки:

х² – 2ах = 0

х(х – 2а) = 0

х = 0 или х – 2а = 0

х = 0 или х = 2а

Получили, что при любом значении параметра а ур-ние имеет два корня. Один из них равен нулю при любом значении а, а второй вычисляется по формуле х = 2а:

при а = 3х = 2•3 = 6

Ответ: есть два корня – 0 и 2а. При а = 2 корни равны 0 и 6.

Пример. Решите ур-ние

р²х – 3рх = р² – 9

Решение. Слева вынесем за скобки множитель рх, а выр-ние справа преобразуем, используя формулу разности квадратов:

рх(р – 3) = (р – 3)(р + 3)

Возникает желание поделить обе части рав-ва на р(р – 3), чтобы выразить х. Однако сразу так делать нельзя, ведь если величина р(р – 3) равна нулю, то получится деление на ноль.

Поэтому сначала изучим случаи, когда один из множителей слева равен нулю. Если р = 0, то мы получим рав-во

0•х•(0 – 3) = (0 – 3) (3 – 0)

0 = – 9

Это неверное тождество, а потому при р = 0 ур-ние корней не имеет.

Если р – 3 = 0, то есть р = 3, получится следующее

3•х•0 = 0•(3 + 3)

0 = 0

Это равенство верно при любом х. Значит, при р = 3 корнем ур-ния является любое число.

Если же р≠ 0 и р ≠ 3, то произведение р(р – 3) также не равно нулю, а потому обе части равенства можно поделить на р(р – 3). Тогда получим

В этом случае ур-ние имеет единственный корень.

Ответ: при р = 0 корней нет; при р = 3 корнем является любое число; при других рх = (р + 3)/р.

Часто в задаче требуется не выразить корень ур-ния через параметр, а лишь оценить количество корней ур-ния или диапазон их значений.

Пример. Сколько корней имеет ур-ние

|х² – 6х + 5| = b

при различных значениях параметра b.

Решение. Будем решать ур-ние графическим методом. Для этого сначала построим график у = |х² – 6х + 5|. В модульных скобках находится обычная квадратичная функция, чьи ветви смотрят вверх. Найдем нули функции:

х² – 6х + 5 = 0

D = b²– 4ас = (– 6)² – 4•1•5 = 36 + 20 = 16

х₁ = (6 – 4)/2 = 1

х₂ = (6 + 4)/2 = 5

Итак, нули ф-ции – это точки 1 и 5. Найдем координату х₀ вершины параболы по формуле:

х₀ = –b/2a = 6/2 = 3

Подставив х₀ в квадратичную ф-цию найдем координату у₀ вершины параболы:

3² – 6•3 + 5 = 9 – 18 + 5 = – 4

Теперь построим квадратичную ф-цию:

Для построения графика, содержащего модуль функции, надо отобразить точки с отрицательными ординатами (они находятся ниже оси Ох) симметрично относительно оси Ох:

Мы построили график левой части ур-ния. График правой части представляет собой горизонтальную прямую у = b. Можно выделить 5 различных случаев взаимного расположения этих графиков:

При b< 0 прямая пролегает ниже графика. Общих точек у графиков нет, а потому ур-ние корней не имеет.

При b = 0 прямая у = 0 касается графика в 2 точках: (1; 0) и (5; 0). Получаем 2 корня.

Если 0 <b< 4, то прямая пересекает график в 4 точках.

При b = 4 прямая у = 4 касается перевернутой вершины параболы, а также пересекает ветви ещё в 2 точках. Итого 3 корня.

Наконец, при b>4 есть горизонтальная прямая пересекает график лишь в 2 точках, то есть получаем 2 корня.

Ответ: нет корней при b< 0; 2 корня при b = 0 и b> 4; 3 корня при b = 4; 4 корня при 0 <b< 4.

Пример. При каком а ур-ние

х⁴ – (а + 2)х² + 3а – 3 = 0

имеет ровно 4 корня?

Решение. Это ур-ние является биквадратным, то есть для его решения нужно произвести замену у = х²:

у² – (а + 2)у + 3а – 3 = 0 (1)

Для того, чтобы исходное ур-ние имело 4 корня, необходимо, чтобы у квадратного уравнения с параметром(1) было два положительных корня: у₁ и у₂. Тогда, проводя обратную замену х² = у₁ и х² = у₂, мы получим два разных квадратных ур-ния, корни которых будут равны

Если же хоть один из двух корней, например, у₁, окажется равным нулю, то величины

Совпадут (они обе будут равны нулю), и останется лишь 3 корня. Если же у₁ будет отрицательным числом, то ур-ние

х² = у₁

вовсе не будет иметь решений, и тогда останется не более 2 корней.

Итак, решим ур-ние (1):

у² – (а + 2)у + 3а – 3 = 0

D = b²– 4ас = (– (а + 2))² – 4•1•(3а – 3) = (а + 2)² – 12 а + 12 =

= а² + 4а + 4 – 12а + 12 = а² – 8а + 16 = а² – 2•4•а + 4² = (а – 4)²

Чтобы у ур-ния (1) было два различных корня, дискриминант должен быть положительным. Величина (а – 4)² положительна при всех значениях а, кроме а = 4, которое обращает дискриминант в ноль. Значит, а ≠ 4.

Извлечем корень из дискриминанта:

Корни ур-ния (1) можно вычислить по формулам:

И у₁, и у₂ должны быть положительными величинами, однако у₁ меньше, чем у₂ (ведь для его вычисления дискриминант брали со знаком «минус», а не «плюс»). Поэтому достаточно записать нер-во:

Получили неравенство, содержащее модуль. Для избавления от модульных скобок в нер-ве рассмотрим 2 случая. Если а – 4>0, то есть а > 4, выполняется равенство

|а – 4| = а – 4

Тогда имеем

а + 2 – (а – 4) > 0

6> 0

Это нер-во выполняется при любом допустимом значении а, поэтому при а >4 исходное ур-ние имеет 4 корня.

Если а < 4, то справедливо соотношение

|а – 4| = – (а – 4)

Тогда получится следующее:

а + 2 – |а – 4|> 0

а + 2 – (– (а – 4)) > 0

а + 2 + а – 4 > 0

2а > 2

а > 1

Итак, при условии, что а< 4, должно выполняться нер-во а > 1. Это значит, что а∊(1; 4). С учетом первого случая, при котором было получено решение

а > 4

можно записать окончательный ответ: а∊(1; 4)∪(4; + ∞).

Ответ: а∊(1; 4)∪(4; + ∞).

Пример. При каких параметрах а у ур-ния

х² – 2(а + 1)х + а² + 2а – 3 = 0

существует два корня, которые принадлежат интервалу (– 5; 5)?

Решение. Данное ур-ние является квадратным. Найдем его дискриминант:

D = b²– 4ас = (– 2(а + 1))² – 4•1•( а² + 2а – 3) = 4(а² + 2а + 1) – 4(а² + 2а – 3) =

= 4(а² + 2а + 1 – а²– 2а + 3) = 4•4 = 16

Получаем, что при любом а дискриминант положителен, а потому уур-ния 2 корня. Вычислить их можно по формулам

Для того, чтобы оба решения уравнения с параметром принадлежали интервалу (– 5; 5), нужно, чтобы меньший из них (это х₁) был больше – 5, больший (это х₂) – меньше – 5:

Значит, должны выполняться два нер-ва

х₁>– 5и х₂<5

а – 1 >– 5 и а + 3 < 5

а >– 4 и а < 2

Эти два нер-ва выполняются, если а∊(– 4; 2)

Ответ: (– 4; 2)