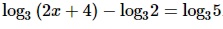Как найти корень уравнения егэ 2016

Найдите корень уравнения — Задание 5 ЕГЭ

Сегодня мы будем тренировать навык решения задания 5 ЕГЭ — найдите корень уравнения. Будем искать корень уравнения. Рассмотрим примеры решения такого рода заданий. Но для начала, давайте вспомним — что значит — найти корень уравнения?

Это значит найти такое, зашифрованное под х число, которое мы подставим вместо x и наше уравнение будет верным равенством.

Например, 3x=9 — это уравнение, а 3 . 3=9 — это уже верное равенство. То есть в данном случае, мы вместо x подставили число 3 — получили верное выражение или равенство, это означает, что мы решили уравнение, то есть нашли данное число x=3, которое превращает уравнение в верное равенство.

Вот этим мы и займемся — будем находить корень уравнения.

Задание 1 — найдите корень уравнения 2 1-4x =32

Это показательное уравнение. Оно решается следующим образом — нужно чтобы и слева, и справа от знака «равно» была степень с одинаковым основанием.

Слева у нас основание степени 2, а справа — степени нет вовсе. Но мы знаем, что 32 — это 2 в пятой степени. То есть, 32=2 5

Таким образом, наше уравнение будет выглядеть так: 2 1-4х =2 5

Слева и справа у нас основания степени одинаковы, значит, чтобы у нас было равенство, должны быть равны и показатели степени:

Получаем обыкновенное уравнение. Решаем обычным способом — все неизвестные оставляем слева, а известные переносим вправо, получим:

Делаем проверку: 2 1-4(-1) =32

Мы нашли корень уравнение. Ответ: х=-1.

Самостоятельно найдите корень уравнения в следующих заданиях:

Задание 2 — найдите корень уравнения 2 5-x = 1/16

Уравнение решаем аналогично — путем приведения левой и правой частей уравнения к одному основанию степени. В нашем случае — к основанию степени 2.

Используем следующее свойство степени:

По этому свойству мы получим для правой части нашего уравнения:

Тогда наше уравнение запишется в виде:

Если равны основания степени, значит, равны и показатели степени:

Сделаем проверку — подставим найденное значение х в исходное уравнение — если мы получим верное равенство, значит, мы решили уравнение правильно.

Мы нашли корень уравнения правильно.

Задание 3 — найдите корень уравнения

Заметим, что справа у нас стоит 1/8, а 1/8 — это

Тогда наше уравнение запишется в виде:

Если основания степени равны, значит, равны и показатели степени, получим простое уравнение:

Ответ: х=5. Проверку сделайте самостоятельно.

Задание 4 — найдите корень уравнения log₃(15-х)=log₃2

Это уравнение решается также как и показательное. Нам нужно, чтобы основания логарифмов слева и справа от знака «равно» были одинаковыми. Сейчас они одинаковы, значит, приравниваем те выражения, которые стоят под знаком логарифмов:

Задание 5 — найдите корень уравнения log₃(3-x)=3

Число 3 — это log₃27. Чтобы было понятно внизу нижним индексом под знаком логарифма стоит число которое возводится в степень, в нашем случае 3, под знаком логарифма стоит число, которое получилось при возведении в степень — это 27, а сам логарифм — это показатель степени, в которую нужно возвести 3, чтобы получить 27.

Смотрите на картинке:

Таким образом, любое число можно записать в виде логарифма. В данном случае очень удобно записать число 3 в виде логарифма с основанием 3. Получим:

Основания логарифмов равны, значит, равны и числа, стоящие под знаком логарифма:

Задание №1. Простейшие уравнения. Профильный ЕГЭ по математике

В задании №1 варианта ЕГЭ вам встретятся всевозможные уравнения: квадратные и сводящиеся к квадратным, дробно-рациональные, иррациональные, степенные, показательные и логарифмические и даже тригонометрические. Видите, как много нужно знать, чтобы справиться с заданием! И еще ловушки и «подводные камни», которые ждут вас в самом неожиданном месте.

Вот список тем, которые стоит повторить:

Уравнения, сводящиеся к квадратным

1. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Кажется, что уравнение очень простое. Но иногда здесь ошибаются даже отличники. А вот шестиклассник бы не ошибся.

С левой частью уравнения все понятно. Дробь умножается на А в правой части — смешанное число Его целая часть равна 19, а дробная часть равна Запишем это число в виде неправильной дроби:

Выбираем меньший корень.

Ответ: — 6,5.

2. Решите уравнение

Возведем в квадрат левую часть уравнения. Получим:

Дробно-рациональные уравнения

3. Найдите корень уравнения

Перенесем единицу в левую часть уравнения. Представим 1 как и приведем дроби к общему знаменателю:

Это довольно простой тип уравнений. Главное — внимательность.

Иррациональные уравнения

Так называются уравнения, содержащие знак корня — квадратного, кубического или n-ной степени.

4. Решите уравнение:

Выражение под корнем должно быть неотрицательно, а знаменатель дроби не равен нулю.

Значит, .

Возведём обе части уравнения в квадрат:

Условие при этом выполняется.

5. Решите уравнение Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

А в этом уравнении есть ловушка. Решите его самостоятельно и после этого читайте дальше.

Выражение под корнем должно быть неотрицательно. И сам корень — величина неотрицательная. Значит, и правая часть должна быть больше или равна нуля. Следовательно, уравнение равносильно системе:

Решение таких уравнений лучше всего записывать в виде цепочки равносильных переходов:

Мы получили, что . Это единственный корень уравнения.

Типичная ошибка в решении этого уравнения такая. Учащиеся честно пишут ОДЗ, помня, что выражение под корнем должно быть неотрицательно:

Возводят обе части уравнения в квадрат. Получают квадратное уравнение: Находят его корни: или Пишут в ответ: -9 (как меньший из корней). В итоге ноль баллов.

Теперь вы знаете, в чем дело. Конечно же, число -9 корнем этого уравнения быть не может.

6. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите больший из корней.

Запишем решение как цепочку равносильных переходов.

Показательные уравнения

При решении показательных уравнений мы пользуемся свойством монотонности показательной функции.

7. Решите уравнение

Вспомним, что Уравнение приобретает вид: Функция монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.

8. Решите уравнение

Функция монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.

9. Решите уравнение

Представим в виде степени с основанием 3 и воспользуемся тем, что

Логарифмические уравнения

Решая логарифмические уравнения, мы также пользуемся монотонностью логарифмической функции: каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, значит, равны и сами числа.

И конечно, помним про область допустимых значений логарифма:

Логарифмы определены только для положительных чисел;

Основание логарифма должно быть положительно и не равно единице.

10. Решите уравнение:

Область допустимых значений: . Значит,

Представим 2 в правой части уравнения как — чтобы слева и справа в уравнении были логарифмы по основанию 5.

Функция монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом

11. Решите уравнение:

Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:

12. Решите уравнение:

Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2. Мы делаем это по формуле перехода к другому основанию:

Записываем решение как цепочку равносильных переходов.

13. Решите уравнение. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

В этом уравнении тоже есть ловушка. Мы помним, что основание логарифма должно быть положительно и не равно единице.

Первое уравнение мы получили просто из определения логарифма.

Квадратное уравнение имеет два корня: и

Очевидно, корень является посторонним, поскольку основание логарифма должно быть положительным. Значит, единственный корень уравнения:

Тригонометрические уравнения (Часть 1 ЕГЭ по математике)

Тригонометрические уравнения? В первой части вариантов ЕГЭ? — Да. Причем это задание не проще, чем задача 13 из второй части варианта Профильного ЕГЭ.

14. Найдите корень уравнения: В ответе запишите наибольший отрицательный корень.

Типичная ошибка — решать это уравнение в уме. Мы не будем так делать! Несмотря на то, что это задание включено в первую части варианта ЕГЭ, оно является полноценным тригонометрическим уравнением, причем с отбором решений.

Сделаем замену Получим:

Получаем решения: Вернемся к переменной x.

Поделим обе части уравнения на и умножим на 4.

Первой серии принадлежат решения

Вторая серия включает решения

Наибольший отрицательный корень — тот из отрицательных, который ближе всех к нулю. Это

15. Решите уравнение В ответе напишите наименьший положительный корень.

Сделаем замену Получим: Решения этого уравнения:

Вернемся к переменной х:

Умножим обе части уравнения на 4 и разделим на

Выпишем несколько решений уравнения и выберем наименьший положительный корень:

Наименьший положительный корень

Мы разобрали основные типы уравнений, встречающихся в задании №1 Профильного ЕГЭ по математике. Конечно, это не все, и видов уравнений в этой задаче существует намного больше. Именно поэтому мы рекомендуем начинать подготовку к ЕГЭ по математике не с задания 1, а с текстовых задач на проценты, движение и работу и основ теории вероятностей.
Успеха вам в подготовке к ЕГЭ!

Задание №7 ЕГЭ по математике базового уровня

Простейшие уравнения

В задании №7 базового уровня ЕГЭ по математике необходимо решить

Простейшие (Protozoa) — тип одноклеточных животных.

Разбор типовых вариантов заданий №7 ЕГЭ по математике базового уровня

Вариант 7МБ1

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Алгоритм выполнения

1. Раскрыть скобки с левой и с правой стороны равенства, применив формулы приведения.
2. Все, выражения, содержащие переменную перенести в левую часть, а не содержащие в правую.
3. Преобразовать левую часть.
4. Преобразовать правую часть.
5. Решить уравнение относительно x, то есть найти неизвестный множитель.

Решение:

Квадрат суммы двух выражений равен сумме квадратов этих выражений плюс удвоенное произведение первого и второго выражений.

(x + 3) 2 = x 2 + 2 · x · 3 + 3 2 = x 2 + 6x + 9

Квадрат разности двух выражений равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражений.

(x – 9) 2 = x 2 – 2 · x · 9 + 9 2 = x 2 – 18x + 81

После преобразования выражение примет

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

x 2 + 6x + 9 = x 2 – 18x + 81

Все выражения, содержащие переменную перенесем в левую часть, а не содержащие – в правую. При переносе из одной части равенства в другую знак меняется на противоположный.

x 2 + 6x – x 2 + 18x = 81 – 9

Преобразуем левую часть. Приведем подобные слагаемые. Объединим в скобки, сохранив знаки, те выражения, где содержится x 2 и x.

x 2 + 6x – x 2 + 18x = (x 2 – x 2 ) + (6x +18x) = 0 + 24x = 24x

Выражение примет вид:

Преобразуем правую часть. 81 – 9 = 72

Выражение примет вид:

Решим уравнение относительно x, то есть найдем неизвестный множитель. Для того чтобы найти неизвестный множитель нужно произведение разделить на известный множитель.

Решение в общем виде:

Вариант 7МБ2

Алгоритм выполнения

1. Раскрыть скобки с левой и с правой стороны равенства, применив формулы приведения.
2. Все, выражения, содержащие переменную перенести в левую часть, а не содержащие в правую.
3. Преобразовать левую часть.
4. Преобразовать правую часть.
5. Решить уравнение относительно x, то есть найти неизвестный множитель.

Решение:

Квадрат суммы двух выражений равен сумме квадратов этих выражений плюс удвоенное произведение первого и второго выражений.

(x + 2) 2 = x 2 + 2 · x · 2 + 2 2 = x 2 + 4x + 4

Квадрат разности двух выражений равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражений.

(x – 2 = x 2 – 2 · x · 8 + 8 2 = x 2 – 16x + 64

После преобразования выражение примет вид:

x 2 + 4x + 4 = x 2 – 16x + 64

Все выражения, содержащие переменную перенесем в левую часть, а не содержащие – в правую. При переносе из одной части равенства в другую знак меняется на противоположный.

x 2 + 4x – x 2 + 16x = 64 – 4

Преобразуем левую часть. Приведем подобные слагаемые. Объединим в скобки, сохранив знаки, те выражения, где содержится x 2 и x.

x 2 + 4x – x 2 + 16x = (x 2 – x 2 ) + (4x +16x) = 0 + 20x = 20x

Выражение примет вид:

Преобразуем правую часть. 64 – 4 = 60

Выражение примет вид:

Решим уравнение относительно x, то есть найдем неизвестный множитель. Для того чтобы найти неизвестный множитель нужно произведение разделить на известный множитель.

Решение в общем виде:

Вариант 7МБ3

Алгоритм выполнения

1. Перенести вычитаемое в правую сторону равенства с противоположным знаком.
2. Преобразовать правую часть с учетом свойства: log_ax + log_ay = log_a (x · y).
3. Приравнять логарифмические выражения. Можно так поступить, так как основания логарифмов в левой и правой части одинаковы.
4. Решить уравнение относительно x.

Решение:

Вариант 7МБ4

Найдите корень уравнения 3 x− 3 = 81.

Алгоритм выполнения

1. Привести выражения в степенях к одинаковому основанию. В данном случае – это 3. Теперь необходимо вспомнить, какой степенью тройки является 81.
2. Когда основания равны, можно приравнять значения степеней

Если вы забыли, то для этого необходимо делить 81 на 3 до тех пор, пока не получим 3. Чтобы получить три из 81, нам нужно поделить 81 на 3 три раза: при первом делении мы получим 27, при втором – 9, при третьем – три.

Значит, 81 это три в четвертой степени. Запишем это:

Решение:

Ответ: 7

Вариант 7МБ5

Найдите корень уравнения log₂( x − 3) = 6 .

Алгоритм выполнения

1. Логарифм по основанию два показывает нам число, в степень которого нам необходимо возвести основание, то есть двойку, чтобы получить число под логарифмом.

Решение:

Вариант 7МБ6

Найдите отрицательный корень уравнения x 2 − x − 6 = 0.

Алгоритм выполнения

1. Вычислить дискриминант
2. Найти корни
3. Выбрать необходимый корень

Решение:

D = -(1) 2 − 4 • 1 • (-6) = 25

Так как нам необходим отрицательный корень – ответ -2

Вариант 7МБ7

Решите уравнение х 2 = –2х + 24.

Если уравнение имеет больше одного

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Алгоритм выполнения

1. Переносим влево часть ур-ния, стоящую справа от знака «=». Получаем кв.уравнение стандартного вида.
2. Поскольку уравнение является приведенным, используем для нахождения корней т.Виета.
3. Записываем в качестве ответа большее из полученных 2 чисел.

Решение:

Поскольку требуется указать больший из корней, то ответом будет 4.

Вариант 7МБ8

Найдите корни уравнения 4 х–6 = 64.

Алгоритм выполнения

1. Представляем 64 как степень с основанием 4, т.е. приводим выражения справа и слева к степеням с одинаковым основанием.
2. Опускаем одинаковые основания и переходим к равенству показателей. Ур-ние стало простейшим линейным.
3. Находим корень ур-ния.

Решение:

Вариант 7МБ9

Найдите корень уравнения log₃ (2x – 5) = 2.

Алгоритм выполнения

1. Преобразуем часть уравнения справа от знака «=», используя св-ва логарифмов log_xx=1 и log_xy n =nlog_xy.
2. Переходим от равенства логарифмов к равенству выражений, стоящих под их знаками.
3. Решаем полученное линейное ур-ние.

Решение:

Вариант 7МБ10

Найдите корень уравнения

Алгоритм выполнения

1. Преобразовываем обе части ур-ния: приводим их к степеням с основанием 3. Для этого используем св-во степеней (1/а) х =а –х .
2. Поскольку основания степеней слева и справа в ур-нии теперь одинаковы, то можем их опустить и приравнять показатели.
3. Решаем полученное линейное ур-ние.

Решение:

Вариант 7МБ11

Найдите корень уравнения (х – 2 = (х – 2) 2 .

Алгоритм выполнения

1. Раскрываем скобки слева и справа, используя ф-

Луб — это сложная проводящая ткань, по которой продукты фотосинтеза (органические вещества) транспортируются из листьев ко всем органам растения (к корневищам, плодам, семенам и т. д.).

Решение:

х 2 – 2 · х ·8 + 8 2 = х 2 – 2 · х · 2 + 2 2

Вариант 7МБ12

Найдите корень уравнения

Алгоритм выполнения

1. Преобразовываем обе части ур-ния так, чтобы привести их к степеням с одинаковым основанием 7. Для выражения слева применяем св-во степеней (1/а) х =а –х .
2. Применяем св-во показат.уравнений: если степени с одинаковыми основаниями равны, то равны и их показатели. Отсюда переходим к линейному ур-нию.
3. Решаем его.

Решение:

Вариант 7МБ13

Решите уравнение х 2 – 25 = 0

Алгоритм выполнения

1. Переносим 25 в правую часть ур-ния.
2. Выражаем из ур-ния х путем извлечения корня из 25.
3. Определяем корни, сравниваем их, определяем больший.

Решение:

Для ответа берем 5.

Вариант 7МБ14

Найдите корень уравнения

Алгоритм выполнения

1. Применим св-во логарифмических равенств: если логарифмы с одинаковыми основания равны, то равны и их подлогарифменные выражения. В результате получаем равенство из выражений, стоящих под знаком логарифма.
2. Решаем полученное линейное ур-ние.

Решение:

Вариант 7МБ15

Найдите корень уравнения

Алгоритм выполнения

1. Приводим обе части ур-ния к степеням с основанием 2. При этом для преобразования выражения слева используем св-во степеней (1/а) х =а –х .
2. Получив слева и справа степени с одинаковым основанием, опускаем это основание и приравниваем показатели этих степеней. Получаем линейное ур-ние.
3. Решаем его.

Решение:

Вариант 7МБ16

Найдите корень уравнения

источники:

http://ege-study.ru/ru/ege/materialy/matematika/zadanie-1-prostejshie-uravneniya/

Задание №7 ЕГЭ по математике базового уровня

Скачать материал

Скачать материал

Описание презентации по отдельным слайдам:

• 

  1 слайд

  Решение уравнений из открытого банка заданий ЕГЭ 2016
  по математике

• 

  2 слайд

  Решение линейных,
  квадратных, кубических уравнений
  Решение тригонометрических
  уравнений
  Рациональные уравнения

  Решение уравнений
  Инструкция
  Аннотация
  Источники
  Решение иррациональных
  уравнений
  Решение логарифмических уравнений
  Решение показательных уравнений

• 

  3 слайд

  8
  9
  1

  2

  3
  4
  5
  6
  7
  Решение линейных, квадратных , кубических уравнений

• 

  4 слайд

  1. Найдите корень уравнения:  

   .
  Решение.

  Ответ : 13
  .

• 

  5 слайд

  2) Найдите корень уравнения:  
  Ответ: -5
  Решение:

• 

  6 слайд

  3) Найдите корень уравнения
  Если уравнение имеет более одного корня, укажите меньший из них.

  Решение:
  По теореме, обратной теореме Виета, сумма корней этого уравнения равна 17, а их произведение равно 72. Значит корни равны 8 и 9.

   Ответ: 8.

• 

  7 слайд

  4)  Найдите корень уравнения:

  Если уравнение имеет более одного корня, укажите меньший из них:

    Ответ :-1,5

• 

  8 слайд

  5)  Решите уравнение:

  Ответ:-6

• 

  9 слайд

  6)   Решите уравнение: 
  Ответ:-4

• 

  10 слайд

  7)
  Найдите корень уравнения
  Если уравнение имеет более одного корня,
  укажите меньший из них:

    Ответ: -7

• 

  11 слайд

  8)Найдите корень уравнения :

  Решение :
  Извлекая кубический корень из обеих частей уравнения, получаем
  х-1=2 , откуда 
  х =2+1
  х=3.

    Ответ: х=3

• 

  12 слайд

  9)  Найдите корень уравнения  .

   Решение :
  Извлекая кубический корень из обеих частей уравнения, получаем

  Х-1= — 2
  Х= -2+1
  Х= -1
  Ответ: -1

• 

  13 слайд

  8
  9
  10
  1
  2

  3

  4
  5
  6
  7
  Решение тригонометрических уравнений

• 

  14 слайд

  1)Решите уравнение
  В ответе укажите наименьший положительный корень.

• 

  15 слайд

  2)Решите уравнение:
  В ответе напишите наибольший отрицательный корень.

• 

  16 слайд

  3) Решите уравнение:

  В ответе напишите наименьший положительный корень.

• 

  17 слайд

  4) Решите уравнение:

• 

  18 слайд

  5) Решите уравнение:

• 

  19 слайд

  6) Решите уравнение:

• 

  20 слайд

  7) Решите уравнение: 5cosx=0

• 

  21 слайд

  Решите уравнение:

• 

  22 слайд

  9) Решите уравнение:

• 

  23 слайд

  10) Решите уравнение:

• 

  24 слайд

  8

  9

  10
  11
  12
  14
  15
  1
  2
  3
  4
  5
  6
  13
  7
  Решение логарифмических уравнений

• 

  25 слайд

  1)Найдите корень уравнения :

• 

  26 слайд

  2)Найдите корень уравнения: 
  log8(x+6) = log8(3x−8).

• 

  27 слайд

  3)Найдите корень уравнения  log9(x+6) = log9(2x−7).

• 

  28 слайд

  4)Найдите корень уравнения log2(13−x) = −4.

• 

  29 слайд

  5)Найдите корень уравнения.

• 

  30 слайд

  6)Найдите корень уравнения log6(x+4) = log6(6x−6).

• 

  31 слайд

  7)Найдите корень уравнения  log3(12−x) = 3log34.

• 

  32 слайд

  8)Найдите корень уравнения  : log2(9−x) = 2log23.

• 

  33 слайд

  9)Найдите корень уравнения  log2(4−x)=8.

• 

  34 слайд

  10)Найдите корень уравнения  log3(5+x) = 3.

• 

  35 слайд

  11)Найдите корень уравнения  log2(8−4x) = −4.

• 

  36 слайд

  12)Найдите корень уравнения log8(x+5) = log8(2x−2).

• 

  37 слайд

  13)Найдите корень уравнения log4(x+6) = log4(5x−14).

• 

  38 слайд

  14)Найдите корень уравнения  log4(8−5x) = 2log43.

• 

  39 слайд

  15)Найдите корень уравнения:

• 

  40 слайд

  8
  9
  10
  1
  2
  3
  4
  5
  6
  7
  Решение показательных уравнений
  11
  12
  13

• 

  41 слайд

  1)Найдите корень уравнения

• 

  42 слайд

  2)Найдите корень уравнения:

• 

  43 слайд

  3)Найдите корень уравнения:

• 

  44 слайд

  4)Найдите корень уравнения:

• 

  45 слайд

  5)Найдите корень уравнения:

• 

  46 слайд

  6)Найдите корень уравнения:

• 

  47 слайд

  7)Найдите корень уравнения:

• 

  48 слайд

  8)Найдите корень уравнения:

• 

  49 слайд

  9)Найдите корень уравнения:

• 

  50 слайд

  10)Найдите корень уравнения:

• 

  51 слайд

  11)Найдите корень уравнения:

• 

  52 слайд

  12)Найдите корень уравнения:

• 

  53 слайд

  13)Найдите корень уравнения:

• 

  54 слайд

  8
  9
  10
  11
  12
  1
  2
  3
  4
  5
  6
  7
  Иррациональные уравнения

• 

  55 слайд

  1)  Найдите корень уравнения 
  Решение.

• 

  56 слайд

  2) Найдите корень уравнения

• 

  57 слайд

  3) Найдите корень уравнения

• 

  58 слайд

  4) Найдите корень уравнения:
  Если корней несколько, в ответе укажите меньший из них

• 

  59 слайд

  5)Найдите корень уравнения :

• 

  60 слайд

  6) Найдите корень уравнения:

• 

  61 слайд

  7) Найдите корень уравнения

• 

  62 слайд

  Найдите корень уравнения

• 

  63 слайд

  9) Найдите корень уравнения:
  Если корней несколько, в ответе укажите меньший из них:

• 

  64 слайд

  10) Найдите корень уравнения

• 

  65 слайд

  11) Найдите корень уравнения

• 

  66 слайд

  12) Найдите корень уравнения

• 

  67 слайд

  8
  9
  1
  2
  3
  4
  5
  6
  7
  Рациональные уравнения

• 

  68 слайд

  1)  Решите уравнение:

• 

  69 слайд

  2) Решите уравнение: .
  Если корней несколько, то в ответе укажите
  больший из них.

  Ответ: 5

• 

  70 слайд

  3)  Решите уравнение:
  Если корней несколько, то в ответе укажите
  больший из них.

  Ответ: 5

• 

  71 слайд

  4)  № 77367 Решите уравнение:
  Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

  Ответ :-0,5

• 

  72 слайд

  5)  Решите уравнение:
  Если уравнение имеет более одного корня, то в ответе запишите больший из корней.
  Решение:
  Заметим, что числители дробей равны. Имеем:

  Ответ:1

• 

  73 слайд

  6)  Найдите корень уравнения: 
  Решение.

  Ответ: 1.

• 

  74 слайд

  7) Найдите корень уравнения:
  Ответ: 0,3
  Решение:
  Последовательно получаем:

• 

  75 слайд

  Решите уравнение:
  Решение.
  Если две дроби с равным числителем равны, то равны их знаменатели. Имеем:

  Ответ:7.

• 

  76 слайд

  9) Решите уравнение:

  Ответ :-6
  Решение.
  Если две дроби с равным числителем равны, то равны их знаменатели. Имеем:

• 

  77 слайд

  Источники и литература
  Сайт Гущина по подготовке к ЕГЭ
  Открытый банк заданий по математике с сайта ФИПИ
  Сайт Александра Ларина.

• 

  78 слайд

  Аннотация:
  Математический тренажер содержит темы:
  Решение линейных, квадратных, кубических, тригонометрических,показательных, логарифмических, иррациональных уравнений.
  Материал предназначен для подготовки к ЕГЭ по математике, а также в качестве тренажера для занятий как в школе, так и дома.
  Целевая аудитория 9-11 класс.

• 

  79 слайд

  На слайде (2) представлены основные темы.
  Вы можете выбрать раздел, кликнув на него мышкой, перейдя на слайд выбранного раздела, кликнув мышкой можно выбрать конкретное задание. Решив данное задание, вы всегда сможете его проверить, кликнув мышкой. Для того, чтобы выбрать следующий вопрос–кликните мышкой и вы вернетесь на домашнюю страницу.
  Инструкция:

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 264 626 материалов в базе

• Выберите категорию:

• Выберите учебник и тему

• Выберите класс:

• Тип материала:

  • Все материалы

  • Статьи

  • Научные работы

  • Видеоуроки

  • Презентации

  • Конспекты

  • Тесты

  • Рабочие программы

  • Другие методич. материалы

Найти материалы

Вам будут интересны эти курсы:

• Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»

• Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»

• Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»

• Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»

• Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»

• Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»

• Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»

• Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»

• Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»

• Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»

• Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»

• Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»

Решения отдельных заданий ЕГЭ по математике от 6 июня 2016 года

Задания вариантов можно найти здесь и здесь.

13.1.

а) Решите уравнение:

б) Укажите корни этого уравнения, принадлежащие отрезку

Решение: + показать

14.1. В правильной треугольной призме сторона основания равна , а боковое ребро равно . На ребре отмечена точка так, что . Точки и   – середины ребер и соответственно. Плоскость параллельна прямой и содержит точки и .
а) Докажите, что прямая перпендикулярна плоскости .

б) Найдите расстояние от точки до плоскости 

Решение: + показать

15.1. Решите неравенство:

Решение: + показать

16.1. В трапеции боковая сторона перпендикулярна основаниям. Из точки на сторону опустили перпендикуляр . На стороне отмечена точка так, что прямые и перпендикулярны.
а) Докажите, что прямые и параллельны.

б) Найдите отношение если угол равен

Решение: + показать

16.2. В треугольнике проведены высоты и . На них из точек и опущены

перпендикуляры
а) Докажите, что прямые и параллельны.
б) Найдите отношение , если угол равен

Решение: + показать

 16.3. В трапеции  точка  – середина основания , точка  – середина боковой стороны . Отрезки  и  пересекаются в точке .
а) Докажите, что площади четырёхугольника  и треугольника  равны.
б) Найдите, какую часть от площади трапеции составляет площадь четырёхугольника , если

Решение: + показать

17.1. 15‐го января планируется взять кредит в банке на сумму млн рублей на месяцев. Условия его возврата таковы:
‐ 1‐го числа каждого месяца долг возрастает на целое число процентов по сравнению с концом предыдущего месяца;

‐ со 2‐го по 14‐е число каждого месяца необходимо выплатить часть долга;
‐ 15‐го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.

Найдите наименьшее значение , при котором общая сумма выплат будет составлять более млн. рублей. 

Решение: + показать

18.1. Определите, при каких значениях параметра уравнение

имеет ровно два различных решения.

Решение: + показать

18.2. Определите, при каких значениях параметра уравнение

имеет ровно три различных решения.

Решение: + показать

18.3. Определите, при каких значениях параметра уравнение

имеет ровно один корень.

Решение: + показать

18.4. Определите, при каких значениях параметра система уравнений

имеет ровно три различных решения.

Решение: + показать

19.1. На доске написаны числа 1, 2, 3, …, 30. За один ход разрешается стереть произвольные три числа, сумма которых меньше 35 и отлична от каждой из сумм троек числа, стёртых на предыдущих ходах.
а) Приведите пример последовательности 5 ходов.

б) Можно ли сделать 10 ходов?
в) Какое наибольшее число ходов можно сделать?

Решение: + показать

---

Задания (часть С) резервного дня сдачи ЕГЭ по математике 2016 можно найти здесь.

Сайты, меню, вход, новости