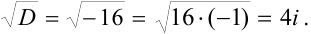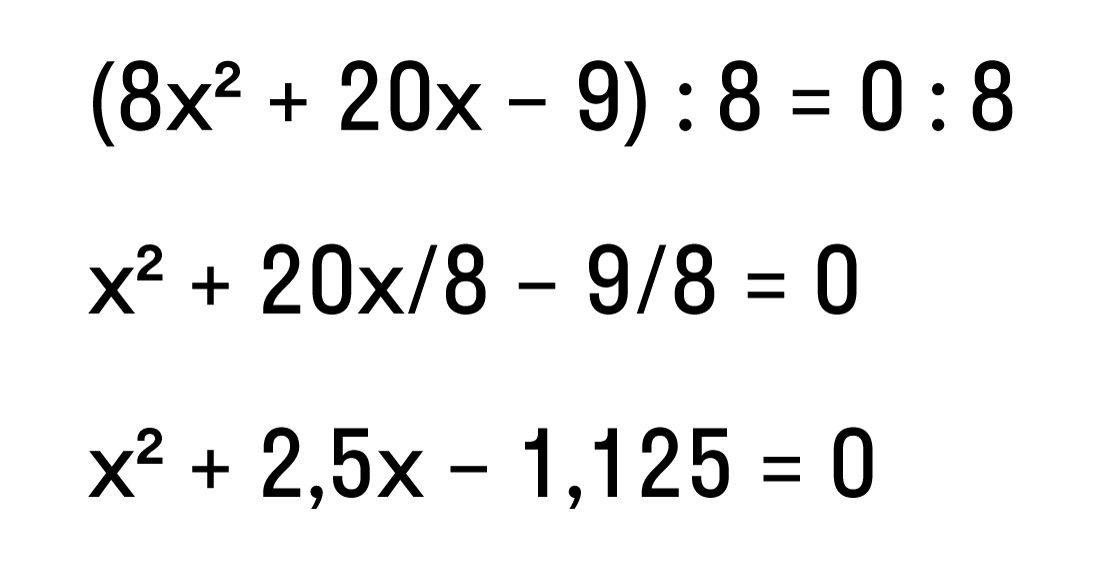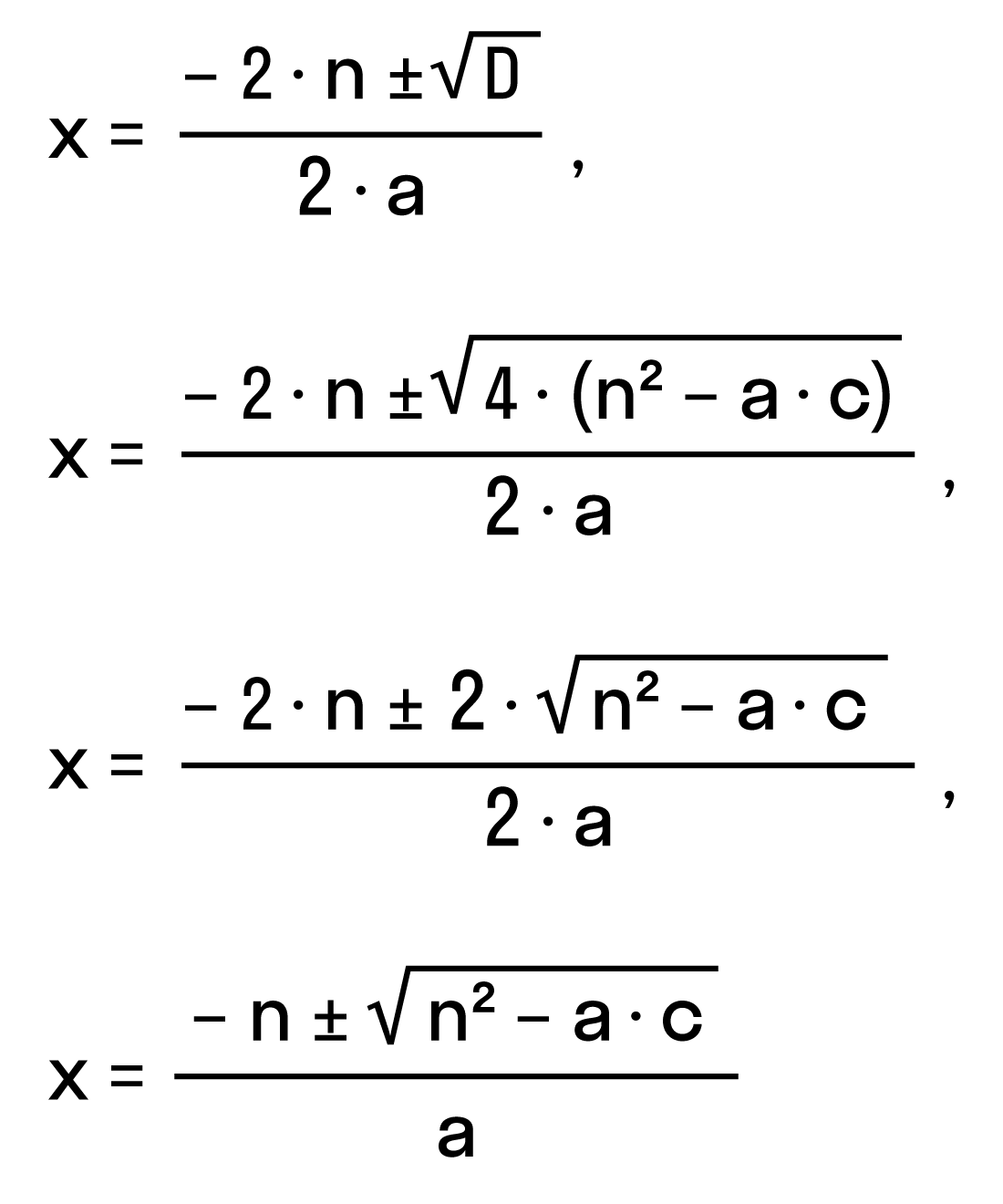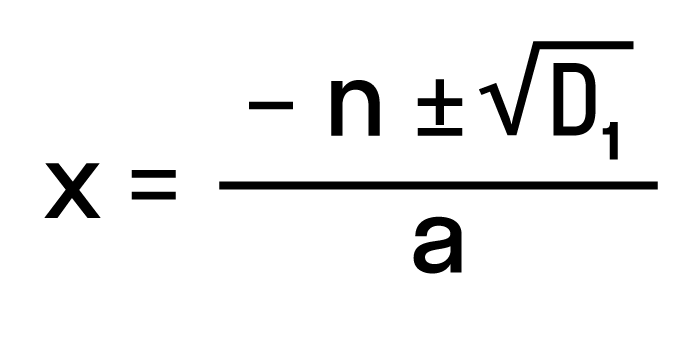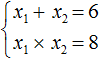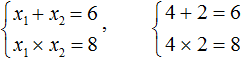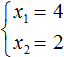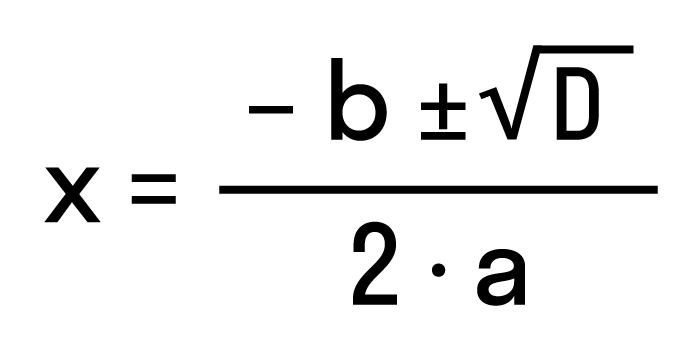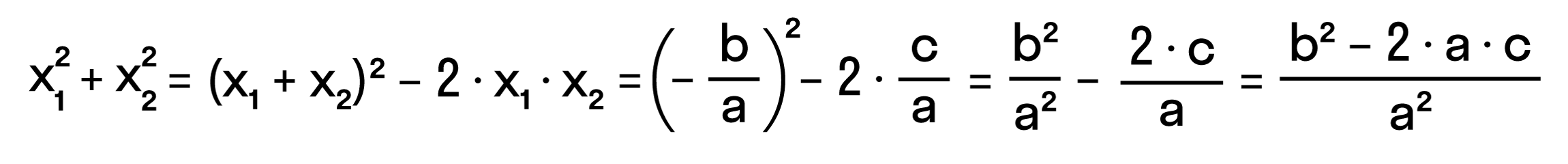Рассмотрим решение квадратных уравнений, дискриминант которых отрицателен:
Пример №42.4.
Решить уравнение: 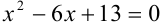
Решение:
Найдем дискриминант: 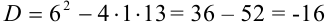
Тогда 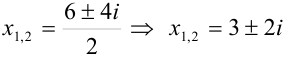
Ответ: 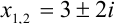
Видим, что если дискриминант квадратного уравнения отрицателен, то уравнение имеет решения на множестве комплексных чисел. В ответе получаются два сопряженных комплексных числа. Это очень важный результат: теперь мы знаем, что абсолютно любое квадратное уравнение имеет два корня на множестве комплексных чисел.
Подобное утверждение, известное под названием «основная теорема алгебры», было доказано Гауссом в конце XVIII века: любое алгебраическое уравнение 

Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Предмет высшая математика
Другие лекции по высшей математике, возможно вам пригодятся:
Например, для трехчлена (3x^2+2x-7), дискриминант будет равен (2^2-4cdot3cdot(-7)=4+84=88). А для трехчлена (x^2-5x+11), он будет равен ((-5)^2-4cdot1cdot11=25-44=-19).
Дискриминант обозначается буквой (D) и часто используется при решении квадратных уравнений. Также по значению дискриминанта можно понять, как примерно выглядит график квадратичной функции (см. ниже).
Дискриминант и корни квадратного уравнения
Значение дискриминанта показывает количество корней квадратного уравнения:
— если (D) положителен – уравнение будет иметь два корня;
— если (D) равен нулю – только один корень;
— если (D) отрицателен – корней нет.
Это не надо учить, к такому выводу несложно прийти, просто зная, что квадратный корень из дискриминанта (то есть, (sqrt{D}) входит в формулу для вычисления корней квадратного уравнения: (x_{1}=)(frac{-b+sqrt{D}}{2a}) и (x_{2}=)(frac{-b-sqrt{D}}{2a}). Давайте рассмотрим каждый случай подробнее.
Если дискриминант положителен
В этом случае корень из него – это некоторое положительное число, а значит (x_{1}) и (x_{2}) будут различны по значению, ведь в первой формуле (sqrt{D}) прибавляется, а во второй – вычитается. И мы имеем два разных корня.
Пример: Найдите корни уравнения (x^2+2x-3=0)
Решение:
|
(x^2+2x-3=0) |
Выписываем коэффициенты: |
|
|
(a=1;) (b=2;) (c=-3;) |
Вычисляем дискриминант по формуле (D=b^2-4ac) |
|
|
(D=2^2-4cdot1cdot(-3)=) |
Найдем корни уравнения |
|
|
(x_{1}=)(frac{-2+sqrt{16}}{2cdot1})(=)(frac{2}{2})(=1) (x_{2}=)(frac{-2-sqrt{16}}{2cdot1})(=)(frac{-6}{2})(=-3) |
Получили два различных корня из-за разных знаков перед (sqrt{D}) |
Ответ: (x_{1}=1); (x_{2}=-3)
На графике квадратичной функции положительный дискриминант будет означать пересечение функции с осью икс ровно в двух точках – корнях уравнения. И это логично. Вдумайтесь – если уравнение (x^2+2x-3=0) имеет корни (x_{1}=1) и (x_{1}=-3), значит при подстановке (1) и (-3) вместо икса, левая часть станет нулем. А значит, если те же самые единицу и минус тройку подставить в функцию (y=x^2+2x-3) получим (y=0). То есть, функция (y=x^2+2x-3) проходит через точки ((1;0)) и ((-3;0)) (подробнее смотри статью Как построить график функции).

Если дискриминант равен нулю
А сколько корней будет, если дискриминант равен нулю? Давайте рассуждать.
Формулы корней выглядят так: (x_{1}=)(frac{-b+sqrt{D}}{2a}) и (x_{2}=)(frac{-b-sqrt{D}}{2a}). И если дискриминант – ноль, то и корень из него тоже ноль. Тогда получается:
(x_{1}=)(frac{-b+sqrt{D}}{2a})(=)(frac{-b+sqrt{0}}{2a})(=)(frac{-b+0}{2a})(=)(frac{-b}{2a})
(x_{2}=)(frac{-b-sqrt{D}}{2a})(=)(frac{-b-sqrt{0}}{2a})(=)(frac{-b-0}{2a})(=)(frac{-b}{2a})
То есть, значения корней уравнения будут совпадать, потому что прибавление или вычитание нуля ничего не меняет.
Пример: Найдите корни уравнения (x^2-4x+4=0)
Решение:
|
(x^2-4x+4=0) |
Выписываем коэффициенты: |
|
|
(a=1;) (b=-4;) (c=4;) |
Вычисляем дискриминант по формуле (D=b^2-4ac) |
|
|
(D=(-4)^2-4cdot1cdot4=) |
Находим корни уравнения |
|
|
(x_{1}=)(frac{-(-4)+sqrt{0}}{2cdot1})(=)(frac{4}{2})(=2) (x_{2}=)(frac{-(-4)-sqrt{0}}{2cdot1})(=)(frac{4}{2})(=2) |
Получили два одинаковых корня, поэтому нет смысла писать их по отдельности – записываем как один. |
Ответ: (x=2)
На графике квадратичной функции нулевой дискриминант означает одну точку пересечения функции с осью икс. Все аналогично изложенному выше: два корня – две точки пересечения, один корень – одна. В частности, функция (y=x^2-4x+4) будет выглядеть вот так:

Если дискриминант отрицателен
В этом случае корень из дискриминанта извлечь нельзя (т.к. квадратный корень из отрицательного числа – невычислим), а значит и корни квадратного уравнения мы вычислить не можем.
Пример: Найдите корни уравнения (x^2+x+3=0)
Решение
|
(x^2+x+3=0) |
Выписываем коэффициенты: |
|
|
(a=1;) (b=1;) (c=3;) |
Вычисляем дискриминант по формуле (D=b^2-4ac) |
|
|
(D=1^2-4cdot1cdot3=) |
Находим корни уравнения |
|
|
(x_{1}=)(frac{-1+sqrt{-11}}{2cdot1})(=…) (x_{2}=)(frac{-1-sqrt{-11}}{2cdot1})(=…) |
Оба корня содержат невычислимое выражение (sqrt{-11}), значит, и сами не вычислимы |
Ответ: нет корней.
То есть, отсутствие корней у квадратного уравнения с отрицательным дискриминантом – не чья-то случайная придумка. Это не потому что «в учебнике так написано», а действительно правда: невозможно найти такое число, чтоб при подстановке его вместо икса в выражение (x^2+x+3) получился ноль.
Матхак: заметим, что если вы решаете обычное квадратное уравнение или неравенство и получаете отрицательный дискриминант, стоит проверить решение еще раз, так как это не частая ситуация в школьном курсе математики.
Ну, а на графиках все просто: нет корней – нет точек пересечения с осью икс!

Что делать если дискриминант отрицательный?
Можно ли извлечь отрицательный дискриминант?
Если дискриминант отрицателен
В этом случае корень из дискриминанта извлечь нельзя (т. к. квадратный корень из отрицательного числа – невычислим), а значит и корни квадратного уравнения мы вычислить не можем.
Что делать если дискриминант меньше нуля?
1. Если дискриминант больше нуля ( ), то квадратное уравнение имеет два различных действительных корня. . Если дискриминант меньше нуля ( ), то квадратное уравнение не имеет действительных корней, а имеет комплексные корни, но нахождение комплексных корней в этой статье рассматривать не будем.
Как решить квадратное уравнение с отрицательным дискриминантом?
Как решать квадратные уравнения через дискриминант
- как найти дискрининант: D = b2 − 4ac;
- если дискриминант отрицательный — зафиксировать, что действительных корней нет;
- если дискриминант равен нулю — вычислить единственный корень уравнения по формуле х = — b2/2a;
30 нояб. 2020 г.
В каком случае дискриминант не имеет корней?
Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. . Если D 0, корней будет два.
Что делать если отрицательный корень?
Правило извлечения нечетной степени из отрицательных чисел: чтобы извлечь корень из отрицательного числа необходимо извлечь корень из противоположного ему положительного числа и поставить перед ним знак минус.
Как искать комплексные корни?
Для решения квадратного трехчлена необходимо вычислить дискриминант (D): D = b2 — 4ac, затем найти корни, которые зависят от знака D.
.
Комплексные корни
- если D больше 0, уравнение имеет 2 вещественных корня;
- при D = 0 у уравнения 1 корень х = -b / 2а;
- при D меньше 0 — 2 мнимых корня (вещественных корней нет).
В каком случае уравнение не имеет корней?
Если уравнение не имеет корней, то обычно так и пишут «уравнение не имеет корней», или применяют знак пустого множества ∅. Если уравнение имеет корни, то их записывают через запятую, или записывают как элементы множества в фигурных скобках.
Как решить уравнение ax2 bx c 0?
Алгоритм решения квадратного уравнения ax2 + bx + c = 0:
- вычислить его значение дискриминанта по формуле D = b2−4ac;
- если дискриминант отрицательный, зафиксировать, что действительных корней нет;
- если дискриминант равен нулю, вычислить единственный корень уравнения по формуле х = — b2/2a;
30 нояб. 2020 г.
Чему равны корни квадратного уравнения?
Теорема Виета гласит, что если $x_1 и x_2$– корни квадратного уравнения, то их сумма равняется –в, а произведение с. Это не совсем то, что нужно для решения, но обратная теорема говорит о том, что, если сумма двух чисел равняется –в, а произведение числу с, то эти числа и есть корни уравнения.
Что делать если в Дискриминанте отрицательное число?
Итак, чтобы решить полное квадратное уравнение, надо вычислить дискриминант D. . Если дискриминант отрицательное число (D Как решать квадратные уравнения?
В отличии от линейных уравнений для решения квадратных уравнений используется специальная формула для нахождения корней. Чтобы решить квадратное уравнение нужно: привести квадратное уравнение к общему виду «ax2 + bx + c = 0».
Почему Дискриминант так называется?
Термин образован от лат. discrimino — «разбираю», «различаю». Понятие «дискриминант квадратичной формы» использовалось в работах Гаусса, Дедекинда, Кронекера, Вебера и др. Термин ввёл Сильвестр.
Решение квадратных уравнений с отрицательным дискриминантом
Рассмотрим решение квадратных уравнений, дискриминант которых отрицателен:
Пример №42.4.
Решить уравнение: 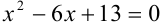
Решение:
Найдем дискриминант: 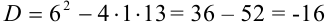
Тогда 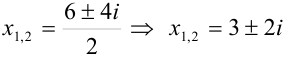
Ответ: 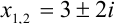
Видим, что если дискриминант квадратного уравнения отрицателен, то уравнение имеет решения на множестве комплексных чисел. В ответе получаются два сопряженных комплексных числа. Это очень важный результат: теперь мы знаем, что абсолютно любое квадратное уравнение имеет два корня на множестве комплексных чисел.
Подобное утверждение, известное под названием «основная теорема алгебры», было доказано Гауссом в конце XVIII века: любое алгебраическое уравнение 

Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:





















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Если дискриминант отрицательный то сколько корней
Дискриминантом квадратного трехчлена называют выражение (b^ -4ac), где (a, b) и (c) – коэффициенты данного трехчлена.
Например, для трехчлена (3x^2+2x-7), дискриминант будет равен (2^2-4cdot3cdot(-7)=4+84=88). А для трехчлена (x^2-5x+11), он будет равен ((-5)^2-4cdot1cdot11=25-44=-19).
Дискриминант обозначается буквой (D) и часто используется при решении квадратных уравнений . Также по значению дискриминанта можно понять, как примерно выглядит график квадратичной функции (см. ниже).
Дискриминант и корни квадратного уравнения
Значение дискриминанта показывает количество корней квадратного уравнения:
– если (D) положителен – уравнение будет иметь два корня;
– если (D) равен нулю – только один корень;
– если (D) отрицателен – корней нет.
Это не надо учить, к такому выводу несложно прийти, просто зная, что квадратный корень из дискриминанта (то есть, (sqrt ) входит в формулу для вычисления корней квадратного уравнения: (x_ =) (frac > ) и (x_ =) (frac > ) . Давайте рассмотрим каждый случай подробнее.
Если дискриминант положителен
В этом случае корень из него – это некоторое положительное число, а значит (x_ ) и (x_ ) будут различны по значению, ведь в первой формуле (sqrt ) прибавляется, а во второй – вычитается. И мы имеем два разных корня.
Пример: Найдите корни уравнения (x^2+2x-3=0)
Решение:
Вычисляем дискриминант по формуле (D=b^2-4ac)
Найдем корни уравнения
Получили два различных корня из-за разных знаков перед (sqrt )
На графике квадратичной функции положительный дискриминант будет означать пересечение функции с осью икс ровно в двух точках – корнях уравнения. И это логично. Вдумайтесь – если уравнение (x^2+2x-3=0) имеет корни (x_ =1) и (x_ =-3), значит при подстановке (1) и (-3) вместо икса, левая часть станет нулем. А значит, если те же самые единицу и минус тройку подставить в функцию (y=x^2+2x-3) получим (y=0). То есть, функция (y=x^2+2x-3) проходит через точки ((1;0)) и ((-3;0)) (подробнее смотри статью Как построить график функции ).
Если дискриминант равен нулю
А сколько корней будет, если дискриминант равен нулю? Давайте рассуждать.
Формулы корней выглядят так: (x_ =) (frac > ) и (x_ =) (frac > ) . И если дискриминант – ноль, то и корень из него тоже ноль. Тогда получается:
То есть, значения корней уравнения будут совпадать, потому что прибавление или вычитание нуля ничего не меняет.
Пример: Найдите корни уравнения (x^2-4x+4=0)
Решение:
Вычисляем дискриминант по формуле (D=b^2-4ac)
Находим корни уравнения
Получили два одинаковых корня, поэтому нет смысла писать их по отдельности – записываем как один.
На графике квадратичной функции нулевой дискриминант означает одну точку пересечения функции с осью икс. Все аналогично изложенному выше: два корня – две точки пересечения, один корень – одна. В частности, функция (y=x^2-4x+4) будет выглядеть вот так:
Если дискриминант отрицателен
В этом случае корень из дискриминанта извлечь нельзя (т.к. квадратный корень из отрицательного числа – невычислим), а значит и корни квадратного уравнения мы вычислить не можем.
Пример: Найдите корни уравнения (x^2+x+3=0)
Решение
Вычисляем дискриминант по формуле (D=b^2-4ac)
Находим корни уравнения
Оба корня содержат невычислимое выражение (sqrt ), значит, и сами не вычислимы
То есть, отсутствие корней у квадратного уравнения с отрицательным дискриминантом – не чья-то случайная придумка. Это не потому что «в учебнике так написано», а действительно правда: невозможно найти такое число, чтоб при подстановке его вместо икса в выражение (x^2+x+3) получился ноль.
Матхак: заметим, что если вы решаете обычное квадратное уравнение или неравенство и получаете отрицательный дискриминант, стоит проверить решение еще раз, так как это не частая ситуация в школьном курсе математики.
Ну, а на графиках все просто: нет корней – нет точек пересечения с осью икс!
Как решать квадратные уравнения?
1. Дискриминант положительный. Это значит, из него можно извлечь корень. Хорошо корень извлекается, или плохо – вопрос другой. Важно, что извлекается в принципе. Тогда у вашего квадратного уравнения – два корня. Два различных решения.
2. Дискриминант равен нулю. Тогда у вас одно решение. Строго говоря, это не один корень, а два одинаковых.
Основные формулы
Рассмотрим квадратное уравнение:
(1) .
Корни квадратного уравнения (1) определяются по формулам:
; .
Эти формулы можно объединить так:
.
Когда корни квадратного уравнения известны, то многочлен второй степени можно представить в виде произведения сомножителей (разложить на множители):
.
Далее считаем, что – действительные числа.
Рассмотрим дискриминант квадратного уравнения:
.
Если дискриминант положителен, , то квадратное уравнение (1) имеет два различных действительных корня:
; .
Тогда разложение квадратного трехчлена на множители имеет вид:
.
Если дискриминант равен нулю, , то квадратное уравнение (1) имеет два кратных (равных) действительных корня:
.
Разложение на множители:
.
Если дискриминант отрицателен, , то квадратное уравнение (1) имеет два комплексно сопряженных корня:
;
.
Здесь – мнимая единица, ;
и – действительная и мнимая части корней:
; .
Тогда
Графическая интерпретация
Если построить график функции
,
который является параболой, то точки пересечения графика с осью будут корнями уравнения
.
При , график пересекает ось абсцисс (ось ) в двух точках.
При , график касается оси абсцисс в одной точке.
При , график не пересекает ось абсцисс.
Ниже приводятся примеры таких графиков.
Полезные формулы, связанные с квадратным уравнением
Вывод формулы для корней квадратного уравнения
Выполняем преобразования и применяем формулы (f.1) и (f.3):
Итак, мы получили формулу для многочлена второй степени в виде:
.
Отсюда видно, что уравнение
выполняется при
и .
То есть и являются корнями квадратного уравнения
.
Примеры определения корней квадратного уравнения
Пример 1
Найти корни квадратного уравнения:
(1.1) .
Запишем квадратное уравнение в общем виде:
.
Сравнивая с нашим уравнением (1.1), находим значения коэффициентов:
.
Находим дискриминант:
.
Поскольку дискриминант положителен, , то уравнение имеет два действительных корня:
;
;
.
Отсюда получаем разложение квадратного трехчлена на множители:
График функции y = 2 x 2 + 7 x + 3 пересекает ось абсцисс в двух точках.
Построим график функции
.
График этой функции является параболой. Она пересевает ось абсцисс (ось ) в двух точках:
и .
Эти точки являются корнями исходного уравнения (1.1).
Пример 2
Найти корни квадратного уравнения:
(2.1) .
Запишем квадратное уравнение в общем виде:
.
Сравнивая с исходным уравнением (2.1), находим значения коэффициентов:
.
Находим дискриминант:
.
Поскольку дискриминант равен нулю, , то уравнение имеет два кратных (равных) корня:
;
.
Тогда разложение трехчлена на множители имеет вид:
.
График функции y = x 2 – 4 x + 4 касается оси абсцисс в одной точке.
Построим график функции
.
График этой функции является параболой. Она касается оси абсцисс (ось ) в одной точке:
.
Эта точка является корнем исходного уравнения (2.1). Поскольку этот корень входит в разложение на множители два раза:
,
то такой корень принято называть кратным. То есть считают, что имеется два равных корня:
.
Пример 3
Найти корни квадратного уравнения:
(3.1) .
Запишем квадратное уравнение в общем виде:
(1) .
Перепишем исходное уравнение (3.1):
.
Сравнивая с (1), находим значения коэффициентов:
.
Находим дискриминант:
.
Дискриминант отрицателен, . Поэтому действительных корней нет.
Можно найти комплексные корни:
;
;
.
График функции не пересекает ось абсцисс. Действительных корней нет.
Построим график функции
.
График этой функции является параболой. Она не пересекает ось абсцисс (ось ). Поэтому действительных корней нет.
Действительных корней нет. Корни комплексные:
;
;
.
Автор: Олег Одинцов . Опубликовано: 19-04-2016
http://lfirmal.com/reshenie-kvadratnyih-uravnenij-s-otritsatelnyim-diskriminantom/
http://games-on-pc.ru/info/esli-diskriminant-otricatelnyj-to-skolko-kornej/
Надеюсь, изучив данную статью, вы научитесь находить корни полного квадратного уравнения.
С помощью дискриминанта решаются только полные квадратные уравнения, для решения неполных квадратных уравнений используют другие методы, которые вы найдете в статье «Решение неполных квадратных уравнений».
Какие же квадратные уравнения называются полными? Это уравнения вида ах2 + b x + c = 0, где коэффициенты a, b и с не равны нулю. Итак, чтобы решить полное квадратное уравнение, надо вычислить дискриминант D.
D = b2 – 4ас .
В зависимости от того какое значение имеет дискриминант, мы и запишем ответ.
Если дискриминант отрицательное число (D < 0),то корней нет.
Если же дискриминант равен нулю, то х = (-b)/2a. Когда дискриминант положительное число (D > 0),
тогда х1 = (-b — √D)/2a , и х2 = (-b + √D)/2a .
Например. Решить уравнение х2 – 4х + 4= 0.
D = 42 – 4 · 4 = 0
x = (- (-4))/2 = 2
Ответ: 2.
Решить уравнение 2х2 + х + 3 = 0.
D = 12 – 4 · 2 · 3 = – 23
Ответ: корней нет.
Решить уравнение 2х2 + 5х – 7 = 0.
D = 52 – 4 · 2 · (–7) = 81
х1 = (-5 — √81)/(2·2)= (-5 — 9)/4= – 3,5
х2 = (-5 + √81)/(2·2) = (-5 + 9)/4=1
Ответ: – 3,5 ; 1.
Итак представим решение полных квадратных уравнений схемой на рисунке1.
По этим формулам можно решать любое полное квадратное уравнение.
ах2 + bx + c, иначе можно допустить ошибку. Например, в записи уравнения х + 3 + 2х2 = 0, ошибочно можно решить, что
а = 1, b = 3 и с = 2. Тогда
D = 32 – 4 · 1 · 2 = 1 и тогда уравнение имеет два корня. А это неверно. (Смотри решение примера 2 выше).
Поэтому, если уравнение записано не многочленом стандартного вида, вначале полное квадратное уравнение надо записать многочленом стандартного вида (на первом месте должен стоять одночлен с наибольшим показателем степени, то есть ах2, затем с меньшим – bx, а затем свободный член с.
При решении приведенного квадратного уравнения и квадратного уравнения с четным коэффициентом при втором слагаемом можно использовать и другие формулы. Давайте познакомимся и с этими формулами. Если в полном квадратном уравнении при втором слагаемом коэффициент будет четным (b = 2k), то можно решать уравнение по формулам приведенным на схеме рисунка 2.
Полное квадратное уравнение называется приведенным, если коэффициент при х2 равен единице и уравнение примет вид х2 + px + q = 0. Такое уравнение может быть дано для решения, либо получается делением всех коэффициентов уравнение на коэффициент а, стоящий при х2.
На рисунке 3 приведена схема решения приведенных квадратных
Пример. Решить уравнение
3х2 + 6х – 6 = 0.
Давайте решим это уравнение применяя формулы приведенные на схеме рисунка 1.
D = 62 – 4 · 3 · (– 6) = 36 + 72 = 108
√D = √108 = √(36 · 3) = 6√3
х1 = (-6 — 6√3 )/(2 · 3) = (6 ( -1- √(3)))/6 = –1 – √3
х2 = (-6 + 6√3 )/(2 · 3) = (6 ( -1+ √(3)))/6 = –1 + √3
Ответ: –1 – √3; –1 + √3
Можно заметить, что коэффициент при х в этом уравнении четное число, то есть b = 6 или b = 2k , откуда k = 3. Тогда попробуем решить уравнение по формулам , приведенным на схеме рисунка D1 = 32 – 3 · (– 6) = 9 + 18 = 27
√(D1) = √27 = √(9 · 3) = 3√3
х1 = (-3 — 3√3)/3 = (3 (-1 — √(3)))/3 = – 1 – √3
х2 = (-3 + 3√3)/3 = (3 (-1 + √(3)))/3 = – 1 + √3
Ответ: –1 – √3; –1 + √3. Заметив, что все коэффициенты в этом квадратном уравнении делятся на 3 и выполнив деление, получим приведенное квадратное уравнение x2 + 2х – 2 = 0 Решим это уравнение, используя формулы для приведенного квадратного 
D2 = 22 – 4 · (– 2) = 4 + 8 = 12
√(D2) = √12 = √(4 · 3) = 2√3
х1= (-2 — 2√3)/2 = (2 (-1 — √(3)))/2 = – 1 – √3
х2= (-2 + 2√3)/2 = (2 (-1+ √(3)))/2 = – 1 + √3
Ответ: –1 – √3; –1 + √3.
Как видим, при решении этого уравнения по различным формулам мы получили один и тот же ответ. Поэтому хорошо усвоив формулы приведенные на схеме рисунка 1 , вы всегда сможете решить любое полное квадратное уравнение.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Понятие квадратного уравнения
Уравнение — это равенство, содержащее переменную, значение которой нужно найти.
Например, х + 8 = 12 — это уравнение, которое содержит переменную х.
Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.
Например, если х = 5, то при подстановке в уравнение мы получим 5 + 8 = 12. 13 = 12 — противоречие. Значит, х = 5 не является корнем уравнения.
А вот если х = 4, то при подстановке в уравнение мы получим 4 + 8 = 12. 12 = 12 — верное равенство. Значит, х = 4 является корнем уравнения.
Решить уравнение — значит найти все его корни или доказать, что их не существует.
Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Чтобы запомнить месторасположение коэффициентов, давайте потренируемся определять их.
Квадратные уравнения могут иметь два корня, один корень или не иметь корней.
Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b2 − 4ac. А вот свойства дискриминанта:
- если D < 0, корней нет;
- если D = 0, есть один корень;
- если D > 0, есть два различных корня.
С этим разобрались. А сейчас посмотрим подробнее на различные виды квадратных уравнений.
Разобраться в теме еще быстрее с помощью опытного преподавателя можно
на курсах по математике в онлайн-школе Skysmart.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас
Приведенные и неприведенные квадратные уравнения
Квадратное уравнение может быть приведенным или неприведенным — все зависит от от значения первого коэффициента.
Приведенное квадратное уравнение — это уравнение, где старший коэффициент, тот который стоит при одночлене высшей степени, равен единице.
Неприведенным называют квадратное уравнение, где старший коэффициент отличается от единицы.
Давайте-ка на примерах — вот у нас есть два уравнения:
- x2 — 2x + 6 = 0
- x2 — x — 1/4 = 0
В каждом из них старший коэффициент равен единице (которую мы мысленно представляем при x2 ), а значит уравнение называется приведенным.
- 2x2 − 4x — 12 = 0 — первый коэффициент отличен от единицы (2), значит это неприведенное квадратное уравнение.
Каждое неприведенное квадратное уравнение можно преобразовать в приведенное, если произвести равносильное преобразование — разделить обе его части на первый коэффициент.
Запоминаем!
У преобразованного уравнения те же корни, что и у первоначального. Ну или вообще нет корней.
Пример 1. Превратим неприведенное уравнение: 8x2 + 20x — 9 = 0 — в приведенное.
Для этого разделим обе части исходного уравнения на старший коэффициент 8:
Ответ: равносильное данному приведенное уравнение x2 + 2,5x — 1,125 = 0.
Пройдите тест и узнайте, какие темы отделяют от пятёрки по математике
Добро пожаловать в школу магии.
О нет! Мальчик-молния случайно попал в школьные часы. Теперь они отстают. Мы все можем задержаться в школе
Жми на стрелки сверху, чтобы путешествовать в истории→
Одна ученица когда-то была в школьной кладовке и видела там схему часов
Но в кладовку просто так не попадёшь→
Реши два примера от волшебной статуи на входе в кладовку
frac{1}{7} + frac{3}{7} =
frac{4}{7}
frac{5}{7}
frac{4}{14}
frac{2}{7}
frac{4}{15} — frac{1}{15} =
frac{1}{3}
frac{1}{5}
frac{3}{30}
frac{1}{10}
Схема у нас!
Деталь можно сделать из проволоки и формы для заливки металла. Найди их на картинке
Теперь осталось взять инструменты у садовника! Он обменяет их на волшебные бобы для его сада
Для починки часов нужны: молоток, отвертка и плоскогубцы.
Ты можешь либо одолжить у садовника набор, либо отдельные инструменты, либо и то, и другое. Какое минимальное количество волшебных бобов ты можешь отдать садовнику?
Ответ:
562 боба
400 бобов
553 боба
Деталь имеет форму прямоугольника со сторонами 5 см и 12 см. Найди периметр и площадь детали, чтобы посчитать, сколько проволоки для неё понадобится
Периметр прямоугольника равен
40 см
26 см
22 см
34 см
Площадь прямоугольника равна
50 см^2
46 см^2
60 см^2
62 см^2
Мальчик-молния выплавил деталь, часы должны работать! Но они почему-то не идут… Кажется, одной шестерёнки не хватает — она куда-то упала
В коробке, шкатулке, ящике и банке находятся пыльца, волчий корень, золото и шестерёнка. Шестерёнка и пыльца не в коробке, ёмкость с волчьим корнем стоит между ящиком и ёмкостью с золотом, в банке не волчий корень и не шестерёнка. Шкатулка стоит около банки и ёмкостью с пыльцой. В какой ёмкости что находится?
Соедини ёмкости с содержимым на картинках ниже
Шестерёнка
Золото
Волчий корень
Пыльца
Ура, мы вставили последнюю шестеренку, и часы пошли! Сегодня уроки закончатся вовремя. Спасибо тебе за помощь!
Дальше узнаешь свои результаты →
Полные и неполные квадратные уравнения
В определении квадратного уравнения есть условие: a ≠ 0. Оно нужно, чтобы уравнение ax2 + bx + c = 0 было именно квадратным. Если a = 0, то уравнение обретет вид линейного: bx + c = 0.
Что касается коэффициентов b и c, то они могут быть равны нулю, как по отдельности, так и вместе. В таком случае квадратное уравнение принято называть неполным.
Неполное квадратное уравнение —— это квадратное уравнение вида ax2 + bx + c = 0, где оба или хотя бы один из коэффициентов b и c равен нулю.
Полное квадратное уравнение — это уравнение, у которого все коэффициенты отличны от нуля.
| Для самых любопытных объясняем откуда появились такие названия: |
|---|
Такие уравнения отличны от полного квадратного тем, что их левые части не содержат либо слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения. |
Решение неполных квадратных уравнений
Как мы уже знаем, есть три вида неполных квадратных уравнений:
- ax2 = 0, ему отвечают коэффициенты b = 0 и c = 0;
- ax2 + c = 0, при b = 0;
- ax2 + bx = 0, при c = 0.
Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам.
Как решить уравнение ax2 = 0
Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax2 = 0.
Уравнение ax2 = 0 равносильно x2 = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x2 = 0 является нуль, так как 02 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.
Таким образом, неполное квадратное уравнение ax2 = 0 имеет единственный корень x = 0.
Пример 1. Решить −6x2 = 0.
Как решаем:
- Замечаем, что данному уравнению равносильно x2 = 0, значит исходное уравнение имеет единственный корень — нуль.
- По шагам решение выглядит так:
−6x2 = 0
x2 = 0
x = √0
x = 0
Ответ: 0.
Как решить уравнение ax2 + с = 0
Обратим внимание на неполные квадратные уравнения вида ax2 + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.
Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами.
Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax2 + c = 0:
- перенесем c в правую часть: ax2 = — c,
- разделим обе части на a: x2 = — c/а.
Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.
Если — c/а < 0, то уравнение x2 = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а < 0 ни для какого числа p равенство р2 = — c/а не является верным.
Если — c/а > 0, то корни уравнения x2 = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)2 = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)2 = — c/а. Ура, больше у этого уравнения нет корней.
| В двух словах |
|---|
|
Неполное квадратное уравнение ax2 + c = 0 равносильно уравнению х2= -c/a, которое:
|
Пример 1. Найти решение уравнения 8x2 + 5 = 0.
Как решать:
- Перенесем свободный член в правую часть:
8x2 = — 5
- Разделим обе части на 8:
x2 = — 5/8
- В правой части осталось число со знаком минус, значит у данного уравнения нет корней.
Ответ: уравнение 8x2 + 5 = 0 не имеет корней.
Как решить уравнение ax2 + bx = 0
Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.
Неполное квадратное уравнение ax2 + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение:
-
Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.
-
Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.
Таким образом, неполное квадратное уравнение ax2 + bx = 0 имеет два корня:
- x = 0;
- x = −b/a.
Пример 1. Решить уравнение 0,5x2 + 0,125x = 0
Как решать:
- Вынести х за скобки
х(0,5x + 0,125) = 0
- Это уравнение равносильно х = 0 и 0,5x + 0,125 = 0.
- Решить линейное уравнение:
0,5x = −0,125,
х = −0,125/0,5 - Разделить:
х = −0,25
- Значит корни исходного уравнения — 0 и −0,25.
Ответ: х = 0 и х = −0,25.
Как разложить квадратное уравнение
С помощью теоремы Виета можно получить формулу разложения квадратного трехчлена на множители. Выглядит она так:
Формула разложения квадратного трехчлена
Если x1 и x2 — корни квадратного трехчлена ax2 + bx + c, то справедливо равенство ax2 + bx + c = a (x − x1) (x − x2).
Дискриминант: формула корней квадратного уравнения
Чтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так:
где D = b2 − 4ac — дискриминант квадратного уравнения.
Эта запись означает:
,
.
Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться.
Алгоритм решения квадратных уравнений по формулам корней
Теперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни.
В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.
Алгоритм решения квадратного уравнения ax2 + bx + c = 0:
- вычислить его значение дискриминанта по формуле D = b2−4ac;
- если дискриминант отрицательный, зафиксировать, что действительных корней нет;
- если дискриминант равен нулю, вычислить единственный корень уравнения по формуле х = −b/2a;
- если дискриминант положительный, найти два действительных корня квадратного уравнения по формуле корней
Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться!
Примеры решения квадратных уравнений
Как решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике.
Пример 1. Решить уравнение −4x2 + 28x — 49 = 0.
Как решаем:
- Найдем дискриминант: D = 282 — 4(-4)(-49) = 784 — 784 = 0
- Так как дискриминант равен нулю, значит это квадратное уравнение имеет единственный корень
- Найдем корень
х = — 28/2(-4)
х = 3,5
Ответ: единственный корень 3,5.
Пример 2. Решить уравнение 54 — 6x2 = 0.
Как решаем:
- Произведем равносильные преобразования. Умножим обе части на −1
54 — 6x2 = 0 | *(-1)
6x2 — 54 = 0
- Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую
6x2 = 54
х2 = 9
х = ±√9
х1 = 3, х2 = — 3
Ответ: два корня 3 и — 3.
Пример 3. Решить уравнение x2— х = 0.
Как решаем:
- Преобразуем уравнение так, чтобы появились множители
х(х — 1) = 0
х₁ = 0, х₂ = 1
Ответ: два корня 0 и 1.
Пример 4. Решить уравнение x2— 10 = 39.
Как решаем:
- Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую
x2— 10 = 39
x2= 39 + 10
x2= 49
х = ±√49
х₁ = 7, х₂ = −7
Ответ: два корня 7 и −7.
Пример 5. Решить уравнение 3x2— 4x+94 = 0.
Как решаем:
- Найдем дискриминант по формуле
D = (-4)2 — 4 * 3 * 94 = 16 — 1128 = −1112
- Дискриминант отрицательный, поэтому корней нет.
Ответ: корней нет.
В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся.
Формула корней для четных вторых коэффициентов
Рассмотрим частный случай. Формула решения корней квадратного уравнения 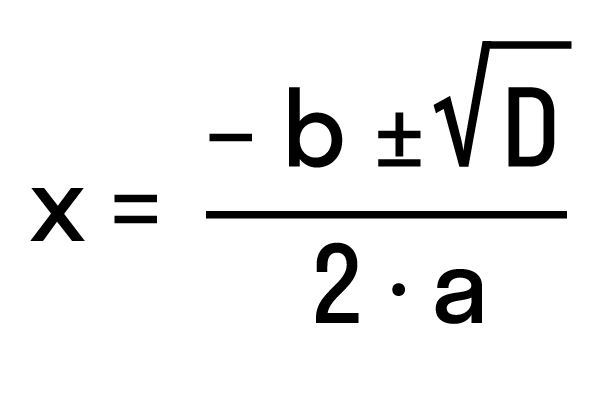
Например, нам нужно решить квадратное уравнение ax2 + 2nx + c = 0. Сначала найдем его корни по известной нам формуле. Вычислим дискриминант D = (2n)2— 4ac = 4n2 — 4ac = 4(n2— ac) и подставим в формулу корней:
Для удобства вычислений обозначим выражение n2 -ac как D1. Тогда формула корней квадратного уравнения со вторым коэффициентом 2·n примет вид:
где D1 = n2— ac.
Самые внимательные уже заметили, что D = 4D1, или D1= D/4. Проще говоря, D1 — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения.
Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:
- вычислить D1= n2— ac;
- если D1< 0, значит действительных корней нет;
- если D1= 0, значит можно вычислить единственный корень уравнения по формуле x = -n/a;
- если же D1> 0, значит можно найти два действительных корня по формуле
Формула Виета
Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так:
Теорема Виета
Сумма корней x2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.
Если дано x2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:
Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.
Рассмотрим теорему Виета на примере: x2 + 4x + 3 = 0.
Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:
Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:
Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:
Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.
Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:
Результат проделанных вычислений в том, что мы убедились в справедливости выражения:
Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она:
Обратная теорема Виета
Если числа x1 и x2 таковы, что их сумма равна второму коэффициенту уравнения x2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа и есть корни x2 + bx + c = 0.
Обычно вся суть обратных теорем в том самом выводе, которое дает первая теорема. Так, при доказательстве теоремы Виета стало понятно, что сумма x1 и x2 равна −b, а их произведение равно c. В обратной теореме это и есть утверждение.
Пример 1. Решить при помощи теоремы Виета: x2 − 6x + 8 = 0.
Как решаем:
- Для начала запишем сумму и произведение корней уравнения. Сумма будет равна 6, так как второй коэффициент равен −6. А произведение корней равно 8.
- Когда у нас есть эти два равенства, можно подобрать подходящие корни, которые будут удовлетворять обоим равенствам системы.
Чтобы проще подобрать корни, нужно их перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x1 и x2 надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.
Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x1 + x2 = 6. А значения 4 и 2 подходят обоим равенствам:
- Значит числа 4 и 2 — корни уравнения x2 − 6x + 8 = 0. p>
Упрощаем вид квадратных уравнений
Если мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту.
Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11x2 — 4 x — 6 = 0, чем 1100x2 — 400x — 600 = 0.
Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100x2 — 400x — 600 = 0, просто разделив обе части на 100.
Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов.
Покажем, как это работает на примере 12x2— 42x + 48 = 0. Найдем наибольший общий делитель абсолютных величин его коэффициентов: НОД (12, 42, 48) = 6. Разделим обе части исходного квадратного уравнения на 6, и придем к равносильному уравнению 2x2 — 7x + 8 = 0. Вот так просто.
А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов. Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения
умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x2 + 4x — 18 = 0.
Также для удобства вычислений можно избавиться от минуса при старшем коэффициенте квадратного уравнения — для этого умножим или разделим обе части на −1. Например, удобно от квадратного уравнения −2x2— 3x + 7 = 0 перейти к решению 2x2 + 3x — 7 = 0.
Связь между корнями и коэффициентами
Мы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты:
Из этой формулы, можно получить другие зависимости между корнями и коэффициентами.
Например, можно применить формулы из теоремы Виета:
- x₁ + x₂ = — b/a,
- x₁* x₂ = c/a.
Для приведенного квадратного уравнения сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней — свободному члену. Например, по виду уравнения 3x2— 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3.
Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты: