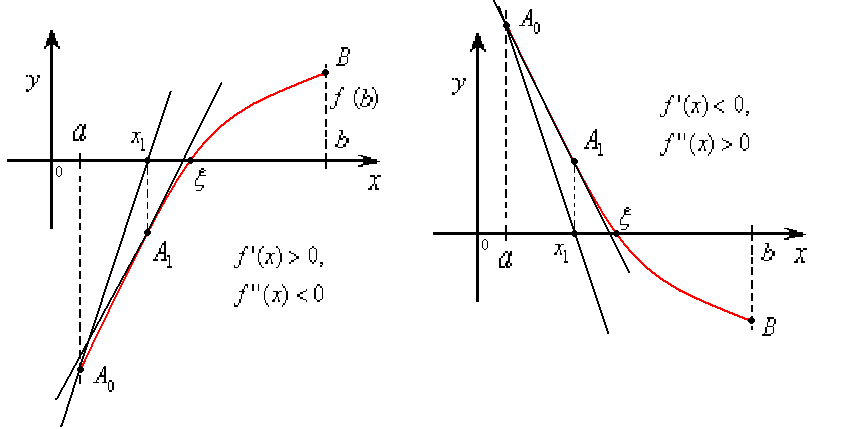Как найти корень уравнения методом касательных

Пусть
корень уравнения
отделен на отрезке,
причемf’(x)
и f’’(x)
и сохраняют
постоянные знаки на всем отрезке
.

Геометрический
смысл метода Ньютона состоит в том, что
дуга кривой
заменяется касательной к этой кривой
(отсюда и второе название метода — «метод
касательных»).

Рассмотрим два
случая:

а)
или

Проведем
касательную к кривой
в точкеB0
(b,f(b))
и найдем абсциссу
точки
пересечения касательной с осью
Ox.
Известно,
что уравнение касательной в точке B0
(b,f(b))
имеет вид:

Поскоку
в нашем случае y=0,
x=x1,то
получаем:
.

Теперь
корень уравнения находится на отрезке
[a,x1].
Применяя снова метод Ньютона, проведем
касательную к кривой в точке B1
(x1,f(x1))
получим:
,
и вообще:.
Очевидно, что каждый следующий член
последовательностиесть более близкое приближенное значение
к корню,
чем предыдущий. Однако всев этом случае остаются больше истинного
значения корня,
т.е.— приближенное значение корняс избытком.

б)Пусть

или,
т.е.

Если
снова провести касательную к кривой
в точкеB,
то она
пересечет ось абсцисс в точке, не
принадлежащей отрезку
.
Потому проведем касательную в точкеA0(a,f(a))
и запишем
ее уравнение

Поскоку
y=0,
x=x1,то
получаем:
.

Очевидно,
корень
находится на отрезке [x1,b].
Повторив процедуру в точке A1
(x1,f(x1)),
получаем:
и вообще.

Итак,
получив последовательность
приближенных
значений искомого корня,
отметим, что каждый последующий член
ее ближе к истинному корню,
чем предыдущий. Отсюда следует, что— приближенное значение корняс недостатком.

Анализ
полученных формул в случае а) и в случае
б) приводит к следующему правилу выбора
начального приближения
корня:

-за
исходную точку
следует
брать тот конец отрезка,
в котором знак функциисовпадает со знаком второй производнойf’’(x).
Очевидно, в
первом случае (случае а))
и начальная точка,
а во втором случаеи начальное приближение есть.

Примечание

  1. Для
    оценки погрешности приближенного
    значения корня
    будем пользоваться формулой:,
    где(эта
    формула используется в методе хорд).

  2. В
    том случае, когда отрезок
    настолько
    мал, что на нем выполняется условие,
    где,
    точность приближения наn-ом
    шаге оценивается следующим образом:
    если
    .

  3. Если
    производная f’(x)
    мало меняется на отрезке
    ,
    то для упрощения вычислений можно
    пользоваться формулой:,
    т.е. значение производной в начальной
    точке достаточно вычислить только один
    раз. Геометрически это означает, что
    касательные в точкеBn
    (xn,f(xn))
    заменяются прямыми, параллельными
    касательной, проведенной к кривой
    в точкеB0(x0,f(x0)).

Пример

Методом
касательных уточнить до
корень уравнения,
расположенный на отрезке [-2,75;-2,5] .

Решение

Имеем
: f(-2,75)=-2,753+3*2,752-3<0,
f’’(x)=6x+6<0,

,
т.е..

Это
означает, что вычисления надо вести по
формуле
.
Находим:f’(x)=3x2+6x,
f’(x0)=f’(-2,75)=(-3)*2,75*(-2,75+2)=6,1875.

Для удобства все
вычисленное сведем в таблицу:

n

xn

3

f(xn)

0

-2,75

-20,797

7,5625

22,6895

-1,111

0,179

1

-2,571

-16,994

6,6100

19,8300

-0,164

0,026

2

-2,545

-16,484

6,4770

19,431

-0,053

0,008

3

-2,537

-16,329

6,4364

19,309

0,020

0,003

4

-2,534

-16,271

6,4212

19,2636

0,007

0,001

5

-2,533

Из
этой таблицы следует, что
и поэтому корень.

Пример

Методом
касательных уточнить до
корень уравнения,
расположенный на отрезке [0,982;1,178].

Решение

Здесь
a=0,982;
b=1,178,
находим
f’(x)=1-cos
x;
. f’’(x)=sinx>0
на [0,982;1,178],
.
Значит,

Вычисления
будем вести по формуле
.
Результаты вычислений сведем в таблицу:

n

xn

—sin
xn

0

1,178

-0,92384

0,00416

0,61723

-0,0065

1

1,1715

-0,92133

0,00017

0,01123

-0,0002

2

1,1713

-0,92127

0,00003

0,61110

-0,00005

3

1,17125

Из
таблицы видно, что
.
Таким образом,.

Соседние файлы в папке Лекции Маркина

  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник
 

Пусть имеется уравнение вида

f(x)= 0

где f(x) — заданная алгебраическая или трансцендентная функция.

Решить уравнение — значит найти все его корни, то есть те значения x, которые обращают уравнение в тождество.
Если уравнение достаточно сложно, то задача точного определения корней является в некоторых случаях нерешаемой. Поэтому ставится задача найти такое приближенное значение корня xПP, которое отличается от точного значения корня x* на величину, по модулю не превышающую указанной точности (малой положительной величины) ε, то есть

│x* – xпр │< ε

Величину ε также называют допустимой ошибкой, которую можно задать по своему усмотрению.

Этапы приближенного решения нелинейных уравнений

Приближенное решение уравнения состоит из двух этапов:

  • Отделение корней, то есть нахождение интервалов из области определения функции f(x), в каждом из которых содержится только один корень уравнения f(x)=0.
  • Уточнение корней до заданной точности.

Отделение корней

Отделение корней можно проводить графически и аналитически.
Для того чтобы графически отделить корни уравнения, необходимо построить график функции f(x). Абсциссы точек его пересечения с осью Ox являются действительными корнями уравнения.

Для примера рассмотрим задачу решения уравнения
Уравнение
где угол x задан в градусах. Указанное уравнение можно переписать в виде
f(x)=0
Для графического отсечения корней достаточно построить график функции
График функции
Из рисунка видно, что корень уравнения лежит в промежутке x∈(6;8).

Аналитическое отделение корней

Аналитическое отделение корней основано на следующих теоремах.
Теорема 1. Если непрерывная функция f(x) принимает на концах отрезка [a; b] значения разных знаков, т.е.
f(a)f(b)<0
то на этом отрезке содержится по крайней мере один корень уравнения.
Теорема 2. Если непрерывная на отрезке [a; b] функция f(x) принимает на концах отрезка значения разных знаков, а производная f'(x) сохраняет знак внутри указанного отрезка, то внутри отрезка существует единственный корень уравнения f(x) = 0.

Уточнение корней

Для уточнения корней может использоваться один из следующих методов:

  • Метод последовательных приближений (метод итераций)
  • Метод Ньютона (метод касательных)
  • Метод секущих (метод хорд)
  • Метод половинного деления (метод дихотомии)

Метод последовательных приближений (метод итераций)

Метод итерации — численный метод решения математических задач, используемый для приближённого решения алгебраических уравнений и систем. Суть метода заключается в нахождении по приближённому значению величины следующего приближения (являющегося более точным). Метод позволяет получить решение с заданной точностью в виде предела последовательности итераций. Характер сходимости и сам факт сходимости метода зависит от выбора начального приближения решения.
Функциональное уравнение может быть записано в виде
x=f(x)
Функцию f(x) называют сжимающим отображением.

Последовательность чисел x0, x1 ,…, xn называется итерационной, если для любого номера n>0 элемент xn выражается через элемент xn-1 по рекуррентной формуле
xn=f(xn-1)
а в качестве x0 взято любое число из области задания функции f(x).

Реализация на C++ для рассмотренного выше примера
Уравнение
Уравнение может быть записано в форме
x=1/sinx

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

#define _USE_MATH_DEFINES
#include <iostream>
#include <cmath>
using namespace std;
double find(double x, double eps)
{
  double rez; int iter = 0;
  cout << «x0= » << x << » «;
  do {
    rez = x;
    x = 1 / (sin(M_PI*x / 180));
    iter++;
  } while (fabs(rez — x) > eps && iter<20000);
  cout << iter << » iterations» << endl;
  return x;
}
int main() 
{
  cout << find(7, 0.00001);
  cin.get(); 
  return 0;
}

Результат выполнения
Результат метода последовательных приближений

Метод Ньютона (метод касательных)

Если известно начальное приближение x0 корня уравнения f(x)=0, то последовательные приближения находят по формуле
метод Ньютона
Графическая интерпретация метода касательных имеет вид
Метод касательных
Реализация на C++
Для заданного уравнения
метод Ньютона
производная будет иметь вид f'(x)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

#define _USE_MATH_DEFINES
#include <iostream>
#include <cmath>
using namespace std;
double find(double x, double eps)
{
  double f, df; int iter = 0;
  cout << «x0= » << x << » «;
  do {
    f = sin(M_PI*x / 180) — 1 / x;
    df = M_PI / 180 * cos(M_PI*x / 180) + 1 / (x*x);
    x = x — f / df;
    iter++;
  } while (fabs(f) > eps && iter<20000);
  cout << iter << » iterations» << endl;
  return x;
}
int main() 
{
  cout << find(1, 0.00001);
  cin.get(); return 0;
}

Результат выполнения
Метод Ньютона

Метод секущих (метод хорд)

Если x0, x1 — приближенные значения корня уравнения f(x) = 0 и выполняется условие
f(a)f(b)
то последующие приближения находят по формуле
Метод хорд
Методом хорд называют также метод, при котором один из концов отрезка закреплен, т.е. вычисление приближения корня уравнения f(x) = 0 производят по формулам:
Метод секущих
Геометрическая интерпретация метода хорд:
Метод хорд
Реализация на C++
В отличие от двух рассмотренных выше методов, метод хорд предполагает наличие двух начальных приближений, представляющих собой концы отрезка, внутри которого располагается искомый корень.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

#define _USE_MATH_DEFINES
#include <iostream>
#include <cmath>
using namespace std;
double find(double x0, double x1, double eps)
{
  double rez = x1, f0, f;
  int iter = 0;
  cout << «x0= » << x0 << » x1= » << x1 << » «;
  do {
    f = sin(M_PI*rez / 180) — 1 / rez;
    f0 = sin(M_PI*x0 / 180) — 1 / x0;
    rez = rez — f / (f — f0)*(rez — x0);
    iter++;
  } while (fabs(f) > eps && iter<20000);
  cout << iter << » iterations» << endl;
  return rez;
}
int main() 
{
  cout << find(1.0, 10.0, 0.000001);
  cin.get(); return 0;
}

Результат выполнения
Реализация метода хорд

Метод половинного деления (метод дихотомии)

Если x0, x1 — приближенные значения корня уравнения f(x) = 0 и выполняется условие
Метод половинного деления
то последующие приближения находятся по формуле
Метод дихотомии
и вычисляется f(xi). Если f(xi)=0, то корень найден. В противном случае из отрезков выбирается тот, на концах которого f(x) принимает значения разных знаков, и проделывается аналогичная операция. Процесс продолжается до получения требуемой точности.

Геометрическая интерпретация метода дихотомии
Метод дихотомии
Реализация на C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

#define _USE_MATH_DEFINES
#include <iostream>
#include <cmath>
using namespace std;
double func(double x)
{
  return (sin(M_PI*x / 180) — 1 / x);
}
double find(double x0, double x1, double eps)
{
  double left = x0, right = x1, x, fl, fr, f;
  int iter = 0;
  cout << «x0= » << x0 << » x1= » << x1 << » «;
  do {
    x = (left + right) / 2;
    f = func(x);
    if (f > 0) right = x;
    else left = x;
    iter++;
  } while (fabs(f) > eps && iter<20000);
  cout << iter << » iterations» << endl;
  return x;
}
int main() 
{
  cout << find(1.0, 10.0, 0.000001);
  cin.get(); return 0;
}

Результат выполнения
Метод дихотомии
Для численного поиска решения также можно использовать генетические алгоритмы.

Назад: Алгоритмизация

Источник

Этот онлайн калькулятор применяет метод Ньютона (также известный как метод касательных) используя калькулятор производных для получения аналитической формулы производной заданной функции (метод Ньютона требует вычисления производной). Под калькулятором можно прочитать краткое описание метода.

PLANETCALC, Метод Ньютона

Метод Ньютона

Критерий останова (погрешность)

Точность вычисления

Знаков после запятой: 4

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Метод Ньютона1

Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643—1727). Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации.

Основная идея метода заключается в следующем: задаётся начальное приближение вблизи предположительного корня, после чего строится касательная к графику исследуемой функции в точке приближения, для которой находится пересечение с осью абсцисс. Эта точка берётся в качестве следующего приближения. Далее процесс повторяется, пока не будет достигнута необходимая точность.

Уравнение касательной к графику функции выглядит следующим образом:
y(x)=f(x_{n})+(x-x_{n})cdot mathrm {tg} ,alpha _{n},
где mathrm {tg} ,alpha _{n} — тангенс угла пересечения касательной с осью абсцисс.

Тангенс угла пересечения касательной с осью абсцисс, frac{Delta y}{Delta x} — не что иное, как значение производной в точке x_n.
С учетом того факта, что в точке пересечения с осью абсцисс значение y равно нулю, можно записать следующее выражение для нахождения точки пересечения (следующей точки приближения):
x_{n+1}=x_{n}-{frac {f(x_{n})}{f'(x_{n})}}

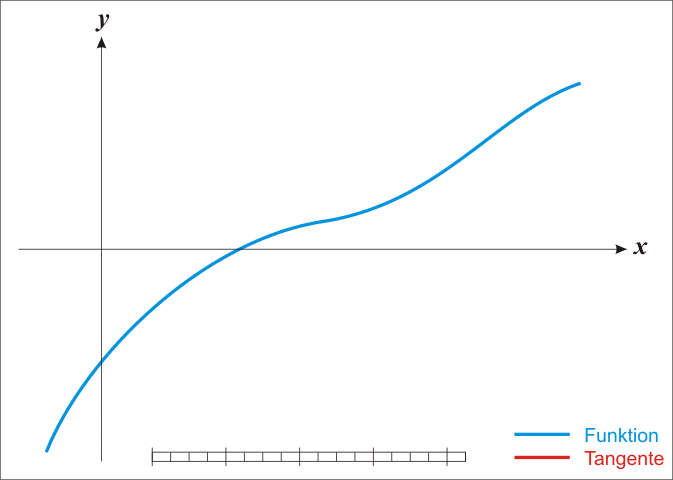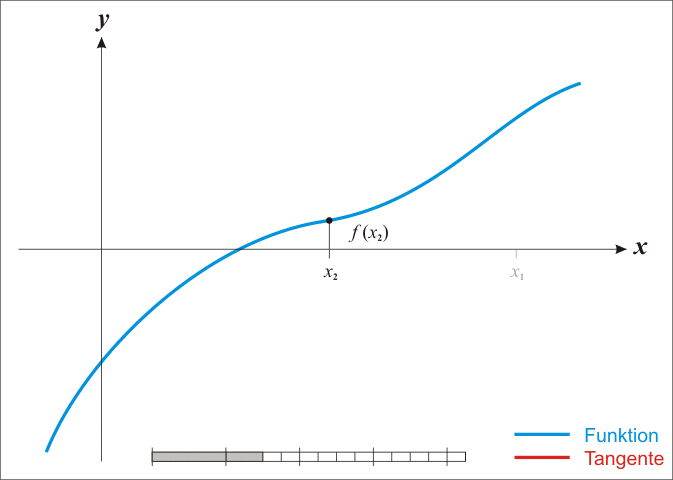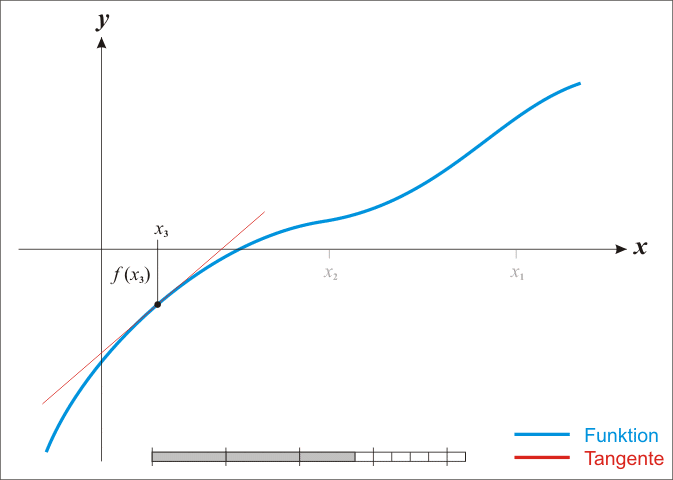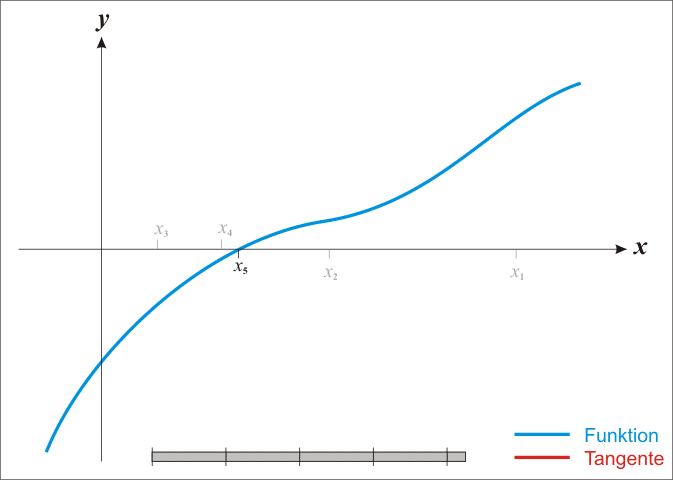
Анимация метода Ньютона (Ralf Pfeifer, https://commons.wikimedia.org/wiki/File:NewtonIteration_Ani.gif)
Анимация метода Ньютона (Ralf Pfeifer, https://commons.wikimedia.org/wiki/File:NewtonIteration_Ani.gif)

Метод Ньютона является очень мощным методом поиска корней функции, так как имеет квадратичную скорость сходимости — количество значащих цифр примерно удваивается с каждым шагом итерации, однако существуют и ограничения, затрудняющие его применение. Так, например, если начальное приближение недостаточно близко к решению, то метод может не сойтись, если производная не непрерывна в точке корня, то метод может расходиться в любой окрестности корня, если не существует вторая производная в точке корня, то скорость сходимости метода может быть заметно снижена, если производная в точке корня равна нулю, то скорость сходимости не будет квадратичной, а сам метод может преждевременно прекратить поиск, и дать неверное для заданной точности приближение.

Теорема Канторовича дает следующие условия применимости метода для поиска корней функции:

  1. функция должна быть ограничена;
  2. функция должна быть гладкой, дважды дифференцируемой;
  3. её первая производная f'(x) равномерно отделена от нуля;
  4. её вторая производная f»(x) должна быть равномерно ограничена.
Источник

Понравилась статья? Поделить с друзьями:
  • Как найти точку пересечения медиан зная координаты
  • Как найти произведение подстановок
  • Как найти человека работающего в милиции
  • Неправильно постирала куртку как исправить
  • Как составить гобелен