Как найти корень уравнения на заданном промежутке - Исправление недочетов и поиск решений вместе с Examum.ru

Чтобы успешно решать тригонометрические уравнения удобно пользоваться методом сведения к ранее решенным задачам. Давайте разберемся, в чем суть этого метода?

В любой предлагаемой задаче вам необходимо увидеть уже решенную ранее задачу, а затем с помощью последовательных равносильных преобразований попытаться свести данную вам задачу к более простой.

Так, при решении тригонометрических уравнений обычно составляют некоторую конечную последовательность равносильных уравнений, последним звеном которой является уравнение с очевидным решением. Только важно помнить, что если навыки решения простейших тригонометрических уравнений не сформированы, то решение более сложных уравнений будет затруднено и малоэффективно.

Кроме того, решая тригонометрические уравнения, никогда не стоит забывать о возможности существования нескольких способов решения.

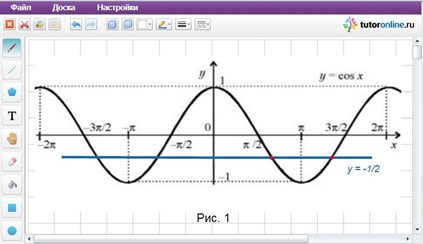
Пример 1. Найти количество корней уравнения cos x = -1/2 на промежутке [0; 2π].

Решение:

I способ. Изобразим графики функций y = cos x и y = -1/2 и найдем количество их общих точек на промежутке [0; 2π] (рис. 1).

Так как графики функций имеют две общие точки на промежутке [0; 2π], то уравнение содержит два корня на данном промежутке.

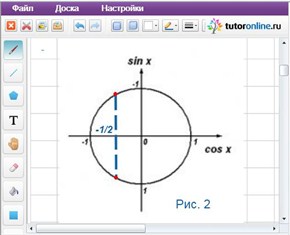
II способ. С помощью тригонометрического круга (рис. 2) выясним количество точек, принадлежащих промежутку [0; 2π], в которых cos x = -1/2. По рисунку видно, что уравнение имеет два корня.

III способ. Воспользовавшись формулой корней тригонометрического уравнения, решим уравнение cos x = -1/2.

cos x = -1/2;

x = ± arccos (-1/2) + 2πk, k – целое число (k € Z);

x = ± (π – arccos 1/2) + 2πk, k – целое число (k € Z);

x = ± (π – π/3) + 2πk, k – целое число (k € Z);

x = ± 2π/3 + 2πk, k – целое число (k € Z).

Промежутку [0; 2π] принадлежат корни 2π/3 и -2π/3 + 2π, k – целое число. Таким образом, уравнение имеет два корня на заданном промежутке.

Ответ: 2.

В дальнейшем тригонометрические уравнения будут решаться одним из предложенных способов, что во многих случаях не исключает применения и остальных способов.

Пример 2. Найти количество решений уравнения tg (x + π/4) = 1 на промежутке [-2π; 2π].

Решение:

Воспользовавшись формулой корней тригонометрического уравнения, получим:

x + π/4 = arctg 1 + πk, k – целое число (k € Z);

x + π/4 = π/4 + πk, k – целое число (k € Z);

x = πk, k – целое число (k € Z);

Промежутку [-2π; 2π] принадлежат числа -2π; -π; 0; π; 2π. Итак, уравнение имеет пять корней на заданном промежутке.

Ответ: 5.

Пример 3. Найти количество корней уравнения cos² x + sin x · cos x = 1 на промежутке [-π; π].

Решение:

Так как 1 = sin² x + cos² x (основное тригонометрическое тождество), то исходное уравнение принимает вид:

cos² x + sin x · cos x = sin² x + cos² x;

sin² x – sin x · cos x = 0;

sin x(sin x – cos x) = 0. Произведение равно нулю, а значит хотя бы один из множителей должен быть равен нулю, поэтому:

sin x = 0 или sin x – cos x = 0.

Так как значение переменной, при которых cos x = 0, не являются корнями второго уравнения (синус и косинус одного и того же числа не могут одновременно быть равными нулю), то разделим обе части второго уравнения на cos x:

sin x = 0 или sin x / cos x — 1 = 0.

Во втором уравнении воспользуемся тем, что tg x = sin x / cos x, тогда:

sin x = 0 или tg x = 1. С помощью формул имеем:

x = πk или x = π/4 + πk, k – целое число (k € Z).

Из первой серии корней промежутку [-π; π] принадлежат числа -π; 0; π. Из второй серии: (π/4 – π) и π/4.

Таким образом, пять корней исходного уравнения принадлежат промежутку [-π; π].

Ответ: 5.

Пример 4. Найти сумму корней уравнения tg² x + сtg² x + 3tg x + 3сtgx + 4 = 0 на промежутке [-π; 1,1π].

Решение:

Перепишем уравнение в следующем виде:

tg² x + сtg² x + 3(tg x + сtgx) + 4 = 0 и сделаем замену.

Пусть tg x + сtgx = a. Обе части равенства возведем в квадрат:

(tg x + сtg x)² = a². Раскроем скобки:

tg² x + 2tg x · сtgx + сtg² x = a².

Так как tg x · сtgx = 1, то tg² x + 2 + сtg² x = a², а значит

tg² x + сtg² x = a² – 2.

Теперь исходное уравнение имеет вид:

a² – 2 + 3a + 4 = 0;

a² + 3a + 2 = 0. С помощью теоремы Виета получаем, что a = -1 или a = -2.

Сделаем обратную замену, имеем:

tg x + сtgx = -1 или tg x + сtgx = -2. Решим полученные уравнения.

tg x + 1/tgx = -1 или tg x + 1/tgx = -2.

По свойству двух взаимно обратных чисел определяем, что первое уравнение не имеет корней, а из второго уравнения имеем:

tg x = -1, т.е. x = -π/4 + πk, k – целое число (k € Z).

Промежутку [-π; 1,1π] принадлежат корни: -π/4; -π/4 + π. Их сумма:

-π/4 + (-π/4 + π) = -π/2 + π = π/2.

Ответ: π/2.

Пример 5. Найти среднее арифметическое корней уравнения sin 3x + sin x = sin 2x на промежутке [-π; 0,5π].

Решение:

Воспользуемся формулой sin α + sin β = 2sin ((α + β)/2) · cos ((α – β)/2), тогда

sin 3x + sin x = 2sin ((3x + x)/2) · cos ((3x – x)/2) = 2sin 2x · cos x и уравнение принимает вид

2sin 2x · cos x = sin 2x;

2sin 2x · cos x – sin 2x = 0. Вынесем общий множитель sin 2x за скобки

sin 2x(2cos x – 1) = 0. Решим полученное уравнение:

sin 2x = 0 или 2cos x – 1 = 0;

sin 2x = 0 или cos x = 1/2;

2x = πk или x = ±π/3 + 2πk, k – целое число (k € Z).

Таким образом, имеем корни

x = πk/2, x = π/3 + 2πk, x = -π/3 + 2πk, k – целое число (k € Z).

Промежутку [-π; 0,5π] принадлежат корни -π; -π/2; 0; π/2 (из первой серии корней); π/3 (из второй серии); -π/3 (из третьей серии). Их среднее арифметическое равно:

(-π – π/2 + 0 + π/2 + π/3 – π/3)/6 = -π/6.

Ответ: -π/6.

Пример 6. Найти количество корней уравнения sin x + cos x = 0 на промежутке [-1,25π; 2π].

Решение:

Данное уравнение является однородным уравнением первой степени. Разделим обе его части на cosx (значение переменной, при которых cos x = 0, не являются корнями данного уравнения, так как синус и косинус одного и того же числа не могут одновременно быть равными нулю). Исходное уравнение имеет вид:

tg x + 1 = 0;

tg x = -1;

x = -π/4 + πk, k – целое число (k € Z).

Промежутку [-1,25π; 2π] принадлежат корни -π/4; (-π/4 + π); и (-π/4 + 2π).

Таким образом, заданному промежутку принадлежат три корня уравнения.

Ответ: 3.

Научитесь делать самое главное – четко представлять план решения задачи, и тогда любое тригонометрическое уравнение будет вам по плечу.

Остались вопросы? Не знаете, как решать тригонометрические уравнения?
Чтобы получить помощь репетитора – зарегистрируйтесь.

Источник

РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ

Простейшими тригонометрическими уравнениями называют уравнения

Чтобы рассуждения по нахождению корней этих уравнений были более наглядными, воспользуемся графиками соответствующих функций.

19.1. Уравнение cos x = a

Объяснение и обоснование

Корни уравненияcosx=a.

2.Частые случаи решения уравнения sin x = a.

Полезно помнить специальные записи корней уравнения при a = 0, a = -1, a = 1, которые можно легко получить, используя как ориентир единичную окружность (рис 2).

Учитывая, что синус равен ординате соответствующей точки единичной окружности, получаем, что sin x = 0 тогда и только тогда, когда соответствующей точкой единичной окружности является точка C или тока D. Тогда

Аналогично sin x = 1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка A, следовательно,

Также sin x = -1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка B, таким образом,

Примеры решения задач

Замечание. Ответ к задаче 1 часто записывают в виде:

19.3. Уравнения tg x = a и ctg x = a

Объяснение и обоснование

1.Корни уравнений tg x = a и ctg x = a

Рассмотрим уравнение tg x = a. На промежутке функция y = tg x возрастает (от -∞ до +∞). Но возрастающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение tg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арктангенса равен: x₁ = arctg a и для этого корня tg x = a.

Функция y = tg x периодическая с периодом π, поэтому все остальные корни отличаются от найденного на πn (n ∈ Z). Получаем следующую формулу корней уравнения tg x = a:

При a=0 arctg 0 = 0, таким образом, уравнение tg x = 0 имеет корни x = πn (n ∈ Z).

Рассмотрим уравнение ctg x = a. На промежутке (0; π) функция y = ctg x убывает (от +∞ до -∞). Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение ctg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арккотангенса равен: x₁=arсctg a.

Функция y = ctg x периодическая с периодом π, поэтому все остальные корни отличаются от найденного на πn (n ∈ Z). Получаем следующую формулу корней уравнения ctg x = a:

таким образом, уравнение ctg x = 0 имеет корни

Примеры решения задач

Вопросы для контроля

Какие уравнения называют простейшими тригонометрическими?
Запишите формулы решения простейших тригонометрических уравнений. В каких случаях нельзя найти корни простейшего тригонометрического уравнения по этим формулам?
Выведите формулы решения простейших тригонометрических уравнений.
Обоснуйте формулы решения простейших тригонометрических уравнений для частных случаев.

Упражнения

Решите уравнение (1-11)

Найдите корни уравнения на заданном промежутке (12-13)

Способы отбора корней в тригонометрических уравнениях

Класс: 10

Автор проекта:
Шелкова Полина,
Класс: 10

Руководитель:
Злобова Людмила Викторовна,
учитель математики

ВВЕДЕНИЕ

Слово «тригонометрия» греческое, оно переводится как «измерение треугольников» (τρίγονον — «тригон» — треугольник и μετρειν — «метрео» — измеряю).

Тригонометрия, как и всякая другая наука, выросла из практической деятельности человека. Потребности развивающегося мореплавания, для которого требовалось умение правильно определять курс корабля в открытом море по положению небесных светил, оказали большое влияние на развитие астрономии и тесно связанной с ней тригонометрией. Предполагают, что основополагающее значение для развития тригонометрии в эпоху ее зарождения, имели работы древнегреческого астронома Гиппарха Никейского (180-125 лет до н. э.) (прил. №3). Систематическое использование полной окружности в 360° установилось в основном благодаря Гиппарху и его таблице хорд (прил. №2). Т.е. таблицы, которые выражают длину хорды для различных центральных углов в круге постоянного радиуса, что является аналогом современных таблиц тригонометрических функций. Впрочем, до нас не дошли оригинальные таблицы Гиппарха, как и почти все, что им написано. И мы, можем составить себе о них представление главным образом по сочинению «Великое построение» или «Альмагесту» знаменитого астронома Клавдия Птолемея, жившего в середине II века н.э.

Несмотря на то, что в работах ученых древности нет «тригонометрии» в строгом смысле этого слова, но по существу они, пользуясь известными им средствами элементарной геометрии, решали те задачи, которыми занимается тригонометрия. Например, задачи на решение треугольников (определение всех сторон и углов треугольника по трем его известным элементам), теоремы Евклида и Архимеда представленные в геометрическом виде, эквивалентны специфическим тригонометрическим формулам. Главным достижением средневековой Индии стала замена хорд синусами. Это позволило вводить различные функции, связанные со сторонами и углами прямоугольного треугольника. Таким образом, в Индии было положено начало тригонометрии, как учению о тригонометрических величинах.

Учёные стран Ближнего и Среднего Востока с VIII века развили тригонометрию своих предшественников. Уже в середине IX века среднеазиатский учёный аль-Хорезми написал сочинение «Об индийском счёте». После того, как трактаты мусульманских ученых были переведены на латынь, многие идеи греческих, индийских и мусульманских математиков стали достоянием европейской, а затем и мировой науки. В дальнейшем потребности географии, геодезии, военного дела, способствовали развитию тригонометрии. Особенно усиленно шло ее развитие в средневековое время. Большая заслуга в формировании тригонометрии как отдельной науки принадлежит азербайджанскому ученому Насир ад-Дину ат-Туси (1201-1274), написавшему «Трактат о полном четырехстороннике». Творения ученых этого периода привели к выделению тригонометрии как нового самостоятельного раздела науки. Однако в их трудах еще не была введена необходимая символика. Современный вид тригонометрия получила в трудах Леонарда Эйлера (1707-1783). На основании трудов Эйлера были составлены учебники тригонометрии, излагавшие ее в строгой научной последовательности (прил. №4). Тригонометрические вычисления применяются во многих областях человеческой деятельности: в геометрии, в физике, в астрономии, в архитектуре, в геодезии, инженерном деле, в акустике, в электронике и т.д.

I РАЗДЕЛ (теоретический)

Тема проекта и её актуальность: почему я выбрала тему «Способы отбора корней в тригонометрических уравнениях»?

Расширить и углубить свои знания, полученные в курсе геометрии 8-9 класса.
Тригонометрические уравнения рассматриваются в курсе алгебры и начал математического анализа 10-11 класса.
Тригонометрические уравнения включены в КИМы ЕГЭ по математике.

Цель проекта: изучить способы отбора корней в тригонометрических уравнениях и выбрать для себя наиболее рациональные подходы для качественной подготовки к ЕГЭ.

Задачи:

познакомиться с историческими сведениями о возникновении тригонометрии, как науки;
изучить соответствующую литературу;
научиться решать тригонометрические уравнения;
найти теоретический материал и изучить методы отбора корней в тригонометрических уравнениях;
научиться отбирать корни в тригонометрических уравнениях, принадлежащим заданному промежутку;
подготовиться к ЕГЭ по математике.

Приёмы отбора корней тригонометрического уравнения на заданном промежутке.

При решении тригонометрических уравнений предлагается провести отбор корней из множества значений неизвестного. В тригонометрическом уравнении отбор корней можно осуществлять следующими способами: арифметическим, алгебраическим, геометрическим и функционально-графическим.

Арифметический способ отбора корней состоит в непосредственной подстановке полученных корней в уравнение, учитывая имеющиеся ограничения, при переборе значений целочисленного параметра.

Алгебраический способ предполагает составление неравенств, соответствующих дополнительным условиям, и их решение относительно целочисленного параметра.

Геометрический способ предполагает использование при отборе корней двух вариантов: тригонометрической окружности или числовой прямой. Тригонометрическая окружность более удобна, когда речь идет об отборе корней на промежутке или в случае, когда значение обратных тригонометрических функций, входящих в решения, не являются табличными. В остальных случаях предпочтительнее модель числовой прямой. Числовую прямую удобно использовать при отборе корней на промежутке, длина которого не превосходит 2 или требуется найти наибольший отрицательный или наименьший положительный корень уравнения.

Функционально-графический способ предполагает отбор корней осуществлять с использование графиков тригонометрических функций. Чтобы использовать данный способ отбора корней, требуется умение схематичного построения графиков тригонометрических функций.

II РАЗДЕЛ (практический)

Покажу практически три наиболее эффективных и рациональных, с моей точки зрения, метода отбора корней на примере решения следующего тригонометрического уравнения:

sinx−cos2x=0; [применили формулу двойного угла: cos2x = cos 2 x−sin 2 x]

sinx−(cos 2 x−sin 2 x)=0;

sinx−(1−sin 2 x−sin 2 x)=0;

Введем новую переменную: sinx = t, -1 ≤ t ≤1, получим

Вернемся к замене:

б) Рассмотрим три способа отбора корней, попадающих в отрезок .

1 способ: обратимся к единичной окружности. Отметим на ней дугу, соответствующую указанному отрезку, т.е. выполним отбор корней арифметическим способом и с помощью тригонометрической окружности:

2 способ: указанный отрезок соответствует неравенству: Подставим в него полученные корни:

3 способ: разместим корни уравнения на числовой прямой. Сначала отметим корни, подставив вместо n, и нуль (0), а потом добавим к каждому корню периоды.

Нам останется только выбрать корни, которые попали в нужный нам отрезок.

ЗАКЛЮЧЕНИЕ

При работе над моим проектом я изучила методы решения тригонометрических уравнений и способы отбора корней тригонометрических уравнений. Выяснила для себя положительные и отрицательные моменты. При апробации этих подходов в отборе корней тригонометрического уравнения, понимаешь, что каждый из этих способов удобен по-своему в том или ином случае. Например, алгебраический способ (решение неравенством) наиболее эффективен, когда промежуток для отбора корней достаточно большой, в тоже время он дает практически стопроцентное нахождение целочисленного параметра для вычисления корней, а применение арифметического способа приводит к громоздким вычислениям. При отборе корней уравнения, удовлетворяющих дополнительным условиям, т.е. когда корни уравнения принадлежат заданному промежутку, мне проще и нагляднее получить корни с помощью тригонометрической окружности, а проверить себя можно арифметическим способом. Замечу, что при решении тригонометрических уравнений трудности, связанные с отбором корней, возрастают, если в уравнении приходится учитывать ОДЗ. Как показывает практика и анкетирование моих одноклассников, из четырёх возможных методов отбора корней тригонометрического уравнения по дополнительным условиям, наиболее предпочтительным является отбор корней по окружности. Анкетирование проходили 12 респондентов, изучающих тригонометрию (прил. №5). Большинство из них отвечали, что этот раздел математики достаточно сложный: большой объем информации, очень много формул, табличных значений, которые нужно знать и уметь применять на практике. Еще как одна из проблем — небольшое количество времени, отведенное на изучение этого сложного раздела математики. И я разделяю их мнение. При такой сложности, многие считают, что тригонометрия важный раздел математики, который находит применение в других науках и практической деятельности человека.

СПИСОК ЛИТЕРАТУРЫ

Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс: учеб для общеобразоват. организаций: базовый и углубленный уровни/ [С.М.Никольский, М.К.Потапов, Н.Н.Решетников и др.]-3 -е изд.- М.: Просвещение, 2016.
Алгебра и начала математического анализа: Учеб для 10-11 кл.общеобразоват. организаций / А.Н.Колмогоров, А.М.Абрамов, Ю.П.Дудницин и др. под редакцией А.Н.Колмогорова — М. Просвещение, 2017.
С.В Кравцев и др. Методы решения задач по алгебре: от простых до самых сложных — М: Издательство: «Экзамен», 2005.
Корянов А.Г., Прокофьев А.А. — Тригонометрические уравнения: методы решения и отбор корней. — М.: Математика ЕГЭ, 2012.

Отбор корней в тригонометрическом уравнение

В этой статье и постараюсь объяснить 2 способа отбора корней в тригонометрическом уравнение: с помощью неравенств и с помощью тригонометрической окружности. Перейдем сразу к наглядному примеру и походу дела будем разбираться.

а) Решить уравнение sqrt(2)cos^2x=sin(Pi/2+x)
б) Найдите все корни этого уравнения, принадлежащие промежутку [-7Pi/2; -2Pi]

Решим пункт а.

Воспользуемся формулой приведения для синуса sin(Pi/2+x) = cos(x)

sqrt(2)cos^2x — cosx = 0

cosx(sqrt(2)cosx — 1) = 0

x1 = Pi/2 + Pin, n ∈ Z

sqrt(2)cosx — 1 = 0

x2 = arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x3 = -arccos(sqrt(2)/2) + 2Pin, n ∈ Z

x2 = Pi/4 + 2Pin, n ∈ Z
x3 = -Pi/4 + 2Pin, n ∈ Z

Решим пункт б.

1) Отбор корней с помощью неравенств

Здесь все делается просто, полученные корни подставляем в заданный нам промежуток [-7Pi/2; -2Pi], находим целые значения для n.

-7Pi/2 меньше или равно Pi/2 + Pin меньше или равно -2Pi

Сразу делим все на Pi

-7/2 меньше или равно 1/2 + n меньше или равно -2

-7/2 — 1/2 меньше или равно n меньше или равно -2 — 1/2

-4 меньше или равно n меньше или равно -5/2

Целые n в этом промежутку это -4 и -3. Значит корни принадлежащие этому промежутку буду Pi/2 + Pi(-4) = -7Pi/2, Pi/2 + Pi(-3) = -5Pi/2

Аналогично делаем еще два неравенства

-7Pi/2 меньше или равно Pi/4 + 2Pin меньше или равно -2Pi
-15/8 меньше или равно n меньше или равно -9/8

Целых n в этом промежутке нет

-7Pi/2 меньше или равно -Pi/4 + 2Pin меньше или равно -2Pi
-13/8 меньше или равно n меньше или равно -7/8

Одно целое n в этом промежутку это -1. Значит отобранный корень на этом промежутку -Pi/4 + 2Pi*(-1) = -9Pi/4.

Значит ответ в пункте б: -7Pi/2, -5Pi/2, -9Pi/4

2) Отбор корней с помощью тригонометрической окружности

Чтобы пользоваться этим способом надо понимать как работает эта окружность. Постараюсь простым языком объяснить как это понимаю я. Думаю в школах на уроках алгебры эта тема объяснялась много раз умными словами учителя, в учебниках сложные формулировки. Лично я понимаю это как окружность, которую можно обходить бесконечное число раз, объясняется это тем, что функции синус и косинус периодичны.

Обойдем раз против часовой стрелки

Обойдем 2 раза против часовой стрелки

Обойдем 1 раз по часовой стрелки (значения будут отрицательные)

Вернемся к нашем вопросу, нам надо отобрать корни на промежутке [-7Pi/2; -2Pi]

Чтобы попасть к числам -7Pi/2 и -2Pi надо обойти окружность против часовой стрелки два раза. Для того, чтобы найти корни уравнения на этом промежутке надо прикидывать и подставлять.

Рассмотри x = Pi/2 + Pin. Какой приблизительно должен быть n, чтобы значение x было где-то в этом промежутке? Подставляем, допустим -2, получаем Pi/2 — 2Pi = -3Pi/2, очевидно это не входит в наш промежуток, значит берем меньше -3, Pi/2 — 3Pi = -5Pi/2, это подходит, попробуем еще -4, Pi/2 — 4Pi = -7Pi/2, также подходит.

Рассуждая аналогично для Pi/4 + 2Pin и -Pi/4 + 2Pin, находим еще один корень -9Pi/4.

Сравнение двух методов.

Первый способ (с помощью неравенств) гораздо надежнее и намного проще для пониманию, но если действительно серьезно разобраться с тригонометрической окружностью и со вторым методом отбора, то отбор корней будет гораздо быстрее, можно сэкономить около 15 минут на экзамене.

источники:

http://urok.1sept.ru/articles/687140

http://reshimvse.com/article.php?id=100

Источник

Слайд 1

Методы отбора корней в тригонометрических уравнениях на заданном промежутке

Слайд 2

Баллы за задание №12 (С-1) 2015 2018 2020 2021 1 балл 90,7% 73, 7% 92,2% 100% 2 балла 69,4% 51,1% 83,5% 100%

Слайд 5

Обязательный минимум знаний sin x = a , -1  a  1 (  a   1) x = arcsin a + 2  n, n  Z x =  — arcsin a + 2  n, n  Z sin x = 1 x =  /2 + 2  k, k  Z sin x = — 1 x = —  /2 + 2  k, k  Z sin x = 0 x =  k, k  Z y x y x x y

Слайд 6

Обязательный минимум знаний cos x = a , -1  a  1 (  a   1) x =  arccos a + 2  n, n  Z arccos (- a) =  — arccos a cos x = 1 x = 2  k, k  Z cos x = — 1 x =  + 2  k, k  Z cos x = 0 x =  /2 +  k, k  Z y x y x y x

Слайд 7

Обязательный минимум знаний tg x = a , a  R x = arctg a +  n, n  Z arctg (- a) = — arctg a ctg x = a , a  R x = arcctg a +  n, n  Z arctg (- a) =  — arctg a

Слайд 8

Рекомендации по решению тригонометрических уравнений Свести уравнение к простейшему Некоторые методы решения тригонометрических уравнений Применение тригонометрических формул Использование формул сокращённого умножения Разложение на множители Сведение к квадратному уравнению относительно sin x, cos x, tg x Введением вспомогательного аргумента Делением обеих частей однородного уравнения первой степени ( asin x +bcosx = 0 ) на cos x Делением обеих частей однородного уравнения второй степени (a sin 2 x +bsin x cos x+ c cos 2 x =0) на cos 2 x

Слайд 9

Различные способы отбора корней cos 2x = ½, x  [-  /2; 3  /2] 2x = ± arccos ½ + 2  n, n  Z 2x = ±  /3 + 2  n, n  Z x = ±  /6 +  n, n  Z Отберём корни с помощью тригонометрической окружности Ответ : —  /6;  /6; 5  /6; 7  /6 Найти корни уравнения, принадлежащие данному промежутку (с помощью тригонометрической окружности)

Слайд 10

Различные способы отбора корней Найти корни уравнения, принадлежащие данному промежутку (арифметический, метод перебора) sin 3x = √3/2, x  [-  /2;  /2] 3x = ( – 1) k  /3 +  k, k  Z x = ( – 1) k  /9 +  k/3, k  Z Отберём корни с помощью перебора значений k: k = 0, x =  /9 – принадлежит промежутку k = 1, x = –  /9 +  /3 = 2  /9 – принадлежит промежутку k = 2, x =  /9 + 2  /3 = 7  /9 – не принадлежит промежутку k = – 1, x = –  /9 –  /3 = – 4  /9 – принадлежит промежутку k = – 2, x =  /9 – 2  /3 = – 5  /9 – не принадлежит промежутку Ответ: -4  /9;  /9; 2  /9

Слайд 11

Различные способы отбора корней tg 3x = – 1 , x  (-  /2;  ) 3x = –  /4 +  n, n  Z x = –  /12 +  n/3, n  Z Отберём корни с помощью неравенства: Ответ: – 5  /12; –  /12;  /4; 7  /12; 11  /12 –  /2 < –  /12 +  n/3 <  , – 1/2 < – 1/12 + n/3 < 1, – 1/2 + 1/12 < n/3 < 1+ 1/12, – 5/12 < n/3 < 13/12, – 5/4 < n < 13/4, n  Z, n = – 1; 0; 1; 2; 3 Найти корни уравнения, принадлежащие данному промежутку ( с помощью неравенства) n = – 1, x = –  /12 –  /3 = – 5  /12 n = 0, x = –  /12 n = 1, x = –  /12 +  /3 =  /4 n = 2, x = –  /12 + 2  /3 = 7  /12 n = 3, x = –  /12 +  = 11  /12

Слайд 12

Различные способы отбора корней Найти корни уравнения, принадлежащие данному промежутку ( с помощью графика) cos x = – √2/2, x  [ – 4; 5  /4] x =  arccos (– √2/2) + 2  n, n  Z x =  3  /4 + 2  n, n  Z Отберём корни с помощью графика: Ответ:  5  /4;  3  /4 x = –  /2 –  /4 = – 3  /4; x = –  –  /4 = – 5  /4

Слайд 13

1. Решить уравнение 7 2cosx = 49 sin2x и указать его корни на отрезке [  ; 5  /2] 7 2cosx = 49 sin2x, 7 2cosx = 7 2sin2x, 2cos x = 2sin 2x, cos x – 2 sinx cosx = 0, cos x (1 – 2sinx) = 0, cos x = 0 , x =  /2 +  k, k  Z или 1 – 2sinx = 0, sin x = ½, x =  /6 + 2  k, k  Z x = 5  /6 + 2  k, k  Z Решим уравнение: Проведём отбор корней с помощью тригонометрической окружности: Ответ: а)  /2 +  k, k  Z, x1 =  /6 + 2  k, k  Z; x2 = 5  /6 + 2  k, k  Z б) 3  /2; 5  /2; 13  /6 x = 2  +  /6 = 13  /6

Слайд 14

4cos 2 x + 8 cos (x – 3  /2) +1 = 0 4cos 2 x + 8 cos (3  /2 – x) +1 = 0, 4cos 2 x – 8 sin x +1 = 0, 4 – 4sin 2 x – 8 sin x +1 = 0, 4sin 2 x + 8sin x – 5 = 0, D/4 = 16 + 20 = 36, sin x = – 2,5  или sin x = ½ x1=  /6 + 2  k, k  Z x2 = 5  /6 + 2  k, k  Z 2. Решить уравнение 4cos 2 x + 8 cos (x – 3  /2) +1 = 0 Найти его корни на отрезке [3  ; 9  2]

Слайд 15

Проведем отбор корней на отрезке [3  ; 9  2] (с помощью графиков) x = 4  +  /6 = 25  /6 Ответ: а) x1 =  /6 + 2  k, k  Z x2 = 5  /6 + 2  k, k  Z б) 25  /6 sin x = ½ Построим графики функций y = sin x и y = ½

Слайд 16

3. Решить уравнение 4 – cos 2 2x = 3 sin 2 2x + 2 sin 4x Найти его корни на отрезке [0; 1] 4 – cos 2 2x = 3 sin 2 2x + 2 sin 4x 4 (sin 2 2x + cos 2 2x ) – cos 2 2x = 3 sin 2 2x + 4 sin 2x cos 2x, sin 2 2x + 3 cos 2 2x – 4 sin 2x cos 2x = 0 Если cos 2 2x = 0, то sin 2 2x = 0, что невозможно, поэтому cos 2 2x  0 и обе части уравнения можно разделить на cos 2 2x. tg 2 2x + 3 – 4 tg 2x = 0, tg 2 2x – 4 tg 2x + 3= 0, tg 2x = 1, 2x =  /4 +  n, n  Z x =  /8 +  n/2, n  Z или tg 2x = 3, 2x = arctg 3 +  k, k  Z x = ½ arctg 3 +  k/2, k  Z

Слайд 17

Проведём отбор корней на отрезке [0; 1] 4 – cos 2 2x = 3 sin 2 2x + 2 sin 4x x =  /8 +  n/2, n  Z или x = ½ arctg 3 +  k/2, k  Z Так как 0 < arctg 3<  /2, 0 < ½ arctg 3<  /4, то ½ arctg 3 является решением Так как 0 <  /8 <  /4 < 1,значит  /8 также является решением Другие решения не попадут в промежуток [0; 1], так как они получаются из чисел ½ arctg 3 и  /8 прибавлением чисел, кратных  /2. Ответ: а)  /8 +  n/2, n  Z ; ½ arctg 3 +  k/2, k  Z б)  /8; ½ arctg 3

Слайд 18

4. Решить уравнение log 5 (cos x – sin 2x + 25) = 2 Найти его корни на отрезке [2  ; 7  /2] log 5 (cos x – sin 2x + 25) = 2 cos x – sin 2x + 25 > 0, cos x – sin 2x + 25 = 25, 25 > 0, cos x – 2sin x cos x = 0, cos x (1 – 2sin x) = 0, cos x = 0, x =  /2 +  n, n  Z или 1 – 2sinx = 0, sin x = 1/2 x =  /6 + 2  k, k  Z x = 5  /6 + 2  k, k  Z Решим уравнение:

Слайд 19

1) x =  /2 +  n, n  Z 2    /2 +  n  7  /2, n  Z 2  1/2 + n  7/2, n  Z 2 – ½  n  7/2 – ½, n  Z 1,5  n  3, n  Z n = 2; 3 x =  /2 + 2  = 5  /2 x =  /2 + 3  = 7  /2 x = 2  +  /6 = 13  /6 x = 3  –  /6 = 17  /6 Проведём отбор корней на отрезке [2  ; 7  /2]: Проведём отбор корней на отрезке 2) sin x = 1/2 Ответ: а)  /2 +  n, n  Z; x1 =  /6 + 2  k, k  Z x2 = 5  /6 + 2  k, k  Z б) 13  /6 ; 5  /2; 7  /2; 17  /6

Слайд 20

5. Решить уравнение 1/sin 2 x + 1/sin x = 2 Найти его корни на отрезке [-5  /2; -3  /2] 1/sin 2 x + 1/sin x = 2 x   k Замена 1/sin x = t, t 2 + t = 2, t 2 + t – 2 = 0, t 1 = – 2, t 2 = 1 Решим уравнение: 1/sin x = – 2, sin x = – ½, x = –  /6 + 2  n, n  Z или x = – 5  /6 + 2  n, n  Z 1/sin x = 1, sin x = 1, x =  /2 + 2  n, n  Z

Слайд 21

1) x = —  /6 + 2  n, n  Z -5  /2  —  /6 + 2  n  -3  /2, n  Z -5/2  -1/6 + 2n  -3/2, n  Z -5/2 +1/6  2n  -3/2 + 1/6, n  Z – 7/3  2n  -4/3, n  Z -7/6  n  -2/3, n  Z n = -1 x = —  /6 — 2  = -13  /6 Рассмотрим остальные серии корней и проведём отбор корней на отрезке алгебраическим методом [-5  /2; -3  /2] Продолжим отбор корней на отрезке Ответ: а)  /2 + 2  n, n  Z ; x1 = —  /6 + 2  k, k  Z x2 = — 5  /6 + 2  k, k  Z б) -13  /6 ; -3  /2 2) x =  /2 + 2  n, n  Z -5  /2   /2 + 2  n  -3  /2, n  Z -5/2  1/2 + 2n  -3/2, n  Z -5/2 — 1/2  2n  -3/2 — 1/2, n  Z – 3  2n  -2, n  Z -1,5  n  -1, n  Z n = -1 x =  /2 — 2  = -3  /2

Слайд 22

6. Решить уравнение |sin x|/sin x + 2 = 2cos x Найти его корни на отрезке [-1; 8] Решим уравнение |sin x|/sin x + 2 = 2cos x 1)Если sin x >0, то |sin x| =sin x Уравнение примет вид: 2 cos x=3, cos x =1,5 – не имеет корней 2) Если sin x <0, то |sin x| =-sin x и уравнение примет вид 2cos x=1, cos x = 1/2, x = ±π/3 +2πk, k  Z Учитывая, что sin x < 0, то остаётся одна серия ответа x = — π/3 +2πk, k  Z Произведём отбор корней на отрезке [-1; 8] k=0, x= — π/3 , — π < -3, — π/3 < -1, -π/3 не принадлежит данному отрезку k=1, x = — π/3 +2π = 5 π/3<8, 5 π/3  [-1; 8] k=2, x= — π/3 + 4π = 11 π/3 > 8, 11 π/3 не принадлежит данному отрезку. Ответ: а) — π/3 +2πk, k  Z б) 5 π/3

Слайд 23

7. Решить уравнение 4sin 3 x=3cos(x- π/2) Найти его корни на промежутке [7  /2; 9  /2) Решим уравнение 4sin 3 x = 3cos(x- π/2) 4sin 3 x = 3cos(π/2-х), 4sin 3 x — 3cos(π/2-х) = 0, 4sin 3 x – 3sin x = 0, sin x (4sin 2 x – 3) = 0, sin x= 0 x=  n, n  Z или 4sin 2 x – 3=0, sin x=√3/2; sin x =-√3/2 sin x=√3/2, x1=  /3 + 2  k, k  Z, x2=4  /3 + 2  k, k  Z. sin x =-√3/2, x1=-  /3 + 2  k, k  Z, x2= -4  /3 + 2  k, k  Z.

Слайд 24

Объединим решения ( см. рисунок) Уравнение можно решить короче, зная формулу sin 3x = 3sinx – 4sin 3 x : 4sin 3 x – 3sin x =0, 3sin x – 4sin 3 x =0, s in 3x = 0, х =  m/3, m  Z или х =  m/3, m  Z

Слайд 25

Проведём отбор корней на промежутке [7  /2; 9  /2) х=  m/3, m  Z. 7  /2 ≤  m/3 < 9  /2, 21/2 ≤ m<27/2, m  Z, 10,5 ≤ m < 13,5, m  Z, m =10; 11; 12, x= 10  /3, x= 11  /3, x= 12  /3 Ответ : а)  m/3, m  Z; б) 10  /3; 11  /3; 12  /3

Слайд 26

8. Решить уравнение √1-sin 2 x= sin x Найти его корни на промежутке [5  /2; 4  ] Решим уравнение √1-sin 2 x= sin x. sin x ≥ 0, 1- sin 2 x = sin 2 x; sin x ≥ 0, sin x≥0, 2sin 2 x = 1; sin x =√2/2; sin x = — √2/2; sin x =√2/2 sin x =√2/2 x=(-1) k  /4 +  k, k  Z

Слайд 27

Проведём отбор корней на отрезке [5  /2; 4  ] x=(-1) k  /4 +  k, k  Z sin x =√2/2 у =sin x и у=√2/2 5  /2 +  /4 = 11  /4 Ответ: а) (-1) k  /4 +  k, k  Z ; б) 11  /4

Слайд 28

9. Решить уравнение (sin2x + 2 sin 2 x)/√-cos x =0 Найти его корни на промежутке [-5  ; -7  /2] Решим уравнение (sin2x + 2 sin 2 x)/√-cos x =0. 1) cos x <0 ,  /2 +2  n

Слайд 29

Отберём корни на заданном отрезке Отберём корни на заданном отрезке [-5  ; -7  /2] x=  +2  n, n  Z ; -5  ≤  +2  n ≤ -7  /2, -5-1 ≤ 2n ≤ -7/2-1, -3≤ n ≤ -9/4, n  Z n = -3, x=  -6  = -5  x= 3  /4 + 2  n, n  Z -5  ≤ 3  /4 + 2  n ≤ -7  /2 -23/8 ≤ n ≤ -17/8, нет такого целого n. Ответ: а)  +2  n, n  Z ; 3  /4 + 2  n, n  Z ; б) -5  .

Слайд 30

10. Решить уравнение 2sin2x =4cos x –sinx+1 Найти его корни на промежутке [  /2; 3  /2 ] Решим уравнение 2sin2x = 4cos x – sinx+1 2sin2x = 4cos x – sinx+1, 4 sinx∙cos x – 4cos x + sin x -1 = 0, 4cos x(sin x – 1) + (sin x – 1) = 0, (sin x – 1)(4cos x +1)=0, sin x – 1= 0, sin x = 1, x =  /2+2  n, n  Z или 4cos x +1= 0, cos x = -0,25 x = ± (  -arccos (0,25)) + 2  n, n  Z Запишем корни этого уравнения иначе x =  — arccos(0,25) + 2  n, x = -(  — arccos(0,25)) + 2  n, n  Z

Слайд 31

Отберём корни с помощью окружности x =  /2+2  n, n  Z, х =  /2; x =  -arccos(0,25)+2  n, х=-(  -arccos(0,25)) +2  n, n  Z, x =  — arccos(0,25), x =  + arccos(0,25) Ответ: а)  /2+2  n,  -arccos(0,25)+2  n, -(  -arccos(0,25)) +2  n, n  Z; б)  /2;  -arccos(0,25);  +arccos(0,25)

Источник

Всероссийский конкурс для школьных педагогов на лучшую образовательную статью «Просто о сложном»

Автор Лисицына Елена Федоровна.

учитель математики

МБОУ «Гимназия№11»

г. Бийска Алтайского кр.

Методы отбора корней в тригонометрических уравнениях

или

Ох уж эта тригонометрия!

Решение тригонометрических уравнений и отбор корней, принадлежащих заданному промежутку — это одна из сложнейших тем математики, которая выносится на Единый Государственный Экзамен в течение уже более 10лет. По результатам анкетирования многие учащиеся затрудняются или вообще не умеют решать тригонометрические уравнения и особенно затрудняются в отборе корней, принадлежащих промежутку. Необходимо также знать тригонометрические формулы, табличные значения тригонометрических функций для решения еще целого ряда заданий Единого Государственного Экзамена по математике. Постоянно работая в 10-11 классах, я регулярно сталкивалась с определенными проблемами при работе с вышеуказанным разделом тригонометрии: долго не могла установить баланс между доступностью изложения материала и достаточностью обоснований развернутого решения этой категории заданий. В моей практике были случаи, когда вполне успевающие по математике учащиеся начинали испытывать неуверенность и просто страх при решении тригонометрических уравнений с отбором корней, будь то принадлежность корней области допустимых значений переменной или указанному в задании промежутку. В результате целенаправленной многолетней работы в этом направлении у меня сложилась определенная методика работы с данным разделом, которая оказалась довольно успешной, что подтверждает следующая таблица результатов выполнения учащимися задания №13 профильного ЕГЭ по математике с 2015 по 2021 г.г. ( в % от общего количества учеников 11-х классов гимназии, сдающих профильный ЕГЭ по математике)

Баллы за задание №13(С-1)	2015	2016	2017	2018	2019	2020	2021
1 балл	52,5%	55,1%	59,0%	68,8%	76,4%	85.8%	92,2%
2 балла	43,6%	47.2№	51,1%	57,2%	63,3%	77,0%	83,5%

В тригонометрическом уравнении отбор корней можно осуществлять следующими способами: арифметическим, алгебраическим, геометрическим и функционально-графическим.

Геометрический способ предполагает использование при отборе корней двух вариантов: тригонометрического круга или числовой прямой. Тригонометрический круг более удобен, когда речь идет об отборе корней на промежутке или в случае, когда значение обратных тригонометрических функций, входящих в решения, не являются табличными. Числовую прямую удобно использовать при отборе корней на промежутке, длина которого превосходит полный оборот или требуется найти наибольший отрицательный или наименьший положительный корень уравнения.

Моя практика показала, что чаще всего можно обойтись применением тригонометрического круга при отборе корней , а в случае, если промежуток превышает по длине полный оборот- алгебраическим способом. При этом, безусловно, следует познакомить учащихся и с остальными способами. Таким образом, работа над данным разделом разделилась у меня на следующие этапы:

1)Знакомство с устройством тригонометрического круга и отработка умений находить числа и промежутки на нем в ходе выполнения следующих упражнений:

2)Отработка навыков работы с тригонометрическим кругом при решении простейших тригонометрических уравнений с отбором корней , которая предполагает выполнение большого количества упражнений по типу приведенных ниже:

3)Отбор корней в одном и том же уравнении разными способами, чтобы учащиеся имели возможность выбора в соответствии со своими предпочтениями, например

Например,
а) Решить уравнение cos2x=sin(π/2+x).
б) Найдите все корни этого уравнения, принадлежащие промежутку [–7π/2; –2π].

Решим пункт а)Воспользуемся формулой приведения для синуса sin(π/2+x) = cos(x);cos2x = cosx ;
cos2x – cosx = 0; cosx(cosx – 1) = 0, т.е.

cosx = 0

cosx – 1 = 0

cosx = 1/ ; cosx = /2

x = arccos(/2) + 2πk, k ∈ Z

x = –arccos(/2) + 2πm, m ∈ Z

x = π/4 + 2πk, k ∈ Z

x = —π/4 + 2πm, m ∈ Z

Решим пункт б).

I . Отбор корней с помощью неравенств

Здесь все делается просто, полученные корни подставляем в заданный нам промежуток [–7π/2; –2π], находим целые значения для n.
–7π/2 ≤ π/2 + πn ≤ –2π;

Сразу делим все на π или умножаем на 1/ π
–7/2 ≤ 1/2 + n ≤ –2;
–7/2 – 1/2 ≤ n ≤ –2 – 1/2 ;
–4 ≤ n ≤ –5/2.
Целые n в этом промежутке это: n=–4 n= –3.

Значит, корни, принадлежащие этому промежутку, будут следующие:

х= π/2 + π(–4) = –7π/2; х=π/2 + π(–3) = –5π/2.
Аналогично решаем еще два неравенства:
–7π/2 ≤ π/4 + 2πk ≤ –2π;
–15/8 ≤ k ≤ –9/8.
Получили, что целых k в этом промежутке нет.
–7π/2 ≤ –π/4 + 2πm ≤ –2π;
–13/8 ≤ m ≤ –7/8.
Получили одно целое n в этом промежутке, m =–1. Значит, отобранный корень на этом промежутке имеет вид: х= –π/4 + 2π·(–1) = –9π/4.
Ответ: –7π/2, –5π/2, –9π/4.

II. Отбор корней с помощью тригонометрической окружности.

Чтобы использовать этот способ надо понимать, как работать с окружностью. Так как функции синус, косинус, тангенс и котангенс периодичны, то окружность, можно обходить бесконечное число раз.

«Обойдем» окружность один раз против часовой стрелки (положительное направление, т.е. значения будут положительные)

«Обойдем» окружность два раза против часовой стрелки (положительное направление т.е. значения будут положительные)

«Обойдем» 1 раз по часовой стрелки (отрицательное направление, т.е. значения будут отрицательные)

Вернемся к вопросу об отборе корней на промежутке

[–7π/2; –2π].
Чтобы попасть к числам –7π/2 и –2π надо «обойти» окружность против часовой стрелки два раза. Для того, чтобы найти корни уравнения на этом промежутке надо прикидывать и подставлять.

Рассмотри x = π/2 + πn. Какой приблизительно должен быть n, чтобы значение x было где–то в этом промежутке? Предположим n= –2, получаем х=π/2 – 2π = –3π/2, очевидно, это не входит в наш промежуток. Значит, берем меньше n=–3, то х= π/2 – 3π = –5π/2, это подходит. Попробуем еще n=–4, то х=π/2 – 4π = –7π/2, также подходит.
Рассуждая аналогично для х=π/4 + 2πk, k ∈ Z и х=–π/4 + 2πm, m ∈ Z находим еще один корень x=–9π/4.

После того, как отбор корней произвели разными способами, прошу проанализировать преимущества каждого из них, получились, в частности такие итоги: первый способ (с помощью неравенств) гораздо надежнее и намного проще для понимания, но нужно уметь решать простейшие неравенства. Если действительно серьезно разобраться с тригонометрической окружностью, то отбор корней по второму методу будет гораздо быстрее. Плюс экономия времени на экзамене.

4)Проведение смотра знаний по данной теме в форме математической игры «Своя игра»

(идея заимствована здесь https://kopilkaurokov.ru/matematika/uroki/okh-uzh-eta-trighonomietriia )

5)Рассмотрение реальных работ участников ЕГЭ прошлых лет, оцененных экспертами, с целью нахождения ошибок при выполнении отбора корней в тригонометрических уравнениях, например оценка эксперта-1 балл. Почему не засчитано решение п.б)?

Вывод: отбор корней нельзя назвать обоснованным, так как перебор остановлен на корне принадлежащем отрезку.

Вывод: при отборе корней отсутствует решение и ошибочно указано число, которое не является корнем тригонометрического уравнения.

В заключение отмечу, что поскольку задание № 13 (или №12 в модели профильного ЕГЭ 2022 года) является самым простым из заданий с развернутым решением, то целенаправленная работа над ним дает возможность большему числу выпускников успешно справиться с ним и получить высокий результат на экзамене.

Список используемых ресурсов:

1. Виленкин Н. Я. Алгебра и математический анализ 10 класс. Учебник для углубленного изучения математики в общеобразовательных учреждениях, Издательство Мнемозина, 13-е изд. стереотипное, 2006. — 336с.

2. Гельфанд И.М., Львовский С.М., Тоом А.Л. Тригонометрия, М. : МЦНМО, 2003.-7-16 с.

3. Захарова, И. Г. Информационные технологии в образовании: учебное пособие для студ. пед. учеб. заведений/ И. Г. Захарова,– М.: Издательский центр «Академия», 2003. – 192 с.

4. Звавич В.И., Пигарев Б.П. Тригонометрические уравнения (решение уравнений + варианты самостоятельных работ)//Математика в школе.№3, С.18-27.

5. А.Н. Колмагорова Алгебра и начала анализа. Учебник для 10-11 классов общеобразовательных учреждений, 17-е изд. – М. : Просвещение, 2008. — 384 с.

6. Королев С.В. Тригонометрия на экзамене по математике, изд. Экзамен, 2006. – 254 с.

7. Марасанов А.Н. О методологическом подходе в обучении тригонометрии/ Н.И. Попов, А.Н. Марасанов// Знание и понимание. Умение. -2008. — №4. — 139-141 с.

8. Марасанов А.Н. Тригонометрия: учебное пособие, 2-е изд., испр и доп. (Н.И. Попов, А.Н. Марасанов.-Йошкар-Ола; Мар. гос. Ун-т, 2009.-114с.)

9. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Тригонометрия. 10 класс, М. : Просвещение, 2008. – 61 с.

10. Мордкович А.Г. Алгебра и начала анализа.10-11 классы. Часть 1.Учебник для учащихся общеобразовательных учреждений(базовый уровень). – 10-е изд., стер. – М. : Мнемозина, 2009. – 399 с.:ил.

11. Мордкович А.Г. Алгебра и начала анализа.10-11 классы. Часть 2. Задачник для учащихся общеобразовательных учреждений(базовый уровень), – 10-е изд., стер. – М. : Мнемозина, 2009. – 399 с.:ил. 69

12. Мирошин В. Отбор корней в тригонометрических уравнениях.//Математика. Приложение к газете «Первое сентября» №17, 2006г.

13. Просветов Г.И. Тригонометрия. Задачи и решения, Альфа-Пресс, 2010. – 72 с.

14. Решетников Н.Н. Тригонометрия в школе: М. Педагогический университет «Первое сентября», 2006, лк 1.

15. Смоляков А.Н., Севрюков П.Ф. Приемы решения тригонометрических уравнений//Математика в школе. 2004. №1. С.24-26.

16. Шабашова О.В. Приемы отбора корней в тригонометрических уравнениях//Математика в школе. 2004. №1. С.20-24.

17. https://ppt-online.org/491236

18. Методические материалы для председателей и членов предметных комиссий субъектов Российской Федерации по проверке выполнения заданий с развёрнутым ответом экзаменационных работ ЕГЭ 2022 года. МАТЕМАТИКА. Федеральный институт педагогических измерений, 2022

19. https://kopilkaurokov.ru/matematika/uroki/okh-uzh-eta-trighonomietriia

Источник

Муниципальное
бюджетное общеобразовательное учреждение

средняя общеобразовательная школа № 1 р.п. Мокшан

Исследовательская работа

по математике

«Методы решения тригонометрических уравнений и способы отбора корней на
заданном промежутке»

Выполнил: Васякин
Михаил, ученик 11 класса

МБОУ СОШ №1 р.п.
Мокшан

Научный
руководитель:

Паркина Наталья
Ивановна,

учитель
математики

МБОУ СОШ №1 р.п.
Мокшан

2018
год

Содержание

Глава I.
О тригонометрических уравнениях и основных методах их решения.

I. Общие правила
решения тригонометрических уравнений:

Применение методов
в практике по решению тригонометрических уравнений

1 метод:
Разложение одной из частей уравнения на множители.

2 метод: Замена
переменной.

3 метод:
Применяется к однородным тригонометрическим уравнениям.

4 метод: Решение
уравнений вида a*cos x + b*sin x = c с помощью введения вспомогательного угла.

5 метод: Метод
подстановки.

6 метод: Решение
тригонометрических уравнений, содержащих обратные тригонометрические функции.

7 метод: Метод
универсальной подстановки.

8 метод:
Функционально-графический способ

9 метод: Решение
тригонометрических уравнений с параметрами.

Глава II.
Приемы отбора корней в тригонометрических уравнениях

Глава III.
Уравнения, предлагавшиеся на ЕГЭ.

Заключение

Приложение 1

Приложение 2

Список
использованной литературы

Введение

«Уравнения
для меня важнее,

потому
что политика — для настоящего,

а
уравнения — для вечности»

Альберт
Эйнштейн

Тригонометрические
уравнения одна из самых сложных тем в школьном курсе математики.
Тригонометрические уравнения возникают при решении задач по планиметрии,
стереометрии, астрономии, физики и в других областях. Тригонометрические
уравнения и неравенства из года в год встречаются среди заданий
централизованного тестирования.

Самое важное
отличие тригонометрических уравнений от алгебраических состоит в том, что в
алгебраических уравнениях конечное число корней, а в тригонометрических –
бесконечное, что сильно усложняет отбор корней. Еще одной особенностью
тригонометрических уравнений является неединственность формы записи ответа.

Долгое время
тригонометрию рассматривали как раздел геометрии, и это порождало у школьников
неверное представление о тригонометрических функциях, границы применимости
которых, к тому же, сводились до минимума.

В настоящее время
тригонометрию изучают в курсе алгебры и начал анализа, хотя основное понятие
тригонометрической функции в учебной литературе по-прежнему задается
геометрическим способом в виду отсутствия у старшеклассников знаний теории
рядов. Таким образом, изучение тригонометрических функций, а в дальнейшем и
тригонометрических уравнений, в школьном курсе имеет некоторые особенности.

При изучении
тригонометрических уравнений в общеобразовательной школе не хватает времени на
рассмотрение уравнений, решаемых нетрадиционными способами. Поэтому мне стало
интересно рассмотреть решения таких уравнений, тем более такие уравнения я
встречал в олимпиадных заданиях и эти знания мне пригодятся в дальнейшем.

С точки зрения
стандартных школьных методов решения тригонометрических уравнений, рассмотрю
новые методы, не изучаемые в школьном курсе. Заинтересовавшись темой решения
тригонометрических уравнений, я самостоятельно стал пробовать решать уравнения
из сборников по математике повышенной сложности, сборников олимпиадных задач и
понял, что моих знаний не хватает для решения многих типов тригонометрических
уравнений. Постараюсь как можно лучше раскрыть методы решения
тригонометрических уравнений путем приведения решений таких уравнений.

Процесс нахождения
решений тригонометрического уравнения состоит из двух основных этапов: преобразования
уравнения до получения простейшего (их системы либо совокупности) и решения
последнего (или последних).

В зависимости от
вида исходного тригонометрического уравнения, существуют различные методы их
решения, и в данной работе подробно рассматривается каждый из них,
сопровождается примерами из вступительных экзаменов и пособий для абитуриентов.

Актуальность темы
заключается в том, что тригонометрические уравнения включены во вторую часть
Единого Государственного Экзамена. Задания такого плана содержат две части:
непосредственное решение уравнения, в результате которого получается
бесконечное множество корней, и последующий отбор корней на предмет
принадлежности конкретному промежутку. Новизна исследования
состоит в том, что показана возможность эффективного решения отдельных
тригонометрических уравнений.

Актуальность
темы определяется тем, что учащиеся должны
разбираться в тех или иных способах решения тригонометрических уравнений и
уметь правильно отбирать нужные корни.

Поэтому, перед
собой я поставил следующую цель:

Систематизировать,
расширить знания и умения, связанные с применением методов решения
тригонометрических уравнений и способов отбора корней в тригонометрических
уравнениях.

Объектом
исследования является изучение тригонометрических
уравнений в заданиях ЕГЭ.

Предмет
исследования — решение тригонометрических уравнений и способы
отбора корней в тригонометрических уравнениях.

В соответствии с
целями, объектом и предметом исследования определены следующие задачи:

1.
Рассмотреть различные типы заданий, содержащие тригонометрические уравнения,
предлагавшиеся на ЕГЭ работ предыдущих лет и при выполнении диагностических
работ, где необходимо выполнить отбор корней, классифицировать их;

2.
Определить наиболее рациональный способ отбора корней для каждого типа заданий;

3.
Рассмотреть рекомендации по решению тригонометрических уравнений из вариантов
ЕГЭ;

4.
Составить презентацию полученных результатов. Сделать выводы.

При
выполнении работы использовались материалы ЕГЭ по математике. Основные
источники получения информации: официальные документы, научная и справочная
литература.

Глава I. О
тригонометрических уравнениях и основных методах их решения.

Определение 1. Тригонометрическим
уравнением называется уравнение, содержащее переменную под знаком
тригонометрических функций.

Простейшие
тригонометрические уравнения — это уравнения вида sin x
= a,

cos x=a, tg x=a, ctg x =
a.

В таких уравнениях
переменная находится под знаком тригонометрической функции, а — данное число.

Решение
тригонометрического уравнения состоит из двух этапов: преобразование уравнения
для получения его простейшего вида и решение полученного простейшего
тригонометрического уравнения.

Для решения тригонометрических
уравнений используется несколько основных формул, около 20 дополнительных, и
всего 8 методов решения. Все эти методы по-своему хороши и применимы для разных
видов тригонометрических уравнений. Главная задача при решении
тригонометрического уравнения состоит в том, чтобы правильно преобразовать его,
свести к какому-нибудь более стандартному варианту подобрать наилучший способ
решения для конкретного случая. То есть, в большинстве своём, главная проблема
заключается в том, что уравнения надо непременно сначала привести к какому-то
виду, прежде чем применить нужный метод решения.[1]

Итак, основных
методов решения тригонометрических уравнений 8:

1)
Разложение одной из частей уравнения на множители.

В данном случае мы
все слагаемые переносим в левую часть, раскладываем её на множители и
приравниваем каждый множитель к нулю.

Недостаток
метода: может
быть применён только к узкому кругу уравнений.

2)
Замена переменной.

В данном случае
уравнение приводят к такому виду, чтобы остался только один вид
тригонометрической функции, а затем заменяют её на новую переменную. После
решения уравнения относительно введённой переменной, остаётся только решить
получившиеся простейшие тригонометрические уравнения согласно базовым формулам.

Преимущество
метода:
может быть применён к любому тригонометрическому уравнению (если только это
целесообразно), так как все тригонометрические функции можно выразить друг
через друга. Может также применяться совместно с другими методами.

Недостаток
метода:
Иногда, пытаясь свести всё уравнение к одному типу тригонометрической функции,
мы получаем слишком сложное уравнение, так как не все функции связаны простыми
зависимостями. К тому же метод нецелесообразен, когда в уравнении много разных
тригонометрических функций.

3)
Метод решения однородных тригонометрических уравнений.

В данном случае мы
сначала приводим уравнения к однородному тригонометрическому уравнению. Затем
делим обе части на cos x/cos²x/cos³x
в зависимости от степени уравнения. Затем производим замену переменной и решаем
методом замены переменной.

Преимущество
метода: очень прост в применении. Одинаков для
всех тригонометрических уравнений одной степени.

Недостаток
метода: Далеко не все тригонометрические
уравнения можно привести к виду однородных.

4)
Решение уравнений вида a*cos x
+ b*sin x
= c с помощью введения
вспомогательного угла.

Недостаток
метода: можно решить только уравнения
определённого вида или сводимые к ним уравнения.

5)
Метод подстановки.

В этом случае
вместо часто повторяющейся разности или суммы двух функций подставляют
переменную, решают уравнение относительно неё, а затем возвращаются к сумме или
разности функций, которая была заменена.

Преимущество
метода: даёт большие результаты в комплексном
использовании вместе с другими методами.

Недостаток
метода: редко применим к сложным уравнениям.

6)
Решение тригонометрических уравнений, содержащих обратные тригонометрические
функции.

7)
Метод универсальной подстановки.

При решении
тригонометрических уравнений можно использовать и так называемую универсальную
тригонометрическую подстановку на основе формул:

Если теперь ввести
обозначение то

С помощью универсальной
подстановки мы можем любое уравнение вида свести к алгебраическому уравнению. Важно при
этом помнить, что, делая замену, мы можем потерять те корни исходного
уравнения, для которых не
определён, то есть значения их мы должны проверять отдельно.

Преимущество:
применим для большинства уравнений. В сопряжении с другими методами едва ли не уникален.

Недостаток:
после применения подстановки сужается область определения уравнения, поэтому
все значения необходимо проверять.

Ограниченность функций (графический способ).

Каждая часть
уравнения рассматривается как отдельная функция, причём первая из них –
тригонометрическая, а вторая – алгебраическая, строятся графики этих функций,
находятся их пересечения.

Преимущество
метода: Наглядность, отсутствие сложных
преобразований.

Недостатки:
Невозможность построения некоторых графиков. Возможность неточностей в
определении координат точек пересечения. Возможность ошибки в построении.[2]

*9)
Решение тригонометрических уравнений с параметрами.

I. Общие правила решения
тригонометрических уравнений:

Также существуют
общие правила решения тригонометрических уравнений. Во время решения необходимо
решать задачи:

1) отсева
посторонних корней,

2) потери корней,

3) пересечения
решений.

Решение
тригонометрических уравнений сводится, как правило, к решению простейших
уравнений:

a) sin x = a.

Все решения можно
описать формулой:

x = (-1)^k
arcsin a + πk, где k – число целое.

b) cos x = a.

Все решения можно
описать формулой:

x = arccos a + 2πk, где k – число целое.

c) tg x = a.

Все решения можно
описать формулой:

x = arctg a + πk,
где k – число целое.

d) ctg x = a.

Все решения можно
описать формулой:

x = arcсtg a + πk,
где k – число целое.

Если a = 0,-1,1 то
для решения уравнений используются следующие частные формулы:

sin x = 0, x = πk,
где k – число целое.

sin x = 1, x = +2πk, где k – число целое.

sin x = -1, x = — + 2πk, где k – число целое.

cos x = 0, x = +πk, где k – число целое.

cos x = 1, x = 2πk,
где k – число целое.

cos x = -1, x = π
+πk, где k – число целое.

tg x = 0, x = πk,
где k – число целое.

ctg x = 0, x = +πk, где k – число целое.

Применение методов в практике по
решению тригонометрических уравнений

1 метод: Разложение одной из частей
уравнения на множители.

При данном методе
решения всё переносится в левую часть уравнения так, чтобы в правой при этом
оставался 0. Затем левая часть уравнения раскладывается на множители и далее
уравнение решается согласно известному правилу: если произведение равно нулю,
значит хотя бы один из множителей равен нулю. Так мы получаем из сложного
уравнения совокупность простых уравнений вида cos t = a, sin t = a, tg t = a,
ctg t = a, для решения которых используются указанные формулы.[3]

Примеры
применения данного метода:

4sin tcos t
– 2cos t
+ 2sin t
— 1 = 0

(2sin t – 1)(2cos t + 1)
= 0

2sin t – 1 = 0 или
2cos t + 1 = 0

sin t = или
cos t = —

Тогда:

t = (-1)^кarcsin + πk, k – число целое или

t = arcos(-) a + 2πk, где k – число целое.

Иначе:

t = (-1)^к
+ πk, k – число целое или

t = + 2πk, где k – число целое.

3tg² t – 2tg t
= 0

tg t (3tg t – 2) = 0

tg t = 0 или
3 tg t – 2 = 0

tg t = 0 или
tg t =

Тогда:

t = arctg 0 + πk =
πk, где k – число целое или

t = arctg + πk, где k – число целое.

ctg t = ctg³ t

ctg t – ctg³ t
= 0

ctg t( – ctg²
t) = 0

ctg t( – ctg t)( + ctg t) = 0

ctg t = 0 или
– ctg t = 0 или
+ ctg t = 0

Тогда:

t = + πk, k – число целое.

t = arcctg + πk, где k– число целое

t = (π– arcctg ) + πk, где k – число целое.

1 – sin xcos x = sin x –
cos x

1 – sin xcos x – sin x +
cos x = 0

(sin x -1) + cos x (sin x – 1) = 0

(cos x + 1)(sin x – 1) = 0

cos x + 1 = 0 или
sin x – 1 = 0

cos x =
-1 или sin x = 1

x ₁ =π
+ πk, где k– число целое.

x ₂ = + 2πn, где n – число целое.

2 метод: Замена переменной.

При данном методе
решения также все слагаемые переносятся в левую часть, в правой остаётся 0, а
тригонометрическая функция в уравнении заменяется переменной. Далее уравнение
решается как обычное квадратное уравнение относительно этой переменной. После
нахождения значений необходимо заменить переменную соответствующей
тригонометрической функцией и найти корни исходного уравнения по формулам.

Примеры применения
данного метода:

1) 3cos²
x = 7(sin x +1)

3 – 3sin² x –
7sin x – 7 = 0

3sin² x + 7sin
x + 4 = 0

Пусть sin x = a,
тогда:

3a² +
7a + 4 = 0

D = 49 – 4*12 = 1

a ₁ = = -1

a ₂ = = = , посторонний корень.

Т.к.
a = sin x, то:

sin x = -1

x = (-1)k+1 * arcsin1 + πk,
k – число целое.

x = (-1)k+1 * + πk, k – число целое.

2) tg² x + 2tg
x – 3 = 0

Пусть
tg x = a, тогда:

a² + 2a – 3 =
0

D = 4 + 12 = 16 = 42

а₁
= =
1

a ₂ = = -3

Т.к
a = tg x, то:

tg x =
-3 или tg x = 1

x = -arctg 3 + πk
или
x = +
πk,
где
k – число целое.

3) + 10 = + 7

2ctg² x + 10 +
5ctg x – 7 = 0

2ctg² x + 5
ctg x + 3 = 0

Пусть ctg x = a,
тогда:

2a² + 5a + 3 =
0

D = 25 – 423 = 1

a1 = = -1

a2 = = -1.5

Т.к.
a = ctg x, то:

ctg x =
-1 или ctg x = — 1.5

x = π – arcctg1 + πk
или x = π – arcctg1.5 + πk, где k – число целое.

x = + πk или x = π –
arcctg1.5 + πk, где k – число целое.

Перепишем
уравнение в виде получили
уравнение, однородное относительно и Рассмотрим два случая:

1) тогда откудачто невозможно, поскольку в этом случае корней нет.

2) тогда разделим обе части уравнения на Пусть Получим откуда Осталось решить уравнения и

Ответ: где

3 метод: Применяется к однородным
тригонометрическим уравнениям.

Определение
однородных тригонометрических уравнений:

Уравнение вида
asin x + bcos x = 0 называют однородным тригонометрическим уравнением первой
степени.

Уравнение вида asin2 x + bsin xcos x+ ccos2 x = 0 называют однородным
тригонометрическим уравнением второй степени.

Уравнение вида asin3 x + bsin2 xcos x+ csin xcos2 x + dcos3 x = 0 называют однородным тригонометрическим
уравнением третей степени.

А вообще
тригонометрическое уравнение называют однородным, если после некоторой замены
полученный многочлен от двух переменных составлен из одночленов одинаковой
степени.

1)Однородные
тригонометрические уравнения первой степени решают так:

Сначала обе части
уравнения делим почленно на cos x, получим:

asin x + bcos x =
0

+ =

Выполнив
преобразования, получим:

atg x + b = 0

tg x =

Отсюда по формуле
находим x.

2)Однородные
тригонометрические уравнения второй степени решают так:

asin² x
+ bsin
xcos
x+ ccos²
x = 0 cos² x

+ + =

Выполнив
преобразования, получим:

аtg² x
+ btg x + c = 0

Далее решаем
уравнение методом замены переменной.(см. пример 4) к этому методу).

3)Однородные
тригонометрические уравнения третей степени решают так:

asin³ x
+ bsin²
xcos
x+ csin
xcos²
x + dcos³
x = 0 cos³ x

+ + + = 0

Выполнив
преобразования, получим:

atg³
x
+ btg²
x
+ ctg х+ d = 0

Далее производим
замену переменной и решаем получившееся кубическое уравнение относительно новой
переменной. Затем возвращаемся к замене и вычисляем по формуле корни уравнения.

Примеры
применения данного метода:

sin²
x
+ 2 sin(π–
x)
cos x
– 3cos²
(2π – x)
= 0

Выполнив
преобразования, получим:

sin²
x
+ 2sin xcos x
– 3cos²
x
= 0 cos²
x

+ — =

tg² x +
2tg x – 3 = 0

Получаем
уравнение, уже решённое нами как пример 2 ко второму методу решения тригонометрических
уравнений.

2) 3sin ² 3x —
√2 3 sin3xcos3x + 5cos² 3x = 2

Данное уравнение
не является однородным уравнением, поэтому сначала его необходимо привести к
виду asin ² x
+ bsinxcos x+ ccos ² x = 0.

sin ²t + cos ²t = 1

Тогда
2sin ²t + 2cos ²t = 2. Заменим
t на 3x. Получим равенство:

2sin ²3x
+ 2cos² 3x= 2

Подставим
выражение из левой части в правую часть исходного уравнения. Получим:

3sin² 3x — 2sin3xcos3x + 5cos²
3x = 2sin ²3x + 2cos ²3x

3sin² 3x — 2sin3xcos3x + 5cos²
3x – 2sin ²3x – 2cos ²3x = 0

sin² 3x — 2sin3xcos3x + 3cos²
3x = 0 cos² 3x

— +
=

tg² 3x – 2tg3x + 3 = 0

Пусть
z = tg3x, тогда:

z² – 2z + 3 = 0

(z-) ² = 0

z =, т.е.
tg 3x =

Тогда
по
формуле
3x = arctg + πk

3x
= π/3 + πk

x
= π/9 + πk/3, где k – число целое

3) 2sin x – 3cos x =
0

2tg x – 3 = 0

tg
x = 1.5

x = arctg 1.5 + πk,
где k – число целое.

4 метод: Решение уравнений вида acos
x + bsin x = c с помощью введения вспомогательного угла.

a*cos
x + b*sin x = c

Разделим обе части
уравнения на = 0.

Легко проверить,
что

+ = 1

этому существует
такой угол , что

cos =, sin =

Если c² a² + b²,
то найдётся такой угол n,что = cos. В этом случае получим уравнение coscos x + sinsin x = cos cos(x –) = cos, равносильное данному. Решая это уравнение,
находим множество решений x = ++ , k – число целое. Если же условие c² a² + b²
не выполняется, то уравнение решений не имеет.

Примеры
применения данного метода:

1) sin
2x
+ cos
2x
+ 1 = 0

+ =

sin 2xcos + cos 2xsin =

sin(2x + ) =

Откуда x = (-1)^k+1 – + , где k – число целое.

2) 12cos x – 5sin
x + 13 = 0

Разделив обе части
уравнения на = 13,
получим

cos x – sin x = -1

Полагая cos= и sin=, записываем cos(x +) = -1, где = arccos = arcsin. Решая это уравнение, находим

x + = +2k, где k – число целое x = —+ +2k, где k – число целое, откуда

x = -arccos + (2k = 1), где k – число целое.

5 метод: Метод подстановки.

Иногда
методом введения вспомогательного угла = решаются уравнения, содержащие одно из выражений
sin x + cos x, sin x – cos x или sin xcos x. При этом вводят подстановку t = sin x +
cos x или t = sin x – cos x и, учитывая, что sin 2x = 2sin xcos x = (sin x + cos x)² – 1
= t² – 1 или

sin 2x = 1 — (sin
x — cos x) ² = 1 – t², приходят к уравнению относительно
переменной t.

Примеры
применения данного метода:

1) sin x + cos x =
1 – sin 2x

Обозначим t = sin
x + cos x, тогда sin 2x = t² – 1, поэтому t = 1 – (t² –
1) t² + +t –
2 = 0, t₁ = 1,t₂ = -2, откуда:

1) sin x + cos x =
1, x₁ = (-1)^k – + k, где k – число целое

2) уравнение sin x
+ cos x = -2 решений не имеет, так как

= cos < 2

Заметим, что при
решении тригонометрических уравнений часто произведения разноимённых или
одноимённых тригонометрических функций вида sinx* cosx, sinx*sinx, cosx*cosx следует записать в виде суммы или разности этих
функций.

6 метод: Решение тригонометрических
уравнений, содержащих обратные тригонометрические функции.

Проводят аналогии
с решением подобных уравнений с прямыми тригонометрическими функциями на основе
определения зависимости между этими функциями.

Примеры
применения данного метода:

1) arcsin x = —

Так как – < — < , то x = sin (-) =

2) arcsin2 x – π/2
arcsin x + π2/18 = 0

Воспользуемся
методом замены: t = arcsin x, тогда

t² –
π/2 t + π2/18 = 0

Решив это
уравнение, получим: t₁ = , t₂ = .

Т.е. arcsin x = или arcsin x = .

Отсюда x₁
= , x₂ = .

7 метод: Метод универсальной
подстановки.

Многие тригонометрические уравнения можно
решить с помощью формул универсальной тригонометрической подстановки:

Следует отметить,
что применение формул может приводить к сужению ОДЗ исходного уравнения,
поскольку не определен в
точках х=π+2πк, поэтому в таких случаях нужно проверять, являются ли
углы х=π+2πк, корнями исходного уравнения.

Пример.
Решим уравнение sin x+
cos x=1

Решение:

Обращение к
функции предполагает,
что ,
то есть х=π+2πn ,.

По формулам
универсальной тригонометрической подстановки исходное уравнение примет вид:

; ; |:2 ;

Ответ: ,; ,

8 метод: Функционально-графический
способ

Пример. Решите
уравнение

cos2π
x=x²−8x+17

Решение: cos2πx=x²−8x+17

cos2πx=
(x−4)²+1 .

Оценим левую и
правую части уравнения:

−1 ≤cos2πx≤
1 и (x−4)²+1≥1 . Следовательно,
равенство достигается, если cos2πx=1
и (x−4)²+1 =1.

Решая второе
уравнение системы, получаем x = 4. Подставляем это значение в
первое уравнение и убеждаемся в верности равенства. Следовательно, x =
4 корень исходного уравнения.

Ответ: x =
4

Решение
нестандартных тригонометрических уравнений

Пример 1. Решим уравнение

Решение. Преобразуем выражение

: .

Уравнение
запишется в виде:

Принимая ,
получаем . , .
Следовательно

Ответ. .

Пример 2. Решим
уравнение:

Решение. Уравнение равносильно смешанной системе:

Но —
не годится.

Ответ. .

Раскрывая знак
модуля получаем более громоздкое решение. А ответ в этом случае принимает вид:

Ответ. .

9 метод: Решение тригонометрических
уравнений с параметрами.

1) В зависимости
от значений параметра a решить уравнение и определить число его корней на отрезке

Допустимые
значения переменной х задаются системой

Исходное уравнение
равносильно уравнению которое
равносильно совокупности двух уравнений

Так как то второе уравнение системы
решений не имеет. Рассмотрим первое уравнение системы. Так как здесь числитель
должен равняться нулю, т.е. то При таких значениях х с учётом области
допустимых значений находим, что . Итак, при из неравенств следует, что Этим неравенствам удовлетворяют девять целых
значений k и, следовательно, исходное уравнение имеет девять решений на
заданном промежутке.

Пустьтогда первое уравнение системы
запишется в виде Исключая
из множества решения
уравнений и получим А тогда решая неравенство находим, что и, таким образом, существует пять целых
решений рассматриваемого неравенства. Рассмотрим случай При таком значении параметра а имеем
уравнение Здесь уже
надо из множества решений исключить
решения уравнений и Сделав это, получим решая же неравенство окончательно находим, что при
исходное неравенство
имеет четыре решения.

Ответ: если , то девять корней если то пять корней если то четыре корня

2) При каких
значениях параметров a и b уравнение имеет единственное решение?

решение задачи
основывается на том факте, что если функция f задана равенством то условия А=В, С=0 являются
необходимыми и достаточными условиями того, чтобы уравнение имело единственное решение. Таким
образом, решение задачи сводится к решению относительно параметров a и b
системы

Из первого
уравнения этой системы находим, что А так как то приходим к рассмотрению систем и

Как легко видеть,
решениями второй системы являются все значения параметра а, определяемые
равенством что же
касается первой системы, то она оказывается несовместной. Отсюда, с учётом
второго уравнения системы поиск требуемых параметров a и b сводится к поиску
решений системы ответ
здесь очевиден.

Ответ: любое.

3) В зависимости
от значений параметров a и b решить уравнение

Обозначив получим систему откуда находим Но так как то и значит

Ответ: если то при других значениях a и b решений нет.

4) В зависимости
от значений параметра а решить уравнение

Допустимыми
значениями переменной х являются все При таких значениях х полагая перепишем уравнение в виде Если то При записанное уравнение равносильно совокупности Дискриминанты обоих
уравнений совокупности совпадают и имеют вид: Поэтому, если то решений у уравнения нет.

Пусть В этом случае решая уравнения
совокупности, находим, что

При имеем В остальных случаях все корни определяются
формулами.[4]

Ответ: если то решений нет; если то если , то при остальных значениях параметра а

Глава II. Приемы
отбора корней в тригонометрических уравнениях

Обучение решению
тригонометрических уравнений предполагает знакомство с приемами отбора корней
из множеств значений неизвестного. Отбор корней в тригонометрическом уравнении
может осуществляться способами: геометрическим, арифметическим и алгебраическим
и функционально-графическим.

Геометрический
способ основан на использовании двух моделей:
тригонометрической окружности и числовой прямой. Тригонометрическая окружность
удобна в случае, когда речь идет об отборе корней на промежутке, длина которого
не превосходит 2, или если требуется
найти наибольший отрицательный или наименьший положительный корень уравнения. В
остальных случаях предпочтительнее модель числовой прямой.

Тригонометрическую
окружность удобно использовать при отборе корней на промежутке длина которого
не превосходит , или в случае, когда
значение обратных тригонометрических функций, входящих в серию решений, не
являются табличными.

Арифметический
способ отбора корней состоит в вычислении
неизвестного при переборе значений параметров из найденных серий решений с
последующей их проверкой по дополнительным условиям.

Алгебраический
способ предполагает составление соответствующих
дополнительным условиям неравенств и их решение относительно параметра.

Алгебраический
способ наиболее эффективен когда промежуток для отбора корней достаточно
большой и применение арифметического способа приводит к сложным и объемным
вычислениям, а геометрический- к громоздким построениям.

Функционально-графический
способ, состоит в том, что при решении
тригонометрических уравнений используют графики тригонометрических функций и отбор
корней осуществляют с использованием этих графиков.

Данный способ
отбора корней требует умение схематичного построения графика тригонометрической
функции и применение формул корней соответствующих уравнений.

Каждый из этих
способов по-своему хорош и удобен для применения в том или ином случае.

Как показывает
практика и анкетирование моих одноклассников, из четырёх возможных подходов к
отбору корней тригонометрического уравнения по дополнительным условиям,
наиболее популярен арифметический.

Отбор
корней уравнения, удовлетворяющих дополнительным условиям

(корни
уравнения принадлежат промежутку)

Пример
2.

Найдите все
решения уравнения sin 2x = cos x , принадлежащие
промежутку

Решение.

sin
2x
= cos x,

2 sin x cos x – cos x =
0,

2 cos x (2 sin x – 1) =
0,

cos x = 0 или
sin x = .

1)cos x = 0, 2)
sin x = ,

x = ; n x = или
x = , n

Отбор
корней выполним арифметическим способом и с помощью
тригонометрической окружности.

1.Если n=0,
то x
= , .

Если n=1,
то x
= , .

Если n=1, то x
= , .

Если n=2, то x
= .

2.Если n=0,
то x
= , или x
= , .

Если n=1,
то для первой серии решений x
= , .

Если n=1, то x
= ,

или x
= , .

Ответ:
, , .

Отбор
корней арифметическим способом приводит к громоздким вычислениям. С помощью
тригонометрической окружности проще и нагляднее получить корни, принадлежащие
данному промежутку.

Пример
3.

Найдите все
решения уравнения , принадлежащие отрезку
[1;2] .

Решение.

Воспользуемся
формулами понижения степени и преобразования суммы функций в произведение:

+ = 1,

cos 4x + cos 6x = 0,

2cos 5x cos x=0,

, или ,

, k

Вторая серия
решений входит в первую серию решений. (Пример 1).

Отбор
корней выполним алгебраическим способом.

Решим двойное
неравенство:

10,

то k=2.

Тогда x
= .

Ответ:.

Отбор
корней уравнения, удовлетворяющих дополнительным условиям

(корни
уравнения удовлетворяют неравенству)

Пример
5.

Найдите
все корни уравнения: удовлетворяющие
неравенству cos x 0 .

Решение.

, ,

Отбор
корней. Изобразим полученные решения на
тригонометрической окружности. Каждому уравнению соответствуют две точки на
тригонометрической окружности. В ответ запишем только решения, расположенные на
дуге окружности, соответствующей неравенству cos x 0 , т.е. лежащие в I и
IV четвертях.

Ответ:
, n,k

Уравнения,
в которых необходимо выполнить отбор корней в соответствии с областью
допустимых значений уравнения

При решении
уравнений этого типа важно обращать внимание на область допустимых значений
входящих в него переменных. В этих заданиях нет требования — осуществить отбор
решений из полученных серий ответов. Решение этих уравнений само собой
подразумевает выполнение отбора корней в соответствии с областью допустимых
значений уравнения.

Пример
6.

Решить
уравнение:

Решение.

О.Д.З sin x , значит

cos x =

cos x = 1 1 + ,

cos x = 0,

cos x ( cos x – 1) = 0,

cos x = 0, cos
x = 1,

, , n, k

Отбор
корней.

Для отбора корней
используем тригонометрическую окружность.

Ответ:; 2; n,k

Пример
8. Решить уравнение

Решение.

О.Д.З. tgx
> 1

Отбор
корней. Функционально-графический способ.

На промежутке , длина которого 2π,
неравенству tgx>1 удовлетворяет одно
число . Следовательно,
удовлетворяют данному уравнению все числа вида +2πn,
n

Ответ:
+2πn,
n

Уравнения,
в которых необходимо выполнить отбор корней в соответствии с областью
допустимых значений уравнения и дополнительным условием

Пример
10.

Укажите
количество корней уравнения ctg3x sin 6x — cos6x — cos12x =
0

на промежутке [0;2].

Решение.

ctg3x sin 6x — cos6x — cos12x =
0. О.Д.З. , .

cos 3x sin 6x – sin 3x cos 6x – sin 3x cos 12x = 0

sin (6x – 3x) — sin 3x cos12x = 0,

sin 3x — sin 3x cos12x = 0,

sin 3x(1 – cos
12x)=0,

, или
1 – cos
12x
= 0,

, т.к. x О.Д.З ,

12x
= 2n,

,
n,k

Отбор
корней.

Проведем отбор
корней, используя тригонометрическую окружность. Для этого полученные значения
в серии решений и серии ограничений изобразим на тригонометрической окружности
и в ответ запишем количество не совпавших в обеих сериях значений переменной х.

Ответ:
6.

Пример11.
Дано уравнение tg²x
+ tgx
+ 6= 0.

а) Решите
уравнение.

б) Укажите корни,
принадлежащие отрезку [-2π; — ].

Решение.

О.Д.З.: $xnefrac{pi}{2}+pi n.$ Тогда
уравнение принимает вид:

t²
+ 5t + 6 =0 t
= -3 или t
= -2

tgx
= -3 или tgx
= -2

x
= — arctg3 +πk, k x = — arctg2
+πn, n

Отбор
корней. Осуществляем отбор решений с
использованием единичной окружности.

Из рисунка видно,
что в интересующий нас промежуток входят только два значения из этих
серий:

Ответ:

Системы
тригонометрических уравнений

Пример
12.

Решите
систему уравнений

Решение.

1)
Решим первое уравнение системы.

О.Д.З
y >0

= 0

sin x =
t ,
где −1 ≤ t ≤
1.

2 − 3t +1 = 0,

t₁ =1,
t₂ =,

sin x =1, sin
x =,

x =
+ 2πn,n ;

2)
Решим
второе уравнение системы.

Так как y >0,
то cos x.

3) Проведем отбор
корней 1 уравнения для условия cos x.

Отсюда, x =
+ 2πn, n ∈
Z

Вернемся к системе

y = cosx

cos = cos

Таким образом,
исходная система имеет решения x = + 2πn, n ∈
Z, y = .

Ответ:
x = + 2πn, n ∈
Z, y = .

Глава III.
Уравнения, предлагавшиеся на ЕГЭ.

Сама задача
решения уравнений порой бывает менее важна, чем нахождение частных решений, удовлетворяющих
некоторому условию (принадлежащие заданному отрезку). В таких задачах после
нахождения множества решений необходимо производить отбор корней. Рассмотрим
пример решения таких задач.[5]

1.
Уравнения, сводящиеся к квадратному.

Решить уравнение:

Решение:
Воспользовавшись основным тригонометрическим тождеством, перепишем уравнение в
виде

Заменой cos=t
уравнение сводится к квадратному: 2t²+
9 t
-5 =0, которое имеет корни t₁= ½ и t₂
= -5. Возвращаясь к переменной х, получим ,

Второе уравнение
корней не имеет, так как |cosx|≥1,

а из первого x=±+6k,kZ

Ответ: =±+6k,kZ

Вывод:
вводя новую переменную, нужно   учитывать, что значения sin x
и cos x
ограничены отрезком      , а иначе появятся посторонние
корни.

2.
Уравнения, решаемые разложением на множители. Задание
С1 ( 2011 г.) [6]

а) Решить
уравнение

б) Указать корни
уравнения, принадлежащие отрезку

Решение:
а) решаем разложением левой части на множители:

группируем и
выносим общий множитель за скобки, получим

Уравнение 1)
решений не имеет.

Второе уравнение
однородное, решается делением почленно на cosx
≠0, получим ,
откуда

б)

Ответ: а) б)

Вывод:

1.При решении
уравнения такого вида, во – первых, нужно знать, что |sinх|≤1
и |cosx|≤1,
и уравнение sinx=-2 решений не имеет;

2.Обосновать
деление на cosx≠о (так как, если cosx=0,то
sinх=0,
а это невозможно);

3.Обоснованно
произвести отбор корней, принадлежащих данному промежутку.

3.Уравнение
на применение формул приведения ( 2010 г.)

а) решить
уравнение;

б) Указать корни,
принадлежащие отрезку

Решение:
Используя формулы приведения, получим:

sin 2 x – cos x =0,

2 sinx cosx- cosx =0,

сosx
(2 sinx -1 )=0, откуда cosx= 0 или
sinx =½,

б) Найдем значения
к, при которых корни будут принадлежать

указанному
промежутку. Решение представим в виде:

б) Найдем значения
к, при которых корни будут принадлежать указанному промежутку.

Ответ: а)

б)

Вывод:

При решении
уравнения такого вида, необходимо знать формулы приведенного уравнения и
правильно её применить; уметь представлять решениена две серии корней; правильно выбрать
корни, принадлежащие заданному отрезку.[7]

4.
Системы тригонометрических уравнений

(2010).
Решить систему уравнений

Решение: О.Д.З

Дробь равна нулю,
если числитель равен 0, а знаменатель не равен 0.

Из уравнения 2sin²x
– 3 sinx
+1 =0, решая методом введения новой переменной, находим

или sin x=1.

1)Пусть ,
тогда и у = cos x
= ›0
( используя основное тригонометрическое тождество)

либо и — нет решения.

2) Пусть sinx
= 1, тогда у = cos x
= 0 – нет решения.

Ответ: и у =

Вывод:

1) нужно
учитывать ограниченность тригонометрических функций;

2) Записывать и
учитывать О.Д.З.

5.
Использование формул приведения.

а) Решите уравнение:

б) Найдите
все корни этого уравнения, принадлежащие промежутку

Решение.

Используя формулу
приведения и
формулу синуса двойного угла ,
получаем:

Заданный
промежуток имеет длину π, поэтому ему принадлежит не больше двух корней
из первой серии, не больше одного корня из второй серии и не больше одного
корня из третьей серии. Во второй серии решений из отрезка нет, из первой
и третьей серии это числа

Ответ:
а) б)

Различные
примеры заданий под №13[8]

6.
а) Решите уравнение cos2x − 3cosx +
2 = 0.

б) Найдите все
корни уравнения, принадлежащие отрезку

Решение.

а) Преобразуем
уравнение:

Получаем   или
   откуда
    или

где

б) На отрезке корни
отберём с помощью единичной окружности.

Получаем и

Ответ: а) б)

7.
а) Решите уравнение

б) Укажите корни
этого уравнения, принадлежащие отрезку

Решение.

б) Укажем корни
этого уравнения, принадлежащие отрезку Покажем
на единичной окружности.

Ответ:
а) б)

8.
а) Решите уравнение

б) Укажите корни
этого уравнения, принадлежащие отрезку

Решение.

Сведём уравнение
к квадратному, используя формулу

Имеем:

б)
С помощью числовой окружности отберём корни, принадлежащие
отрезку (см.
рис.), получим число

Ответ:
а) б)

9.
а) Решите уравнение .

б) Укажите его
корни, принадлежащие отрезку

Решение.

Сделаем замену
,
получим квадратное уравнение корнями
которого являются числа    и
Уравнение
  не
имеет решений, а из уравнения    находим
искомые корни:

или
;
.

Найдем корни, принадлежащие
отрезку Решим
неравенства:

или
;

Соответствующие
найденным значениям параметров корни: и
.

Ответ:
а).
б) Заданному отрезку принадлежат
корни и
.

10.
а)
Решите уравнение

б)
Укажите корни, принадлежащие отрезку

Решение.

Сделаем замену
и
получим квадратное уравнение откуда,
Уравнение
не
имеет решений, а из уравнения находим

Найдем корни, принадлежащие
отрезку

Отрезку принадлежат
корни

Ответ:
a) б)

Вывод: Ответ
записать с учётом О.Д.З.

№11 Найдем
все решения уравнения, принадлежащие промежутку [-π;π]

cos 2x
+ sin²x
= cos x

решениями являются числа вида

x
= и
x
= 2πn,
n

Отбор корней можно проводить различными
способами. Например,

I способ:   k
= 0        x =                              n
= 0        x = 0

                  k
= 1        x =                           n
= ± 1     x = ± 2π

k = -1 x = n = ±
2 x = ±2π

k
= -2 x = если
‌ |‌‌‌‌‌n|
> 2, то x

k
= 2 x =

если ‌ |k|
> 2, то x

Ответ:
решениями уравнения из промежутка [-π;π] являются х =

II способ: x ,
т.е. –π ≤ х ≤ π

Значит, –π ≤ ≤ π
–π ≤ 2πп ≤ π

–1 ≤ ≤
1 –1 ≤ 2п ≤ 1

– ≤ k
≤ – ≤ n
≤

k—
целое число, значит, n
– целое число, значит,

k
= -1; 0 n
=0

Таким образом, искомыми корнями являются
числа при k = -1 х = ,

при k
= 0 х = ,

при n
= 0 х = 0.

Ответ:
х =

№12.
Найдем число корней уравнения cos²
2х + cos²
6х = 1, принадлежащие отрезку

При решении этого уравнения учащиеся могут
воспользоваться формулой понижения степени.

Так в данном уравнении две серии решений:

х = и х =

и после отбора корней получается, что п
= 0; 1; 2; 3, k = 0; 1. Если бы буква
была одна, то можно допустить ошибку: посчитать, что различных корней
всего четыре, тогда как окончательно уравнение имеет 6 различных корней из
промежутка . [9]

Заключение

В проделанной мною работе были изучены различные
методы решения тригонометрических уравнений, рассмотрены рекомендации по
отбору корней тригонометрических уравнений.

Я рассмотрел 9 основных методов решения
тригонометрических уравнений, выявил положительные и отрицательные черты этих
методов, решил уравнения, которые не подлежат решению стандартными способами,
выявил другие методы решения тригонометрических уравнений.

При решении тригонометрических уравнений следует умело
анализировать зависимости между различными тригонометрическими функциями и уметь
творчески подходить к работе.

Основная схема, которой мы будем руководствоваться
при решении тригонометрических уравнений следующая: решение заданного уравнения
сводится к решению элементарных уравнений. Средства решения: преобразования,
разложения на множители, замена неизвестных. Ведущий принцип: не терять корней.
Это означает, что при переходе к следующему уравнению (уравнениям) мы не
опасаемся появления лишних (посторонних) корней, а заботимся лишь о том, чтобы
каждое последующее уравнение нашей «цепочки» (или совокупность
уравнений в случае ветвления) являлось следствием предыдущего. Одна из
особенностей тригонометрических уравнений заключается в том, что ответ во
многих случаях может быть записан различными способами.

Одним из возможных методов отбора корней является
проверка. Сразу заметим, что в случае тригонометрических уравнений трудности,
связанные с отбором корней, с проверкой, как правило, резко возрастают по
сравнению с алгебраическими уравнениями. Ведь проверять приходится серии,
состоящие из бесконечного числа членов.

Способы
отбора корней в тригонометрических уравнениях:

1.
Арифметический способ: перебор значений
целочисленного параметра и вычисление корней.

2.
Алгебраический способ: решение неравенства
относительно неизвестного целочисленного параметра и вычисление корней.

3.
Геометрический способ:

—
изображение корней на тригонометрической окружности с последующим отбором с
учетом имеющихся ограничений;

—
изображение корней на числовой прямой с последующим отбором с учетом имеющихся
ограничений.

4.
Функционально-графический способ:отбор
корней с использованием графика простейшей тригонометрической функции.

Рекомендации
при отборе корней в тригонометрических уравнениях:

Арифметический
способ самый простой, но он становится не
эффективным в следующих случаях:

-заданные
ограничения охватывают большой промежуток, и последовательный перебор значений
приводит к громоздким вычислениям;

-серии
решений содержат нетабличные значения обратных тригонометрических функций;

-требуется
определить количество корней уравнения, удовлетворяющих дополнительным
условиям.

Тригонометрическую
окружность удобно использовать при отборе корней на промежутке, длина которого
не превосходит 2π, или в случае, когда значения обратных тригонометрических
функций, входящих в серию решений, не являются табличными.

При
отборе корней, если есть О. Д. З., необходимо выполнить сначала отбор по О. Д.
З. а затем по условию к уравнению.

Данная
работа имеет большое практическое значение, т.к. тригонометрические уравнения
часто содержатся в материалах ЕГЭ и экзаменов для поступления в вузы, а в
школьном курсе математике недостаточно изучаются. Исследование может быть
употреблено как материал для проведения предметных факультативов по алгебре или
при подготовке к ЕГЭ.

Приложение 1

Основные
формулы тригонометрии

1)
основное тригонометрическое тождество sin²α
+cos²
α= 1,

Деля это уравнение
на квадрат косинуса и синуса соответственно имеем

2)формулы
двойного аргумента sin2α
=2 sinα cos
α,

cos 2α
= cos² α — sin²α,

cos
2α = 1- 2sin²α,

3)формулы
понижения степени:

sin ² x
=

cos ² x =

4)
формулы синуса и коссинуса суммы и разности двух аргументов:

sin(α+β)=sinα
cos β
+cos
α sin β

sin(α-β)=sinα
cos β
—cos
α sin β

cos(α+β)=cosα
cos β
+sin
α sin β

cos(α-β)=sinα
cos β
+sinα
sin β

5)Формулы
приведения

Формулами
приведения называются формулы следующего вида:

$f left( frac{(2n+1) pi}{2} + alpharight) = pm g (alpha),,$

$f left( frac{(2n+1) pi}{2} - alpharight) = pm g (alpha).,$

6.
Формулы суммы и разности тригонометрических функций

$sin alpha pm sin beta = 2 sin frac{alpha pm beta}{2} cos frac{alpha mp beta}{2}$

$cos alpha + cos beta = 2 cos frac{alpha+beta}{2} cos frac{alpha-beta}{2}$

$cos alpha - cos beta = - 2 sin frac{alpha+beta}{2} sin frac{alpha-beta}{2}$

$operatorname{tg} alpha pm operatorname{tg} beta = frac{sin (alpha pm beta)}{cos alpha cos beta}$

$1 pm sin {2 alpha} = (sin alpha pm cos alpha)^2 .$

7.
Чётность

Косинус— чётная,
синус, тангенс и котангенс— нечётные,
то есть:

8.
Непрерывность

Синус и косинус — непрерывные
функции. Тангенс и имеет точки
разрыва , котангенс 0; ±π; ±2π;…

9.
Периодичность

Функции y
= cos x,
y
= sin x — периодические с
периодом 2π,

функции y
= tg x и
y
= ctg x —
c периодом π.

10.
Знаки тригонометрических функций по четвертям

Приложение 2

(Таблица
значений тригонометрических функций некоторых углов)

Угол (a)	*Тригонометрическая функция*
*Градусы*	*Радианы*	*sin a*	*cos a*	*tg a*	*ctg a*	*sec a*	*cosec a*
0°	0	0	1	0	∞	1	∞
30°							2
45°				1	1
60°						2
90°		1	0	∞	0	∞	1
120°						-2
135°				-1	-1
150°							2
180°		0	-1	0	∞	-1	∞
210°							-2
225°				1	1
240°						-2
270°		-1	0	∞	0	∞	-1
300°						2
315°				-1	-1
330°							-2
360°		0	1	0	∞	1	∞

Список использованной литературы

1.
Гилемханов Р.Г. О преподавании
тригонометрии в 10 классе//Математика в школе. 2001-№ 6 -с. 26-28.

2.
Глазков Ю. А. Математика. ЕГЭ: сборник
заданий и методических рекомендаций/ Ю. А. Глазков, И. К. Варшавский, М. Я.
Гаиашвили. – М.: Издательство «Экзамен», 2016

3.
ЕГЭ. Контрольно-измерительные материалы.
М: Просвещение, 2002-2017г.

4.
ЕГЭ: 4000 задач с ответами по математике.
Все задания «Закрытый сегмент». Базовый и профильный уровни /И.В.Ященко,
И.Р.Высоцкий, А.В.Забелин и др.; под редакцией И.В.Ященко. – М.: Издательство
«Экзамен», 2016. – 640 с. (Серия «Банк заданий ЕГЭ»)

5.
Крамор В.С. Повторяем и систематизируем
школьный курс алгебры и начал анализа. Москва, «Просвещение», 1994.

6.
Крамор В.С. Тригонометрические функции. —
М.: Просвещение, 1979.

7.
Математика. ЕГЭ – 2017: экспресс – курс
для подготовки к экзамену/ Дмитрий Гущин. – М, : Издательский дом «Учительская
газета», 2017. – 256 с. (Библиотечка «Учительской газеты». Готовимся к ЕГЭ с
лучшими учителями России)

8.
Синакевич С.В. Тригонометрические
уравнения — М.: Учпедгиз, 1959.

9.
Цукарь А.Я. Упражнения практического
характера по тригонометрии //Математика в школе. 1993-№3- с 12-15.

10.
Электронный ресурс «Математика»/ URL:
http://www.webmath.ru/poleznoe/trig_formules.php

11.
Электронный ресурс «Решу ЕГЭ»/ URL:
http://reshuege.ru/

Источник

Способы отбора корней в тригонометрических уравнениях

Автор проекта: Шелкова Полина, Класс: 10

ВВЕДЕНИЕ

I РАЗДЕЛ (теоретический)

II РАЗДЕЛ (практический)

ЗАКЛЮЧЕНИЕ

Отбор корней в тригонометрическом уравнение

Глава I. О тригонометрических уравнениях и основных методах их решения.

I. Общие правила решения тригонометрических уравнений:

Применение методов в практике по решению тригонометрических уравнений

1 метод: Разложение одной из частей уравнения на множители.

2 метод: Замена переменной.

3 метод: Применяется к однородным тригонометрическим уравнениям.

4 метод: Решение уравнений вида a*cos x + b*sin x = c с помощью введения вспомогательного угла.

5 метод: Метод подстановки.

6 метод: Решение тригонометрических уравнений, содержащих обратные тригонометрические функции.

7 метод: Метод универсальной подстановки.

8 метод: Функционально-графический способ

9 метод: Решение тригонометрических уравнений с параметрами.

Глава II. Приемы отбора корней в тригонометрических уравнениях

Глава III. Уравнения, предлагавшиеся на ЕГЭ.

Заключение

Приложение 1

Приложение 2

Список использованной литературы

Автор проекта:
Шелкова Полина,
Класс: 10

Глава I. О
тригонометрических уравнениях и основных методах их решения.

I. Общие правила решения
тригонометрических уравнений:

Применение методов в практике по
решению тригонометрических уравнений

1 метод: Разложение одной из частей
уравнения на множители.

3 метод: Применяется к однородным
тригонометрическим уравнениям.

4 метод: Решение уравнений вида acos
x + bsin x = c с помощью введения вспомогательного угла.

6 метод: Решение тригонометрических
уравнений, содержащих обратные тригонометрические функции.

7 метод: Метод универсальной
подстановки.

8 метод: Функционально-графический
способ

9 метод: Решение тригонометрических
уравнений с параметрами.

Глава II. Приемы
отбора корней в тригонометрических уравнениях

Глава III.
Уравнения, предлагавшиеся на ЕГЭ.