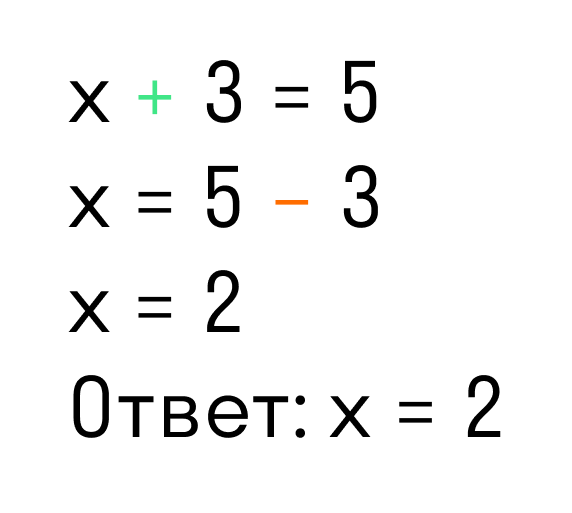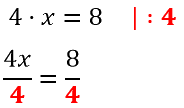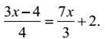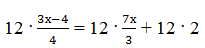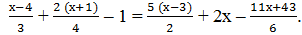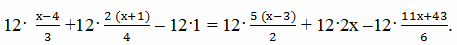Основные понятия уравнения
Определение
Уравнением называют равенство, в котором одна из переменных неизвестна, и её нужно найти. Значение этой неизвестной должно быть таким, чтобы равенство было верным.
К примеру: 3+4=7 это числовое равенство, при вычислении которого с левой стороны получается 7=7.
Уравнением же будет называться следующее равенство: 3+х=7, поскольку есть неизвестная переменная х, её значение можно найти.
Из этого уравнения следует, что переменная х=4, только при таком его значении равенство 3+х=7, будет верным.
Неизвестные переменные принято писать в виде маленьких латинских букв, можно любыми, но чаще используют x,y,z.
Получается, чтобы равенство сделать уравнением необходимо, чтобы в нем была буква, значение которой неизвестно.
Как мы понимаем существует множество примеров уравнений с разными арифметическими действиями.
Пример: х + 5 = 1= 9; z — 2 = 7; 9 * y = 18, 6 : f = 2
Помимо этого существуют уравнения со скобками. К таким уравнениям относится 8 : (х — 4) = 2 * (8 — х), неизвестных может быть несколько, они могут быть, как слева уравнения, так и справа или в обеих частях.
Помимо таких простых уравнений они могут быть с корнями, логарифмами, степенями и тд.
Уравнение может содержать несколько переменными, тогда их принято называть, соответственно уравнениями с двумя, тремя и более переменными.
Пример:
3 * а = 15 : х — уравнение с двумя переменными:
8 — а = 5 * х — z — уравнение с тремя переменными.
Корень уравнения
Мы часто слышим фразу на уроках математики, «найдите корень уравнения», давайте разберёмся, что же это значит.
Пример:
В примере 3+х=7, можно представить вместо буквы число, и уравнение тогда станет равенством, оно может быть либо верным, либо неверным, если поставить х=3, то первичное равенство примет вид 3+3 = 7 и станет неверным, а если х= 4 то равенство 3+4=7 будет верным, а значит х = 4 будет называться корнем или по другому решением уравнения 3+х=7.
Определение.
Отсюда можно выделить следующее определение: корень уравнения — это такое значение неизвестной переменной, при котором числовое равенство будет верным.
Стоит отметить, что корней может быть несколько или не быть вовсе.
Рассмотрим подробнее пример который не будет иметь корней. Таким примером станет 0 * х = 7, сколько бы чисел мы сюда не подставляли равенство не будет верным, так как умножая на ноль будет ноль, а не 7.
Но существуют и уравнения с множественным числом корней, к примеру, х — 3 = 6, в таком уравнении только один корень 9, а в уравнении квадратного вида х2 = 16, два корня 4 и -4, можно привести пример и с тремя корнями х * (х — 1) * (х — 2) = 0, в данном случае три решения ноль, два и один.
Для того чтобы верно записать результат уравнения мы пишем так:
- Если корня нет, пишем уравнение корней не имеет;
- Если есть и их несколько, они либо прописываются через запятые, либо в фигурных скобках, например, так: {-2, 3, 5};
- Еще одним вариантом написания корней, считается запись в виде простого равенства, к примеру неизвестная х а корни 3,5 тогда результат прописывается так: х=3, х=5.
- или прибавляя индекс снизух1 =3 , х2 = 5. данным способом указывается номер корня;
- Если решений уравнения бесконечное множество, то запись будет либо в виде числового промежутка от и до, или общепринятыми обозначениями. множество натуральных чисел N, целых – Z, действительных — R.
Стоит отметить, что если уравнение имеет два и более корней, то чаще употребляется понятие решение уравнения. Рассмотрим определение уравнения с несколькими переменными.
Решение уравнения с двумя и более переменными, означает, что эти несколько значений превращают уравнение в верное равенство.
Примеры:
Представим, что мы имеем следующее уравнение х + а = 5, такое уравнение имеет две переменные. Если мы поставим вместо них числа 3 и 6 то равенство не будет верным, соответственно и данные числа не являются решением для данного примера. А если взять числа 2 и 3 то равенство превратится в верное, а числа 2 и 3 будут решением уравнения. Представленные уравнения с несколькими переменными, тоже могут или не иметь корня вообще или наоборот иметь множество решений.
Правила нахождения корней
Таких правил существует несколько рассмотрим их ниже.
Пример 1
Допустим мы имеем уравнение 4 + х = 10, чтобы найти корень уравнения или значение х в данном случае необходимо найти неизвестное слагаемое, для этого есть следующее правило или формула. Для нахождения неизвестного слагаемого, нужно из суммы вычесть известное значение.
Решение:
х = 10 — 4
х = 6
Чтобы проверить является ли 6 решением, мы ставим его на место неизвестной переменной х в исходное уравнение, получаем следующее равенство 4 + 6 = 10, такое равенство является верным, что означает число корня уравнения, равно 6.
Пример 2
Возьмём уравнение вида х — 5 = 3, в данном примере х это неизвестное уменьшаемое, для того чтобы его найти необходимо следовать следующему правилу:
Для нахождения уменьшаемого необходимо сложить разность и вычитаемое.
Решение:
х = 3 + 5
х = 8
Проверяем правильность нахождения корня уравнения, подставляем, вместо переменной неизвестной, найденное число 8, получаем равенство 8 — 5 = 3, так как оно верное, то и корень уравнения найден правильно.
Пример 3
Берём уравнение, в котором неизвестное х будет вычитаемое к примеру: 8 — х = 4. для того чтобы найти х необходимо воспользоваться правилом:
Для нахождения вычитаемого, нужно из уменьшаемого вычесть разность.
Решение:
х = 8 — 4
х = 4
Проверяем правильность нахождения корня уравнения, для этого полученное значение ставим вместо неизвестного вычитаемого в исходный пример, и получаем следующее равенство 8 — 4 = 4, равенство верно, значит и корень найден правильно.
Нет времени решать самому?
Наши эксперты помогут!
Пример 4
Возьмём уравнение вида х * 3 = 9, в данном уравнении неизвестна переменная х, является множимым. Для того, чтобы найти корень такого уравнения необходимо использовать следующее правило.
Для нахождения неизвестного множимого, нужно произведение разделить на множитель.
Решение:
х = 9 : 3
х = 3
Для проверки подставим найденное значение х в исходное уравнение, получим равенство 3 * 3 =9, так как равенство является верным, то и решение уравнения верное.
Такое же правило действует и для множителя, чтобы его найти необходимо произведение разделить на множимое.
Пример 5
Возьмём уравнение следующего вида: х : 2 = 10 , в данном уравнении х- это неизвестное делимое, 2 — делитель, а 10 — частное. Для нахождения неизвестного значения х, воспользуемся правилом:
Чтобы найти делимое, необходимо частное умножить на делитель.
Решение:
х = 10 * 2
х = 20
Проверим, вместо неизвестного х, поставим его значение 20, получим следующее равенство 20: 2 = 10. Равенство верное, значит и решение было верным.
Пример 6
Теперь рассмотрим пример с делителем.
Возьмём уравнение 22: х = 11, где х неизвестный делитель. Для того чтобы его найти существует правило:
При нахождении неизвестного делителя нужно делимое разделить на частное.
Решение:
х = 22 : 11
х = 2
Проверяем, 2 ставим на место неизвестного х в исходное уравнение, получаем равенство 22 : 2 = 11. Так как равенство верно, то мы нашли верный корень уравнения.
Пример применения правил в более сложном уравнении: 2х — 5 =5
Решение:
2х = 5 + 5
2х = 10
х = 10 : 2
х = 5
Проверяем, для этого полученное значение х = 5, ставим в исходное уравнение, получаем равенство 2 * 5 — 5 = 5, так как равенство верно, корень найден правильно.
Квадратные уравнения
Существует также уравнения квадратного вида, например: 2х2 = 32, для того, чтобы найти неизвестное или корень квадратного уравнения, в таком уравнении необходимо:
Решение:
х2 = 32 : 2
х2 = 16
х = √16
х = 4
Проверим, для этого полученное значение подставим в исходное уравнение, и получим равенство 242 = 32. так как равенство верное, то и решение уравнения верно.
Как мы видим нахождение корня уравнения не такой сложный процесс, главное запомнить правила. Стоит отметить, что помимо решения различного вида задач, уравнения применяются в других различных науках. Применение уравнений можно найти в экономике, в физике, химии, биологии и других. При их помощи можно вычислить и описать процессы, происходящие вокруг нас.
Калькулятор квадратных корней
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.
Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.
Решить уравнение значит найти все возможные корни или убедиться, что их нет.
Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Какие бывают виды уравнений
Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.
Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.
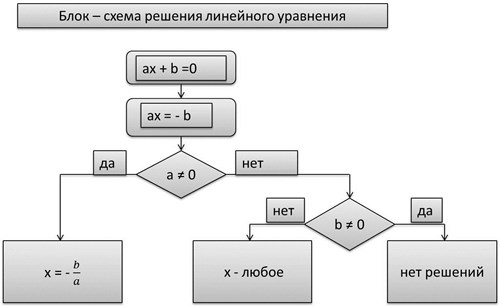
Линейное уравнение выглядят так: ах + b = 0, где a и b — действительные числа. Вот, что поможет в решении:
-
если а ≠ 0 — уравнение имеет единственный корень: х = -b : а;
-
если а = 0 — уравнение корней не имеет;
-
если а и b равны нулю, то корнем уравнения является любое число.
Квадратное уравнение выглядит так: ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.
Числовой коэффициент — число, которое стоит при неизвестной переменной.
Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:
- кубические,
- уравнения четвертой степени,
- иррациональные и рациональные,
- системы линейных алгебраических уравнений и другие.
Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.
Как решать простые уравнения
Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.
1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.
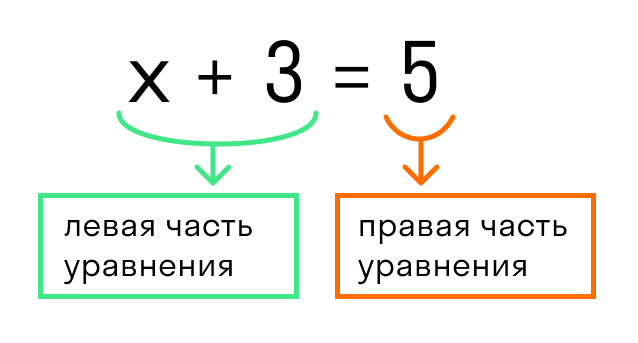
Для примера рассмотрим простейшее уравнение: x+3=5.
Начнем с того, что в каждом уравнении есть левая и правая часть.
Перенесем 3 из левой части в правую и меняем знак на противоположный.
Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.
Решим еще один пример: 6x = 5x + 10.
Как решаем:
-
Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.
6x — 5x = 10
-
Приведем подобные и завершим решение.
x = 10
Ответ: x = 10.
2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.
Применим правило при решении примера: 4x=8.
При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.
Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.
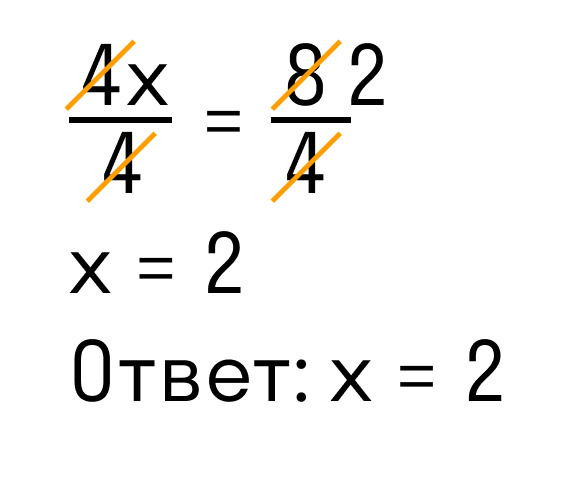
Разделим каждую часть на 4. Как это выглядит:
Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:
Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: -4x = 12
Как решаем:
- Разделим обе части на -4, чтобы коэффициент при неизвестной стал равен единице.
-4x = 12 | : (-4)
x = −3
Ответ: x = −3.
Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.
Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.
Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.
| Алгоритм решения простого линейного уравнения |
|---|
|
Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.
Примеры линейных уравнений
Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!
Пример 1. Как правильно решить уравнение: 6х + 1 = 19.
Решаем так:
-
ЮПеренести 1 из левой части в правую со знаком минус.
6х = 19 − 1
-
Выполнить вычитание.
6х = 18
-
Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.
х = 3
Ответ: 3.
Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3(х − 4) + 2х − 1.
Решаем так:
-
Раскрыть скобки
5х − 15 + 2 = 3х − 12 + 2х − 1
-
Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены. Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.
5х − 3х − 2х = −12 − 1 + 15 − 2
-
Приведем подобные члены.
0х = 0
Ответ: х — любое число.
Пример 3. Решить: 4х = 1/8.
Решаем так:
-
Разделим обе части уравнения на множитель стоящий перед переменной х, то есть на 4.
х = 1/8 : 4
х = 1/32
Ответ: 1/32.
Пример 4. Решить: 4(х + 2) = 6 − 7х.
Решаем так:
-
4х + 8 = 6 − 7х
-
4х + 7х = 6 − 8
-
11х = −2
-
х = −2 : 11
-
х = −2/11
Ответ: −2/11 или −(0,18). О десятичных дробях можно почитать в другой нашей статье.
Пример 5. Решить:
Решаем так:
-
-
3(3х — 4) = 4 · 7х + 24
-
9х — 12 = 28х + 24
-
9х — 28х = 24 + 12
-
-19х = 36
-
х = 36 : (-19)
-
х = — 36/19
Ответ: 1 17/19.
Пример 6. Как решить линейное уравнение: х + 7 = х + 4.
Решаем так:
-
Сгруппировать в левой части неизвестные члены, в правой — свободные члены:
х – х = 4 — 7
-
Приведем подобные члены.
0 * х = — 3
Ответ: нет решений.
Пример 7. Решить: 2(х + 3) = 5 − 7х.
Решаем так:
-
2х + 6 = 5 − 7х
-
2х + 7х = 5 − 6
-
9х = −1
-
х = −1/9
Ответ: −1/9.
Уравнения бывают разные. Вы изучите их многие виды в курсе математике, но все они решаются по одним правилам, эти правила мы сейчас рассмотрим подробно.
Что такое уравнение? Смысл и понятия.
Узнаем сначала все понятия, связанные с уравнением.
Определение:
Уравнение – это равенство, содержащее переменные и числовые значения.
Переменные (аргументы уравнения) или неизвестные уравнения – их обозначают в основном латинскими буквами (x, y, z, f и т.д.). При подстановки числового значения переменной в уравнение получаем верное равенство – это корень уравнения.
Решить уравнение – это значит найти все корни уравнения или доказать, что у данного уравнения нет корней.
Корни уравнения – это значение переменной при котором уравнение превращается в верное равенство.
Рассмотрим теперь, все термины на простом примере:
x+1=3
В данном случае x – переменная или неизвестное значение уравнения.
Можно устно решить данное уравнение. Какое надо число прибавить к 1, чтобы получить 3? Конечно, число 2. То есть наша переменная x =2. Корень уравнения равен 2. Проверим правильно ли мы решили уравнение? Чтобы проверить уравнение, нужно вместо переменной подставить полученный корень уравнения.
2+1=3
Получили верное равенство. Значит, правильно нашли корни уравнения.
Но бывают более сложные уравнения, которые устно не решить. Нужно прибегать к правилам решения уравнений. Рассмотрим правила решения уравнений ниже, которые объяснят нам как решать уравнения.
Правила уменьшения или увеличения уравнения на определенное число.
Чтобы понять правило рассмотрим подробно простой пример:
Решите уравнение x+2=7
Решение:
Чтобы решить данное уравнение нужно левую и правую часть уменьшить на 2. Это нужно сделать для того, чтобы переменная x осталась слева, а известные (т.е. числа) справа. Что значит уменьшить на 2? Это значит отнять от левой части двойку и одновременно от правой части отнять двойку. Если мы делаем какое-то действие, например, вычитание применяя его одновременно к левой части уравнения и к правой, то уравнение не меняет смысл.
x+2-2=7-2
x+0=7-2
x=7-2
Нужно остановиться на этом моменте подробно. Другими словами, мы +2 перенесли с левой части на правую и знак поменяли стало число -2.
x=5
Как проверить правильно ли вы нашли корень уравнения? Ведь не все уравнения будут простыми как данное. Чтобы проверить корень уравнения его значение нужно поставить в само уравнение.
Проверка:
Вместо переменной x подставим 5.
x+2=7
5+2=7
Получили верное равенство, значит уравнение решено верно.
Ответ: 5.
Разберем следующий пример:
Решите уравнение x-4=12.
Решение:
Чтобы решить данное уравнение нужно увеличить левую и правую часть уравнения на 4, чтобы переменная x осталось в левой стороне, а известные (т.е. числа) в правой стороне. Прибавим к левой и правой части число 4. Получим:
x-4+4=12+4
x=12+4
Другими словами, мы -4 перенесли из левой части уравнения в правую и получили +4. При переносе через равно знаки меняются на противоположные.
x=16
Теперь выполним проверку, вместо переменной x подставим в уравнение полученное число 16.
x-4=12
16-4=12
Ответ: 16
Очень важно понять правила переноса частей уравнения через знак равно. Не всегда нужно переносить числа, иногда нужно перенести переменные или даже целые выражения.
Рассмотрим пример:
Решите уравнение 4+3x=2x-5
Решение:
Чтобы решить уравнение необходимо неизвестные перенести в одну сторону, а известные в другую. То есть переменные с x будут в левой части, а числа в правой части.
Сначала перенесем 2x с правой стороны в левую сторону уравнения и получим -2x.
4+3x=2x-5
4+3x-2x=-5
Далее 4 с левой стороны уравнения перенесем на правую сторону и получим -4
4+3x-2x=-5
3x-2x=-5-4
Теперь, когда все неизвестные в левой стороне, а все известные в правой стороне посчитаем их.
(3-2)x=-9
1x=-9 или x=-9
Сделаем проверку, правильно ли решено уравнение? Для этого вместо переменной x в уравнение подставим -9.
4+3x=2x-5
4+3⋅(-9)=2⋅(-9)-5
4-27=-18-5
-23=-23
Получилось верное равенство, уравнение решено верно.
Ответ: корень уравнения x=-9.
Правила уменьшения или увеличения уравнения в несколько раз.
Данное правило подходит тогда, когда вы уже посчитали все неизвестные и известные, но какой-то коэффициент остался перед переменной. Чтобы избавится от не нужного коэффициента мы применяем правило уменьшения или увеличения в несколько раз коэффициент уравнения.
Рассмотрим пример:
Решите уравнение 5x=20.
Решение:
В данном уравнение не нужно переносить переменные и числа, все компоненты уравнения стоят на месте. Но нам мешает коэффициент 5 который стоит перед переменной x. Мы не можем его просто взять и перенести в правую сторону уравнения, потому что между число 5 и переменно x стоит умножение 5⋅х. Если бы между переменной и числом стоял знак плюс или минус, мы могли бы 5 перенести вправо. Но мы так поступить не можем. За то мы можем все уравнение уменьшить в 5 раз или поделить на 5. Обязательно делим правую и левую сторону одновременно.
5x=20
5x:5=20:5
5:5x=4
1x=4 или x=4
Делаем проверку уравнения. Вместо переменной x подставляем 4.
5x=20
5⋅4=20
20=20 получили верное равенство, корень уравнение найден правильно.
Ответ: x=4.
Рассмотрим следующий пример:
Найдите корни уравнения .
Решение:
Так как перед переменной x стоит коэффициент необходимо от него избавиться. Надо все уравнение увеличить в 3 раза или умножить на 3, обязательно умножаем левую часть уравнения и правую часть.
1x=21 или x=21
Сделаем проверку уравнения. Подставим вместо переменной x полученный корень уравнения 21.
7=7 получено верное равенство.
Ответ: корень уравнения равен x=21.
Следующий пример:
Найдите корни уравнения
Решение:
Сначала перенесем -1 в правую сторону уравнения относительно знака равно, а в левую сторону и знаки у них поменяются на противоположные.
Теперь нужно все уравнение умножить на 5, чтобы в коэффициенте перед переменной x убрать из знаменателя 5.
3x=45
Далее делим все уравнение на 3.
3x:3=45:3
(3:3)x=15
1x=15 или x=15
Сделаем проверку. Подставим в уравнение найденный корень.
5=5
Ответ: x=15
Как решать уравнения? Алгоритм действий.
Подведем итог разобранной теме уравнений, рассмотрим общие правила решения уравнений:
- Перенести неизвестные в одну сторону, а известные в другую сторону уравнения относительно равно.
- Преобразовать и посчитать подобные в уравнении, то есть переменные с переменными, а числа с числами.
- Избавиться от коэффициента при переменной если нужно.
- В итоге всех действий получаем корень уравнение. Выполняем проверку.
Эти правила действуют на любой вид уравнения (линейный, квадратный, логарифмический, тригонометрический, рациональные, иррациональные, показательные и другие виды). Поэтому важно понять эти простые правила и научиться ими пользоваться.
Корнем уравнения называют число, подстановка которого в уравнение вместо переменной (обычно (x)), дает одинаковые значения выражений справа и слева от знака равно.
Решая, например, уравнение (2x+1=x+4) находим ответ: (x=3). Если подставить тройку вместо икса, получатся одинаковые значения слева и справа:
(2x+1=x+4)
(2cdot3+1=3+4)
(7=7)
И никакое другое число, кроме тройки такого равенства нам не даст. Значит, число (3) – единственный корень уравнения.
Еще раз: корень – это НЕ ИКС! Икс – это переменная, а корень – это число, которое превращает уравнение в верное равенство (в примере выше – тройка). И при решении уравнений мы это неизвестное число (или числа) ищем.
Пример: Является ли (5) корнем уравнения (x^{2}-2x-15=0)?
Решение: Подставим (5) вместо икса:
(5^{2}-2cdot5-15=0)
(25-10-15=0)
(0=0)
По обе стороны от равно — одинаковые значения (ноль), значит 5 действительно корень.
Матхак: на контрольных таким способом можно проверить верно ли вы нашли корни.
Пример: Какое из чисел (0, pm1, pm2), является корнем для (2x^{2}+15x+22=0)?
Решение: Проверим подстановкой каждое из чисел:
|
проверяем (0): |
(2cdot0^{2}+15cdot0+22=0) |
|
(0+0+22=0) |
|
| (22=0) — не сошлось, значит (0) не подходит | |
|
проверяем (1): |
(2cdot1^{2}+15cdot1+22=0) |
| (2+15+22=0) | |
| (39=0) — опять не сошлось, то есть и (1) не корень | |
|
проверяем (-1): |
(2cdot(-1)^{2}+15cdot(-1)+22=0) |
| (2-15+22=0) | |
| (9=0) — снова равенство неверное, (-1) тоже мимо | |
|
проверяем (2): |
(2cdot2^{2}+15cdot2+22=0) |
|
(2cdot4+30+22=0) |
|
|
(60=0) — и вновь не то, (2) также не подходит |
|
|
проверяем (-2): |
(2cdot(-2)^{2}+15cdot(-2)+22=0) |
|
|
(2cdot4-30+22=0) |
| (0=0) — сошлось, значит (-2) — корень уравнения |
Очевидно, что решать уравнения перебором всех возможных значений – безумие, ведь чисел бесконечно много. Потому были разработаны специальные методы нахождения корней. Так, например, для линейных уравнений достаточно одних только равносильных преобразований, для квадратных – уже используются формулы дискриминанта и т.д. Каждому типу уравнений – свой метод.
Ответы на часто задаваемые вопросы
Вопрос: Может ли корень уравнения быть равен нулю?
Ответ: Да, конечно. Например, уравнение (3x=0) имеет единственный корень — ноль. Можете проверить подстановкой.
Вопрос: Когда в уравнении нет корней?
Ответ: В уравнении может не быть корней, если нет таких значений для икса, которые сделают уравнение верным равенством. Яркий примером тут может быть уравнение (0cdot x=5). Это уравнение не имеет корней, так как значение икса здесь не играет роли (из-за умножения на ноль) — все равно левая часть будет всегда равна нулю. А ноль не равен пятерке. Значит, корней нет.
Вопрос: Что значит «найдите меньший корень уравнения»?
Ответ: Это значит, что нужно решить уравнение, и в ответ указать его меньший корень. Например, уравнение (x^2-5x-6=0) имеет два корня: (x_1=-1) и (x_2=6). Меньший из корней: (-1). Вот его и надо будет записать в ответ. Если бы спрашивали про больший корень, то надо было бы записать (6).
Уравнение с одним неизвестным, которое после раскрытия скобок и приведения подобных членов принимает вид
aх + b = 0, где a и b произвольные числа, называется линейным уравнением с одним неизвестным. Cегодня разберёмся, как эти линейные уравнения решать.
Например, все уравнения:
2х + 3= 7 – 0,5х; 0,3х = 0; x/2 + 3 = 1/2 (х – 2) — линейные.
Значение неизвестного, обращающее уравнение в верное равенство называется решением или корнем уравнения.
Например, если в уравнении 3х + 7 = 13 вместо неизвестного х подставить число 2 , то получим верное равенство 3· 2 +7 = 13. Значит, значение х = 2 есть решение или корень уравнения.
А значение х = 3 не обращает уравнение 3х + 7 = 13 в верное равенство, так как 3· 2 +7 ≠ 13. Значит, значение х = 3 не является решением или корнем уравнения.
Решение любых линейных уравнений сводится к решению уравнений вида
aх + b = 0.
Перенесем свободный член из левой части уравнения в правую, изменив при этом знак перед b на противоположный, получим
aх = ‒ b.
Если a ≠ 0, то х = ‒ b/a .
Пример 1. Решите уравнение 3х + 2 =11.
Перенесем 2 из левой части уравнения в правую, изменив при этом знак перед 2 на противоположный, получим
3х = 11 – 2.
Выполним вычитание, тогда
3х = 9.
Чтобы найти х надо разделить произведение на известный множитель, то есть
х = 9 : 3.
Значит, значение х = 3 является решением или корнем уравнения.
Ответ: х = 3.
Если а = 0 и b = 0, то получим уравнение 0х = 0. Это уравнение имеет бесконечно много решений, так как при умножении любого числа на 0 мы получаем 0,но b тоже равно 0. Решением этого уравнения является любое число.
Пример 2. Решите уравнение 5(х – 3) + 2 = 3 (х – 4) + 2х ‒ 1.
Раскроем скобки:
5х – 15 + 2 = 3х – 12 + 2х ‒ 1.
Сгруппируем в левой части члены, содержащие неизвестные, а в правой ‒ свободные члены:
5х – 3х ‒ 2х = – 12 ‒ 1 + 15 ‒ 2.
Приведем подобные члены:
0х = 0.
Ответ: х — любое число.
Если а = 0 и b ≠ 0, то получим уравнение 0х = — b. Это уравнение решений не имеет, так как при умножении любого числа на 0 мы получаем 0, но b ≠ 0 .
Пример 3. Решите уравнение х + 8 = х + 5.
Сгруппируем в левой части члены, содержащие неизвестные, а в правой ‒ свободные члены:
х – х = 5 ‒ 8.
Приведем подобные члены:
0х = ‒ 3.
Ответ: нет решений.
На рисунке 1 изображена схема решения линейного уравнения
Составим общую схему решения уравнений с одной переменной. Рассмотрим решение примера 4.
Пример 4. Пусть надо решить уравнение
1) Умножим все члены уравнения на наименьшее общее кратное знаменателей, равное 12.
2) После сокращения получим
4 (х – 4) + 3·2 (х + 1) ‒ 12 = 6·5 (х – 3) + 24х – 2 (11х + 43)
3) Чтобы отделить члены, содержащие неизвестные и свободные члены, раскроем скобки:
4х – 16 + 6х + 6 – 12 = 30х – 90 + 24х – 22х – 86 .
4) Сгруппируем в одной части члены, содержащие неизвестные, а в другой – свободные члены:
4х + 6х – 30х – 24х + 22х = ‒ 90 – 86 + 16 – 6 + 12.
5) Приведем подобные члены:
‒ 22х = ‒ 154.
6) Разделим на – 22 , Получим
х = 7.
Как видим, корень уравнения равен семи.
Вообще такие уравнения можно решать по следующей схеме:
а) привести уравнение к целому виду;
б) раскрыть скобки;
в) сгруппировать члены, содержащие неизвестное, в одной части уравнения, а свободные члены ‒ в другой;
г) привести подобные члены;
д) решить уравнение вида aх = b,которое получили после приведения подобных членов.
Однако эта схема не обязательна для всякого уравнения. При решении многих более простых уравнений приходится начинать не с первого, а со второго (Пример. 2), третьего (Пример. 1, 3) и даже с пятого этапа, как в примере 5.
СЛОЖНА-А-А 🙀 Ты же знаешь, что если не разобраться в теме сейчас, то потом придется исправлять оценки. Беги на бесплатное онлайн-занятие с репетитором (подробности тут + 🎁).
Пример 5. Решите уравнение 2х = 1/4.
Находим неизвестное х = 1/4 : 2,
х = 1/8 .
Рассмотрим решение некоторых линейных уравнений, встречающихся на основном государственном экзамене.
Пример 6. Решите уравнение 2 (х + 3) = 5 – 6х.
Решение
2х + 6 = 5 – 6х
2х + 6х = 5 – 6
8х = ‒1
х = ‒1 : 8
х = ‒ 0, 125
Ответ: ‒ 0, 125
Пример 7. Решите уравнение – 6 (5 – 3х) = 8х – 7.
Решение
– 30 + 18х = 8х – 7
18х – 8х = – 7 +30
10х = 23
х = 23 : 10
х = 2,3
Ответ: 2,3
Пример 8. Решите уравнение
Решение:
3(3х – 4) = 4 · 7х + 24
9х – 12 = 28х + 24
9х – 28х = 24 + 12
-19х = 36
х = 36 : (-19)
х = — 36/19
Ответ: — 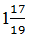
Пример 9. Найдите f(6), если f (x + 2) = 37-х
Решение
Так как надо найти f(6), а нам известно f (x + 2),
то х + 2 = 6.
Решаем линейное уравнение х + 2 = 6,
получаем х = 6 – 2, х = 4.
Если х = 4, тогда
f(6) = 37-4 = 33 = 27
Ответ: 27.
Молодец! Раз ты дочитал это до конца, вероятно, ты все отлично усвоил. Но если вдруг что-то еще непонятно — попробуй онлайн-занятие с репетитором (подробности тут + 🎁).
Если у Вас остались вопросы, есть желание разобраться с решением уравнений более основательно, записывайтесь на мои уроки в РАСПИСАНИИ. Буду рада Вам помочь!
Также TutorOnline советует посмотреть новый видеоурок от нашего репетитора Ольги Александровны, который поможет разобраться как с линейными уравнениями, так и с другими.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.