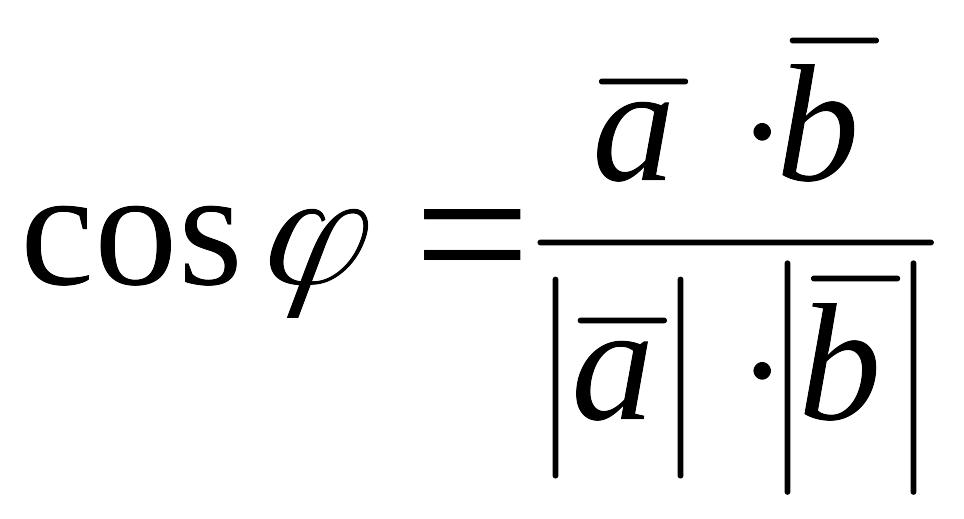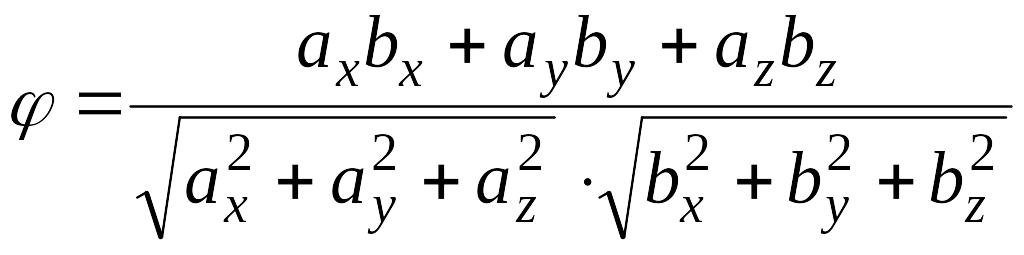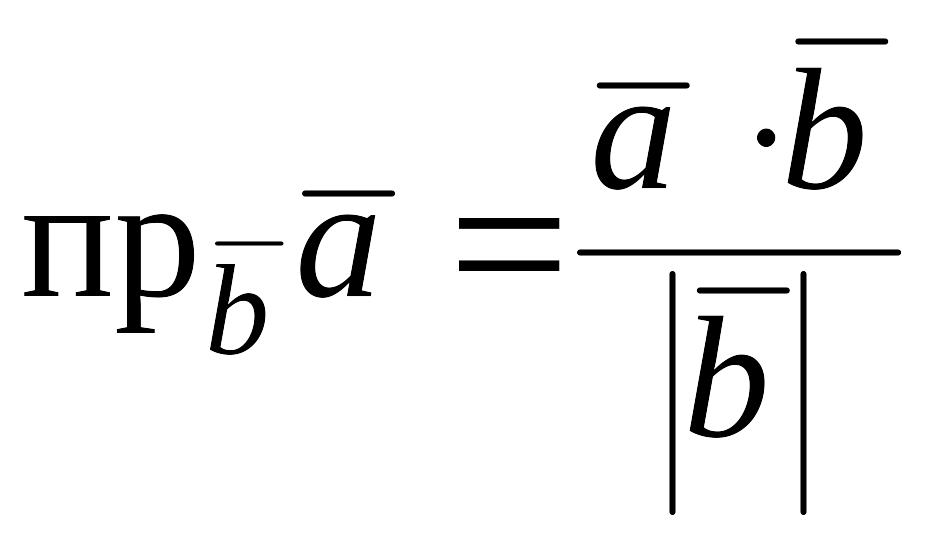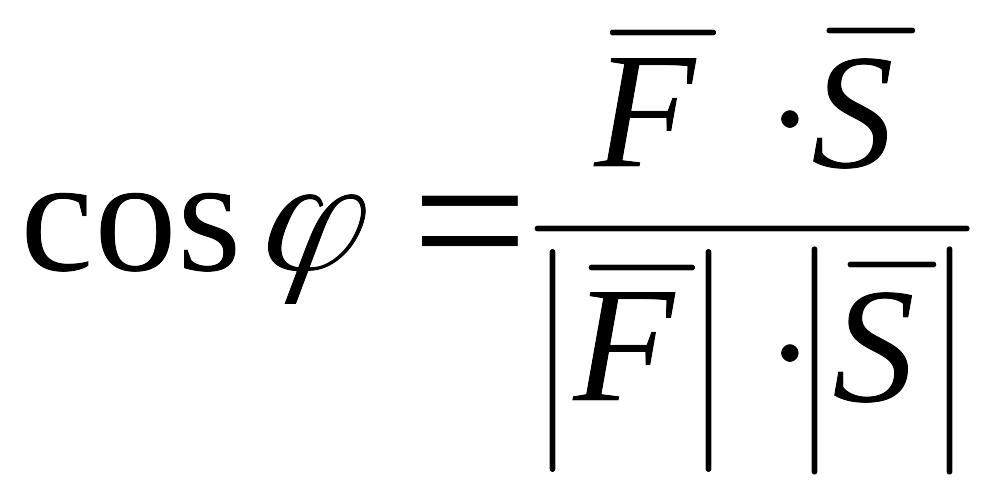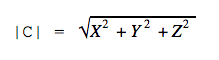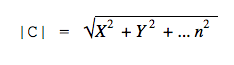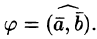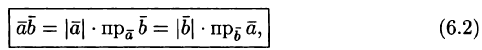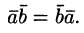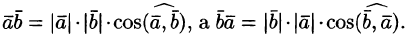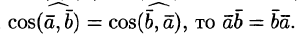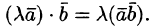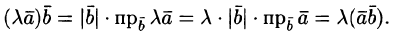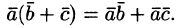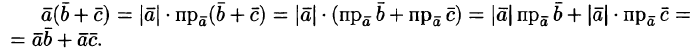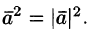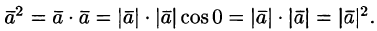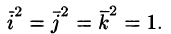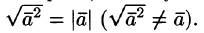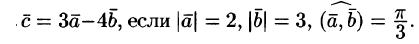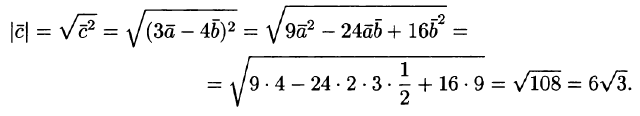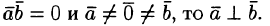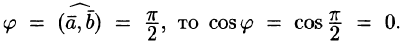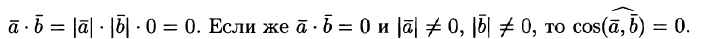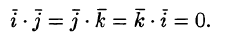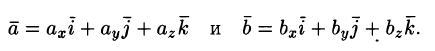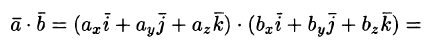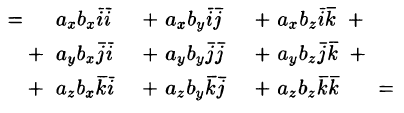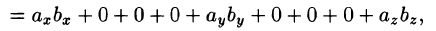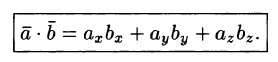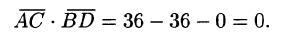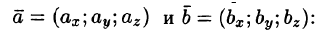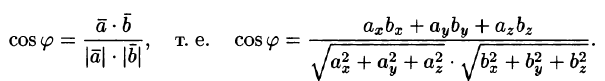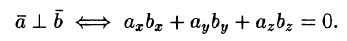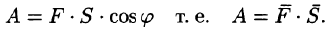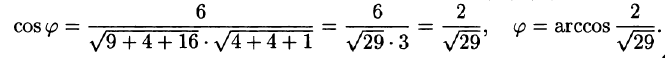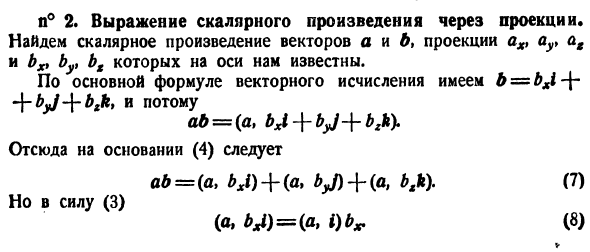Как найти корень вектора в квадрате - Исправление недочетов и поиск решений вместе с Examum.ru

6.1. Определение скалярного произведения

Определение.
Скалярным
произведением двух
ненулевых векторов

называется число,
равное
произведению длин этих векторов на
косинус угла между ними.

Обозначается

,

(или

).
Итак, по определению,

,
(6.1)

где

Формуле
(6.1) можно придать иной вид. Так как

,
(см. рис. 6.1), a

,
то получаем:

,
(6.2)

т.
е. скалярное произведение двух векторов
равно модулю одного из них, умноженному
на проекцию другого на ось, сонаправленную
с первым вектором.

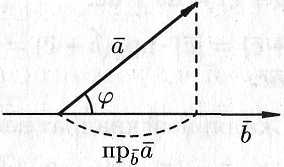
Рис. 6.1.

6.2. Свойства скалярного произведения

Скалярное
произведение обладает переместительным
свойством:

,
а

.

И
так как

,
как произведение
чисел и

,
то

2.
Скалярное произведение обладает
сочетательным свойством относительно
скалярного множителя:

.

3.
Скалярное произведение обладает
распределительным свойством:

4.
Скалярный квадрат вектора равен квадрату
его длины:

.

В
частности:

.

Если
вектор

возвести скалярно в квадрат и затем
извлечь корень, то получим не первоначальный
вектор, а его модуль

,
т. е.

(
).

Пример
6.1.
Найти
длину вектора

,
если

,

,

.

Решение.

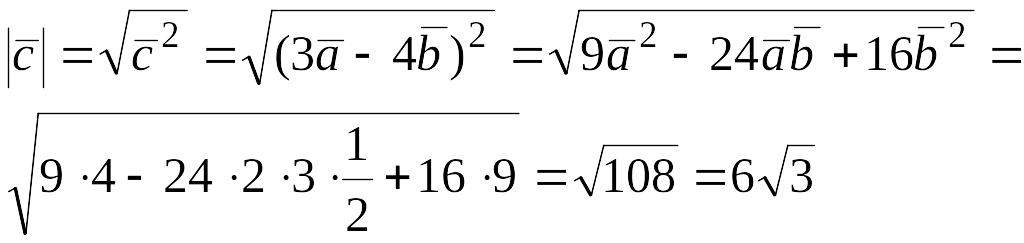
5.
Если векторы

(ненулевые) взаимно перпендикулярны,
то их скалярное произведение равно
нулю, т. е. если

,
то

.
Справедливо и обратное утверждение:
если

и

,
то

Так
как

,
то

.
Следовательно,

.
Если же

и

,

,
то

.
Отсюда

,
т.e.

В
частности:
.

6.3. Выражение скалярного произведения через координаты

Пусть заданы два
вектора

Найдем
скалярное произведение векторов,
перемножая их как многочлены (что законно
в силу свойств линейности скалярного
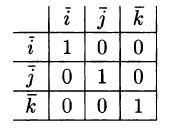
произведения) и пользуясь таблицей
скалярного произведения векторов

,

,

:

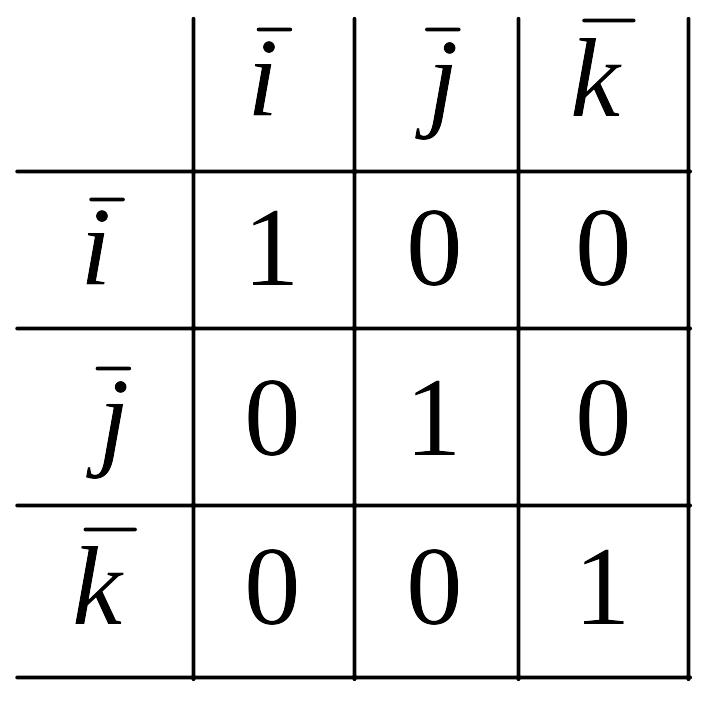
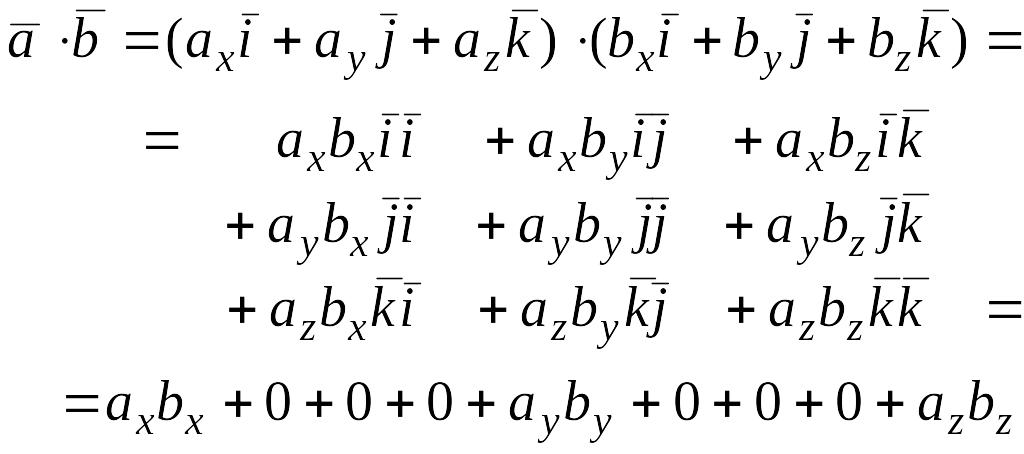
т.
e.

Итак,
скалярное
произведение векторов равно сумме
произведений их одноименных координат.

Пример
6.2.
Доказать,
что диагонали четырехугольника, заданного
координатами вершин

,

,

,

,
взаимно перпендикулярны.

Решение.
Составим вектора

и

,
лежащие на диагоналях данного
четырехугольника. Имеем:

и

.
Найдем скалярное произведение этих
векторов:

Отсюда
следует, что

.
Диагонали
четырехугольника

взаимно перпендикулярны.

6.4. Некоторые приложения скалярного произведения

Угол
между векторами.

Определение
угла

между ненулевыми векторами

и

:

,
т.е.

.

Отсюда
следует условие перпендикулярности
ненулевых векторов

и

:

Проекция
вектора на заданное направление.

Нахождение
проекции вектора

на направление, заданное вектором

,
может
осуществляться по формуле

, т.е.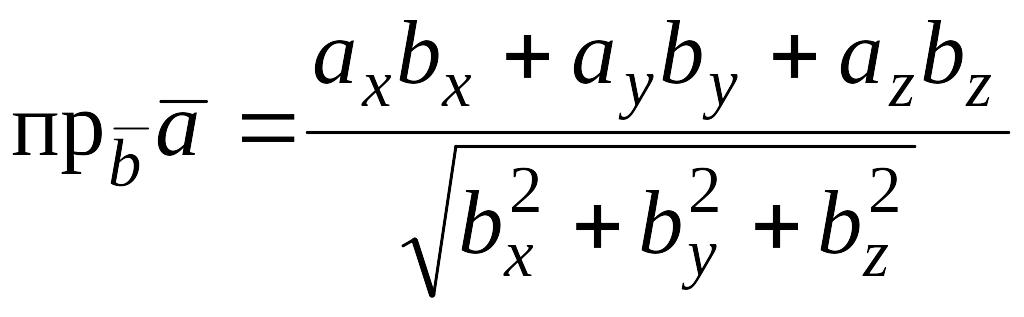

Работа
постоянной силы.

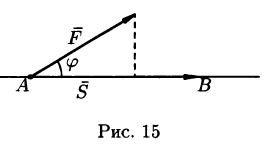
Пусть
материальная точка перемещается
прямолинейно из положения

в положение

под действием постоянной силы

,
образующей угол

с перемещением

(см. рис. 6.2).

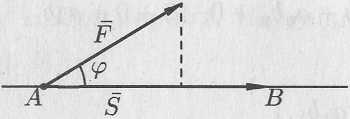
Рис. 6.2.

Из
физики известно, что работа силы

при перемещении

равна

т.е.

.

Таким
образом, работа постоянной силы при
прямолинейном перемещении ее точки
приложения равна скалярному произведению
вектора силы на вектор перемещения.

Пример
6.3.
Вычислить
работу, произведенную силой

,
если точка ее приложения перемещается
прямолинейно из положения

в положение

.
Под каким углом к

направлена сила

Решение.
Находим

.
Стало быть,

(ед.
работы).

Угол

между

находим по формуле

,
т. е.

,
.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Операции с векторами

Как сложить и перемножить векторы (и зачем).

Мы постепенно показываем вам математику за пределами школьной программы. Начинали со знакомства с векторами, теперь сделаем следующий шаг.

Напомним основные мысли:

Вектор — это абстрактное понятие, которое представляет собой организованную последовательность каких-то чисел.
В виде вектора можно представить координаты предмета в каком-то пространстве; площадь квартиры и её стоимость; цифровые данные анкеты какого-то человека и динамику цен на нефть.
Если по-простому, то векторы нужны, чтобы обрабатывать большое количество организованных чисел. Представьте, что вектор — это коробка с конфетами, только вместо конфет — числа. Каждое число стоит в своей ячейке.
Машинное обучение основано на перемножении матриц, которые, в свою очередь, можно представить как наборы векторов. Так что векторы лежат в глубине всех модных и молодёжных технологий ИИ.

С векторами можно совершать некоторые математические операции. Вот о них и поговорим.

Правильно — векторы

Математики часто говорят во множественном числе «вектора», но по словарю правильно «векторы». Это такой профессиональный жаргон, как «договора», «бухгалтера» и «сервера». Мы будем использовать «векторы», но если вы окажетесь в постковидном математическом баре, лучше говорите «вектора».

Сложение

Представим четыре вектора, которые лежат в двухмерном пространстве и пока что не связаны между собой. Нарисуем эти векторы и обозначим их буквами X, Y, Z, K.

Поскольку векторы находятся в одном пространстве, координаты каждого состоят из одинакового количества чисел. У нас пример с двухмерным пространством и два числа. Выглядеть это будет так: X = (6, 4); Y = (3, −2); Z = (−7, −5); K = (−10, 4).

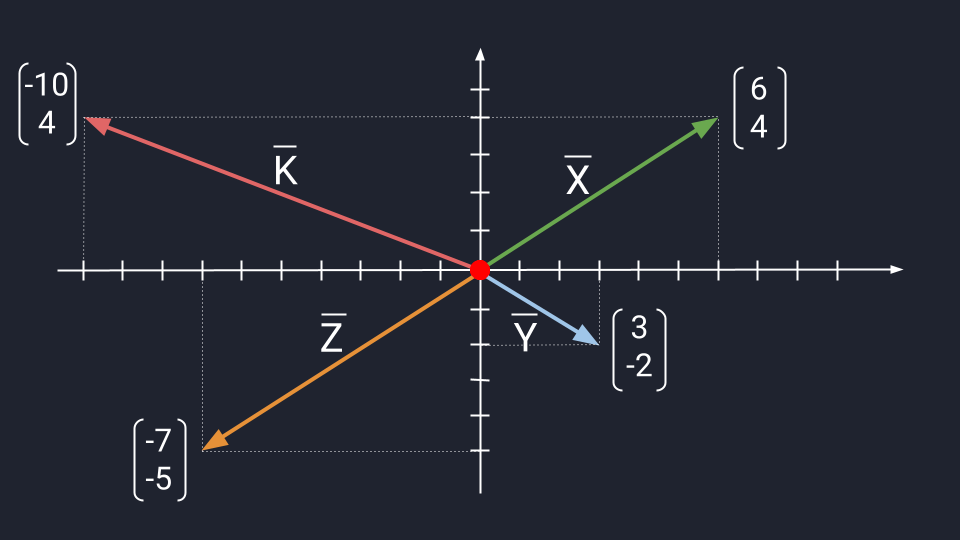
Векторы X, Y, Z, K в двухмерном пространстве

Если у нас несколько векторов с одинаковым количеством чисел, то эти числа можно поэлементно складывать. Для этого мы берём первое число одного вектора, складываем его с первым числом другого вектора и так далее.

Предположим, нам нужно сложить векторы X и Y.

X = (6, 4)
Y = (3, −2)
X + Y = (9, 2)

Вроде просто: складываешь последовательно все координаты, результаты сложения складываешь в исходные коробочки. Так можно делать с любым количеством координат. Помните, что вектор — это необязательно стрелка в двумерном пространстве. Она может быть и в десятимерном пространстве — с точки зрения математики это неважно.

Например, вот сложение векторов с пятью координатами:

X = (6, 4, 11, 14, 99)
Y = (3, -2, 10, -10, 1)
X + Y = (9, 2, 21, 4, 100)

Интуитивное изображение сложения

Для интуитивного восприятия удобно использовать векторы с двумя координатами. Их удобно рисовать на координатной плоскости и таким образом смотреть на геометрию.

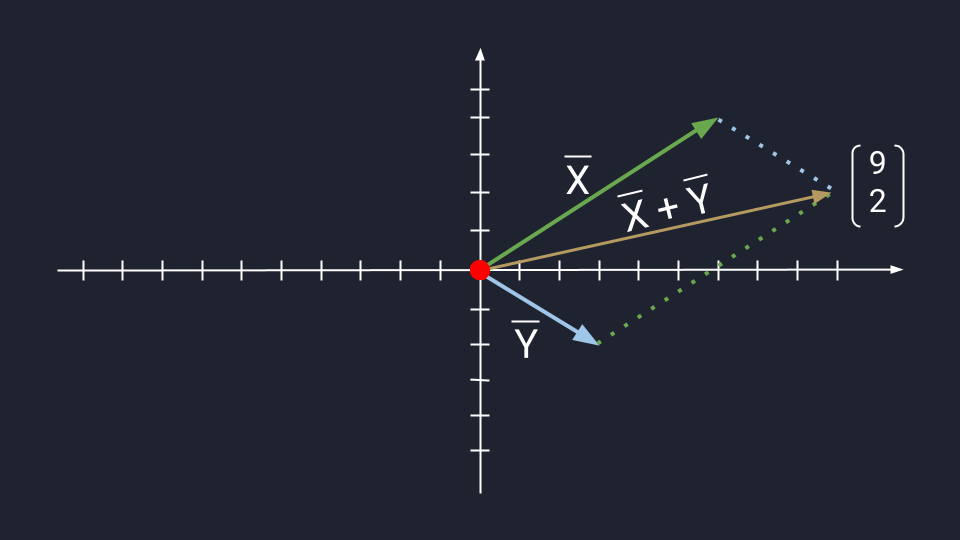
Например, можно на плоскости показать, как будет работать сложение двух векторов. Для этого есть два метода: метод треугольника и метод параллелограмма.

Метод треугольника: ставим векторы Х и Y в очередь друг за другом. Для этого берём вектор Х, ставим за ним вектор Y и получаем новый вектор. Новый вектор начинается в хвосте вектора Х и заканчивается на стрелке вектора Y. Этот вектор — результат сложения. Представьте, что это ребёночек двух векторов.

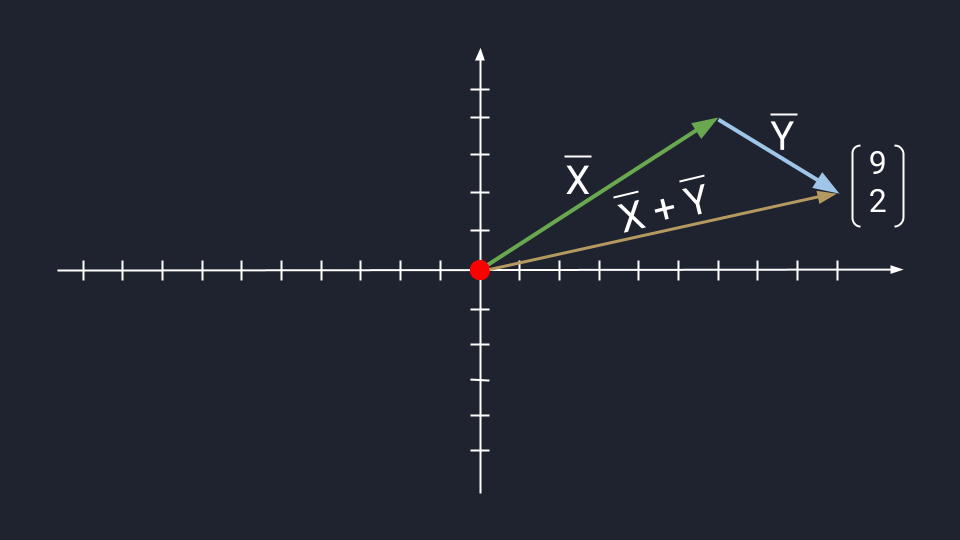
Сложение векторов по методу треугольника: X = (6, 4); Y = (3, −2); Х + Y = (9, 2)

Чтобы воспользоваться методом параллелограмма, нам нужно поставить векторы Х и Y в одну исходную точку. Дальше мы дублируем векторы Х и Y, формируем параллелограмм и получаем новый вектор. В новом векторе соединяем исходную точку с исходной точкой дублирующих векторов — стрелка проходит посередине параллелограмма. Длина нового вектора — это сумма векторов Х и Y.

Сложение по методу параллелограмма и треугольника даёт одинаковый результат. Поэтому выбирайте вариант, который больше подходит под задачу.

Сложение векторов по методу параллелограмма: X = (6, 4); Y = (3, -2); Х + Y = (9, 2)

Вычитание

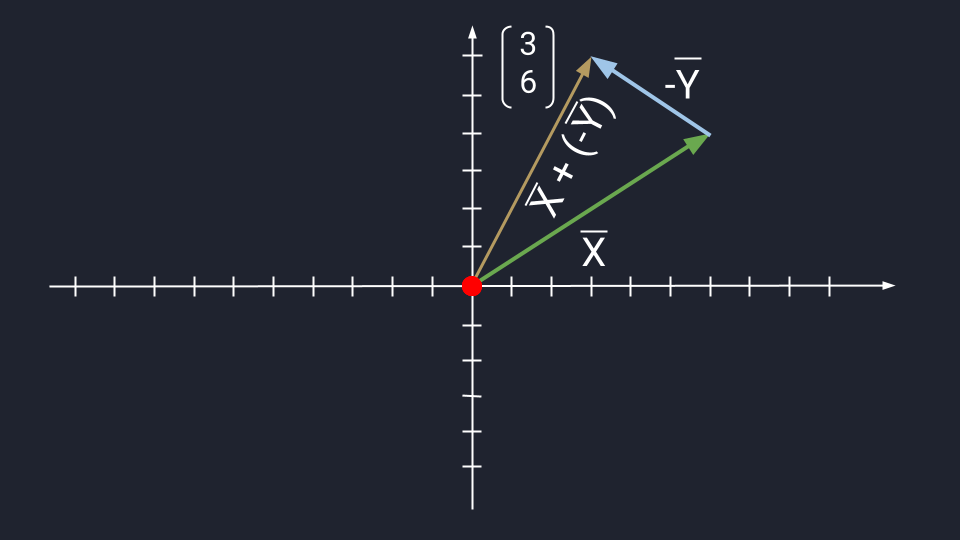
Вычитание векторов немного сложнее. Чтобы вычесть векторы, нужно «развернуть» вычитаемый вектор и сложить его с исходным. «Развернуть» — то есть направить в обратную сторону, «перевернув» знаки координат. Получится конструкция вроде такой: Х + (−Y)

Дальше используются правила сложения. Пошагово это выглядит так:

У нас есть X = (6, 4) и Y = (3, −2).
Превращаем формулу Х − Y в формулу Х + (−Y).
Разворачиваем вектор Y. Было: Y = (3, −2). Стало: −Y = (−3, 2).
Считаем: X + (−Y) = (3, 6).

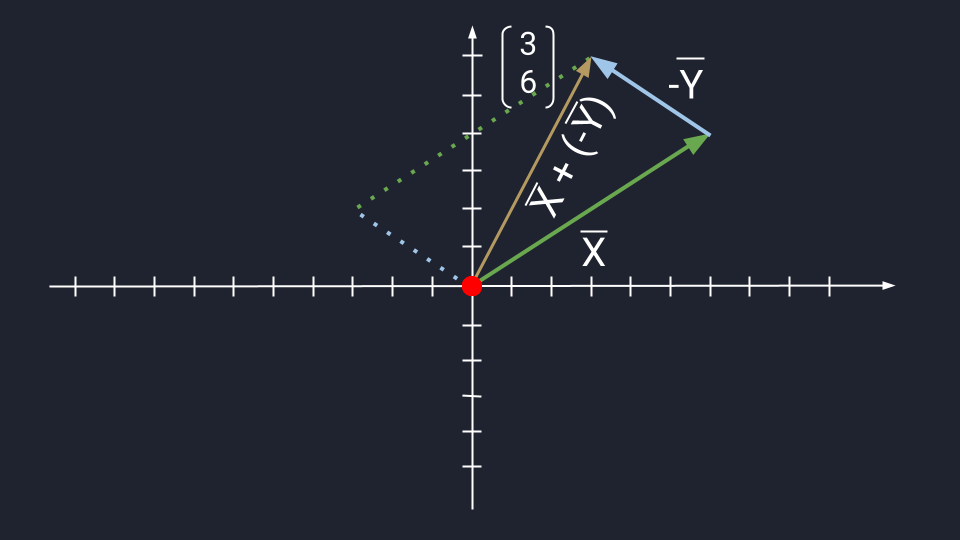
Теперь посмотрим, как выглядит вычитание векторов на графике:

Вычитание векторов по методу треугольника: X = (6, 4); −Y = (−3, 2); X + (−Y) = (3, 6) Вычитание векторов по методу параллелограмма: X = (6, 4); −Y = (−3, 2); X + (−Y) = (3, 6)

Длина вектора

Длина вектора — это одно число, которое измеряется расстоянием от кончика до стрелки вектора. Длину вектора нельзя путать с координатами. Координаты — это несколько чисел, которые указывают на расположение стрелки вектора. По координатам можно определить только конечную точку вектора. Например, если X = (6, 2), то стрелка будет находиться в точке 6 по оси Х. Или другой пример: если Y = (6, 5), то стрелка этого вектора будет находиться в точке 5 по оси Y.

Предположим, нам известны начальные точки векторов X и Y. Пусть это будет точка 2 по оси X и точка 2 по оси Y. Так мы можем легко посчитать длину отрезков:

X = 6 − 2 = 4
Y = 5 − 2 = 3

Иногда приходится рассчитывать длину третьего вектора, который привязан к двум другим векторам. Это легко сделать с помощью теоремы Пифагора — это когда квадрат гипотенузы равен сумме квадратов катетов. В нашем случае катетами будут длины векторов X и Y. Вспоминаем школьную формулу и считаем:

|C|2 = 42 + 32 = 25
|C| = √25 = 5 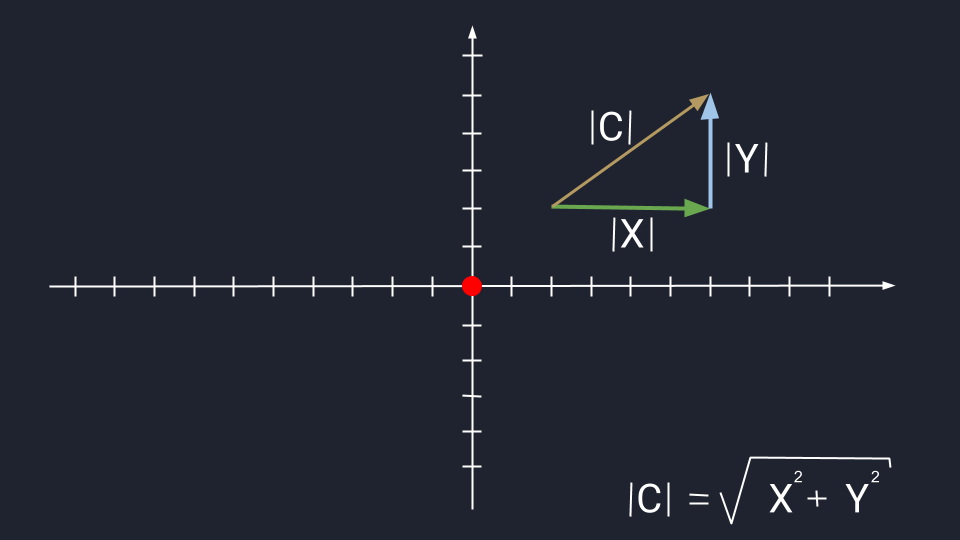Длина вектора считается по формуле прямоугольного треугольника. Чтобы было проще представить — перенесите векторы на систему координат

Это формула для двумерного пространства. В трёхмерном пространстве формула похожая: нужно сложить квадраты трёх координат и вычислить квадратный корень из суммы.

В пространстве с большим числом измерений формула выглядит сложнее, но по сути то же: складываем все квадраты координат и получаем квадратный корень из этой суммы.

Умножение и деление вектора на число

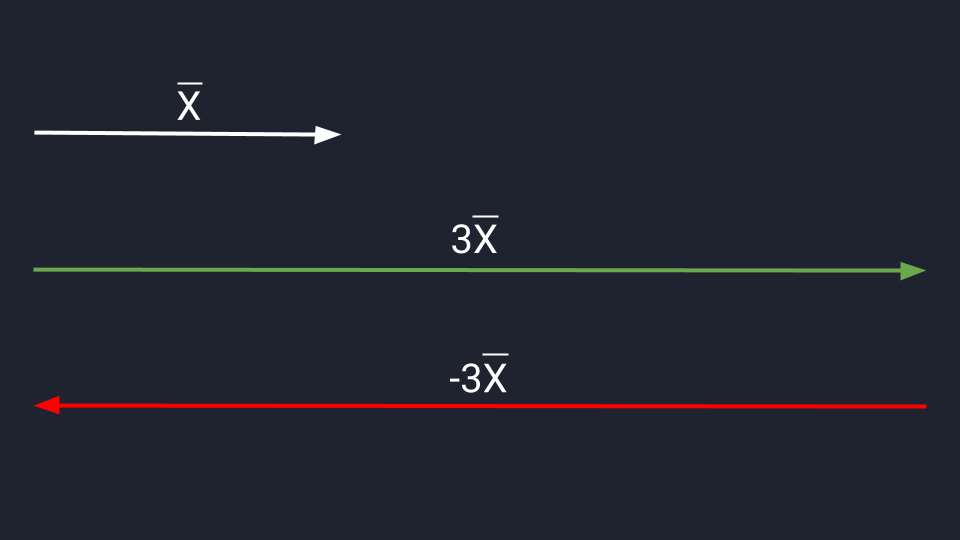
Умножение и деление позволяют изменить длину и направление вектора. Если мы умножим вектор Х на три, то увеличим его длину в три раза. Если умножим на минус три — увеличим длину и изменим его направление на противоположное.

Умножение вектора на число

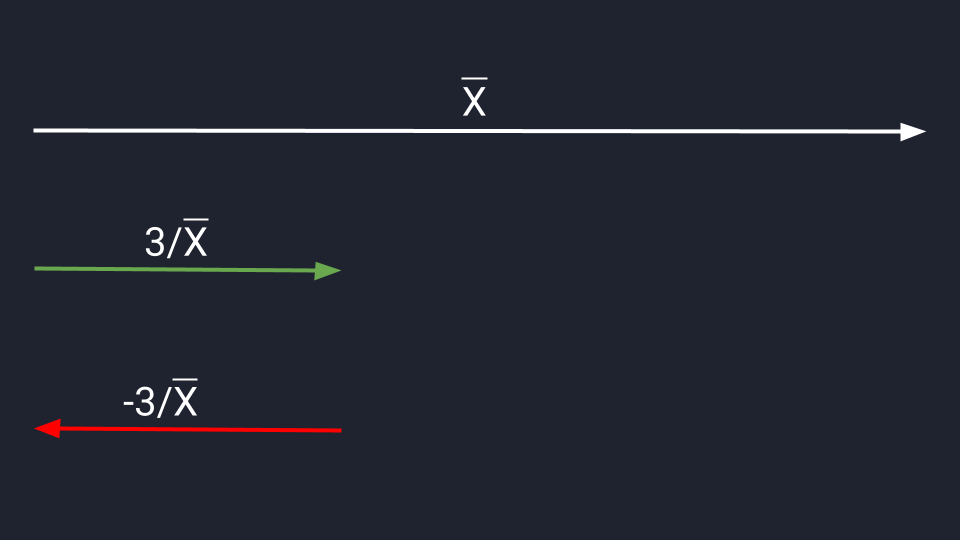
Для деления сохраняются аналогичные правила. Делим вектор Х на три и сокращаем длину в три раза. Делим на минус три — сокращаем и разворачиваем.

Деление вектора на число

Да вроде несложно!

Пока ничего сложного. Но если углубляться, вы узнаете, что:

векторы можно умножать на векторы тремя способами в зависимости от задачи и от того, что мы понимаем под умножением;
если от векторов перейти к матрицам, то перемножение матриц имеет несколько более сложную и довольно неинтуитивную математику;
а перемножение матриц — это и есть машинное обучение.

Что дальше

В следующей статье рассмотрим линейную зависимость векторов. Чтобы не скучать — посмотрите интервью с Анастасией Никулиной. Анастасия сеньор-дата-сайентист в Росбанке и по совместительству блогер с интересной историей.

Как я отказался от вычисления квадратного корня

Очень часто при цифровой обработке сигналов необходимо вычислить длину вектора, обычно это делается по формуле A=SQRТ(X^2+Y^2). Здесь возвести в квадрат значение не сложно, но операция вычисления квадратного корня не является простой операцией, особенно для микроконтроллеров. Кроме того, алгоритмы вычисления корня выполняются не стабильное время, и для алгоритмов, в которых таких вычислений много, становится сложно прогнозировать время, необходимое для вычислений.

С такой задачей столкнулся и я. О том, как я отказался от процедуры вычисления корня, читайте ниже.

Для начала рассмотрим четыре вектора, они лежат в разных четвертях.

Сведем все в одну четверть — в первую. Для этого возьмем координату Y и если она отрицательная, то превратим ее в положительную. В случае если она и так положительная, то оставим все без изменений.

На самом деле, поскольку у меня абсолютные координаты и значения указаны в целых числах без знака, то вычислим модуль.

Если Y>2047, то Y=Y-2047
Если Y 2047, то X=X-2047
Если X X, то угол вектора лежит в области 45-90 градусов, а если Y X, то TEMP=Y, Y=X, X=TEMP (меняем X и Y местами).
Если Y Таблица

Младшее значение 0x800h, что означает 2048. Cтаршее 0xB50, и оно означает 2896.
2896/2048 = 1.414, что соответствует 1/cos(45).

Для получения индекса массива необходимо умножить Y на 2048 и разделить на Х.

Полученный индекс укажет на ячейку массива, из этой ячейки извлекаем значение, умножаем X на него и делим на 2048. Полученный результат есть длина вектора.

Хочу заметить, что деление и умножение на 2048 выполняется сдвигом, и еще одно деление и умножение выполняется специальными командами или алгоритмами, если в используемой платформе нет команд умножения и/или деления.

В моем случае применялся микроконтроллер STM32F103, который имел команды деления и умножения.

Подведем итог алгоритма.

Проверка знака по Y и разворот, если необходимо.
Проверка знака по X и разворот, если необходимо.
Сравнение X и Y и обмен местами, если необходимо.
Проверка X на 0.
Умножение Y на 2048 сдвигом.
Деление Y на X.
Прибавляем полученное значение к адресу массива и читаем значение K.
Умножаем X на K.
Делим X на 2048 сдвигом.

Получившаяся программа на языке ассемблер для STM32F103.

Приведу пример работы алгоритма в сравнении с классическим методом для двух из четырех векторов, которые показаны на изображениях выше.

Возьмем синий вектор (из третьей области).

Его координаты X=-45,Y=-126 (можно проверить по пикселям)

(-45)^2+(-126)^2=2025+15876=17901
SQRT(17901)=133 (усечено до целого)

пункт 1: 2002>2047? -> нет. X=2047-2002=45
пункт 2: 1921>2047? -> нет. Y=2047-1921=126
пункт 3: 126>45 -> да. меняем местами X=126, Y=45
пункт 4: X=0 -> нет. продолжаем
пункт 5: Y=Y*2048, Y=45*2048=92160
пункт 6: I=Y/X, I=92160/126=731
Пункт 7: в таблице 255 строк по 8 значений, ищем 731е значение.
Это 91я строка и 3е значение, которое равно 0x087e, или 2174 в десятичном
виде.
Пункт 8: X=X*2174, X=126*2174=273924
Пункт 9: A=X/2048, A=273924/2048=133 (усечено до целого)

Теперь возьмем зеленый вектор (из четвертой области).

Его координаты X=-170,Y=95 (можно проверить по пикселям).

(-170)^2+(95)^2=28900+9025=37925
SQRT(37925)=194 (усечено до целого)

пункт 1: 1877>2047? -> нет. X=2047-1877=170
пункт 2: 2142>2047? -> да. Y=2142-2047=95
пункт 3: 95>170 -> нет. оставляем как есть.
пункт 4: X=0 -> нет. продолжаем
пункт 5: Y=Y*2048, Y=95*2048=194560
пункт 6: I=Y/X, I=194560/170=1144
Пункт 7: в таблице ищем 1144е значение.
Это 143я строка и 0е значение, которое равно 0x092A, или 2346 в десятичном виде.
Пункт 8: X=X*2346, X=170*2346=398820
Пункт 9: A=X/2048, A=398820/2048=194 (усечено до целого)

Подобный алгоритм можно использовать в ЦОС (как я), например, можно заметно ускорить Быстрое Преобразование Фурье. Также можно использовать в компьютерной графике, где используется трассировка лучей. Возможно и еще есть применение.

Как найти длину вектора

Формула

Чтобы найти длину вектора, заданного своими координатами, нужно извлечь корень квадратный из суммы квадратов его координат. Если вектор задан на плоскости и имеет координаты $bar=left(a_ ; a_right)$, его длина вычисляется по формуле:

Примеры вычисления длины вектора

Задание. Найти длину вектора $bar=(-3 ; 4)$

Решение. Для нахождения длины вектора, заданного на плоскости, воспользуемся формулой

Ответ. $|bar|=5$

Задание. В пространстве заданы точки $A(3 ;-2 ;-1)$ и $ B(1 ; 2 ;-5)$. Найти длину вектора $overline$

Решение. Найдем сначала координаты вектора $overline$. Для этого из координат конца вычислим соответствующие координаты начала, получим:

нахождения длины вектора $overline$ воспользуемся формулой:

Подставляя в эту формулу координаты вектора, получим

Ответ. $|overline|=6$

источники:

http://habr.com/ru/post/496782/

http://www.webmath.ru/poleznoe/formules_13_4.php

Источник

Определение скалярного произведения:

Скалярным произведением двух ненулевых векторов 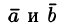называется число, равное произведению длин этих векторов на косинус угла между ними.

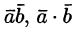
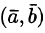
Обозначается (или ). Итак, по определению,

где

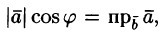
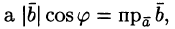
Формуле (6.1) можно придать иной вид. Так как (см. рис. 14), то получаем:

т. е. скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.

Свойства скалярного произведения

1.Скалярное произведение обладает переместительным свойством:

И так как 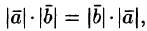как произведение чисел и

2.Скалярное произведение обладает сочетательным свойством относительно скалярного множителя:

3.Скалярное произведение обладает распределительным свойством:

4.Скалярный квадрат вектора равен квадрату его длины:

В частности:

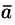
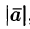
Если вектор возвести скалярно в квадрат и затем извлечь корень, то получим не первоначальный вектор, а его модуль , т. е.

Пример:

Найти длину вектора

Решение:

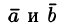
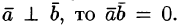
5.Если векторы (ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т. е. если Справедливо и обратное утверждение: если

Так как

Следовательно,

Отсюда 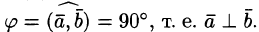В частности:

Выражение скалярного произведения через координаты

Пусть заданы два вектора

Найдем скалярное произведение векторов, перемножая их как многочлены (что законно в силу свойств линейности скалярного произведения) и пользуясь таблицей скалярного произведения векторов i, j, k:

т. e.

Итак, скалярное произведение векторов равно сумме произведений их одноименных координат.

Пример:

Доказать, что диагонали четырехугольника, заданного координатами вершин A(-4;- 4; 4), В(-3;2;2), С(2;5;1), D(3; -2; 2), взаимно перпендикулярны.

Решение:

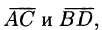
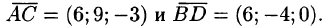
Составим вектора лежащие на диагоналях данного четырехугольника. Имеем: Найдем скалярное произведение этих векторов:

Отсюда следует, что 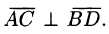Диагонали четырехугольника ABCD взаимно перпендикулярны.

Некоторые приложения скалярного произведения

Угол между векторами

Определение угла (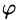 между ненулевыми векторами

Отсюда следует условие перпендикулярности ненулевых векторов

Проекция вектора на заданное направление

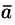
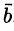
Нахождение проекции вектора на направление, заданное вектором , может осуществляться по формуле

Работа постоянной силы

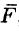
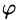
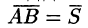
Пусть материальная точка перемещается прямолинейно из положения А в положение В под действием постоянной силы , образующей угол с перемещением (см. рис. 15).

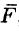
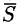
Из физики известно, что работа силы при перемещении равна

Таким образом, работа постоянной силы при прямолинейном перемещении ее точки приложения равна скалярному произведению вектора силы на вектор перемещения.

Пример:

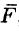
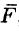
Вычислить работу, произведенную силой =(3; 2; 4), если точка ее приложения перемещается прямолинейно из положения A(2; 4; 6) в положение В (4; 2; 7). Под каким углом к АВ направлена сила ?

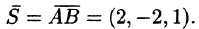
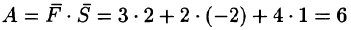
Решение: Находим Стало быть,

(ед. работы).

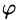
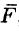
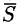
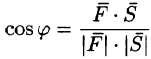
Угол между и находим по формуле т. е.

Скалярное произведение векторов

Смотрите также:

Предмет высшая математика

Решение заданий и задач по предметам:

Математика
Высшая математика
Математический анализ
Линейная алгебра

Дополнительные лекции по высшей математике:

Тождественные преобразования алгебраических выражений
Функции и графики
Преобразования графиков функций
Квадратная функция и её графики
Алгебраические неравенства
Неравенства
Неравенства с переменными
Прогрессии в математике
Арифметическая прогрессия
Геометрическая прогрессия
Показатели в математике
Логарифмы в математике
Исследование уравнений
Уравнения высших степеней
Уравнения высших степеней с одним неизвестным
Комплексные числа
Непрерывная дробь (цепная дробь)
Алгебраические уравнения
Неопределенные уравнения
Соединения
Бином Ньютона
Число е
Непрерывные дроби
Функция
Исследование функций
Предел
Интеграл
Двойной интеграл
Тройной интеграл
Интегрирование
Неопределённый интеграл
Определенный интеграл
Криволинейные интегралы
Поверхностные интегралы
Несобственные интегралы
Кратные интегралы
Интегралы, зависящие от параметра
Квадратный трехчлен
Производная
Применение производной к исследованию функций
Приложения производной
Дифференциал функции
Дифференцирование в математике
Формулы и правила дифференцирования
Дифференциальное исчисление
Дифференциальные уравнения
Дифференциальные уравнения первого порядка
Дифференциальные уравнения высших порядков
Дифференциальные уравнения в частных производных
Тригонометрические функции
Тригонометрические уравнения и неравенства
Показательная функция
Показательные уравнения
Обобщенная степень
Взаимно обратные функции
Логарифмическая функция
Уравнения и неравенства
Положительные и отрицательные числа
Алгебраические выражения
Иррациональные алгебраические выражения
Преобразование алгебраических выражений
Преобразование дробных алгебраических выражений
Разложение многочленов на множители
Многочлены от одного переменного
Алгебраические дроби
Пропорции
Уравнения
Системы уравнений
Системы уравнений высших степеней
Системы алгебраических уравнений
Системы линейных уравнений
Системы дифференциальных уравнений
Арифметический квадратный корень
Квадратные и кубические корни
Извлечение квадратного корня
Рациональные числа
Иррациональные числа
Арифметический корень
Квадратные уравнения
Иррациональные уравнения
Последовательность
Ряды сходящиеся и расходящиеся
Тригонометрические функции произвольного угла
Тригонометрические формулы
Обратные тригонометрические функции
Теорема Безу
Математическая индукция
Показатель степени
Показательные функции и логарифмы
Множество
Множество действительных чисел
Числовые множества
Преобразование рациональных выражений
Преобразование иррациональных выражений
Геометрия
Действительные числа
Степени и корни
Степень с рациональным показателем
Тригонометрические функции угла
Тригонометрические функции числового аргумента
Тригонометрические выражения и их преобразования
Преобразование тригонометрических выражений
Комбинаторика
Вычислительная математика
Прямая линия на плоскости и ее уравнения
Прямая и плоскость
Линии и уравнения
Прямая линия
Уравнения прямой и плоскости в пространстве
Кривые второго порядка
Кривые и поверхности второго порядка
Числовые ряды
Степенные ряды
Ряды Фурье
Преобразование Фурье
Функциональные ряды
Функции многих переменных
Метод координат
Гармонический анализ
Вещественные числа
Предел последовательности
Аналитическая геометрия
Аналитическая геометрия на плоскости
Аналитическая геометрия в пространстве
Функции одной переменной
Высшая алгебра
Векторная алгебра
Векторный анализ
Векторы
Векторное произведение векторов
Смешанное произведение векторов
Операции над векторами
Непрерывность функций
Предел и непрерывность функций нескольких переменных
Предел и непрерывность функции одной переменной
Производные и дифференциалы функции одной переменной
Частные производные и дифференцируемость функций нескольких переменных
Дифференциальное исчисление функции одной переменной
Матрицы
Линейные и евклидовы пространства
Линейные отображения
Дифференциальные теоремы о среднем
Теория устойчивости дифференциальных уравнений
Функции комплексного переменного
Преобразование Лапласа
Теории поля
Операционное исчисление
Системы координат
Рациональная функция
Интегральное исчисление
Интегральное исчисление функций одной переменной
Дифференциальное исчисление функций нескольких переменных
Отношение в математике
Математическая логика
Графы в математике
Линейные пространства
Первообразная и неопределенный интеграл
Линейная функция
Выпуклые множества точек
Система координат

Источник

Вектор – это направленный прямолинейный отрезок, то есть отрезок, имеющий
определенную длину и определенное направление. Пусть точка А – начало вектора, а точка B – его конец, тогда вектор обозначается символом или . Вектор называется противоположным
вектору и может быть
обозначен .

Сформулируем ряд базовых определений.

Длиной
или модулем
вектора  называется
длина отрезка и обозначается . Вектор нулевой длины (его суть — точка) называется нулевым  и направления
не имеет. Вектор единичной длины, называется единичным. Единичный вектор,
направление которого совпадает с направлением вектора , называется ортом вектора  .

Векторы
называются коллинеарными, если они лежат на одной прямой или на
параллельных прямых, записывают. Коллинеарные векторы могут иметь совпадающие или
противоположные направления. Нулевой вектор считают коллинеарным любому
вектору.

Векторы
называются равными , если они коллинеарны, одинаково направлены и имеют
одинаковые длины.

Три вектора в пространстве называются компланарными,
если они лежат в одной плоскости или на параллельных плоскостях. Если среди
трех векторов хотя бы один нулевой или два любые коллинеарны, то такие векторы
компланарны.

Рассмотрим в
пространстве прямоугольную систему координат 0xyz. Выделим на осях координат 0x, 0y, 0z единичные векторы (орты) и
обозначим их через соответственно.
Выберем произвольный вектор

пространства и совместим его начало с началом
координат. Спроектируем вектор
на координатные
оси и обозначим проекции через a_x, a_y, a_z
соответственно. Тогда нетрудно показать, что

. (2.25)

Эта
формула является основной в векторном исчислении и называется разложением
вектора по ортам координатных осей. Числа a_x, a_y, a_z называются координатами вектора . Таким образом, координаты вектора являются его
проекциями на оси координат. Векторное равенство (2.25) часто записывают в
виде

. Мы будем использовать обозначение вектора в фигурных
скобках, чтобы визуально легче различать координаты вектора и координаты точки.
С использованием формулы длины отрезка, известной из школьной геометрии, можно
найти выражение для вычисления модуля вектора

:

, (2.26)

то
есть модуль вектора равен корню квадратному из суммы квадратов его координат.

Обозначим углы между вектором
и осями
координат через α, β, γ соответственно. Косинусы этих углов называются
для вектора направляющими, и для них выполняется соотношение:Верность данного равенства можно показать с помощью
свойства проекции вектора на ось, которое будет рассмотрено в нижеследующем
пункте 4.

Пусть в трехмерном пространстве заданы векторы своими
координатами. Имеют место следующие
операции над ними: линейные (сложение, вычитание, умножение на число и
проектирование вектора на ось или другой вектор); не линейные – различные
произведения векторов (скалярное, векторное, смешанное).

1. Сложение двух векторов производится покоординатно, то
есть если

Данная
формула имеет место для произвольного конечного числа слагаемых.

Геометрически
два вектора складываются по двум правилам:

а) правило треугольника –
результирующий вектор суммы двух векторов соединяет начало первого из них с
концом второго при условии, что начало второго совпадает с концом первого
вектора; для суммы векторов –
результирующий вектор суммы соединяет начало первого из них с концом последнего
вектора-слагаемого при условии, что начало последующего слагаемого совпадает с
концом предыдущего;

б)
правило
параллелограмма (для двух
векторов) – параллелограмм строится на векторах-слагаемых как на сторонах,
приведенных к одному началу; диагональ параллелограмма исходящая из их общего начала, является суммой
векторов.

2. Вычитание двух векторов производится
покоординатно, аналогично сложению, то есть если , то

Геометрически два
вектора складываются по уже упомянутому правилу параллелограмма с учетом того, что разностью векторов
является диагональ, соединяющая концы векторов, причем результирующий вектор
направлен из конца вычитаемого в конец уменьшаемого вектора.

Важным следствием
вычитания векторов является тот факт, что если известны координаты начала и
конца вектора, то для вычисления координат вектора необходимо из координат его конца
вычесть координаты его начала. Действительно, любой вектор пространства может быть
представлен в виде разности двух векторов, исходящих из начала координат: . Координаты векторов и совпадают с
координатами точек А и В, так как начало координат О(0;0;0). Таким образом, по правилу
вычитания векторов следует произвести вычитание координат точки А из координат точки В.

3. Умножение вектора на число λ покоординатно:.

При λ>0
– вектор сонаправлен ; λ<0 – вектор противоположно направлен ; |λ|>1 – длина вектора увеличивается в λ раз; |λ|<1 – длина вектора уменьшается в λ раз.

4. Пусть в пространстве задана
направленная прямая (ось l), вектор задан
координатами конца и начала. Обозначим проекции точек A и B на ось l
соответственно через A’ и B’.

Проекцией вектора на ось l называется длина вектора , взятая со
знаком «+», если вектор и ось l сонаправлены, и со
знаком «–», если и l противоположно направлены.

Если
в качестве оси l взять некоторый другой вектор , то получим проекцию вектора на вектор .

Рассмотрим некоторые
основные свойства проекций:

1) проекция вектора на ось l равна произведению модуля
вектора на косинус угла
между вектором и осью, то есть ;

2.) проекция вектора на ось
положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и
равна нулю, если этот угол – прямой;

3) проекция суммы нескольких
векторов на одну и ту же ось равна сумме проекций на эту ось.

Сформулируем определения и
теоремы о произведениях векторов, представляющих нелинейные операции над
векторами.

5. Скалярным произведением векторов и называется
число (скаляр), равное произведению длин этих векторов на косинус угла φ между
ними, то есть

. (2.27)

Очевидно, что скалярный квадрат любого ненулевого вектора равен квадрату его длины, так как в этом случае угол , поэтому его косинус (в 2.27) равен 1.

Теорема 2.2. Необходимым и достаточным условием
перпендикулярности двух векторов является равенство нулю их скалярного
произведения

Следствие. Попарные скалярные произведения единичных орт равны нулю, то есть

Теорема 2.3. Скалярное произведение двух векторов ,
заданных своими координатами, равно сумме произведений их одноименных координат, то есть

(2.28)

С помощью скалярного произведения векторов можно
вычислить угол между ними.
Если заданы два ненулевых вектора
своими координатами , то косинус угла φ между ними:

(2.29)

Отсюда
следует условие перпендикулярности ненулевых векторов
и :

(2.30)

Нахождение проекции вектора на направление,
заданное вектором , может осуществляться по формуле

(2.31)

С помощью скалярного произведения векторов находят
работу постоянной силы на
прямолинейном участке пути.

Предположим, что под действием постоянной силы материальная точка перемещается прямолинейно из
положения А в положение B. Вектор силы образует угол φ с вектором перемещения (рис. 2.14). Физика утверждает, что работа силы при перемещении
равна .

Следовательно, работа постоянной силы
при прямолинейном перемещении точки ее приложения равна скалярному произведению
вектора силы на вектор перемещения.

Пример
2.9. С
помощью скалярного произведения векторов найти угол при вершине A параллелограмма ABCD, построенного на векторах

Решение. Вычислим модули векторов и их скалярное произведение
по теореме (2.3):

Отсюда согласно формуле (2.29) получим косинус
искомого угла

Пример 2.10. Затраты сырьевых и материальных ресурсов, используемых
на производство одной тонны творога, заданы в таблице 2.2 (руб.).

Какова общая цена этих ресурсов, затрачиваемых на изготовление одной
тонны творога?

Таблица 2.2

Решение. Введем в рассмотрение два вектора: вектор затрат
ресурсов на тонну продукции и вектор цены единицы
соответствующего ресурса .

Тогда . Общая цена
ресурсов , что представляет собой скалярное произведение
векторов . Вычислим его по формуле (2.28) согласно теореме 2.3:

Таким образом, общая цена затрат на производство одной
тонны творога составляет 279 541,5 рублей

Примечание. Действия с векторами, осуществленные в примере 2.10,
можно выполнить на персональном компьютере. Для нахождения скалярного
произведения векторов в MS Excel используют функцию СУММПРОИЗВ( ), где в качестве
аргументов указываются адреса диапазонов элементов матриц, сумму произведений
которых необходимо найти. В MathCAD
скалярное произведение двух векторов выполняется при помощи соответствующего
оператора панели инструментов Matrix

Пример 2.11. Вычислить работу, произведенную силой , если точка ее приложения перемещается прямолинейно
из положения A(2;4;6) в положение A(4;2;7). Под каким углом к AB направлена сила ?

Решение. Находим вектор перемещения, вычитая из координат его конца координаты
начала

. По формуле (2.28) (единиц работы).

Угол φ между и
находим по
формуле (2.29), то есть

6. Три некомпланарных вектора , взятые в указанном порядке, образуют правую
тройку, если при наблюдении из конца третьего вектора кратчайший
поворот от первого вектора ко второму
вектору совершается против часовой стрелки, и левую,
если по часовой стрелке.

Векторным
произведением вектора на вектор называется
вектор , удовлетворяющий следующим условиям:

– перпендикулярен векторам и ;

– имеет длину, равную , где φ – угол, образованный векторами
и ;

– векторы образуют правую
тройку (рис. 2.15).

Теорема 2.4. Необходимым и достаточным
условием коллинеарности двух векторов является равенство нулю их векторного
произведения

Теорема 2.5. Векторное произведение векторов , заданных своими координатами, равно определителю
третьего порядка вида

(2.32)

Примечание. Определитель (2.25)
раскладывается по свойству 7 определителей

Следствие 1. Необходимым и достаточным условием коллинеарности двух
векторов является пропорциональность их соответствующих координат

Следствие 2. Векторные произведения единичных орт равны

Следствие 3. Векторный квадрат любого вектора равен нулю

Геометрическая
интерпретация векторного произведения состоит в том, что длина результирующего
вектора численно равна площади S
параллелограмма, построенного на векторах–сомножителях как на сторонах,
приведенных к одному началу. Действительно, согласно определению, модуль
векторного произведения векторов равен . С другой стороны, площадь параллелограмма,
построенного на векторах и , также равна

. Следовательно,

. (2.33)

Также с помощью векторного произведения можно
определить момент силы относительно точки и линейную скорость вращения.

Пусть в точке A приложена
сила  и пусть O –
некоторая точка пространства (рис. 2.16). Из курса физики известно, что моментом
силы  относительно
точки O называется вектор , который проходит через точку O и удовлетворяет следующим условиям:

— перпендикулярен плоскости, проходящей через точки O, A, B;

— его модуль численно равен произведению силы на плечо .

— образует правую тройку с векторами и .

Следовательно,
момент силы относительно
точки O представляет собой векторное произведение

. (2.34)

Линейная скорость точки М твердого тела, вращающегося с
угловой скоростью вокруг
неподвижной оси, определяется формулой Эйлера , O – некоторая неподвижная

точка оси (рис. 2.17).

Пример 2.12. С помощью
векторного произведения найти площадь треугольника ABC, построенного на векторах
, приведенных к одному началу.

Решение. Найдем векторное произведение заданных векторов по
формуле (2.32).

. Согласно формуле (2.33) модуль векторного
произведения двух неколлинеарных векторов численно равен площади
параллелограмма, построенного на данных векторах как на сторонах, приведенных к
общему началу, то есть . Тогда площадь треугольника
. Следовательно, искомая площадь равна (единиц
площади)

7. Рассмотрим произведение трех векторов , составленное следующим образом: . Здесь первые два вектора перемножаются векторно, а
результирующий вектор – скалярно на третий. Такое произведение называется смешанным
произведением трех векторов
(векторно–скалярным произведением).

Теорема 2.6. Необходимым и достаточным условием компланарности
трех векторов является равенство нулю их смешанного произведения

Теорема 2.7. Если три вектора заданы своими координатами, то их смешанное
произведение представляет собой определитель третьего порядка, составленный из
координат векторов- сомножителей соответственно, то есть

(2.35)

Нетрудно показать, что объем параллелепипеда,
построенного на векторах как на
сторонах, приведенных к общему началу, численно равен модулю смешенного
произведения этих векторов .

Объем треугольной пирамиды, построенной на этих же
векторах, равен

(2.36)

Пример 2.13. Вершинами пирамиды служат точки . Вычислить объем пирамиды.

Решение. Найдем
координаты векторов

. Вычислим смешанное произведение этих векторов:

По формуле (2.36) объем пирамиды, построенной на
векторах равен
(единиц объема)

Рассмотрим очень важный вопрос о
разложении вектора по базису. Приведем
следующие определения.

Система векторов называется
линейно зависимой, если существуют такие числа , хотя бы одно из которых отлично от нуля, что имеет
место равенство

(2.37)

Отсюда всегда можно один из линейно
зависимых векторов выразить через линейную комбинацию остальных. Действительно,
допустим для определенности, что . Тогда на это число разделим равенство (2.37), имеем:

получим выражение вектора через
остальные векторы

Линейно независимыми называют векторы, если равенство
(2.37) выполняется только тогда, когда
все

В системе векторов число линейно
независимых векторов равняется рангу матрицы, которая составлена из координат
этих векторов (смотри раздел I.5).

Базисом n – мерного
пространства E_n называют любую совокупность линейно независимых векторов n – мерного пространства.

Произвольный вектор n
– мерного пространства можно представить
в виде линейной комбинации векторов базиса

таким образом:

Числа
называются координатами
вектора в базисе
векторов .

Линейное пространство называется
конечномерным и имеет размерность n, если в этом
пространстве существует система из n линейно независимых векторов (базис) такая,
что каждое ее расширение приводит к линейной зависимости системы.

Например, в трехмерном пространстве
существует базис единичных орт  такой, что любое расширение этой системы
линейно независимых векторов, то есть каждый вектор  трехмерного
пространства, приводит к линейной зависимости векторов (является линейной
комбинацией орт ): Коэффициенты {x₁, x₂, x₃} такого разложения вектора
по ортам  являются координатами вектора  в трехмерном
пространстве.

Вопросы для самопроверки

Источник

Два вектора

a→

b→

всегда образуют угол.

Угол между векторами может принимать значения от

0°

до

180°

включительно.

Если векторы не параллельны, то их можно расположить на пересекающихся прямых.

Векторы могут образовать:

1. острый угол;

2. тупой угол;

3. прямой угол (векторы перпендикулярны).

Если векторы расположены на параллельных прямых, то они могут образовать:

4. угол величиной

0°

(векторы сонаправлены);

5. угол величиной

180°

(векторы противоположно направлены).

Если один из векторов или оба вектора нулевые, то угол между ними будет равен

0°

Угол между векторами записывают так:

Скалярное произведение векторов

Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними:

a→⋅b→=a→⋅b→⋅cosa→b→ˆ

Результат скалярного произведения векторов является числом (в отличие от результата рассмотренных ранее действий с векторами — сложения, вычитания и умножения на число. В таких случаях результатом был вектор). При умножении вектора на вектор получается число, так как длины векторов — это числа, косинус угла — число — соответственно, их произведение также будет являться числом.

1. Если угол между векторами острый, то скалярное произведение будет положительным числом (так как косинус острого угла — положительное число).

Если векторы сонаправлены, то угол между ними будет равен

0°

, а косинус равен (1), скалярное произведение также будет положительным.

2. Если угол между векторами тупой, то скалярное произведение будет отрицательным (так как косинус тупого угла — отрицательное число).

Если векторы направлены противоположно, то угол между ними будет равен

180°

. Скалярное произведение также отрицательно, так как косинус этого угла равен (-1).

Справедливы и обратные утверждения:

1. Если скалярное произведение векторов — положительное число, то угол между данными векторами острый.

2. Если скалярное произведение векторов — отрицательное число, то угол между данными векторами тупой.

Особенный третий случай!

Обрати внимание!

3. Если угол между векторами прямой, то скалярное произведение векторов равно нулю, так как косинус прямого угла равен (0).

Обратное суждение: если скалярное произведение векторов равно нулю, то эти векторы перпендикулярны.

Вектор, умноженный на самого себя, будет числом, которое называется скалярным квадратом вектора. Скалярный квадрат вектора равен квадрату длины данного вектора и обозначается как

a→2

Свойства скалярного произведения

Для любых векторов и любого числа справедливы следующие свойства:

a→2≥0

, к тому же

a→2>0

, если

a→≠0→

2. Переместительный, или коммутативный, закон скалярного произведения:

a→⋅b→=b→⋅a→

3. Распределительный, или дистрибутивный, закон скалярного произведения:

a→+b→⋅c→=a→⋅c→+b→⋅c→

4. Сочетательный, или ассоциативный, закон скалярного произведения:

k⋅a→⋅b→=k⋅a→⋅b→

Использование скалярного произведения

Удобно использовать скалярное произведение векторов для определения углов между прямыми и между прямой и плоскостью.

Угол между прямыми

Ознакомимся с ещё одним определением.

Вектор называют направляющим вектором прямой, если он находится на прямой или параллелен этой прямой.

Чтобы определить косинус угла между прямыми, надо определить косинус угла между направляющими векторами этих прямых, то есть найти векторы, параллельные прямым, и определить косинус угла между векторами.

Для этого необходимо рассмотреть определение скалярного произведения, если векторы даны в координатной системе.

Если

a→x1;y1;z1

b→x2;y2;z2

, то

a→⋅b→=x1⋅x2+y1⋅y2+z1⋅z2

Прежде была рассмотрена формула определения длины вектора в координатной форме.

Теперь, объединив эти формулы, получим формулу для определения косинуса угла между векторами в координатной форме. Так как из формулы скалярного произведения следует, что

cosα=a→⋅b→a→⋅b→

, то

cosα=x1⋅x2+y1⋅y2+z1⋅z2x12+y12+z12 ⋅x22+y22+z22

Угол между прямой и плоскостью

Введём понятие о нормальном векторе плоскости.

Нормальный вектор плоскости — это любой ненулевой вектор, лежащий на прямой, перпендикулярной к данной плоскости.

Используя следующий рисунок, легко доказать, что косинус угла

между нормальным вектором

n→

данной плоскости и неким вектором

b→

равен синусу угла

между прямой и плоскостью, так как

вместе образуют угол в

90°

При нахождении косинуса угла между

n→

b→

можно использовать это число как синус угла между прямой, на которой лежит вектор

b→

, и плоскостью.

Источник