Как найти кореньиз 2 - Исправление недочетов и поиск решений вместе с Examum.ru

Square root of 2 can be calculated as Square root of any other number. The square root of a number is a positive algebraic expression represented by the symbol ‘√‘ and is written as √x or x^½. Square root of 2 is an irrational number represented as √2 or 2^½. It when multiplied by itself, will result in the number 2. The value of this expression i.e. √2 is 1.414… Its value can’t be determined exactly because it can not be represented as a fraction i.e. in the form of a/b where a and b are integers and b can’t be zero. So, Square root of 2 is considered an irrational number.

Similarly, Is π an irrational number? can be found here.

Value of Square Root of 2

The value of Square root of 2 is widely used in mathematics as 1.414 because it contains an infinite number of decimals. Hence, to make mathematical computations easy, we use only 3 digits after decimal places. Sometimes 99/70 is also used as a value for Square root of 2.

Computing Square Roots

The square root of a number is the value that when multiplied by itself, results in the number taken as input. To compute the square root, we first need to check if the number is a perfect square. Perfect Squares are the numbers, the roots of which are whole numbers. For example, 4, 9, 25, 36, 49, etc. It is easier to compute the square root of a perfect square number as compared to a non-perfect square number. To compute the root of a non-perfect number, we need to apply the formula of the long division method.

How to Calculate the Long Division Method?

To compute the square root of a number using the long division method, go through the steps given below:

Step 1: First we need to divide the number into groups of two starting from right to left.

For example: To compute the value of √132496, we divide the digits into groups like 13, 24, and 96.

Step 2: Now we need to find the highest number that when multiplied by itself results in the number less than or equal to the first pair of digits.

Here, we need a number that when multiplied by itself results in a product ≤ 13. So, the highest number that can be selected is 3.

Step 3: Now compute the remainder and then write the next pair of digits next to the remainder. This will become our dividend for the next step.

Step 4: To create the divisor, first we will multiply the quotient by 2 and write the product as the digit for the tens place of the divisor. For the unit’s place, we will again perform Step 2.

Step 5: Now perform Step 3 and Step 4 again and then again repeat Step 2 to create the divisor. Continue the same until the remainder becomes zero.

The quotient formed will be the square root of the number.

What are irrational numbers
Real Numbers

How to Find Square Root of 2?

It is always easier to compute the square root of perfect squares but to compute the square root of a non-perfect square, we need to perform the long division method. To compute the square root of 2, we need to follow the steps given below:

Step 1: Write 2 as 2.000000 to make it easier to divide

Step 2: Now look for the perfect square less than 2 i.e. 1 and divide the number with it.

Step 3: Now the quotient and the remainder are 1. We will place a decimal in the quotient and bring down the pair of zeroes for further division.

Step 4: Now add the quotient with the existing divisor, this will become the digit at the tens place for our next divisor.

Step 5: For the unit’s place, we need to find a value that can be placed at the unit place of both quotient and the divisor such that the new divisor when multiplied with the unit digit of the quotient results in the highest number less than the remainder.

Now. bring down the next pair of zeros and repeat the steps 4th and 5th. This can be done for infinite steps as the exact value of the square root of 2 goes up to infinite decimal places. We can compute the result up to 4 decimal places as that can be used for approx. value of the square root.

FAQs on Square Root of 2

Question 1: Why is the Square Root of 2 an Irrational Number?

Answer:

2 is a prime number which signifies that pair of 2 does not exist. i.e. √2 can never be written in the form of p/q. Therefore, square root of 2 is irrational.

Question 2: Is the number 2 a Perfect Square?

Answer:

2 is a prime number this implies that the square root of 2 cannot be expressed as a product of two equal integers. Therefore, 2 is not a perfect square.

Question 3: Is 1.414 the exact value of √2?

Answer:

√2 is an irrational number so it cannot be expressed in the form of a proper decimal number. The value of √2 is a non-terminating decimal which is given as

√2 = 1.41421356237309504880168872420969807856967187537694…

But for the sake of calculation, it is taken as 1.414

Question 4: What is the value of √3?

Answer:

√3 is an irrational number so its exact value is never determined. But it can be approximated to √3 = 1.732(approx)

Last Updated :
25 Aug, 2022

Like Article

Save Article

Источник

Для определения квадратного корня из числа 2, необходимо найти такое число, которое было бы корнем такого уравнения:

x² = 2.

График функции √x представляет из себя:

Исходя из данного графика, понятно, что √2 имеет дробное значение, которое находится в промежутке между 1 и 2.

√2 можно вычислить графическим способом, он будет примерно равен 1,4 (для этого нужно провести линии от осей X и Y).

Ещё более точное значение можно получить с помощью формулы в электронных таблицах Microsoft Excel: √2 будет приблизительно =

модератор выбрал этот ответ лучшим

TextExpert
[128K]

6 лет назад

Некоторое положительное число (действительное), которое, будучи умноженным на такое-же, дает 2 — это и будет результат вычисления корня из двух. Целым такое число быть не может — считается, что оно было самым первым иррациональным видом числа, которое стало известно людям. Если обратиться к калькулятору, то оно составит:

Как его запомнить? Есть мнемонические способы, когда запоминается некое стихотворение, каждое слово в котором дает цифру по числу входящих в него букв. Например, так:

Десять лет назад (в 2007 году) был вычислен 200 миллиардный знак после запятой, это делал компьютер, причем долго — всего на 7 часов меньше, чем две недели.

Lunatica
[14.4K]

7 лет назад

Квадратный корень из 2 самому вычислить также тяжело, как из пяти, шести, семи и так далее (то есть невозможно самому подобрать число, которое, если помножить само на себя, получает данную цифру). Получается число 1.41421356237, но приблизительно это 1,41.

Нэпэйшни
[18.2K]

6 лет назад

Квадратный корень из двух это вешественное число при умножении на себя дает число равное 2.Значение этого числа было еще известно 1800—1600 до н. э. Вычисляется корень в виде обыкновенной или десятичнои дроби.Корень из двух равен 1.41421356237

Для этого есть специальные таблицы, где корни большинства простых чисел, представлены готовыми с точностью, обычно до третьего знака после запятой.

Корень 2 (двух) равен 1,414 Именно это число помноженное само на себя даст нам 2 (точнее 1,99)

Красное облако
[248K]

5 лет назад

Если точно, то вот чему равен корень из двух 1,41421356237 (целых одиннадцать цифр, после запятой, для любителей точности и точных цифр), но как правило цифру округляют, то есть, корень из двух равен 1,41-у.

Streight
[21.6K]

6 лет назад

В математике существует не так много чисел, квадратный корень из которых был бы равен целому числу. В ситуации с числом 2, если ее возвести в корень уравнения, то получим число 1 с множеством символов после запятой. Обычно корни из подобных чисел принято округлять. В случае с корнем из числа 2 при округлении до сотых значение будет 1,41

Это сугубо примерное значение и обозначается на носителе, как ~1,41

Nelli4ka
[114K]

6 лет назад

Если округлять до сотых, то корень из двух — это 1,41.

Можно также это число приблизительно представить в виде дроби — 99/70 (где 99 — числитель, а 70 — знаменатель).

Вероятно, корень из двух — это первое иррациональное число, с которым столкнулись древние математики. Так, известно, что корень из двух — это диагональ квадрата, в котором одна сторона (а значит, и все остальные стороны) равна единице.

Galina7v7
[120K]

7 лет назад

Так как первые квадраты в ряду равны 1 и 4 ,то корень из 2 число приблизительное и неточное,и лежит между 1-V1 ,и 2=V4,но ближе к 1 ,та как квадрат лежит ближе к квадрату=1,а не к 4.Еще можно проанализировать относительно квадрата 1,5:1,5^2=2,25что говорит о том,что V2<1,5.Ну далее не обойтись без таблицы или калькулятора:V2=1,4142…=1.41 во всех вычислениях.И это достаточная точность.

[пользователь заблокирован]
[1.4K]

5 лет назад

Чтобы вычислить квадратный корень из 2, нужно определить число, которое при умножении само на себя дает цифру 2.

Все знают, что 1² = 1 и 2² = 4. Поэтому искомое значение является бесконечной десятичной дробью и находится между 1 и 2.

Значение корня из 2 можно легко узнать с помощью таблиц Брадиса.

Если округлять до сотых, то получается, что √2 = 1,41.

Григорий бэха
[0]

3 года назад

Есть проверенный метод если у вас современный телефон то в калькуляторе будет знак корня нажимаем на него ставим(2) и нажимаем равно и получится 1,4142135624

Shurik2015
[5.5K]

7 лет назад

1,41421356237 это равенство корень из 2 (можете перепроверить на всяк случай),хотя где ж вы нашли такое задание?

alexm12
[257K]

7 лет назад

Примерно 1,41…

Там бесконечная непериодическая десятичная дробь получается.

Знаете ответ?

Источник

Извлечем корень квадратный числа «2» или как находить корень второй степени из числа «два». Извлечь на калькуляторе корень квадратный из «двух».

Корень квадратный из 2 равен 1.4142135623731

Как извлечь квадратный корень из двух с примером, онлайн.

Как как находить корень квадратный из числа 2.
Извлечь корень квадратный из 2.

Округлим до десятых корень из 2!
Округлим до сотых корень из 2!

Второй корень квадратный из 2
Разложить число 2 на числа.
Пример как разложить 2 на числа.
Онлайн квадратный корень из 2..

Как как находить корень квадратный из числа 2..

Нам нужно получить корень квадратный из «двух», единственный способ, кроме «разложения на числа»(если число раскладывается), но его нужно тоже знать… поэтому, самый простой способ — это калькулятор!

Что нужно сделать …:

Откройте калькулятор.

Вбиваем число — 2, из которого нужно получить квадратный корень.

Ищем и нажимаем знак квадратного корня.

Получаем квадратный корень из числа «2»:

1.4142135623731

Извлечь корень квадратный из 2.

Извлеченный квадратный корень из числа «два» :

1.4142135623731

Видим, что извлеченный корень квадратный из числа «2» не является целым!

Количество знаков извлеченного корня из числа «2» после запятой:

Проверяем правильность извлечения корня!

Если возвести корень на калькуляторе квадратный во вторую степень 1.4142135623731², то получим 2.Результат: 1.4142135623731 * 1.4142135623731 = 2

Округлим до десятых корень квадратный из «2»!

Округлим полученный корень из «двух» до десятых!
Окргуленение до сотых — это означает, что чисел после запятой будет 1:1.4

Округлим до сотых корень из «2»!

Округлим полученный корень из «двух» до сотых!
Окргуленение до сотых — это означает, что чисел после запятой будет 2:1.41

Как записать корень квадратный из 2.

Можно записывать корень «квадратный» используя знак корня(символ).
Этот символ «√» ставим первым, рядом с ним, справа — число «2» из которого нужно извлечь корень. Третьим… равно и собственно, что получилось :

√ 2 = 1.4142135623731

Используя css знак корня можно стилизовать(здесь подробности).
Порядок записи компонентов выражения аналогична первому пункту!

Чтобы указать степень корня, слева от него ставят степень корня.

Второй корень квадратный из 2.

Помним, что у квадратного корня из «двух» есть второе значением со знаком минус:

— 1.4142135623731 * — 1.4142135623731 = 2

Разложить число 2 на числа.

Давайте разложим число «2» на числа! Число «2» разложится автоматически на числа!
Если число «2» нельзя разложить на числа, то будет соответствующее сообщение.
Как и где проверить, что «2» не раскладывается ? Смотри здесь.

Число 2 — является простым!
Оно делится только на 1 и на себя!
Поэтому… вы не сможете его разложить на числа!
Есть отдельная страница на данную тему… можете проверить самостоятельно!

Пример как разложить 2 на числа.

Рассмотрим разложение на числа на примере

Что значит разложить на числа «2» под корнем?

Не буду рассказывать заново см. здесь.
Но что делать с представленными числами?
Если есть 2 повторяющихся числа, то это число можно вынести за корень.

Например : разложим «2» под корнем!

Смотрим на вторую строчку, там число, которое повторяются.
Под корнем убираем два, и переносим за корень. см. третью строчку!

Онлайн квадратный корень из 2..

Как извлечь корень квадратный из «2» онлайн? Нужно сделать пару действий:

Без калькулятора — никак! Открываем.

Нужно набрать ваше число — 2, из которого хотите получить квадратный корень.

Кликаем знак квадратного корня.

Калькулятор выдаст результат полученный извлечением квадратного корня из числа «2»:

1.4142135623731

Не благодарите, но ссылкой можете поделиться!

COMMENTS+

BBcode

Источник

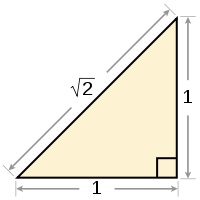
Квадратный корень из 2 равен длине гипотенузы в прямоугольном треугольнике с длиной катетов 1.

Квадратный корень из числа 2 — положительное вещественное число, которое при умножении само на себя даёт число 2. Обозначение: Приведём значение корня из 2 с 65 знаками после запятой:

1,414 213 562 373 095 048 801 688 724 209 698 078 569 671 875 376 948 073 176 679 737 99…

Геометрически корень из 2 можно представить как длину диагонали квадрата со стороной 1 (это следует из теоремы Пифагора). Вероятно, это было первое известное в истории математики иррациональное число (то есть число, которое нельзя точно представить в виде дроби).

Квадратный корень из 2.

Хорошим и часто используемым приближением к sqrt{2} является дробь $tfrac{99}{70}$ . Несмотря на то, что числитель и знаменатель дроби лишь двузначные целые, оно отличается от реального значения меньше, чем на 1/10000.

Система счисления	Оценка числа √2
Иррациональные числа γ — ζ(3) — √2 — √3 — √5 — φ — α — e — π — δ

Двоичная	1.0110101000001001111…
Десятичная	1.4142135623730950488…
Шестнадцатеричная	1.6A09E667F3BCC908B2F…
Непрерывная дробь	$1 + cfrac{1}{2 + cfrac{1}{2 + cfrac{1}{2 + cfrac{1}{2 + ddots}}}}$

Содержание

1 История
2 Алгоритмы вычисления
3 Свойства квадратного корня из двух
4 Доказательство иррациональности
5 Непрерывная дробь
6 Использование в других областях
- 6.1 Размер бумаги
- 6.2 Космические скорости
7 Мнемоническое правило
8 См. также
9 Примечания

[править] История

Вавилонская глиняная табличка с вычислениями в 60-ричной системе: диагональ квадрата, равная 42/60+25/60²+35/60³ (≈0,7071) получается умножением длины стороны квадрата 30 (=1/2 по таблице обратных величин^[1]) на коэффициент 1+24/60+51/60²+10/60³ (≈√2).

Вавилонская глиняная табличка (ок. 1800—1600 до н. э.) даёт приближённое значение sqrt{2} в четырёх шестидесятеричных цифрах, что составляет 8 десятичных цифр:

$1 + frac{24}{60} + frac{51}{60^2} + frac{10}{60^3} = 1.41421overline{296}.$

Другое раннее приближение этого числа в древнеиндийском математическом тексте, Шульба-сутры (ок. 800—200 до н. э.) даётся следующим образом:

$1 + frac{1}{3} + frac{1}{3 cdot 4} - frac{1}{3 cdot4 cdot 34} = frac{577}{408} approx 1.414215686.$

Пифагорейцы обнаружили, что диагональ квадрата несоизмерима с его стороной, или на современном языке, что квадратный корень из двух является иррациональным. Мало что известно с определённостью о времени и обстоятельствах этого выдающегося открытия, но традиционно его авторство приписывается Гиппасу из Метапонта.

[править] Алгоритмы вычисления

Существует множество алгоритмов для вычисления значения квадратного корня из двух. В результате алгоритма получается приблизительное значение sqrt{2} в виде обыкновенной или десятичной дроби. Самый популярный алгоритм для этого, который используется во многих компьютерах и калькуляторах, это вавилонский метод вычисления квадратных корней. Он состоит в следующем:

$a_{n+1} = frac{a_n + frac{2}{a_n}}{2}=frac{a_n}{2}+frac{1}{a_n}.$

Чем больше повторений в алгоритме (то есть, чем больше «n»), тем лучше приближение квадратного корня из двух. Каждое повторение приблизительно удваивает количество правильных цифр. Приведём несколько первых приближений:

3/2 = 1.5
17/12 = 1.416…
577/408 = 1.414215…
665857/470832 = 1.4142135623746…

В 1997 году Ясумаса Канада вычислил значение √2 до 137,438,953,444 десятичных знаков после запятой. В феврале 2007 года рекорд был побит: Шигеру Кондо вычислил 200 миллиардов десятичных знаков после запятой в течение 13 дней и 14 часов, используя процессор 3.6 GHz с 16 ГБ ОЗУ. Среди математических констант только было вычислено более точно.

[править] Свойства квадратного корня из двух

Половина √2 приблизительно равна 0.70710 67811 86548; эта величина даёт в геометрии и тригонометрии координаты единичного вектора,образующего угол 45° с координатными осями:

$frac{sqrt{2}}{2} = sqrt{frac{1}{2}} = frac{1}{sqrt{2}} = cos(45^circ) = sin(45^circ).$

Одно из интересных свойств √2 состоит в следующем:

.Потому что

Это является результатом свойства серебряного сечения.

Другое интересное свойство √2:

Квадратный корень из двух может быть выражен в мнимых единицах i используя только квадратные корни и арифметические операции:

$frac{sqrt{i}+i sqrt{i}}{i}$

и $frac{sqrt{-i}-i sqrt{-i}}{-i}.$

Квадратный корень из 2 является единственным числом, отличным от 1, чья бесконечная тетрация равна его квадрату.

$sqrt{2}^ {sqrt{2}^ {sqrt{2}^ { cdot^ {cdot^ cdot}}}} = 2$

Квадратный корень из двух может быть также использован для приближения π:

$2^msqrt{2-sqrt{2+sqrt{2+cdots+sqrt{2}}}} to pitext{ as }m to infty,$

С точки зрения высшей алгебры, sqrt{2} является корнем многочлена x^2-2 и поэтому является целым алгебраическим числом. Множество чисел вида , где ~a, b — рациональные числа, образует алгебраическое поле. Оно обозначается и является подполем поля вещественных чисел.

[править] Доказательство иррациональности

Применим доказательство от противного: допустим, sqrt{2} рационален, то есть представляется в виде несократимой дроби $frac{m}{n}$ , где и — целые числа. Возведём предполагаемое равенство в квадрат:

$sqrt{2} = frac{m}{n} Rightarrow 2 = frac{m^2}{n^2} Rightarrow m^2 = 2n^2$

Отсюда следует, что m^2 чётно, значит, чётно и . Пусть m=2r , где целое. Тогда

Следовательно, n^2 чётно, значит, чётно и . Мы получили, что и чётны, что противоречит несократимости дроби $frac{m}{n}$ . Значит, исходное предположение было неверным, и sqrt{2} — иррациональное число.

[править] Непрерывная дробь

Квадратный корень из двух может быть представлен в виде непрерывной дроби:

$! sqrt{2} = 1 + cfrac{1}{2 + cfrac{1}{2 + cfrac{1}{2 + cfrac{1}{2 + ddots}}}}.$

Подходящие дроби данной непрерывной дроби дают приближённые значения, быстро сходящиеся к точному квадратному корню из двух. Способ их вычисления прост: если обозначить предыдущую подходящую дробь $frac {m}{n}$ , то последующая имеет вид $frac {m+2 n}{m+n}$ . Скорость сходимости здесь меньше, чем у метода Ньютона, но вычисления гораздо проще. Выпишем несколько первых приближений:

$frac {3}{2}; frac {7}{5}; frac {17}{12}; frac {41}{29}; frac {99}{70}; frac {239}{169}; frac {577}{408}; frac {1393}{985}; frac {3363}{2378} dots$

Квадрат последней приведенной дроби равен (округлённо) 2,000000177.

[править] Использование в других областях

[править] Размер бумаги

Квадратный корень из двух является пропорцией формата бумаги ISO 216. Это соотношение гарантирует, что разрезав лист пополам параллельно к его короткой стороне в результате получатся два листа той же пропорции. Наиболее широко известный формат стандарта ISO — формат A4.

[править] Космические скорости

Вторая космическая скорость v₂ (параболическая скорость) в раза больше первой v₁ (круговой скорость).

[править] Мнемоническое правило

Для того, чтобы запомнить приближенное значение корня из двух, можно заучить фразу «Я Маша, я дура, но я вот взяла корень из двух». Если записать количество букв в каждом слове поговорки, то получатся цифры, составляющие десятичную запись корня из двух.

[править] См. также

Иррациональность
Теорема Виета

[править] Примечания

↑ Выгодский М.Я. § 8. Таблицы обратных величин. Деление // Арифметика и алгебра в древнем мире. — 2-е изд. — М.: Наука, 1967. — С. 113—126.

Источник

Квадратный корень из 2 равен длине гипотенузы в прямоугольном треугольнике с длиной катетов 1.

1,414 213 562 373 095 048 801 688 724 209 698 078 569 671 875 376 948 073 176 679 737 99…

Квадратный корень из 2.

Система счисления	Оценка числа √2
Иррациональные числа γ — ζ(3) — √2 — √3 — √5 — φ — α — e — π — δ

Двоичная	1.0110101000001001111…
Десятичная	1.4142135623730950488…
Шестнадцатеричная	1.6A09E667F3BCC908B2F…
Непрерывная дробь	$1 + cfrac{1}{2 + cfrac{1}{2 + cfrac{1}{2 + cfrac{1}{2 + ddots}}}}$

Содержание

1 История
2 Алгоритмы вычисления
3 Свойства квадратного корня из двух
4 Доказательство иррациональности
5 Непрерывная дробь
6 Размер бумаги
7 См. также

История

Вавилонская глиняная табличка с примечаниями.

$1 + frac{24}{60} + frac{51}{60^2} + frac{10}{60^3} = 1.41421overline{296}.$

$1 + frac{1}{3} + frac{1}{3 cdot 4} - frac{1}{3 cdot4 cdot 34} = frac{577}{408} approx 1.414215686.$

Алгоритмы вычисления

$a_{n+1} = frac{a_n + frac{2}{a_n}}{2}=frac{a_n}{2}+frac{1}{a_n}.$

3/2 = 1.5
17/12 = 1.416…
577/408 = 1.414215…
665857/470832 = 1.4142135623746…

Свойства квадратного корня из двух

$frac{sqrt{2}}{2} = sqrt{frac{1}{2}} = frac{1}{sqrt{2}} = cos(45^circ) = sin(45^circ).$

Одно из интересных свойств √2 состоит в следующем:

.Потому что

Это является результатом свойства серебряного сечения.

Другое интересное свойство √2:

$frac{sqrt{i}+i sqrt{i}}{i}$

и $frac{sqrt{-i}-i sqrt{-i}}{-i}.$

$sqrt{2}^ {sqrt{2}^ {sqrt{2}^ { cdot^ {cdot^ cdot}}}} = 2$

Квадратный корень из двух может быть также использован для приближения π:

$2^msqrt{2-sqrt{2+sqrt{2+cdots+sqrt{2}}}} to pitext{ as }m to infty,$

Доказательство иррациональности

$sqrt{2} = frac{m}{n} Rightarrow 2 = frac{m^2}{n^2} Rightarrow m^2 = 2n^2$

Отсюда следует, что m^2 чётно, значит, чётно и . Пусть m=2r , где целое. Тогда

Непрерывная дробь

Квадратный корень из двух может быть представлен в виде непрерывной дроби:

$! sqrt{2} = 1 + cfrac{1}{2 + cfrac{1}{2 + cfrac{1}{2 + cfrac{1}{2 + ddots}}}}.$

$frac {3}{2}; frac {7}{5}; frac {17}{12}; frac {41}{29}; frac {99}{70}; frac {239}{169}; frac {577}{408}; frac {1393}{985}; frac {3363}{2378} dots$

Квадрат последней приведенной дроби равен (округлённо) 2,000000177.

Размер бумаги

Квадратный корень из двух является пропорцией формата бумаги ISO 216. Соотношение сторон таково, что при разрезании листа пополам параллельно его короткой стороне получатся два листа той же пропорции.

См. также

Иррациональность
Теорема Виета

Источник

Value of Square Root of 2

Computing Square Roots

How to Calculate the Long Division Method?

Read More

How to Find Square Root of 2?

FAQs on Square Root of 2

Как извлечь квадратный корень из двух с примером, онлайн.

Как как находить корень квадратный из числа 2..

Извлечь корень квадратный из 2.

Проверяем правильность извлечения корня!

Округлим до десятых корень квадратный из «2»!

Округлим до сотых корень из «2»!

Как записать корень квадратный из 2.

Второй корень квадратный из 2.

Разложить число 2 на числа.

Пример как разложить 2 на числа.

Что значит разложить на числа «2» под корнем?

Например : разложим «2» под корнем!

Онлайн квадратный корень из 2..

Содержание

[править] История

[править] Алгоритмы вычисления

[править] Свойства квадратного корня из двух

[править] Доказательство иррациональности

[править] Непрерывная дробь

[править] Использование в других областях

[править] Размер бумаги

[править] Космические скорости

[править] Мнемоническое правило

[править] См. также

[править] Примечания

Содержание

История

Алгоритмы вычисления

Свойства квадратного корня из двух

Доказательство иррациональности

Непрерывная дробь

Размер бумаги

См. также