Как найти корни аналитически

Аналитический способ отделения
корней основан на следующей теореме:

Теорема 1.1.

  1. » Если функция F(x), определяющая
    уравнениеF(x)=0, на концах отрезка[a;b]принимает значения разных
    знаков, т.е.F(a)*F(b)<0(3), то на
    этом отрезке содержится, по крайней
    мере, один корень уравнения»[4].

  2. «Если функция F(x)строго монотонна,
    то корень на[a,b]единственный(F’(a)*F’(b)>0 (4)).

Для отделения корней аналитическим
способом выбирается отрезок [A;B], на
котором находятся все интересующие
вычислителя корни уравнения. Причем на
отрезке[A;B]функцияF(x)определена,
непрерывна иF(a)*F(b)<0. Требуется
указать все частичные отрезки[a;b],
содержащие по одному корню.

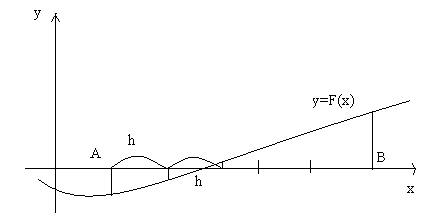
Будем вычислять значение функции F(x),
начиная с точкиx=A, двигаясь вправо
с некоторым шагомh. ЕслиF(x)*F(x+h)<0,
то на отрезке[x;x+h] существует
корень:»[1]

Если F(xk)=0, xk-точный
корень.(5)

На практике данный способ реализуется
следующим образом:например дана
такая задача: на основании найденного
отрезка изоляции (см.графический
способ отделения корней):

  1. доказать существование и единственность
    корня на полученном отрезке с помощью:

    1. Mathcad;

    2. Excel.

  2. отделить корни уравнения cos(2x)+x-5=0аналитическим способом с шагом 1 на
    отрезке [-10;10], используя:

    1. Mathcad;

    2. Excel.

Рассмотрим полученный отрезок изоляции
[5;6].

Для доказательства существования
корня на отрезке изоляции необходимо
выполнить следующие действия:

  1. Запустить MS Excel.

  2. Ввести в ячейки А1, В1 и С1 соответственно
    «x», «y=cos(2x)+x-5» и «ответ».

  3. В А2 и А3 ввести граничные значения
    отрезка изоляции.

  4. В В2 ввести формулу =COS(2*A2)+A2-5 и методом
    протягивания заполнить В3.

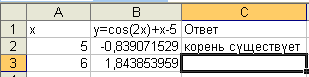
  5. В С2 ввести формулу =ЕСЛИ(B2*B3<0;»корень
    существует»;»корень не существует»).

Таким образом, на отрезке изоляции
корень существует:

Для доказательства единственности
корня на отрезке изоляции необходимо
выполнить следующие действия:

  1. Продолжить работу в том же документе
    MS Excel.

  2. Заполнить D1 и E1 соответственно:
    «y’=-sin(2x)*2+1» и «ответ» (причем выражение
    y’=-sin(2x)*2+1 – это производная первого
    порядка от функции y=cos(2x)+x-5).

  3. Ввести в D2 формулу =-SIN(2*A2)*2+1 и методом
    протягивания заполнить D3.

  4. Ввести в E2 =ЕСЛИ(D2*D3>0;»корень на
    данном отрезке единственный»;»Корень
    не единственный»).

В результате получаем:

Таким образом доказано существование
и единственность корня на отрезке
изоляции.

Чтобы отделить корни уравнения
аналитическим способом с помощью MS
Excel, необходимо выполнить следующее:

  1. Заполнить ячейки A1:D1 соответственно:
    «x», «y=cos(2x)+x-5», «h», «ответ».

  2. В С2 ввести значение 1.

  3. Ввести в А2 значение -10.

  4. Ввести в А3 =A2+$C$2 и методом протягивания
    заполнить ячейки А4:А22.

  5. В В2 ввести =COS(2*A2)+A2-5 и методом протягивания
    заполнить диапазон В3:В22.

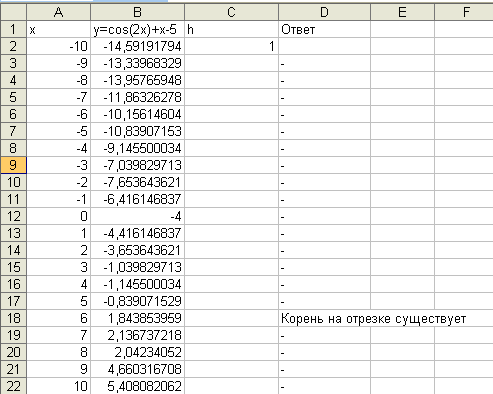
  6. В С3 ввести формулу =ЕСЛИ(B2*B3<0;»Корень
    на отрезке существует»;ЕСЛИ(B3=0;»точный
    корень»;»-«)) и методом протягивания
    заполнить диапазон ячеек С4:С22.

В результате получаем следующее:

Ответ: Корень уравнения существует на
отрезке [5;6].

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #

    17.02.2016593.41 Кб41чм.doc

  • #
  • #
  • #
  • #
  • #
Источник
 

Пусть имеется уравнение вида

f(x)= 0

где f(x) — заданная алгебраическая или трансцендентная функция.

Решить уравнение — значит найти все его корни, то есть те значения x, которые обращают уравнение в тождество.
Если уравнение достаточно сложно, то задача точного определения корней является в некоторых случаях нерешаемой. Поэтому ставится задача найти такое приближенное значение корня xПP, которое отличается от точного значения корня x* на величину, по модулю не превышающую указанной точности (малой положительной величины) ε, то есть

│x* – xпр │< ε

Величину ε также называют допустимой ошибкой, которую можно задать по своему усмотрению.

Этапы приближенного решения нелинейных уравнений

Приближенное решение уравнения состоит из двух этапов:

  • Отделение корней, то есть нахождение интервалов из области определения функции f(x), в каждом из которых содержится только один корень уравнения f(x)=0.
  • Уточнение корней до заданной точности.

Отделение корней

Отделение корней можно проводить графически и аналитически.
Для того чтобы графически отделить корни уравнения, необходимо построить график функции f(x). Абсциссы точек его пересечения с осью Ox являются действительными корнями уравнения.

Для примера рассмотрим задачу решения уравнения
Уравнение
где угол x задан в градусах. Указанное уравнение можно переписать в виде
f(x)=0
Для графического отсечения корней достаточно построить график функции
График функции
Из рисунка видно, что корень уравнения лежит в промежутке x∈(6;8).

Аналитическое отделение корней

Аналитическое отделение корней основано на следующих теоремах.
Теорема 1. Если непрерывная функция f(x) принимает на концах отрезка [a; b] значения разных знаков, т.е.
f(a)f(b)<0
то на этом отрезке содержится по крайней мере один корень уравнения.
Теорема 2. Если непрерывная на отрезке [a; b] функция f(x) принимает на концах отрезка значения разных знаков, а производная f'(x) сохраняет знак внутри указанного отрезка, то внутри отрезка существует единственный корень уравнения f(x) = 0.

Уточнение корней

Для уточнения корней может использоваться один из следующих методов:

  • Метод последовательных приближений (метод итераций)
  • Метод Ньютона (метод касательных)
  • Метод секущих (метод хорд)
  • Метод половинного деления (метод дихотомии)

Метод последовательных приближений (метод итераций)

Метод итерации — численный метод решения математических задач, используемый для приближённого решения алгебраических уравнений и систем. Суть метода заключается в нахождении по приближённому значению величины следующего приближения (являющегося более точным). Метод позволяет получить решение с заданной точностью в виде предела последовательности итераций. Характер сходимости и сам факт сходимости метода зависит от выбора начального приближения решения.
Функциональное уравнение может быть записано в виде
x=f(x)
Функцию f(x) называют сжимающим отображением.

Последовательность чисел x0, x1 ,…, xn называется итерационной, если для любого номера n>0 элемент xn выражается через элемент xn-1 по рекуррентной формуле
xn=f(xn-1)
а в качестве x0 взято любое число из области задания функции f(x).

Реализация на C++ для рассмотренного выше примера
Уравнение
Уравнение может быть записано в форме
x=1/sinx

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

#define _USE_MATH_DEFINES
#include <iostream>
#include <cmath>
using namespace std;
double find(double x, double eps)
{
  double rez; int iter = 0;
  cout << «x0= » << x << » «;
  do {
    rez = x;
    x = 1 / (sin(M_PI*x / 180));
    iter++;
  } while (fabs(rez — x) > eps && iter<20000);
  cout << iter << » iterations» << endl;
  return x;
}
int main() 
{
  cout << find(7, 0.00001);
  cin.get(); 
  return 0;
}

Результат выполнения
Результат метода последовательных приближений

Метод Ньютона (метод касательных)

Если известно начальное приближение x0 корня уравнения f(x)=0, то последовательные приближения находят по формуле
метод Ньютона
Графическая интерпретация метода касательных имеет вид
Метод касательных
Реализация на C++
Для заданного уравнения
метод Ньютона
производная будет иметь вид f'(x)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

#define _USE_MATH_DEFINES
#include <iostream>
#include <cmath>
using namespace std;
double find(double x, double eps)
{
  double f, df; int iter = 0;
  cout << «x0= » << x << » «;
  do {
    f = sin(M_PI*x / 180) — 1 / x;
    df = M_PI / 180 * cos(M_PI*x / 180) + 1 / (x*x);
    x = x — f / df;
    iter++;
  } while (fabs(f) > eps && iter<20000);
  cout << iter << » iterations» << endl;
  return x;
}
int main() 
{
  cout << find(1, 0.00001);
  cin.get(); return 0;
}

Результат выполнения
Метод Ньютона

Метод секущих (метод хорд)

Если x0, x1 — приближенные значения корня уравнения f(x) = 0 и выполняется условие
f(a)f(b)
то последующие приближения находят по формуле
Метод хорд
Методом хорд называют также метод, при котором один из концов отрезка закреплен, т.е. вычисление приближения корня уравнения f(x) = 0 производят по формулам:
Метод секущих
Геометрическая интерпретация метода хорд:
Метод хорд
Реализация на C++
В отличие от двух рассмотренных выше методов, метод хорд предполагает наличие двух начальных приближений, представляющих собой концы отрезка, внутри которого располагается искомый корень.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

#define _USE_MATH_DEFINES
#include <iostream>
#include <cmath>
using namespace std;
double find(double x0, double x1, double eps)
{
  double rez = x1, f0, f;
  int iter = 0;
  cout << «x0= » << x0 << » x1= » << x1 << » «;
  do {
    f = sin(M_PI*rez / 180) — 1 / rez;
    f0 = sin(M_PI*x0 / 180) — 1 / x0;
    rez = rez — f / (f — f0)*(rez — x0);
    iter++;
  } while (fabs(f) > eps && iter<20000);
  cout << iter << » iterations» << endl;
  return rez;
}
int main() 
{
  cout << find(1.0, 10.0, 0.000001);
  cin.get(); return 0;
}

Результат выполнения
Реализация метода хорд

Метод половинного деления (метод дихотомии)

Если x0, x1 — приближенные значения корня уравнения f(x) = 0 и выполняется условие
Метод половинного деления
то последующие приближения находятся по формуле
Метод дихотомии
и вычисляется f(xi). Если f(xi)=0, то корень найден. В противном случае из отрезков выбирается тот, на концах которого f(x) принимает значения разных знаков, и проделывается аналогичная операция. Процесс продолжается до получения требуемой точности.

Геометрическая интерпретация метода дихотомии
Метод дихотомии
Реализация на C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

#define _USE_MATH_DEFINES
#include <iostream>
#include <cmath>
using namespace std;
double func(double x)
{
  return (sin(M_PI*x / 180) — 1 / x);
}
double find(double x0, double x1, double eps)
{
  double left = x0, right = x1, x, fl, fr, f;
  int iter = 0;
  cout << «x0= » << x0 << » x1= » << x1 << » «;
  do {
    x = (left + right) / 2;
    f = func(x);
    if (f > 0) right = x;
    else left = x;
    iter++;
  } while (fabs(f) > eps && iter<20000);
  cout << iter << » iterations» << endl;
  return x;
}
int main() 
{
  cout << find(1.0, 10.0, 0.000001);
  cin.get(); return 0;
}

Результат выполнения
Метод дихотомии
Для численного поиска решения также можно использовать генетические алгоритмы.

Назад: Алгоритмизация

Источник

Численные методы поиска корней алгебраических и трансцендентных уравнений

     Уравнение называется алгебраическим, если его можно представить в виде:

1

    Формула (1.1) – каноническая форма записи алгебраического уравнения. Если уравнение f(x)=0 не удается привести к виду (1.1) заменой переменных, то уравнение называется трансцендентным.

    Решить уравнение означает найти такие значения x , при которых уравнение превращается в тождество.

    Известно, что уравнение (1.1) имеет ровно n корней – вещественных или комплексных. Если n =1, 2, 3 [и иногда 4 (биквадратное уравнение], то существуют точные методы решения уравнения (1.1). Если же n >4 или уравнение – трансцендентное, то таких методов не существует, и решение уравнения ищут приближенными методами. Всюду при дальнейшем изложении будем предполагать, что f(x) – непрерывная функция. Методы, которые мы рассмотрим, пригодны для поиска некратных (то есть изолированных) корней.

1.1 Отделение корня

    Решение уравнения состоит из двух этапов: 1 – отделение корня, 2 – его уточнение.

    Отделить корень – значит указать такой отрезок [a , b] , на котором содержится ровно один корень уравнения f(x)=0.

1

    Не существует алгоритмов отделения корня, пригодных для любых функций f (x). Если удастся подобрать такие a и b , что

                                                                             1) f (a) f(b) < 0                                                    (1.2)

                                                                             2) f ( x ) – непрерывная на [ a , b ] функция        (1.3)

                                                                             3) f ( x ) – монотонная на [ a , b ] функция         (1.4)

то можно утверждать, что на отрезке [a , b] корень отделен.

    Условия (1.2) –(1.4) – достаточные условия того, что корень на [a , b] отделен, то есть если эти условия выполняются, то корень отделен, но невыполнение, например, условий (1.3) или (1.4) не всегда означает, что корень не отделен.

    Корень можно отделить аналитически и графически.

    Пример. Аналитически отделить положительный корень уравнения x3-7x-5=0 Решение. Составим таблицу

x

0

1

2

3

y=x3-7x-5

-5

-11

-11

1

1

Графический метод отделения корня

1 

1

1.2 Уточнение корня методом деления отрезка пополам

    Уточнить корень – значит найти его приближенное значение с заданной погрешностью e .

    Самый простой метод, пригодный для любых непрерывных функций – метод деления отрезка пополам.

    Предположим, что отрезок [a , b], на котором отделен корень уравнения, уже найден.

1

    Пусть, например, f(a)>0, f(b)<0. Вычислим точку x=(a+b)/2. Если вместо корня взять точку x, то погрешность, которую мы при этом допустим, не превысит величины e1=(b-a)/2. Если эта погрешность не превышает некоторую заданную погрешность e , с которой нужно уточнить корень уравнения, то вычисления прекращаем и можно записать: ?=x ±(b-a)/2 . В противном случае определяем новый отрезок [a , b], на котором отделен корень нашего уравнения. Для этого определим знак функции в точке х. В нашем примере f (x )>0. Новый отрезок – отрезок [x , b], так как на концах этого отрезка функция имеет разные знаки. Переобозначим один из концов отрезка – в нашем случае положим a = x — и повторим процедуру для нового отрезка [a , b].

1.3 Метод хорд

    Идея метода состоит в следующем. Проводим прямую через точки с координатами (a ,f(a)), (b ,f(b)). Находим точку пересечения прямой с осью Х. Определяем знак функции в этой точке. Далее проводим прямую через те точки, абсциссы которых содержат корень уравнения ? . Вычисления прекращаются, как только выполнится условие |xn+1-xn|< e .

    Итерационная формула имеет вид:

1

2

1.4 Метод касательных

    Дополнительные предположения: f(x) дважды непрерывно дифференцируема на отрезке [a , b], на котором отделен корень; f'(x) и f»(x) сохраняют постоянные знаки на отрезке [a , b].

    За х0 выбирается точка, в которой выполняется условие

                                                                                 f(x0)f«(x0)>0                                                 (1.6)

    Это либо точка a , либо точка b . Далее вычисляются точки

                                                                                xn+1=xn-f(xn)/f‘(xn)                                        (1.7)

до тех пор, пока не выполнится условие

                                                                                     |xn+1-xn|< e

    Тогда xn+1 — приближенное значение корня с погрешностью e.

3

      Метод касательных можно упростить, если вычисления вести по формуле (1.8):

                                                                         xn+1=xn-f(xn)/f‘(x0)                                    (1.8)

    Производная здесь вычисляется один раз. Сначала проводится касательная к кривой, а затем прямые, параллельные этой касательной. Метод обычно сходится медленнее, чем метод касательных.

3

    Методы хорд и касательных можно объединить, и тогда получится комбинированный метод: с одной стороны к корню мы будем приближаться методом хорд, с другой – методом касательных. Условия сходимости у двух последних методов те же, что и у метода касательных.

3

1.5 Метод итераций

    Уравнение f(x)=0 преобразуется к виду

 x= j (x)                                                          (1.9)

    Например, вместо 5x-ln(x)-sin(x)=0 можно написать x=(ln(x)+sin(x))/5.

    Достаточным условием сходимости метода итераций является

|j‘(x)|<1                 11                                  (1.10)

    Если условие (1.10) выполняется, то формула для расчетов выглядит так:

xn+1= j (xn)                                                       (1.11)

    Вычисления прекращаются, как только выполнится условие

|xn+1-xn|< e

    Тогда корень уравнения ?=xn+1 ±e

1

    Все итерационные методы обладают свойствами «самоисправляемости»: если в процессе вычислений мы допустили ошибку, но не вышли из области сходимости, а в дальнейшем вели вычисления правильно, то корень будет уточнен с заданной погрешностью за конечное число итераций.

Источник

Понравилась статья? Поделить с друзьями:
  • Как по унрз найти
  • Как быстро найти объявление на авито
  • Как найти жену азербайджанку
  • Как найти среднедневной заработок при расчете отпускных
  • Как найти площадь по палетке 4 класс