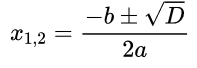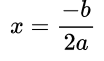Как найти корни дискриминанта по теореме виета

Определение

Уравнение вида ax²+bx+c=0, где a,b,c – любые числа, причем a≠0, называют квадратным уравнением. Числа a,b,c принято называть коэффициентами, при этом a – первый коэффициент, b – второй коэффициент, c – свободный член.

Квадратное уравнение может иметь не более двух корней. Решить такое уравнение – это значит найти все его корни или доказать, что их нет.

Дискриминант

Количество корней квадратного уравнения зависит от такого элемента, как дискриминант (обозначают его буквой D).

Нахождение корней квадратного уравнения

Дискриминант – это такой математический инструмент, который позволяет нам определять количество корней. Он выражается определенной формулой:

D=b²–4ac

• Если D>0, то уравнение имеет два различных корня. Их находят по формуле:

• Если D<0, то уравнение не имеет корней.
• Если D=0, то уравнение имеет два равных корня, их записывают и находят как один:

Рассмотрим решение квадратных уравнений на примерах.

Пример №1. Решить уравнение х²–2х–3=0. Определяем коэффициенты: а=1, b=–2, c=–3. Находим дискриминант: D=b²–4ac=(–2)²–41(–3)=4+12=16. Видим, что дискриминант положительный, значит, уравнение имеет два различных корня, находим их:

Пример №2. Решить уравнение 5х²+2х+1=0. Определяем коэффициенты: а=5, b=2, c=1. D=b²–4ac=2²–4=4–20=–16, D<0, уравнение не имеет корней.

Пример №3. Решить уравнение х²–6х+9=0. Определяем коэффициенты: а=1, b=–6, c=9.

D=b²–4ac=(–6)²–4=36–36=0, D=0, 1 корень

Теорема Виета

Приведенные квадратные уравнения

Среди квадратных уравнений встречаются такие, у которых первый коэффициент равен 1 (обратим внимание на пример 1 и 3), такие уравнения называются приведенными.

Приведенные квадратные уравнения можно решать не только с помощью дискриминанта, но и с помощью теоремы Виета.

Теорема Виета

Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком; произведение корней равно третьему коэффициенту.

х₁+х₂= –b

х₁•х₂= с

Корни с помощью данной теоремы находятся устно способом подбора. Рассмотрим это на примерах.

Пример №4. Решить уравнение х²–10х+21=0. Выпишем коэффициенты: а=1, b=–10, c=21. Применим теорему Виета:

х₁+х₂=–(–10)=10

х₁х₂=21

Начинаем с произведения корней, которое является положительным числом, значит оба корня либо отрицательные, либо положительные. Предполагаем, что это могут быть либо 3 и 7, либо противоположные им числа. Теперь смотрим на сумму, она является положительным числом, поэтому нам подходит пара чисел 3 и 7. Проверяем: 3+7=10, 37=21. Значит, корнями данного уравнения являются числа 3 и 7.

Пример №5. Решить уравнение: х²+5х+4=0. Выпишем коэффициенты: а=1, b=5, c=4. По теореме Виета:

х₁+х₂=–5

х₁х₂=4

Видим, что произведение корней равно 4, значит оба корня либо отрицательные, либо положительные. Видим, что сумма отрицательная, значит, будем брать два отрицательных числа, нам подходят –1 и –4. Проверим:

–1+(–4)=–5

(–1)(–4)=4

Ответ: –1 и –4

Алла Василевская | Просмотров: 13k

Квадратное уравнение

Это уравнение вида ax2+bx+c=0ax^2 + bx + c = 0,

где aa – коэффициент перед x2x^2,

bb – коэффициент перед xx,

cc – свободное число.

Существуют разные способы нахождения корней квадратного уравнения. Пожалуй, самый основной и распространенный способ – через вычисление дискриминанта. В этом случае он рассчитывается по формуле:

D=b2–4acD = b^2 – 4ac

Если второй коэффициент уравнения четный, можно решать уравнение через kk, тогда будет другая формула дискриминанта:

D1=k2–acD_1 = k^2 – ac

Если первый коэффициент уравнения равен 1, то можно воспользоваться теоремой Виета, которая имеет 2 условия:

x1+x2=−bx_1 + x_2 = -b
x1⋅x2=cx_1 cdot x_2 = c

Но если мы захотим решить уравнение основным способом, ошибки не будет. Нахождение корней уравнения через дискриминант – универсальный способ, а остальные введены для удобства вычислений.

Задача 1

Решим уравнение: 3×2+7x−6=0.3x^2 + 7x — 6 = 0.

Обозначим коэффициенты:

a=3a = 3,

b=7b = 7,

c=−6c = -6

Далее находим дискриминант по формуле:

D=b2–4acD = b^2 – 4ac

D=72–4∗3∗(−6)=49+72=121=112D = 7^2 – 4 * 3 * (-6) = 49 + 72 = 121 = {11}^2

D>0D > 0 – значит, уравнение имеет 2 корня.

Находим корни уравнения по следующим формулам:

x1=(−b+√D)/2ax_1 = (-b + √D) / 2a
x2=(−b−√D)/2ax_2 = (-b — √D) / 2a

Подставляем численные значения:

x1=(−7+11)/2∗3=4/6=23x_1 = (-7 + 11) / 2*3 = 4 / 6 = frac{2}{3}

x2=(−7–11)/2∗3=−18/6=−3x_2 = (-7 – 11) / 2*3 = -18 / 6 = -3

Ответ: x1=23x_1 = frac{2}{3}, x2=−3x_2 = -3.

Задача 2

Решим уравнение: −x2+7x+8=0.-x^2 + 7x + 8 = 0.

Обозначим коэффициенты:

a=−1a = -1,

b=7b = 7,

c=8.c = 8.

Далее находим дискриминант по формуле:

D=b2–4acD = b^2 – 4ac

D=72–4⋅(−1)⋅8=49+32=81=92D = 7^2 – 4 cdot (-1) cdot 8 = 49 + 32 = 81 = 9^2

D>0D > 0 – значит, уравнение имеет 2 корня.

Находим корни уравнения по следующим формулам:

x1=(−b+√D)/2ax_1 = (-b + √D) / 2a
x2=(−b−√D)/2ax_2 = (-b — √D) / 2a

Подставляем численные значения:

x1=(−7+9)/2∗(−1)=2/(−2)=−1x_1 = (-7 + 9) / 2 * (-1) = 2 / (-2) = -1
x2=(−7–9)/2∗(−1)=−16/(−2)=8x_2 = (-7 – 9) / 2 * (-1) = -16 / (-2) = 8

Ответ: x1=−1x_1 = -1, x2=8x_2 = 8.

Задача 3

Решим уравнение: 4×2+4x+1=0.4x^2 + 4x + 1 = 0.

Обозначим коэффициенты:
a=4a = 4,

b=4b = 4,

c=1.c = 1.

Далее находим дискриминант по формуле: D=b2–4acD = b^2 – 4ac

D=42–4⋅4⋅1=16–16=0D = 4^2 – 4 cdot 4 cdot 1 = 16 – 16 = 0

D=0D = 0 – значит, уравнение имеет 1 корень.

Находим корень уравнения по следующей формуле: x=−b/2ax = -b / 2a

Подставляем численные значения:

x=−4/2⋅4=−4/8=−1/2=−0,5x = -4 / 2 cdot 4 = -4 / 8 = -1 / 2 = -0,5

Ответ: x=−0,5.x = -0,5.

Задача 4

Решим уравнение: 2×2+x+1=0.2x^2 + x + 1 = 0.

Обозначим коэффициенты:
a=2a = 2,

b=1b = 1,

c=1.c = 1.

Далее находим дискриминант по формуле: D=b2–4acD = b^2 – 4ac

D=12–4∗2∗1=1–8=−7D = 1^2 – 4 * 2 * 1 = 1 – 8 = -7

D<0D < 0 – значит, уравнение корней не имеет.

Ответ: корней нет.

Решение квадратного уравнения через k

Если у квадратного уравнения коэффициент bb четный, то можно решать уравнение через kk, при этом k=12bk = frac{1}{2} b.

Задача 5

Решим уравнение: −x2+2x+8=0.-x^2 + 2x + 8 = 0.

Обозначим коэффициенты:

a=−1a = -1,

b=2b = 2,

c=8c = 8

bb – четное.

k=12b=1k = frac {1}{2} b = 1.

Далее находим дискриминант по формуле: D1=k2–acD_1 = k^2 – ac

D1=12–(−1)∗8=1+8=9=32D_1 = 1^2 – (-1) * 8 = 1 + 8 = 9 = 3^2

D1>0D_1 > 0 – значит, уравнение имеет 2 корня.

Находим корни уравнения по следующим формулам:

x1=(−k+D1)/ax_1 = (-k + {sqrt D}_1) / a
x2=(−k−D1)/ax_2 = (-k — {sqrt D}_1) / a

Подставляем численные значения:

x1=(−1+3)/(−1)=2/(−1)=−2x_1 = (-1 + 3) / (-1) = 2 / (-1) = -2
x2=(−1–3)/(−1)=−4/(−1)=4x_2 = (-1 – 3) / (-1) = -4 / (-1) = 4

Ответ: x_1 = -2, x_2 = 4.

Задача 6

Решим уравнение: 9×2–6x+1=0.9x^2 – 6x + 1 = 0.

Обозначим коэффициенты:
a=9a = 9,

b=−6b = -6,

c=1c = 1

bb – четное.

K=12b=−3.K = frac{1}{2} b = -3.

Далее находим дискриминант по формуле: D1=k2–acD_1 = k^2 – ac

D1=(−3)2–9∗1=9–9=0D_1 = {(-3)}^2 – 9 * 1 = 9 – 9 = 0

D1=0D_1 = 0 – значит, уравнение имеет 1 корень.

Находим корень уравнения по следующей формуле: x=−k/ax = -k / a

Подставляем численные значения:

x=3/9=13x = 3 / 9 = frac{1}{3}

Ответ: x=13.x = frac{1}{3}.

Нахождение корней уравнения по теореме Виета

Если в квадратном уравнении a=1a = 1, то можно найти корни уравнения по теореме Виета.

Задача 7

Найдем корни уравнения: x2+3x+2=0.x^2 + 3x + 2 = 0.

Обозначим коэффициенты:
a=1a = 1,

b=3b = 3,

c=2c = 2.

Запишем 2 условия теоремы Виета:

x1+x2=−bx_1 + x_2 = -b
x1∗x2=cx_1 * x_2 = c

Теперь методом подбора найдем 2 числа, которые будут соответствовать этим условиям. Вероятно, это числа -2 и -1.

Значит, корни уравнения равны:

x1=−2x_1 = -2
x2=−1x_2 = -1

Ответ: x1=−2x_1 = -2, x2=−1x_2 = -1.

Задача 8

Найдем корни уравнения: x2–5x+6=0.x^2 – 5x +6 = 0.

Обозначим коэффициенты:

a=1a = 1,

b=−5b = -5,

c=6c = 6

Запишем 2 условия теоремы Виета:

x1+x2=−bx_1 + x_2 = -b
x1∗x2=cx_1 * x_2 = c

Теперь методом подбора найдем 2 числа, которые будут соответствовать этим условиям. Вероятно, это числа 2 и 3.

Значит, корни уравнения равны:

x1=2x_1 = 2
x2=3x_2 = 3

Ответ: x1=2x_1 = 2, x2=3.x_2 = 3.

Тест по теме «Примеры решения квадратных уравнений»

О квадратных уравнениях в правильном порядке

Как вам преподавали квадратные уравнения в школе? Это был 7-8 класс, примерно. Вероятнее всего, вам рассказали что есть формулы корней через дискриминант, что направление ветвей зависит от старшего коэффициента. Через пару занятий дали теорему Виета. Счастливчикам еще рассказали про метод переброски. И на этом решили отпустить.

Вы довольны такой базой? Вам не рассказали ни геометрический смысл, ни как это получить.

Спустя некоторое время обдумывания сей несправедливости, я решил написать эту статью и тем самым закрыть гештальт о фрагментарности знаний.

Вы не найдете здесь ничего нового по факту, но, возможно, это даст посмотреть на такое простое понятие с другой стороны.

Начнем с конца

Когда я перечислял темы, касающиеся квадратных уравнений, я делал это примерно в том же порядке, в котором изучают их в школе. Но такой порядок не оправдан с точки зрения обучения, и вот почему:

• Дискриминант дается просто как данность (за редким исключением, когда показывают вывод этих формул через приведение к полному квадрату)

• Мощнейшая по своей сути теорема Виета дается в конце и только как эвристический способ решения

Гораздо проще начать с теоремы Виета.

Рассмотрим квадратный трехчлен

В силу основной теоремы алгебры (примем её как данность, так как её действительно тяжело доказать), мы знаем, что у этого уравнения должно быть два корня. Допустим, что это некоторые числа . Тогда можно переписать изначальное уравнение как выражение его корней:

Оба эти уравнения эквиваленты, так как они оба зануляются в (первое по определению , второе по построению).

Раскрывая скобки, мы получим следующее:

Откуда приравняв соответствующие коэффициенты с имеющимися, получим знаменитую систему:

Мы только что доказали теорему Виета на случай квадратного трехчлена. Это потрясающий результат: мы начинаем получать некоторую информацию о корнях, которые, как мы предположили, существуют. И этот результат мы будем использовать далее.

Геометрия параболы

Вершина

Здесь можно было бы рассказать весь первый курс алгебры университета: о фокусах, директрисах, о конических сечениях, первой и второй производной…

Но раз мы ограничились школьной программой (7-8 класс, если быть точным), то и рассуждения у нас будут простые.

Самая, на мой субъективный взгляд, интересная точка параболы – это её вершина. Она уникальным образом задает положение параболе и дает понимание о том, как устроены корни.

Но формулу для нее мы не знаем, до первых понятий о производной нам еще 3 года в среднем. Будем выкручиваться.

Парабола – симметричная фигура. До того момента, как мы сдвинули ее относительно оси , ось служит для нее осью симметрии. Когда же мы начинаем ее сдвигать, становится видно, что она продолжает быть симметричной, но уже относительно оси, проходящей через вершину.

Тогда от вершины в обе стороны до корней равные расстояния, а это значит, что вершина параболы лежит ровно между корнями. Тогда координата вершины это среднее между ее корнями

Пока что мы не знаем наши корни. Но благодаря теореме Виета мы знаем, чему равна сумма корней!

Потрясающий результат, который нам пригодится далее.

Ещё немного про корни

Мы знаем, что корни, графически, это те точки, в которых кривая пересекает ось . Очень полезное знание, учитывая, что смотря на параболу, исключительно визуально, мы понимаем что у нас может быть 3 случая:

1. Корней нет, при этом

   1. Либо значение в вершине больше нуля и старший коэффициент больше нуля

   2. Либо значение в вершине меньше нуля и старший коэффициент меньше нуля

2. Корень один, но кратности 2 (не забываем основную теорему алгебры), и значение в вершине равно нулю

3. Корня два

Второй случай тривиален, до третьего мы еще дойдем. Интересно математически взглянуть на первый. Найдем значение квадратного трехчлена в вершине:

И теперь все же рассмотрим первый случай: парабола висит над осью ветвями вверх.

Домножим первое неравенство на . Учитывая, что , знак неравенства сменится на противоположный:

Это условие, при котором корней нет.

Рассмотрим вкратце противоположный случай: парабола висит под осью ветвями вниз.

Какая-то магия. Получается, что это условие инвариантно относительно положения параболы. Но тем оно лучше.

На данном этапе прошу заметить, что это только условие отсутствия действительных корней. Да, это похоже на дискриминант, но давайте представим, что вы этого не знаете.

Понятие дискриминанта

Мы уже многое поняли о корнях: в какой они связи с коэффициентами, когда они не существуют, каким образом они лежат относительно вершины. Все это безумно полезно, но это все до сих пор не способ найти значения алгебраически.

Давайте будем отталкиваться от того, что мы уже знаем: от вершины. Если бы мы каким-то образом знали расстояние между корнями, то могли бы однозначно найти и сами корни.

Таки что мешает нам это сделать? Но как настоящие математики, давайте находить квадрат расстояния между корнями. Не теряя общности, будем считать, что – больший корень. Тогда

Пока что выглядит не очень, но на что-то это очень сильно похоже. Не видите? Давайте выделим полный квадрат, но по сумме, а не по разности: добавим , но чтобы все осталось в точности так же, это же и вычтем.

Все еще не видите? Воспользуемся снова теоремой Виета:

Мы получили квадрат расстояния между корнями с учетом растяжения коэффициентом .

Так мы теперь можем найти корни! Вершина параболы да половину расстояния между корнями в обе стороны:

Или, немного преобразовав

Квадрат расстояния между корнями квадратного трехчлена и есть дискриминант.

В общем случае, дискриминант — более сложное понятие, связанное с кратными корнями. Но для квадратного уравнения в 7 классе этого достаточно.

Теперь, если рассуждать о дискриминанте как о расстоянии, становится логично и понятно, почему если он равен нулю, то корень всего один; а если отрицательный, то действительных корней вообще нет.

Заключение

Заметьте, что единственное, что мы предположили, что корня два и они существуют. Единственное, что приняли на веру, это основную теорему алгебры. До всего остального мы дошли исключительно умозрительными заключениями и простейшей алгеброй.

Как по мне, это именно то, как должны преподавать эту тему в школе.

Что такое квадратные уравнения?

А теперь подробно с примерами обсудим квадратные уравнения.

Любые уравнения, сводящиеся к виду (ax^2+bx+c=0), называются квадратными. Где буквы ( b,; с) — любые числа, (aneq0). Почему (aneq0) мы обсудим ниже.

Обратите внимание на порядок слагаемых в квадратном уравнении:
(a) — всегда стоит первая и обязательно умножается на (x^2), она называется старшим коэффициентом (или первым);
(b) — принадлежит второму слагаемому и всегда умножается просто на переменную (x), это у нас второй коэффициент;
(c) — называют свободным членом, она не умножается ни на какую переменную.

В дальнейшем старайтесь приводить квадратное уравнение к виду (ax^2+bx+c=0), чтобы слагаемые стояли именно в таком порядке. Это очень важно при решении уравнений, и поможет избежать множества ошибок.

Потренируемся определять значения коэффициентов ( a, ; b,; с), чтобы запомнить порядок:

Пример 1
$$2x^2+3x+4=0;$$
$$a=2 quad b=3 quad c=4.$$

Пример 2
$$5x^2-3x-0,7=0;$$
$$a=5 quad b=-3 quad c=-0,7.$$

Пример 3
$$-x^2+2x+10=0;$$
Минус перед (x^2) можно представить в виде (-x^2=-1*x^2). Единицу обычно не пишут, поэтому минус перед первым слагаемым означает, что (a=-1):
$$a=-1 quad b=2 quad c=10.$$

Пример 4
$$3+x^2-5x=0;$$
Слагаемые стоят в неправильном порядке. Так коэффициенты находить неудобно, поэтому переставим все слагаемые в нужном порядке. От перемены мест слагаемых сумма не меняется:
$$x^2-5x+3=0;$$
$$a=1 quad b=-5 quad c=3.$$

Пример 5
$$2x^2-3x=0;$$
В уравнении нет свободного члена (c), поэтому он будет равен (0):
$$a=2 quad b=-3 quad c=0.$$

Пример 6
$$-4x^2+1=0;$$
А здесь уже нет второго коэффициента (b):
$$a=-4 quad b=0 quad c=1.$$

Уравнения, приведенные в примерах №5 и 6, называются неполными квадратными уравнениями, так как в них коэффициенты (b) или (c) равны нулю.

А вот если в уравнении коэффициенты ( a, ; b,; с) не равны 0, то такое уравнение называется полным.

От того, полное ли квадратное уравнение или неполное, зависит, как мы будем его решать. Начнем с неполных уравнений, они немного легче, но почему-то как раз в них все часто ошибаются.

Неполные квадратные уравнения

Неполное квадратное уравнение — это уравнение, в котором один из коэффициентов (b) или (c) равен нулю, (aneq0).

Как решать квадратное уравнение (ax^2+bx=0)?

Рассмотрим уравнение, в котором (c=0), оно будет иметь вид:
$$ax^2+bx=0;$$
Чтобы его решить, нужно вынести общий множитель (x) за скобки:
$$x(ax+b)=0;$$
И вспомнить правило, что произведение равно нулю, когда хотя бы один из множителей равен нулю. Здесь два множителя: (x) и ((ax+b)). Приравниваем их к нулю и решаем каждое по-отдельности:
$$x=0;$$
Тут решать-то нечего, сразу дан корень.
Второе:
$$ax+b=0;$$
Обычное линейное уравнение:
$$ax=-b;$$
$$x=frac{-b}{a};$$

Получили, что уравнение имеет сразу два корня:(x=0) и (x=frac{-b}{a}).

Разберем на примере:

Пример 7
$$2x^2+8x=0;$$
Выносим общий множитель (x):
$$x(2x+8)=0;$$
$$quad x_1=0 quad и quad 2x+8=0;$$
$$2x+8=0;$$
$$2x=-8;$$
$$x_2=-4.$$
Ответ: (x_1=0 quad и quad x_2=-4.)

Как решать квадратное уравнение (ax^2+с=0)?

Вот с такими уравнениями надо быть очень внимательными. Важно помнить, что любое число (выражение), возведенное в квадрат, всегда больше или равно нуля, оно не может быть отрицательным.

Общая схема решения уравнений вида (ax^2+с=0):

• Выражаем (x^2) из уравнения:
  $$ax^2+c=0;$$
  $$ax^2=-c;$$
  $$x^2=frac{-c}{a};$$
• Если (-frac{c}{a} geq 0):
  $$x_1=sqrt{-frac{c}{a}};$$
  $$x_2=-sqrt{-frac{c}{a}};$$
• Если (-frac{c}{a} lt 0):
  РЕШЕНИЙ НЕТ.

Пример 8
$$2x^2-8=0;$$
$$2x^2=8;$$
$$x^2=frac{8}{2};$$
$$x^2=4;$$
$$x=pmsqrt{4};$$
$$x_1=2;$$
$$x_2=-2;$$
Ответ: (x_1=2 quad и quad x_2=-2.)

Пример 9
$$4x^2+36=0;$$
$$2x^2=-36;$$
$$x^2=frac{-36}{2}=-18;$$
Так как (-18 < 0), а (x^2) не может быть отрицательным, то это уравнение не имеет корней.
Ответ: Нет корней.

Пример 10
$$frac{1}{2}x^2-frac{1}{18}=0;$$
$$frac{1}{2}x^2=frac{1}{18};$$
Чтобы избавиться от (frac{1}{2}), умножим уравнение слева и справа на (2):
$$x^2=frac{2}{18};$$
$$x^2=frac{1}{9};$$
$$x=pmsqrt{frac{1}{9}};$$
$$x_1=frac{1}{3};$$
$$x_2=-frac{1}{3};$$
Ответ: (x_1=frac{1}{3} quad и quad x_2=-frac{1}{3}.)

Решение квадратных уравнений через дискриминант

Квадратные уравнения (ax^2+bx+c=0), у которых все коэффициенты ( a, ; b,; с) не равны 0, называются полными квадратными уравнениями.

Чтобы их решать, нужно уметь находить дискриминант квадратного уравнения. Ничего страшного в этом нет, несмотря на странное называние. Дискриминантом уравнения (ax^2+bx+c=0) называют выражение:
$$D=b^2-4ac;$$

1. Если дискриминант получился больше нуля ((D ge 0)), то квадратное уравнение имеет два корня, которые можно найти по формулам:
   $$x_1=frac{-b+sqrt{D}}{2a};$$
   $$x_2=frac{-b-sqrt{D}}{2a};$$
2. Если дискриминант равен нулю ((D=0)), то квадратное уравнение имеет один корень:
   $$x=frac{-b}{2a};$$
3. Если дискриминант меньше нуля ((D<0)), то квадратное уравнение не имеет корней.

Примеры квадратных уравнений

Пример 11
$$2x^2-9x+4=0;$$
Прежде чем решать уравнение, я рекомендую выписать все коэффициенты:
$$a=2 quad b=-9 quad c=4.$$
Используя значения коэффициентов, можем посчитать дискриминант:
$$D=b^2-4ac=(-9)^2-4*2*4=81-32=49;$$
Ура, дискриминант посчитан и он больше нуля! Значит корней будет два, найдем их по формулам:
$$x_1=frac{-b+sqrt{D}}{2a}=frac{-(-9)+sqrt{49}}{2*2}=frac{9+7}{4}=frac{16}{4}=4;$$
$$x_2=frac{-b-sqrt{D}}{2a}=frac{-(-9)—sqrt{49}}{2*2}=frac{9-7}{4}=frac{2}{4}=frac{1}{2};$$
Ответ: (x_1=4 quad и quad x_2=frac{1}{2}.)

Пример 12
$$10x^2+x-21=0;$$
$$a=10 quad b=1 quad c=-21.$$
$$D=b^2-4ac=1^2-4*10*(-21)=1+840=841;$$
$$x_1=frac{-b+sqrt{D}}{2a}=frac{-1+sqrt{841}}{2*10}=frac{-1+29}{20}=frac{28}{20}=frac{7}{5};$$
$$x_2=frac{-b-sqrt{D}}{2a}=frac{-1-sqrt{841}}{2*10}=frac{-1-29}{20}=frac{-30}{20}=frac{-3}{2};$$
Ответ: (x_1=frac{7}{5} quad и quad x_2=-frac{3}{2}.)

Пример 13
$$(x-7)^2=2x^2+11x+23;$$
Это уравнение еще нужно привести к стандартному виду, для этого раскроем скобки по формуле «квадрат разности» ((a-b)^2=a^2-2ab+b^2):
$$x^2-14x+49=2x^2+11x+23;$$
Перекинем все слагаемые в левую часть, не забывая при этом менять знак на противоположный:
$$x^2-14x+49-2x^2-11x-23=0;$$
Приводим подобные слагаемые:
$$-x^2-25x+26=0;$$
$$a=-1 quad b=-25 quad c=26.$$
$$D=b^2-4ac=(-25)^2-4*(-1)*26=625+104=729;$$
$$x_1=frac{-b+sqrt{D}}{2a}=frac{-(-25)+sqrt{729}}{2*(-1)}=frac{25+27}{-2}=frac{52}{-2}=-26;$$
$$x_2=frac{-b-sqrt{D}}{2a}=frac{-(-25)-sqrt{729}}{2*(-1)}=frac{25-27}{-2}=frac{-2}{-2}=1;$$
Ответ: (x_1=-26 quad и quad x_2=1.)

Пример 14
$$3x^2+7x+6=0;$$
$$a=3 quad b=7 quad c=6.$$
$$D=b^2-4ac=7^2-4*3*6=49-72=-23;$$
Стоп! Дискриминант получился отрицательный, это означает, что у этого квадратного уравнения не будет корней.
Ответ: Нет корней.

Пример 15
$$4x^2-4x+1=0;$$
$$a=4 quad b=-4 quad c=1.$$
$$D=b^2-4ac=(-4)^2-4*4*1=16-16=0;$$
Дискриминат получился равен нулю. В этом случае у квадратного уравнения будет всего один корень, который можно найти по формуле:
$$x=frac{-b}{2a}=frac{-(-4)}{2*4}=frac{4}{8}=frac{1}{2};$$
Ответ: (x=frac{1}{2}.)

Полезно знать! Если дискриминант получился равен нулю, то перед вами формула полного квадрата. Это значит, что квадратный многочлен можно разложить по формуле ((apm b)^2=a^2pm 2ab+b^2).
И пример №15 можно решить, используя эту формулу:
$$4x^2-4x+1=0;$$
$$(2x-1)^2=0;$$
Квадрат равен нулю только в том случае, если выражение под квадратом равно нулю:
$$2x-1=0;$$
$$2x=1;$$
$$x=frac{1}{2};$$
Ответ получили точно такой же, как и при решении через дискриминант.

Дискриминант деленный на 4

Квадратные уравнения иногда удобно решать по упрощенной формуле дискриминанта. Но применять ее можно не во всех случаях, а только, если коэффициент (b) в уравнении (ax^2+bx+c=0) четный (делится на 2).

Итак, представим, что коэффициент (b) четный, тогда дискриминант можно посчитать по формуле:
$$D_4=left(frac{b}{2}right)^2-ac;$$
А корни уравнения находятся по формулам:
$$x_1=frac{-frac{b}{2}+sqrt{D_4}}{a};$$
$$x_2=frac{-frac{b}{2}-sqrt{D_4}}{a};$$
Кстати, обычный дискриминант (D) отличается от (D_4) в 4 раза:
$$D_4=frac{D}{4}=frac{b^2-4ac}{4}=frac{b^2}{4}-frac{4ac}{4}=left(frac{b}{2}right)^2-ac;$$
Поэтому (D_4) называют «дискриминантом деленным на 4».

Эти формулы нужны, чтобы, когда это возможно, сократить вычисления. Разберем на примере:

Пример 16
$$7x^2-20x-1067=0;$$
$$a=7 quad b=-20 quad c=-1067.$$
(b=-20) — четный, поэтому воспользуемся дискриминантом деленным на 4:
$$D_4=left(frac{b}{2}right)^2-ac=left(frac{-20}{2}right)^2-7*(-1067)=(-10)^2+7469=100+7469=7569;$$
$$x_1=frac{-frac{b}{2}+sqrt{D_4}}{a}=frac{-frac{-20}{2}+sqrt{7569}}{7}=frac{10+87}{7}=frac{97}{7};$$
$$x_2=frac{-frac{b}{2}-sqrt{D_4}}{a}=frac{-frac{-20}{2}-sqrt{7569}}{7}=frac{10-87}{7}=frac{-77}{7}=-11;$$
Ответ: (x_1=frac{97}{7} quad и quad x_2=-11.)

Возникает вопрос, зачем вообще нужен этот (D_4), если все можно считать через обычный дискриминант? Если бы мы считали пример №16 как обычно, то наш дискриминант, который и так получился не маленьким — ((D_4=7659)), был бы в четыре раза больше. А чем больше числа, тем сложнее расчеты.

Теорема Виета для решения квадратных уравнений

Теорема Виета — это еще один способ упростить решение полных квадратных уравнений. Ее очень часто используют для решения несложных квадратных уравнений в уме и для анализа квадратного многочлена, особенно это актуально в сложных заданиях с параметром в ЕГЭ.

Прежде чем сформулировать теорему Виета, познакомимся с приведенными квадратными уравнениями.

Приведенное квадратное уравнение

Квадратные уравнения (ax^2+bx+c=0), у которых коэффициент (a) при (x^2) равен (1), называют приведенными.

Например:
$$x^2+4x-3=0;$$
$$x^2-140x-65=0;$$
Любое полное квадратное уравнение всегда можно свести к приведенному. Для этого надо поделить все уравнение на коэффициент (a):

Пример 17
Привести квадратное уравнение к приведенному.
$$3x^2-15x+9=0;$$
Разделим уравнение на (a=3). (Так можно делать: если левую и правую части уравнения поделить на одно и то же число, то корни уравнения от этого не изменятся.)
$$frac{3x^2-15x+9}{3}=frac{0}{3};$$
В результате каждое слагаемое поделится на (3):
$$frac{3x^2}{3}-frac{15x}{3}+frac{9}{3}=0;$$
$$x^2-5x+3=0;$$

Формулы Виета

Сумма корней приведенного квадратного уравнения (x^2+bx+c=0) равна второму коэффициенту (b) со знаком минус, а произведение корней равно свободному члену (c).

Пусть (x_1), и (x_2) — корни квадратного уравнения (x^2+bx+c=0), тогда справедливы формулы:
$$ begin{cases}
x_1+x_2=-b; \
x_1*x_2=c. \
end{cases}$$
На первый взгляд может показаться, что это очень запутанно, но на самом деле, теорема Виета часто помогает решить уравнение в уме. Попробуем на практике:

Пример 18
$$x^2+4x+3=0;$$
$$a=1 quad b=4 quad c=3.$$
Воспользуемся теоремой Виета и выпишем формулы:
$$ begin{cases}
x_1+x_2=-b; \
x_1*x_2=c. \
end{cases}$$
Подставим коэффициенты:
$$ begin{cases}
x_1+x_2=-4; \
x_1*x_2=3. \
end{cases}$$

Нужно найти такие (x_1) и (x_2), которые удовлетворяют и первому, и второму уравнениям в системе. Подобрать корни достаточно просто: рассмотрим второе уравнение, какие два числа дают при умножении (3ку)?

Либо: (3=1*3);
Либо: (3=(-1)*(-3)).

Осталось проверить, будут ли найденные множители удовлетворять первому уравнению в системе, просто подставим их:
$$1+3 neq -4;$$
$$-1+(-3) = -4;$$
Вот мы и нашли корни системы уравнений: (x_1=-1) и (x_2=-3). А самое главное, мы нашли корни исходного квадратного уравнения.
Ответ: (x_1=-1 quad и quad x_2=-3.)

Если потренироваться, то все эти вычисления можно легко проводить в уме, если коэффициенты небольшие. Главное запомнить, что произведение корней должно быть равно свободному члену (c), а сумма корней равна ((-b)).

Теорема Виета, если (aneq1)

По теореме Виета можно решать не только приведенные квадратные уравнения (у которых (a=1)). Но перед тем, как применять формулы Виета, надо привести уравнение к приведенному, поделив на первый коэффициент (a):
$$ax^2+bx+c=0; quad mid :a$$
$$frac{ax^2}{a}+frac{bx}{a}+frac{c}{a};$$
$$x^2+frac{b}{a}*x+frac{c}{a};$$
Получили приведенное квадратное уравнение, для которого можно записать формулы Виета, где вторым коэффициентом будет (frac{b}{a}), а свободным членом (frac{c}{a}):
$$ begin{cases}
x_1+x_2=-frac{b}{a}; \
x_1*x_2=frac{c}{a}. \
end{cases}$$

Пример 19
$$12x^2+x-1=0;$$
$$a=12 quad b=1 quad c=-1.$$
Коэффициент (a=12 neq 1), поэтому разделим все уравнение на (a=12):
$$12x^2+x-1=0; quad mid :12$$
$$x^2+frac{1}{12}x-frac{1}{12}=0;$$
$$a=1 quad b=frac{1}{12} quad c=-frac{1}{12}.$$

Теорема Виета:
$$ begin{cases}
x_1+x_2=-frac{1}{12}; \
x_1*x_2=-frac{1}{12}. \
end{cases}$$

Подбираем корни:
$$x_1=-frac{1}{3};$$
$$x_2=frac{1}{4};$$

Ответ: (x_1=-frac{1}{3} quad и quad x_2=frac{1}{4}.)

Теорема Виета удобна, когда у квадратного уравнения небольшие коэффициенты и можно легко подобрать корни. В остальных случаях лучше пользоваться дискриминантом.

Квадратное уравнение – уравнение вида , где

Числа называются коэффициентами квадратного уравнения.

Квадратное уравнение может иметь два действительных корня, один действительный корень или ни одного.

Количество корней квадратного уравнения зависит от знака выражения, которое называется дискриминант.

Дискриминант квадратного уравнения: .

Если > 0, квадратное уравнение имеет два корня: и .

Если = 0, квадратное уравнение имеет единственный корень .

Если < 0, квадратное уравнение не имеет действительных корней.

Чтобы решать квадратные уравнения, надо уметь:

1. Правильно определять коэффициенты квадратного уравнения.
2. Находить дискриминант и определять количество корней.
3. Находить корни уравнения по формуле.

Определим коэффициенты в следующих квадратных уравнениях.

1)

Коэффициентом является числа:  .

2)

В этом уравнении коэффициенты – это числа:

Обратите внимание на слагаемые и : x — это не коэффициент, а переменная.

3)

А в этом уравнееии нужно быть внимательными, потому что коэффициенты — дробные числа:

Квадратные уравнения вида , в которых коэффициент , называются приведенными.

Запишем несколько квадратных уравнений и проверим, сколько корней они имеют.

Задача 1.

Решение:

В этом уравнении , , .

Дискриминант уравнения равен > 0. Уравнение имеет два корня.

Задача 2.

Решение:

В этом уравнении .

Дискриминант уравнения равен . Уравнение имеет единственный корень.

Заметим, что в левой части уравнения находится выражение, которое называют полным квадратом. В самом деле, . Мы применили формулу сокращенного умножения.

Уравнение имеет единственный корень .

Задача 3.

Решение:

В этом уравнении .

Дискриминант уравнения равен < 0. Корней нет.

Задача 4. Решим уравнение:

Решение:

Дискриминант уравнения равен > 0.

Уравнение имеет два корня.

Корни уравнения:

Задача 5. Решим уравнение:

Решение:

Дискриминант положительный, поэтому уравнение имеет два корня:

Рассмотрим другой пример.

Задача 6.

Дискриминант положительный, уравнение имеет два корня. Находим их по формуле корней квадратного уравнения:

Что делать в том случае, если корень из дискриминанта не является целым числом? Тогда корни квадратного уравнения будут записаны выражением, в котором содержится квадратный корень. Такие выражения называются иррациональными.

Задача 7. Решим уравнение: 

Решение:

Обратите внимание, что слагаемые в правой части записаны не в том порядке, в котором они указаны в общем виде квадратного уравнения. Поэтому, прежде чем начать решать, перепишем уравнение в следующем виде: 

Найдем дискриминант: Уравнение имеет один корень:

Задача 8. И еще одно уравнение: 

Решение:

Найдем дискриминант 

Дискриминант отрицательный, поэтому квадратное уравнение не имеет корней.

Так и запишем в ответе: корней нет.

Теорема Виета

Полезная теорема для решения квадратных уравнений – теорема Виета.

Если и  – корни уравнения , то , .

Теорему Виета удобно использовать, когда коэффициент при равен 1, то есть квадратное уравнение приведенное.

Например,

Коэффициенты этого уравнения . Значит, сумма корней и равна 5, а произведение корней равно 6. Эти два числа подобрать нетрудно, потому что

Тогда

Теорема Виета помогает проверить, правильно ли мы решили квадратное уравнение.

Например, в нашем уравнении сумма корней равна , а произведение корней равно .

Квадратное уравнение можно решить несколькими способами. Можно вычислять дискриминант, или воспользоваться теоремой Виета, а иногда можно просто угадать один из корней. Или оба корня.

Неполные квадратные уравнения

Квадратное уравнение, в котором один из коэффициентов b или с (или они оба) равны нулю, называется неполным. В таких случаях искать дискриминант не обязательно. Можно решить проще.

Задача 9. Рассмотрим уравнение: .

Решение:

В этом уравнении и . Очевидно, – единственный корень уравнения.

Задача 10. Рассмотрим квадратное уравнение: . Здесь , а другие коэффициенты нулю не равны.

Решение:

Проще всего разложить левую часть уравнения на множители по формуле разности квадратов. Получим:

Произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.

Значит,   или

Вот похожее уравнение: .

Поскольку , уравнение можно записать в виде:

Отсюда или
.

Пусть теперь не равно нулю и .

Задача 11.  Рассмотрим квадратное уравнение: .

Левую часть уравнения можно разложить на множители, вынеся за скобки. Получим:

.

Произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.

Значит, или .

Задача 12.  Решим уравнение: .

Разложить по формуле разности квадрата не получится, тогда попробуем перенести слагаемое 4 в правую часть уравнения.

.

Мы знаем, что нет такого действительного числа, квадрат которого был бы отрицательным числом. Значит, уравнение не имеет действительных корней.

Напомним, что решить уравнение – значит найти все его корни или доказать, что их нет.

Разложение квадратного трехчлена на множители

.

Здесь и – корни квадратного уравнения .

Запомните эту формулу. Она необходима для решения квадратичных и дробно-рациональных неравенств.

Например, уравнение

.

Его корни

,

.

.

Полезные лайфхаки для решения квадратных уравнений.

1) Намного проще решать квадратное уравнение, если коэффициент , который умножается на , положителен. Кажется, что это мелочь, да? Но сколько ошибок на ЕГЭ возникает из-за того, что старшеклассник игнорирует эту «мелочь».

Например, уравнение
.

Намного проще умножить его на – 1, чтобы коэффициент стал положительным. Получим:
.

Дискриминант этого уравнения равен
.

Корни уравнения: .

2)Прежде чем решать квадратное уравнение, посмотрите на него внимательно. Может быть, можно сократить обе его части на какое-нибудь не равное нулю число?

Вот, например, уравнение .

Разделим все коэффициенты этого квадратного уравнения на 5. Получим .

Уравнение упростилось. Остается решить его.

Или такое уравнение.

Задача 13.  .

Можно сразу посчитать дискриминант и корни. А можно заметить, что все коэффициенты и делятся на 17. Поделив обе части уравнения на 17, получим:

.

Здесь можно и не считать дискриминант, а сразу угадать первый корень: . А второй корень легко находится по теореме Виета.

3)Работать с дробными коэффициентами неудобно. Например, уравнение
.

Вы уже догадались, что надо сделать. Умножить обе части уравнения на 100! Получим:

.

Корни этого уравнения равны 1 и -6.

Задача 14.  Решим уравнение:

Умножим обе части уравнения на 2. Получим:

.

Теперь решение этого квадратного уравнения можно осуществить с помощью любого уже известного нам способа. Корни этого уравнения -11 и -1.

Смотри также: Квадратичная функция