Задание №12. Уравнения — профильный ЕГЭ по математике
Задание 12 Профильного ЕГЭ по математике – это решение уравнений. Чаще всего, конечно, это тригонометрические уравнения. Но встречаются и другие типы – показательные, логарифмические, комбинированные.
Сейчас задание 12 Профильного ЕГЭ на решение уравнения состоят из двух пунктов: собственно решения и отбора корней на определенном отрезке.
Что нужно знать, чтобы справиться с этой задачей на ЕГЭ? Вот необходимые темы для повторения.
Что необходимо помнить при решении уравнений?
1) Помним про область допустимых значений уравнения! Если в уравнении есть дроби, корни, логарифмы или арксинусы с арккосинусами — сразу записываем ОДЗ. А найдя корни, проверяем, входят они в эту область или нет. Есть в уравнении есть — помним, что он существует, только если
2) Стараемся записывать решение в виде цепочки равносильных переходов.
3) Если есть возможность сделать замену переменной — делаем замену переменной! Уравнение сразу станет проще.
4) Если еще не выучили формулы тригонометрии — пора это сделать! Много формул не нужно. Самое главное — тригонометрический круг, формулы синусов и косинусов двойных углов, синусов и косинусов суммы (разности), понижения степени. Формулы приведения не надо зубрить наизусть! Надо знать, как они получаются.
5) Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.
Например, вы нашли серию решений , где — целое, а найти надо корни на отрезке На указанном промежутке лежит точка . От нее и будем отсчитывать. Получим:
6) Получив ответ, проверьте его правильность. Просто подставьте найденные решения в исходное уравнение!
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
Упростим левую часть по формуле приведения.
Вынесем за скобки. Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.
б) Отметим на тригонометрическом круге найденные серии решений и отрезок
Видим, что указанному отрезку принадлежат решения
Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.
Например, вы нашли серию решений , где — целое, а найти надо корни на отрезке На указанном промежутке лежит точка От нее и отсчитываем.
2. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Это уравнение — комбинированное. Кроме тригонометрии, применяем свойства степеней.
Степени равны, их основания равны. Значит, равны и показатели.
Это ответ в пункте (а).
б) Отберем корни, принадлежащие отрезку
Отметим на тригонометрическом круге отрезок и найденные серии решений.
Видим, что указанному отрезку принадлежат точки и из серии
Точки серии не входят в указанный отрезок.
А из серии в указанный отрезок входит точка
Ответ в пункте (б):
3. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Применим формулу косинуса двойного угла:
Перенесем всё в левую часть уравнения и разложим по формуле разности квадратов.
Обратите внимание: мы отметили серии решений на тригонометрическом круге. Это помогло нам увидеть, как их записать одной формулой.
б) Для разнообразия отберем корни на отрезке с помощью двойного неравенства.
Какой способ отбора корней лучше — с помощью тригонометрического круга или с помощью двойного неравенства? У каждого из них есть «плюсы» и «минусы».
Пользуясь тригонометрическим кругом, вы не ошибетесь. Вы видите и интервал, и сами серии решений. Это наглядный способ.
Зато, если интервал больше, чем один круг, удобнее отбирать корни с помощью двойного неравенства. Например, надо найти корни из серии на отрезке Это больше 10 кругов! Конечно, в таком случае лучше решить двойное неравенство.
4. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Самое сложное здесь — область допустимых значений (ОДЗ). Условие заметно сразу. А условие появляется, поскольку в уравнении есть
Уравнение равносильно системе:
Отберем решения с помощью тригонометрического круга. Нам нужны те серии решений, для которых 
Ответ в пункте а)
б) Отметим на тригонометрическом круге найденные серии решений и отрезок
Как обычно, ориентируемся на начало круга. Видим, что указанному промежутку принадлежат точки
5. а) Решите уравнение
б) Найдите корни, принадлежащие отрезку
Выражение под корнем должно быть неотрицательно, а произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.
Это значит, что уравнение равносильно системе:
Решим эту систему с помощью тригонометрического круга. Отметим на нем углы, для которых или . Заметим, что среди них находятся и углы, для которых
Числа серии не могут быть корнями исходного уравнения, т.к. для этих чисел не выполнено условие . Остальные серии решений нас устраивают.
Тогда в ответ в пункте (а) войдут серии решений:
б) Отберем корни, принадлежащие отрезку любым способом — с помощью тригонометрического круга или с помощью двойного неравенства.
Отбор корней в тригонометрическом уравнение
В этой статье и постараюсь объяснить 2 способа отбора корней в тригонометрическом уравнение: с помощью неравенств и с помощью тригонометрической окружности. Перейдем сразу к наглядному примеру и походу дела будем разбираться.
а) Решить уравнение sqrt(2)cos^2x=sin(Pi/2+x)
б) Найдите все корни этого уравнения, принадлежащие промежутку [-7Pi/2; -2Pi]
Решим пункт а.
Воспользуемся формулой приведения для синуса sin(Pi/2+x) = cos(x)
sqrt(2)cos^2x — cosx = 0
cosx(sqrt(2)cosx — 1) = 0
x1 = Pi/2 + Pin, n ∈ Z
sqrt(2)cosx — 1 = 0
x2 = arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x3 = -arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x2 = Pi/4 + 2Pin, n ∈ Z
x3 = -Pi/4 + 2Pin, n ∈ Z
Решим пункт б.
1) Отбор корней с помощью неравенств
Здесь все делается просто, полученные корни подставляем в заданный нам промежуток [-7Pi/2; -2Pi], находим целые значения для n.
-7Pi/2 меньше или равно Pi/2 + Pin меньше или равно -2Pi
Сразу делим все на Pi
-7/2 меньше или равно 1/2 + n меньше или равно -2
-7/2 — 1/2 меньше или равно n меньше или равно -2 — 1/2
-4 меньше или равно n меньше или равно -5/2
Целые n в этом промежутку это -4 и -3. Значит корни принадлежащие этому промежутку буду Pi/2 + Pi(-4) = -7Pi/2, Pi/2 + Pi(-3) = -5Pi/2
Аналогично делаем еще два неравенства
-7Pi/2 меньше или равно Pi/4 + 2Pin меньше или равно -2Pi
-15/8 меньше или равно n меньше или равно -9/8
Целых n в этом промежутке нет
-7Pi/2 меньше или равно -Pi/4 + 2Pin меньше или равно -2Pi
-13/8 меньше или равно n меньше или равно -7/8
Одно целое n в этом промежутку это -1. Значит отобранный корень на этом промежутку -Pi/4 + 2Pi*(-1) = -9Pi/4.
Значит ответ в пункте б: -7Pi/2, -5Pi/2, -9Pi/4
2) Отбор корней с помощью тригонометрической окружности
Чтобы пользоваться этим способом надо понимать как работает эта окружность. Постараюсь простым языком объяснить как это понимаю я. Думаю в школах на уроках алгебры эта тема объяснялась много раз умными словами учителя, в учебниках сложные формулировки. Лично я понимаю это как окружность, которую можно обходить бесконечное число раз, объясняется это тем, что функции синус и косинус периодичны.
Обойдем раз против часовой стрелки
Обойдем 2 раза против часовой стрелки
Обойдем 1 раз по часовой стрелки (значения будут отрицательные)
Вернемся к нашем вопросу, нам надо отобрать корни на промежутке [-7Pi/2; -2Pi]
Чтобы попасть к числам -7Pi/2 и -2Pi надо обойти окружность против часовой стрелки два раза. Для того, чтобы найти корни уравнения на этом промежутке надо прикидывать и подставлять.
Рассмотри x = Pi/2 + Pin. Какой приблизительно должен быть n, чтобы значение x было где-то в этом промежутке? Подставляем, допустим -2, получаем Pi/2 — 2Pi = -3Pi/2, очевидно это не входит в наш промежуток, значит берем меньше -3, Pi/2 — 3Pi = -5Pi/2, это подходит, попробуем еще -4, Pi/2 — 4Pi = -7Pi/2, также подходит.
Рассуждая аналогично для Pi/4 + 2Pin и -Pi/4 + 2Pin, находим еще один корень -9Pi/4.
Сравнение двух методов.
Первый способ (с помощью неравенств) гораздо надежнее и намного проще для пониманию, но если действительно серьезно разобраться с тригонометрической окружностью и со вторым методом отбора, то отбор корней будет гораздо быстрее, можно сэкономить около 15 минут на экзамене.
http://reshimvse.com/article.php?id=100
Пример:
а) реши уравнение
sinx=cos2x
.
б) Найди все корни этого уравнения, принадлежащие отрезку
2π;7π2
.
a) Уравнение прежде всего иррациональное, поэтому решается возведением обеих частей в квадрат. С учётом области определения получаем:
sinx=cos2x;sinx≥0,cos2x≥0.
Стоит заметить, что рассматривать оба неравенства в системе нам не нужно, так как мы будем решать уравнение. Поэтому можно оставить только одно — более простое неравенство:
sinx=cos2x;(1)sinx≥0.
Решим уравнение системы ((1)). Прежде всего избавимся от двойного угла в уравнении:
sinx=cos2x;sinx−cos2x=0;sinx−(cos2x−sin2x)=0;sinx−(1−sin2x−sin2x)=0;sinx−(1−2sin2x)=0;2sin2x+sinx−1=0;sinx=−1,sinx=12.
(sin x= -1) исключаем, так как это значение не входит в область определения, а решения второго уравнения обозначим на тригонометрической окружности.
Рис. (1). Решения уравнения на единичной окружности
Эти решения можно записать в виде:
x=π6+2πn,n∈ℤ,x=5π6+2πm,m∈ℤ.
б) Рассмотрим три способа отбора корней, попадающих в отрезок
2π;7π2
.
(1) способ:
вернёмся к единичной окружности. Отметим на ней дугу, соответствующую указанному промежутку, подпишем начало и конец, отметим точки окружности, представляющие серии решений и принадлежащие дуге, укажем их значения, принадлежащие промежутку.
2π+π6=13π6,2π+5π6=17π6.
Рис. (2). Отбор корней с помощью единичной окружности
Обрати внимание!
Нельзя отмечать и подписывать посторонние точки на окружности!
(2) способ:
указанный отрезок соответствует неравенству
2π≤x≤7π2
. Подставим в него полученные корни:
| 2π≤π6+2πn≤7π2,n∈ℤ:π;2≤16+2n≤72,n∈ℤ−16;2−16≤2n≤72−16,n∈ℤ;116≤2n≤206,n∈ℤ:2;1112≤n≤2012,n∈ℤ;1112≤n≤1812,n∈ℤ;n=1;π6+2π⋅1=13π6 | 2π≤5π6+2πm≤7π2,m∈ℤ:π;2≤56+2m≤72,m∈ℤ−56;2−56≤2m≤72−56,m∈ℤ;76≤2m≤166,m∈ℤ:2;712≤m≤1612,m∈ℤ;712≤m≤1412,m∈ℤ;m=1;5π6+2π⋅1=17π6 |
Обрати внимание!
Обязательно выдели целые части дробей для оценки значений (n) и (m)!
(3) способ:
разместим корни уравнения на числовой прямой. Сначала отметим корни, подставив вместо (n) и (m) (0), а потом добавим к каждому корню периоды. На числовой прямой должен быть выделен заданный отрезок, обозначены его концы, отмечены все последовательные значения серий корней, начиная с точек, расположенных левее промежутка, и заканчивая точками, расположенными правее промежутка.
Рис. (3). Отбор корней с помощью координатной прямой
Нам останется только выбрать корни, которые попали в нужный нам отрезок.
Ответ: а)
π6+2πn,n∈ℤ;5π6+2πm,m∈ℤ
; б)
13π6,17π6.
Рекомендуем при решении тригонометрических уравнений использовать несколько разных способов отбора. Это поможет тебе убедиться в правильности отбора корней и выработать навык выбора наиболее удобного способа.
Источники:
Рис. 1. Решения уравнения на единичной окружности. © ЯКласс.
Рис. 2. Отбор корней с помощью единичной окружности. © ЯКласс.
Рис. 3. Отбор корней с помощью координатной прямой. © ЯКласс.
Как решать задание 13
О чем задача?
Задачи на решение тригонометрических уравнений, более сложных, чем в задании 5. В большинстве задач требуется не только решить уравнение, но и отобрать корни, принадлежащие определенному отрезку.
Как решать?
Шаг 1. Найдите область определения
Шаг 2. Приведите уравнение к виду простейших тригонометрических уравнений
Для того чтобы привести уравнение к виду простейших тригонометрических уравнений, применяйте следующие стандартные приемы:
Мы свели исходное уравнение к совокупности простейших тригонометрических уравнений [ cos x = − 1 , cos x = − 1 2 . left[begin cos x = -1 <,>\cos x = -frac<1> <2><.>endright. [ cos x = − 1 , cos x = − 2 1 .
Шаг 3. Решите простейшие тригонометрические уравнения
О решении простейших тригонометрических уравнений читайте в отдельной статье .
Убедитесь, что найденные вами корни принадлежат области определения уравнения.
Остается решить уравнение cos x = − 1 2 cos x =-frac<1> <2>cos x = − 2 1 .
Шаг 4. Выберите корни, принадлежащие отрезку, данному в условии
Корни, принадлежащие данному в условии отрезку, можно найти либо методом перебора, либо путем решения неравенства относительно k k k .
Найдем подходящие корни методом перебора. Для этого рассмотрим две серии корней по отдельности.
Способы отбора корней в тригонометрических уравнениях
Класс: 10
Автор проекта:
Шелкова Полина,
Класс: 10
Руководитель:
Злобова Людмила Викторовна,
учитель математики
ВВЕДЕНИЕ
Слово «тригонометрия» греческое, оно переводится как «измерение треугольников» (τρίγονον — «тригон» — треугольник и μετρειν — «метрео» — измеряю).
Тригонометрия, как и всякая другая наука, выросла из практической деятельности человека. Потребности развивающегося мореплавания, для которого требовалось умение правильно определять курс корабля в открытом море по положению небесных светил, оказали большое влияние на развитие астрономии и тесно связанной с ней тригонометрией. Предполагают, что основополагающее значение для развития тригонометрии в эпоху ее зарождения, имели работы древнегреческого астронома Гиппарха Никейского (180-125 лет до н. э.) (прил. №3). Систематическое использование полной окружности в 360° установилось в основном благодаря Гиппарху и его таблице хорд (прил. №2). Т.е. таблицы, которые выражают длину хорды для различных центральных углов в круге постоянного радиуса, что является аналогом современных таблиц тригонометрических функций. Впрочем, до нас не дошли оригинальные таблицы Гиппарха, как и почти все, что им написано. И мы, можем составить себе о них представление главным образом по сочинению «Великое построение» или «Альмагесту» знаменитого астронома Клавдия Птолемея, жившего в середине II века н.э.
Несмотря на то, что в работах ученых древности нет «тригонометрии» в строгом смысле этого слова, но по существу они, пользуясь известными им средствами элементарной геометрии, решали те задачи, которыми занимается тригонометрия. Например, задачи на решение треугольников (определение всех сторон и углов треугольника по трем его известным элементам), теоремы Евклида и Архимеда представленные в геометрическом виде, эквивалентны специфическим тригонометрическим формулам. Главным достижением средневековой Индии стала замена хорд синусами. Это позволило вводить различные функции, связанные со сторонами и углами прямоугольного треугольника. Таким образом, в Индии было положено начало тригонометрии, как учению о тригонометрических величинах.
Учёные стран Ближнего и Среднего Востока с VIII века развили тригонометрию своих предшественников. Уже в середине IX века среднеазиатский учёный аль-Хорезми написал сочинение «Об индийском счёте». После того, как трактаты мусульманских ученых были переведены на латынь, многие идеи греческих, индийских и мусульманских математиков стали достоянием европейской, а затем и мировой науки. В дальнейшем потребности географии, геодезии, военного дела, способствовали развитию тригонометрии. Особенно усиленно шло ее развитие в средневековое время. Большая заслуга в формировании тригонометрии как отдельной науки принадлежит азербайджанскому ученому Насир ад-Дину ат-Туси (1201-1274), написавшему «Трактат о полном четырехстороннике». Творения ученых этого периода привели к выделению тригонометрии как нового самостоятельного раздела науки. Однако в их трудах еще не была введена необходимая символика. Современный вид тригонометрия получила в трудах Леонарда Эйлера (1707-1783). На основании трудов Эйлера были составлены учебники тригонометрии, излагавшие ее в строгой научной последовательности (прил. №4). Тригонометрические вычисления применяются во многих областях человеческой деятельности: в геометрии, в физике, в астрономии, в архитектуре, в геодезии, инженерном деле, в акустике, в электронике и т.д.
I РАЗДЕЛ (теоретический)
Тема проекта и её актуальность: почему я выбрала тему «Способы отбора корней в тригонометрических уравнениях»?
- Расширить и углубить свои знания, полученные в курсе геометрии 8-9 класса.
- Тригонометрические уравнения рассматриваются в курсе алгебры и начал математического анализа 10-11 класса.
- Тригонометрические уравнения включены в КИМы ЕГЭ по математике.
Решение тригонометрических уравнений и отбор корней, принадлежащих заданному промежутку — это одна из сложнейших тем математики, которая выносится на Единый Государственный Экзамен. По результатам анкетирования многие учащиеся затрудняются или вообще не умеют решать тригонометрические уравнения и особенно затрудняются в отборе корней, принадлежащих промежутку. Немаловажно также знать, тригонометрические формулы, табличные значения тригонометрических функций для решения целого ряда заданий Единого Государственного Экзамена по математике.
Цель проекта: изучить способы отбора корней в тригонометрических уравнениях и выбрать для себя наиболее рациональные подходы для качественной подготовки к ЕГЭ.
Задачи:
- познакомиться с историческими сведениями о возникновении тригонометрии, как науки;
- изучить соответствующую литературу;
- научиться решать тригонометрические уравнения;
- найти теоретический материал и изучить методы отбора корней в тригонометрических уравнениях;
- научиться отбирать корни в тригонометрических уравнениях, принадлежащим заданному промежутку;
- подготовиться к ЕГЭ по математике.
Приёмы отбора корней тригонометрического уравнения на заданном промежутке.
При решении тригонометрических уравнений предлагается провести отбор корней из множества значений неизвестного. В тригонометрическом уравнении отбор корней можно осуществлять следующими способами: арифметическим, алгебраическим, геометрическим и функционально-графическим.
Арифметический способ отбора корней состоит в непосредственной подстановке полученных корней в уравнение, учитывая имеющиеся ограничения, при переборе значений целочисленного параметра.
Алгебраический способ предполагает составление неравенств, соответствующих дополнительным условиям, и их решение относительно целочисленного параметра.
Геометрический способ предполагает использование при отборе корней двух вариантов: тригонометрической окружности или числовой прямой. Тригонометрическая окружность более удобна, когда речь идет об отборе корней на промежутке или в случае, когда значение обратных тригонометрических функций, входящих в решения, не являются табличными. В остальных случаях предпочтительнее модель числовой прямой. Числовую прямую удобно использовать при отборе корней на промежутке, длина которого не превосходит 2 или требуется найти наибольший отрицательный или наименьший положительный корень уравнения.
Функционально-графический способ предполагает отбор корней осуществлять с использование графиков тригонометрических функций. Чтобы использовать данный способ отбора корней, требуется умение схематичного построения графиков тригонометрических функций.
II РАЗДЕЛ (практический)
Покажу практически три наиболее эффективных и рациональных, с моей точки зрения, метода отбора корней на примере решения следующего тригонометрического уравнения:
sinx−cos2x=0; [применили формулу двойного угла: cos2x = cos 2 x−sin 2 x]
sinx−(cos 2 x−sin 2 x)=0;
sinx−(1−sin 2 x−sin 2 x)=0;
Введем новую переменную: sinx = t, -1 ≤ t ≤1, получим
Вернемся к замене:
б) Рассмотрим три способа отбора корней, попадающих в отрезок 
1 способ: обратимся к единичной окружности. Отметим на ней дугу, соответствующую указанному отрезку, т.е. выполним отбор корней арифметическим способом и с помощью тригонометрической окружности:
2 способ: указанный отрезок соответствует неравенству: Подставим в него полученные корни:
3 способ: разместим корни уравнения на числовой прямой. Сначала отметим корни, подставив вместо n, и нуль (0), а потом добавим к каждому корню периоды.
Нам останется только выбрать корни, которые попали в нужный нам отрезок.
ЗАКЛЮЧЕНИЕ
При работе над моим проектом я изучила методы решения тригонометрических уравнений и способы отбора корней тригонометрических уравнений. Выяснила для себя положительные и отрицательные моменты. При апробации этих подходов в отборе корней тригонометрического уравнения, понимаешь, что каждый из этих способов удобен по-своему в том или ином случае. Например, алгебраический способ (решение неравенством) наиболее эффективен, когда промежуток для отбора корней достаточно большой, в тоже время он дает практически стопроцентное нахождение целочисленного параметра для вычисления корней, а применение арифметического способа приводит к громоздким вычислениям. При отборе корней уравнения, удовлетворяющих дополнительным условиям, т.е. когда корни уравнения принадлежат заданному промежутку, мне проще и нагляднее получить корни с помощью тригонометрической окружности, а проверить себя можно арифметическим способом. Замечу, что при решении тригонометрических уравнений трудности, связанные с отбором корней, возрастают, если в уравнении приходится учитывать ОДЗ. Как показывает практика и анкетирование моих одноклассников, из четырёх возможных методов отбора корней тригонометрического уравнения по дополнительным условиям, наиболее предпочтительным является отбор корней по окружности. Анкетирование проходили 12 респондентов, изучающих тригонометрию (прил. №5). Большинство из них отвечали, что этот раздел математики достаточно сложный: большой объем информации, очень много формул, табличных значений, которые нужно знать и уметь применять на практике. Еще как одна из проблем — небольшое количество времени, отведенное на изучение этого сложного раздела математики. И я разделяю их мнение. При такой сложности, многие считают, что тригонометрия важный раздел математики, который находит применение в других науках и практической деятельности человека.
СПИСОК ЛИТЕРАТУРЫ
- Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс: учеб для общеобразоват. организаций: базовый и углубленный уровни/ [С.М.Никольский, М.К.Потапов, Н.Н.Решетников и др.]-3 -е изд.- М.: Просвещение, 2016.
- Алгебра и начала математического анализа: Учеб для 10-11 кл.общеобразоват. организаций / А.Н.Колмогоров, А.М.Абрамов, Ю.П.Дудницин и др. под редакцией А.Н.Колмогорова — М. Просвещение, 2017.
- С.В Кравцев и др. Методы решения задач по алгебре: от простых до самых сложных — М: Издательство: «Экзамен», 2005.
- Корянов А.Г., Прокофьев А.А. — Тригонометрические уравнения: методы решения и отбор корней. — М.: Математика ЕГЭ, 2012.
источники:
http://urok.1sept.ru/articles/687140
Отбор корней с помощью тригонометрического круга
В заданиях, где требуется отобрать корни тригонометрического уравнения, принадлежащие определенному числовому промежутку, можно использовать тригокруг. Этот метод отбора корней является наиболее распространенным. Его плюсы заключаются в том, что это визуальный метод, т. е. отбор корней происходит наглядно, но у этого есть и свои недостатки – углов бесконечное множество, из которых только 360° можно визуализировать на тригокруге, поэтому может возникнуть путаница с количеством оборотов по нему.
«ОБОРОТЫ» ПО ТРИГОКРУГУ И СООТВЕТВЕТСТВУЮЩИЕ ИМ УГЛЫ:
АЛГОРИТМ ОТБОРА КОРНЕЙ С ПОМОЩЬЮ ТРИГОКРУГА
-
Отмечаем получившийся угол на тригокруге. Это будет серия ответов – бесконечное количество углов, визуально находящееся на тригокруге в одной точке.
-
Отмечаем нужную дугу, т. е. обозначаем указанный промежуток, в котором нужно отобрать корни.
-
Определяем корни, попадающие в эту дугу.
-
Находим искомые углы учитывая обороты – прибавляем соответствующее количество периодов к отмеченному на окружности углу.
Пример:
Даны корни уравнения:
(x_{1} = frac{pi}{3} + 2pi n, nmathbb{in Z})
(x_{2} = frac{2pi}{3} + 2pi n, nmathbb{in Z})
Найдите корни, принадлежащие отрезку (leftlbrack — pi, frac{3pi}{2} rightrbrack).
-
Каждый из этих корней включает в себя бесконечное количество углов. Отметим эти серии ответов на тригокруге:
-
При этом мы знаем, что нужные корни должны находиться на промежутке (leftlbrack — pi, frac{3pi}{2} rightrbrack). Этот промежуток занимает больше, чем один оборот. Обозначим его так:
-
Так как промежуток занимает больше одного круга, каждая серия ответов так или иначе попадет в этот него.
-
Теперь определим, на каком обороте серии ответов попадут именно в этот промежуток. Если мы будем идти по тригокругу от (- pi) до (frac{3pi}{2}), то попадем в точки с сериями ответов по одному разу – в первом обороте после нуля. Тогда получим следующие углы:
Запишем ответ.
Ответ: (frac{pi}{3});( frac{2pi}{3}).
Важно! Чтобы решение было обоснованным, очень важно отметить всё на круге: и точки, и углы, и промежуток.
Вы можете заказать подробное решение вашей задачи !!!
Равенство, содержащее неизвестную под знаком тригонометрической функции (`sin x, cos x, tg x` или `ctg x`), называется тригонометрическим уравнением, именно их формулы мы и рассмотрим дальше.
Простейшими называются уравнения `sin x=a, cos x=a, tg x=a, ctg x=a`, где `x` — угол, который нужно найти, `a` — любое число. Запишем для каждого из них формулы корней.
1. Уравнение `sin x=a`.
При `|a|>1` не имеет решений.
При `|a| leq 1` имеет бесконечное число решений.
Формула корней: `x=(-1)^n arcsin a + pi n, n in Z`
2. Уравнение `cos x=a`
При `|a|>1` — как и в случае с синусом, решений среди действительных чисел не имеет.
При `|a| leq 1` имеет бесконечное множество решений.
Формула корней: `x=pm arccos a + 2pi n, n in Z`
Частные случаи для синуса и косинуса в графиках.
3. Уравнение `tg x=a`
Имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arctg a + pi n, n in Z`
4. Уравнение `ctg x=a`
Также имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arcctg a + pi n, n in Z`
Формулы корней тригонометрических уравнений в таблице
Для синуса:


Методы решения тригонометрических уравнений
Решение любого тригонометрического уравнения состоит из двух этапов:
- с помощью преобразовать его до простейшего;
- решить полученное простейшее уравнение, используя выше написанные формулы корней и таблицы.
Рассмотрим на примерах основные методы решения.
Алгебраический метод.
В этом методе делается замена переменной и ее подстановка в равенство.
Пример. Решить уравнение: `2cos^2(x+frac pi 6)-3sin(frac pi 3 — x)+1=0`
`2cos^2(x+frac pi 6)-3cos(x+frac pi 6)+1=0`,
делаем замену: `cos(x+frac pi 6)=y`, тогда `2y^2-3y+1=0`,
находим корни: `y_1=1, y_2=1/2`, откуда следуют два случая:
1. `cos(x+frac pi 6)=1`, `x+frac pi 6=2pi n`, `x_1=-frac pi 6+2pi n`.
2. `cos(x+frac pi 6)=1/2`, `x+frac pi 6=pm arccos 1/2+2pi n`, `x_2=pm frac pi 3-frac pi 6+2pi n`.
Ответ: `x_1=-frac pi 6+2pi n`, `x_2=pm frac pi 3-frac pi 6+2pi n`.
Разложение на множители.
Пример. Решить уравнение: `sin x+cos x=1`.
Решение. Перенесем влево все члены равенства: `sin x+cos x-1=0`. Используя , преобразуем и разложим на множители левую часть:
`sin x — 2sin^2 x/2=0`,
`2sin x/2 cos x/2-2sin^2 x/2=0`,
`2sin x/2 (cos x/2-sin x/2)=0`,
- `sin x/2 =0`, `x/2 =pi n`, `x_1=2pi n`.
- `cos x/2-sin x/2=0`, `tg x/2=1`, `x/2=arctg 1+ pi n`, `x/2=pi/4+ pi n`, `x_2=pi/2+ 2pi n`.
Ответ: `x_1=2pi n`, `x_2=pi/2+ 2pi n`.
Приведение к однородному уравнению
Вначале нужно данное тригонометрическое уравнение привести к одному из двух видов:
`a sin x+b cos x=0` (однородное уравнение первой степени) или `a sin^2 x + b sin x cos x +c cos^2 x=0` (однородное уравнение второй степени).
Потом разделить обе части на `cos x ne 0` — для первого случая, и на `cos^2 x ne 0` — для второго. Получим уравнения относительно `tg x`: `a tg x+b=0` и `a tg^2 x + b tg x +c =0`, которые нужно решить известными способами.
Пример. Решить уравнение: `2 sin^2 x+sin x cos x — cos^2 x=1`.
Решение. Запишем правую часть, как `1=sin^2 x+cos^2 x`:
`2 sin^2 x+sin x cos x — cos^2 x=` `sin^2 x+cos^2 x`,
`2 sin^2 x+sin x cos x — cos^2 x -` ` sin^2 x — cos^2 x=0`
`sin^2 x+sin x cos x — 2 cos^2 x=0`.
Это однородное тригонометрическое уравнение второй степени, разделим его левую и правую части на `cos^2 x ne 0`, получим:
`frac {sin^2 x}{cos^2 x}+frac{sin x cos x}{cos^2 x} — frac{2 cos^2 x}{cos^2 x}=0`
`tg^2 x+tg x — 2=0`. Введем замену `tg x=t`, в результате `t^2 + t — 2=0`. Корни этого уравнения: `t_1=-2` и `t_2=1`. Тогда:
- `tg x=-2`, `x_1=arctg (-2)+pi n`, `n in Z`
- `tg x=1`, `x=arctg 1+pi n`, `x_2=pi/4+pi n`, ` n in Z`.
Ответ. `x_1=arctg (-2)+pi n`, `n in Z`, `x_2=pi/4+pi n`, `n in Z`.
Переход к половинному углу
Пример. Решить уравнение: `11 sin x — 2 cos x = 10`.
Решение. Применим формулы двойного угла, в результате: `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x/2+10 cos^2 x/2`
`4 tg^2 x/2 — 11 tg x/2 +6=0`
Применив описанный выше алгебраический метод, получим:
- `tg x/2=2`, `x_1=2 arctg 2+2pi n`, `n in Z`,
- `tg x/2=3/4`, `x_2=arctg 3/4+2pi n`, `n in Z`.
Ответ. `x_1=2 arctg 2+2pi n, n in Z`, `x_2=arctg 3/4+2pi n`, `n in Z`.
Введение вспомогательного угла
В тригонометрическом уравнении `a sin x + b cos x =c`, где a,b,c — коэффициенты, а x — переменная, разделим обе части на `sqrt {a^2+b^2}`:
`frac a{sqrt {a^2+b^2}} sin x +` `frac b{sqrt {a^2+b^2}} cos x =` `frac c{sqrt {a^2+b^2}}`.
Коэффициенты в левой части имеют свойства синуса и косинуса, а именно сумма их квадратов равна 1 и их модули не больше 1. Обозначим их следующим образом: `frac a{sqrt {a^2+b^2}}=cos varphi`, ` frac b{sqrt {a^2+b^2}} =sin varphi`, `frac c{sqrt {a^2+b^2}}=C`, тогда:
`cos varphi sin x + sin varphi cos x =C`.
Подробнее рассмотрим на следующем примере:
Пример. Решить уравнение: `3 sin x+4 cos x=2`.
Решение. Разделим обе части равенства на `sqrt {3^2+4^2}`, получим:
`frac {3 sin x} {sqrt {3^2+4^2}}+` `frac{4 cos x}{sqrt {3^2+4^2}}=` `frac 2{sqrt {3^2+4^2}}`
`3/5 sin x+4/5 cos x=2/5`.
Обозначим `3/5 = cos varphi` , `4/5=sin varphi`. Так как `sin varphi>0`, `cos varphi>0`, то в качестве вспомогательного угла возьмем `varphi=arcsin 4/5`. Тогда наше равенство запишем в виде:
`cos varphi sin x+sin varphi cos x=2/5`
Применив формулу суммы углов для синуса, запишем наше равенство в следующем виде:
`sin (x+varphi)=2/5`,
`x+varphi=(-1)^n arcsin 2/5+ pi n`, `n in Z`,
`x=(-1)^n arcsin 2/5-` `arcsin 4/5+ pi n`, `n in Z`.
Ответ. `x=(-1)^n arcsin 2/5-` `arcsin 4/5+ pi n`, `n in Z`.
Дробно-рациональные тригонометрические уравнения
Это равенства с дробями, в числителях и знаменателях которых есть тригонометрические функции.
Пример. Решить уравнение. `frac {sin x}{1+cos x}=1-cos x`.
Решение. Умножим и разделим правую часть равенства на `(1+cos x)`. В результате получим:
`frac {sin x}{1+cos x}=` `frac {(1-cos x)(1+cos x)}{1+cos x}`
`frac {sin x}{1+cos x}=` `frac {1-cos^2 x}{1+cos x}`
`frac {sin x}{1+cos x}=` `frac {sin^2 x}{1+cos x}`
`frac {sin x}{1+cos x}-` `frac {sin^2 x}{1+cos x}=0`
`frac {sin x-sin^2 x}{1+cos x}=0`
Учитывая, что знаменатель равным быть нулю не может, получим `1+cos x ne 0`, `cos x ne -1`, ` x ne pi+2pi n, n in Z`.
Приравняем к нулю числитель дроби: `sin x-sin^2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
- `sin x=0`, `x=pi n`, `n in Z`
- `1-sin x=0`, `sin x=-1`, `x=pi /2+2pi n, n in Z`.
Учитывая, что ` x ne pi+2pi n, n in Z`, решениями будут `x=2pi n, n in Z` и `x=pi /2+2pi n`, `n in Z`.
Ответ. `x=2pi n`, `n in Z`, `x=pi /2+2pi n`, `n in Z`.
Тригонометрия, и тригонометрические уравнения в частности, применяются почти во всех сферах геометрии, физики, инженерии. Начинается изучение в 10 классе, обязательно присутствуют задания на ЕГЭ, поэтому постарайтесь запомнить все формулы тригонометрических уравнений — они вам точно пригодятся!
Впрочем, даже запоминать их не нужно, главное понять суть, и уметь вывести. Это не так и сложно, как кажется. Убедитесь сами, просмотрев видео.
Обязательный минимум знаний
sin x = a, -1 a 1 (a 1)
x = arcsin a + 2 n, n Z
x = — arcsin a + 2 n, n Z
или
x = (- 1)k arcsin a + k, k Z
arcsin (- a) = — arcsin a
sin x = 1
x = /2 + 2 k, k Z
sin x = 0
x = k, k Z
sin x = — 1
x = — /2 + 2 k, k Z
y
y
x
y
x
x
Обязательный минимум знаний
cos x = a, -1 a 1 (a 1)
x = arccos a + 2 n, n Z
arccos (- a) = — arccos a
cos x = 1
x = 2 k, k Z
cos x = 0
x = /2 + k, k Z
y
y
x
cos x = — 1
x = + 2 k, k Z
y
x
x
Обязательный минимум знаний
tg x = a, a R
x = arctg a + n, n Z
ctg x = a, a R
x = arcctg a + n, n Z
arctg (- a) = — arctg a
arctg (- a) = — arctg a Свести уравнение к одной функции
Свести к одному аргументу
Некоторые методы решения
тригонометрических уравнений
Применение тригонометрических формул
Использование формул сокращённого умножения
Разложение на множители
Сведение к квадратному уравнению относительно sin x, cos x, tg x
Введением вспомогательного аргумента
Делением обеих частей однородного уравнения первой степени
(asin x +bcosx = 0) на cos x
Делением обеих частей однородного уравнения второй степени
(a sin2 x +bsin x cos x+ c cos2x =0) на cos2 x
Устные упражнения Вычислите
arcsin ½
arcsin (- √2/2)
arccos √3/2
arccos (-1/2)
arctg √3
arctg (-√3/3)
= /6
= — /4
= /6
= — arccos ½ = — /3 = 2 /3
= /3
= — /6
(с помощью тригонометрической окружности)
cos 2x = ½, x [- /2; 3 /2]
2x = ± arccos ½ + 2 n, n Z
2x = ± /3 + 2 n, n Z
x = ± /6 + n, n Z
Отберём корни с помощью тригонометрической окружности
Ответ: — /6; /6; 5 /6; 7 /6
Различные способы отбора корней
Найти корни уравнения, принадлежащие данному промежутку
sin 3x = √3/2, x [- /2; /2]
3x = (– 1)k /3 + k, k Z
x = (– 1)k /9 + k/3, k Z
Отберём корни с помощью перебора значений k:
k = 0, x = /9 – принадлежит промежутку
k = 1, x = – /9 + /3 = 2 /9 – принадлежит промежутку
k = 2, x = /9 + 2 /3 = 7 /9 – не принадлежит промежутку
k = – 1, x = – /9 – /3 = – 4 /9 – принадлежит промежутку
k = – 2, x = /9 – 2 /3 = – 5 /9 – не принадлежит промежутку
Ответ: -4 /9; /9; 2 /9
Различные способы отбора корней
Найти корни уравнения, принадлежащие данному промежутку
(с помощью неравенства)
tg 3x = – 1, x (- /2;)
3x = – /4 + n, n Z
x = – /12 + n/3, n Z
Отберём корни с помощью неравенства:
– /2 < – /12 + n/3 < ,
– 1/2 < – 1/12 + n/3 < 1,
– 1/2 + 1/12 < n/3 < 1+ 1/12,
– 5/12 < n/3 < 13/12,
– 5/4 < n < 13/4, n Z,
n = – 1; 0; 1; 2; 3
n = – 1, x = – /12 – /3 = – 5 /12
n = 0, x = – /12
n = 1, x = – /12 + /3 = /4
n = 2, x = – /12 + 2 /3 = 7 /12
n = 3, x = – /12 + = 11 /12
Ответ: – 5 /12; – /12; /4; 7 /12; 11 /12
10. Различные способы отбора корней
Найти корни уравнения, принадлежащие данному промежутку
(с помощью графика)
cos x = – √2/2, x [–4; 5 /4]
x = arccos (– √2/2) + 2 n, n Z
x = 3 /4 + 2 n, n Z
Отберём корни с помощью графика:
x = – /2 – /4 = – 3 /4; x = – – /4 = – 5 /4
Ответ: 5 /4; 3 /4
11. 1. Решить уравнение 72cosx = 49sin2x и указать его корни на отрезке [; 5/2]
1. Решить уравнение 72cosx = 49sin2x
и указать его корни на отрезке [ ; 5 /2]
Решим уравнение:
72cosx = 49sin2x,
72cosx = 72sin2x,
2cos x = 2sin 2x,
cos x – 2 sinx cosx = 0,
cos x (1 – 2sinx) = 0,
cos x = 0 ,
x = /2 + k, k Z
или
1 – 2sinx = 0,
sin x = ½,
x = (-1)n /6 + n, n Z
Проведём отбор корней с помощью
тригонометрической окружности:
x = 2 + /6 = 13 /6
Ответ:
а) /2 + k, k Z, (-1)n /6 + n, n Z
б) 3 /2; 5 /2; 13 /6
12. 2. Решить уравнение 4cos2 x + 8 cos (x – 3/2) +1 = 0 Найти его корни на отрезке
2. Решить уравнение 4cos2 x + 8 cos (x – 3 /2) +1 = 0
Найти его корни на отрезке
4cos2 x + 8 cos (x – 3 /2) +1 = 0
4cos2x + 8 cos (3 /2 – x) +1 = 0,
4cos2x – 8 sin x +1 = 0,
4 – 4sin2 x – 8 sin x +1 = 0,
4sin 2x + 8sin x – 5 = 0,
D/4 = 16 + 20 = 36,
sin x = – 2,5
или
sin x = ½
x = (-1)k /6 + k, k Z
13. Проведем отбор корней на отрезке (с помощью графиков)
Проведем отбор корней на отрезке
(с помощью графиков)
sin x = ½
Построим графики функций y = sin x и y = ½
x = 4 + /6 = 25 /6
Ответ: а) (-1)k /6 + k, k Z; б) 25 /6
14. 3. Решить уравнение Найти его корни на отрезке
4 – cos2 2x = 3 sin2 2x + 2 sin 4x
4 (sin2 2x + cos2 2x) – cos2 2x = 3 sin2 2x + 4 sin 2x cos 2x,
sin2 2x + 3 cos2 2x – 4 sin 2x cos 2x = 0
Если cos2 2x = 0, то sin2 2x = 0, что невозможно, поэтому
cos2 2x 0 и обе части уравнения можно разделить на cos2 2x.
tg22x + 3 – 4 tg 2x = 0,
tg22x – 4 tg 2x + 3= 0,
tg 2x = 1,
2x = /4 + n, n Z
x = /8 + n/2, n Z
или
tg 2x = 3,
2x = arctg 3 + k, k Z
x = ½ arctg 3 + k/2, k Z
15.
4 – cos2 2x = 3 sin2 2x + 2 sin 4x
x = /8 + n/2, n Z или x = ½ arctg 3 + k/2, k Z
Так как 0 < arctg 3< /2,
0 < ½ arctg 3< /4, то ½ arctg 3
является решением
Так как 0 < /8 < /4 < 1,значит /8
также является решением
Другие решения не попадут в
промежуток , так как они
получаются из чисел ½ arctg 3 и /8
прибавлением чисел, кратных /2.
Ответ: а) /8 + n/2, n Z ; ½ arctg 3 + k/2, k Z
б) /8; ½ arctg 3
16. 4. Решить уравнение log5(cos x – sin 2x + 25) = 2 Найти его корни на отрезке
4. Решить уравнение log5(cos x – sin 2x + 25) = 2
Найти его корни на отрезке
Решим уравнение:
log5(cos x – sin 2x + 25) = 2
ОДЗ: cos x – sin 2x + 25 > 0,
cos x – sin 2x + 25 = 25, 25 > 0,
cos x – 2sin x cos x = 0,
cos x (1 – 2sin x) = 0,
cos x = 0,
x = /2 + n, n Z
или
1 – 2sinx = 0,
sin x = 1/2
x = (-1)k /6 + k, k Z
17.
Проведём отбор корней на отрезке
Проведём отбор корней на отрезке :
1) x = /2 + n, n Z
2 /2 + n 7 /2, n Z
2 1/2 + n 7/2, n Z
2 – ½ n 7/2 – ½, n Z
1,5 n 3, n Z
n = 2; 3
x = /2 + 2 = 5 /2
x = /2 + 3 = 7 /2
2) sin x = 1/2
x = 2 + /6 = 13 /6
x = 3 – /6 = 17 /6
Ответ: а) /2 + n, n Z ; (-1)k /6 + k, k Z
б) 13 /6 ; 5 /2; 7 /2; 17 /6
18. 5. Решить уравнение 1/sin2x + 1/sin x = 2 Найти его корни на отрезке [-5/2; -3/2]
5. Решить уравнение 1/sin2x + 1/sin x = 2
Найти его корни на отрезке [-5 /2; -3 /2]
Решим уравнение:
1/sin2x + 1/sin x = 2
x k
Замена 1/sin x = t,
t2 + t = 2,
t2 + t – 2 = 0,
t1= – 2, t2 = 1
1/sin x = – 2,
sin x = – ½,
x = – /6 + 2 n, n Z
или
x = – 5 /6 + 2 n, n Z
1/sin x = 1,
sin x = 1,
x = /2 + 2 n, n Z
Исключается эта серия корней, т.к. -150º+ 360ºn выходит за пределы
заданного промежутка [-450º; -270º]
19.
Продолжим отбор корней на отрезке
Рассмотрим остальные серии корней и проведём отбор корней
на отрезке [-5 /2; -3 /2] ([-450º; -270º]):
1) x = — /6 + 2 n, n Z
2) x = /2 + 2 n, n Z
-5 /2 — /6 + 2 n -3 /2, n Z
-5 /2 /2 + 2 n -3 /2, n Z
-5/2 -1/6 + 2n -3/2, n Z
-5/2 1/2 + 2n -3/2, n Z
-5/2 +1/6 2n -3/2 + 1/6, n Z
-5/2 — 1/2 2n -3/2 — 1/2, n Z
– 7/3 2n -4/3, n Z
– 3 2n -2, n Z
-7/6 n -2/3, n Z
-1,5 n -1, n Z
n = -1
n = -1
x = — /6 — 2 = -13 /6 (-390º)
x = /2 — 2 = -3 /2 (-270º)
Ответ: а) /2 + 2 n, n Z ; (-1)k+1 /6 + k, k Z
б) -13 /6 ; -3 /2
20. 6. Решить уравнение |sin x|/sin x + 2 = 2cos x Найти его корни на отрезке [-1; 8]
Решим уравнение
|sin x|/sin x + 2 = 2cos x
1)Если sin x >0, то |sin x| =sin x
Уравнение примет вид:
2 cos x=3,
cos x =1,5 – не имеет корней
2) Если sin x <0, то |sin x| =-sin x
и уравнение примет вид
2cos x=1, cos x = 1/2,
x = ±π/3 +2πk, k Z
Учитывая, что sin x < 0, то
остаётся одна серия ответа
x = — π/3 +2πk, k Z
Произведём отбор корней на
отрезке [-1; 8]
k=0, x= — π/3 , — π < -3, — π/3 < -1,
-π/3 не принадлежит данному
отрезку
k=1, x = — π/3 +2π = 5π/3<8,
5 π/3 [-1; 8]
k=2, x= — π/3 + 4π = 11π/3 > 8,
11π/3 не принадлежит данному
отрезку.
Ответ: а) — π/3 +2πk, k Z
б) 5
π/3
21. 7. Решить уравнение 4sin3x=3cos(x- π/2) Найти его корни на промежутке
8. Решить уравнение √1-sin2x= sin x
Найти его корни на промежутке
Решим уравнение √1-sin2x= sin x.
sin x ≥ 0,
1- sin2x = sin2x;
sin x ≥ 0,
2sin2x = 1;
sin x≥0,
sin x =√2/2; sin x = — √2/2;
sin x =√2/2
x=(-1)k /4 + k, k Z
sin x =√2/2
25. Проведём отбор корней на отрезке
Проведём отбор корней на отрезке
x=(-1)k /4 + k, k Z
sin x =√2/2
у =sin x и у=√2/2
5 /2 + /4 = 11 /4
Ответ: а) (-1)k /4 + k, k Z ;б) 11 /4
26. 9. Решить уравнение (sin2x + 2 sin2x)/√-cos x =0 Найти его корни на промежутке [-5; -7/2]
9. Решить уравнение (sin2x + 2 sin2x)/√-cos x =0
Найти его корни на промежутке [-5 ; -7 /2]
Решим уравнение
(sin2x + 2 sin2x)/√-cos x =0.
1) ОДЗ: cos x <0 ,
/2 +2 n
2) sin2x + 2 sin2x =0,
2 sinx∙cos x + 2 sin2x =0,
sin x (cos x+ sin x) =0,
sin x=0, x= n, n Z
или
cos x+ sin х=0 | : cos x,
tg x= -1, x= — /4 + n, n Z
C учётом ОДЗ
x= n, n Z, x= +2 n, n Z;
x= — /4 + n, n Z,
x= 3 /4 + 2 n, n Z
27. Отберём корни на заданном отрезке
Отберём корни на заданном
отрезке [-5 ; -7 /2]
x= +2 n, n Z ;
-5 ≤ +2 n ≤ -7 /2,
-5-1 ≤ 2n ≤ -7/2-1,
-3≤ n ≤ -9/4, n Z
n = -3, x= -6 = -5
x= 3 /4 + 2 n, n Z
-5 ≤ 3 /4 + 2 n ≤ -7 /2
-23/8 ≤ n ≤ -17/8, нет такого
целого n.
Ответ: а) +2 n, n Z ;
3 /4 + 2 n, n Z ;
б) -5 .
28. 10. Решить уравнение 2sin2x =4cos x –sinx+1 Найти его корни на промежутке [/2; 3/2]
10. Решить уравнение 2sin2x =4cos x –sinx+1
Найти его корни на промежутке [ /2; 3 /2]
Решим уравнение
2sin2x = 4cos x – sinx+1
2sin2x = 4cos x – sinx+1,
4 sinx∙cos x – 4cos x + sin x -1 = 0,
4cos x(sin x – 1) + (sin x – 1) = 0,
(sin x – 1)(4cos x +1)=0,
sin x – 1= 0, sin x = 1, x = /2+2 n, n Z
или
4cos x +1= 0, cos x = -0,25
x = ± (-arccos (0,25)) + 2 n, n Z
Запишем корни этого уравнения иначе
x = — arccos(0,25) + 2 n,
x = -(- arccos(0,25)) + 2 n, n Z
29. Отберём корни с помощью окружности
x = /2+2 n, n Z, х = /2;
x = -arccos(0,25)+2 n,
х=-(-arccos(0,25)) +2 n, n Z,
x = — arccos(0,25),
x = + arccos(0,25)
Ответ: а) /2+2 n,
-arccos(0,25)+2 n,
-(-arccos(0,25)) +2 n, n Z;
б) /2;
-arccos(0,25); +arccos(0,25)
Задача №1
Логика простая: будем поступать так, как поступали раньше не взирая на то, что теперь у тригонометрических функций стал более сложный аргумент!
Если бы мы решали уравнение вида:
То мы бы записали вот такой ответ:
Или (так как)
Но теперь в роли у нас выступаем вот такое выражение:
Тогда можно записать:
Наша с тобою цель — сделать так, чтобы слева стоял просто, без всяких «примесей»!
Давай постепенно от них избавляться!
Вначале уберём знаменатель при: для этого домножим наше равенство на:
Теперь избавимся от, разделив на него обе части:
Теперь избавимся от восьмёрки:
Полученное выражение можно расписать как 2 серии решений (по аналогии с квадратным уравнением, где мы либо прибавляем, либо вычитаем дискриминант)
Нам нужно найти наибольший отрицательный корень! Ясно, что надо перебирать.
Рассмотрим вначале первую серию:
Ясно, что если мы будем брать то в результате мы будем получать положительные числа, а они нас не интересуют.
Значит нужно брать отрицательным. Пусть.
При корень будет уже:
А нам нужно найти наибольший отрицательный!! Значит идти в отрицательную сторону здесь уже не имеет смысла. И наибольший отрицательный корень для этой серии будет равен.
Теперь рассматриваем вторую серию:
И опять подставляем: , тогда:
Не интересует!
Тогда увеличивать больше не имеет смысла! Будем уменьшать! Пусть, тогда:
Подходит!
Пусть. Тогда
Тогда — наибольший отрицательный корень!
Ответ:
Задача №2
Опять решаем, не взирая на сложный аргумент косинуса:
Теперь снова выражаем слева:
Умножаем обе стороны на
Делим обе стороны на
Всё, что осталось — это перенести вправо, изменив её знак с минуса на плюс.
У нас опять получается 2 серии корней, одна с, а другая с.
Нам нужно найти наибольший отрицательный корень. Рассмотрим первую серию:
Ясно, что первый отрицательный корень мы получим при, он будет равен и будет наибольшим отрицательным корнем в 1 серии.
Для второй серии
Первый отрицательный корень будет получен также при и будет равен. Так как, то — наибольший отрицательный корень уравнения.
Ответ:
.
Задача №3
Решаем, не взирая на сложный аргумент тангенса.
Вот, вроде бы ничего сложного, не так ли?
Как и раньше, выражаем в левой части:
Ну вот и замечательно, здесь вообще всего одна серия корней! Опять найдём наибольший отрицательный.
Ясно, что он получается, если положить. И корень этот равен.
Ответ:
Теперь попробуй самостоятельно решить следующие задачи.
Домашняя работа или 3 задачи для самостоятельного решения.
- Ре-ши-те урав-не-ние.
- Ре-ши-те урав-не-ние.
В от-ве-те на-пи-ши-те наи-мень-ший по-ло-жи-тель-ный ко-рень. - Ре-ши-те урав-не-ние.
В от-ве-те на-пи-ши-те наи-мень-ший по-ло-жи-тель-ный ко-рень.
Готов? Проверяем. Я не буду подробно описывать весь алгоритм решения, мне кажется, ему и так уделено достаточно внимания выше.
Ну что, всё правильно? Ох уж эти гадкие синусы, с ними всегда какие-то беды!
Ну что же, теперь ты умеешь решать простейшие тригонометрические уравнения!
Сверься с решениями и ответами:
Задача №1
Выразим
Наименьший положительный корень получится, если положить, так как, то
Ответ:
Задача №2
Наименьший положительный корень получится при.
Он будет равен.
Ответ:
.
Задача №3
При получаем, при имеем.
Ответ:
.
Эти знания помогут тебе решать многие задачи, с которыми ты столкнёшься в экзамене.
Если же ты претендуешь на оценку «5», то тебе просто необходимо перейти к чтению статьи для среднего уровня,
которая будет посвящена решению более сложных тригонометрических уравнений (задание С1).
СРЕДНИЙ УРОВЕНЬ
В этой статье я опишу решение тригонометрических уравнений более сложного типа
и как производить отбор их корней. Здесь я буду опираться на следующие темы:
- Тригонометрические уравнения для начального уровня (см выше).
Более сложные тригонометрические уравнения — это основа задач повышенной сложности. В них требуется как решить само уравнение в общем виде, так и найти корни этого уравнения, принадлежащие некоторому заданному промежутку.
Решение тригонометрических уравнений сводится к двум подзадачам:
- Решение уравнения
- Отбор корней
Следует отметить, что второе требуется не всегда, но все же в большинстве примеров требуется производить отбор. А если же он не требуется, то тебе скорее можно посочувствовать — это значит, что уравнение достаточно сложное само по себе.
Мой опыт разбора задач С1 показывает, что они как правило делятся на вот такие категории.
Четыре категории задач повышенной сложности (ранее С1)
- Уравнения, сводящиеся к разложению на множители.
- Уравнения, сводящиеся к виду.
- Уравнения, решаемые заменой переменной.
- Уравнения, требующие дополнительного отбора корней из-за иррациональности или знаменателя.
Говоря по-простому: если тебе попалось одно из уравнений первых трех типов
, то считай, что тебе повезло. Для них как правило дополнительно нужно подобрать корни, принадлежащие некоторому промежутку.
Если же тебе попалось уравнение 4 типа
, то тебе повезло меньше: с ним нужно повозиться подольше и повнимательнее, зато довольно часто в нем не требуется дополнительно отбирать корни. Тем не менее данный тип уравнений я буду разбирать в следующей статье, а эту посвящу решению уравнений первых трех типов.
Уравнения, сводящиеся к разложению на множители
Самое важное, что тебе нужно помнить, чтобы решать уравнения этого типа это
Как показывает практика, как правило, этих знаний достаточно. Давай обратимся к примерам:
Пример 1. Уравнение, сводящиеся к разложению на множители с помощью формул приведения и синуса двойного угла
- Ре-ши-те урав-не-ние
- Най-ди-те все корни этого урав-не-ния, при-над-ле-жа-щие от-рез-ку
Здесь, как я и обещал, работают формулы приведения:
Тогда мое уравнение примет вот такой вид:
Тогда мое уравнение примет следующую форму:
Недальновидный ученик мог бы сказать: а теперь я сокращу обе части на, получаю простейшее уравнение и радуюсь жизни! И будет горько заблуждаться!
ЗАПОМНИ: НИКОГДА НЕЛЬЗЯ СОКРАЩАТЬ ОБЕ ЧАСТИ ТРИГОНОМЕТРИЧЕСКОГО УРАВНЕНИЯ НА ФУНКЦИЮ, СОДЕРЖАЩУЮ НЕИЗВЕСТНУЮ! ТАКИМ ОБРАЗОМ, ТЫ ТЕРЯЕШЬ КОРНИ!
Так что же делать? Да все просто, переносить все в одну сторону и выносить общий множитель:
Ну вот, на множители разложили, ура! Теперь решаем:
Первое уравнение имеет корни:
А второе:
На этом первая часть задачи решена. Теперь нужно отобрать корни:
Промежуток вот такой:
Или его еще можно записать вот так:
Ну что, давай отбирать корни:
Вначале поработаем с первой серией (да и проще она, что уж говорить!)
Так как наш промежуток — целиком отрицательный, то нет нужды брать неотрицательные, все равно они дадут неотрицательные корни.
Возьмем, тогда — многовато, не попадает.
Пусть, тогда — снова не попал.
Еще одна попытка — , тогда — есть, попал! Первый корень найден!
Стреляю еще раз: , тогда — еще раз попал!
Ну и еще разок: : — это уже перелет.
Так что из первой серии промежутку принадлежат 2 корня: .
Работаем со второй серией (возводим
в степень по правилу):
Недолет!
Снова недолет!
Опять недолет!
Попал!
Перелет!
Таким образом, моему промежутку принадлежат вот такие корни:
Вот по такому алгоритму мы и будем решать все другие примеры. Давай вместе потренируемся еще на одном примере.
Пример 2. Уравнение, сводящиеся к разложению на множители с помощью формул приведения
- Решите уравнение
Решение:
Опять пресловутые формулы приведения:
Опять не вздумай сокращать!
Первое уравнение имеет корни:
А второе:
Теперь снова поиск корней.
Начну со второй серии, мне про нее уже все известно из предыдущего примера! Посмотри и убедись, что корни, принадлежащие промежутку следующие:
Теперь первая серия и она попроще:
Если — подходит
Если — тоже годится
Если — уже перелет.
Тогда корни будут следующие:
Самостоятельная работа. 3 уравнения.
Ну что, техника тебе ясна? Решение тригонометрических уравнений уже не кажется таким сложным? Тогда быстренько прорешай следующие задачки самостоятельно, а потом мы с тобой будем решать другие примеры:
- Решите уравнение
Най-ди-те все корни этого урав-не-ния, при-над-ле-жа-щие промежутку. - Ре-ши-те урав-не-ние
Ука-жи-те корни урав-не-ния, при-над-ле-жа-щие от-рез-ку - Ре-ши-те урав-не-ние
Най-ди-те все корни этого урав-не-ния, при-над-ле-жа-щие про-ме-жут-ку.
Уравнение 1.
И снова формула приведения:
Первая серия корней:
Вторая серия корней:
Начинаем отбор для промежутка
Ответ:
, .
Уравнение 2. Проверка самостоятельной работы.
Довольно хитрая группировка на множители (применю формулу синуса двойного угла):
тогда или
Это общее решение. Теперь надо отбирать корни. Беда в том, что мы не можем сказать точное значение угла, косинус которого равен одной четверти. Поэтому я не могу просто так избавиться от арккосинуса — вот такая досада!
Что я могу сделать, так это прикинуть, что так как, то.
Составим таблицу: промежуток:
Ну что же, путем мучительных поисков мы пришли к неутешительному выводу о том, что наше уравнение имеет один корень на указанном промежутке: displaystyle arccosfrac{1}{4}-5pi
Уравнение 3. Проверка самостоятельной работы.
Уравнение пугающего вида. Однако решается довольно просто путем применения формулы синуса двойного угла:
Сократим на 2:
Сгруппируем первое слагаемое со вторым и третье с четвертым и вынесем общие множители:
Ясно, что первое уравнение корней не имеет, а теперь рассмотрим второе:
Вообще я собирался чуть позже остановиться на решении таких уравнений, но раз уж подвернулось, то делать нечего, надо решать…
Уравнения вида:
Данное уравнение решается делением обеих частей на:
Таким образом, наше уравнение имеет единственную серию корней:
Нужно найти те из них, которые принадлежат промежутку: .
Опять построим табличку, как я делал и ранее:
Ответ:
.
Уравнения, сводящиеся к виду:
Ну вот, теперь самое время переходить ко второй порции уравнений, тем более, что я уже и так проболтался в чем состоит решение тригонометрических уравнений нового типа. Но не лишним будет повторить, что уравнение вида
Решается делением обеих частей на косинус:
- Ре-ши-те урав-не-ние
Ука-жи-те корни урав-не-ния, при-над-ле-жа-щие от-рез-ку. - Ре-ши-те урав-не-ние
Ука-жи-те корни урав-не-ния, при-над-ле-жа-щие про-ме-жут-ку.
Пример 1.
Первое — ну совсем простое. Перенесем вправо и применим формулу косинуса двойного угла:
Ага! Уравнение вида: . Делю обе части на
Делаем отсев корней:
Промежуток:
Ответ:
Пример 2.
Все тоже довольно тривиально: раскроем скобки справа:
Основное тригонометрическое тождество:
Синус двойного угла:
Окончательно получим:
Отсев корней: промежуток.
Ответ:
.
Ну как тебе техника, не слишком сложна? Я надеюсь, что нет. Сразу можно оговориться: в чистом виде уравнения, которые тут же сводятся к уравнению относительно тангенса, встречаются довольно редко. Как правило, этот переход (деление на косинус) является лишь частью более сложной задачи. Вот тебе пример
, чтобы ты мог поупражняться:
- Ре-ши-те урав-не-ние
- Най-ди-те все корни этого урав-не-ния, при-над-ле-жа-щие от-рез-ку.
Давай сверяться:
Уравнение решается сразу же, достаточно поделить обе части на:
Отсев корней:
Ответ:
.
Так или иначе, нам еще предстоит встретиться с уравнениями того вида, которые мы только что разобрали. Однако нам еще рано закругляться: остался еще один «пласт» уравнений, которые мы не разобрали. Итак:
Решение тригонометрических уравнений заменой переменной
Здесь все прозрачно: смотрим пристально на уравнение, максимально его упрощаем, делаем замену, решаем, делаем обратную замену! На словах все очень легко. Давай посмотрим на деле:
Пример.
- Решить уравнение: .
- Най-ди-те все корни этого урав-не-ния, при-над-ле-жа-щие от-рез-ку.
Ну что же, здесь замена сама напрашивается к нам в руки!
Тогда наше уравнение превратится вот в такое:
Первое уравнение имеет корни:
А второе вот такие:
Теперь найдем корни, принадлежащие промежутку
Ответ:
.
Давай вместе разберем чуть более сложный пример
:
- Ре-ши-те урав-не-ние
- Ука-жи-те корни дан-но-го урав-не-ния, при-над-ле-жа-щие про-ме-жут-ку.
Здесь замена сразу не видна, более того, она не очень очевидна. Давай вначале подумаем: а что мы можем сделать?
Можем, например, представить
А заодно и
Тогда мое уравнение примет вид:
А теперь внимание, фокус:
Давай разделим обе части уравнения на:
Внезапно мы с тобой получили квадратное уравнение относительно! Сделаем замену, тогда получим:
Уравнение имеет следующие корни:
Неприятная вторая серия корней, но ничего не поделаешь! Производим отбор корней на промежутке.
Нам также нужно учитывать, что
Так как и, то
Ответ:
Для закрепления, прежде чем ты сам будешь решать задачи, вот тебе еще упражнение
:
- Ре-ши-те урав-не-ние
- Най-ди-те все корни этого урав-не-ния, при-над-ле-жа-щие про-ме-жут-ку.
Здесь нужно держать ухо востро: у нас появились знаменатели, которые могут быть нулевыми! Поэтому надо быть особо внимательными к корням!
Прежде всего, мне нужно преобразовать уравнение так, чтобы я мог сделать подходящую замену. Я не могу придумать сейчас ничего лучше, чем переписать тангенс через синус и косинус:
Теперь я перейду от косинуса к синусу по основному тригонометрическому тождеству:
И, наконец, приведу все к общему знаменателю:
Теперь я могу перейти к уравнению:
Но при (то есть при).
Теперь все готово для замены:
Тогда или
Однако обрати внимание, что если, то при этом!
Кто от этого страдает? Беда с тангенсом, он не определен, когда косинус равен нулю (происходит деление на ноль).
Таким образом, корни уравнения следующие:
Теперь производим отсев корней на промежутке:
Таким образом, наше уравнение имеет единственный корень на промежутке, и он равен.
Видишь: появление знаменателя (также, как и тангенса, приводит к определенным затруднениям с корнями! Тут нужно быть более внимательным!).
Ну что же, мы с тобой почти закончили разбор тригонометрических уравнений, осталось совсем немного — самостоятельно решить две задачи. Вот они.
- Решите уравнение
Най-ди-те все корни этого урав-не-ния, при-над-ле-жа-щие от-рез-ку. - Ре-ши-те урав-не-ние
Ука-жи-те корни этого урав-не-ния, при-над-ле-жа-щие от-рез-ку.
Решил? Не очень сложно? Давай сверяться:
- Работаем по формулам приведения:
Подставляем в уравнение:
Перепишем все через косинусы, чтобы удобнее было делать замену:
Теперь легко сделать замену:
Ясно, что — посторонний корень, так как уравнение решений не имеет. Тогда:
Ищем нужные нам корни на промежутке
Ответ:
. -
Здесь замена видна сразу:
Тогда или
— подходит! — подходит! — подходит! — подходит! — много! — тоже много! Ответ:
Ну вот, теперь все! Но решение тригонометрических уравнений на этом не заканчивается, за бортом у нас остались самые сложные случаи: когда в уравнениях присутствует иррациональность или разного рода «сложные знаменатели». Как решать подобные задания мы рассмотрим в статье для продвинутого уровня.
ПРОДВИНУТЫЙ УРОВЕНЬ
В дополнение к рассмотренным в предыдущих двух статьях тригонометрическим уравнениям, рассмотрим еще один класс уравнений, которые требуют еще более внимательного анализа. Данные тригонометрические примеры содержат либо иррациональность, либо знаменатель, что делает их анализ более сложным
. Тем не менее ты вполне можешь столкнуться с данными уравнениями в части С экзаменационной работы. Однако нет худа без добра: для таких уравнений уже, как правило, не ставится вопрос о том, какие из его корней принадлежат заданному промежутку. Давай не будем ходить вокруг да около, а сразу тригонометрические примеры.
Пример 1.
Решить уравнение и найти те корни, которые принадлежат отрезку.
Решение:
У нас появляется знаменатель, который не должен быть равен нулю! Тогда решить данное уравнение — это все равно, что решить систему
Решим каждое из уравнений:
А теперь второе:
Теперь давай посмотрим на серию:
Ясно, что нам не подходит вариант, так как при этом у нас обнуляется знаменатель (см. на формулу корней второго уравнения)
Если же — то все в порядке, и знаменатель не равен нулю! Тогда корни уравнения следующие: , .
Теперь производим отбор корней, принадлежащих промежутку.
| — не подходит | — подходит | |
| — подходит | — подходит | |
| перебор | перебор |
Тогда корни следующие:
Видишь, даже появление небольшой помехи в виде знаменателя существенно отразилось на решении уравнения: мы отбросили серию корней, нулящих знаменатель. Еще сложнее может обстоять дело, если тебе попадутся тригонометрические примеры имеющие иррациональность.
Пример 2.
Решите уравнение:
Решение:
Ну хотя бы не надо отбирать корни и то хорошо! Давай вначале решим уравнение, не взирая на иррациональность:
И что, это все? Нет, увы, так было бы слишком просто! Надо помнить, что под корнем могут стоять только неотрицательные числа. Тогда:
Решение этого неравенства:
Теперь осталось выяснить, не попала ли ненароком часть корней первого уравнения туда, где не выполяется неравенство.
Для этого можно опять воспользоваться таблицей:
| : , но | Нет! | |
| Да! | ||
| Да! |
Таким образом, у меня «выпал» один из корней! Он получается, если положить. Тогда ответ можно записать в следующем виде:
Ответ:
Видишь, корень требует еще более пристального внимания! Усложняем: пусть теперь у меня под корнем стоит тригонометрическая функция.
Пример 3.
Как и раньше: вначале решим каждое отдельно, а потом подумаем, что же мы наделали.
Теперь второе уравнение:
Теперь самое сложное — выяснить, не получаются ли отрицательные значения под арифметическим корнем, если мы подставим туда корни из первого уравнения:
Число надо понимать как радианы. Так как радиана — это примерно градусов, то радианы — порядка градусов. Это угол второй четверти. Косинус второй четверти имеет какой знак? Минус. А синус? Плюс. Так что можно сказать про выражение:
Оно меньше нуля!
А значит — не является корнем уравнения.
Теперь черед.
Сравним это число с нулем.
Котангенс — функция убывающая в 1 четверти (чем меньше аргумент, тем больше котангенс). радианы — это примерно градусов. В то же время
так как, то, а значит и
,
Ответ:
.
Может ли быть еще сложнее? Пожалуйста! Будет труднее, если под корнем по-прежнему тригонометрическая функция, а вторая часть уравнения — снова тригонометрическая функция.
Чем больше тригонометрических примеров, тем лучше, смотри дальше:
Пример 4.
Корень не годится, ввиду ограниченности косинуса
Теперь второе:
В то же время по определению корня:
Надо вспомнить единичную окружность: а именно те четверти, где синус меньше нуля. Какие это четверти? Третья и четвертая. Тогда нас будут интересовать те решения первого уравнения, которые лежат в третьей или четвертой четверти.
Первая серия дает корни, лежащие на пересечении третьей и четвертой четверти. Вторая же серия — ей диаметрально противоположная — и порождает корни, лежащие на границе первой и второй четверти. Поэтому эта серия нам не подходит.
Ответ:
,
И опять тригонометрические примеры с «трудной иррациональностью»
. Мало того, что у нас снова под корнем тригонометрическая функция, так теперь она еще и в знаменателе!
Пример 5.
Ну, ничего не поделаешь — поступаем как и раньше.
Теперь работаем со знаменателем:
Я не хочу решать тригонометрическое неравенство, а потому поступлю хитро: возьму и подставлю в неравенство мои серии корней:
Если — четное, то имеем:
так как, то все углы вида лежат в четвертой четверти. И снова сакральный вопрос: каков знак синуса в четвертой четверти? Отрицательный. Тогда неравенство
Если же -нечетное, то:
В какой четверти лежит угол? Это угол второй четверти. Тогда все углы — снова углы второй четверти. Синус там положительный. Как раз то, что надо! Значит, серия:
Подходит!
Точно так же разбираемся со второй серией корней:
Подставляем в наше неравенство:
Если — четное, то
Углы первой четверти. Синус там положительный, значит серия подходит. Теперь если — нечетное, то:
тоже подходит!
Ну вот, теперь записываем ответ!
Ответ:
Ну вот, это был, пожалуй, наиболее трудоемкий случай. Теперь я предлагаю тебе задачи
для самостоятельного решения.
Тренировка
- Решите и найдите все корни уравнения, принадлежащие отрезку.
Решения:
-
Первое уравнение:
или
ОДЗ корня:Второе уравнение:
Отбор корней, которые принадлежат промежутку
Ответ:
Или
или
Но
Рассмотрим: . Если — четное, то
— не подходит!
Если — нечетное, : — подходит!
Значит, наше уравнение имеет такие серии корней:
или
Отбор корней на промежутке:
| — не подходит | — подходит | |
| — подходит | — много | |
| — подходит | много |
Ответ:
, .
Или
Так как, то при тангенс не определен. Тут же отбрасываем эту серию корней!
Вторая часть:
В то же время по ОДЗ требуется, чтобы
Проверяем найденные в первом уравнении корни:
Если знак:
Углы первой четверти, где тангенс положительный. Не подходит!
Если знак:
Угол четвертой четверти. Там тангенс отрицательный. Подходит. Записываем ответ:
Ответ:
, .
Мы вместе разобрали в этой статье сложные тригонометрические примеры, но тебе стоит прорешать уравнения самому.
КРАТКОЕ ИЗЛОЖЕНИЕ И ОСНОВНЫЕ ФОРМУЛЫ
Тригонометрическое уравнение — это уравнение, в котором неизвестная находится строго под знаком тригонометрической функции.
Существует два способа
решения тригонометрических уравнений:
Первый способ
— с использованием формул.
Второй способ
— через тригонометрическую окружность.
Позволяет измерять углы, находить их синусы, косинусы и прочее.
а)
Решите уравнение 2(sin x-cos x)=tgx-1.
б)
left[ frac{3pi }2;,3pi right].
Показать решение
Решение
а)
Раскрыв скобки и перенеся все слагаемые в левую часть, получим уравнение 1+2 sin x-2 cos x-tg x=0.
Учитывая, что cos x neq 0,
слагаемое 2 sin x
можно заменить на 2 tg x cos x,
получим уравнение 1+2 tg x cos x-2 cos x-tg x=0,
которое способом группировки можно привести к виду (1-tg x)(1-2 cos x)=0.
1)
1-tg x=0,
tg x=1,
x=fracpi 4+pi n, n in mathbb Z;
2)
1-2 cos x=0,
cos x=frac12,
x=pm fracpi 3+2pi n, n in mathbb Z.
б)
С помощью числовой окружности отберём корни, принадлежащие промежутку left[ frac{3pi }2;, 3pi right].
x_1=fracpi 4+2pi =frac{9pi }4,
x_2=fracpi 3+2pi =frac{7pi }3,
x_3=-fracpi 3+2pi =frac{5pi }3.
Ответ
а)
fracpi 4+pi n,
pmfracpi 3+2pi n, n in mathbb Z;
б)
frac{5pi }3,
frac{7pi }3,
frac{9pi }4.
Условие
а)
Решите уравнение (2sin ^24x-3cos 4x)cdot sqrt {tgx}=0.
б)
Укажите корни этого уравнения, принадлежащие промежутку left(0;,frac{3pi }2right] ;
Показать решение
Решение
а)
ОДЗ: begin{cases} tgxgeqslant 0\xneq fracpi 2+pi k,k in mathbb Z. end{cases}
Исходное уравнение на ОДЗ равносильно совокупности уравнений
left[!!begin{array}{l} 2 sin ^2 4x-3 cos 4x=0,\tg x=0. end{array}right.
Решим первое уравнение. Для этого сделаем замену cos 4x=t,
t in [-1; 1].
Тогда sin^24x=1-t^2.
Получим:
2(1-t^2)-3t=0,
2t^2+3t-2=0,
t_1=frac12,
t_2=-2, t_2notin [-1; 1].
cos 4x=frac12,
4x=pm fracpi 3+2pi n,
x=pm fracpi {12}+frac{pi n}2, n in mathbb Z.
Решим второе уравнение.
tg x=0,, x=pi k, k in mathbb Z.
При помощи единичной окружности найдём решения, которые удовлетворяют ОДЗ.
Знаком «+»
отмечены 1
-я и 3
-я четверти, в которых tg x>0.
Получим: x=pi k, k in mathbb Z;
x=fracpi {12}+pi n, n in mathbb Z;
x=frac{5pi }{12}+pi m, m in mathbb Z.
б)
Найдём корни, принадлежащие промежутку left(0;,frac{3pi }2right].
x=fracpi {12},
x=frac{5pi }{12};
x=pi ;
x=frac{13pi }{12};
x=frac{17pi }{12}.
Ответ
а)
pi k, k in mathbb Z;
fracpi {12}+pi n, n in mathbb Z;
frac{5pi }{12}+pi m, m in mathbb Z.
б)
pi;
fracpi {12};
frac{5pi }{12};
frac{13pi }{12};
frac{17pi }{12}.
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Условие
а)
Решите уравнение: cos ^2x+cos ^2fracpi 6=cos ^22x+sin ^2fracpi 3;
б)
Укажите все корни, принадлежащие промежутку left(frac{7pi }2;,frac{9pi }2right].
Показать решение
Решение
а)
Так как sin fracpi 3=cos fracpi 6,
то sin ^2fracpi 3=cos ^2fracpi 6,
значит, заданное уравнение равносильно уравнению cos^2x=cos ^22x,
которое, в свою очередь, равносильно уравнению cos^2x-cos ^2 2x=0.
Но cos ^2x-cos ^22x=
(cos x-cos 2x)cdot (cos x+cos 2x)
и
cos 2x=2 cos ^2 x-1,
поэтому уравнение примет вид
(cos x-(2 cos ^2 x-1)),cdot
(cos x+(2 cos ^2 x-1))=0,
(2 cos ^2 x-cos x-1),cdot
(2 cos ^2 x+cos x-1)=0.
Тогда либо 2 cos ^2 x-cos x-1=0,
либо 2 cos ^2 x+cos x-1=0.
Решая первое уравнение как квадратное уравнение относительно cos x,
получаем:
(cos x)_{1,2}=frac{1pmsqrt 9}4=frac{1pm3}4.
Поэтому либо cos x=1,
либо cos x=-frac12.
Если cos x=1,
то x=2kpi , k in mathbb Z.
Если cos x=-frac12,
то x=pm frac{2pi }3+2spi , s in mathbb Z.
Аналогично, решая второе уравнение, получаем либо cos x=-1,
либо cos x=frac12.
Если cos x=-1,
то корни x=pi +2mpi , m in mathbb Z.
Если cos x=frac12,
то x=pm fracpi 3+2npi , n in mathbb Z.
Объединим полученные решения:
x=mpi , m in mathbb Z;
x=pm fracpi 3 +spi , s in mathbb Z.
б)
Выберем корни, которые попали в заданный промежуток, с помощью числовой окружности.
Получим: x_1 =frac{11pi }3,
x_2=4pi ,
x_3 =frac{13pi }3.
Ответ
а)
mpi, m in mathbb Z;
pm fracpi 3 +spi , s in mathbb Z;
б)
frac{11pi }3,
4pi ,
frac{13pi }3.
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Условие
а)
Решите уравнение 10cos ^2frac x2=frac{11+5ctgleft(dfrac{3pi }2-xright) }{1+tgx}.
б)
Укажите корни этого уравнения, принадлежащие интервалу left(-2pi ; -frac{3pi }2right).
Показать решение
Решение
а)
1.
Согласно формуле приведения, ctgleft(frac{3pi }2-xright) =tgx.
Областью определения уравнения будут такие значения x
, что cos x neq 0
и tg x neq -1.
Преобразуем уравнение, пользуясь формулой косинуса двойного угла 2 cos ^2 frac x2=1+cos x.
Получим уравнение: 5(1+cos x) =frac{11+5tgx}{1+tgx}.
Заметим, что frac{11+5tgx}{1+tgx}=
frac{5(1+tgx)+6}{1+tgx}=
5+frac{6}{1+tgx},
поэтому уравнение принимает вид: 5+5 cos x=5 +frac{6}{1+tgx}.
Отсюда cos x =frac{dfrac65}{1+tgx},
cos x+sin x =frac65.
2.
Преобразуем sin x+cos x
по формуле приведения и формуле суммы косинусов: sin x=cos left(fracpi 2-xright),
cos x+sin x=
cos x+cos left(fracpi 2-xright)=
2cos fracpi 4cos left(x-fracpi 4right)=
sqrt 2cos left(x-fracpi 4right) =
frac65.
Отсюда cos left(x-fracpi 4right) =frac{3sqrt 2}5.
Значит, x-fracpi 4=
arccos frac{3sqrt 2}5+2pi k, k in mathbb Z,
или x-fracpi 4=
-arccos frac{3sqrt 2}5+2pi t, t in mathbb Z.
Поэтому x=fracpi 4+arccos frac{3sqrt 2}5+2pi k,k in mathbb Z,
или x =fracpi 4-arccos frac{3sqrt 2}5+2pi t,t in mathbb Z.
Найденные значения x
принадлежат области определения.
б)
Выясним сначала куда попадают корни уравнения при k=0
и t=0.
Это будут соответственно числа a=fracpi 4+arccos frac{3sqrt 2}5
и b=fracpi 4-arccos frac{3sqrt 2}5.
1.
Докажем вспомогательное неравенство:
frac{sqrt 2}{2}<frac{3sqrt 2}2<1.
Действительно, frac{sqrt 2}{2}=frac{5sqrt 2}{10}<frac{6sqrt2}{10}=frac{3sqrt2}{5}.
Заметим также, что left(frac{3sqrt 2}5right) ^2=frac{18}{25}<1^2=1,
значит frac{3sqrt 2}5<1.
2.
Из неравенств (1)
по свойству арккосинуса получаем:
arccos 1
0
Отсюда fracpi 4+0<fracpi 4+arccos frac{3sqrt 2}5<fracpi 4+fracpi 4,
0<fracpi 4+arccos frac{3sqrt 2}5<fracpi 2,
0
Аналогично, -fracpi 4
0=fracpi 4-fracpi 4<fracpi 4-arccos frac{3sqrt 2}5<
fracpi 4<fracpi 2,
0
При k=-1
и t=-1
получаем корни уравнения a-2pi
и b-2pi.
Bigg(a-2pi =-frac74pi +arccos frac{3sqrt 2}5,,
b-2pi =-frac74pi -arccos frac{3sqrt 2}5Bigg).
При этом -2pi
2pi Значит, эти корни принадлежат заданному промежутку left(-2pi , -frac{3pi }2right).
При остальных значениях k
и t
корни уравнения не принадлежат заданному промежутку.
Действительно, если kgeqslant 1
и tgeqslant 1,
то корни больше 2pi.
Если kleqslant -2
и tleqslant -2,
то корни меньше -frac{7pi }2.
Ответ
а)
fracpi4pm arccosfrac{3sqrt2}5+2pi k, kinmathbb Z;
б)
-frac{7pi}4pm arccosfrac{3sqrt2}5.
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Условие
а)
Решите уравнение sin left(fracpi 2+xright) =sin (-2x).
б)
Найдите все корни этого уравнения, принадлежащие промежутку ;
Показать решение
Решение
а)
Преобразуем уравнение:
cos x =-sin 2x,
cos x+2 sin x cos x=0,
cos x(1+2 sin x)=0,
cos x=0,
x =fracpi 2+pi n, n in mathbb Z;
1+2 sin x=0,
sin x=-frac12,
x=(-1)^{k+1}cdot fracpi 6+pi k, k in mathbb Z.
б)
Корни, принадлежащие отрезку ,
найдём с помощью единичной окружности.
Указанному промежутку принадлежит единственное число fracpi 2.
Ответ
а)
fracpi 2+pi n, n in mathbb Z;
(-1)^{k+1}cdot fracpi 6+pi k, k in mathbb Z;
б)
fracpi 2.
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Условие
не входит в ОДЗ.
Значит, sin x neq 1.
Разделим обе части уравнения на множитель (sin x-1),
отличный от нуля. Получим уравнение frac 1{1+cos 2x}=frac 1{1+cos (pi +x)},
или уравнение 1+cos 2x=1+cos (pi +x).
Применяя в левой части формулу понижения степени, а в правой — формулу приведения, получим уравнение 2 cos ^2 x=1-cos x.
Это уравнение с помощью замены cos x=t,
где -1 leqslant t leqslant 1
сводим к квадратному: 2t^2+t-1=0,
корни которого t_1=-1
и t_2=frac12.
Возвращаясь к переменной x
, получим cos x = frac12
или cos x=-1,
откуда x=frac pi 3+2pi m,
m in mathbb Z,
x=-frac pi 3+2pi n,
n in mathbb Z,
x=pi +2pi k,
k in mathbb Z.
б)
Решим неравенства
1) -frac{3pi }2 leqslant frac{pi }3+2pi m leqslant -frac pi 2 ,
2) -frac{3pi }2 leqslant -frac pi 3+2pi n leqslant -frac pi {2,}
3) -frac{3pi }2 leqslant pi+2pi k leqslant -frac pi 2 ,
m,
n,
k in mathbb Z.
1)
-frac{3pi }2 leqslant frac{pi }3+2pi m leqslant -frac pi 2 ,
-frac32 leqslant
frac13+2m leqslant
-frac12 -frac{11}6 leqslant
2m leqslant
-frac56 ,
-frac{11}{12} leqslant m leqslant -frac5{12}.
left [-frac{11}{12};-frac5{12}right]
.
2)
-frac {3pi} 2 leqslant -frac{pi }3+2pi n leqslant -frac{pi }{2},
-frac32 leqslant -frac13 +2n leqslant -frac12 ,
-frac76 leqslant 2n leqslant -frac1{6},
-frac7{12} leqslant n leqslant -frac1{12}.
Нет целых чисел, принадлежащих промежутку left[ -frac7{12} ; -frac1{12} right].
3)
-frac{3pi }2 leqslant pi +2pi kleqslant -frac{pi }2,
-frac32 leqslant 1+2kleqslant -frac12,
-frac52 leqslant 2k leqslant -frac32,
-frac54 leqslant k leqslant -frac34.
Этому неравенству удовлетворяет k=-1,
тогда x=-pi.
Ответ
а)
frac pi 3+2pi m;
-frac pi 3+2pi n;
pi +2pi k,
m,
n,
k in mathbb Z;
б)
-pi .
В этой статье и постараюсь объяснить 2 способа отбора корней в тригонометрическом уравнение
: с помощью неравенств и с помощью тригонометрической окружности. Перейдем сразу к наглядному примеру и походу дела будем разбираться.
А) Решить уравнение sqrt(2)cos^2x=sin(Pi/2+x)
б) Найдите все корни этого уравнения, принадлежащие промежутку [-7Pi/2; -2Pi]
Решим пункт а.
Воспользуемся формулой приведения для синуса sin(Pi/2+x) = cos(x)
Sqrt(2)cos^2x = cosx
Sqrt(2)cos^2x — cosx = 0
Cosx(sqrt(2)cosx — 1) = 0
X1 = Pi/2 + Pin, n ∈ Z
Sqrt(2)cosx — 1 = 0
Cosx = 1/sqrt(2)
Cosx = sqrt(2)/2
X2 = arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x3 = -arccos(sqrt(2)/2) + 2Pin, n ∈ Z
X2 = Pi/4 + 2Pin, n ∈ Z
x3 = -Pi/4 + 2Pin, n ∈ Z
Решим пункт б.
1) Отбор корней с помощью неравенств
Здесь все делается просто, полученные корни подставляем в заданный нам промежуток [-7Pi/2; -2Pi], находим целые значения для n.
7Pi/2 меньше или равно Pi/2 + Pin меньше или равно -2Pi
Сразу делим все на Pi
7/2 меньше или равно 1/2 + n меньше или равно -2
7/2 — 1/2 меньше или равно n меньше или равно -2 — 1/2
4 меньше или равно n меньше или равно -5/2
Целые n в этом промежутку это -4 и -3. Значит корни принадлежащие этому промежутку буду Pi/2 + Pi(-4) = -7Pi/2, Pi/2 + Pi(-3) = -5Pi/2
Аналогично делаем еще два неравенства
7Pi/2 меньше или равно Pi/4 + 2Pin меньше или равно -2Pi
-15/8 меньше или равно n меньше или равно -9/8
Целых n в этом промежутке нет
7Pi/2 меньше или равно -Pi/4 + 2Pin меньше или равно -2Pi
-13/8 меньше или равно n меньше или равно -7/8
Одно целое n в этом промежутку это -1. Значит отобранный корень на этом промежутку -Pi/4 + 2Pi*(-1) = -9Pi/4.
Значит ответ в пункте б: -7Pi/2, -5Pi/2, -9Pi/4
2) Отбор корней с помощью тригонометрической окружности
Чтобы пользоваться этим способом надо понимать как работает эта окружность. Постараюсь простым языком объяснить как это понимаю я. Думаю в школах на уроках алгебры эта тема объяснялась много раз умными словами учителя, в учебниках сложные формулировки. Лично я понимаю это как окружность, которую можно обходить бесконечное число раз, объясняется это тем, что функции синус и косинус периодичны.
Обойдем раз против часовой стрелки
Обойдем 2 раза против часовой стрелки
Обойдем 1 раз по часовой стрелки (значения будут отрицательные)
Вернемся к нашем вопросу, нам надо отобрать корни на промежутке [-7Pi/2; -2Pi]
Чтобы попасть к числам -7Pi/2 и -2Pi надо обойти окружность против часовой стрелки два раза. Для того, чтобы найти корни уравнения на этом промежутке надо прикидывать и подставлять.
Рассмотри x = Pi/2 + Pin. Какой приблизительно должен быть n, чтобы значение x было где-то в этом промежутке? Подставляем, допустим -2, получаем Pi/2 — 2Pi = -3Pi/2, очевидно это не входит в наш промежуток, значит берем меньше -3, Pi/2 — 3Pi = -5Pi/2, это подходит, попробуем еще -4, Pi/2 — 4Pi = -7Pi/2, также подходит.
Рассуждая аналогично для Pi/4 + 2Pin и -Pi/4 + 2Pin, находим еще один корень -9Pi/4.
Сравнение двух методов.
Первый способ (с помощью неравенств) гораздо надежнее и намного проще для пониманию, но если действительно серьезно разобраться с тригонометрической окружностью и со вторым методом отбора, то отбор корней будет гораздо быстрее, можно сэкономить около 15 минут на экзамене.




























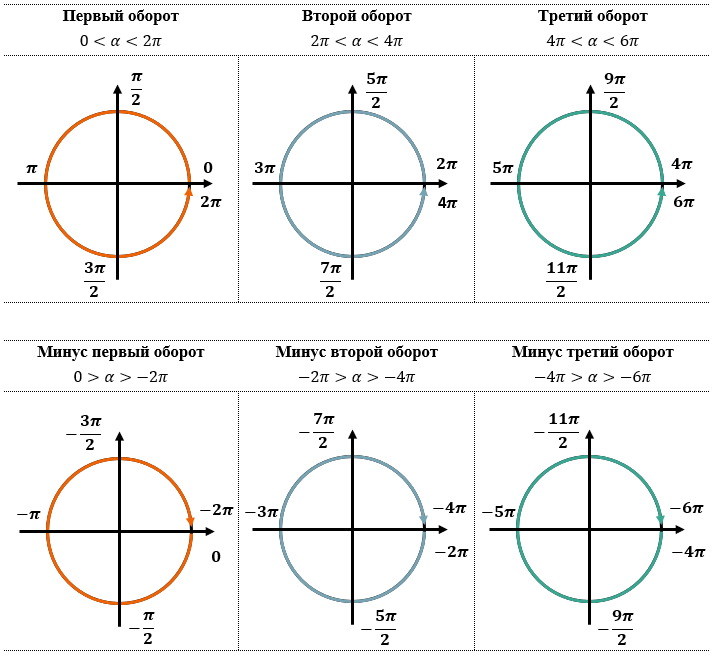
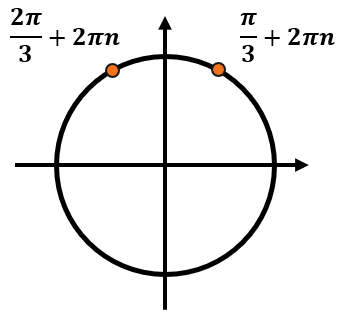
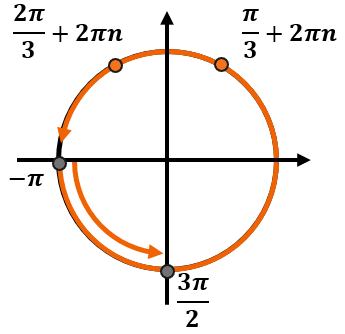
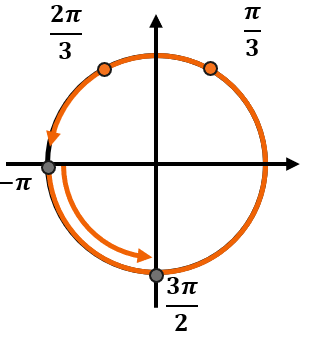






.png)




