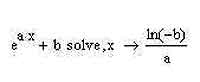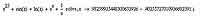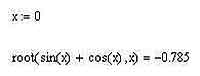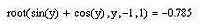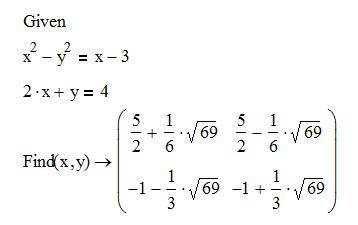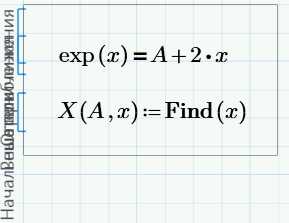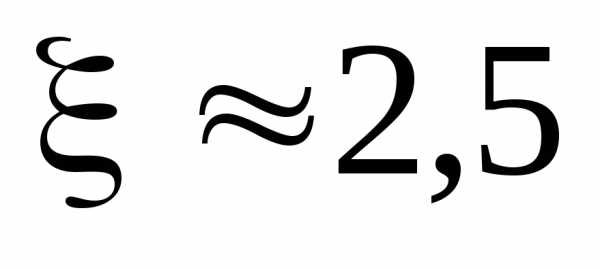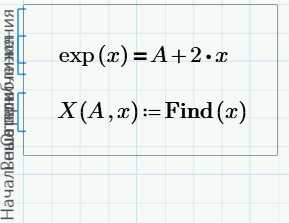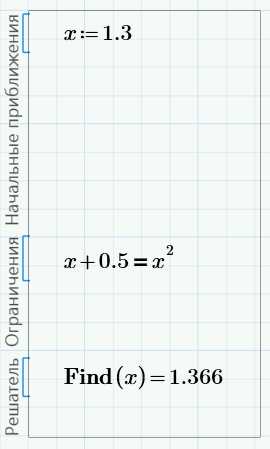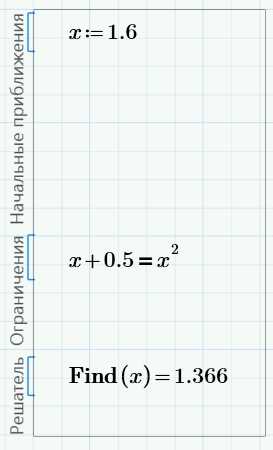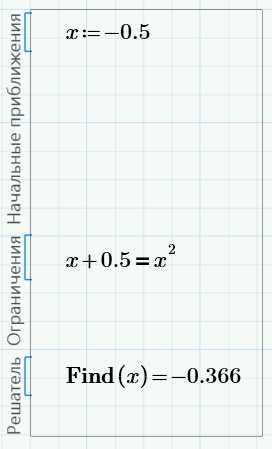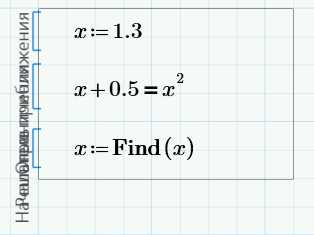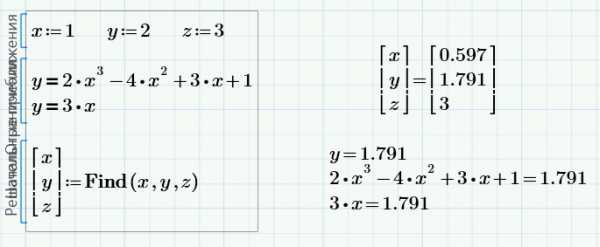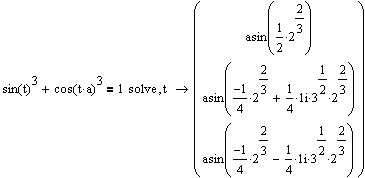Решение уравнений в MathCad
Для решения уравнений в Mathcad можно воспользоваться двумя способами:
Использование метода Given — Find:
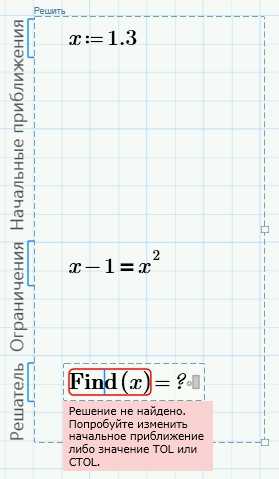
Это наиболее распространенный способ решения обычных алгебраических уравнений. Он достаточно прост. В рабочем поле записываем слово Given. Это служебное слово. Оно подключает определенные программные модули mathcad для обработки исходных данных, необходимых для решения уравнения численными методами.
Затем указывается начальное приближение для искомой переменной. Это нужно для увеличения скорости и точности решения уравнения. Если начальное приближение не задать, то mathcad по умолчанию примет его равным нулю
Рис. 1. Ввод данных в поле mathcad
Далее вводится уравнение. Его можно записать в явном или неявном виде. Само уравнение набирается с клавиатуры вручную с использованием панели Calculator. Из этой панели можно взять основные математические операции: дроби, тригонометрию, факториалы и прочее. Уравнение нужно записывать с использованием логического символа «ровно». На панели Boolean он выделен жирным шрифтом (см. рис. 2)
Рис. 2. Панели Boolean и Calculator
После уравнения вводится функция Find(x) (где х — переменная). Это функция, которая возвращает результат. Значение функции Find(x) можно присвоить какой-либо переменной с помощью символа «:=» и использовать ее далее в расчетах
Для получения результата, после Find(x) следует поставить символ «→» либо «=» из панели Evaluation (см. рис. 3). Причем, если вы используете символ «→«, то mathcad определит все корни уравнения и сформирует матрицу результатов. Но если вы используете символ «=«, то mathcad выведет единственный корень, который был наиболее близок к начальному приближению. Так что, если вы не знаете сколько корней имеет уравнение, то лучше использовать стрелочку
Рис. 3. Панель «Evaluation»
В зависимости от сложности уравнения через определенное время MathCad выведет результат. На рис.4 можно рассмотреть синтаксис и различие результатов выводимых mathcad. Обратите внимание, что выводимые результаты одного и того же уравнения различны
Рис. 4. Результат численного решения уравнения
Mathcad позволяет решать уравния в символьном виде. Например, если мы заменим все числовые константы на неизвестные параметры и решим уравнение относительно x, то результат выведется в символьном виде (см. рис. 5). Причем, обратите внимание, что в данном случае нам не нужно вводить начальное приближение и мы должны использовать символ «→» для вывода результата
Рис. 5. Результат символьного решения уравнения
Использование метода Solve:
Этот метод отличается от выше рассмотренного синтаксисом. На свободном поле вводим уравнение с использованием логического символа «ровно» из панели Boolean. После ввода уравнения, не смещая курсор ввода, на панели Symbolic нажимаем кнопку solve (см. рис. 6)
Рис. 6. Панель Symbolic
Затем ставим запятую и вводим переменную, относительно которой нужно решить уравнение (в нашем случае это x). Нажимаем Enter на клавиатуре и смотрим результат (см. рис. 7)
Рис. 7. Результат решения уравнения методом Solve
Обратите внимание, что метод подходит как для численного так и для символьного представления результатов
Как показывает моя личная инженерная практика, иногда не удается решить уравнения с помощью Given — Find, но получается в Solve. При этом, к сожалению, метод Solve не очень удобен для далнейшего использования результатов решения уравнения
Donec eget ex magna. Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fergiat. Pellentesque in mi eu massa lacinia malesuada et a elit. Donec urna ex, lacinia in purus ac, pretium pulvinar mauris. Curabitur sapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Duis dapibus rutrum facilisis. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam tristique libero eu nibh porttitor fermentum. Nullam venenatis erat id vehicula viverra. Nunc ultrices eros ut ultricies condimentum. Mauris risus lacus, blandit sit amet venenatis non, bibendum vitae dolor. Nunc lorem mauris, fringilla in aliquam at, euismod in lectus. Pellentesque habitant morbi tristique senectus et netus et malesuada fames ac turpis egestas. In non lorem sit amet elit placerat maximus. Pellentesque aliquam maximus risus, vel venenatis mauris vehicula hendrerit.
Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fersapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique lorem ipsum dolor.
Нахождение корней кубического уравнения в среде Microsoft Office Excel 2003, Mathcad 13, Turbo Pascal 7.0
Страницы работы
Содержание работы
Балтийский Государственный Технический Университет «ВоенМех» им. Д.Ф. Устинова
Кафедра прикладной математики и информатики
Курсовая работа по дисциплине «Информатика»
Нахождение корней кубического уравнения в среде Microsoft Office Excel 2003, Mathcad 13, Turbo Pascal 7.0.
Студент Ефимов Евгений Михайлович Е19108
Преподаватель Гнидин Вячеслав Васильевич
Санкт – Петербург 2010
Решение кубического уравнения
· Работа в среде Microsoft Office Excel 3
· Работа в среде Mathcad 13 4
· Работа в среде Turbo Pascal 7.0 5
· Вывод по результатам работы 9
Работавсреде Microsoft Office Excel
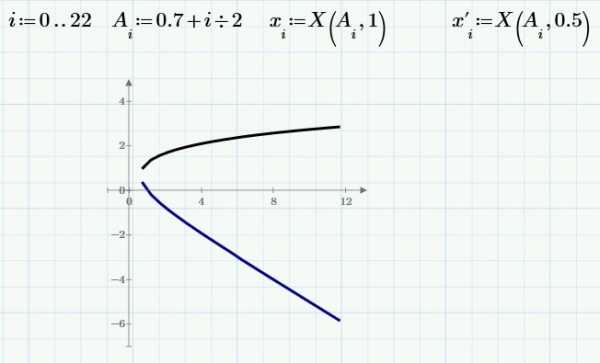
С помощью графика, построенного по точкам в среде Excel, я нахожу промежутки, при которых корни уравнения находятся внутри этих промежутков.
Кубическое уравнение вида a + b + cx + d = 0 имеет коэффициенты, равные:
A = 1 B= 2,28 C= -1,9347 D= -3,907574
Работа в среде Mathcad 13
2) Построение графика
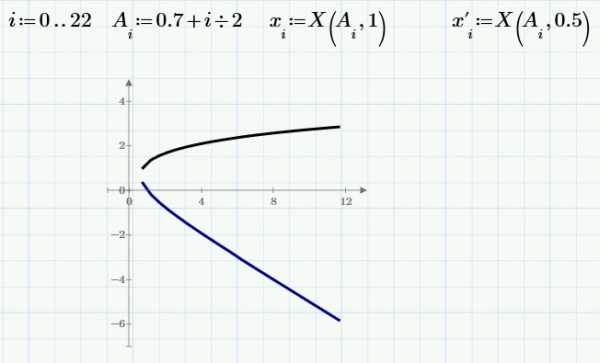
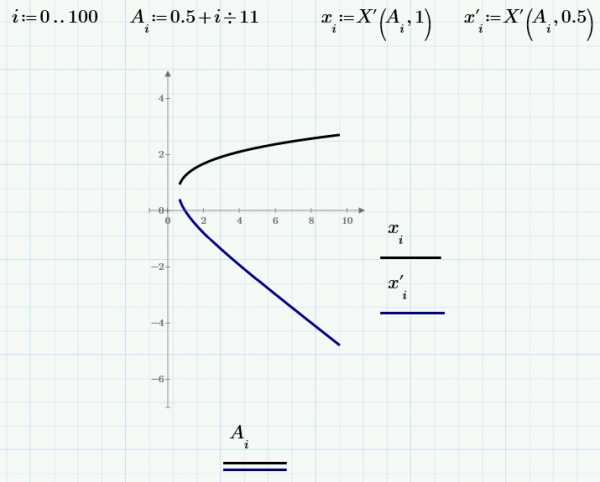
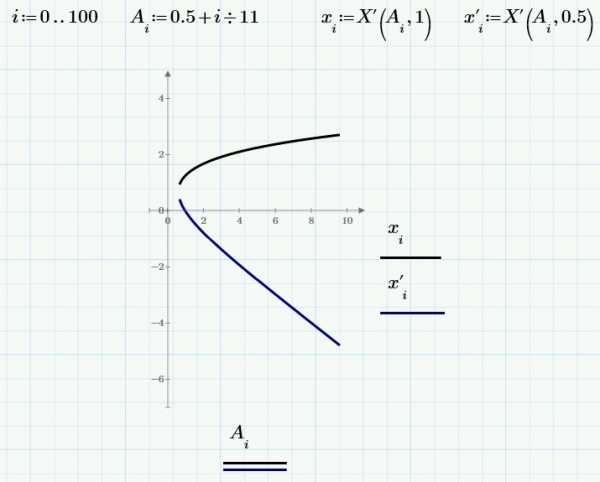
Задав функцию и промежутки в среде MathCAD 13, я построил график.
С помощью встроенной функции «Given -Find» в среде MathCAD 13 вычислил корни кубического уравнения.
Составление программы, позволяющую находить корни кубического уравнения с заданной точностью на известных промежутках.
Т.к. с достаточно высокой точностью известны промежутки, на которых находятся корни уравнения, то решено было использовать наиболее простой алгоритм: нахождение минимального по модулю значения функции на заданном промежутке с помощью прямой подстановки; шаг значений переменной задаёт необходимую точность.
const k1=1; k2=2.28; k3=-1.9347; k4=-3.907574;
var a,b,c,fa,fc,eps:real; key:integer; f:text;
Как найти корни кубического уравнения в маткаде
Уравнение и системы уравнений в математическом пакете Mathcad в символьном виде решаются с использованием специального оператора символьного решения solve в сочетании со знаком символьного равенства, который может быть также введен с рабочей панели “Символика”. Например:
Аналогичные действия при решении уравнений в Mathcad можно выполнить, используя меню “Символика”. Для этого необходимо записать вычисляемое выражение. Затем выделить переменную, относительно которой решается уравнение, войти в меню Символика, Переменная, Разрешить. Например:
В случае, если необходимо упростить полученный результат, используется знак равенства [=]. Например:
При решении некоторых уравнений, результат включает большое количество символов. Mathcad сохраняет его в буфере, а на дисплей выводитcя сообщение: “This array has more elements than can be displayed at one time. Try using the “submatrix” function” – “Этот массив содержит больше элементов, чем может быть отображено одновременно. Попытайтесь использовать функцию “submatrix””. В этом случае рекомендуется использовать численное решение. Или, в случае необходимости, символьное решение может быть выведено и отображено на дисплее.
Символьное решение может быть получено с использованием блока given … find. В этом случае при записи уравнения для связи его левой и правой части использует символ логического равенства “=” с панели инструментов Boolean, например:
Аналогичным способом решаются системы уравнений в символьном виде. Ниже приводятся примеры решения систем уравнений в символьном виде различными способами. При использовании оператора символьного решения solve в сочетании со знаком символьного равенства 
Пример использования блока given…find для решения системы уравнений:
http://vunivere.ru/work59449
http://allmathcad.com/ru/reshenie-uravnenij-i-sistem-uravnenij.html
Решение уравнений на бумаге — это задача, с которой каждый знаком еще со школьной скамьи. Сначала мы учились решать простые линейные уравнения, деля а на b и получая x, потом — системы уравнений, затем переходили к квадратным уравнениям. Находим дискриминант, извлекаем корень, делим, складываем… Все это вам знакомо, не так ли? Знакомы, наверное, и трансцендентные уравнения: тригонометрические, логарифмические (они же показательные), смешанные…
Системы трансцендентных уравнений — это вообще песня, причем песня из серии «этот стон у нас песней зовется». Люди давно уже пришли к выводу, что решать уравнения с помощью компьютера — отнюдь не роскошь, а вполне разумный подход к делу. Только раньше каждый, кто желал решить уравнение, должен был уметь программировать и владеть при этом какими-нибудь численными методами — например, методом Гаусса для решения систем линейных уравнений или методом Зейделя для решения трансцендентных. Сейчас эти все методы, конечно, тоже используются, но большая часть пользователей могут забыть их как страшный сон — все эти вычисления возможны в MathCAD’е, и именно о том, как их выполнять в этом замечательном математическом пакете, я сейчас и расскажу.
Аналитическое решение уравнений
Довольно значительное число уравнений поддаются аналитическому решению — т.е. решению в обобщенном виде, когда корни уравнения представляются в виде какой-то формулы, выражающей их зависимость от входящих в уравнение функций и различных коэффициентов перед ними. При этом, однако, надо заметить, что такой подход применим отнюдь не ко всем уравнениям — большая часть трансцендентных уравнений не может быть решена аналитически. Поэтому мы сейчас будем говорить преимущественно о полиномиальных уравнениях, известных также под названием алгебраических. Алгебраическим называется уравнение, которое можно преобразовать так, что в левой части будет многочлен от одной или нескольких неизвестных, а в правой — нуль. Степень многочлена называется степенью уравнения. Простейшие алгебраические уравнения: линейное уравнение — уравнение 1-й степени с одним неизвестным ax + b = 0, имеющее один действительный корень; квадратное уравнение — уравнение 2-й степени ax2 + bx + c = 0, которое в зависимости от значения коэффициентов может иметь либо два различных, либо два совпадающих действительных корня либо не иметь действительных корней. Вообще алгебраическое уравнение степени n не может иметь более n корней, что доказывается в рамках основной теоремы алгебры, которую в ВУЗах проходят в курсе математического анализа.
Что ж, давайте, пожалуй, перейдем к практике. То есть запустим MathCAD, включим панель символьных вычислений (Symbolic) — о том, как это сделать, уже было рассказано ранее в первой статье про MathCAD. На этой панели нам с вами понадобится оператор solve — именно он отвечает за аналитическое решение уравнений. Общий вид этого оператора такой: уравнение solve, переменная > решение. Здесь уравнение — это именно то уравнение, решение которого мы хотим найти в общем виде, а переменная — это символ, обозначающий в нашем уравнении переменную величину. Его нужно указывать для того, чтобы MathCAD (не такой уж он умный, как иногда кажется!) мог отличить переменную от коэффициентов. Давайте попробуем найти решение обычного квадратного уравнения ax2 + bx + c = 0. Для этого нажмите на кнопку Solve на панели инструментов символьных вычислений и на то место, где должно быть записано уравнение, введите наше квадратное уравнение. Здесь есть два тонких момента. Во-первых, чтобы записать «x2», нужно после x нажать Shift + 6 — тогда вы перейдете от записи переменных к записи показателя степени. Чтобы затем переключиться в режим записи других слагаемых в уравнении, достаточно нажать на клавиатуре стрелку вправо. Вообще навигация по записям в MathCAD при помощи стрелок вполне прозрачная — вы передвигаетесь стабильно в том направлении, куда указывает стрелка, и перескакиваете в показатели степени и индексы автоматически. Во-вторых, при записи уравнения в операторе solve «равно» нужно не обычное, а логическое — оно записывается с клавиатуры комбинацией Ctrl + =. При этом, если правая часть вашего уравнения равна нулю, то и ноль, и знак равенства можно опускать — MathCAD посчитает, что уравнение записано в стандартном виде, и успешно (если это, конечно, возможно) решит его. Итак, давайте посмотрим, что получилось от «скармливания» оператору solve нашего с вами квадратного уравнения.
Как видите, ничего неожиданного не произошло: MathCAD честно воспользовался известными всем еще из школьного курса алгебры формулами Виета, а решения уравнения записал в виде вектора-столбца. Несложно самостоятельно убедиться в том, что MathCAD знает и формулы Кордано для решения кубических уравнений — их он также может решать с произвольными коэффициентами. Правда, конечно, решения получаются несравненно более громоздкими, а потому я их здесь не буду приводить. Это же справедливо и для уравнений четвертой степени, для которых также существуют аналитические решения. Решение других видов уравнений (например, показательных) в аналитическом виде также вполне возможно. Например, если мы запишем уравнение eax + b = 0, то MathCAD совершенно справедливо сообщит, что решением этого уравнения будет выражение ln(-b)/a. Точно так же можно решать простые тригонометрические уравнения.
Численное решение уравнений с помощью функции solve
Но, конечно, такие красивые результаты в максимально обобщенной форме мы сможем получать далеко не всегда. Уже на уравнениях пятой степени MathCAD спотыкается, и произвольные коэффициенты приходится заменять постоянными. Впрочем, в этом ничего страшного нет — даже уравнения третьей степени со всеми произвольными коэффициентами решать вряд ли имеет смысл, поскольку гораздо проще подставить коэффициенты и получить нормальные числа в решении — в конце концов, общие формулы для решения алгебраических выражений используются именно из-за того, что живому человеку гораздо проще подставить числа в готовую формулу, чем подбирать каждый раз корни уравнения. С компьютерами дело обстоит в большинстве случаев с точностью до наоборот — получить численное решение уравнения зачастую гораздо проще, чем аналитическое. Оператор solve умеет находить и численные решения уравнений. Если аналитическое решение получить не удается, он автоматически подключает систему нахождения численных решений уравнений. Так что, если мы запишем совершенно невообразимое для нормального человека уравнение x25 + sin(x) + ln(x) + ex + 1/x = 0, то MathCAD, и глазом не моргнув, выдаст нам результат вычислений.
Но численное решение уравнений с помощью функции solve — честно говоря, не лучшая идея. Некоторые виды уравнений она решает из рук вон плохо — в первую очередь, конечно же, это относится к уравнениям тригонометрическим. Начнем с того, что эта функция выдает решение только для одного периода в то время, как большая часть решений тригонометрических уравнений описывается с помощью специального целочисленного параметра, выражающего номер периода. Но это, в общем-то, не самое худшее, поскольку иногда использование solve приводит к получению совершенно неверного результата, который при подстановке его в уравнение дает совершенно неверное значение. Конечно, это является минусом MathCAD’а, но положение дел совсем не фатально. Если использовать специальные методы решения трансцендентных уравнений, то численные результаты будут совершенно адекватными. Можно также пойти по другому пути, например, преобразуя выражения с помощью символьного процессора MathCAD (о том, как это делается, я еще расскажу в дальнейшем), а затем уже решая с помощью solve более простые уравнения, получившиеся в результате этих преобразований. Численное решение уравнений требует от пользователя понимания того, что он ожидает в результате этого решения получить. Поэтому прежде, чем приступать к рассказу о самом процессе численного решения, я расскажу об одной полезной функции, которая пригодится для численного решения простых трансцендентных уравнений.
Решение уравнений с помощью функции root
Эта очень хорошая и полезная во всех смыслах функция имеет лишь одно ограничение — она может найти всего один корень. К сожалению, несущественным это ограничение назвать, честно говоря, сложно. Впрочем, вы увидите, что и его запросто можно обойти — разработчики MathCAD, по крайней мере, предусмотрели такую возможность, и ею вполне можно воспользоваться, если, конечно, в этом есть необходимость. Функция root имеет следующий вид: root(функция, переменная). Функция — это фактически левая часть уравнения в стандартном виде, т.е. уравнения, в котором левая часть равна нулю. Переменная — это, конечно же, тот символ, который обозначает в функции переменную величину. Для использования функции root нужно задать начальное приближение — то есть число, отталкиваясь от которого, функция root будет искать корни нашего уравнения. От начального приближения может весьма существенно зависеть и сам результат работы функции root, особенно если искомые корни уравнения находятся сравнительно близко. Начальное приближение задается очень просто: набираем имя нашей переменной до функции root, ставим двоеточие (MathCAD самостоятельно преобразует его в знак присвоения «:=»), пишем число, соответствующее нашему начальному приближению.
В принципе, вместо начального приближения можно задать интервал, в пределах которого должно лежать решение, отыскиваемое нами с помощью функции root. Для этого после имени переменной в списке параметров функции нужно (через запятую, конечно же) указать начало и конец интервала, на котором должно располагаться решение. У этого способа есть только одно существенное но: числа, определяющие начало и конец этого интервала, должны иметь разные знаки. При этом, если уравнение не имеет действительных корней, то и интервал нужно задавать в комплексной форме. Мнимая единица при этом записывается как i или как j.
Как видите, для численного нахождения уравнений с помощью функции root необходимо довольно точно представлять, где именно должны располагаться корни уравнения — сделать это можно, например, с помощью графика функции, на котором с помощью трассировки можно определить нули функции. Но о том, как строить графики и как ими потом пользоваться, как-нибудь в другой раз.
SF, spaceflyer@tut.by
Компьютерная газета. Статья была опубликована в номере 14 за 2008 год в рубрике soft
Уравнение и системы уравнений в математическом пакете Mathcad в символьном виде решаются с использованием специального оператора символьного решения solve в сочетании со знаком символьного равенства, который может быть также введен с рабочей панели “Символика”. Например:
Аналогичные действия при решении уравнений в Mathcad можно выполнить, используя меню “Символика”. Для этого необходимо записать вычисляемое выражение. Затем выделить переменную, относительно которой решается уравнение, войти в меню Символика, Переменная, Разрешить. Например:
В случае, если необходимо упростить полученный результат, используется знак равенства [=]. Например:
При решении некоторых уравнений, результат включает большое количество символов. Mathcad сохраняет его в буфере, а на дисплей выводитcя сообщение: “
This array has more elements than can be displayed at one time. Try using the “submatrix” function” – “Этот массив содержит больше элементов, чем может быть отображено одновременно. Попытайтесь использовать функцию “submatrix””. В этом случае рекомендуется использовать численное решение. Или, в случае необходимости, символьное решение может быть выведено и отображено на дисплее.
Символьное решение может быть получено с использованием блока given … find. В этом случае при записи уравнения для связи его левой и правой части использует символ логического равенства “=” с панели инструментов Boolean, например:
Аналогичным способом решаются системы уравнений в символьном виде. Ниже приводятся примеры решения систем уравнений в символьном виде различными способами. При использовании оператора символьного решения
solve в сочетании со знаком символьного равенства система уравнений должна быть задана в виде вектора, который вводится вместо левого маркера оператора solve, а перечень переменных, относительно которых решается система, вместо правого маркера. Например:
Пример использования блока given…find для решения системы уравнений:
allmathcad.com
Уравнения с одним неизвестным в Mathcad
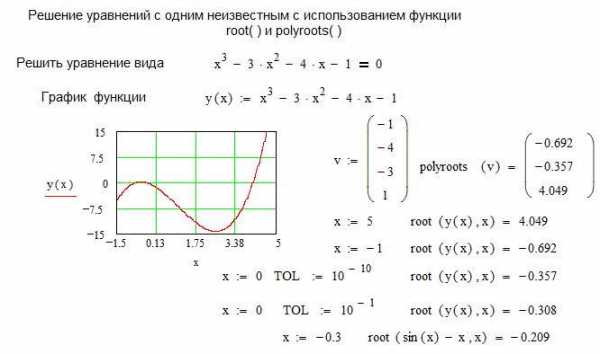
Простейший способ найти корень уравнения с одним неизвестным в Mathcad обеспечит функция root ( ). Аргументами функции root ( ) являются вид функции определяющей решаемое уравнение и имя переменой, относительно которой ищется решение — root (f(x),x) Если уравнение в Mathcad содержит несколько корней, то функция обеспечивает нахождение единственного корня, ближайшего к заданному начальному значению для искомой переменной. Точность вычислений может быть увеличена или уменьшена посредством задания значения переменной
TOL, равной по умолчанию 10-3 и определённой в меню Math, Options (Математика, Опции). Установленное значение TOL также оказывает влияние на точность вычислений.
В случае, если решаемое уравнение в Mathcad представлено полиномом, то все его решения могут быть получены с помощью функции polyroots (v). В качестве аргументов этой функции выступает вектор коэффициентов полинома –v, а результат представляется в виде вектора корней полинома. На листинге представлен пример нахождения корней уравнений с использованием функций root ( ) и polyroots ( ).
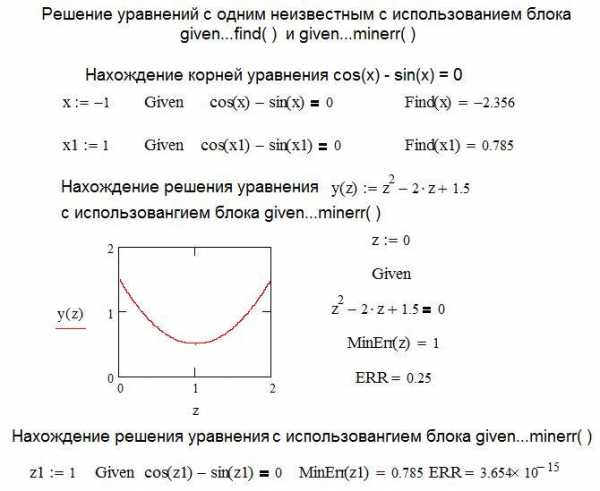
Другим способом решения уравнений в Mathcad является применение специального вычислительного блока, начинающегося с ключевого слова given с использованием функций find( ) и minerr ( ).
Блок имеет следующую структуру:
Начальное значение искомой переменной
given
Решаемое уравнение
Выражение с использованием функции find( ) или minerr ( )
Нахождение корней уравнения в Mathcad с использованием блока given…find ( ) в чем – то аналогично использованию функции root ( ). В Mathcad задается начальное значение для искомой переменной, после находится решение, ближайшее к заданному начальному условию. Использовании блока given…minerr ( ) имеет существенные особенности. Решение будет найдено в любом случае, даже при его отсутствии. Дело в том, что ищется не решение системы, а минимальная невязка уравнений. На листинге рассмотрена функция, заведомо не имеющая действительных корней и при использовании блока
given…minerr ( ) найдено решение, значение, которое наиболее приближено к оси х, то есть обеспечивает минималь-ную невязку. Значение невязки (ошибки) показывает системная переменная ERR.
allmathcad.com
Решение системы уравнений в Mathcad
Первоначально рассмотрим СЛАУ в Mathcad. Для их решения может использоваться блок given …find() или специальная функция lsolve(). Применение блока given …find() предопределяет необходимость задания начальных значений искомых переменных. Далее после ключевого слова given описывается СЛАУ и с помощью find() находится решение. Следует указать, что в том случае, когда
СЛАУ в Mathcad имеет бесконечное множество решений блок given …find() дает конкретный результат, что несомненно следует отнести к недостаткам. В случае отсутствия решения будет выдано сообщение “Matrix is singular. Cannot compute its inversу – Матрица сингулярная. Нельзя вычислить эту инверсию”.
Применение функции lsolve( ) позволяет избежать этого недостатка. Функция lsolve(M,b) имеет два аргумента. M – матрица коэффициентов при неизвестных, b – вектор свободных членов. На листинге приведен пример решения СЛАУ.
Пример решения СЛАУ:

given…find() и given…minerr () для решения систем нелинейных уравнений.
allmathcad.com
Урок 24. Решение уравнений в Mathcad – использование функций
Решение уравнений является важным для решения практических задач. Поэтому уделим уравнениям еще один урок.
Блок решения в функции
Если Вы хотите исследовать изобразить на графике поведение уравнения в зависимости от значения определенного параметра, Вам, возможно, придется решить систему уравнений много раз. Вы можете сделать это, используя блок решения в функции. Покажем на примере: предположим, мы хотим исследовать поведение решения следующего уравнения в зависимости от различных значения параметра
A:
Блоку решения не нужно ни значение параметра, ни начальное приближение, поскольку решение есть функция этих двух значений. Эти значения мы будем задавать при вызове функции.
Функцию можно использовать сколько угодно раз:
Использовать функцию можно с диапазоном переменных:
Такая техника решения не самая надежная. Если хотя бы одно решение не может быть найдено, Вы не получите и решений для других параметров (это произойдет, если задать
A<0.7). Поэтому лучше заранее проверить свою функцию.
Сообщения об ошибке можно избежать, написав маленькую программу:
Если блок решения выдает сообщение об ошибке, на выходе получим значение NaN (Not a Number – «Не Число»), которое просто не отображается на графике:
Построим две ветки уравнения с использованием этого приема:
Когда переменных много
Расчеты часто содержат несколько переменных, но Вам, возможно, придется использовать лишь некоторые из них. В качестве примера рассмотрим систему восьми уравнений, где нам нужно получить только значения X и Y. Начальные приближения следует задать для всех переменных:
Решение представляет собой вектор из восьми элементов, но нам нужны лишь элементы с индексами 0 и 1.
Минимизация ошибки
Find() – не единственный решатель в Mathcad. Еще один полезным решателем является Minnerr(), находящий решения, которые минимизируют ошибку в системе уравнений. Рассмотрим пример: есть набор данных, которые мы хотим аппроксимировать уравнением Бейтмена:
Мы хотим подобрать три константы в уравнении Бейтмена таким образом, чтобы ошибка приближения была минимальна. У нас есть семь уравнений (по одной для каждого эксперимента) и три константы, так что в системе избыток данных. Minerr() может обработать эту проблему:
Замечания:
- Три константы являются переменными для этой системы.
- Переменные не могут иметь счетных индексов.
- У параметров (t и c) могут быть счетные индексы.
Возможно, Вам хотелось бы использовать цикл
for для семи уравнений, но в блоке решений этого сделать нельзя.
Для полностью определенных систем (с одинаковым числом независимых уравнений и неизвестных) функция Minerr() дает тот же ответ, что и Find().
Резюме
В этом уроке мы определили способы расширенного использования блоков решения:
- Вы можете определить вывод блока решения как функцию. Таким образом в блок решения можно передавать параметры и начальные приближения.
- Если при вычислении точек для графика хотя бы одно решение не будет найдено, то график не будет построен. Этой ошибки можно избежать, написав небольшую программу с использованием “try/on error”, которая выводит NaN (Not a Number – Не Число), если результат отсутствует.
- Для двух и более неизвестных (и уравнений) вывод блока решения является вектором. Если нужен один или два элемента этого вектора, их можно вывести, используя подстрочные индексы.
- Вместо функции Find() можно использовать Minerr() – она минимизирует ошибку для заданного набора ограничений, в том числе, если данные избыточны. Minerr() часто может дать приближенный результат, когда Find() выдает ошибку.
Другие интересные материалы
sapr-journal.ru
2. Решение уравнений в Mathcad
2.1. Численное решение уравнения
Для простейших уравнений
вида f(x) = 0
решение в Mathcad находится с помощью
функции root
root(
f(х1,
x2,
…),
х1,
a,
b
)
Возвращает значение х1,
принадлежащее отрезку [a,
b],
при котором выражение или функция f(х)
обращается в 0. Оба
аргумента этой функции должны быть
скалярами. Функция возвращает скаляр.
Аргументы:
f(х1,
x2,
…)
— функция,
определенная где-либо в рабочем документе,
или выражение. Выражение должно возвращать
скалярные значения.
х1
— — имя переменной,
которая используется в выражении. Этой
переменной перед использованием функции
root
необходимо присвоить
числовое значение. Mathcad использует его
как начальное приближение при поиске
корня.
a,
b
– необязательны, если
используются, то должны быть вещественными
числами, причем a
< b.
Наиболее распространен
графический способ
определения начальных приближений.
Принимая во внимание, что действительные
корни уравнения f(x)
= 0 — это точки пересечения графика функции
f(x)
с осью абсцисс, достаточно построить
график функции f(x)
и отметить точки пересечения f(x)
с осью Ох,
или отметить на оси Ох
отрезки, содержащие по одному корню.
Построение графиков часто удается
сильно упростить, заменив уравнение
f(x)
= 0 равносильным
ему уравнением:
|
, |
где функции
f1(x)
и f2(x)
— более простые, чем функция
f(x).
Тогда, построив графики функций у
=
f1(x)
и у
= f2(x),
искомые корни получим как абсциссы
точек пересечения этих графиков.
Пример.
Графически отделить
корни уравнения:
Уравнение (1) удобно
переписать в виде равенства:
lg x=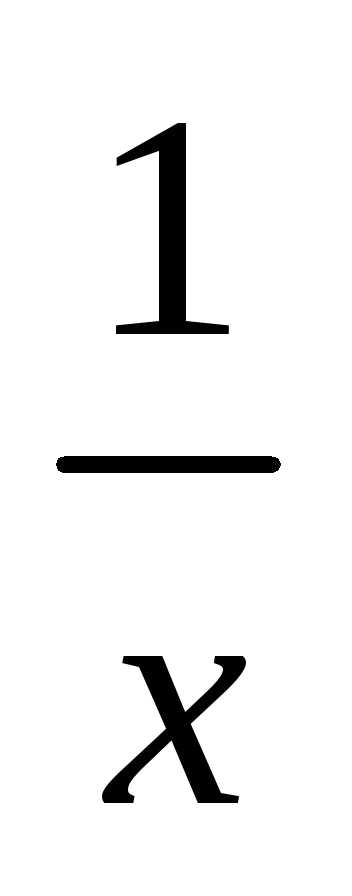
Отсюда ясно, что корни
уравнения (1) могут быть найдены как
абсциссы точек пересечения логарифмической
кривой y
= lg x и
гиперболы y
=
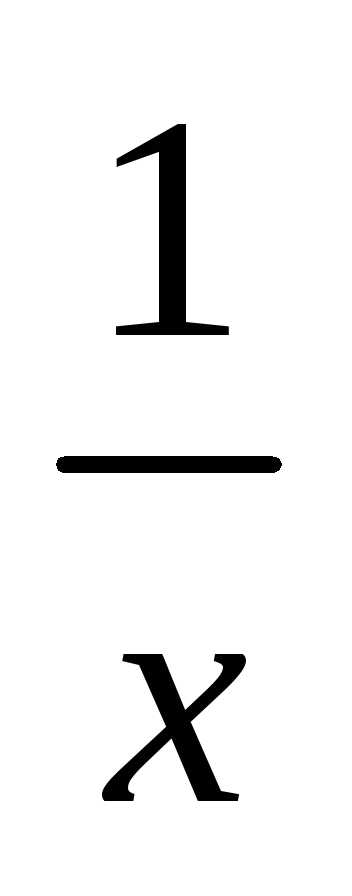
Построив эти кривые, приближенно найдем
единственный корень
уравнения (1) или определим его содержащий
отрезок [2, 3].
Упражнение 1.
Построить график
функции f(x)
(Таблица 1) и приблизительно
определить один из корней уравнения.
Решить уравнение f(x)=
0 с
помощью встроенной функции Mathcad root.
Таблица 1
Варианты упражнения 1
-
x3
+ x2
-2sin(x)
=05x
— 8ln(x) = 8x2
+ x — cos(3x) = 1x2
— sin(4x) = 03x
— 2ln(x) = 52x
-2,2x =0x2
— 2x -sin(3x) =1x
— sin(x)
-0.25
= 03x —
ex
= 03x
— 2ln(x) = 5ex
+ e-3x
= 4x
+4sin(x) = 22.7x
— 1.5ln(x) = 2.8x3
+ x2
-2sin(x)
=0ex
-6x =3
studfiles.net
Решение уравнений в MathCad – использование функций
Одной из самых важных математических задач является решение уравнений. Поэтому нам стоит остановиться на них еще подробнее.
Блок решения в функциях
Если вам нужно просмотреть на графике действие уравнения, относительно определенных параметров, вам, судя по всему, придется решить данное уравнение огромное количество раз. Давайте обратимся к визуальному примеру. Попробуем просмотреть поведение решения уравнений в зависимости от разных значений параметра А.
Блок решения не нуждается в значениях параметров, изначальных приближениях. Решением будет считаться функция двух указанных значений. Их мы будем оформлять во время вызова функций.
Каждая функция может быть использованной неограниченное количество раз.
Так, можно воспользоваться функцией с диапазонами переменных.
Данная методика решения задач не считается самой проверенной и надежной. Если хотя бы одно решение не удастся найти, пользователь не сможет перейти к решению остальных параметров. Вот почему нужно быть максимально уверенным в правильности заданных функций.
Чтобы избежать появления ошибок, достаточно написать небольшую программу.
Когда блок решения начинает выдавать ошибки, мы получим значение NaN (Not a Number – «Не Число». Впрочем, на графике мы его не увидим.
Теперь разработаем две ветки уравнения при использовании данного опционала:
Что делать в случаях, когда переменных много
Бывают расчеты, в которых вмещено несколько переменных. Вполне возможно, что когда-то с ними столкнетесь и вы. Для примера мы возьмем систему, которая состоит из восьми уравнений. Нам понадобится получить только X и Y. Сначала же зададим всем переменным начальное приближение.
Решение становится вектором из восьми пунктов. Нам потребуются исключительно те элементы, которые вмещают индексы 0 и 1.
Устранение ошибки
Теперь давайте на примере просмотрим набор данных, которые будут аппроксимированны в соответствии с уравнениями Бейтмена.
Сейчас мы собираемся разработать три константы при помощи уравнения Бейтмена таким образом, чтобы актуальная ошибка приближения была минимизирована. Что мы имеем? Систему из семи уравнений. Каждая из них соответствует отдельному эксперименту. Также у нас есть три константы, а, следовательно, система пострадала от преизбытка данных. Опция Minerr () станет оптимальным инструментом для обработки данной проблемы.
Константы – это переменные нашей системы. Переменные не имеют математических индексов. Параметры имеют индексы счетного типа.
archicad-autocad.com
Урок 23. Нелинейные уравнения в Mathcad
Mathcad может решать системы линейных и нелинейных уравнений с помощью встроенных алгоритмов. На самом деле, «решать» — не совсем верное определение того, что делает программа. Лучше рассуждать так: Вы задаете приближенное значение, затем программа уточняет эту оценку. Поэтому, используя такую технологию решения, нужно знать, что Вы делаете. Вы должны понимать, как ведет себя функция, которую исследуете. Иначе Вы можете быть разочарованы.
Изучение «решения» начнем с уравнений с одной переменной. В этом случае поведение уравнения можно понять, построив график. Позже мы рассмотрим системы уравнений.
Уравнения с одной переменной
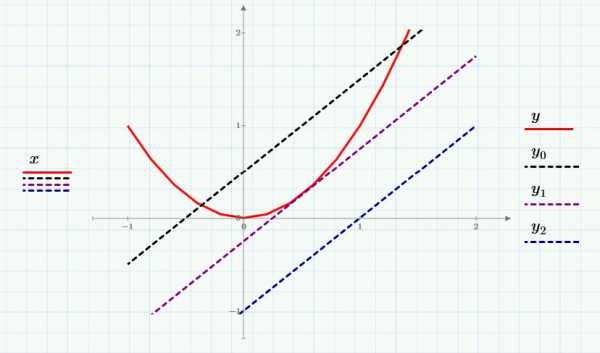
Уравнение, которое мы рассмотрим, достаточно простое:
Рассмотрим это уравнение как пересечение прямой линии (левая часть) и парабола (правая часть). Построим графики трех прямых линий и посмотрим, что произошло:
Первая (самая верхняя) линия дважды пересекается с параболой около точек x=-0.3 и x=1.3. У второй линии – одно пересечение (или два близко расположенных) возле точки x=0.5. Пересечений с третьей прямой (самой нижней) нет.
Решения
Сначала рассмотрим самую верхнюю линию. Чтобы получить решение, нам нужен Блок решения (вкладка Математика –> Области –> Блок решения). Заполним блок для решения первого уравнения:
Здесь есть три области для различных записей:
— начальные приближения;
— ограничения;
— решатель.
В области ограничений мы записали уравнение, которое хотим решить. В первой области мы задали приближенное решение этого уравнения. Функция Find(), которую мы записали в последней области – это решатель.
Как видно, решение 1.366 – это правое пересечение прямой и параболы. Начальное приближение не критично – можно ввести 1.6, щелкнуть мышью вне блока и получить тот же результат:
Изменим начальное приближение на значение, близкое к левому пересечению, скажем, -0.5. Решение изменится на -0.366:
Измените начальное приближение обратно на 1.3.
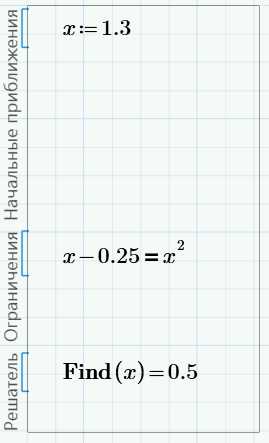
Теперь поменяем константу 0.5 в уравнении на -0.25. Решение изменится на 0.5:
Этот же ответ мы будем получать для любого значения начального приближения – это единственное решение.
Наконец, изменим константу в уравнении на -1 (последнее уравнение). Щелкнем вне блока и получим сообщение об ошибке:
Решения нет. Изменим константу обратно на 0.5.
Вывод решения
Переменные в блоке решений локальны. Вы не можете использовать их значения вне блока. Вернемся к уравнению, где приближенное значение задано 1.3. Мы решили уравнение, чтобы найти более точное решение x=1.366. Однако если мы попробуем вывести значение x, мы получим вектор, которые определили для нашего графика.
Если Вы хотите использовать результат решения в дальнейших вычислениях, нужно присвоить функцию решателя переменной:
Тогда получим верный результат:
Решение систем уравнений
Для примера решим систему трех уравнений: два линейных и одно кубическое. Здесь три неизвестных – начальное приближение даем для всех трех:
Все три ответа можно вывести в вектор:
Удалите последнее из трех уравнений. Решение все равно будет найдено, с учетом двух оставшихся уравнений:
Однако, такое решение может быть не тем, которое Вам нужно.
Обратите внимание еще на некоторые детали. В блоке решения используются два вида знака «равно»: знак присваивания для начальных приближений и для решателя Find, и знак булева равенства в уравнении. Эта разница очень важна. Еще один момент – щелкните по слову Find в области решателя, откройте вкладку Математика. В строке Обозначения должно быть отмечено «Ключевое». Некоторые другие ключевые слова мы рассмотрим в последующих уроках.
Растворимость вещества
Рассмотрим растворение вещества DOH. Это двухстадийный процесс: сначала растворяется твердая фаза, затем растворенные части диссоциируют на D и OH. Малую растворимость можно повысить, добавив небольшое количество сильной кислоты HA. Она диссоциирует, и ионы водорода вступают в реакцию с гидроксильной группой:
Как зависит общая растворимость D от количества добавленной кислоты? Концентрацию будем считать в моль/л. Концентрация насыщения нерастворенной кислоты:
Начнем с концентрации кислоты:
Константы равновесия реакции:
Блок решения начинается с трех неизвестных и их начальных приближений:
Решение:
Общая концентрация вещества:
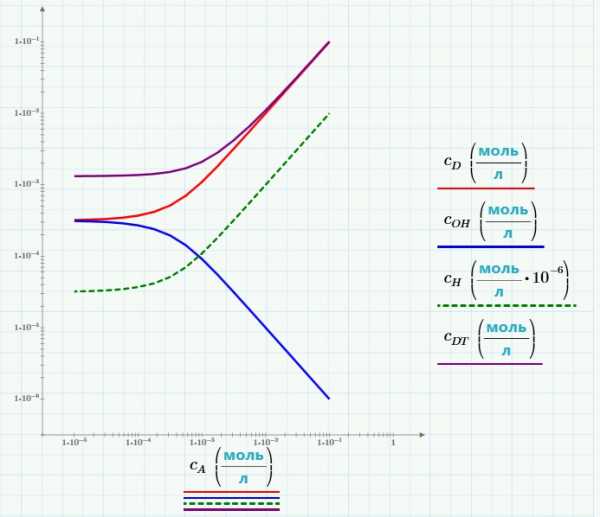
Расчет для построения графика (подробнее о таких расчетах поговорим в следующем уроке):
График показывает концентрацию как функцию от количества добавленной кислоты. Концентрация ионов водорода на порядки меньше, чем концентрации других элементов. Поэтому мы изменили масштаб в миллион раз, чтобы показать этот график в тех же осях:
Если концентрация кислоты мала, решение содержит низкую концентрацию DOH, которая диссоциирует только частично. При увеличении концентрации кислоты, все больше и больше вещества диссоциирует.
Резюме
- Если есть уравнение или система уравнений, Вы можете дать приближенное решение, а Mathcad улучшит эту оценку. Такой способ используется в Блоке решения.
- Первая часть блока решения – начальные приближения, т.е. Ваши оценки. Здесь используется знак присваивания «:=». Эти значения могут быть помещены и до блока.
- В области «Ограничения» (уравнения) нужно использовать булево равенство [Ctrl+=]. Это единственный знак, по обе стороны от которого могут быть выражения.
- Блок решения заканчивается функцией для решения. Мы рассмотрели Find(), которая содержит неизвестные, которые нужно найти.
- Чтобы использовать результат решения в дальнейших расчетах, присвойте Find() переменной. Это может быть как одна переменная, так и вектор.
- Для решения системы нелинейных уравнений нужно быть внимательным. Число уравнений должно быть равно числу неизвестных. Кроме того, приближенные значения должны быть как можно ближе к решению.
- Если решение не было найдено, не спешите обвинять Mathcad. Нелинейные уравнения являются головной болью для любого языка программирования. Попробуйте понять поведение Ваших уравнений, прежде чем приступать – часто уравнения могут не иметь решения.
Другие интересные материалы
sapr-journal.ru
DEP
, для алгебраических уравнений до четвертой степени включительно функция solve должна возвращать точные корни. В некоторых случаях эта функция может найти точные корни и для уравнений более высоких степеней. (Если коэффициенты — числа с плавающей точкой, то возвращается результат с плавающей точкой.)
Казалось бы, имея возможность получить корни с заданной точностью, можно найти приближенные значения невязки с заданной точностью, как например в Мaple (использована версия 7.0, но версия тут не важна).
Код:
> P:= z^5 -1: Z:= evalf[32](solve(P));
Z =
1., .30901699437494742410229341718282+.95105651629515357211643933337938*I,
-.80901699437494742410229341718282+.58778525229247312916870595463905*I,
-.80901699437494742410229341718282-.58778525229247312916870595463905*I,
.30901699437494742410229341718282-.95105651629515357211643933337938*I
> seq(eval[32](P, z=Z[k]), k=1..5);
0., -.1e-31-.77781757615511713920653428365785e-32*I,
-.6e-31+.94876071991504312973751185717278e-31*I,
-.6e-31-.94876071991504312973751185717278e-31*I,
-.1e-31+.77781757615511713920653428365785e-32*I
Для случая коэффициентов с плавающей точкой
Код:
> Digits:= 32:
> P:= z^5 -1.0: Z:= solve(P);
Z = 1., -.80901699437494742410229341718282-.58778525229247312916870595463907*I,
-.80901699437494742410229341718282+.58778525229247312916870595463907*I,
.30901699437494742410229341718282-.95105651629515357211643933337938*I,
.30901699437494742410229341718282+.95105651629515357211643933337938*I
> seq(eval[33](P, z=Z[k]), k=1..5);
0., 0.-.13972252156122383769449788012377e-31*I,
0.+.13972252156122383769449788012377e-31*I,
-.1e-31+.77781757615511713920653428365785e-32*I,
-.1e-31-.77781757615511713920653428365785e-32*I
Однако в Mathcad 13 неожиданно для меня невязка при символьном вычислении оказывается большой. См. прикрепление.
| Вложения: |
| MathCAD13_Polynom_roots_symbolic.PNG [ 46.18 Кб | Просмотров: 0 ]
|
Исследование
функции является одним из важнейших
приложений теории пределов, непрерывности
функции и производных. Полная схема
исследования функции и построения ее
графика объединяет в себе три этапа:
-
Элементарное
исследование. -
Исследование
графика функции с помощью первой
производной. -
Исследование
графика функции с помощью второй
производной.
При этом на каждом
из этапов решаются частные задачи,
которые позволяют в целом получить
свойства функции и оценить ее поведение
в различных областях ее определения:
-
Элементарное
исследование.
-
Найти область
определения функции. -
Исследовать
функцию на симметричность, периодичность,
четность и нечетность. -
Вычислить
предельные значения функции в ее
граничных точках. -
Выяснить
существование асимптот и получить их
уравнения в том случае, если они есть. -
Определить,
если это не вызовет особых затруднений,
точки пересечения графика функции с
координатными осями. -
Сделать
эскиз графика функции, используя
полученные результаты.
-
Исследование
графика функции с помощью первой
производной:
-
Найти
точки, подозрительные на экстремум из
решения уравнений
и
.
-
Точки,
«подозрительные» на экстремум,
исследовать с помощью достаточного
условия существования экстремума,
определить вид экстремума. -
Вычислить
значения функции в точках экстремума. -
Найти
интервалы монотонности функции. -
Нанести
на эскиз графика экстремальные точки. -
Уточнить
вид графика функции согласно полученным
результатам.
-
Исследование
графика функции с помощью второй
производной.
-
Найти
точки, «подозрительные» на точки
перегиба из решения уравнений: y”(х)=0
и y”(х)=. -
Точки,
«подозрительные» на перегиб, исследовать
с помощью достаточного условия. -
Вычислить
значения функции в точках перегиба. -
Найти
интервалы выпуклости и вогнутости
графика функции. -
Нанести
на эскиз графика точки перегиба. -
Окончательно
построить график функции.
Если
исследование проведено без ошибок, то
результаты всех этапов должны
согласовываться друг с другом. Если же
согласование отсутствует, необходимо
проверить правильность результатов
отдельных этапов и исправить найденные
ошибки.
Очевидно,
что проведение полного анализа – очень
трудоемкая задача. А решение некоторых
вопросов, например, проверка функции
на периодичность, требует знаний из
областей математики, не входящих в
учебную программу. Тем не менее, пакет
MathCAD
может оказать большую помощь при
исследовании функций, особенно в тех
случаях, где требуется решение уравнений
и неравенств. А технология построения
графиков функций, используемая системой
MathCAD,
позволяет проверять найденные решения
практически на любом из этапов
исследования.
6.1. Решение уравнений
Многие
задачи, с которыми приходилось сталкиваться
в школьном курсе математики, задавались
и решались в символьном виде. Тем или
иным образом преобразовывались и
упрощались выражения, использовались
определенные стандартные формулы и
методы, умножались, делились, сокращались
– и в результате выражения приводились
к какому-то несложному аналитическому
результату. Так, например, при решении
квадратного уравнения использовались
формулы Виета. Пытаясь аналитически
найти корни кубического уравнения,
исходные выражения разлагались на
линейные множители (или, в крайнем
случае, использовали формулу Кардано).
Для бикубических уравнений заменялся
квадрат искомой переменной на новую
переменную и в результате получалось
квадратной уравнение.
Решение
задач в аналитическом виде имеет массу
преимуществ перед решением численным
способом. Во-первых,
в этом случае ответ может быть вычислен
без какой-либо погрешности. Во-вторых,
при получении результата в виде
аналитического выражения имеются куда
более широкие возможности его последующего
использования (например, в качестве
формулы). В-третьих,
числовой результат, полученный при
вычислении выражения, представленного
в символьном виде, куда более нам понятен,
чем десятичная дробь, получаемая при
использовании численных методов. Увы,
но аналитическим
решением обладает очень ограниченное
количество задач.
Уравнение в
первоначальном понимании – это равенство
двух функций
,
рассматриваемых в общей области их
определения. При желании это равенство
можно записать в виде,
где.Такой вид
называют стандартным.
Решить уравнение
– это значит, найти точки, в которых
функция f(x)
принимает нулевые значения.
В MathCAD реализовано
три принципиально отличающихся друг
от друга подхода к решению уравнений:
применение численных алгоритмов,
использование символьных преобразований
и графический метод [19].
Чтобы найти корни
уравнения в виде выражения, требуется
выразить одну переменную через все
остальные (или коэффициенты). Сделать
же это обычно можно только в том случае,
если уравнение включает переменные
невысокой степени и не содержит
разнородных функций. Такие уравнения
специально подбираются в учебниках, и
их можно более или менее просто решить
на бумаге.
Но на практике
часто существует необходимость находить
корни таких
уравнений, пытаться решать которые с
помощью традиционных приемов символьной
алгебры совершенно бесперспективно.
Численно же можно решить практически
любое уравнение. Однако, как отмечалось
выше, получаемое при использовании
численного метода значение корня в виде
числа с плавающей точкой куда менее
информативно, чем выражение аналитического
решения. Опыт показывает, что простые
уравнения лучше решать в символьном
виде, более сложные — численно. Обычно
численный метод используется, если
MathCAD
не сможет решить уравнение аналитически.
Имеются
такие
уравнения, которые нельзя решить ни
аналитически (так как они слишком
сложны), ни численно (чаще всего потому,
что соответствующая функция не является
непрерывной). В таких случаях решение
ищут по графику, используя специальные
инструменты панели Graph (Графические).
Данный способ довольно трудоемок, однако
он способен обеспечить точность, мало
уступающую точности численных методов.
Для численного
решения
нелинейного
уравнения
можно
использовать встроенную функциюroot
и блок
решенияGiven
– find….
Остановимся
на функции
root,
которая имеет вид, представленный на
рис. 6.1.
root(f(x),
x,[a,b])
где
– левая часть уравнения;х
– имя переменной, относительно которой
решается уравнение; a,
b
– левый и правый концы отрезка, на
котором находится корень уравнения
(наличие квадратных скобок в описании
указывает на то, что эти параметры
являются необязательными). Поиск корня
уравнения осуществляется итерационным
методом с заданной точностью (точность
по умолчанию равна
).
Переустановить значение точности можно
с помощью задания нового значения
системной переменнойTOL,
которая отвечает за точность. Перед
использованием встроенной функции root
нужно задать начальное значение
переменной – искомого корня. Если
уравнение имеет несколько корней, то
целесообразно начальное значение
выбирать исходя из отрезка, определяющего
местоположение корня.
Рис. 6.1. Окно мастера
функций, открытое для вызова функции
root
Пример 1.
Найти корень уравнения вида
в численном виде при начальном значении
и заданной точности
.
Решение.
Процесс решения задачи можно свести к
выполнению следующих шагов:
-
Определить функцию
для решения. -
Задать начальное
значение корня. -
Переустановить
точность – в данном случае не требуется,
так как она соответствует точности,
взятой «по умолчанию». -
Вызвать функцию
root
для решения.
Фрагмент с решением
задачи в системе представлен ниже на
листинге.
Для аналитического
решения
уравнений в системе MathCAD можно
воспользоваться одним из двух способов:
-
С помощью оператора
solve,
расположенного на панели Symbolic
(Символьные). -
С помощью команды
solve
из подменю Symbolics→Variable.
В первом случае
для нахождения корня уравнения, необходимо
выполнить следующую последовательность
действий:
-
Введите оператор
solve
(решить)
с помощью одноименной команды панели
Symbolic
(Символьные).
В результате будет представлен шаблон
вида:
В левом маркере
задайте вид решаемого уравнения.
В качестве знака
равенства следует
использовать логическое равенство
(Bold Equal
– вводится сочетанием <Ctrl>
+<=>).
Если уравнение
приведено к стандартному виду, то
достаточно будет в этот маркер вписать
лишь его левую часть. При этом выражение
будет приравнено к нулю автоматически.
Также в левый маркер можно внести и имя
функции – в этом случае будут найдены
выражения, определяющие ее нули. Форма
записи уравнения через функцию удобна
в том случае, если оно имеет большую
длину.
-
В правый маркер
внесите переменную, относительно
которой должно быть решено уравнение,
как это показано на рис. 6.2.
Ответ оператор
solve
возвращает в виде выражения (численного
или буквенного), которое вполне можно
использовать в дальнейших вычислениях.
Если решений имеется несколько, то
возвращается содержащий их вектор.
При символьном
решении уравнений нет особой разницы,
сколько переменных содержит уравнение.
Ответ ищется в виде выражения, и поэтому
для системы неважно, будет ли оно
содержать буквенные или численные
элементы. Исходя из этого, вы можете
найти корни как уравнения нескольких
переменных, так и уравнения с параметрами
или буквенными коэффициентами.
Во втором случае,
чтобы решить уравнение в символьном
виде, нужно ввести уравнение (знак <=>
следует брать с панели Boolean),
выделить переменную, выбрать команду
solve
из подменю
Symbolics→Variable,
как это показано на рис. 6.3.
|
|
а) |
|
|
b) |
Рис. 6.2. Символьное
решение уравнения с использованием
панели инструментов Symbolic
Рис. 6.3. Символьное
решение уравнения
с использованием
подменю Variable
Пример 2.
Требуется найти корни уравнения вида
в
символьном виде. Следует иметь в виду,
что при решении тригонометрических
уравнений система находит только частное
решение приn=0.
Решение.
Процесс решения задачи можно свести к
выполнению следующих шагов:
-
Выполнить команду
solve,
расположенную на панели Symbolics
(Символьные). -
Заполнить
предоставленный шаблон. -
Проанализировать
результат, предоставленный системой
в виде, как это показано на рис. 6.4.
Рис. 6.4. Символьное
решение уравнения с использованием
команду solve
Как это видно из
предоставленного системой решения,
уравнение имеет три корня — один
действительный и два комплексных. Ответ
в аналитическом виде не всегда является
удобным для анализа, поэтому пересчитываем
его с помощью команды float,
расположенной на панели Symbolics
(Символьные),
в десятичную дробь с точностью до
4
знаков:
.
В результате
решение примет вид, как это показано на
рис. 6.5.
Рис. 6.5. Символьное
решение уравнения с использованием
команд solve
и float
Пример 3.
Требуется найти корни уравнения вида
в символьном виде.
Решение.
Процесс решения, как это показано в
предыдущей задаче, можно свести к
выполнению следующих шагов:
-
Выполнить команду
solve,
расположенную на панели Symbolics
(Символьные). -
Заполнить
предоставленный шаблон. -
Результат решения
предоставлен на рис. 6.6.
Рис. 6.6. Символьное
решение уравнения с использованием
команд solve
В предоставленном
решении используется ссылка
на функцию с именем W
– функцию
Ламберта. Функция Ламберта. Это функция
обратная функции
.
Чтобы найти значениеW
и использовать
найденное
значение в предоставленном решении,
можно также воспользоваться оператором
float,
как это показано на рис. 6.7.
Рис. 6.7. Символьное
решение уравнения с использованием
команд solve
и float
Пример 4.
Требуется найти корни уравнений вида:
-
;
-
в
символьном виде. Здесь
– логарифм по основанию 2, а
– логарифм по
основанию 10.
Решение
выполняется
по стандартной схеме, как это показано
в предыдущих примерах. Результаты
решения представлены на рис. 6.8.
Рис. 6.8. Символьное
решение уравнений с использованием
команды solve
Как это видно из
рис. 6.8, первое уравнение имеет 4
действительных корня, а второе уравнение
не имеет решение – об этом система
выдала сообщение (при этом цвет символов
в уравнении изменился на красный, а
сообщение об отсутствии решения
поместилось в прямоугольную область
желтого цвета). Действительно, анализ
области определения для уравнения 2
(приведен на рис. 6.9) показывает, что эта
область пуста, т.е. нет таких значений
x,
при которых имелось бы решение уравнения.
Поэтому при решении уравнений целесообразно
предварительно находить область
определения функции.
|
|
|
|
Рис. 6.9. Построение
области определения для функции b)
из примера 4
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #