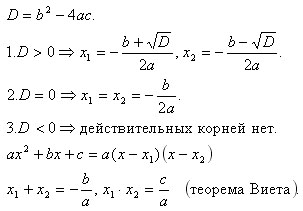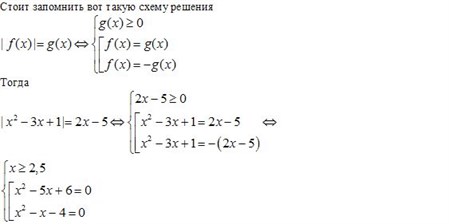Как найти корни квадратного уравнения формула

Решение квадратных уравнений

6 июля 2011

Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.

Квадратное уравнение — это уравнение вида ax² + bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.

Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:

1. Не имеют корней;
2. Имеют ровно один корень;
3. Имеют два различных корня.

В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант.

Дискриминант

Пусть дано квадратное уравнение ax² + bx + c = 0. Тогда дискриминант — это просто число D = b² − 4ac.

Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:

1. Если D < 0, корней нет;
2. Если D = 0, есть ровно один корень;
3. Если D > 0, корней будет два.

Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:

Задача. Сколько корней имеют квадратные уравнения:

1. x² − 8x + 12 = 0;
2. 5x² + 3x + 7 = 0;
3. x² − 6x + 9 = 0.

Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8)² − 4 · 1 · 12 = 64 − 48 = 16

Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 3² − 4 · 5 · 7 = 9 − 140 = −131.

Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6)² − 4 · 1 · 9 = 36 − 36 = 0.

Дискриминант равен нулю — корень будет один.

Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.

Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.

Корни квадратного уравнения

Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:

Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D < 0, корней нет — ничего считать не надо.

Задача. Решить квадратные уравнения:

1. x² − 2x − 3 = 0;
2. 15 − 2x − x² = 0;
3. x² + 12x + 36 = 0.

Первое уравнение:
x² − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2)² − 4 · 1 · (−3) = 16.

D > 0 ⇒ уравнение имеет два корня. Найдем их:

Второе уравнение:
15 − 2x − x² = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2)² − 4 · (−1) · 15 = 64.

D > 0 ⇒ уравнение снова имеет два корня. Найдем их

[begin{align} & {{x}_{1}}=frac{2+sqrt{64}}{2cdot left( -1 right)}=-5; \ & {{x}_{2}}=frac{2-sqrt{64}}{2cdot left( -1 right)}=3. \ end{align}]

Наконец, третье уравнение:
x² + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12² − 4 · 1 · 36 = 0.

D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:

[x=frac{-12+sqrt{0}}{2cdot 1}=-6]

Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.

Неполные квадратные уравнения

Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:

1. x² + 9x = 0;
2. x² − 16 = 0.

Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:

Уравнение ax² + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.

Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax² = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.

Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax² + c = 0. Немного преобразуем его:

Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c/a) ≥ 0. Вывод:

1. Если в неполном квадратном уравнении вида ax² + c = 0 выполнено неравенство (−c/a) ≥ 0, корней будет два. Формула дана выше;
2. Если же (−c/a) < 0, корней нет.

Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c/a) ≥ 0. Достаточно выразить величину x² и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.

Теперь разберемся с уравнениями вида ax² + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:

Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:

Задача. Решить квадратные уравнения:

1. x² − 7x = 0;
2. 5x² + 30 = 0;
3. 4x² − 9 = 0.

x² − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x₁ = 0; x₂ = −(−7)/1 = 7.

5x² + 30 = 0 ⇒ 5x² = −30 ⇒ x² = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.

4x² − 9 = 0 ⇒ 4x² = 9 ⇒ x² = 9/4 ⇒ x₁ = 3/2 = 1,5; x₂ = −1,5.

Смотрите также:

1. Теорема Виета
2. Следствия из теоремы Виета
3. Тест на тему «Значащая часть числа»
4. Метод коэффициентов, часть 1
5. Однородные тригонометрические уравнения: общая схема решения
6. Задача B4: строительные бригады

Квадратное уравнение

Это уравнение вида ax2+bx+c=0ax^2 + bx + c = 0,

где aa – коэффициент перед x2x^2,

bb – коэффициент перед xx,

cc – свободное число.

Существуют разные способы нахождения корней квадратного уравнения. Пожалуй, самый основной и распространенный способ – через вычисление дискриминанта. В этом случае он рассчитывается по формуле:

D=b2–4acD = b^2 – 4ac

Если второй коэффициент уравнения четный, можно решать уравнение через kk, тогда будет другая формула дискриминанта:

D1=k2–acD_1 = k^2 – ac

Если первый коэффициент уравнения равен 1, то можно воспользоваться теоремой Виета, которая имеет 2 условия:

x1+x2=−bx_1 + x_2 = -b
x1⋅x2=cx_1 cdot x_2 = c

Но если мы захотим решить уравнение основным способом, ошибки не будет. Нахождение корней уравнения через дискриминант – универсальный способ, а остальные введены для удобства вычислений.

Задача 1

Решим уравнение: 3×2+7x−6=0.3x^2 + 7x — 6 = 0.

Обозначим коэффициенты:

a=3a = 3,

b=7b = 7,

c=−6c = -6

Далее находим дискриминант по формуле:

D=b2–4acD = b^2 – 4ac

D=72–4∗3∗(−6)=49+72=121=112D = 7^2 – 4 * 3 * (-6) = 49 + 72 = 121 = {11}^2

D>0D > 0 – значит, уравнение имеет 2 корня.

Находим корни уравнения по следующим формулам:

x1=(−b+√D)/2ax_1 = (-b + √D) / 2a
x2=(−b−√D)/2ax_2 = (-b — √D) / 2a

Подставляем численные значения:

x1=(−7+11)/2∗3=4/6=23x_1 = (-7 + 11) / 2*3 = 4 / 6 = frac{2}{3}

x2=(−7–11)/2∗3=−18/6=−3x_2 = (-7 – 11) / 2*3 = -18 / 6 = -3

Ответ: x1=23x_1 = frac{2}{3}, x2=−3x_2 = -3.

Задача 2

Решим уравнение: −x2+7x+8=0.-x^2 + 7x + 8 = 0.

Обозначим коэффициенты:

a=−1a = -1,

b=7b = 7,

c=8.c = 8.

Далее находим дискриминант по формуле:

D=b2–4acD = b^2 – 4ac

D=72–4⋅(−1)⋅8=49+32=81=92D = 7^2 – 4 cdot (-1) cdot 8 = 49 + 32 = 81 = 9^2

D>0D > 0 – значит, уравнение имеет 2 корня.

Находим корни уравнения по следующим формулам:

x1=(−b+√D)/2ax_1 = (-b + √D) / 2a
x2=(−b−√D)/2ax_2 = (-b — √D) / 2a

Подставляем численные значения:

x1=(−7+9)/2∗(−1)=2/(−2)=−1x_1 = (-7 + 9) / 2 * (-1) = 2 / (-2) = -1
x2=(−7–9)/2∗(−1)=−16/(−2)=8x_2 = (-7 – 9) / 2 * (-1) = -16 / (-2) = 8

Ответ: x1=−1x_1 = -1, x2=8x_2 = 8.

Задача 3

Решим уравнение: 4×2+4x+1=0.4x^2 + 4x + 1 = 0.

Обозначим коэффициенты:
a=4a = 4,

b=4b = 4,

c=1.c = 1.

Далее находим дискриминант по формуле: D=b2–4acD = b^2 – 4ac

D=42–4⋅4⋅1=16–16=0D = 4^2 – 4 cdot 4 cdot 1 = 16 – 16 = 0

D=0D = 0 – значит, уравнение имеет 1 корень.

Находим корень уравнения по следующей формуле: x=−b/2ax = -b / 2a

Подставляем численные значения:

x=−4/2⋅4=−4/8=−1/2=−0,5x = -4 / 2 cdot 4 = -4 / 8 = -1 / 2 = -0,5

Ответ: x=−0,5.x = -0,5.

Задача 4

Решим уравнение: 2×2+x+1=0.2x^2 + x + 1 = 0.

Обозначим коэффициенты:
a=2a = 2,

b=1b = 1,

c=1.c = 1.

Далее находим дискриминант по формуле: D=b2–4acD = b^2 – 4ac

D=12–4∗2∗1=1–8=−7D = 1^2 – 4 * 2 * 1 = 1 – 8 = -7

D<0D < 0 – значит, уравнение корней не имеет.

Ответ: корней нет.

Решение квадратного уравнения через k

Если у квадратного уравнения коэффициент bb четный, то можно решать уравнение через kk, при этом k=12bk = frac{1}{2} b.

Задача 5

Решим уравнение: −x2+2x+8=0.-x^2 + 2x + 8 = 0.

Обозначим коэффициенты:

a=−1a = -1,

b=2b = 2,

c=8c = 8

bb – четное.

k=12b=1k = frac {1}{2} b = 1.

Далее находим дискриминант по формуле: D1=k2–acD_1 = k^2 – ac

D1=12–(−1)∗8=1+8=9=32D_1 = 1^2 – (-1) * 8 = 1 + 8 = 9 = 3^2

D1>0D_1 > 0 – значит, уравнение имеет 2 корня.

Находим корни уравнения по следующим формулам:

x1=(−k+D1)/ax_1 = (-k + {sqrt D}_1) / a
x2=(−k−D1)/ax_2 = (-k — {sqrt D}_1) / a

Подставляем численные значения:

x1=(−1+3)/(−1)=2/(−1)=−2x_1 = (-1 + 3) / (-1) = 2 / (-1) = -2
x2=(−1–3)/(−1)=−4/(−1)=4x_2 = (-1 – 3) / (-1) = -4 / (-1) = 4

Ответ: x_1 = -2, x_2 = 4.

Задача 6

Решим уравнение: 9×2–6x+1=0.9x^2 – 6x + 1 = 0.

Обозначим коэффициенты:
a=9a = 9,

b=−6b = -6,

c=1c = 1

bb – четное.

K=12b=−3.K = frac{1}{2} b = -3.

Далее находим дискриминант по формуле: D1=k2–acD_1 = k^2 – ac

D1=(−3)2–9∗1=9–9=0D_1 = {(-3)}^2 – 9 * 1 = 9 – 9 = 0

D1=0D_1 = 0 – значит, уравнение имеет 1 корень.

Находим корень уравнения по следующей формуле: x=−k/ax = -k / a

Подставляем численные значения:

x=3/9=13x = 3 / 9 = frac{1}{3}

Ответ: x=13.x = frac{1}{3}.

Нахождение корней уравнения по теореме Виета

Если в квадратном уравнении a=1a = 1, то можно найти корни уравнения по теореме Виета.

Задача 7

Найдем корни уравнения: x2+3x+2=0.x^2 + 3x + 2 = 0.

Обозначим коэффициенты:
a=1a = 1,

b=3b = 3,

c=2c = 2.

Запишем 2 условия теоремы Виета:

x1+x2=−bx_1 + x_2 = -b
x1∗x2=cx_1 * x_2 = c

Теперь методом подбора найдем 2 числа, которые будут соответствовать этим условиям. Вероятно, это числа -2 и -1.

Значит, корни уравнения равны:

x1=−2x_1 = -2
x2=−1x_2 = -1

Ответ: x1=−2x_1 = -2, x2=−1x_2 = -1.

Задача 8

Найдем корни уравнения: x2–5x+6=0.x^2 – 5x +6 = 0.

Обозначим коэффициенты:

a=1a = 1,

b=−5b = -5,

c=6c = 6

Запишем 2 условия теоремы Виета:

x1+x2=−bx_1 + x_2 = -b
x1∗x2=cx_1 * x_2 = c

Теперь методом подбора найдем 2 числа, которые будут соответствовать этим условиям. Вероятно, это числа 2 и 3.

Значит, корни уравнения равны:

x1=2x_1 = 2
x2=3x_2 = 3

Ответ: x1=2x_1 = 2, x2=3.x_2 = 3.

Тест по теме «Примеры решения квадратных уравнений»

В предыдущих уроках мы разбирали
«Как решать линейные уравнения», то есть
уравнения первой степени. В этом уроке мы разберем, что называют квадратным уравнением и как его решать.

Что называют квадратным уравнением

Примеры квадратных уравнений

• 5x² − 14x + 17 = 0
• −x² + x + = 0
• x² + 0,25x = 0
• x² − 8 = 0

Чтобы найти «a», «b» и «c»
нужно сравнить свое уравнение с общим видом квадратного уравнения
«ax² + bx + c = 0».

Давайте потренируемся определять
коэффициенты «a», «b»
и «c» в квадратных уравнениях.

Уравнение	Коэффициенты
5x2 − 14x + 17 = 0	a = 5 b = −14 с = 17
−7x2 − 13x + 8 = 0	a = −7 b = −13 с = 8
−x2 + x + 1 3 = 0	a = −1 b = 1 с = 1 3
x2 + 0,25x = 0	a = 1 b = 0,25 с = 0
x2 − 8 = 0	a = 1 b = 0 с = −8

Как решать квадратные уравнения

В отличии от линейных уравнений для решения квадратных уравнений используется специальная
формула для нахождения корней.

Давайте на примере разберем, как применять формулу для нахождения корней квадратного уравнения. Решим квадратное уравнение.

x² − 3x − 4 = 0

Уравнение «
x² − 3x − 4 = 0
» уже приведено к общему виду «ax² + bx + c = 0» и не требует дополнительных упрощений.
Для его решения нам достаточно применить формулу нахождения корней квадратного уравнения.

Определим коэффициенты «a», «b» и
«c» для этого уравнения.

Уравнение	Коэффициенты
x2 − 3x − 4 = 0	a = 1 b = −3 с = −4

Подставим их в формулу и найдем корни.

x² − 3x − 4 = 0

x_1;2 =

x_1;2 =

−(−3) ± √(−3)2 − 4 · 1· (−4)

2 · 1

x_1;2 =

x_1;2 =

x_1;2 =

x1 =	x2 =
x1 =	x2 =
x1 = 4	x2 = −1

Ответ: x₁ = 4; x₂ = −1

В формуле «x_1;2 = » часто заменяют подкоренное выражение
«b² − 4ac» на букву «D» и называют
дискриминантом. Более подробно понятие дискриминанта рассматривается в уроке
«Что такое дискриминант».

---

Рассмотрим другой пример квадратного уравнения.

x² + 9 + x = 7x

В данном виде определить коэффициенты «a», «b» и
«c» довольно сложно.
Давайте вначале приведем уравнение к общему виду «ax² + bx + c = 0».

Используем
правило переноса и
упростим подобные
члены.

x² + 9 + x = 7x
x² + 9 + x − 7x = 0
x² + 9 − 6x = 0
x² − 6x + 9 = 0

Теперь можно использовать формулу для корней.

x_1;2 =

−(−6) ± √(−6)2 − 4 · 1 · 9

2 · 1

x_1;2 =

x_1;2 =

x_1;2 =

x =

x = 3

Ответ: x = 3

---

Бывают случаи, когда в квадратных уравнениях нет корней. Такая ситуация возникает, когда в формуле под корнем
оказывается отрицательное число.

Мы помним из определения квадратного корня о том,
что извлекать квадратный корень из отрицательного числа
нельзя.

Рассмотрим пример квадратного уравнения, у которого нет корней.

5x² + 2x = − 3
5x² + 2x + 3 = 0

x_1;2 =

−2 ± √22 − 4 · 3 · 5

2 · 5

x_1;2 =

x_1;2 =

Ответ: нет действительных корней.

Итак, мы получили ситуацию, когда под корнем стоит отрицательное число.
Это означает, что в уравнении нет корней. Поэтому в ответ мы так и записали «Нет действительных корней».

Неполные квадратные уравнения

Иногда встречаются квадратные уравнения, в которых отсутсвуют в явном виде коэффициенты «b» и/или
«c». Как например, в таком уравнении:

4x² − 64 = 0

Такие уравнения называют неполными квадратными уравнениями. Как их решать рассмотрено в уроке
«Неполные квадратные уравнения».

---

Ваши комментарии

Оставить комментарий:

---

В наши дни онлайн обучение становится все востребование. Такой вид самоусовершенствования имеет ряд преимуществ. Главной мотивацией к обучению является доступ к материалу благодаря мультимедийным ресурсам. К тому же, ученик получает необходимые знания с помощью чтения, что более эффективно, чем прослушивание. Очень важно подобрать качественный ресурс (сайт), где будет изложено решение нужной задачи.

Рассмотрим решение квадратных уравнений.

Квадратное уравнение имеет вид ax² + bx + c = 0,
где x – переменная;
а и b – коэффициенты;
с – свободный член уравнения.

Квадратные уравнения называют приведенными, если а = 1. Неполное квадратное уравнение, если b или с равны нулю.

График квадратичной функции – парабола. Если значение а – положительное, то ветви параболы направлены вверх, отрицательное – вниз. При положительном коэффициенте b – вершина находится в левой полуплоскости, при отрицательном – в правой. Точки пересечения графика с осью абсцисс – корни квадратного уравнения. Соответственно, когда уравнение корней не имеет, парабола не пересекает ось абсцисс. Если уравнение имеет один корень, то вершина параболы (одна точка) касается оси абсцисс.

Как видно из решения, найти корни квадратного уравнения достаточно просто. При доступном изложении материала, можно выучить любой урок. Безусловно, занятия в школе онлайн обучение заменить не сможет, но быть вспомогательным инструментом вполне. Особенно такой способ актуален для школьников с ограниченными возможностями, программа для которых создается индивидуально, что намного эффективнее по сравнению с надомным обучением. К тому же, обучение онлайн всегда дешевле, чем занятия с репетитором, а со стороны родителей может осуществляться контроль за уровнем усваивания материала ребенком.

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Остались вопросы?

Задайте свой вопрос и получите ответ от профессионального преподавателя.

Неполные квадратные уравнения имеют (2) вида:

Неполные квадратные уравнения можно решать с помощью формул дискриминанта, но рациональнее выбрать специальные способы:

(т. к. произведение двух чисел равно (0) только тогда, когда хотя бы один из множителей равен (0)). 
 

Это значит, что