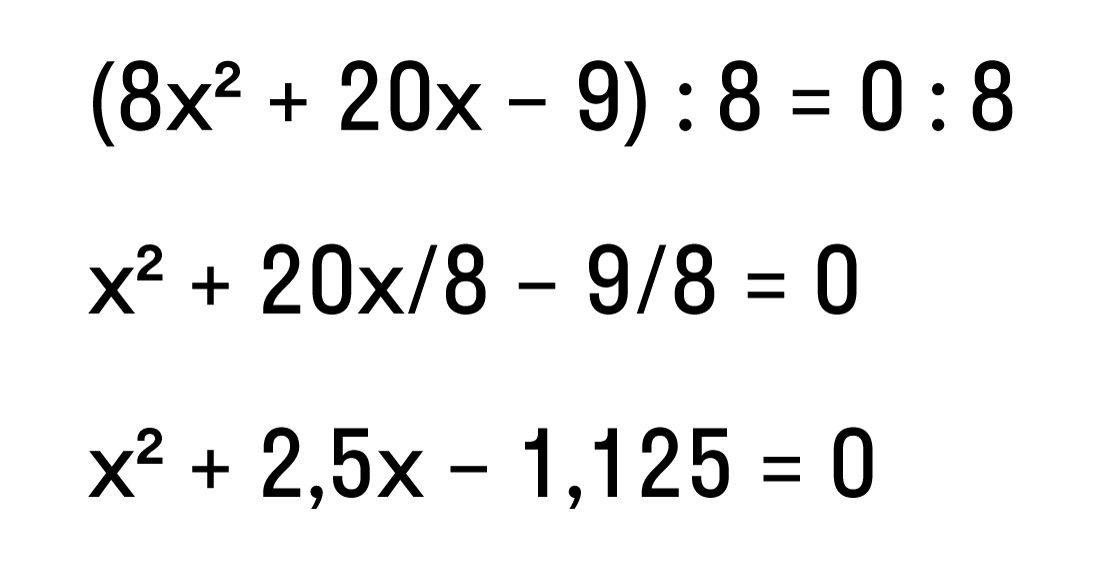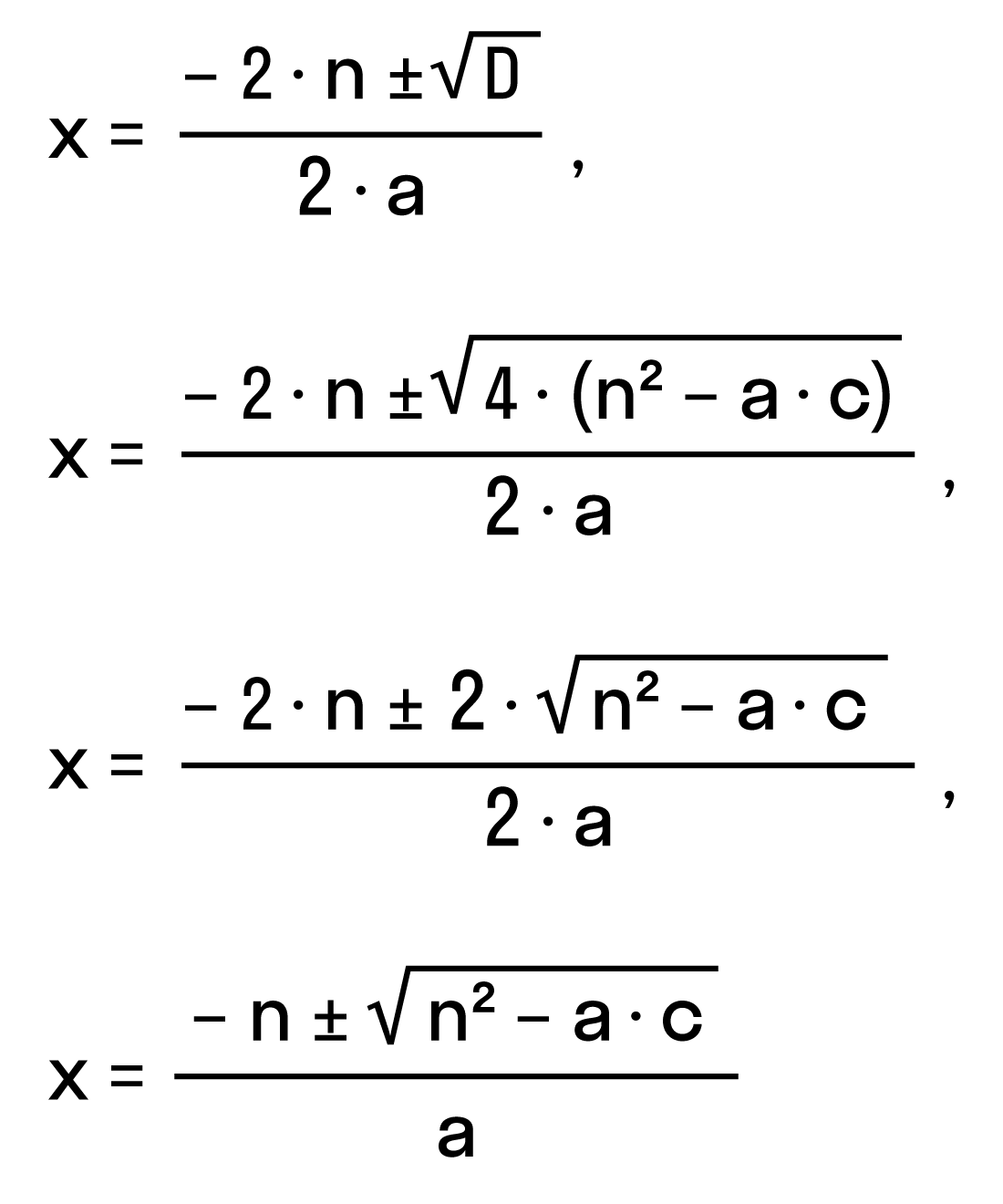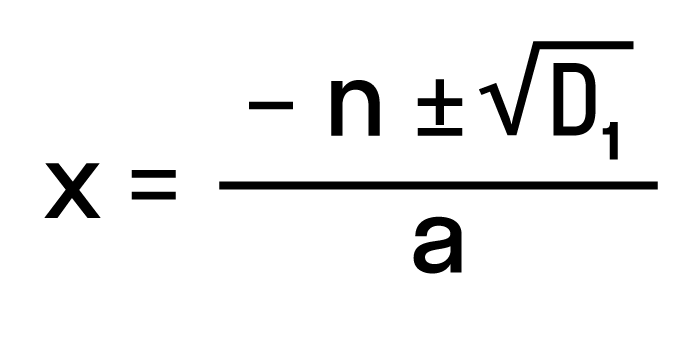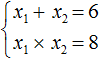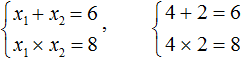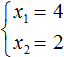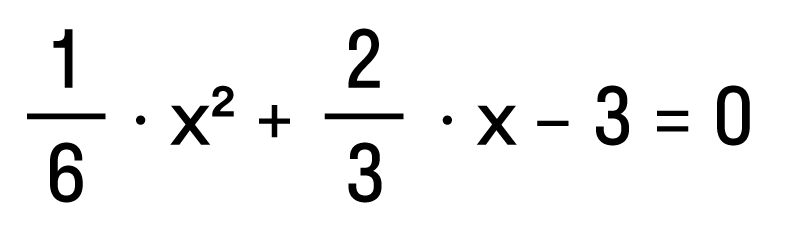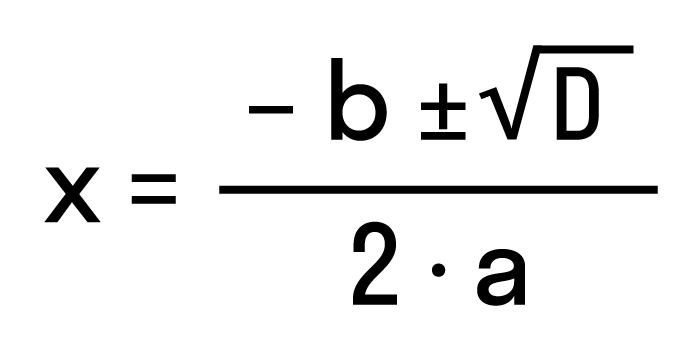Как найти корни квадратного уравнения методом подбора

Различные способы решения квадратных уравнений

Разделы: Математика

Цели урока:

Систематизировать различные способы решения квадратных уравнений, дать представление учащимся о важных вехах истории развития математики;

Обучать поискам нескольких способов решения одной задачи и умению выбирать из них наиболее оптимальный;

Развивать навыки работы с дополнительной литературой, историческим материалом;

Показать многообразие и красоту математических решений.

Тип урока: урок систематизации и обобщения.

Ход урока

Устная работа:
Определите, имеет ли уравнение корни. Если имеет, то ответьте на вопросы:

а) Сколько корней имеет уравнение?

б) Рациональными или иррациональными являются его корни?

в) Каковы знаки корней?

г) Если корни разных знаков, то какой из них имеет больший модуль?

3 x 2 + 7х +2 =0; 3 – 8у + 2 = 0; 5 x 2 – 3х +2 =0; 2 x 2 – 10х – 5 =0.

Решите квадратное уравнение подбором корней:

x 2 + 9х +20 =0; x 2 – 17х + 30 =0; x 2 + 7х – 60=0; x 2 – 11х + 24 =0.

Учитель: Сегодня на уроке мы рассмотрим различные способы решения квадратных уравнений в разные исторические эпохи на примере одной задачи-решения квадратного уравнения.

Ученик 1: Методы решения квадратных уравнений были известны еще в древние времена. Они излагались в вавилонских рукописях царя Хаммурапи (XX в. до н.э.), в трудах древнегреческого математика Евклида (III в. до н. э), в древних китайских и японских трактатах. Многие математики древности решали квадратные уравнения геометрическим способом: квадрат и 10 его корней равны 39.

Для решения уравнения x 2 + 10х = 39 поступали следующим образом. Пусть АВ = х, ВС=5, ( 10:2). На стороне АС = АВ + ВС строился квадрат, который разбивался на четыре части. Очевидно, что сумма площадей трех частей равна x 2 + 10х или 39. Если к этой площади прибавить площадь четвертой части, то 39+25=64 – площадь всего квадрата. Но, эта же площадь равна = 64, х + 5 = 8, х = 3. Таким образом, число 3 является корнем квадратного уравнения, так как отрицательных чисел тогда не знали.

Ученик 2: А вот как решал эту же задачу ал-Хорезми в 825 году. Строим квадрат со стороной х и на его сторонах – четыре прямоугольника высотой 10/4. В углах фигуры построим четыре квадрата со стороной 10/4. Подсчитаем площадь получившегося большого квадрата:

x 2 + 4 · 10/4 · х + = x 2 + 10х + · 4.

По условию x 2 + 10х = 39, т.е. площадь получившегося большого квадрата равна

39 + + · 4 = 39 + 25 = 64. Значит, его сторона равна 8, тогда

х + 2· 10/4 = 8, х = 3 (Ал-Хорезми не признавал отрицательных чисел).

Ученик 3: В III в. н. э. квадратное уравнение x 2 – 20х + 96 = 0 решал великий древнегреческий математик Диофант.

Пусть сумма двух чисел 20, а произведение 96.Допустим, что разность этих чисел 2z. Так как их сумма 20, то если разделить ее пополам, каждая из полученных делением частей будет равна половине суммы, то есть 10. И если половину разности – z прибавить к одной из полученных от деления половине и вычесть из другой, то опять получается сумма 20 и разность 2z.

Пусть большее из искомых чисел равно z + 10, тогда меньшее — 10–z. Их сумма 20, а разность 2z. Произведение искомых чисел равно 96. Таким образом,

(10 + z)(10 –z) = 96, 100 – = 96, = 4, z = 2. Следовательно, большее число равно 12, а меньшее 8.

Давайте пробуем решить квадратное уравнение x 2 + 10х = 39 методом Диофанта.

1. Пусть x 2 + 10х – 39 =0;
2. Положим разность искомых чисел 2z;
3. –5 — половина коэффициента при х с противоположным знаком;
4. Положим х1 = z – 5, х2 = z + 5. Тогда (z – 5)(z + 5) = 39, – 25 = 39,

= 64, z =8.

Отсюда, х1 = 8–5=3, х2 = 8+5=13. Полученные корни 13 и 3 “устроили” бы Диофанта, т.к. оба натуральные. Но, используя теорему Виета, мы видим, что х1·х2 = –39, а это означает, что корни должны быть разного знака. Значит, не каждое уравнение можно решить этим методом.

Ученик 4: Неполные квадратные уравнения и частные виды полных квадратных уравнений умели решать вавилоняне и египтяне (2 тыс. лет до н.э.). Некоторые виды квадратных уравнений решали и древнегреческие математики, используя геометрический подход. Примеры решения уравнений без обращения к геометрии дает Диофант Александрийский (III в. н. э.). В своем трактате хорезмский тематик Мухаммед ал-Хорезми в 825 г. Разъясняет приемы решения квадратных уравнений. После трудов немецкого математика М. Штифеля (1487 – 1567 гг.), нидерландца А. Жирара (1595 – 1632 гг.), Р.Декарта и Н.Ньютона, способ решения квадратных уравнений принял современный вид. А в 1591 г. Ф.Виет вывел формулы, выражающие зависимость корней квадратного уравнения от его коэффициентов и сформулировал свою знаменитую теорему.

Ученик 5: Франсуа Виет родился в 1540 г. Во Франции, в Фонтене – ле – Конт. По образованию юрист. Он много занимался адвокатской деятельностью, а с 1571 г. по 1584 г. Был советником короля Георга III и Георга IV. Но, все свободное время, весь свой досуг он отдавал занятиям математикой. Особенно усиленно он начал работать в области математики с 1584 г., после отстранения от должности при королевском дворе. Виет детально изучил труды как древних так и современных ему математиков и создал по существу новую алгебру. Он ввел в нее буквенную символику. После открытия Виета, стало возможным записывать правила в виде формул.

Учитель: Именно с 1591 г. мы пользуемся формулами при решении квадратных уравнений. Решим квадратное уравнение x 2 + 10х – 39 =0 современными способами.

x 2 + 10х – 39 = 0,
а = 1, b = 10, с = –39.
D = – 4ac; D = 100 + 156 = 256, D > 0.

Х1,2 = (; Х1 = (-10 + 16)/2 = 3; Х2 = (-10 — 16)/2 = -13.

Ученик 6: Следует отметить, что второй коэффициент в данном уравнении четный, что позволяет использовать иную формулу для решения данного уравнения.

x 2 + 10х – 39 =0 ,
а = 1, k= 5, с = –39.
D1 = – ac; D1 = 25 + 39 = 64, D1> 0.

Х1,2 =( ; Х1 = (-5 + 8)/1 = 3; Х2 = (-5 — 8)/1 = -13.

Ученик 7: Данное уравнение можно решить, используя теорему, обратную теореме Виета.

x 2 + 10х – 39 = 0,

Учитель: Существуют ли другие способы решения квадратных уравнений?

Ученик: Квадратные уравнения можно решать, используя свойства “суммы коэффициентов”. Если a + b + c = 0, х1 = 1, х2 = c/а; или если a – b – c = 0, то х1 = –1, х2 = – с/а. Но, данное квадратное уравнение нельзя решить, используя эти соотношения. Например, изменим в рассмотренном уравнении свободный член:

x 2 + 10х – 11 = 0;
a = 1; b = 10; с = –11; 1 + 10 – 11 = 0;
х1 = 1; х2 = –11.

Учитель: Приведите примеры уравнений, решаемых с применением второго утверждения.

Например: –10 x 2 + 29х + 39 =0; x 2 – 2005х – 2006 = 0.

Учитель: В учебнике мы встречаем задания, где четко обозначено, как решить квадратное уравнение. В предложенных вам задачах вы не только решите уравнение, но и узнаете интересные факты.

1.Известно, что учет населения проводился в Египте и в Китае еще до нашей эры. Решив квадратное уравнение 4x 2 – 24х + 39 =0 , вы определите в каком это было тысячелетии до н.э.

2. На основе статистических данных можно выделить регионы с максимальным сбросом загрязненных вод: это Краснодарский край и Москва. Сколько процентов общего количества загрязненных вод дают эти регионы, вы узнаете, решив уравнение x 2 – 19х + 88 =0 .

3. Кислотные осадки разрушают сооружения из мрамора и других материалов. Исторические памятники Греции и Рима, простояв тысячелетия, за последние годы разрушаются прямо на глазах. “Мировой рекорд” принадлежит одному шотландскому городку, где 10 апреля 1974 года выпал дождь, скорее напоминающий столовый уксус, чем воду. Устно решите уравнения, найдите верный ответ и соответствующую ему букву и прочитайте название этого “знаменитого” городка. (Питлохри).

Теорема Виета для квадратного уравнения

О чем эта статья:

Основные понятия

Квадратное уравнение — это ax 2 + bx + c = 0, где a — первый коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Существует три вида квадратных уравнений:

• не имеют корней;
• имеют один корень;
• имеют два различных корня.

Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Формула для его поиска записывается так: D = b 2 − 4ac. Его свойства:

• если D 0, есть два различных корня.

В случае, когда второй коэффициент четный, можно воспользоваться формулой нахождения дискриминанта , где .

В математике теоремой принято называть утверждение, у которого ранее было сформулировано доказательство.

Формула Виета

Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так:

Рассмотрим квадратное уравнение, в котором первый коэффициент равен 1: . Такие уравнения называют приведенными квадратными уравнениями. Сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.

Если дано x 2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:

Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.

Рассмотрим теорему Виета на примере: x 2 + 4x + 3 = 0.

Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:

Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:

Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x 2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:
2 + 4x + 3 = 0″ height=»215″ src=»https://lh5.googleusercontent.com/E_X403ETh_88EANRWdQN03KRT8yxP2HO4HoCrxj__c8G0DqmNJ1KDRqtLH5Z1p7DtHm-rNMDB2tEs41D7RHpEV5mojDTMMRPuIkcW33jVNDoOe0ylzXdHATLSGzW4NakMkH2zkLE» width=»393″>

Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.
2 + 4x + 3 = 0″ height=»52″ src=»https://lh5.googleusercontent.com/VzGPXO9B0ZYrr9v0DpJfXwuzeZtjYnDxE_ma76PUC8o7jVWwa8kZjTJhq2Lof0TiJXAp_ny3yRwI_OyRzeucv9xUZ63yoozGPP4xd4OxvElVT7Pt-d6xL5w17e_mQNs5qZJQiwfG» width=»125″>

Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:
2 + 4x + 3 = 0″ height=»52″ src=»https://lh4.googleusercontent.com/Cq-LCFmY3YGNSan1VF3l3CqIeojoJYAvGAiTBWnzyoZu_xJFrF5NfQ3xCe59apJklw6uYbmQ4lAkBTeC-TJmEGicN3rgGtsezhuqdNiOWjZT39NziOB5uOmQr3cr9-5fNnepdZDo» width=»112″>

Результат проделанных вычислений в том, что мы убедились в справедливости выражения:

Обучение на курсах по математике помогает быстрее разобраться в новых темах и подтянуть оценки в школе.

Доказательство теоремы Виета

Дано квадратное уравнение x 2 + bx + c = 0. Если его дискриминант больше нуля, то оно имеет два корня, сумма которых равна второму коэффициенту с противоположным знаком, а произведение корней равно свободному члену:

Докажем, что следующие равенства верны

• x₁ + x₂ = −b,
• x₁ * x₂ = c.

Чтобы найти сумму корней x₁ и x₂ подставим вместо них то, что соответствует им из правой части формул корней. Напомним, что в данном квадратном уравнении x 2 + bx + c = 0 старший коэффициент равен единице. Значит после подстановки знаменатель будет равен 2.

Объединим числитель и знаменатель в правой части.

Раскроем скобки и приведем подобные члены:

Сократим дробь полученную дробь на 2, остается −b:

Мы доказали: x₁ + x₂ = −b.

Далее произведем аналогичные действия, чтобы доказать о равенстве x₁ * x₂ свободному члену c.

Подставим вместо x₁ и x₂ соответствующие части из формул корней квадратного уравнения:

Перемножаем числители и знаменатели между собой:

Очевидно, в числителе содержится произведение суммы и разности двух выражений. Поэтому воспользуемся тождеством (a + b) * (a − b) = a 2 − b 2 . Получаем:

Далее произведем трансформации в числителе:

Нам известно, что D = b2 − 4ac. Подставим это выражение вместо D.

Далее раскроем скобки и приведем подобные члены:

Сократим:

Мы доказали: x₁ * x₂ = c.

Значит сумма корней приведённого квадратного уравнения x 2 + bx + c = 0 равна второму коэффициенту с противоположным знаком (x₁ + x₂ = −b), а произведение корней равно свободному члену (x₁ * x₂= c). Теорема доказана.

Обратная теорема Виета

Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Она формулируется так:

Обратная теорема Виета

Если числа x₁ и x₂ таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа являются корнями x 2 + bx + c = 0.

Обратные теоремы зачастую сформулированы так, что их утверждением является заключение первой теоремы. Так, при доказательстве теоремы Виета стало понятно, что сумма x₁ и x₂ равна −b, а их произведение равно c. В обратной теореме это является утверждением.

Докажем теорему, обратную теореме Виета

Корни x₁ и x₂ обозначим как m и n. Тогда утверждение будет звучать следующим образом: если сумма чисел m и n равна второму коэффициенту x 2 + bx + c = 0, взятому с противоположным знаком, а произведение равно свободному члену, то числа m и n являются корнями x 2 + bx + c = 0.

Зафиксируем, что сумма m и n равна −b, а произведение равно c.

Чтобы доказать, что числа m и n являются корнями уравнения, нужно поочередно подставить буквы m и n вместо x, затем выполнить возможные тождественные преобразования. Если в результате преобразований левая часть станет равна нулю, то это будет означать, что числа m и n являются корнями x 2 + bx + c = 0.

Выразим b из равенства m + n = −b. Это можно сделать, умножив обе части на −1:

Подставим m в уравнение вместо x, выражение −m − n подставим вместо b, а выражение mn — вместо c:

При x = m получается верное равенство. Значит число m является искомым корнем.

1. Аналогично докажем, что число n является корнем уравнения. Подставим вместо x букву n, а вместо c подставим m * n, поскольку c = m * n.

   При x = n получается верное равенство. Значит число n является искомым корнем.

Мы доказали: числа m и n являются корнями уравнения x 2 + bx + c = 0.

Примеры

Для закрепления знаний рассмотрим примеры решения уравнений по теореме, обратной теореме Виета.

Дано: x 2 − 6x + 8 = 0.

Для начала запишем сумму и произведение корней уравнения. Сумма будет равна 6, так как второй коэффициент равен −6. А произведение корней равно 8.
2 − 6x + 8 = 0″ height=»59″ src=»https://lh6.googleusercontent.com/tFokx3SM93Hwlr7ZM9BqX1xiHKv_2dUIB9MoNa8RAwSTmQKXdCcqcFXxTZmxNGw7bOVek-RzRXqBkoCqnYMiqIYVwKhfnHeU-7mA03feEqJTlyKB7e-OsTTKgPaOlddfiaTGszcv» width=»99″>

Имея эти два равенства можно подобрать подходящие корни, которые будут удовлетворять как равенству обоим равенствам системы.

Подбор корней удобнее выполнять с помощью их произведения. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x₁ и x₂ надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.

Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x₁ + x₂ = 6. Значения 4 и 2 подходят обоим равенствам:

Значит числа 4 и 2 являются корнями уравнения x 2 − 6x + 8 = 0.
2 − 6x + 8 = 0″ height=»57″ src=»https://lh3.googleusercontent.com/rohB7Bvd-elMhTxEUuOhKqLJjqLAvo9VlJxZvOnMeDAHARfKT-SYOWb1WXTTWEN2h0oKbLl6wH7lc0IWL_vH3Si2AJGAGXVn8TPFDT_J1Wu2WeoQ-WP1qgXjCnZ99tWUkK2BOvF2″ width=»64″>

Неприведенное квадратное уравнение

Теорема Виета выполняется только тогда, когда квадратное уравнение является приведённым, то есть его первый коэффициент равен единице:

ax 2 + bx + c = 0, где а = 1.

Если квадратное уравнение не является приведенным, но задание связано с применением теоремы, нужно обе части разделить на коэффициент, который располагается перед x 2 .

1. Получилось следующее приведенное уравнение:

Получается, второй коэффициент при x равен, свободный член —. Значит сумма и произведение корней будут иметь вид:

Рассмотрим пример неприведенного уравнения: 4x 2 + 5x + 1 = 0. Разделим обе его части на коэффициент перед x 2 , то есть на 4.

Получилось приведённое квадратное уравнение. Второй коэффициент которого равен, а свободный член.

Тогда в соответствии с теоремой Виета получаем:

Метод подбора помогает найти корни: −1 и

Квадратное уравнение. Дискриминант. Теорема Виета.

теория по математике 📈 уравнения

Уравнение вида ax 2 +bx+c=0, где a,b,c – любые числа, причем a≠0, называют квадратным уравнением. Числа a,b,c принято называть коэффициентами, при этом a – первый коэффициент, b – второй коэффициент, c – свободный член.

Квадратное уравнение может иметь не более двух корней. Решить такое уравнение – это значит найти все его корни или доказать, что их нет.

Дискриминант

Количество корней квадратного уравнения зависит от такого элемента, как дискриминант (обозначают его буквой D).

Нахождение корней квадратного уравнения

Дискриминант – это такой математический инструмент, который позволяет нам определять количество корней. Он выражается определенной формулой:

D=b 2 –4ac

Если D>0, то уравнение имеет два различных

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Пример №1. Решить уравнение х 2 –2х–3=0. Определяем коэффициенты: а=1, b=–2, c=–3. Находим дискриминант: D=b 2 –4ac=(–2) 2 –41(–3)=4+12=16. Видим, что дискриминант положительный, значит, уравнение имеет два различных корня, находим их:

Пример №2. Решить уравнение 5х 2 +2х+1=0. Определяем коэффициенты: а=5, b=2, c=1. D=b 2 –4ac=2 2 –4=4–20=–16, D 2 –6х+9=0. Определяем коэффициенты: а=1, b=–6, c=9.

D=b 2 –4ac=(–6) 2 –4=36–36=0, D=0, 1

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Теорема Виета

Среди квадратных уравнений встречаются такие, у которых первый коэффициент равен 1 (обратим внимание на пример 1 и 3), такие уравнения называются приведенными.

Приведенные квадратные уравнения можно решать не только с помощью дискриминанта, но и с помощью теоремы Виета.

Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком; произведение корней равно третьему коэффициенту.

Корни с помощью данной теоремы находятся устно способом подбора. Рассмотрим это на примерах.

Пример №4. Решить уравнение х 2 –10х+21=0. Выпишем коэффициенты: а=1, b=–10, c=21. Применим теорему Виета:

Начинаем с произведения корней, которое является положительным числом, значит оба корня либо отрицательные, либо положительные. Предполагаем, что это могут быть либо 3 и 7, либо противоположные им числа. Теперь смотрим на сумму, она является положительным числом, поэтому нам подходит пара чисел 3 и 7. Проверяем: 3+7=10, 37=21. Значит, корнями данного уравнения являются числа 3 и 7.

Пример №5. Решить уравнение: х 2 +5х+4=0. Выпишем коэффициенты: а=1, b=5, c=4. По теореме Виета:

Видим, что произведение корней равно 4, значит оба корня либо отрицательные, либо положительные. Видим, что сумма отрицательная, значит, будем брать два отрицательных числа, нам подходят –1 и –4. Проверим:

Данное уравнение является квадратным. Но в его условии присутствует квадратный

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Записываем обязательно в начале решения, что подкоренное выражение может быть только равным нулю или положительным числом (правило извлечения квадратного

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Решаем полученное неравенство: − х ≥ − 5 , отсюда х ≤ 5 . Следовательно, для ответа мы будем выбирать значения, которые меньше или равны 5.

Решаем наше квадратное уравнение, перенося все слагаемые из правой части в левую, изменяя при этом знаки на противоположные и приводя подобные слагаемые (выражения с квадратным корнем взаимоуничтожаются):

х 2 − 2 х + √ 5 − х − √ 5 − х − 24 = 0

Получим приведенное квадратное уравнение, корни которого можно найти подбором по теореме Виета:

х 2 − 2 х − 24 = 0

Итак, корнями уравнения х 2 − 2 х − 24 = 0 будут числа -4 и 6.

Теперь выбираем корень, обращая внимание на наше ограничение на х, т.е. корень должен быть меньше или равен 5. Таким образом, запишем, что 6 – это посторонний корень, так как 6 н е ≤ 5 , а число минус 4 записываем в ответ нашего уравнения, так как − 4 ≤ 5 .

pазбирался: Даниил Романович | обсудить разбор | оценить

Понятие квадратного уравнения

Уравнение — это равенство, содержащее переменную, значение которой нужно найти.

Например, х + 8 = 12 — это уравнение, которое содержит переменную х.

Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.

Например, если х = 5, то при подстановке в уравнение мы получим 5 + 8 = 12. 13 = 12 — противоречие. Значит, х = 5 не является корнем уравнения.

А вот если х = 4, то при подстановке в уравнение мы получим 4 + 8 = 12. 12 = 12 — верное равенство. Значит, х = 4 является корнем уравнения.

Решить уравнение — значит найти все его корни или доказать, что их не существует.

Квадратное уравнение — это уравнение вида ax² + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Чтобы запомнить месторасположение коэффициентов, давайте потренируемся определять их.

Квадратные уравнения могут иметь два корня, один корень или не иметь корней.

Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b² − 4ac. А вот свойства дискриминанта:

• если D < 0, корней нет;
• если D = 0, есть один корень;
• если D > 0, есть два различных корня.

С этим разобрались. А сейчас посмотрим подробнее на различные виды квадратных уравнений.

Разобраться в теме еще быстрее с помощью опытного преподавателя можно
на курсах по математике в онлайн-школе Skysmart.

Приведенные и неприведенные квадратные уравнения

Квадратное уравнение может быть приведенным или неприведенным — все зависит от от значения первого коэффициента.

Приведенное квадратное уравнение — это уравнение, где старший коэффициент, тот который стоит при одночлене высшей степени, равен единице.

Неприведенным называют квадратное уравнение, где старший коэффициент отличается от единицы.

Давайте-ка на примерах — вот у нас есть два уравнения:

• x² — 2x + 6 = 0
• x² — x — 1/4 = 0

В каждом из них старший коэффициент равен единице (которую мы мысленно представляем при x² ), а значит уравнение называется приведенным.

• 2x² − 4x — 12 = 0 — первый коэффициент отличен от единицы (2), значит это неприведенное квадратное уравнение.

Каждое неприведенное квадратное уравнение можно преобразовать в приведенное, если произвести равносильное преобразование — разделить обе его части на первый коэффициент.

Пример 1. Превратим неприведенное уравнение: 8x² + 20x — 9 = 0 — в приведенное.

Для этого разделим обе части исходного уравнения на старший коэффициент 8:

Ответ: равносильное данному приведенное уравнение x² + 2,5x — 1,125 = 0.

Пройдите тест и узнайте, какие темы отделяют от пятёрки по математике

Полные и неполные квадратные уравнения

В определении квадратного уравнения есть условие: a ≠ 0. Оно нужно, чтобы уравнение ax² + bx + c = 0 было именно квадратным. Если a = 0, то уравнение обретет вид линейного: bx + c = 0.

Что касается коэффициентов b и c, то они могут быть равны нулю, как по отдельности, так и вместе. В таком случае квадратное уравнение принято называть неполным.

Неполное квадратное уравнение —— это квадратное уравнение вида ax² + bx + c = 0, где оба или хотя бы один из коэффициентов b и c равен нулю.

Полное квадратное уравнение — это уравнение, у которого все коэффициенты отличны от нуля.

Решение неполных квадратных уравнений

Как мы уже знаем, есть три вида неполных квадратных уравнений:

• ax² = 0, ему отвечают коэффициенты b = 0 и c = 0;
• ax² + c = 0, при b = 0;
• ax² + bx = 0, при c = 0.

Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам.

Как решить уравнение ax² = 0

Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax² = 0.

Уравнение ax² = 0 равносильно x² = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x² = 0 является нуль, так как 0² = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.

Таким образом, неполное квадратное уравнение ax² = 0 имеет единственный корень x = 0.

Пример 1. Решить −6x² = 0.

Как решаем:

1. Замечаем, что данному уравнению равносильно x² = 0, значит исходное уравнение имеет единственный корень — нуль.
2. По шагам решение выглядит так:

   −6x² = 0

   x² = 0

   x = √0

   x = 0

Ответ: 0.

Как решить уравнение ax² + с = 0

Обратим внимание на неполные квадратные уравнения вида ax² + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.

Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами.

Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax² + c = 0:

• перенесем c в правую часть: ax² = — c,
• разделим обе части на a: x² = — c/а.

Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.

Если — c/а < 0, то уравнение x² = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а < 0 ни для какого числа p равенство р2 = — c/а не является верным.

Если — c/а > 0, то корни уравнения x² = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)² = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)² = — c/а. Ура, больше у этого уравнения нет корней.

Пример 1. Найти решение уравнения 8x² + 5 = 0.

Как решать:

1. Перенесем свободный член в правую часть:

   8x² = — 5

2. Разделим обе части на 8:

   x² = — 5/8

3. В правой части осталось число со знаком минус, значит у данного уравнения нет корней.

Ответ: уравнение 8x² + 5 = 0 не имеет корней.

Как решить уравнение ax² + bx = 0

Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.

Неполное квадратное уравнение ax² + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение:

1. Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.

2. Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.

Таким образом, неполное квадратное уравнение ax² + bx = 0 имеет два корня:

• x = 0;
• x = −b/a.

Пример 1. Решить уравнение 0,5x² + 0,125x = 0

Как решать:

1. Вынести х за скобки

   х(0,5x + 0,125) = 0

2. Это уравнение равносильно х = 0 и 0,5x + 0,125 = 0.
3. Решить линейное уравнение:

   0,5x = −0,125,
   х = −0,125/0,5

4. Разделить:

   х = −0,25

5. Значит корни исходного уравнения — 0 и −0,25.

Ответ: х = 0 и х = −0,25.

Как разложить квадратное уравнение

С помощью теоремы Виета можно получить формулу разложения квадратного трехчлена на множители. Выглядит она так:

Дискриминант: формула корней квадратного уравнения

Чтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так:

где D = b² − 4ac — дискриминант квадратного уравнения.

Эта запись означает:

,

.

Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться.

Алгоритм решения квадратных уравнений по формулам корней

Теперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни.

В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.

Алгоритм решения квадратного уравнения ax² + bx + c = 0:

• вычислить его значение дискриминанта по формуле D = b²−4ac;
• если дискриминант отрицательный, зафиксировать, что действительных корней нет;
• если дискриминант равен нулю, вычислить единственный корень уравнения по формуле х = −b/2a;
• если дискриминант положительный, найти два действительных корня квадратного уравнения по формуле корней

Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться!

Примеры решения квадратных уравнений

Как решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике.

Пример 1. Решить уравнение −4x² + 28x — 49 = 0.

Как решаем:

1. Найдем дискриминант: D = 28² — 4(-4)(-49) = 784 — 784 = 0
2. Так как дискриминант равен нулю, значит это квадратное уравнение имеет единственный корень
3. Найдем корень

   х = — 28/2(-4)

   х = 3,5

Ответ: единственный корень 3,5.

Пример 2. Решить уравнение 54 — 6x² = 0.

Как решаем:

1. Произведем равносильные преобразования. Умножим обе части на −1

   54 — 6x² = 0 | *(-1)

   6x² — 54 = 0

2. Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую

   6x² = 54

   х² = 9

   х = ±√9

   х₁ = 3, х₂ = — 3

Ответ: два корня 3 и — 3.

Пример 3. Решить уравнение x²— х = 0.

Как решаем:

1. Преобразуем уравнение так, чтобы появились множители

   х(х — 1) = 0

   х₁ = 0, х₂ = 1

Ответ: два корня 0 и 1.

Пример 4. Решить уравнение x²— 10 = 39.

Как решаем:

1. Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую

   x²— 10 = 39

   x²= 39 + 10

   x²= 49

   х = ±√49

   х₁ = 7, х₂ = −7

Ответ: два корня 7 и −7.

Пример 5. Решить уравнение 3x²— 4x+94 = 0.

Как решаем:

1. Найдем дискриминант по формуле

   D = (-4)² — 4 * 3 * 94 = 16 — 1128 = −1112

2. Дискриминант отрицательный, поэтому корней нет.

Ответ: корней нет.

В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся.

Формула корней для четных вторых коэффициентов

Рассмотрим частный случай. Формула решения корней квадратного уравнения 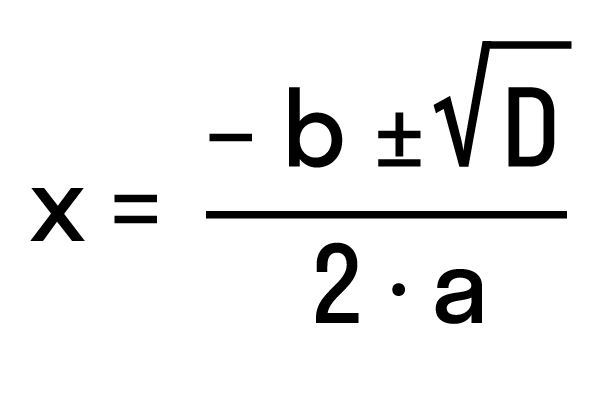, где D = b² — 4ac, помогает получить еще одну формулу, более компактную, при помощи которой можно решать квадратные уравнения с четным коэффициентом при x. Рассмотрим, как появилась эта формула.

Например, нам нужно решить квадратное уравнение ax² + 2nx + c = 0. Сначала найдем его корни по известной нам формуле. Вычислим дискриминант D = (2n)²— 4ac = 4n² — 4ac = 4(n²— ac) и подставим в формулу корней:

Для удобства вычислений обозначим выражение n² -ac как D₁. Тогда формула корней квадратного уравнения со вторым коэффициентом 2·n примет вид:

где D₁ = n²— ac.

Самые внимательные уже заметили, что D = 4D₁, или D₁= D/4. Проще говоря, D₁ — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения.

Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:

• вычислить D₁= n²— ac;
• если D₁< 0, значит действительных корней нет;
• если D₁= 0, значит можно вычислить единственный корень уравнения по формуле x = -n/a;
• если же D₁> 0, значит можно найти два действительных корня по формуле

Формула Виета

---

Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так: 

Если дано x² + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:

Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.

Рассмотрим теорему Виета на примере: x² + 4x + 3 = 0.

Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:

Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:

Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x² + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:

Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.

Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:

Результат проделанных вычислений в том, что мы убедились в справедливости выражения:

Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она:

Обычно вся суть обратных теорем в том самом выводе, которое дает первая теорема. Так, при доказательстве теоремы Виета стало понятно, что сумма x₁ и x₂ равна −b, а их произведение равно c. В обратной теореме это и есть утверждение.

Пример 1. Решить при помощи теоремы Виета: x² − 6x + 8 = 0.

Как решаем:

1. Для начала запишем сумму и произведение корней уравнения. Сумма будет равна 6, так как второй коэффициент равен −6. А произведение корней равно 8.

   

2. Когда у нас есть эти два равенства, можно подобрать подходящие корни, которые будут удовлетворять обоим равенствам системы.

   Чтобы проще подобрать корни, нужно их перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x₁ и x₂ надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.

   Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x₁ + x₂ = 6. А значения 4 и 2 подходят обоим равенствам:

   

3. Значит числа 4 и 2 — корни уравнения x² − 6x + 8 = 0. p>

Упрощаем вид квадратных уравнений

Если мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту.

Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11x² — 4 x — 6 = 0, чем 1100x² — 400x — 600 = 0.

Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100x² — 400x — 600 = 0, просто разделив обе части на 100.

Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов.

Покажем, как это работает на примере 12x²— 42x + 48 = 0. Найдем наибольший общий делитель абсолютных величин его коэффициентов: НОД (12, 42, 48) = 6. Разделим обе части исходного квадратного уравнения на 6, и придем к равносильному уравнению 2x² — 7x + 8 = 0. Вот так просто.

А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов. Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения

умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x² + 4x — 18 = 0.

Также для удобства вычислений можно избавиться от минуса при старшем коэффициенте квадратного уравнения — для этого умножим или разделим обе части на −1. Например, удобно от квадратного уравнения −2x²— 3x + 7 = 0 перейти к решению 2x² + 3x — 7 = 0.

Связь между корнями и коэффициентами

Мы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты:

Из этой формулы, можно получить другие зависимости между корнями и коэффициентами.

Например, можно применить формулы из теоремы Виета:

• x₁ + x₂ = — b/a,
• x₁* x₂ = c/a.

Для приведенного квадратного уравнения сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней — свободному члену. Например, по виду уравнения 3x²— 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3.

Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты:

Цели урока:

1. Систематизировать различные способы решения
   квадратных уравнений, дать представление
   учащимся о важных вехах истории развития
   математики;
2. Обучать поискам нескольких способов решения
   одной задачи и умению выбирать из них наиболее
   оптимальный;
3. Развивать навыки работы с дополнительной
   литературой, историческим материалом;
4. Показать многообразие и красоту математических
   решений.

Тип урока: урок систематизации и обобщения.

Ход урока

Устная работа:

1. Определите, имеет ли уравнение корни. Если
   имеет, то ответьте на вопросы:

а) Сколько корней имеет уравнение?

б) Рациональными или иррациональными являются
его корни?

в) Каковы знаки корней?

г) Если корни разных знаков, то какой из них
имеет больший модуль?

3 x² + 7х +2 =0; 3 – 8у + 2 = 0; 5 x² – 3х +2 =0; 2 x²
– 10х – 5 =0.

2. Решите квадратное уравнение подбором корней:

x² + 9х +20 =0; x² – 17х + 30 =0; x² + 7х –
60=0; x² – 11х + 24 =0.

Учитель: Сегодня на уроке мы рассмотрим
различные способы решения квадратных уравнений
в разные исторические эпохи на примере одной
задачи-решения квадратного уравнения.

Ученик 1: Методы решения квадратных уравнений
были известны еще в древние времена. Они
излагались в вавилонских рукописях царя
Хаммурапи (XX в. до н.э.), в трудах древнегреческого
математика Евклида (III в. до н. э), в древних
китайских и японских трактатах. Многие
математики древности решали квадратные
уравнения геометрическим способом: квадрат и 10
его корней равны 39.

Для решения уравнения x² + 10х = 39 поступали
следующим образом. Пусть АВ = х, ВС=5, ( 10:2). На
стороне АС = АВ + ВС строился квадрат, который
разбивался на четыре части. Очевидно, что сумма
площадей трех частей равна x² + 10х или 39. Если
к этой площади прибавить площадь четвертой
части, то 39+25=64 – площадь всего квадрата. Но, эта
же площадь равна = 64, х + 5 = 8, х = 3. Таким образом, число 3
является корнем квадратного уравнения, так как
отрицательных чисел тогда не знали.

Ученик 2: А вот как решал эту же задачу
ал-Хорезми в 825 году. Строим квадрат со стороной х
и на его сторонах – четыре прямоугольника
высотой 10/4. В углах фигуры построим четыре
квадрата со стороной 10/4. Подсчитаем площадь
получившегося большого квадрата:

x² + 4 · 10/4 · х + = x² + 10х + · 4.

По условию x² + 10х = 39, т.е. площадь
получившегося большого квадрата равна

39 + + · 4
= 39 + 25 = 64. Значит, его сторона равна 8, тогда

х + 2· 10/4 = 8, х = 3 (Ал-Хорезми не признавал
отрицательных чисел).

Ученик 3: В III в. н. э. квадратное уравнение x²
– 20х + 96 = 0 решал великий древнегреческий
математик Диофант.

Пусть сумма двух чисел 20, а произведение
96.Допустим, что разность этих чисел 2z. Так как их
сумма 20, то если разделить ее пополам, каждая из
полученных делением частей будет равна половине
суммы, то есть 10. И если половину разности – z
прибавить к одной из полученных от деления
половине и вычесть из другой, то опять получается
сумма 20 и разность 2z.

Пусть большее из искомых чисел равно z + 10, тогда
меньшее — 10–z. Их сумма 20, а разность 2z.
Произведение искомых чисел равно 96. Таким
образом,

(10 + z)(10 –z) = 96, 100 – = 96, = 4, z = 2. Следовательно, большее
число равно 12, а меньшее 8.

Давайте пробуем решить квадратное уравнение x²
+ 10х = 39 методом Диофанта.

1. Пусть x² + 10х – 39 =0;
2. Положим разность искомых чисел 2z;
3. –5 — половина коэффициента при х с
   противоположным знаком;
4. Положим х1 = z – 5, х2 = z + 5. Тогда (z – 5)(z + 5) = 39, – 25 = 39,

= 64, z =8.

Отсюда, х1 = 8–5=3, х2 = 8+5=13. Полученные корни 13 и 3
“устроили” бы Диофанта, т.к. оба натуральные. Но,
используя теорему Виета, мы видим, что х1·х2 = –39, а
это означает, что корни должны быть разного
знака. Значит, не каждое уравнение можно решить
этим методом.

Ученик 4: Неполные квадратные уравнения и
частные виды полных квадратных уравнений умели
решать вавилоняне и египтяне (2 тыс. лет до н.э.).
Некоторые виды квадратных уравнений решали и
древнегреческие математики, используя
геометрический подход. Примеры решения
уравнений без обращения к геометрии дает Диофант
Александрийский (III в. н. э.). В своем трактате
хорезмский тематик Мухаммед ал-Хорезми в 825 г.
Разъясняет приемы решения квадратных уравнений.
После трудов немецкого математика М. Штифеля (1487
– 1567 гг.), нидерландца А. Жирара (1595 – 1632 гг.),
Р.Декарта и Н.Ньютона, способ решения квадратных
уравнений принял современный вид. А в 1591 г. Ф.Виет
вывел формулы, выражающие зависимость корней
квадратного уравнения от его коэффициентов и
сформулировал свою знаменитую теорему.

Ученик 5: Франсуа Виет родился в 1540 г. Во
Франции, в Фонтене – ле – Конт. По образованию
юрист. Он много занимался адвокатской
деятельностью, а с 1571 г. по 1584 г. Был советником
короля Георга III и Георга IV. Но, все свободное
время, весь свой досуг он отдавал занятиям
математикой. Особенно усиленно он начал работать
в области математики с 1584 г., после отстранения от
должности при королевском дворе. Виет детально
изучил труды как древних так и современных ему
математиков и создал по существу новую алгебру.
Он ввел в нее буквенную символику. После открытия
Виета, стало возможным записывать правила в виде
формул.

Учитель: Именно с 1591 г. мы пользуемся
формулами при решении квадратных уравнений.
Решим квадратное уравнение x² + 10х – 39 =0
современными способами.

x²+ 10х – 39 = 0,
а = 1, b = 10, с = –39.
D = – 4ac; D
= 100 + 156 = 256, D > 0.

Х1,2 = (;
Х1 = (-10 + 16)/2 = 3; Х2 = (-10 — 16)/2 = -13.

Ответ: -13; 3.

Ученик 6: Следует отметить, что второй
коэффициент в данном уравнении четный, что
позволяет использовать иную формулу для решения
данного уравнения.

x² + 10х – 39 =0 ,
а = 1, k= 5, с = –39.
D1 = – ac; D1
= 25 + 39 = 64, D1> 0.

Х1,2 =( ;
Х1 = (-5 + 8)/1 = 3; Х2 = (-5 — 8)/1 = -13.

Ответ: -13; 3.

Ученик 7: Данное уравнение можно решить,
используя теорему, обратную теореме Виета.

x² + 10х – 39 = 0,

Х1 = 3, х2 = -13.

Ответ: -13; 3.

Учитель: Существуют ли другие способы
решения квадратных уравнений?

Ученик: Квадратные уравнения можно решать,
используя свойства “суммы коэффициентов”. Если
a + b + c = 0, х1 = 1, х2 = c/а; или если a – b – c = 0, то х1 = –1,
х2 = – с/а. Но, данное квадратное уравнение нельзя
решить, используя эти соотношения. Например,
изменим в рассмотренном уравнении свободный
член:

x² + 10х – 11 = 0;
a = 1; b = 10; с = –11; 1 + 10 – 11 = 0;
х1 = 1; х2 = –11.

Учитель: Приведите примеры уравнений,
решаемых с применением второго утверждения.

Например: –10 x² + 29х + 39 =0; x²– 2005х – 2006
= 0.

Учитель: В учебнике мы встречаем задания, где
четко обозначено, как решить квадратное
уравнение. В предложенных вам задачах вы не
только решите уравнение, но и узнаете интересные
факты.

1.Известно, что учет населения проводился в
Египте и в Китае еще до нашей эры. Решив
квадратное уравнение 4x² – 24х + 39 =0 , вы
определите в каком это было тысячелетии до н.э.

2. На основе статистических данных можно
выделить регионы с максимальным сбросом
загрязненных вод: это Краснодарский край и
Москва. Сколько процентов общего количества
загрязненных вод дают эти регионы, вы узнаете,
решив уравнение x² – 19х + 88 =0 .

3. Кислотные осадки разрушают сооружения из
мрамора и других материалов. Исторические
памятники Греции и Рима, простояв тысячелетия, за
последние годы разрушаются прямо на глазах.
“Мировой рекорд” принадлежит одному
шотландскому городку, где 10 апреля 1974 года выпал
дождь, скорее напоминающий столовый уксус, чем
воду. Устно решите уравнения, найдите верный
ответ и соответствующую ему букву и прочитайте
название этого “знаменитого” городка.
(Питлохри).

В заключение, вам предлагается выполнить
самостоятельную работу:

Учитель: Подведем итог. На уроке мы
рассмотрели различные способы решения
квадратных уравнений. Квадратные уравнения –
это фундамент, на котором держится алгебра.
Известен способ решения даже с помощью циркуля и
линейки. С этим методом можно познакомиться на
занятиях факультатива.

Литература:

1. Дробышев Ю.А. Изучение квадратных уравнений на
   основе историко –генетического метода/Ю.А.
   Дробышев // Математика школе.
2. Мордкович А.Г. Алгебра 8 класс в двух частях.
   Ч.1./А.Г. Мордкович: учеб. для общеобразоват.
   учреждений. – 4-е изд. – М.: немозина,2002.
3. Мордкович А.Г. Алгебра 8 класс в двух частях.
   Ч.2./А.Г. Мордкович: задачник для общеобразоват.
   учреждений. – 4-е изд. – М.: немозина,2002.
4. С.А. Литвинова, и др. За страницами учебника
   математики 8-11 классы. – 2-е изд., дополненное – М.:
   Глобус, Волгоград: Панорама,2008.-С.76-82.
5. Энциклопедия для детей. Т.11. Математика/ Под ред.
   М.Д. Аксенова. – М.: Аванта+,2000.
6. Юшкевич А.П.История математики в средние
   века/А.П.Юшкевич. – М.: Физматгиз,1961. – С.194-195.

Решение квадратных уравнений

6 июля 2011

Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.

Квадратное уравнение — это уравнение вида ax² + bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.

Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:

1. Не имеют корней;
2. Имеют ровно один корень;
3. Имеют два различных корня.

В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант.

Дискриминант

Пусть дано квадратное уравнение ax² + bx + c = 0. Тогда дискриминант — это просто число D = b² − 4ac.

Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:

1. Если D < 0, корней нет;
2. Если D = 0, есть ровно один корень;
3. Если D > 0, корней будет два.

Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:

Задача. Сколько корней имеют квадратные уравнения:

1. x² − 8x + 12 = 0;
2. 5x² + 3x + 7 = 0;
3. x² − 6x + 9 = 0.

Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8)² − 4 · 1 · 12 = 64 − 48 = 16

Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 3² − 4 · 5 · 7 = 9 − 140 = −131.

Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6)² − 4 · 1 · 9 = 36 − 36 = 0.

Дискриминант равен нулю — корень будет один.

Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.

Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.

Корни квадратного уравнения

Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:

Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D < 0, корней нет — ничего считать не надо.

Задача. Решить квадратные уравнения:

1. x² − 2x − 3 = 0;
2. 15 − 2x − x² = 0;
3. x² + 12x + 36 = 0.

Первое уравнение:
x² − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2)² − 4 · 1 · (−3) = 16.

D > 0 ⇒ уравнение имеет два корня. Найдем их:

Второе уравнение:
15 − 2x − x² = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2)² − 4 · (−1) · 15 = 64.

D > 0 ⇒ уравнение снова имеет два корня. Найдем их

[begin{align} & {{x}_{1}}=frac{2+sqrt{64}}{2cdot left( -1 right)}=-5; \ & {{x}_{2}}=frac{2-sqrt{64}}{2cdot left( -1 right)}=3. \ end{align}]

Наконец, третье уравнение:
x² + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12² − 4 · 1 · 36 = 0.

D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:

[x=frac{-12+sqrt{0}}{2cdot 1}=-6]

Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.

Неполные квадратные уравнения

Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:

1. x² + 9x = 0;
2. x² − 16 = 0.

Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:

Уравнение ax² + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.

Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax² = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.

Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax² + c = 0. Немного преобразуем его:

Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c/a) ≥ 0. Вывод:

1. Если в неполном квадратном уравнении вида ax² + c = 0 выполнено неравенство (−c/a) ≥ 0, корней будет два. Формула дана выше;
2. Если же (−c/a) < 0, корней нет.

Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c/a) ≥ 0. Достаточно выразить величину x² и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.

Теперь разберемся с уравнениями вида ax² + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:

Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:

Задача. Решить квадратные уравнения:

1. x² − 7x = 0;
2. 5x² + 30 = 0;
3. 4x² − 9 = 0.

x² − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x₁ = 0; x₂ = −(−7)/1 = 7.

5x² + 30 = 0 ⇒ 5x² = −30 ⇒ x² = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.

4x² − 9 = 0 ⇒ 4x² = 9 ⇒ x² = 9/4 ⇒ x₁ = 3/2 = 1,5; x₂ = −1,5.

Смотрите также:

1. Теорема Виета
2. Следствия из теоремы Виета
3. Тест на тему «Значащая часть числа»
4. Метод коэффициентов, часть 1
5. Однородные тригонометрические уравнения: общая схема решения
6. Задача B4: строительные бригады

После того, как вы внимательно изучите, как решать квадратные уравнения обычным образом с помощью
формулы для корней
можно рассмотреть другой способ решения квадратных уравнений — с помощью теоремы Виета.

Перед тем, как изучить теорему Виета, хорошо потренируйтесь в
определении коэффициентов
«a», «b» и «с» в квадратных уравнениях.
Без этого вам будет трудно применить теорему Виета.

Когда можно применить теорему Виета

Не ко всем квадратным уравнениям имеет смысл использовать эту теорему.
Применять теорему Виета имеет смысл только к приведённым квадратным уравнениям.

Обратите внимание, что разница с обычным общим видом
квадратного уравнения «ax² + bx + c = 0» в том, что в
приведённом уравнении «x² + px + q = 0» коэффициент
«а = 1».

Если сравнить приведенное квадратное уравнение «x² + px + q = 0» с обычным общим видом квадратного
уравнения «ax² + bx + c = 0», то становится видно,
что
«p = b», а «q = c».

Теперь давайте на примерах разберем, к каким уравнениям можно применять теорему Виета, а где это не целесообразно.

Уравнение	Коэффициенты	Вывод
x2 − 7x + 1 = 0	a = 1 p = −7 q = 1	Так как «a = 1» можно использовать теорему Виета.
3x2 − 1 + x = 0 Приведем уравнение к общему виду: 3x2 + x − 1 = 0	a = 3 p = 1 q = −1	Так как «a = 3» не следует использовать теорему Виета.
−x2 = −3 + 2x Приведем уравнение к общему виду: −x2 + 3 − 2x = 0 −x2 − 2x + 3 = 0	a = −1 p = −2 q = 3	Так как «a = −1» не следует использовать теорему Виета.

Как использовать теорему Виета

Теперь мы готовы перейти к самому методу Виета для решения квадратных уравнений.

Чтобы было проще запомнить формулу Виета, следует запомнить:
«Коэффициент «p» —
значит плохой, поэтому он берется со знаком минус».

---

Рассмотрим пример.

x² + 4x − 5 = 0

Так как в этом уравнении «a = 1», квадратное уравнение
считается приведённым, значит, можно
использовать метод Виета.
Выпишем коэффициенты «p» и «q».

• p = 4
• q = −5

Запишем теорему Виета для квадратного уравнения.

	x1 + x2 = −4
x1 · x2 = −5

Методом подбора мы приходим к тому, что корни уравнения
«x₁ = −5» и «x₂ = 1». Запишем ответ.

Ответ: x₁ = −5; x₂ = 1

---

Рассмотрим другой пример.

x² + x − 6 = 0

Старший коэффициент «a = 1» поэтому можно применять теорему Виета.

	x1 + x2 = −1
x1 · x2 = −6

Методом подбора получим, что корни уравнения
«x₁ = −3» и «x₂ = 2». Запишем ответ.

Ответ: x₁ = −3; x₂ = 2

---

Деление уравнение на первый коэффициент

Рассмотрим уравнение, которое по заданию требуется решить, используя теорему Виета.

2x² − 16x − 18 = 0

Сейчас в уравнении «a = 2»,
поэтому перед тем, как использовать теорему Виета нужно сделать так, чтобы «a = 1».

Для этого достаточно разделить все уравнение на «2».
Таким образом, мы сделаем квадратное уравнение приведённым.

2x² − 16x − 18 = 0            | (:2)
2x²(:2) − 16x(:2) − 18(:2) = 0
x² − 8x − 9 = 0

Теперь «a = 1» и можно смело записывать формулу Виета и находить корни методом подбора.

	x1 + x2 = −(−8)
x1 · x2 = −9

Методом подбора получим, что корни уравнения
«x₁ = 9» и «x₂ = −1». Запишем ответ.

Ответ: x₁ = 9; x₂ = −1

---

Бывают задачи, где требуется найти не только корни уравнения, но и коэффициенты самого уравнения. Например, как в такой задаче.

Корни «x₁» и
«x₂» квадратного уравнения
«x² + px + 3 = 0» удовлетворяют
условию «x₂ = 3x₁».
Найти «p», «x₁»,
«x₂».

Запишем теорему Виета для этого уравнения.

По условию дано, что
«x₂ = 3x₁».
Подставим это выражение в систему вместо «x₂».

	x1 + 3x1 = −p
x1 · 3x1 = 3

Решим полученное квадратное уравнение «x₁² = 1»
методом подбора и найдем «x₁».

   x₁² = 1

• (Первый корень) x₁ = 1
• (Второй корень) x₁ = −1

Мы получили два значения «x₁».
Для каждого из полученных значений найдем «p» и запишем все полученные результаты в ответ.

(Первый корень) x₁ = 1

Найдем
«x₂»

x₁ · x₂ = 3
1 · x₂ = 3
x₂ = 3

Найдем «p»

x₁ + x₂ = −p
1 + 3 = −p
4 = −p
p = −4;
(Второй корень) x₁ = −1

Найдем «x₂»

x₁ · x₂ = 3
−1 · x₂ = 3
                 −x₂ = 3         | ·(−1)
x₂ = −3

Найдем «p»

x₁ + x₂ = −p
−1 + −3 = −p
−4 = −p
p = 4

Ответ: (x₁ = 1; x₂ = 3; p = −4)     и    
(x₁ = −1; x₂ = −3; p = 4)

---

Теорема Виета в общем виде

В школьном курсе математики теорему Виета используют только для приведённых уравнений,
где старший коэффициент «a = 1», но, на самом деле, теорему Виета можно применить к любому квадратному уравнению.

В общем виде теорема Виета для квадратного уравнения выглядит так:

Убедимся в правильности этой теоремы на примере. Рассмотрим неприведённое квадратное уравнение.

3x² + 3x − 18 = 0

Используем для него теорему Виета в общем виде.

	x1 + x2 = −1
x1 · x2 = −6

Методом подбора получим, что корни уравнения
«x₁ = −3» и «x₂ = 2». Запишем ответ.

Ответ: x₁ = −3; x₂ = 2

В заданиях школьной математики мы не рекомендуем использовать теорему Виета в общем виде.

Другими словами, реальную пользу теорема Виета приносит только для приведённых квадратных уравнений, в
которых «a = 1».
Именно в таких случаях она не усложняет жизнь, а позволят без дополнительных расчетов быстро найти корни.

---

Ваши комментарии

Оставить комментарий:

---