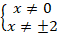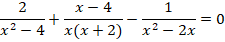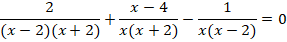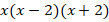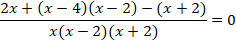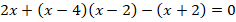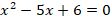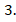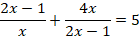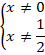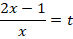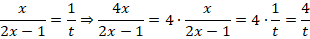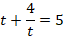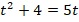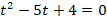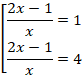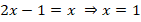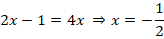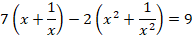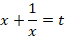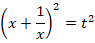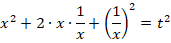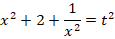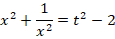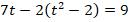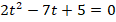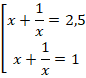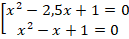Решение дробных уравнений с преобразованием в квадратные уравнения
Дробным уравнением называется уравнение, в котором хотя бы одно из слагаемых — дробь, в знаменателе которой присутствует неизвестное. Например, дробным уравнением является уравнение .
Решать дробные уравнения удобно в следующем порядке:
- найти общий знаменатель дробей, входящих в уравнение, если каждая дробь имеет смысл,
- заменить данное уравнение целым, умножив обе его часть на общий знаменатель,
- решить получившееся целое уравнение,
- исключить из его корней те, которые обращают в нуль общий знаменатель.
Пример 1. Решить дробное уравнение:
.
Решение. Воспользуемся основным свойством дроби с представим левую и правую части этого уравнения в виде дробей с одинаковым знаменателем:
.
Эти дроби равны при тех и только тех значениях, при которых равны их числители, а знаменатель отличен от нуля. Если знаменатель равен нулю, то дроби, а следовательно, и уравнение не имеет смысла.
Таким образом, чтобы найти корни данного уравнения, нужно решить уравнение
.
Упростив уравнение (раскрыв скобки и приведя подобные члены), получим квадратное уравнение
.
.
Найденные корни не обращают знаменатель в нуль, поэтому они являются корнями исходного дробного уравнения.
Пример 2. Решить дробное уравнение:
.
Решение. Найдём общий знаменатель дробей, входящих в данное дробное уравнение. Общий знаменатель —
.
Заменим исходное уравнение целым. Для этого умножим обе его части на общий знаменатель. Получим:
Выполним необходимые преобразования в полученном уравнении и придём к квадратному уравнению
.
.
Если x = -3 , то найденный на первом шаге знаменатель обращается в нуль:
,
то же самое, если x = 3 .
Следовательно, числа -3 и 3 не являются корнями исходного уравнения, а, поскольку никакие другие корни не найдены, данное уравнение не имеет решения.
Пример 3. Решить дробное уравнение:
.
Решение. Найдём общий знаменатель дробей, входящих в данное уравнение. Для этого знаменатели дробей разложим на множители:
.
Общий знаменатель — выражение
Заменим исходное уравнение целым, умножив обе его части на общий знаменатель. Получим:
Выполнив преобразования, придём к квадратному уравнению
.
.
Ни один из корней не обращает общий знаменатель в нуль. Следовательно, числа -4 и 9 — корни данного уравнения.
Пример 4. Решить дробное уравнение:
.
Решение. Введём новую переменную, обозначив . Получим уравнение с переменной y :
.
Корни этого уравнения:
или .
Из уравнения находим, что
.
Из уравнения находим, что
.
Итак, данное уравнение имеет четыре корня:
, .
Решение уравнений с дробями
О чем эта статья:
5 класс, 6 класс, 7 класс
Понятие дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это рациональное число, представленное в виде a/b, где a — числитель дроби, b — знаменатель. Есть два формата записи:
- обыкновенный вид — ½ или a/b,
- десятичный вид — 0,5.
Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.
Дроби бывают двух видов:
- Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5.
- Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.
Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.
Основные свойства дробей
Дробь не имеет значения, если делитель равен нулю.
Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.
Дроби a/b и c/d называют равными, если a × d = b × c.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:
- Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
- Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Решить уравнение значит найти все его корни или убедиться, что корней нет.
Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа.
Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Понятие дробного уравнения
Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:
Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.
Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:
На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.
Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.
Как решать уравнения с дробями
1. Метод пропорции
Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.
Итак, у нас есть линейное уравнение с дробями:
В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.
После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.
2. Метод избавления от дробей
Возьмем то же самое уравнение, но попробуем решить его по-другому.
В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:
- подобрать число, которое можно разделить на каждый из знаменателей без остатка;
- умножить на это число каждый член уравнения.
Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!
Вот так просто мы получили тот же ответ, что и в прошлый раз.
Что еще важно учитывать при решении
- если значение переменной обращает знаменатель в 0, значит это неверное значение;
- делить и умножать уравнение на 0 нельзя.
Универсальный алгоритм решения
Определить область допустимых значений.
Найти общий знаменатель.
Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.
Раскрыть скобки, если нужно и привести подобные слагаемые.
Решить полученное уравнение.
Сравнить полученные корни с областью допустимых значений.
Записать ответ, который прошел проверку.
Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.
Примеры решения дробных уравнений
Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.
Пример 1. Решить дробное уравнение: 1/x + 2 = 5.
- Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
- Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
Решим обычное уравнение.
Пример 2. Найти корень уравнения
- Область допустимых значений: х ≠ −2.
- Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
Переведем новый множитель в числитель..
Сократим левую часть на (х+2), а правую на 2.
Пример 3. Решить дробное уравнение:
-
Найти общий знаменатель:
Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:
Выполним возможные преобразования. Получилось квадратное уравнение:
Решим полученное квадратное уравнение:
Получили два возможных корня:
Если x = −3, то знаменатель равен нулю:
Если x = 3 — знаменатель тоже равен нулю.
Дробно-рациональные уравнения
Что такое дробно-рациональные уравнения
Дробно-рациональными уравнениями называют такие выражения, которые представляется возможным записать, как:
при P ( x ) и Q ( x ) в виде выражений, содержащих переменную.
Таким образом, дробно-рациональные уравнения обязательно содержат как минимум одну дробь с переменной в знаменателе с любым модулем.
9 x 2 — 1 3 x = 0
1 2 x + x x + 1 = 1 2
6 x + 1 = x 2 — 5 x x + 1
Уравнения, которые не являются дробно-рациональными:
Как решаются дробно-рациональные уравнения
В процессе решения дробно-рациональных уравнений обязательным действием является определение области допустимых значений. Найденные корни следует проверить на допустимость, чтобы исключить посторонние решения.
Алгоритм действий при стандартном способе решения:
- Выписать и определить ОДЗ.
- Найти общий знаменатель для дробей.
- Умножить каждый из членов выражения на полученный общий параметр (знаменатель), сократить дроби, которые получились в результате, чтобы исключить знаменатели.
- Записать уравнение со скобками.
- Раскрыть скобки для приведения подобных слагаемых.
- Найти корни полученного уравнения.
- Выполним проверку корней в соответствии с ОДЗ.
- Записать ответ.
Пример 1
Разберем предложенный алгоритм на практическом примере. Предположим, что имеется дробно-рациональное уравнение, которое требуется решить:
x x — 2 — 7 x + 2 = 8 x 2 — 4
Начать следует с области допустимых значений:
x 2 — 4 ≠ 0 ⇔ x ≠ ± 2
Воспользуемся правилом сокращенного умножения:
x 2 — 4 = ( x — 2 ) ( x + 2 )
В результате общим знаменателем дробей является:
Выполним умножение каждого из членов выражения на общий знаменатель:
x x — 2 — 7 x + 2 = 8 x 2 — 4
x ( x — 2 ) ( x + 2 ) x — 2 — 7 ( x — 2 ) ( x + 2 ) x + 2 = 8 ( x — 2 ) ( x + 2 ) ( x — 2 ) ( x + 2 )
После сокращения избавимся от скобок и приведем подобные слагаемые:
x ( x + 2 ) — 7 ( x — 2 ) = 8
x 2 + 2 x — 7 x + 14 = 8
Осталось решить квадратное уравнение:
Согласно ОДЗ, первый корень является лишним, так как не удовлетворяет условию, по которому корень не равен 2. Тогда в ответе можно записать:
Примеры задач с ответами для 9 класса
Требуется решить дробно-рациональное уравнение:
x x + 2 + x + 1 x + 5 — 7 — x x 2 + 7 x + 10 = 0
x x + 2 + x + 1 x + 5 — 7 — x x 2 + 7 x + 10 = 0
Определим область допустимых значений:
О Д З : x + 2 ≠ 0 ⇔ x ≠ — 2
x 2 + 7 x + 10 ≠ 0
D = 49 — 4 · 10 = 9
x 1 ≠ — 7 + 3 2 = — 2
x 2 ≠ — 7 — 3 2 = — 5
Квадратный трехчлен x 2 + 7 x + 10 следует разложить на множители, руководствуясь формулой:
a x 2 + b x + c = a ( x — x 1 ) ( x — x 2 )
x x + 2 + x + 1 x + 5 — 7 — x ( x + 2 ) ( x + 5 ) = 0
Заметим, что общим знаменателем для дробей является: ( x + 2 ) ( x + 5 ) . Умножим на этот знаменатель уравнение:
x x + 2 + x + 1 x + 5 — 7 — x ( x + 2 ) ( x + 5 ) = 0
Сократим дроби, избавимся от скобок, приведем подобные слагаемые:
x ( x + 2 ) ( x + 5 ) x + 2 + ( x + 1 ) ( x + 2 ) ( x + 5 ) x + 5 —
— ( 7 — x ) ( x + 2 ) ( x + 5 ) ( x + 2 ) ( x + 5 ) = 0
x ( x + 5 ) + ( x + 1 ) ( x + 2 ) — 7 + x = 0
x 2 + 5 x + x 2 + 3 x + 2 — 7 + x = 0
2 x 2 + 9 x — 5 = 0
Потребуется решить квадратное уравнение:
2 x 2 + 9 x — 5 = 0
Первый корень не удовлетворяет условиям ОДЗ, поэтому в ответ нужно записать только второй корень.
Дано дробно-рациональное уравнение, корни которого требуется найти:
4 x — 2 — 3 x + 4 = 1
В первую очередь следует переместить все слагаемые влево и привести дроби к минимальному единому знаменателю:
4 ( x + 4 ) x — 2 — 3 ( x — 2 ) x + 4 — 1 ( x — 2 ) ( x + 4 ) = 0
4 ( x + 4 ) — 3 ( x — 2 ) — ( x — 2 ) ( x + 4 ) ( x — 2 ) ( x + 4 ) = 0
4 x + 16 — 3 x + 6 — ( x 2 + 4 x — 2 x — 8 ) ( x — 2 ) ( x + 4 ) = 0
x + 22 — x 2 — 4 x + 2 x + 8 ( x — 2 ) ( x + 4 ) = 0
Заметим, что получилось нулевое значение для дроби. Известно, что дробь может равняться нулю, если в числителе нуль, а знаменатель не равен нулю. На основании этого можно составить систему:
— x 2 — x + 30 ( x — 2 ) ( x + 4 ) = 0 ⇔ — x 2 — x + 30 = 0 ( x — 2 ) ( x + 4 ) ≠ 0
Следует определить такие значения для переменной, при которых в дроби знаменатель будет обращаться в нуль. Такие значения необходимо удалить из ОДЗ:
( x — 2 ) ( x + 4 ) ≠ 0
Далее можно определить значения для переменных, которые при подстановке в уравнение обращают числитель в нуль:
— x 2 — x + 30 = 0 _ _ _ · ( — 1 )
Получилось квадратное уравнение, которое можно решить:
Сравнив корни с условиями области допустимых значений, можно сделать вывод, что оба корня являются решениями данного уравнения.
Нужно решить дробно-рациональное уравнение:
x + 2 x 2 — 2 x — x x — 2 = 3 x
На первом шаге следует перенести все слагаемые в одну сторону и привести дроби к минимальному единому знаменателю:
x + 2 1 x ( x — 2 ) — x x x — 2 — 3 ( x — 2 ) x = 0
x + 2 — x 2 — 3 ( x — 2 ) x ( x — 2 ) = 0
x + 2 — x 2 — 3 x + 6 x ( x — 2 ) = 0
— x 2 — 2 x + 8 x ( x — 2 ) = 0 ⇔ — x 2 — 2 x + 8 = 0 x ( x — 2 ) ≠ 0
Перечисленные значения переменной обращают знаменатель в нуль. По этой причине их необходимо удалить из области допустимых значений.
— x 2 — 2 x + 8 = 0 _ _ _ · ( — 1 )
Корни квадратного уравнения:
x 1 = — 4 ; x 2 = 2
Заметим, что второй корень не соответствует ОДЗ. Таким образом, в ответе остается только первый корень.
Найти корни уравнения:
x 2 — x — 6 x — 3 = x + 2
Согласно стандартному алгоритму решения дробно-рациональных уравнений, выполним перенос всех слагаемых в одну сторону. Далее необходимо привести к дроби к наименьшему общему знаменателю:
x 2 — x — 6 1 x — 3 — x ( x — 3 ) — 2 ( x — 3 ) = 0
x 2 — x — 6 — x ( x — 3 ) — 2 ( x — 3 ) x — 3 = 0
x 2 — x — 6 — x 2 + 3 x — 2 x + 6 x — 3 = 0
0 x x — 3 = 0 ⇔ 0 x = 0 x — 3 ≠ 0
Такое значение переменной, при котором знаменатель становится равным нулю, нужно исключить из области допустимых значений:
Заметим, что это частный случай линейного уравнения, которое обладает бесконечным множеством корней. При подстановке какого-либо числа на место переменной х в любом случае числовое равенство будет справедливым. Единственным недопустимым значением для х в данном задании является число 3, которое не входит в ОДЗ.
Ответ: х — любое число, за исключением 3.
Требуется вычислить корни дробно-рационального уравнения:
5 x — 2 — 3 x + 2 = 20 x 2 — 4
На первом этапе необходимо выполнить перенос всех слагаемых влево, привести дроби к минимальному единому знаменателю:
5 ( x + 2 ) x — 2 — 3 ( x — 2 ) x + 2 — 20 1 ( x — 2 ) ( x + 2 ) = 0
5 ( x + 2 ) — 3 ( x — 2 ) — 20 ( x — 2 ) ( x + 2 ) = 0
5 x + 10 — 3 x + 6 — 20 ( x — 2 ) ( x + 2 ) = 0
2 x — 4 ( x — 2 ) ( x + 2 ) = 0 ⇔ 2 x — 4 = 0 ( x — 2 ) ( x + 2 ) ≠ 0
( x — 2 ) ( x + 2 ) ≠ 0
Данные значения переменной х являются недопустимыми, так как в этом случае теряется смысл дроби в связи с тем, что знаменатель принимает нулевое значение.
Заметим, что 2 не входит в область допустимых значений. В связи с этим, можно заключить, что у уравнения отсутствуют корни.
Ответ: корни отсутствуют
Нужно найти корни уравнения:
x — 3 x — 5 + 1 x = x + 5 x ( x — 5 )
Начнем с определения ОДЗ:
— 5 ≠ 0 x ≠ 0 x ( x — 5 ) ≠ 0 x ≠ 5 x ≠ 0
При умножении обеих частей уравнения на единый знаменатель всех дробей и сокращении аналогичных выражений, которые записаны в числителе и знаменателе, получим:
x — 3 x — 5 + 1 x = x + 5 x ( x — 5 ) · x ( x — 5 )
( x — 3 ) x ( x — 5 ) x — 5 + x ( x — 5 ) x = ( x + 5 ) x ( x — 5 ) x ( x — 5 )
( x — 3 ) x + x = x + 5
Прибегая к арифметическим преобразованиям, можно записать уравнение в упрощенной форме:
x 2 — 3 x + x — 5 = x + 5 → x 2 — 2 x — 5 — x — 5 = 0 → x 2 — 3 x — 10 = 0
Для дальнейших действий следует определить, к какому виду относится полученное уравнение. В нашем случае уравнение является квадратным с коэффициентом при x 2 , который равен 1. Таким образом, целесообразно воспользоваться теоремой Виета:
x 1 · x 2 = — 10 x 1 + x 2 = 3
В этом случае подходящими являются числа: -2 и 5.
Второе значение не соответствует области допустимых значений.
http://skysmart.ru/articles/mathematic/reshenie-uravnenij-s-drobyami
http://wika.tutoronline.ru/algebra/class/9/drobnoraczionalnye-uravneniya
Дробно рациональные уравнения. Решения
Уравнение которые можно свести к дроби f(x)/g(x)=0 называется дробно рациональным уравнением.
Решение дробно рациональных уравнений не слишком сложная задача если Вы знаете методику, а она достаточно проста.
Если уравнение имеет несколько слагаемых то переносим их по одну сторону знака равенства и сводим к общему знаменателю. В результате получим дробную функцию f(x)/g(x), которая равна нулю
Следующим шагом находим корни числителя. Отвергаем среди них те, которые не принадлежат области допустимых значений (нули знаменателя) и записываем правильный ответ.
В теории все просто, однако на практике и у школьников и у студентов возникают проблемы при сведены к общему знаменателю, отыскании корней и т.д. Для ознакомления с решением рассмотрим несколько распространенных задач.
Примеры дробно рациональных уравнений
Пример 1. Найти корни уравнения
Решение: По методике переносим слагаемые и сводим к общему знаменателю
Приравниваем числитель и знаменатель к нулю и находим корни. Первое уравнение можем решить по теореме Виета
Второе раскладываем на множители
Если от корней числителя отбросить нули знаменателя то получим только одно решение x=-7.
Внимание: Всегда проверяйте совпадают ли корни числителя и знаменателя. Если такие есть то не учитывайте их в ответе.
Ответ: х=-7.
————————————
Пример 2. Решить уравнение
Решение: Задано дробное рациональное уравнение. Находим сначала корни числителя, для этого решаем квадратное уравнение
Вычисляем дискриминант
и корни уравнения
Получили три нуля числителя .
Квадратное уравнение в знаменателе проще и можем решить по теореме Виета
Числитель и знаменатель не имеют общих корней поэтому все три найденные значения будут решениями.
————————————
Пример 3. Найти корни уравнения
Решение: Переносим слагаемое за знак равенства
и сводим к общему знаменателю
Раскрываем в числителе скобки и сводим к квадратному уравнению
Полученное дробно рациональное уравнение эквивалентно системе двух уравнений
Корни первого вычисляем через дискриминант
Нули второго находим без проблем
Исключаем из решений числителя значение и получим.
Ответ: х=3.
————————————
Задачи на движение
Задача 4. Вертолет пролетел по ветру расстояние 120 км и обратно вернулся, потратив на весь путь 6 час. Найдите скорость ветра если скорость в штиль составляет 45 км/час.
Решение:
Обозначим скорость ветра через х км/час. Тогда за ветром скорость вертолета составит (45+х) км/час, и в обратном направлении (45-х) км/час. По условию задачи вертолет потратил 6 часов на дорогу.
Разделив расстояние на скорость и просуммировав получим время
Получили дробно рациональное уравнение схема решения которого неоднократно повторялась
Решением второго уравнения будут значения x=-45; x=45.
Корни числителя найдем после упрощений
С физических соображений первое решение отвергаем.
Ответ: скорость ветра 15 км/час.
————————————
Задачи о совместной работе
Задача 2. Два лесорубы работая вместе выполнили норму вырубки за 4 дня. Сколько дней нужно на выполнение этой работы каждому лесорубу отдельно если первому для вырубки нормы нужно на 6 дней меньше чем другому?
Решение: Пусть первый лесоруб выполняет норму по х дней. Тогда второму необходимо (х+6) дней.
Это означает что за один день первый выполнит , а второй — часть всей нормы. По условию выполняют норму за 4 дня, то есть оба в день могут выполнить нормы.
Составляем и решаем уравнение
Данное дробно рациональное уравнение эквивалентно системе двух уравнений
Одно решение не соответствует физической сути задачи. Время второго лесоруба
х+6=6+6=12 (дней)
Ответ: Работу первый лесоруб выполнит за 6 дней, а второй за 12.
————————————
Подобных дробно рациональных уравнений можно рассмотреть множество, схема их решения неизменна. В теоретических задачах правильно составляйте уравнение и не заблуждайтесь при сведении к общему знаменателю. Все остальное сводится к решению преимущественно линейных или квадратных уравнений.
yukhym.com
Дробно-рациональные уравнения | Алгебра
Дробн0-рациональные уравнения (дробные рациональные уравнения или просто дробные уравнения) — это уравнения c одной переменной вида
где f(x) и g(x) — рациональные выражения, хотя бы одно из которых содержит алгебраическую дробь (то есть в таких уравнениях в знаменателе есть переменная).
В общем виде дробно-рациональные уравнения решают по следующей схеме:
1) Все слагаемые переносим в одну сторону.
2) Дроби приводим к НОЗ (наименьшему общему знаменателю).
3) После упрощения решаем уравнение типа «дробь равна нулю«.
В частных случаях дробно-рациональные уравнения могут быть решены с помощью замены переменной либо разложением на множители.
Начнем с рассмотрения примеров общего случая.
Решить дробно-рациональные уравнения:
Переносим все слагаемые в левую часть уравнения и приводим дроби к наименьшему общему знаменателю:
Пришли к уравнению типа «дробь равна нулю» Дробь равна нулю, если числитель равен нулю, а знаменатель отличен от нуля, поэтому это уравнение равносильно системе:
Находим значения переменной, при которых знаменатель обращается в нуль, и исключаем их из области допустимых значений:
Теперь находим значения переменных, при которых числитель обращается в нуль:
Это — квадратное уравнение. Его корни
Оба корня удовлетворяют условиям x≠2, x≠ -4.Ответ: 5; -6.
Переносим все слагаемые в одну сторону и приводим дроби к наименьшему общему знаменателю:
— при этих значениях переменной знаменатель обращается в нуль, поэтому их исключаем из ОДЗ.
Из двух корней квадратного уравнения
— второй не входит в ОДЗ. Поэтому в ответ включаем лишь первый корень.
Ответ: -4.
Переносим все слагаемые в одну сторону и приводим дроби к НОЗ:
Значение переменной, при котором знаменатель обращается в нуль, исключаем из ОДЗ:
Уравнение
— частный случай линейного уравнения. Оно имеет бесконечное множество решений: какое бы число мы не подставили вместо x, получим верное числовое равенство. Единственное значение x, который не входит в множество решений данного уравнения — 3.
Ответ: x — любое число, кроме 3.
Переносим все слагаемые в левую часть и приводим дроби к наименьшему общему знаменателю:
— при этих значениях переменной дробь не имеет смысла, поскольку знаменатель обращается в нуль.
Так как 2 не входит в ОДЗ, данное уравнение не имеет корней.
Ответ: корней нет.
www.algebraclass.ru
Решение целых и дробно рациональных уравнений
Давайте познакомимся с рациональными и дробными рациональными уравнениями, дадим их определение, приведем примеры, а также разберем наиболее распространенные типы задач.
Yandex.RTB R-A-339285-1
Рациональное уравнение: определение и примеры
Знакомство с рациональными выражениями начинается в 8 классе школы. В это время на уроках алгебры учащиеся все чаще начинают встречать задания с уравнениями, которые содержат рациональные выражения в своих записях. Давайте освежим в памяти, что это такое.
Определение 1
Рациональное уравнение – это такое уравнение, в обеих частях которого содержатся рациональные выражения.
В различных пособиях можно встретить еще одну формулировку.
Определение 2
Рациональное уравнение – это такое уравнение, запись левой части которого содержит рациональное выражение, а правая – нуль.
Определения, которые мы привели для рациональных уравнений, являются равнозначными, так как говорят об одно и том же. Подтверждает правильность наших слов тот факт, что для любых рациональных выражений P и Q уравнения P=Q и P−Q=0 будут равносильными выражениями.
А теперь обратимся к примерам.
Пример 1
Рациональные уравнения:
x=1, 2·x−12·x2·y·z3=0, xx2+3·x-1=2+27·x-a·(x+2), 12+34-12x-1=3.
Рациональные уравнения точно также, как и уравнения других видов, могут содержать любое количество переменных от 1 до нескольких. Для начала мы рассмотрим простые примеры, в которых уравнения будут содержать только одну переменную. А затем начнем постепенно усложнять задачу.
Рациональные уравнения делятся на две большие группы: целые и дробные. Посмотрим, какие уравнения будут относиться к каждой из групп.
Определение 3
Рациональное уравнение будет являться целым в том случае, если в записи левой и правой его частей содержатся целые рациональные выражения.
Определение 4
Рациональное уравнение будет являться дробным в том случае, если одна или обе его части содержат дробь.
Дробно рациональные уравнения в обязательном порядке содержат деление на переменную или же переменная имеется в знаменателе. В записи целых уравнений такого деления нет.
Пример 2
3·x+2=0 и (x+y)·(3·x2−1)+x=−y+0,5 – целые рациональные уравнения. Здесь обе части уравнения представлены целыми выражениями.
1x-1=x3 и x:(5·x3+y2)=3:(x−1):5 – это дробно рациональные уравнения.
К числу целых рациональных уравнений можно отнести линейные и квадратные уравнения.
Решение целых уравнений
Решение т
zaochnik.com
5. Дробно рациональные уравнения
Дробно
рациональные уравнения. Решения
Уравнение
которые можно свести к дроби
f(x)/g(x)=0 называется дробно рациональным
уравнением.
Решение дробно
рациональных уравнений не слишком
сложная задача если Вы знаете методику,
а она достаточно проста.
Если
уравнение имеет несколько слагаемых
то переносим их по одну сторону знака
равенства и сводим к общему знаменателю.
В результате получим дробную функцию
f(x)/g(x), которая равна нулю
Следующим
шагом находим корни числителя. Отвергаем
среди них те, которые не принадлежат
области допустимых значений (нули
знаменателя) и записываем правильный
ответ.
В
теории все просто, однако на практике
и у школьников и у студентов возникают
проблемы при сведены к общему знаменателю,
отыскании корней и т.д. Для ознакомления
с решением рассмотрим несколько
распространенных задач.
Примеры
дробно рациональных уравнений
Пример
1.
Найти корни уравнения
Решение:
По методике переносим слагаемые и сводим
к общему знаменателю
Приравниваем
числитель и знаменатель к нулю и находим
корни. Первое уравнение можем решить
по теореме Виета
Второе
раскладываем на множители
Если
от корней числителя отбросить нули
знаменателя то получим только одно
решение x=-7.
Внимание:
Всегда проверяйте совпадают ли корни
числителя и знаменателя. Если такие
есть то не учитывайте их в ответе.
Ответ:
х=-7.
————————————
Пример
2. Решить уравнение
Решение:
Задано дробное рациональное уравнение.
Находим сначала корни числителя, для
этого решаем квадратное уравнение
Вычисляем
дискриминант
и
корни уравнения
Получили
три нуля числителя
.
Квадратное
уравнение в знаменателе проще и можем
решить по теореме Виета
Числитель
и знаменатель не имеют общих корней
поэтому все три найденные значения
будут
решениями.
————————————
Пример
3. Найти корни уравнения
Решение:
Переносим слагаемое за знак равенства
и
сводим к общему знаменателю
Раскрываем
в числителе скобки и сводим к квадратному
уравнению
Полученное
дробно рациональное уравнение эквивалентно
системе двух уравнений
Корни
первого вычисляем через дискриминант
Нули
второго находим без проблем
Исключаем
из решений числителя значение
и
получим.
Ответ:
х=3.
————————————
Задачи
на движение
Задача
4. Вертолет пролетел по ветру расстояние
120 км и обратно вернулся, потратив на
весь путь 6 час. Найдите скорость ветра
если скорость в штиль составляет 45
км/час.
Решение:
Обозначим скорость ветра через х
км/час. Тогда за ветром скорость вертолета
составит (45+х) км/час, и в обратном
направлении (45-х) км/час. По условию
задачи вертолет потратил 6 часов на
дорогу.
Разделив расстояние на
скорость и просуммировав получим время
Получили
дробно рациональное уравнение схема
решения которого неоднократно
повторялась
Решением
второго уравнения будут значения x=-45;
x=45.
Корни
числителя найдем после упрощений
С
физических соображений первое решение
отвергаем.
Ответ:
скорость ветра 15 км/час.
————————————
Задачи
о совместной работе
Задача
2. Два лесорубы работая вместе выполнили
норму вырубки за 4 дня. Сколько дней
нужно на выполнение этой работы каждому
лесорубу отдельно если первому для
вырубки нормы нужно на 6 дней меньше чем
другому?
Решение:
Пусть первый лесоруб выполняет норму
по х дней. Тогда второму необходимо
(х+6) дней.
Это означает что за один
день первый выполнит
,
а второй -часть всей нормы. По условию выполняют
норму за 4 дня, то есть оба в день могут
выполнитьнормы.Составляем
и решаем уравнение
Данное
дробно рациональное уравнение эквивалентно
системе двух уравнений
Одно
решение
не
соответствует физической сути задачи.
Время второго лесоруба
х+6=6+6=12 (дней)
Ответ:
Работу первый лесоруб выполнит за 6
дней, а второй за 12.
————————————
Подобных
дробно рациональных уравнений можно
рассмотреть множество, схема их решения
неизменна. В теоретических задачах
правильно составляйте уравнение и не
заблуждайтесь при сведении к общему
знаменателю. Все остальное сводится к
решению преимущественно линейных или
квадратных уравнений.
Следует
приобрести навык в решении дробно-рациональных
уравнений путём выполнения ряда
тренировочных упражнений. Тренировочные
упражнения предлагаются трёх уровней
сложности: А – обязательный минимум
знаний по этой теме, В – упражнения
среднего уровня сложности, С – упражнения
повышенной степени сложности.
|
№ |
Уравнения |
Ответы |
|
Уровень |
||
|
1 |
5 |
|
|
2 |
-2; |
|
|
3 |
-9; 1 |
|
|
4 |
-0,5; 1 |
|
|
5 |
0,5 |
|
|
6 |
-1 |
|
|
7 |
-4,7; |
|
|
8 |
-4; 7 |
|
|
9 |
-; |
|
|
10 |
2 |
|
№ |
Уравнения |
Ответы |
|
Уровень |
||
|
1 |
7 |
|
|
2 |
-0,25 |
|
|
3 |
Нет |
|
|
4 |
0; 1 |
|
|
5 |
-1; 5 |
|
|
6 |
-1 |
|
|
7 |
(x+4)(x2-1) |
5 |
|
8 |
— |
|
|
9 |
4 |
|
|
10 |
1 |
|
№ |
Уравнения |
Ответы |
|
Уровень |
||
|
1 |
-2 |
|
|
2 |
1; 4; |
|
|
3 |
x2+x+1= |
-2; 1 |
|
4 |
1; 8 |
|
|
5 |
x2-5x+ |
1; 2; |
|
6 |
2 |
|
|
7 |
||
|
8 |
-3; 1 |
|
|
9 |
0,2; |
|
|
10 |
Нет |
studfiles.net
Решение (корни) квадратного уравнения
Квадратным уравнением называется уравнение вида ax² + bx + c = 0,
где x — переменная, которая в уравнении присутствует в квадрате, a, b, c — некоторые числа, причём a ≠ 0.
Например, квадратным является уравнение
2x² — 3x + 1 = 0,
в котором a = 2, b = — 3, c = 1.
В квадратном уравнении ax² + bx + c = 0
коэффициент a называют первым коэффициентом, b — вторым коэффициентом, c — свободным членом.
Уравнения вида ax² + bx = 0,
где c =0,
ax² + c = 0,
где b =0, и
ax² = 0,
где a =0 и b =0,
называются неполными квадратными уравнениями.
Найти корни квадратного уравнения значит решить квадратное уравнение.
Для вычисления корней квадратного уравния служит выражение b² — 4ac,
которое называется дискриминантом квадратного уравнения и обозначается буквой D.
Корни квадратного уравнения имеют следующие сферы применения:
— для разложении квадратного трёхлена на множители, что, в свою очередь, является
приёмом упрощения выражений (например, сокращения дробей, вынесение за скобки общего знаменателя и т.д.) в частности,
при нахождении пределов, производных и интегралов;
— для решения задач на соотношения параметров меняющегося объекта (корни квадратного уравнения,
чаще всего один, являются обычно конечным решением).
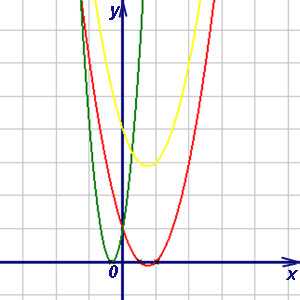
График квадратичного трёхлена ax² + bx + c —
левой части квадратного уравнения — представляет собой параболу, ось симметрии которой параллельна
оси 0y. Число точек пересечения параболы с осью
0x определяет число корней квадратного уравнения. Если точек
пересечения две, то квадратное уравнение имеет два действительных корня, если точка пересечения
одна, то квадратное уравнение имеет один действительный корень, если парабола не пересекает
ось 0x, то квадратное уравнение не имеет действительных
корней. На рисунке ниже изображены три упомянутых случая.
Как видно на рисунке, красная парабола пересекает ось 0x
в двух точках, зелёная — в одной точке, а жёлтая парабола не имеет точек пересечения с осью
0x.
1. Если дискриминант больше нуля (),
то квадратное уравнение имеет два различных действительных корня.
Они вычисляются по формулам:
и
.
Часто пишется так: .
2. Если дискриминант равен нулю (),
то квадратное уравнение имеет только один действительный корень, или, что то же самое — два равных действительных корня,
которые равны .
3. Если дискриминант меньше нуля (),
то квадратное уравнение не имеет действительных корней, а имеет комплексные корни, но нахождение комплексных корней
в этой статье рассматривать не будем. В общем случае правильным решением является констатация того,
что квадратное уравнение не имеет действительных корней.
Пример 1. Определить, сколько действительных корней имеет квадратное уравнение:
.
Решение. Найдём дискриминант:
.
Дискриминант больше нуля, следовательно, квадратное уравнение имеет два действительных корня.
Путём преобразования в квадратное уравнение следует решать и дробные
уравнения, в которых хотя бы одно из слагаемых — дробь, в знаменателе которой присутствует неизвестное, например, .
О том, как это делается — в материале Решение дробных уравнений с преобразованием в квадратное уравнение.
Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.
Пример 2. Определить, сколько действительных корней имеет квадратное уравнение:
.
Решение. Найдём дискриминант:
.
Дискриминант равен нулю, следовательно, квадратное уравнение имеет один действительный корень.
Пример 3. Определить, сколько действительных корней имеет квадратное уравнение:
.
Решение. Найдём дискриминант:
.
Дискриминант меньше нуля, следовательно, квадратное уравнение не имеет действительных корней.
Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.
Находить корни квадратного уравнения требуется при решении многих
задач высшей математики, например, при нахождении пределов,
интегралов, исследовании
функций на возрастание и убывание и других.
Пример 4. Найти корни квадратного уравнения:
.
В примере 1 нашли дискриминант этого уравнения:
,
Решение квадратного уравнения найдём по формуле для корней:
Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.
Корни приведённого квадратного уравнения
Формула корней приведённого уравнения имеет вид:
.
Существуют формулы, связывающие корни квадратного уравнения с его
коэффициентами. Они впервые были получены французским математиком Ф.Виетом.
Теорема Виета. Если квадратное уравнение
ax² + bx + c = 0
имеет действительные корни, то их сумма равна — b/a,
а произведение равно с/a:
Следствие. Если приведённое квадратное уравнение
x² + px + q = 0
имеет действительные корни и
, то
Пояснение формул: сумма корней приведённого квадратного уравнения равна второму
коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному
члену.
Следовательно, теорему Виета можно применять и для поиска корней
приведённого квадратного уравнения.
Если известны корни квадратного уравнения, то трёхчлен, представляющий собой левую часть уравнения, можно
разложить на множители по следующей формуле:
.
Этот приём часто используется для упрощения выражений, особенно сокращения дробей.
Пример 9. Упростить выражение:
.
Решение. Числитель данной дроби можем рассматривать как квадратный трёхчлен в отношении x
и разложить его на множители, предварительно найдя его корни. Найдём дискриминант квадратного уравнения:
.
Корни квадратного уравнения будут следующими:
.
Разложим квадратный многочлен на множители:
.
Упростили выражение, проще не бывает:
.
Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.
Пример 10. Упростить выражение:
.
Решение. И числитель, и знаменатель — квадратные трёхчлены. Значит, их можно разложить
на множители, предварительно найдя корни соответствующих квадратных уравнений. Находим дискриминант первого квадратного уравнения:
.
Корни первого квадратного уравнения будут следующими:
.
Находим дискриминант второго квадратного уравнения:
.
Так как дискриминант равен нулю, второе квадратное уравнение имеет два совпадающих корня:
.
Подставим корни квадратных уравнений, разложим числитель и знаменатель на множители и получим:
.
Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.
Упрощать выражения путём решения квадратных уравнений требуется
при решении многих задач высшей математики, например, при
нахождении пределов,
интегралов,
исследовании
функций на возрастание и убывание и других.
Разумеется, квадратного трёхчлена может может и не быть в выражении в первоначальном виде,
он может быть получен в процессе предварительных преобразований выражения.
Формула корней квадратного уравнения «переоткрывалась» неоднократно. Один
из первых дошедших до наших дней выводов этой формулы принажлежит индийскому математику
Брахмагупте (около 598 г.). Среднеазиатский учёный аль-Хорезми (IX в.) получил эту формулу
методом выделения полного квадрата с помощью геометрической иллюстрации. Суть его рассуждений
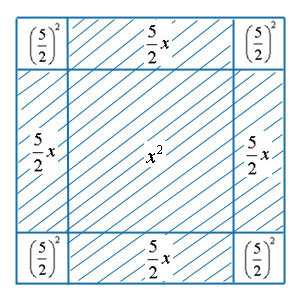
видна из рисунка ниже (он рассматривает уравнение x² + 10x = 39).
Площадь большого квадрата равна (x + 5)².
Она складывается из площади x² + 10x
заштрихованной фигуры, равной левой части рассматриваемого уравнения, и площади четырёх
квадратов со стороной 5/2, равной 25. Получается следующее уравнение и его решение:
Пример 11. Отрезок ткани стоит 180 у.ед. Если бы ткани в отрезке было на 2,5 м больше
и цена отрезка оставалась бы прежней, то цена 1 м ткани была бы на 1 у.ед. меньше. Сколько ткани в отрезке?
Решение. Примем количество ткани в отрезке за x и получим уравнение:
Приведём обе части уравнения к общему знаменателю:
Произведём дальнейшие преобразования:
Получили квадратное уравнение, которое и решим:
Ясно, что количество ткани не может быть отрицательным, поэтому в качестве ответа из двух корней квадратного уравнения подходит лишь один корень — положительный.
Ответ: в отрезке 20 м ткани.
Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.
Пример 12. Товар, количество которого 187,5 кг, взвешивают в одинаковых ящиках.
Если в каждом ящике количество товара уменьшить на 2 кг, то следовало бы использовать на 2 ящика больше и при этом
2 кг товара остались бы невзвешенными. Сколько кг товара взвешивают в каждом ящике?
Решение. Примем за x количество товара, взвешиваемого в одном ящике. Тогда получим уравнение:
Приведём обе части уравнения к общему знаменателю, произведём дальнейшие преобразования и получим квадратное уравнение.
Процесс записывается так:
Найдём дискриминант:
Найдём корни квадратного уравнения:
Количество товара не может быть отрицательным, поэтому в качестве ответа из двух корней квадратного уравнения подходит лишь положительный корень.
Ответ: в одном ящике взвешивают 12,5 кг ткани.
Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.
Другие темы в блоке «Школьная математика»
function-x.ru
Решение дробных рациональных уравнений
Сегодня мы разберемся, как решать дробные рациональные уравнения.
Посмотрим: из уравнений
(1) 2х + 5 = 3(8 – х),
(2) ,
(3)
(4)
дробными рациональными уравнениями являются только (2) и (4), а (1) и (3) это целые уравнения.
Предлагаю решить уравнение (4), а затем сформулировать правило.
Поскольку уравнение дробное, то надо найти общий знаменатель. В этом уравнении это выражение 6(х – 12)(х – 6). Затем мы умножаем обе части уравнения на общий знаменатель:
После сокращения получаем целое уравнение:
6(х – 6)2 – 6(х – 12)2 = 5(х – 12)(х – 6).
Решив это уравнение надо обязательно проверить не обращают ли полученные корни в нуль знаменатели дробей в исходном уравнении.
Раскрываем скобки:
6х2 – 72х + 216 – 6х2 + 144х – 864 = 5х2 – 90х + 360, упрощаем уравнение: 5х2 – 162х + 1008 = 0.
Находим корни уравнения
D = 6084, √D = 78,
х1= (162 – 78)/10= 84/10 = 8,4 и х2 = (162 + 78)/10 = 240/10 = 24.
При х = 8,4 и 24 общий знаменатель 6(х – 12)(х – 6) ≠ 0, значит эти числа являются корнями уравнения (4).
Ответ: 8,4; 24.
Решив предложенное уравнение, приходим к следующим положениям:
1) Находим общий знаменатель.
2) Умножаем обе части уравнения на общий знаменатель.
3) Решаем полученное целое уравнение.
4) Проверяем, какие из корней обращают общий знаменатель в нуль и исключаем их из решения.
Посмотрим теперь на примере, как работают полученные положения.
Решить уравнение:
1) Общий знаменатель: х2 – 1
2) Умножаем обе части уравнения на общий знаменатель, получаем целое уравнение: 6 – 2(х + 1) = 2(х2 – 1) – (х + 4)(х – 1)
3) Решаем уравнение: 6 – 2х – 2 = 2х2 – 2 – х2 – 4х + х + 4
х2 – х – 2 = 0
х1 = — 1 и х2 = 2
4) При х = -1, общий знаменатель х2 – 1 = 0. Число -1 корнем не является.
При х = 2, общий знаменатель х2 – 1 ≠ 0. Число 2 – корень уравнения.
Ответ: 2.
Как видите, наши положения работают. Не бойтесь, у вас все получится! Самое главное правильно найдите общий знаменатель и аккуратно выполните преобразования. Надеемся, что при решение дробных рациональных уравнений у вас всегда будут получаться правильные ответы. Если у вас остались вопросы или вы хотите попрактиковаться в решении подобных уравнений, записывайтесь на уроки к автору этой статьи, репетитору Валентине Галиневской.
Также рекомендуем посмотреть новый видеоурок по данной теме от нашего репетитора Ольги Лукашонок.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
Как решать квадратные уравнения? | Александр Будников
Что такое квадратное уравнение? Виды квадратных уравнений. Примеры.
Обычно квадратные уравнения – одна из самых любимых учениками тем школьной математики. Почему? Потому, что алгоритм решения любого квадратного уравнения достаточно прост и универсален. Работает безотказно. Однако простора для дурацких ошибок при решении квадратных уравнений тоже хватает, да… Так что будем разбираться, что к чему.)
Начнём с названия.
Ключевым словом в понятии квадратное уравнение является слово «квадратное». Что оно означает? Оно означает то, что в уравнении обязательно должен присутствовать икс в квадрате. В любом случае. Также в уравнении могут быть (или не быть – как уж повезёт) просто икс (в первой степени) и просто число (свободный член). Но это ещё не всё. При этом в уравнении не должно быть иксов в кубе, в четвёртой и любых других степенях, больших двойки.
В самом общем виде квадратное уравнение выглядит так:
Здесь a, b, c – какие-то числа. Любые.) Числа b и c могут быть совсем-совсем любыми, а вот а – любым числом, кроме нуля. Почему – объясню чуть ниже.
Например:
Здесь a=1; b=4; c=-5
Или такое:
Здесь a=-2; b=-5; c=3
Или:
Здесь a=0,5; b=-2; c=2
И так далее…
В этих уравнениях слева присутствует полный набор слагаемых: есть икс в квадрате (с коэффициентом a), есть просто икс (с коэффициентом b), а также есть свободный член c. Такие квадратные уравнения в математике так и называются — полными.
А ещё бывают и такие квадратные уравнения, где чего-то не хватает. Что у нас произойдёт, если, например, обнулить коэффициент b (b=0)? У нас исчезнет икс в первой степени.
Получится, к примеру, что-то типа:
x2–9 = 0
x2+25 = 0
И так далее…
А если c=0? Тогда у нас пропадёт свободный член:
x2-4x = 0
—x2+10x = 0
И т.д. и т.п.
А если уж оба коэффициента a и b станут равны нулю, то тогда совсем всё просто получится:
0,1x2 = 0
-3x2 = 0
Такие квадратные уравнения, где какого-то из членов не хватает, называются (вы не поверите) неполными.)
Таким образом, квадратные уравнения бывают двух основных видов – полные и неполные.
А теперь ответ на вопрос, почему коэффициент a не может быть равен нулю. А давайте подумаем, что у нас произойдёт, если мы обнулим коэффициент а? Да! У нас пропадёт икс в квадрате! Наше уравнение превратится в линейное. И решаться будет уже совсем по-другому…
Общая формула корней квадратного уравнения.
Квадратные уравнения решаются достаточно просто. По одной единственной универсальной формуле. Всего одной!
И теперь у меня для вас есть две новости – хорошая и плохая. С какой начнём? Принято с плохой начинать? Что ж, ладно…
Новость плохая. Строгий аналитический вывод общей формулы корней квадратного уравнения достаточно громоздок и основан на процедуре выделения полного квадрата. В большинстве школьных учебников вывод общей формулы корней всё-таки приводят, но я считаю что эта процедура – очередной вынос мозга простому среднестатистическому школьнику. Поэтому в данном уроке я его (вывод) всё-таки опущу.)
Новость хорошая. Запоминать аналитический вывод формулы корней квадратного уравнения в общем виде и не требуется. Вообще! Гораздо важнее запомнить саму формулу и научиться её применять на практике. Вот мы и попрактикуемся. И уравнения порешаем.)
«Формула! Где формула?! Ты достал формулу?» — слышу громкие возгласы, как в старом добром рекламном ролике начала 2000-х…
Достаю, достаю! Из широких штанин… О-па! Вот она, формула!)
Вот такая формула. Да, я не спорю, довольно громоздкая. Но и уравнение мы решаем всё-таки квадратное, а не более простое линейное…
Как вы видите, для поиска корней квадратного уравнения нам необходимы только коэффициенты a, b, c. И всё. Больше ничего. Аккуратно подставляем все коэффициенты в формулу и считаем наши корни.
Что такое дискриминант? Формула и смысл дискриминанта.
Выражение b2-4ac, стоящее в формуле под знаком квадратного корня, называется дискриминант. До боли знакомое и родное слово для большинства старшеклассников. Слова «решаем через дискриминант» звучат обнадёживающе и вселяют оптимизм!)
Обычно дискриминант обозначается буковкой D:
Тогда, с учётом данного обозначения, общая формула корней станет выглядеть вот так:
Сам по себе дискриминант, как правило, прост и безотказен в обращении. Но… В чём его смысл? Почему для, скажем, —b или 2a не вводятся какие-то специальные термины и обозначения? Буквы – они и в Африке буквы… А тут – такое красивое слово! Дискриминант…
А дело вот в чём. При решении любого квадратного уравнения по общей формуле возможны всего три ситуации.
1. Дискриминант положительный (D>0).
Это означает, что из него можно извлечь корень. Красиво корень извлекается или некрасиво – вопрос другой. Главное, что извлекается в принципе.
Тогда наше квадратное уравнение всегда имеет два различных корня.
Вот они:
Два – потому, что общая формула в этой ситуации разбивается на два отдельных случая. А именно – какой знак, плюс или минус, берётся перед радикалом. Каждый случай даёт свой корень.
2. Дискриминант равен нулю (D=0)
Как вы думаете, чему в этом случае будет равен корень из дискриминанта? Нулю, конечно же! А поскольку от прибавления/вычитания нуля в числителе ничего не меняется, то наше уравнение имеет один корень:
Вообще, строго говоря, это не один корень, а два одинаковых. Но в упрощённом виде, когда нам надо просто решить уравнение и получить ответ, принято говорить об одном решении. Поэтому в ответе не заморачиваются и пишут просто одинокий икс, безо всякой индексации х1,2 .
Однако в более солидных темах (например, в решении неравенств методом интервалов) этот пунктик, с двумя одинаковыми (или, по-научному, кратными) корнями, настолько важен, что я буду про него напоминать снова и снова.
3. Дискриминант отрицательный (D<0)
Из отрицательных чисел извлекать квадратный корень в средней школе не учат. Это означает, что уравнение не имеет корней. Ну и ладно. На нет, как говорится, и суда нет.
Как решать квадратные уравнения?
Начнём с полных квадратных уравнений.
Полные квадратные уравнения
Полное квадратное уравнение (любое!) решается всегда в четыре основных этапа.
1. Приводим уравнение к стандартному виду:
Всё просто: выстраиваем левую часть уравнения по убыванию степеней икса. На первом месте пишем слагаемое с иксом в квадрате, на втором месте – с иксом в первой степени и, наконец, свободный член. Справа – обязательно должен быть ноль! Если справа тусуются ещё какие-то члены, то переносим их в левую часть и приводим подобные.
Конечно, если уравнение уже дано в стандартном виде, то первый этап делать не нужно.)
Как только уравнение представлено в стандартном виде, приступаем ко второму этапу.
2. Внимательно осматриваем уравнение и определяем (правильно!) коэффициенты a, b и c.
Если опыта пока что мало, во избежание досадных ошибок бывает очень полезным выписать их отдельно.
3. Считаем дискриминант по формуле D = b2-4ac.
Внимание! На данном этапе сразу же извлекаем корень из дискриминанта! Если красиво извлекается, конечно.)
4. Подставляем все значения в общую формулу, считаем корни уравнения и записываем ответ.
Вот и весь алгоритм. Простой и безотказный. Ну что, тренируемся на кошках?
Например, надо решить вот такое уравнение:
7x2 – x – 8 = 0
Работаем прямо по пунктам.
1. Приводим уравнение к стандартному виду.
Уравнение уже дано нам в стандартном виде. Стало быть, уже готово к решению. Слева – полный набор членов, выстроенных по убыванию степеней, а справа – ноль. Посему переходим сразу ко второму этапу.
2. Внимательно осматриваем уравнение и определяем (правильно!) коэффициенты a, b и c.
Вот и пишем:
a = 7; b = -1; c = -8
3. Считаем дискриминант по формуле D = b2-4ac.
Аккуратно подставляем наши коэффициенты a, b и с в формулу дискриминанта. Подставляем со своими знаками! Частенько именно в знаках коэффициентов народ и путается. Точнее, не столько в самих знаках, сколько в подстановке отрицательных значений в формулу дискриминанта. Вот и не ленимся, аккуратно пишем все знаки и скобочки. Трудов много не отнимет, зато гарантированно убережёт от досадных промахов:
D = b2-4ac = (-1)2 – 4·7·(-8) = 1+224 = 225
Извлекаем корень из дискриминанта:
Отлично, корень извлекается чисто. Теперь переходим к последнему, самому главному этапу – считаем наши корни.
4. Подставляем все значения в общую формулу, аккуратно считаем корни уравнения и записываем ответ.
Опять же, аккуратно подставляем все числа в формулу, со всеми знаками и скобочками:
И считаем:
Вот и всё. Это ответ.)
Кстати сказать, если вы просто решаете квадратное уравнение, то нет особой нужды отдельно считать дискриминант. Можно работать напрямую с общей формулой, просто аккуратно подставляя в неё коэффициенты a, b и с.
В нашем случае можно было бы сразу записать:
Но такое оформление чревато тем, что, впопыхах, можно где-нибудь потерять минус. Оно вам надо? Посему лучше считайте дискриминант отдельно – ошибок меньше будет. Естественно, посчитав дискриминант, не забывайте про корень.) Специально акцентирую внимание на этом моменте, потому что сам дискриминант народ обычно считает правильно, а вот корень извлечь частенько забывает… К тому же, привыкнув к отдельному поиску дискриминанта, вы быстрее запомните его общую формулу – в более серьёзных заданиях пригодится. Например, в задачах с параметрами. Такие задачи – высший пилотаж на ЕГЭ!
Естественно, бывают и сюрпризы. Не без этого… И к ним (к сюрпризам) тоже надо быть готовым, да. Чтобы не растеряться, в случае чего…) Рассмотрим первый сюрприз. Самый безобидный.
Например, дано нам такое уравнение:
x2 + 1 = 4x
Как обычно, работаем прямо по алгоритму.
1. Приводим уравнение к стандартному виду.
Уравнение пока не готово к решению. Справа нужен ноль, а у нас справа тусуется 4х. Не беда: переносим 4х влево и выстраиваем члены по убыванию степеней:
x2 – 4х + 1 = 0
2. Внимательно осматриваем уравнение и определяем (правильно!) коэффициенты a, b и c.
В нашем случае:
a = 1; b = -4; c = 1
3. Считаем дискриминант по формуле D = b2-4ac.
D = b2-4ac = (-4)2 – 4·1·1 = 12
А вот и первый сюрприз.) Дискриминант не является точным квадратом целого числа! И корень из дискриминанта извлекается плохо:
Что делать? Не решается уравнение? Ну да, как же!
Ничего страшного.) Работаем прямо с корнем. Естественно, если есть возможность, то выносим всё, что извлекается, за знак корня:
4. Подставляем все значения в общую формулу, аккуратно считаем корни уравнения и записываем ответ.
Поехали:
Корни нашего уравнения получились иррациональными. Ну и ничего страшного. Бывает.) Такой уж пример.
Открою небольшой секрет. Обычно задания на квадратные уравнения составляются так, чтобы корень из дискриминанта извлекался ровно и, тем самым, корни в ответе получались красивыми – либо целыми, либо рациональными. И народ постепенно привыкает к таким простым примерам наивно полагая, что дискриминант всегда обязан получаться точным квадратом. Не обязан! Более того, суровая реальность такова, что некрасивый дискриминант (а вместе с ним и лохматые иррациональные корни) – скорее правило, чем исключение! И если вы захотите задать какое-нибудь квадратное уравнение, выбрав в нём коэффициенты a, b и с случайным образом, то с вероятностью 99% корни вашего квадратного уравнения будут числами иррациональными.
Но иррациональных корней вовсе не надо бояться.) Ибо они – точно такие же числа, как и все остальные. Кстати говоря, в более серьёзных заданиях (неравенствах, задачах с параметрами) иррациональные корни встречаются сплошь и рядом. И с ними надо обязательно уметь работать – сравнивать, изображать на числовой оси и т.д. И мы тоже поработаем! В соответствующих уроках.)
Как видите, процедура решения полных квадратных уравнений проблем не вызывает. Всё просто, быстро, не больно.) Главное – аккуратно подставляйте коэффициенты в формулу дискриминанта и общую формулу корней. И считайте себе.) И что, думаете, ошибиться нельзя? Ну да, как же…
Вот краткий перечень глупых ошибок при решении квадратных уравнений:
1. Путаница в знаках. Ошибки в подстановке отрицательных коэффициентов в формулу дискриминанта и в общую формулу корней.
2. Забывают извлечь корень из дискриминанта.
3. При работе с общей формулой корней в знаменатель дроби частенько подставляется не 2а, как положено, а просто двойка. Привыкает, видите ли, народ к простым уравнениям, с первым коэффициентом единичкой (а=1). Внимательнее надо быть, да.)
Ну и, разумеется, базовые тождественные преобразования уравнений никто не отменял, да.)
Например, дано такое уравнение:
Уравнение, в принципе, уже дано нам в стандартном виде. Слева – квадратный трёхчлен, построенный по убыванию степеней, справа – ноль.
Наши коэффициенты будут:
a = -1/3; b = 3/2; c = -5
Можно приступать к решению. Только это… коэффициенты – дробные. Неудобно как-то…
Согласен, неудобно! Всё-таки лучше, когда уравнение безо всяких дробей, в линеечку.) Вот и избавимся сначала от дробей. На что надо домножить обе части уравнения, чтобы и двойка сократилась и тройка? На 6! Вот и домножаем. Слева получим:
А что будет справа? Справа будет ноль. Ноль на что ни умножай – всё равно ноль будет. Хорошее число.)
Итого получим:
-2х2 + 9х – 30 = 0
И опять не бросаемся решать, считать дискриминант и прочее. Минус перед иксом в квадрате – нехорош. Забыть его очень легко. Посему избавимся от этого минуса умножением обеих частей на (-1). Проще говоря, поменяем слева все знаки:
2х2 — 9х + 30 = 0
Ну вот. А теперь – по накатанной колее. Выписываем коэффициенты:
a = 2; b = -9; c = 30
Считаем дискриминант:
D = b2-4ac = (-9)2 – 4·2·30 = 81-240 = -159
Вот так штука! А дискриминант-то отрицательный! Не можем мы корень из отрицательного числа извлечь. И сами корни посчитать, стало быть, тоже не можем, да. Стало быть, ответ – решений нет.
Это был второй сюрприз. Надеюсь, теперь отрицательный дискриминант в каком-нибудь примере вас нисколько не смутит.)
Это всё что касается полных квадратных уравнений. Теперь переходим к неполным.)
Неполные квадратные уравнения
Неполными, напоминаю, называются квадратные уравнения, где чего-то не хватает – или bx или с. Или обоих членов сразу.
Например:
х2 – 3х = 0
х2 – 16 = 0
И так далее.)
Неполные квадратные уравнение также можно решать через дискриминант, по общей формуле. Надо только правильно догадаться, чему равняются коэффициенты a, b и с.
Догадались? В первом случае a = 1, b = -3, а свободный член с вообще отсутствует! Что это означает? В математике это означает, что с=0! Вот и всё.)
Во втором уравнении всё аналогично, только нулю будет равно не с, а b!
И все дела.)
Но неполные уравнения можно решать гораздо проще. Безо всяких дискриминантов и безо всяких формул! Зачем же из пушки по воробьям…
Например, такое уравнение:
х2 – 3х = 0
Что здесь можно сделать в левой части? Сильнее всего напрашивается вынести икс за скобки и разложить левую часть на множители. Давайте вынесем:
х(х-3) = 0
И что дальше? А то, что произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю! Вот и приравниваем (в уме!) каждый из множителей к нулю и получаем:
х1 = 0
х2 = 3
И все дела! Это и будут корни нашего уравнения. Оба годятся.) При подстановке каждого из них в исходное уравнение мы получим железное равенство 0=0. Как видите, решение куда проще, чем через дискриминант!
Теперь рассмотрим другое уравнение:
х2 – 16 = 0
А здесь что можно сделать? Можно -16 перенести вправо:
х2 = 16
Остаётся корень извлечь из 16 и – ответ готов:
Тоже два корня: х1 = -4; х2 = 4.
И так решаются все неполные квадратные уравнения. Либо с помощью вынесения икса за скобки и разложения на множители, либо же переносом свободного члена вправо с последующим извлечением корня. Спутать эти два способа – надо очень хорошо постараться.) Ибо в первом случае вам пришлось бы корень из икса извлекать, что как-то не очень, а во втором случае выносить за скобки нечего…
Подытожим тему практическими советами.
1. Перед решением любого квадратного уравнения приводим его к стандартному виду, выстраиваем левую часть по убыванию степеней.
2. Если в уравнении имеются дробные коэффициенты, избавляемся от дробей умножением всего уравнения на нужный множитель.
3. Если коэффициент перед иксом в квадрате отрицательный, избавляемся от минуса умножением всего уравнения на (-1).
Ну что, наш урок окончен. Теперь можно и порешать.)
Решить уравнения:
2x2 – 7x + 3 = 0
х2 – x – 30 = 0
х2 + 6х + 9 = 0
х2 – 7x = 0
х2 + 4x + 5 = 0
-2x2 + 98 = 0
x2 + 0,05x – 0,05 = 0
Ответы (в беспорядке):
х1 = -5; x2 = 6
x1 =-0,2; x2 = 0,5
x1 = 0; x2 = 7
x1 = -0,25; x2 = 0,2
корней нет
x1 = 0,5; x2 = 3
x = -3
x1 = -7; x2 = 7
Всё сошлось? Великолепно! Значит, квадратные уравнения – не ваша беда.) Все получились, а последние два – нет? Значит, проблема – в тождественных преобразованиях. Кликните по ссылке, почитайте – и будет вам счастье!)
abudnikov.ru
From Wikipedia, the free encyclopedia
In mathematics, a quadratic equation is a polynomial equation of the second degree. The general form is
where a ≠ 0.
The quadratic equation on a number 
If the roots are real, there is an alternative technique that obtains a rational approximation to one of the roots by manipulating the equation directly. The method works in many cases, and long ago it stimulated further development of the analytical theory of continued fractions.
Simple example[edit]
Here is a simple example to illustrate the solution of a quadratic equation using continued fractions. We begin with the equation
and manipulate it directly. Subtracting one from both sides we obtain
This is easily factored into
from which we obtain
and finally
Now comes the crucial step. We substitute this expression for x back into itself, recursively, to obtain
But now we can make the same recursive substitution again, and again, and again, pushing the unknown quantity x as far down and to the right as we please, and obtaining in the limit the infinite continued fraction
By applying the fundamental recurrence formulas we may easily compute the successive convergents of this continued fraction to be 1, 3/2, 7/5, 17/12, 41/29, 99/70, 239/169, …, where each successive convergent is formed by taking the numerator plus the denominator of the preceding term as the denominator in the next term, then adding in the preceding denominator to form the new numerator. This sequence of denominators is a particular Lucas sequence known as the Pell numbers.
Algebraic explanation[edit]
We can gain further insight into this simple example by considering the successive powers of
That sequence of successive powers is given by
and so forth. Notice how the fractions derived as successive approximants to √2 appear in this geometric progression.
Since 0 < ω < 1, the sequence {ωn} clearly tends toward zero, by well-known properties of the positive real numbers. This fact can be used to prove, rigorously, that the convergents discussed in the simple example above do in fact converge to √2, in the limit.
We can also find these numerators and denominators appearing in the successive powers of
The sequence of successive powers {ω−n} does not approach zero; it grows without limit instead. But it can still be used to obtain the convergents in our simple example.
Notice also that the set obtained by forming all the combinations a + b√2, where a and b are integers, is an example of an object known in abstract algebra as a ring, and more specifically as an integral domain. The number ω is a unit in that integral domain. See also algebraic number field.
General quadratic equation[edit]
Continued fractions are most conveniently applied to solve the general quadratic equation expressed in the form of a monic polynomial
which can always be obtained by dividing the original equation by its leading coefficient. Starting from this monic equation we see that
But now we can apply the last equation to itself recursively to obtain
If this infinite continued fraction converges at all, it must converge to one of the roots of the monic polynomial x2 + bx + c = 0. Unfortunately, this particular continued fraction does not converge to a finite number in every case. We can easily see that this is so by considering the quadratic formula and a monic polynomial with real coefficients. If the discriminant of such a polynomial is negative, then both roots of the quadratic equation have imaginary parts. In particular, if b and c are real numbers and b2 − 4c < 0, all the convergents of this continued fraction «solution» will be real numbers, and they cannot possibly converge to a root of the form u + iv (where v ≠ 0), which does not lie on the real number line.
General theorem[edit]
By applying a result obtained by Euler in 1748 it can be shown that the continued fraction solution to the general monic quadratic equation with real coefficients
given by
either converges or diverges depending on both the coefficient b and the value of the discriminant, b2 − 4c.
If b = 0 the general continued fraction solution is totally divergent; the convergents alternate between 0 and 
- If the discriminant is negative, the fraction diverges by oscillation, which means that its convergents wander around in a regular or even chaotic fashion, never approaching a finite limit.
- If the discriminant is zero the fraction converges to the single root of multiplicity two.
- If the discriminant is positive the equation has two real roots, and the continued fraction converges to the larger (in absolute value) of these. The rate of convergence depends on the absolute value of the ratio between the two roots: the farther that ratio is from unity, the more quickly the continued fraction converges.
When the monic quadratic equation with real coefficients is of the form x2 = c, the general solution described above is useless because division by zero is not well defined. As long as c is positive, though, it is always possible to transform the equation by subtracting a perfect square from both sides and proceeding along the lines illustrated with √2 above. In symbols, if
just choose some positive real number p such that
Then by direct manipulation we obtain
and this transformed continued fraction must converge because all the partial numerators and partial denominators are positive real numbers.
Complex coefficients[edit]
By the fundamental theorem of algebra, if the monic polynomial equation x2 + bx + c = 0 has complex coefficients, it must have two (not necessarily distinct) complex roots. Unfortunately, the discriminant b2 − 4c is not as useful in this situation, because it may be a complex number. Still, a modified version of the general theorem can be proved.
The continued fraction solution to the general monic quadratic equation with complex coefficients
given by
converges or not depending on the value of the discriminant, b2 − 4c, and on the relative magnitude of its two roots.
Denoting the two roots by r1 and r2 we distinguish three cases.
- If the discriminant is zero the fraction converges to the single root of multiplicity two.
- If the discriminant is not zero, and |r1| ≠ |r2|, the continued fraction converges to the root of maximum modulus (i.e., to the root with the greater absolute value).
- If the discriminant is not zero, and |r1| = |r2|, the continued fraction diverges by oscillation.
In case 2, the rate of convergence depends on the absolute value of the ratio between the two roots: the farther that ratio is from unity, the more quickly the continued fraction converges.
This general solution of monic quadratic equations with complex coefficients is usually not very useful for obtaining rational approximations to the roots, because the criteria are circular (that is, the relative magnitudes of the two roots must be known before we can conclude that the fraction converges, in most cases). But this solution does find useful applications in the further analysis of the convergence problem for continued fractions with complex elements.
See also[edit]
- Lucas sequence
- Methods of computing square roots
- Pell’s equation
References[edit]
- H. S. Wall, Analytic Theory of Continued Fractions, D. Van Nostrand Company, Inc., 1948 ISBN 0-8284-0207-8
Рациональное уравнение, в котором левая или правая части являются дробными выражениями, называется дробным.
Для решения дробного уравнения, необходимо:
1. найти общий знаменатель дробей, входящих в уравнение;
2. умножить обе части уравнения на общий знаменатель;
3. решить получившееся целое уравнение;
4. исключить из его корней те, которые обращают в ноль общий знаменатель.
Пример:
реши дробное уравнение
3x−1+2=4−xx−1
.
1. Находим значения переменной, при которых уравнение не имеет смысл:
.
2. Находим общий знаменатель дробей и умножаем на него обе части уравнения:
3x−1+2x−11=4−xx−1;3+2(x−1)x−1=4−xx−1|⋅x−1.
3. Решаем полученное уравнение:
3+2(x−1)=4−x;3+2x−2=4−x;3x=3;x=1.
4. Исключаем те корни, при которых общий знаменатель равен нулю.
В первом пункте получилось, что при (x = 1) уравнение не имеет смысла, поэтому число (1) не может являться корнем данного дробного уравнения. Следовательно, у данного уравнения вообще нет корней.
При решении уравнения можно использовать основное свойство пропорции.
Основное свойство пропорции:
еслиab=mn, тоa⋅n=b⋅m
.
16x−12=19x+18;6x−12≠0;9x+18≠0;x≠2;x≠−2.16x−12=19x+18;1⋅9x+18=1⋅6x−12;9x+18=6x−12;3x=−30;x=−10;−10≠2;−10≠−2. Кореньx=−10. Проверка:16⋅−10−12=?19⋅−10+18;1−60−12=?1−90+18;1−72=?1−72.
Дробно-рациональные уравнения, сводящиеся к квадратным.

Дробно-рациональные уравнения, сводящиеся к квадратным.
1. Решить уравнение:
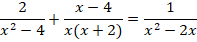
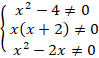
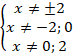
Разложим знаменатели на множители:
Приведем все дроби к общему знаменателю
Дробь равна 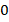
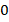
Раскрыв скобки и приведя подобные слагаемые, получаем квадратное уравнение:
Найдем корни квадратного уравнения:
Х1=2, х2=3
Корень 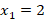
Ответ:
2. Решить уравнение:
Выпишем условие (*) 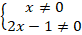
Обратим внимание, что неизвестная 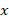
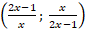
Тогда:
Исходное уравнение будет иметь вид:
Чтобы избавиться от дроби, умножим обе части уравнения на 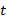
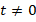
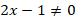
Получили квадратное уравнение, решениями которого являются:
t = 1, t = 4
Вернемся к замене:
Решаем первое уравнение:
Решаем второе уравнение:
Полученные корни удовлетворяют удовлетворяют (*). Ответ: 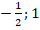
3. Решить уравнение:
Решение.
Выпишем условие (*)
В подобных уравнениях стандартной является замена:
Чтобы выразить 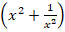
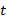
После замены исходное уравнение будет иметь вид:
Преобразуя это выражение, получаем квадратное уравнение:
Найдем корни уравнения:
t = 2,5; t = 1
Вернемся к замене:
Поскольку 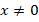
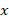
Первое уравнение имеет решения:
x = 2; x = 0,5
Оба решения удовлетворяют условие (*).
Второе уравнение не имеет корней.
Ответ: