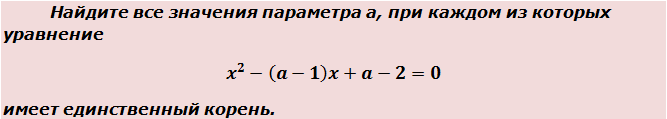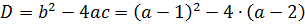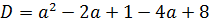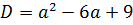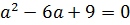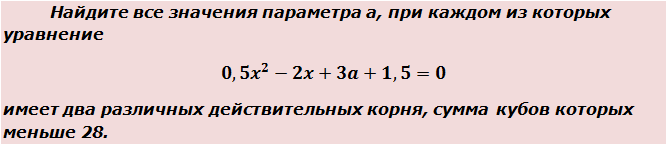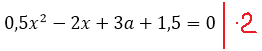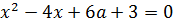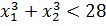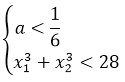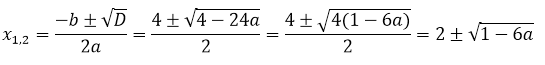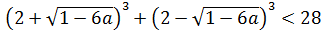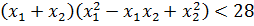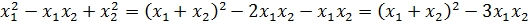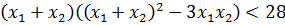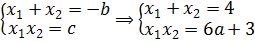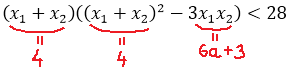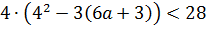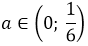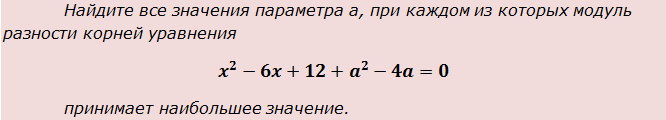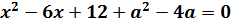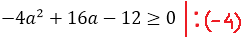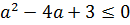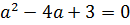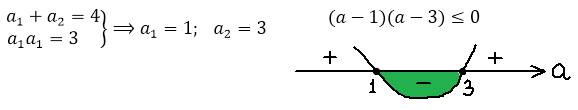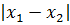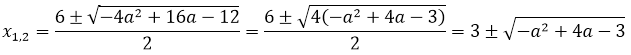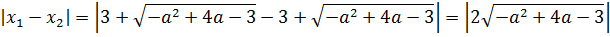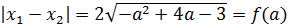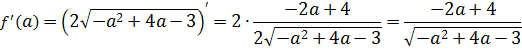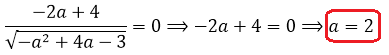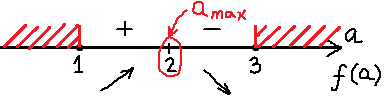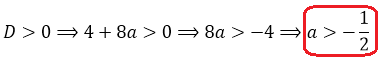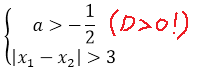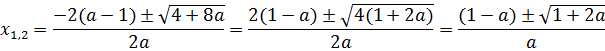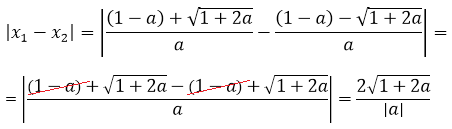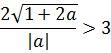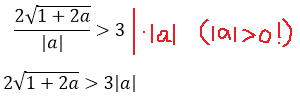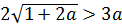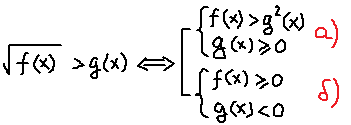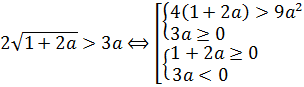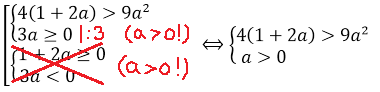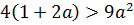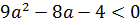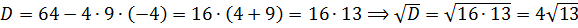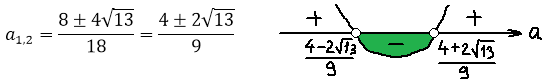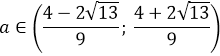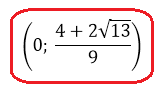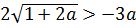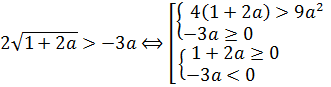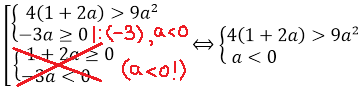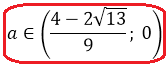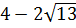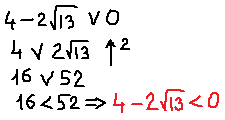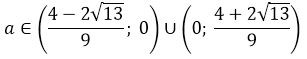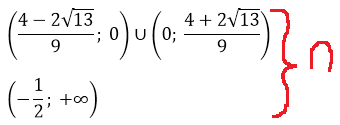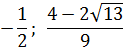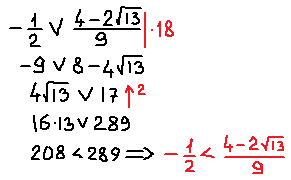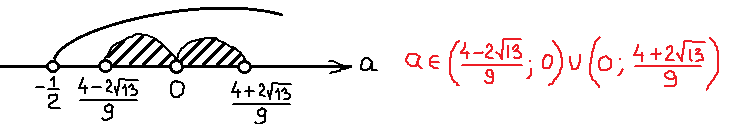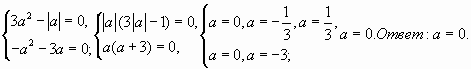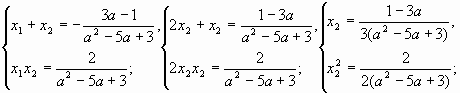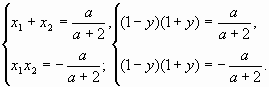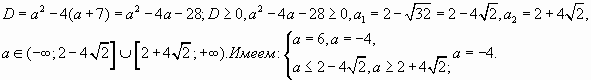Как найти корни квадратного уравнения с параметром - Исправление недочетов и поиск решений вместе с Examum.ru

Чтобы решить квадратное уравнение с параметром, нужно понять, при каких значениях параметра существуют корни, и найти их, выразив через параметр. Обычно это делается просто через анализ дискриминанта. (см. пример 1)
Но иногда в задачах с параметром просят найти такие значения параметра, при которых корни принадлежат определенному числовому промежутку. Например:

Найдите такие значения параметра, чтобы оба корня были меньше некоторого числа (γ): (x_1≤x_2<γ).
Только один из корней принадлежит какому-то промежутку ((γ;β):)
2 случая: (γ<x_1<β≤x_2;) или (x_1≤γ<x_2<β.)
Некоторое число (∝) лежит между корнями: ((x_1<γ<x_2)).
И т.д. Условия могут быть различными.

Теперь разберемся, как при помощи математики записать те или иные условия. Разберем условие: (x_1≤x_2<γ). Точно такие же рассуждения будут справедливы и для других условий.

Очевидно, что (D≥0), для того, чтобы корни существовали (либо один, либо два корня — то и то нас устраивает – именно поэтому знак неравенства больше либо равно).
Чтобы некоторое число лежало вне отрезка ((x_1,x_2)), необходимо рассмотреть два случая: ветки параболы направлены вверх ((a>0)); ветки параболы направлены вниз ((a<0)).
- (a>0). Значит, между корнями функция принимает отрицательные значения, а вне этого отрезка – положительные. Так как наше число (γ) должно по условию лежать вне отрезка ((x_1,x_2)), то (f(γ)>0).
- (a<0). Значит, между корнями функция принимает положительные значения, а вне этого отрезка – отрицательные. Так как наше число (γ) должно по условию лежать вне отрезка ((x_1,x_2)), то (f(γ)<0).

Используем небольшую хитрость, чтобы описать оба этих условия: (a*f(γ)>0). Этим условием мы накладываем ограничение, что наши корни должны лежать слева или справа от числа (γ).

В итоге получаем:

если (a*f(γ)<0), то (γ∈(x_1,x_2)),

если (a*f(γ)>0), то (γ∉(x_1,x_2)).

Нам осталось наложить условие, чтобы наши корни были слева от числа (γ). Здесь нужно просто сравнить положение вершины нашей параболы (x_0) относительно (γ). Заметим, что вершина лежит между точками (x_1) и (x_2). Если (x_0<γ), то в системе с предыдущими условиями это будет означать, что число (γ) лежит справа от отрезка ((x_1,x_2)) и соответственно удовлетворяет условию задачи (x_1≤x_2<γ).

Таким образом, для того, чтобы решить задачу с условием (x_1≤x_2<γ) необходимо решить следующую систему:

$$begin{cases} D≥0,\ a*f(γ)>0, \x_0<γ.end{cases}$$

То, что дискриминант неотрицательный дает нам существование корней. Второе неравенство указывает, что (γ∉(x_1,x_2)). И последнее в совокупности с первыми двумя, что оба корня лежат слева от (γ).
Аналогичные рассуждения можно провести для любых условий. Настоятельно рекомендую разобраться во всех пунктах и откуда возникает вышеуказанная система неравенств, и вы легко сможете проводить анализ квадратных уравнений с параметром.

Ниже приведена таблица, в которой разобраны все варианты расположения нулей квадратичной функции на числовой прямой и соответствующие им условия. (см. таблицу)

Пример 1

При каких значениях параметра a уравнение
$$a(a+3) x^2+(2a+6)x-3a-9=0$$
имеет более одного корня?

Решение:

1 случай:
Если (a(a+3)=0), то уравнение будет линейным. При (a=0) исходное уравнение превращается в (6x-9=0), корень которого (x=1,5). Таким образом, при (a=0) уравнение имеет один корень.

При (a=-3) получаем (0*x^2+0*x-0=0), корнями этого уравнения являются любые рациональные числа. Уравнение имеет бесконечное количество корней.

2 случай:
Если (a≠0; a≠-3), то получим квадратное уравнение. При положительном дискриминанте уравнение будет иметь более одного корня:
$$D>0$$ $$D/4=(a+3)^2+3a(a+3)^2>0$$ $$(a+3)^2 (3a+1)>0$$ $$a>-frac{1}{3}.$$
С учетом (a≠0;) (a≠-3), получим, что уравнение имеет два корня при (a∈(-frac{1}{3};0)∪(0;+∞)).

Объединив оба случая получим (внимательно прочитайте, что от нас требуется):

Ответ: (a ∈ {-3} ∪(-frac{1}{3};0)∪(0;+∞)).

Пример 2

Найти все значения параметра a, при которых корни уравнения
$$(a+1) x^2-(a^2+2a)x-a-1=0$$
принадлежат отрезку ([-2;2]).

Решение:

1 случай: Если (a=-1), то (0*x^2-x+1-1=0) отсюда (x=0). Это решение принадлежит ([-2;2]).

2 случай: При (a≠-1), получаем квадратное уравнение, с условием, что все корни принадлежат ([-2;2]). Для решения введем функцию (f(x)=(a+1) x^2-(a^2+2a)x-a-1) и запишем систему, которая задает требуемые условия:

$$begin{cases} (a+1)*f(-2) ≥ 0, \(a+1)*f(2) ≥ 0, \D≥0, \-2 < x_0 < 2.end{cases}$$

(x_0=frac{a^2+2a}{2(a+1)}) -вершина параболы.

$$ f(-2)=(a+1)*4-(a^2+2a)*(-2)-a-1=2a^2+7a+3; $$
$$ f(2)=(a+1)*4-(a^2+2a)*(2)-a-1=-2a^2-a+3; $$
$$ D=(a^2+2a)^2+4(a+1)^2=(a^2+2a+2)^2=(1+(a+1)^2 )^2>0.$$

Подставляем полученные выражения в систему:

$$ begin{cases} (a+1)(2a^2+7a+3) ≥ 0, \(a+1)(-2a^2-a+3) ≥ 0,\ -2 < frac{a^2+2a}{2(a+1)} < 2. end{cases} $$
Или
$$ begin{cases} 2(a+1)(a+3)(a+0,5) ≥ 0,\ -2(a+1)(a-1)(a+1,5) ≥ 0,\ frac{(a-1-sqrt{5})(a-1+sqrt{5})}{2(a+1)} < 0,\ frac{(a+3-sqrt{5})(a+3+sqrt{5})}{2(a+1)} > 0.end{cases} $$

Ответ: ([-3;-1,5]∪[-0,5;1]).

Пример 3

Решить уравнение (sqrt{x-5}=x+a), где (a) параметр.

Решение:

После равносильных преобразований получим систему:

$$ begin{cases} x-5=(x+a)^2, \x≥-a; end{cases} $$
$$ begin{cases} x^2+(2a-1)x+(a^2+5)=0, \x≥-a. end{cases} $$

Наша задача свелась к исследованию квадратного многочлена:

$$ f(x)=x^2+(2a-1)x+(a^2+5). $$

Для этого найдем дискриминант, вершину параболы и (f(-a)).
$$ D=(2a-1)^2-4(a^2+5)=-4a-19;$$
$$ {x}_{0}=-frac{2a-1}{2}=frac{1-2a}{2}; $$
$$ f(-a)=a+5.$$

Из второго неравенства системы следует, что нас устраивают случаи, когда ({x}_{1} < -a ≤ {x}_{2}) (нас будет устраивать только один корень ({x}_{2})) и (-a ≤ {x}_{1} ≤ {x}_{2}) (под условие системы будут подходить оба корня), где ({x}_{1},{x}_{2})- нули (f(x)).

Обратим внимание, что коэффициент при (x^2) положителен, т.е. ветки параболы направлены вверх.

Первый случай: ({x}_{1} < -a ≤ {x}_{2}) (см. таблицу)

$$ f(-a)≤0 ⇔ a+5≤0 ⇔ a≤-5;$$

Таким образом, при (a ≤ -5) мы имеем одно решение:

$$ x=frac{1-2a+sqrt{-4a-19}}{2}. $$

Второй случай: (-a ≤ {x}_{1} ≤ {x}_{2}) (см. таблицу)

$$ begin{cases} f(-a)≥0, \D≥0, \{x}_{0}>-a; end{cases} $$
$$ begin{cases} a+5≥0, \-4a-19≥0, \ frac{1-2a}{2}>-a; end{cases} $$
$$ begin{cases} a≥-5, \a≤-frac{19}{4}, \ 1>0. end{cases} $$

Получаем, что при (a∈[-5;-4.75]) уравнение имеет два решения:

$$ {x}_{1,2}=frac{1-2a±sqrt{-4a-19}}{2}. $$

Ответ: при (a≤-5) $$ x=frac{1-2a+sqrt{-4a-19}}{2};$$
при (a∈[-5;-4.75]) $$ {x}_{1,2}=frac{1-2a±sqrt{-4a-19}}{2}; $$
при (a>-4.75) решений нет.

Источник

МИНИСТЕРСТВО ОБОРОНЫ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ
ГОСУДАРСТВЕННОЕ КАЗЁННОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

«ОРЕНБУРГКОЕ
ПРЕЗИДЕНТСКОЕ КАДЕТСКОЕ УЧИЛИЩЕ»

РЕШЕНИЕ КВАДРАТНЫХ
УРАВНЕНИЙ С ПАРАМЕТРАМИ

(методическое
пособие для воспитанников и преподавателей)

Составила
преподаватель математики

высшей
квалификационной категории

Зевина Елена Петровна

2013г.

УДК 372.

Зевина Е.П.: РЕШЕНИЕ КВАДРАТНЫХ
УРАВНЕНИЙ С ПАРАМЕТРАМИ.

Методическое
пособие для воспитанников и преподавателей.

–
Оренбург: ФГКОУ Оренбургское ПКУ, 2013. –32с.

В
пособии представлен опыт практической деятельности преподавателя училища по
методике обучения решению квадратных уравнений с параметрами.

Методическое
пособие содержит задачи с параметрами, при решении которых возникают наибольшие
затруднения во время обучения. Методами решения таких задач уделяется минимум
внимания, и целью данного пособия является помощь учащимся в устранении данного
пробела.

Данное
методическое пособие составлено по итогам многолетней практики работы и
подготовки учащихся к сдаче экзамена по математике в формате ЕГЭ и ГИА.

Рассмотрено
на заседании методического совета ФГКОУ Оренбургское ПКУ.

ФГОУ «Оренбургское
президентское кадетское училище», 2013

Содержание

1.
Введение. . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

2.
§1. Квадратные уравнения с параметром . .
. . . . . . . . . . . . . . . . . . . . . . 5

1.1
Понятие уравнения с параметром . . . .. .
. . . . . . . .
. . . . . . . . . . . . . 5

1.2
Квадратные уравнения . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . 5

1.3
Теорема Виета . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . .. . . . . . . . . . 6

3.
§2. Примеры
решения квадратных уравнений с параметром . . . . . . . . . 7

4.
§3.
Задачи для самостоятельной работы по решению квадратных

уравнений с параметром . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . 14

5.
§4. Решение уравнений
с параметром, приводимых к квадратным. . . .15

6.
§5. Задачи для
самостоятельной работы по решению уравнений,

приводимых к квадратным . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . .17

7.
§6. Задачи, связанные с расположением
корней квадратного трехчлена.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . 18

8.
§7. Задачи для
самостоятельного решения, связанные с

расположением корней квадратного трехчлена . . . . . . . . . . . . . . . . . .
25

9.
Заключение. . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26

10.
Список использованной литературы . . . . .
. . . . . . . . . . . . . . . . . . . . . . . 27

Введение

У большинства выпускников
и абитуриентов задачи с параметрами вызывают серьезные затруднения (как решать
задачу и как довести решение до правильного ответа). Трудности при решении
таких задач обусловлены во-первых: решением не по шаблону, во- вторых:
рассмотрением различных случаев, в которых методы решения существенно
отличаются друг от друга; в-третьих: хорошими знаниями свойств функций и
правильным выделением тех свойств, которые нужно применить.

Предлагаемое пособие
построено так, чтобы учащиеся самостоятельно могли понять логику решения задач
с параметрами, и научились их решать.

Пособие разбито на
параграфы, в конце которых приведены упражнения для самостоятельного решения.
Разобраны примеры, которые расположены в последовательности «от простого к
сложному», при этом предполагается, что учащийся имеет хорошие знания по
математике и изучает пособие последовательно.

Пособие может быть
использовано как для самостоятельной подготовки к вступительным экзаменам, так
и в качестве пособия на индивидуальных и групповых занятиях.

Функции вида , где –
квадратный трехчлен, в школьном курсе математики придается большое значение.
Для нее строго доказываются все свойства, нужные в теории и для решения задач. Безукоризненное
знание необходимых свойств квадратного трехчлена требуется от каждого
абитуриента, так как квадратный трехчлен с параметром часто включается в
варианты письменных работ и в тесты для собеседования на вступительных
экзаменах в ВУЗы. Как правило, большая часть абитуриентов с этими задачами не
справляется. Значит, им надо уделять больше внимания на факультативных занятиях
в школе, на страницах печати.

§1.
Квадратные уравнения с параметром

1.1 Понятие уравнения с
параметром

Определение.
Пусть задано уравнение , если ставится задача,
для каждого действительного значения решить уравнение
относительно , то это уравнение
называют уравнением с переменной и параметром
.

Решить уравнение с параметром
– это значит, для каждого действительного значения найти значение , удовлетворяющее данному
уравнению.

Назовем
контрольными значениями параметра (КЗП) те его значения, при
которых обращается в нуль: 1) старший коэффициент в уравнении или неравенстве; 2)
знаменатель дроби; 3) дискриминант квадратного уравнения.

1.2 Квадратные уравнения

Определение. Квадратным
уравнением называют уравнение вида

(1)

где – переменная, и , , – некоторые
действительные числа или выражения, зависящие от параметров.

Левая
часть уравнения является квадратным трехчленом, то есть многочленом второй
степени.

Корни
квадратного уравнения (1) находят по формуле

(2)

Выражение называют дискриминантом
квадратного уравнения (1).

В
случае, когда второй коэффициент квадратного уравнения четное число , корни удобно находить
по формуле

(3)

Число корней квадратного уравнения
зависит от дискриминанта:

если
, то уравнение имеет два
различных действительных корня;

если , то уравнение имеет два
равных действительных корня

или
один корень, но двойной кратности.

если , то уравнение не
имеет действительных корней.

При
решении неполного квадратного уравнения , где удобно пользоваться
разложением на множители левой части уравнения:

1.3 Теорема Виета

При
решении полных квадратных уравнений применяют теорему Виета: если и – корни
квадратного уравнения , где , то справедливы формулы
для суммы и произведения этих корней:

, .

(4)

Формулы (4) называют формулами
Виета.

Верно и обратное
утверждение: если числа и удовлетворяют равенствам
(4), то эти числа являются корнями квадратного уравнения.

Формулы
Виета верны и для приведенного квадратного уравнения . В этом случае они
приобретают вид:

, .

Квадратный
трехчлен можно разложить на линейные множители:

1) если
, то ;

2) если
, то .

§2.
Примеры решения квадратных уравнений с параметром

Пример 1.
Найти все значения параметра а, для которых квадратное уравнение

1)
имеет два различных корня;

2)
не имеет корней;

3)
имеет один корень.

Решение. Так как по
условию старший коэффициент , то уравнение является
квадратным. Найдем его дискриминант: .

Контрольными
значениями параметра будут те значения, при которых дискриминант равен нулю.

КЗП: или .

Далее определим знак дискриминанта,
а для этого заметим, что он представляет собой квадратичную функцию, графиком
которой является парабола, причем ветви её направлены вверх.

Знак
:
1) + 2) 3) 2) + 1)

               – 4
      –            4                   а

Возможны
три случая.

1)
Если , то и уравнение имеет два различных
действительных корня

2)
Если или , то и уравнение имеет один двукратный
корень , причем если , то , а если , то .

3) Если , то и уравнение не имеет
действительных корней.

Ответ:
при ;

при
корней нет;

при
;

при
.

Пример 2. Решить уравнение .

Решение. Поскольку старший
коэффициент данного уравнения зависит от параметр , то это уравнение нельзя
считать квадратным. Поэтому найдем первое контрольное значение параметра, приравняв
старший коэффициент к нулю.

КЗП:
.

1)
Если , то исходное уравнение
принимает вид:

то
есть становится линейным и его корнем является .

2)
Если , то исходное уравнение
является квадратным, поэтому вычислим его дискриминант :

Найдём
другие контрольные значения параметра, из условия, что дискриминант
квадратного уравнения равен нулю.

КЗП:
или .

Определим знак
дискриминанта. Поскольку он представляет собой квадратичную функцию, то графиком
его является парабола c ветвями
направленными вниз.

Знак а) б)
+ в) б) а)

– 1 6 – b

Возможны
следующие три подслучая.

а)
Если , то , а значит, уравнение не имеет
корней.

б)
Если или , то и найти значение корня
уравнения можно по формуле , то есть

при
получим ,

при
получим .

в)
Если , то и уравнение имеет два различных
корня

В
ходе решения данного квадратного уравнения получили три контрольных значения
параметра b, которые наносим на
числовую прямую для удобства записи ответа.

1 2 6 b

Ответ:
при корней нет;

при ;

при
;

при
.

Пример 3. Найти все значения
параметра, для которых квадратное уравнение имеет хотя бы один общий
корень с уравнением .

Решение. В первом
уравнении старший коэффициент – это выражение, содержащее параметр с.
Поэтому первым контрольным значением параметра с будет то, при
котором старший коэффициент уравнения равен нулю.

КЗП:
.

Возможны
два случая.

1)
Если , то получим уравнение , которое не имеет
решений.

2)
Если , уравнение является
квадратным и найдём его дискриминант:

Дискриминант представляет собой выражение
первой степени. Найдем второе контрольное значение параметра, приравняв к нулю.

КЗП:
.

Определим
знак .

а) б)
+

– –1 с

Итак,
возможны два подслучая.

а)
Если , то и уравнение корней не
имеет.

б)
Если , то уравнение имеет два
различных корня

Рассмотрим
второе уравнение . Его корнями являются
числа и .

По
условию задачи хотя бы один из найденных корней должен быть также корнем уравнения
, то есть при подстановке
найденного корня в это уравнение должно получиться тождество.

Если
, то получаем равенство:

откуда
. Аналогично найдём значение
с, при котором корнем уравнения является .

Имеем

=0,

Значит,
при и уравнение имеет, по крайней мере,
один общий корень с уравнением .

Ответ:
и .

Пример 4. Дано уравнение . Доказать, что если , , – попарно различные
действительные корни этого уравнения, то

Решение. По условию , , – попарно различные
действительные корни уравнения , поэтому одновременно выполняются
следующие равенства:

Почленно
вычитая из первого равенства сначала второе, а затем третье равенство, получим:

Поскольку по условию корни уравнения , , – попарно различные, то и , следовательно,

и .

Тогда
и разность этих выражений также равна нулю:

Так
как , то .

Подставив
в равенство , найдем, что .

Тогда
из исходного уравнения следует, что . Что требовалось
доказать.

Пример 5. При каких
значениях параметра с уравнение

имеет
более двух корней?

Решение. Квадратное
уравнение имеет более двух корней, если все его коэффициенты равны нулю (см. пример
4), поэтому

Первое
уравнение имеет корни и ; корнями второго
уравнения являются числа и , а третьего – и .

Общим
для всех является корень .

Ответ:
.

Пример 6. Решить
относительно х уравнение .

Решение. Раскрыв скобки,
получим уравнение вида:

Приравняв
старший коэффициент к нулю, найдем контрольное значение параметра.

КЗП:

– 2) 0 3) + а

Возможны
три случая:

1)
Если , то уравнение примет вид
. Это уравнение решений не имеет.

2)
Если , то разделив обе части
исходного уравнения на а, получим уравнение вида:

Преобразуем его,
выделив в левой части уравнения полный квадрат:

корнями этого
уравнения являются и .

3)
Если , то и уравнение корней не имеет.

Ответ: при , ,

при
корней нет.

Пример 7. При каких
значениях параметра m
корни уравнения

равны по модулю и
противоположны по знаку?

Решение. 1 способ –
найти все значения параметра т, при которых уравнение имеет два корня, найти
эти корни, а затем определить при каких значениях параметра m
корни уравнения противоположные числа.

2 способ. Сначала найти
при каких значениях параметра т уравнение имеет два корня, затем по
теореме Виета найти их сумму

Так
как корни уравнения противоположные числа, то их сумма равна нулю,
следовательно, , откуда .

Ответ:
.

Пример 8. Решите уравнение
относительно
х.

Решение. Данное
уравнение является неполным квадратным, поэтому приведём его к виду: .

Рассмотрим
следующие случаи в зависимости от знака параметра .

1)
Если , то , следовательно,
уравнение имеет два корня

и
.

2)
Если , то уравнение примет вид
и имеет один двукратный
корень .

3)
Если , то , следовательно, уравнение
корней не имеет.

Ответ:
при , ,

при
;

при
корней нет.

Пример 9. При каких
значениях параметра а уравнение

имеет
более одного корня?

Решение. Найдем
контрольные значения параметра, приравняв старший коэффициент к нулю.

КЗП:
, или .

1)
Если ,
то данное уравнение примет вид

или , откуда .

2)
Если , то уравнение
примет вид

или ,

решением
последнего уравнения является любое действительное число.

3)
Если и , то данное уравнение является
квадратным, поэтому найдём дискриминант:

По условию данное
уравнение должно иметь более одного корня, поэтому найдём, при каких значениях
параметра а дискриминант , то есть

Так как , то , тогда или .

Ответ: при и при уравнение имеет более
одного корня.

§3.
Задачи для самостоятельной работы

по решению квадратных
уравнений с параметром

1.
Найти все значения параметра а, при
каждом из которых уравнение

не имеет решений. .

2. Найти
все значения параметра а, при каждом из которых уравнение

имеет два различных
корня.

3. При
каких значениях параметра m
оба корня уравнения

равны нулю? .

4. При
каких значениях параметра а сумма квадратов величин, обратных корням
уравнения , меньше обоих корней
уравнения

? .

5.
Найти все значения параметра а, при
которых уравнения

имеют хотя бы один общий корень? .

6. Найти
все значения параметра а, при которых один корень квадратного уравнения в два раза больше
другого. .

7.
Для каждого значения параметра a решить
относительно х следующие уравнения:

§4.
Решение уравнений с параметром,
приводимых к квадратным.

Пример 1. Решите
уравнение .

Решение. Дробь равна нулю тогда,
когда числитель дроби равен нулю, а знаменатель отличен от нуля. Найдём сначала
допустимые значения для переменной: .

Тогда
, это квадратное уравнение,
так как его старший коэффициент равен 1. Найдём дискриминант:

Определим
контрольное значение параметра, приравняв дискриминант к нулю.

КЗП:
.

1)
Если , то и уравнение имеет один
двукратный корень , который принадлежит
области допустимых значений.

2)
Если , то и уравнение имеет два
корня

и .

Выясним,
при каких значениях параметра с эти корни удовлетворяют условию .

Если
, то при условии, что или .

Найдём
корни уравнения при значениях параметра и .

Если
, то корень уравнения
находим по формуле

а
если , то по формуле .

Ответ:
при и ;

при
и ;

при
;

при
.

Пример 2. Решите
относительно х уравнение .

Решение. Преобразуем данное уравнение
следующим образом:

;

Определим
контрольное значение параметра, при котором знаменатель дроби равен нулю.

КЗП:
.

1)
Если , то уравнение решений не
имеет.

2)
Если , то при условии, что или .

Решим
квадратное уравнение .

Найдем
дискриминант

КЗП:
.

а)
Если , то и уравнение имеет один
двукратный корень, который находим по формуле . Так как , то и он удовлетворяет
условию .

б)
Если , то и уравнение имеет
два корня

и .

Так
как , то определим, при каких
значениях параметра а найденные корни удовлетворяют этому условию.

Если
, то при условии, что , то есть .

Если
, то при условии, что или .

Найдём
корни уравнения при значениях параметра и .

При
корнем уравнения будет , а при по формуле находим, что .

Ответ:
при , и ;

при
, и ;

при
;

при
решений нет.

§5.
Задачи для самостоятельной работы

по решению уравнений,
приводимых к квадратным

1.
Решить уравнение

(–6,
при –5, при 2, при;

3,
при ; или во всех остальных
случаях)

2.
При каких значениях параметра а
уравнение

имеет единственное
решение? (при , , )

3.
Найдите все значения а, при которых
вершины парабол

лежат по разные
стороны от прямой .

§6. Задачи, связанные с расположением
корней квадратного трехчлена.

При
решении задач с параметрами приходится работать с тремя типами моделей:

1) вербальная
модель – словесное описание задачи;

2) геометрическая
модель – график квадратичной функции;

3) аналитическая
модель – система неравенств, при помощи которой описывается геометрическая
модель.

Важно
уметь устанавливать связь между этими моделями. Это означает, что для любого
свойства, сформулированного на алгебраическом языке, нужно уметь давать
геометрическую интерпретацию и, наоборот, по поведению графика параболы дать
общую оценку коэффициентов квадратного трехчлена и его корней. Например,

если
старший коэффициент квадратного трехчлена меньше нуля, то ветви параболы
направлены вниз;

если
, то трехчлен имеет
различные действительные корни и парабола пересекает ось абсцисс в двух точках;

если
график функции находится выше оси
абсцисс, то и .

Последнюю
геометрическую модель можно описать еще тремя способами: неравенство выполняется
при любом х; неравенство не
имеет решений; трехчлен не
имеет действительных корней и его старший коэффициент положителен.

Многие
задачи решают по следующему алгоритмическому предписанию:

1)
уравнение записывают в виде ;

2)
находят контрольные значения параметра и для
каждого случая строят параболу (геометрическую модель);

3)
геометрическую модель описывают системой
неравенств (аналитическая модель);

4)
решают систему неравенств.

Рассмотрим
несколько примеров теоретического плана, показывающих некоторые общие подходы к
решению задач о расположении корней квадратного трехчлена.

Пусть – квадратный трёхчлен. Рассмотрим
случай, когда старший коэффициент .

Обозначим корни
квадратного уравнения через и , причём .

Пусть и В – некоторые
числа на оси Ох.

Задача 1.
При каких условиях оба корня квадратного уравнения, не
обязательно различные, меньше некоторого числа ?

Решение.
Обозначим через абсциссу вершины
параболы, .

Так
как графиком квадратного трёхчлена является парабола, то построим
геометрическую модель данной задачи.

Оба
корня и квадратного уравнения меньше
некоторого числа тогда
и только тогда, когда выполняются следующие условия:

или

2)
Корни и квадратного уравнения лежат
по разные стороны от числа тогда и только тогда,
когда выполняются следующие условия:

или

3) Оба корня и квадратного уравнения больше
некоторого числа тогда
и только тогда, когда выполняются следующие условия:

или

4) Оба корня и квадратного уравнения лежат
между числами и В тогда и
только тогда, когда выполняются следующие условия:

или

5)
Корни и квадратного уравнения лежат
по разные стороны отрезка на оси Ох тогда
и только тогда, когда выполняются следующие условия:

или

6) Квадратное уравнение
имеет два различных корня и и только один из
них принадлежит интервалу или, другими словами,
для
того, чтобы парабола пересекала интервал оси Ох только
в одной точке, необходимо и достаточно, чтобы значения
квадратного трехчлена

в точках А и В
были разных знаков, то есть искомое условие имеет вид:

Очевидно,
что если

то
в рассматриваемом интервале лежит больший корень, а если

то
рассматриваемому интервалу принадлежит меньший корень.

7) Квадратное уравнение
имеет два отрицательных корня при условиях:

Квадратное уравнение
имеет два положительных корня при условиях:

Из приведенных примеров достаточно
ясно виден общий подход к решению задач рассматриваемого вида. Как правило,
задачи с ограничениями на корни квадратного трехчлена сводятся к системе
рациональных неравенств, которая легко решается методом интервалов. При этом
для определения условий, накладываемых на коэффициенты квадратного трехчлена,
рассматриваются следующие его свойства:

·
расположение параболы относительно оси Ох;

·
значения квадратного трехчлена в некоторых
заданных точках;

·
положение оси симметрии параболы
относительно некоторых заданных точек.

Пример 1.
Найдите все значения параметра а, при которых корни уравнения действительные,
различные и оба больше а.

Решение. Графическая
интерпретация задачи показана на рисунке. Обозначим через

Уравнение
будет
иметь
два различных действительных корня, которые
одновременно больше а, тогда и только тогда, когда выполняются следующие
условия:

Решая
полученную систему методом интервалов, найдем .

Ответ:
.

Пример 2. Найдите все
значения параметра а, при которых корни квадратного уравнения неположительные.

Решение. Так как уравнение
квадратное, то . Обозначим через .

Рассмотрим
два случая.

1)
Пусть . Для того чтобы
уравнение

имело
неположительные корни, необходимо и

достаточно
выполнение следующих условий:

Применив
к системе метод интервалов, получим .

2)
Пусть . Тогда положение
параболы определяется условиями:

Решением этой системы является пустое
множество.

Ответ:
.

Пример 3. При каких
значениях а уравнение

имеет
корни разных знаков?

Решение. Для того чтобы парабола
– график

функции
,

пересекала
ось Ox,
в точках, между которыми

лежит
начало координат, необходимо и достаточно,

чтобы
квадратный трехчлен принимал в точке отрицательное значение,
поэтому искомое условие имеет вид:

или .

Ответ:
.

Пример 4. При каких значениях
параметра оба корня уравнения принадлежат отрезку ?

Решение. Так как оба корня уравнения

принадлежат отрезку ,

то
положение параболы

определяется
условиями:

Данную
систему решаем методом интервалов, получаем .

Ответ:
.

Пример 5. При каких
значениях параметра а больший корень уравнения принадлежит промежутку ?

Решение. Положение параболы,
являющейся графиком квадратного трехчлена , при котором только лишь
её правая ветвь пересекает промежуток оси Оx определяется условиями:

Û
Û Û

Ответ:
.

Пример 6. При каких
значениях параметра а все корни уравнения лежат
вне отрезка ?

Решение. При данное уравнение имеет
вид и,
следовательно, корней не имеет.

Если , то квадратный трехчлен

всегда имеет два корня
разных знаков, так как .

Положение
параболы показано на рисунке.

Необходимые
и достаточные условия имеют

вид:

Ответ:
.

Пример 7. Найти все
значения параметра m,
при которых один из корней уравнения находится между числами
0 и 2, а второй между 3 и 5.

Решение. Найдём дискриминант
квадратного уравнения

Так
как , то уравнение имеет два
корня: и . Очевидно, что , поэтому

Ответ:

§7.
Задачи для самостоятельного решения,

связанные с расположением
корней квадратного трехчлена.

1.
Найдите все значения параметра а,
при каждом из которых все корни уравнений и различны и между двумя
корнями одного из них находится ровно один корень другого.

2.
Найдите все значения параметра а,
при которых корни уравнения

неотрицательны.

3.
При каких значениях параметра а
существует единственный корень уравнения , удовлетворяющий условию
?

4.
Найдите все значения параметра k,
при которых корни уравнения

имеет два корня, причем
один из них меньше 1, а другой больше 2.

5.
Сколько решений, удовлетворяющих условию , имеет уравнение в зависимости от значений
параметра а?

Заключение

Параметр – это величина,
значения которой служат для различения элементов некоторого множества между
собой, при этом он требует к себе осторожного и вдумчивого отношения. Ведь,
являясь фиксированным, но неизвестным числом, параметр ограничивает степень свободы
общения с ним. Задачи с параметром – это задачи исследовательского характера,
которые требуют хорошего понимания изучаемого теоретического материала.

Автор надеется, что данное
методическое пособие будет полезно кадетам как в процессе изучения рассмотренных
тем, так и для успешной сдачи экзаменов.

Список использованной литературы:

1. Математика
для старшеклассников. Методы решения задач с параметрами /А.И. Азаров,С.А.
Барвенков-Мн.:»Аверсэв»,2003-272с.

2. Большой
энциклопедический словарь. Математика. — М.: Научное издательство «Большая Российская
Энциклопедия», 1998.

3. Задачи
с параметрами. Горнштейн П.И., Полонский В.Б., Якир М.С. – М.: Илекса,
Харьков: Гимназия, 2003.

4. Задачи
с параметрами. Егерман Е – Математика №2, 2003.

5. Задачи
с параметром, сводящиеся к квадратным уравнениям/ Мещерякова Г.П.. – Математика
в школе №5, 2001.

6. Математика:
интенсивный курс подготовки к экзамену. Черкасов О.Ю., Якушев А.Г. – М.:
Рольф, 1997.

7. .
Задачи с параметром. Линейные уравнения и их системы: 8-9 классы. Шевкин А.В –
М.: ТИД «Русское слово – РС», 2003.

Источник

Задачи с параметрами. Простейшие задачи на квадратный трёхчлен.

Сегодня мы рассмотрим задачи на квадратный трёхчлен, про который, в зависимости от параметра, надо будет что-то выяснить. Это «что-то» может быть самым разнообразным, насколько только хватит фантазии у составителей задачи. Это самый простой тип задач с параметрами. И, если на ЕГЭ вам попалась такая — считайте, что вам повезло!

Но, прежде чем приступать к разбору самих задач, ответьте сами себе на такие простые вопросы:

— Что такое квадратное уравнение, как оно выглядит и как решается?

— Что такое дискриминант и куда его пристроить?

— Что такое теорема Виета и где её можно применить?

Если вы верно отвечаете на эти простые вопросы, то 50% успеха в решении параметрических задач на квадратный трёхчлен вам обеспечены! А остальные 50% — это обычная алгебра и арифметика: раскрытие скобок, приведение подобных, решение уравнений, неравенств и систем и т.д.

Итак, приступим!

Для начала рассмотрим совсем безобидную задачку. Для разминки.

Пример 1

Приступаем к решению. Во-первых, чтобы в будущем не накосячить в коэффициентах, всегда полезно выписать их отдельно. Прямо в столбик. Вот так:

a = 1

b = -(a-1)

c = a-2

Да-да! Часть коэффициентов в уравнении (а именно — b и с) зависит от параметра. В этом как раз и состоит вся фишка таких задач. А теперь снова въедливо перечитываем условие. Ключевой зацепкой в формулировке задания являются слова «единственный корень». И когда же квадратное уравнение имеет единственный корень? Подключаем наши теоретические знания о квадратных уравнениях. Только в одном единственном случае — когда его дискриминант равен нулю.

Так и пишем:

D = 0

Осталось составить выражение для дискриминанта и приравнять его к нулю. Поехали!

Теперь надо приравнять наш дискриминант к нулю:

Можно, конечно, решать это квадратное уравнение через дискриминант, а можно немного схитрить. На что у нас похожа левая часть, если как следует присмотреться? Она у нас похожа на квадрат разности (a-3)²!

Респект внимательным! Верно! Если заменить наше выражение слева на (a-3)², то уравнение будет решаться в уме!

(a — 3)² = 0

a — 3 = 0

a = 3

Вот и всё. Это значит, что единственный корень наше квадратное уравнение с параметром будет иметь только в одном единственном случае — когда значение параметра «а» равно тройке.)

Ответ: 3

Это был разминочный пример. Чтобы общую идею уловить.) Теперь будет задачка посерьёзнее.

Пример 2

Вот такая задачка. Начинаем распутывать. Первым делом выпишем наше квадратное уравнение:

0,5x² — 2x + 3a + 1,5 = 0

Самым логичным шагом, было бы умножить обе части на 2. Тогда у нас исчезнут дробные коэффициенты и само уравнение станет посимпатичнее. Умножаем:

Выписываем в столбик наши коэффициенты a, b, c:

a = 1

b = -4

c = 6a+3

Видно, что коэффициенты a и b у нас постоянны, а вот свободный член с зависит от параметра «а»! Который может быть каким угодно — положительным, отрицательным, целым, дробным, иррациональным — всяким!

А теперь, чтобы продвинуться дальше, вновь подключаем наши теоретические познания в области квадратных уравнений и начинаем рассуждать. Примерно так:

«Для того чтобы сумма кубов корней была меньше 28, эти самые корни, во-первых, должны существовать. Сами по себе. В принципе. А корни у квадратного уравнения существуют, тогда и только тогда, когда его дискриминант неотрицательный. Кроме того, в задании говорится о двух различных корнях. Эта фраза означает, что наш дискриминант обязан быть не просто неотрицательным, а строго положительным!»

Если вы рассуждаете таким образом, то вы движетесь правильным курсом! Верно.) Составляем условие положительности для дискриминанта:

D = (-4)² — 4·1·(6a+3) = 16-24a-12 = 4-24a

4-24a > 0

-24a > -4

a < 1/6

Полученное условие говорит нам о том, что два различных корня у нашего уравнения будет не при любых значениях параметра «а», а только при тех, которые меньше одной шестой! Это глобальное требование, которое должно выполняться железно. Неважно, меньше 28 наша сумма кубов корней или больше. Значения параметра «а», большие или равные 1/6, нас заведомо не устроят. Гуд.) Соломки подстелили. Движемся дальше.

Теперь приступаем к загадочной сумме кубов корней. По условию она у нас должна быть меньше 28. Так и пишем:

Значит, для того чтобы ответить на вопрос задачи, нам надо совместно рассмотреть два условия:

А дальше начинаем отдельно работать с этой самой суммой кубов. Есть два способа такой работы: первый способ для трудолюбивых и второй способ — для внимательных.

Способ для трудолюбивых заключается в непосредственном нахождении корней уравнения через параметр. Прямо по общей формуле корней. Вот так:

Теперь составляем нужную нам сумму кубов найденных корней и требуем, чтобы она была меньше 28:

А дальше — обычная алгебра: раскрываем сумму кубов по формуле сокращённого умножения, приводим подобные, сокращаем и т.д. Если бы корни нашего уравнения получились покрасивее, без радикалов, то такой «лобовой» способ был бы неплох. Но проблема в том, что наши корни выглядят немного страшновато. И подставлять их в сумму кубов как-то неохота, да. Поэтому, для того чтобы избежать этой громоздкой процедуры, я предлагаю второй способ — для внимательных.

Для этого раскрываем сумму кубов корней по соответствующей формуле сокращенного умножения. Прямо в общем виде:

А дальше проделываем вот такой красивый фокус: во вторых скобках выражаем сумму квадратов корней через сумму корней и их произведение. Вот так:

Итого:

Казалось бы, и что из этого? Сейчас интересно будет! Давайте, посмотрим ещё разок на наше уравнение. Как можно внимательнее:

Чему здесь равен коэффициент при x²? Правильно, единичке! А как такое уравнение называется? Правильно, приведённое! А, раз приведённое, то, стало быть, для него справедлива теорема Виета:

Вот и ещё одна теорема нам пригодилась! Теперь, прямо по теореме Виета, подставляем сумму и произведение корней в наше требование для суммы кубов:

Осталось раскрыть скобки и решить простенькое линейное неравенство:

4·(16-18a-9) < 28

64–72a+36 < 28

-72a < 28-64+36

-72a < 0

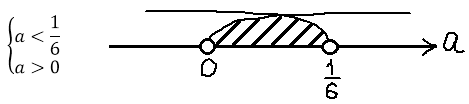
a > 0

Вспоминаем, что ещё у нас есть глобальное требование a < 1/6. Значит, наше полученное множество a > 0 необходимо пересечь с условием a < 1/6. Рисуем картинку, пересекаем, и записываем окончательный ответ.

Ответ:

Да. Вот такой маленький интервальчик. От нуля до одной шестой… Видите, насколько знание теоремы Виета, порой, облегчает жизнь!

Вот вам небольшой практический совет: если в задании говорится о таких конструкциях, как сумма, произведение, сумма квадратов, сумма кубов корней, то пробуем применить теорему Виета. В 99% случаев решение значительно упрощается.

Это были довольно простые примеры. Чтобы суть уловить. Теперь будут примеры посолиднее.

Например, такая задачка из реального варианта ЕГЭ:

Пример 3

Что, внушает? Ничего не боимся и действуем по нашему излюбленному принципу: «Не знаешь, что нужно, делай что можно!»

Опять аккуратно выписываем все коэффициенты нашего квадратного уравнения:

a = 1

b = -6

c = a²-4a

А теперь вчитываемся в условие задачи и находим слова «модуль разности корней уравнения». Модуль разности нас пока не волнует, а вот слова «корней уравнения» примем во внимание. Раз говорится о корнях (неважно, двух одинаковых или двух различных), то наш дискриминант обязан быть неотрицательным! Так и пишем:

D ≥ 0

Что ж, аккуратно расписываем наш дискриминант через параметр а:

D = (-6)² — 4·1·(12 + a²-4a) = 36 — 48 — 4а²+ 16а = -4а²+16а-12.

А теперь решаем квадратное неравенство. По стандартной схеме, через соответствующее квадратное уравнение и схематичный рисунок параболы:

Значит, для того чтобы у нашего уравнения в принципе имелись хоть какие-то корни, параметр а должен находиться в отрезке [-1; 3]. Это железное требование. Хорошо. Запомним.)

А теперь приступаем к этому самому модулю разности корней уравнения. От нас хотят, чтобы вот такая штука

принимала бы наибольшее значение. Для этого, ничего не поделать, но теперь нам всё-таки придётся находить сами корни и составлять их разность: x₁ — x₂. Теорема Виета здесь в этот раз бессильна.

Что ж, считаем корни по общей формуле:

Дальше составляем модуль разности этих самых корней:

Теперь вспоминаем, что корень квадратный — величина заведомо неотрицательная. Стало быть, без ущерба для здоровья, модуль можно смело опустить. Итого наш модуль разности корней выглядит так:

И эта функция f(a) должна принимать наибольшее значение. А для поиска наибольшего значения у нас есть такой мощный инструмент, как производная! Вперёд и с песнями!)

Дифференцируем нашу функцию и приравниваем производную к нулю:

Получили единственную критическую точку a = 2. Но это ещё не ответ, так как нам ещё надо проверить, что найденная точка и в самом деле является точкой максимума! Для этого исследуем знаки нашей производной слева и справа от двойки. Это легко делается простой подстановкой (например, а = 1,5 и а = 2,5).

Слева от двойки производная положительна, а справа от двойки — отрицательна. Это значит, что наша точка a = 2 и вправду является точкой максимума. Заштрихованная зона на картинке означает, что нашу функцию мы рассматриваем только на отрезке [1; 3]. Вне этого отрезка нашей функции f(a) попросту не существует. Потому, что в заштрихованной области наш дискриминант отрицательный, и разговоры о каких-либо корнях (и о функции тоже) бессмысленны. Это понятно, думаю.

Всё. Вот теперь наша задача полностью решена.

Ответ: 2.

Здесь было применение производной. А бывают и такие задачи, где приходится решать уравнения либо неравенства с так ненавистными многими учениками модулями и сравнивать некрасивые иррациональные числа с корнями. Главное — не бояться! Разберём похожую злую задачку (тоже из ЕГЭ, кстати).

Пример 4

Итак, приступаем. Первым делом замечаем, что параметр а ни в коем случае не может быть равен нулю. Почему? А вы подставьте в исходное уравнение вместо а нолик. Что получится?

Получили линейное уравнение, имеющее единственный корень x=2. А это уже совсем не наш случай. От нас хотят, чтобы уравнение имело два различных корня, а для этого нам необходимо, чтобы оно, как минимум, было хотя бы квадратным.)

Итак, а ≠ 0.

При всех остальных значениях параметра наше уравнение будет вполне себе квадратным. И, следовательно, чтобы оно имело два различных корня, необходимо (и достаточно), чтобы его дискриминант был положительным. То есть, первое наше требование будет D > 0.

А далее по накатанной колее. Считаем дискриминант:

D = 4(a-1)² — 4a(a-4) = 4a²-8a+4-4a²+16a = 4+8a

Вот так. Значит, наше уравнение имеет два различных корня тогда и только тогда, когда параметр a > -1/2. При прочих «а» у уравнения будет либо один корень, либо вообще ни одного. Берём на заметку это условие и движемся дальше.

Далее в задаче идёт речь о расстоянии между корнями. Расстояние между корнями, в математическом смысле, означает вот такую величину:

Зачем здесь нужен модуль? А затем, что любое расстояние (что в природе, что в математике) — величина неотрицательная. Причём здесь совершенно неважно, какой именно корень будет стоять в этой разности первым, а какой вторым: модуль — функция чётная и сжигает минус. Точно так же, как и квадрат.

Значит, ответом на вопрос задачи является решение вот такой системы:

Теперь, ясен перец, нам надо найти сами корни. Здесь тоже всё очевидно и прозрачно. Аккуратно подставляем все коэффициенты в нашу общую формулу корней и считаем:

Отлично. Корни получены. Теперь начинаем формировать наше расстояние:

Наше расстояние между корнями должно быть больше трёх, поэтому теперь нам надо решить вот такое неравенство:

Неравенство — не подарок: модуль, корень… Но и мы всё-таки уже решаем серьёзную задачу №18 из ЕГЭ! Делаем всё что можно, чтобы максимально упростить внешний вид неравенства. Мне здесь больше всего не нравится дробь. Поэтому первым делом я избавлюсь от знаменателя, умножив обе части неравенства на |a|. Это можно сделать, поскольку мы, во-первых, в самом начале решения примера договорились, что а ≠ 0, а во-вторых, сам модуль — величина неотрицательная.

Итак, смело умножаем обе части неравенства на положительное число |a|. Знак неравенства сохраняется:

Вот так. Теперь в нашем распоряжении имеется иррациональное неравенство с модулем. Ясное дело, для того чтобы решить его, надо избавляться от модуля. Поэтому придётся разбивать решение на два случая — когда параметр а, стоящий под модулем, положителен и когда отрицателен. Другого пути избавиться от модуля у нас, к сожалению, нет.

Итак!

Случай 1 (a>0, |a|=a)

В этом случае наш модуль раскрывается с плюсом, и неравенство (уже без модуля!) принимает следующий вид:

Неравенство имеет структуру: «корень больше функции». Такие иррациональные неравенства решаются по следующей стандартной схеме:

Отдельно рассматривается случай а), когда обе части неравенства возводятся в квадрат и правая часть неотрицательна и отдельно — случай б), когда правая часть всё-таки отрицательна, но зато сам корень при этом извлекается.) И решения этих двух систем объединяются.

Тогда, в соответствии с этой схемой, наше неравенство распишется вот так:

А теперь можно существенно упростить себе дальнейшую работу. Для этого вспомним, что в случае 1 мы рассматриваем только a>0. С учётом этого требования, вторую систему можно вообще вычеркнуть из рассмотрения, поскольку, второе неравенство в ней (3a<0) эквивалентно неравенству a<0, а условия a>0 и a<0 — это два взаимно исключающих требования.

Упрощаем нашу совокупность с учётом главного условия a>0:

Вот так. А теперь решаем самое обычное квадратное неравенство:

Нас интересует промежуток между корнями. Стало быть,

Отлично. Теперь этот промежуток пересекаем со вторым условием системы a>0:

Есть. Таким образом, первым кусочком ответа к нашему неравенству (а пока не ко всей задаче!) будет вот такой интервал:

Всё. Случай 1 разложен по полочкам. Переходим к случаю 2.

Случай 2 (a<0, |a|=-a)

В этом случае наш модуль раскрывается с минусом, и неравенство принимает следующий вид:

Опять имеем структуру: «корень больше функции». Применяем нашу стандартную схему с двумя системами (см. выше):

С учётом общего требования a<0, мы снова, как и в предыдущем случае, проводим максимальные упрощения: вычёркиваем вторую систему в силу противоречивости двух требований -3а < 0 и нашего общего условия a<0 для всего случая 2.

А дальше снова решаем обычное квадратное неравенство:

И опять сокращаем себе работу. Ибо оно у нас уже решено в процессе разбора случая 1! Решение этого неравенства выглядело вот так:

Осталось лишь пересечь этот интервал с нашим новым условием a<0.

Пересекаем:

Вот и второй кусочек ответа готов:

Кстати сказать, как я узнал, что ноль лежит именно между нашими иррациональными корнями? Легко! Очевидно, что правый корень заведомо положителен. А что касается левого корня, то я просто в уме сравнил иррациональное число

с нулём. Вот так:

А теперь объединяем оба найденных интервала. Ибо мы решаем совокупность (а не систему):

Готово дело. Эти два интервала — это пока ещё только решение неравенства

Кто забыл, данное неравенство отвечает у нас за расстояние между корнями нашего уравнения. Которое должно больше 3. Но! Это ещё не ответ!

Ещё у нас есть условие положительного дискриминанта! Неравенство a>-1/2, помните? Это значит, что данное множество нам ещё надо пересечь с условием a>-1/2. Иными словами, теперь мы должны пересечь два множества:

Но есть одна проблемка. Мы не знаем, как именно расположено на прямой число -1/2 относительно левого (отрицательного) корня. Для этого нам придётся сравнить между собой два числа:

Поэтому сейчас берём черновик и начинаем сравнивать наши числа. Примерно так:

Это значит, что дробь -1/2 на числовой прямой находится левее нашего левого корня. И картинка к окончательному ответу задачи будет какая-то вот такая:

Всё, задача полностью решена и можно записывать окончательный ответ.

Ответ:

Ну как? Уловили суть? Тогда решаем самостоятельно.)

1. Найдите все значения параметра b, при которых уравнение

ax² + 3x +5 = 0

имеет единственный корень.

2. Найдите все значения параметра а, при каждом из которых больший корень уравнения

x² — (14a-9)x + 49a² — 63a + 20 = 0

меньше 9.

3. Найдите все значения параметра а, при каждом из которых сумма квадратов корней уравнения

x² — 4ax + 5a = 0

равна 6.

4. Найдите все значения параметра а, при каждом из которых уравнение

x² + 2(a-2)x + a + 3 = 0

имеет два различных корня, расстояние между которыми больше 3.

Ответы (в беспорядке):

Источник

Решение задач с параметром вызывает
затруднения у учащихся, так как практических
заданий по данной теме в школьных учебниках
недостаточно.

Цели разработки темы

формирование устойчивого интереса к
познавательному процессу при изучении
математики и оценка возможности овладения
предметом с точки зрения дальнейшей перспективы;
обеспечение прочного и сознательного усвоения
учащимися системой математических знаний,
умений и навыков;
формирование качества мышления, характерного
для математической деятельности и необходимые
человеку для жизни в современном обществе;
выявление и развитие математических
способностей учащихся.
Задачи разработки темы:
показать универсальные алгоритмы для решения
квадратных уравнений с параметром;
научить приемам решения различного класса
задач с параметром, способствовать овладению
технических и интеллектуальных математических
умений на уровне свободного их использования;
использование новых современных
педагогических технологий обучения.

В математике параметр – это постоянная
величина, выраженная буквой, сохраняющая свое
постоянное значение лишь в условиях данной
задачи (“параметр” с греческого “parametron” –
отмеривающий)..

Если ставится задача для каждого значения
параметра а из некоторого числового
множества А решить уравнение F(х;а)= 0
относительно х, то это уравнение называют
уравнением с переменной х и параметром а,
а множество А – областью изменения параметра.
Под областью определения уравнения F(х;а)=0
с параметром а понимаются такие системы
значений х и а, при которых F(х;а)
имеет смысл. Все значения параметра а, при
которых F(х;а) не имеет смысла, включать в
число значений параметра, при которых уравнение
не имеет решений. Под областью изменения
параметра (если не сделано специальных оговорок)
берется множество всех действительных чисел, а
задачу решения уравнения с параметром
формулировать следующим образом: решить
уравнение F(х;а)=0 (с переменной х и параметром а) –
это значит на множестве действительных чисел
решить семейство уравнений, получающихся из
данного уравнения при всех действительных
значениях параметра или установить, что решений
нет.

В связи с тем, что выписать каждое уравнение из
бесконечного семейства уравнений невозможно, но
каждое уравнение семейства должно быть решено,
следовательно, необходимо по некоторому
целесообразному признаку разбить множество
всех значений параметра на подмножества и решить
затем заданное уравнение на каждом из этих
подмножеств. Для разбиения множества значений
параметра на подмножества, удобно пользоваться
теми значениями параметра, при которых или при
переходе через которые происходят качественные
изменения уравнения. Такие значения параметра
называются контрольными.

1. КВАДРАТНЫЕ УРАВНЕНИЯ С ПАРАМЕТРОМ

Задачи с параметрами можно разделить на два
больших класса:

задачи, в которых необходимо при всех значениях
параметра из некоторого множества решить
уравнение;
задачи, в которых требуется найти все значения
параметра, при каждом из которых решение
уравнения удовлетворяют некоторым условиям.

В зависимости от типа задачи изменяется и вид
ответа. В первом случае в решении и ответе должны
быть рассмотрены все возможные значения
параметров. Если хотя бы одно значение
какого-либо параметра не исследовано, решение
задачи не может быть признано полным.

Во втором случае в ответе перечисляются только
те значения параметра, при которых выполнены
условия задачи, а при решении подобных задач
обычно решать заданное уравнение нет
необходимости.

Уравнение вида Ах² + Вх + С= 0 , где А, В,
С — выражения, зависимые от параметра, х – переменная
— называется квадратным уравнением с параметром.

Уравнение вида ах²+вх+с=0, где , а, в, с – действительные
числа, называют квадратным уравнением. D=в²-4ас
называется дискриминантом квадратного
уравнения (“дискриминант” по – латыни
“различитель”).

В зависимости от значения дискриминанта
возможны три случая:

D > 0. Данное квадратное уравнение имеет два
действительных корня

D=0. Данное уравнение имеет корень двойной
кратности

D<0. Данное уравнение не имеет
действительных корней.

Для уравнения ах²+2кх+с=0 со вторым
коэффициентом (в=2к) четным, для нахождения
корней удобно пользоваться формулами: , где D₁=
=к²-ас.

№ 1.1. Определите все значения параметра а при
которых уравнение ах²+2(а+1)х+а+3=0 имеет
два неравных корня.

Решение.

Если а=0, то имеем 0·х²+2(0+1)х+0+3=0, 2х+3=0 — данное
уравнение является линейным, х=-1,5 – единственный
корень. Итак, а=0 не удовлетворяет условию задачи.

Если а?0, то уравнение имеет два различных
корня, когда дискриминант >0.

Найдем=(а+1)²-а(а+3)=-а+1,-а+1>0,
а<1. С учетом а 0 ответ: .

№ 1.2. Определите все значения параметра а, при
котором уравнение 2ах²-4(а+1)х+4а+1=0 имеет
один корень.

Решение.

Если а=0, то имеем 2·0·х²-4(0+1)х+4·0+1=0, -4х+1=0 —
данное уравнение является линейным, х=0,25 –
единственный корень. Итак, а=0 удовлетворяет
условию задачи.

Если а 0, то исходное
уравнение является квадратным и имеет
единственный корень при =0. Найдем =(2(a+1))²-2a(4а+1) = -4a²+6a+4,4a²+6a+4=0,
а₁=2, а₂=-0,5.

С учетом а=0, запишем ответ: а=-0,5, а=0, а=2.

№ 1.3. При каких значениях параметра а квадратное
уравнение (5а-1)х²-(5а+2)х+3а-2=0 не имеет
корней?

Решение.

Если 5а-1=0,а=0,2, то имеем (5*0,2-1)х²-(5*0,2+2)х+3*0,2-2=0,

-3х-1,4=0 — данное уравнение является линейным, х = — единственный
корень.

Итак, а=0,2 не удовлетворяет условию задачи.

Если а 0,2, то квадратное
уравнение не имеет корней, если дискриминант
квадратного уравнения D<0. Найдем D=(5а+2)²-4(5a-1)(3а-2)=-35a²+72a-4,-35a²+72a-4<0,

35a²-72a+4>0, а₁=2, а₂=, (а-2)(а-)>0. С учетом а 0,2 ответ:

№ 1.4. Определите все значения параметра а при
которых уравнение (2а-1)х²+ах+2а-3=0 имеет
не более одного решения.

Решение.

Если 2а-1=0,а=0,5, то имеем (2·0,5-1)х²+0,5·х+2·0,5-3=0,
0,5х-2=0 — данное уравнение является линейным, х=4 —
единственный корень.

Итак, а=0,5 удовлетворяет условию задачи.

Если а 0,5, то квадратное
уравнение имеет не более одного решения, если
дискриминант квадратного уравнения D0.

Найдем D=а²-4(2a-1)(2а-3)=-15a²+32a-12, -15a²+32a-120,

15a²-32a+12?0, а₁=, а₂=, (а-)(а-)
0.

С учетом а 0,5, имеем .

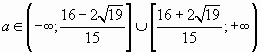
С учетом а=0,5, запишем ответ: .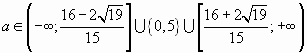

2. НЕПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯ С
ПАРАМЕТРОМ.

Квадратное уравнение ах²+вх+с=0, где а 0 называется неполным,
если хотя бы один из коэффициентов в или с
равен 0.

Общая схема решения неполных квадратных
уравнений с параметрами.

ах²=0, где а 0, в=0,
с=0. Если а 0 ,то
уравнение примет вид: х²=0, х=0.

Следовательно, уравнение имеет два совпадающих
корня, равных нулю.

Если а=0, то х — любое действительное
число.

ах²+с=0, где а0, в=0, с0. Если а0,то уравнение примет вид: следовательно, уравнение
имеет корни, то они равны по абсолютной величине,
но противоположны по знаку; < 0, то , следовательно, уравнение
корней не имеет. Если а=0 и с0, то уравнение действительных корней не
имеет.

ах²+вх=0, где а0, в0, с=0. Если а0,то уравнение примет вид: х(а+в)=0,или Если а=0, то вх=0,
х=0.

№ 2.1. При каких значениях параметра а оба
корня уравнения 2х²+(3а²-|а|)х-а²-3а=0
равны нулю?

Решение.

Оба корня квадратного уравнения равны нулю,
когда

№ 2.2. При каких значениях параметра а, корни
уравнения 2 х²-(5а-3)х+1=0 равны по модулю,
но противоположны по знаку?

Решение.

Корни квадратного уравнения равны по модулю, но
противоположны по знаку, когда 5а-3=0,а=0,6, но с
учетом того, что имеем уравнение 2х²+1=0, х²=-0,5,
которое корней не имеет. Ответ: .

№ 2.3. При каких значениях параметра а один
из двух различных корней уравнения 3х²+х+2а-3=0
равен нулю?

Решение.

Параметр должен удовлетворять условию: 2а-3=0,
а=1,5. Ответ: а=1,5.

№ 2.4. При каких значениях параметра а корни
уравнения 3х²+(а²-4а)х+а-1=0 равны по
модулю, но противоположны по знаку?

Решение.

Корни квадратного уравнения равны по модулю, но
противоположны по знаку, когда:

Ответ: а=0.

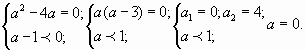
№ 2.5. Решить относительно х неполное
квадратное уравнение х²-2а+1=а.

Решение.

х²=а+2а-1; х²=3а-1.

Если 3а-1=0, а=
,то уравнение имеет два совпадающих корня, равных
нулю.

Если 3а-1<0, а<, то уравнение корней не имеет.

Если 3а-1>0. а>, то уравнение имеет два корня .

Ответ: при арешений
нет; при а= х=0;
при

3. ИССЛЕДОВАНИЕ И РЕШЕНИЕ КВАДРАТНЫХ
УРАВНЕНИЙ С ПАРАМЕТРОМ.

№ 3.1. Исследовать и решить уравнение с
параметром х²–2(а-1)х+2а+1=0.

Решение.

Найдем дискриминант: D=(а — 1)² -2а – 1= а²-2а+1-2а-1= а²— 4а.

D > 0, а²—
4а > 0, а (а -4) > 0, а < 0 или а > 4, то уравнение
имеет два действительных корня ;

D =0, а (а-4)=0,
а=0, то х=а-1, х=0-1, х=-1, а=4,то х=а-1, х=4-1, х=3;

D < 0, а(а-4)
< 0, 0 < а < 4, то уравнение не имеет корней.

Ответ: при а
; при а=0 х=-1;

при а=4 х=3; при а корней нет.

№ 3.2. Исследовать и решить уравнение с
параметром (а–1)х²+2(а+1)х+а–2= 0.

Решение.

1) При а-1=0, а=1 имеем линейное уравнение 4х-1=0, х=– единственное
решение.

2) При а 1 уравнение
является квадратным, найдем дискриминант:

D₁ = (а+1)²-(а–1)(2а-2)=а²+2а+1-а²+2а+а-2=5а-1.

D₁>0. 5а-1>0, а>, а 1, то
уравнение имеет два корня .

D₁=0. 5а-1=0, а=, то уравнение имеет два равных корня .

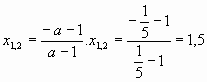
D₁ < 0. 5а-1< 0, а<, то уравнение не имеет
действительных корней.

Ответ: при а
корней нет; при а = х=1,5; при а=1 х =;

при а .

№ 3.3. Исследовать и решить уравнение с
параметром х²+2х- 8–а(х–4)=0.

Решение.

х²+2х-8–ах+4а=0; х²+(2-а)х+4а-8=0.
Уравнение является квадратным.

Найдем дискриминант: D=(2-а)²-4(4а-8)=4-4а+а²-16а+32=
а²-20а+36.

D>0. а²20а+36>0, (а-18)(а -2)>0, а <2 или а >18,
то уравнение имеет два действительных корня .

D=0. (а-18)(а-2)=0, а=2, то ; а=18, то ;

D < 0. (а-18)(а-2)< 0, 2< а <18, то уравнение не имеет
действительных корней.

Ответ: при а
; при а=2 х=0;
при а=18 х=8; при а корней нет.

4. РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ С
ПРИМЕНЕНИЕМ теоремы ВИЕТА.

Если в квадратном уравнении коэффициент при х²
равен 1, то уравнение принимает вид х²+px+q,
где p и q — некоторые числа называется
приведенным квадратным уравнением.

Теорема Виета: Сумма корней приведенного
квадратного уравнения равна второму
коэффициенту, взятому с противоположным знаком,
а произведение корней равно свободному члену.

х²+px+q=0, где х₁ и х₂ – корни
квадратного уравнения, то х₁ + х₂=-p; х₁
х₂=q.

ах²+вх+с=0, где х₁ и х₂ – корни
квадратного уравнения, то

Справедливо утверждение, обратное теореме
Виета.

Теорема: Если числа p и q таковы, что их
сумма равна -p, а произведение равно q. то
эти числа являются корнями уравнения х²+px+q=0.

№ 4.1. При каком значении параметра а сумма
обратных величин действительных корней
уравнения 2х²-2ах+а²-2=0 равна ?

Решение

Пусть х₁ и х₂ – корни квадратного
уравнения, по условию _.

По теореме Виета: 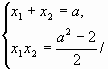Используя соотношения между корнями и
условие задачи, имеем:

Найдем дискриминант квадратного уравнения:

Имеем: 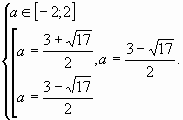Ответ:
при

№ 4.2. В уравнении (а²-5а+3)х²+(3а-1)х+2=0 определите
а так, чтобы один из корней был вдвое больше
другого.

Решение.

Пусть х₁ и х₂ – корни квадратного
уравнения, по условию х₁ =2 х_2.Заметим,
что кратное сравнение выполняется только для
положительных чисел.

По теореме Виета и условию задачи имеем
систему:

Составим и решим уравнение:

Можно вычислить дискриминант данного
уравнения, а затем проверить, удовлетворяет ли
данное значение параметра а условию, что
дискриминант неотрицателен, а так же, что корни
положительны. Однако в данной задаче значительно
проще сделать проверку, подставив это значение а
в исходное уравнение.

При Корни
отрицательны и кратно не сравниваются, поэтому
задача решений не имеет. Ответ: решений нет.

№ 4.3. Найти все значения параметра а, при
которых квадратное уравнение (а+2)х²–ах-а=0
имеет два корня, расположенных на числовой
прямой симметрично относительно точки х=1.

Решение.

При а+2=0, а=-2, то 2х+2=0, х=-1 – единственное решение,
следовательно данное значение а не
удовлетворяет условию задачи.

При а-2. Пусть х₁ и х₂
– корни квадратного уравнения, по условию х₁
=1-у, х_2.=1+у, где у – некоторое действительное
число.

По теореме Виета имеем:

Решим первое уравнение системы: 2(а+2)=а, а=-4.

Найдем дискриминант данного квадратного
уравнения:

Данное значение а=-4 удовлетворяет полученным
значениям. Ответ: а=-4.

Ответ: при а = — 4.

ИСПОЛЬЗУЕМАЯ ЛИТЕРАТУРА.
Азаров А.И., Барвенов С.А., Федосенко В.С. Методы
решения задач с параметрами. Минск; “Аверсэв”.
2005.
Амелькин В. В., Рабцевич В. Л. Задачи с
параметрами. Минск; “Асар”. 1996.
Данкова И. Н., Бондаренко Т. Е., Емелина Л. Л.,
Плетнева О. К.Предпрофильная подготовка учащихся
9 классов по математике. Москва; “5 за знания”.2006.
Литвиненко В. Н., Мордкович А. Г.. Практикум по
элементарной математике. Москва;
“Просвещение”.1991.
Родионов Е. М. Решение задач с параметрами.
Москва; “Русь – 90”. 1995.
Студенецкая В. Н., Сагателова Л. С. Математика 8 –
9классы: сборник элективных курсов. Волгоград;
“Учитель”. 2006.
Шарыгин И. Ф. Решение задач. Москва;
“Просвещение”. 1994.
Шахмейстер А. Х. Уравнения и неравенства с
параметрами. Санкт-Петербург; “Петроглиф”. 2006.

Источник

Дорогой друг! Если ты никогда не решал задач с параметрами – прочитай статьи «Что такое параметр» и «Графический способ решения задач с параметрами». Квадратные уравнения, а тем более неравенства с параметрами только на первый взгляд кажутся простыми. Чтобы уверенно решать их, надо знать определенные приемы. О некоторых мы расскажем.

И заодно – стоит повторить темы «Квадратные уравнения» и «Квадратичные неравенства».

Разберем сначала подготовительные задачи. А в конце – реальную задачу ЕГЭ.

1. Найдите все значения a, при которых уравнение $left ( a-2 right )x^{2}+2left ( a-2 right )x+2=0$ не имеет действительных корней.

Всегда ли это уравнение является квадратным относительно переменной х? – Нет, не всегда. В случае, когда коэффициент при $x^{2}$ равен нулю, оно станет линейным.

Рассмотрим два случая – когда это уравнение квадратное и когда оно линейное.

Тогда уравнение примет вид 2 = 0. Такое уравнение не имеет действительных корней, что удовлетворяет условию задачи.

Уравнение будет квадратным. Квадратное уравнение не имеет действительных корней тогда и только тогда, когда его дискриминант отрицательный.

Найдем дискриминант :

$D=b^{2}-4ac=4left ( a-2 right )^{2}-8left ( a-2 right )$ < 0.

$left ( a-2 right )^{2}-2left ( a-2 right )$ < 0

< 0

Решив неравенство, получим

С учетом пункта 1, получим ответ: .

2. Найдите все значения a, при каждом из которых сумма квадратов действительных корней уравнения

$x^{2}-ax+a-2=0$

минимальна.

Мы привыкли находить корни квадратного уравнения по известной формуле, с помощью дискриминанта. Однако для задач с параметрами такой способ подходит не всегда. А вот теорема Виета нам поможет.

В условии сказано: «Сумма квадратов действительных корней…» Это значит, во-первых, что корни есть, а во-вторых, их должно быть два. А это будет в случае, когда дискриминант положителен ( > 0).

Если $x_{1}$ и $x_{2}$ – корни квадратного уравнения
$ax^{2}+bx+c=0$ , то по теореме Виета:

$left{begin{matrix}x_{1}+x_{2}=frac{-b}{a}\!!!!!!!x_{1}x_{2}=frac{c}{a}end{matrix}right.$

В нашем случае:

Решим первое неравенство системы

Квадратный трехчлен в левой части не имеет корней, так как дискриминант равен -32, то есть отрицателен. Поэтому неравенство будет выполняться для всех действительных значений .

Возведем второе уравнение системы в квадрат:

$left{begin{matrix}x_{1}^{2}+2x_{1}x_{2}+x_{2}^{2}=a^{2}\!!!!!!!!!!!!!x_{1}x_{2}=a-2end{matrix}right.$

Из этих двух уравнений выразим сумму квадратов $x_{1}$ и $x_{2}$ .

$x_{1}^{2}+2left ( a-2 right )+x_{2}^{2}=a^{2}$

$x_{1}^{2}+x_{2}^{2}=a^{2}-2left ( a-2 right )$

$x_{1}^{2}+x_{2}^{2}=a^{2}-2a+4$

Значит, сумму квадратов корней уравнения можно выразить через параметр

$S=a^{2}-2a+4$

График функции — парабола, ее ветви направлены вверх, минимум будет достигаться в ее вершине. Найдем вершину параболы: $a=frac{2}{2}=1$

Ответ: 1

3) Найдите все значения , при каждом из которых все решения уравнения

$left ( a-3 right )x^{2}-2ax+5a=0$

положительны.

Как и в первой задаче, уравнение является квадратным, кроме случая, когда a-3=0 . Рассмотрим этот случай отдельно

1) a=3 . Получим линейное уравнение

x=2,5

У него единственный корень, причем положительный. Это удовлетворяет условию задачи.

2) При aneq 3 уравнение будет квадратным. Нам надо, чтобы решения существовали, причем были положительными. Раз решения есть, то Dgeq 0 .

Покажем один из приемов решения квадратичных уравнений и неравенств с параметрами. Он основан на следующих простых утверждениях:

— Оба корня квадратного уравнения $boldsymbol{x_{1}}$ и $boldsymbol{x_{2}}$ положительны тогда и только тогда, когда их сумма положительна и произведение положительно.

Очевидно, что сумма и произведение двух положительных чисел также положительны. И наоборот – если сумма и произведение двух чисел положительны, то и сами числа положительны.

— Оба корня квадратного уравнения $boldsymbol{x_{1}}$ и $boldsymbol{x_{2}}$ отрицательны тогда и только тогда, когда их сумма отрицательна, а произведение положительно.

Корни квадратного уравнения $boldsymbol{x_{1}}$ и $boldsymbol{x_{2}}$ имеют разные знаки тогда и только тогда, когда их произведение отрицательно.

Сумма и произведение корней входят в формулировку теоремы Виета, которой мы и воспользуемся. Получим

Второе и третье неравенства имеют одинаковое решение . Решение первого неравенства:
.

Решение системы: .

С учетом пункта 1 получим ответ

Ответ:

4. При каких значениях параметра a уравнение $left ( a-1 right )4^{x}+left ( 2a-3 right )6^{x}=left ( 3a-4 right )9^{x}$

имеет единственное решение?

Уравнение является показательным, причем однородным. Мы умеем решать такие уравнения! Разделим обе части на $9^{x}neq 0$ .

Получим:

$left ( a-1 right )left ( frac{2}{3} right )^{2x}+left ( 2a-3 right )left ( frac{2}{3} right )^{x}=3a-4$

Сделаем замену

$left ( a-1 right )t^{2}+left ( 2a-3 right )t-left (3a-4 right )=0$

Для того, чтобы исходное уравнение имело единственное решение, нужно, чтобы уравнение относительно t имело ровно один положительный корень.

1) В случае a=1 уравнение будет линейным

-t+1=0

t=1

Значит, a=1 подходит. В этом случае уравнение имеет единственный положительный корень.

2) Если aneq 1 , уравнение будет квадратным.

Его дискриминант

$D=left ( 2a-3 right )^{2}+4left ( a-1 right )left ( 3a-4 right )=16a^{2}-40a+25=left ( 4a-5 right )^{2}$

Дискриминант является полным квадратом и поэтому всегда неотрицателен. Уравнение имеет либо один, либо два корня. В этом случае несложно найти корни в явном виде.

$t_{1}=frac{3-2a+4a-5}{2left ( a-1 right )}=frac{2a-2}{2a-2}=1$

$t_{2}=frac{3-2a-4a+5}{2left ( a-1 right )}=frac{4-3a}{a-1}=1$

Один корень получился не зависящим от параметра, причем положительным. Это упрощает задачу.

Для того, чтобы уравнение имело единственный положительный корень, нужно, чтобы либо второй был отрицательным, либо равным нулю, либо чтобы корни совпадали. Рассмотрим все случаи.

а) $t_{2}leq 0Rightarrow frac{4-3a}{a-1}leq 0$

Тогда $ain left ( -infty;;1 right )cup left [ frac{4}{3};+infty right )$

б) $t_{1}=t_{2}=1Rightarrow frac{4-3a}{a-1}=1$
a=1,25

Объединив все случаи, получим ответ.

Ответ: $ain left ( -infty;;1 right ]cup left { 1,25 right }cup left [ frac{4}{3};+infty right )$

И наконец – реальная задача ЕГЭ.

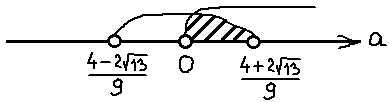
5. При каких значениях a система $left{begin{matrix}left ( a-1 right )x^{2}+2ax+a+4leq 0\ax^{2}+2left ( a+1 right )x+a+1geq 0end{matrix}right.$ имеет единственное решение?

Решением квадратного неравенства может быть:

1) отрезок

2) 2 луча

3) точка

4) ∅

В каких случаях система двух квадратных неравенств имеет единственное решение:

1) единственная общая точка двух лучей-решений ( или интервалов-решений)

2) одно из неравенств имеет решение – точку, которая является решением второго неравенства

Рассмотрим первый случай.

Решим систему

$left{begin{matrix}left ( a-1 right )x^{2}+2ax+a+4leq 0\ax^{2}+2left ( a+1 right )x+a+1geq 0end{matrix}right.Rightarrowleft{begin{matrix}D_{1}=4a^{2}-4left ( a-1 right )left ( a+4 right )\D_{2}=4left ( a+1 right )^{2}-4aleft ( a+1 right )end{matrix}right.$

Если $x_{0}$ является решением 1 и 2 уравнений, то $x_{0}$ является решением уравнения $x^{2}+2x-3=0$ (вытекает из второго первое) ⇒ $x_{0}=1$ или $x_{0}=-3.$

Если $x_{0}=1Rightarrow a=-frac{3}{4}$ , при этом система примет вид:

$left{begin{matrix}left ( -frac{3}{4} -1right )left ( x-1 right )left ( x+frac{13}{7} right )leq 0\!!!!!!-frac{3}{4}left ( x-1 right )left ( x+frac{1}{3} right )geq 0end{matrix}right.Leftrightarrowleft{begin{matrix}left ( x-1 right )left ( x+frac{13}{7} right )geq 0\left ( x-1 right )left ( x+frac{1}{3} right )leq 0end{matrix}right.$

Второй корень первого уравнения:
$frac{a+4}{a-1}=frac{-frac{3}{4}+4}{-frac{3}{4}-1}=-frac{13}{7}$

Второй корень второго первого:
$frac{a+1}{a}=-frac{1}{3}$

Единственное решение x=1.

Если $x_{0}=-3Rightarrow a=frac{5}{4}$ , при этом система примет вид:

$left{begin{matrix}left ( x+3 right )left ( x+7 right )leq 0\left ( x+3 right )left ( x+frac{3}{5} right )geq 0end{matrix}right.$ – бесконечно много решений, не подходит.

Рассмотрим второй случай.

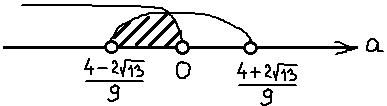
$left ( a-1 right )x^{2}+2ax+a+4leq 0$ – решением является точка, если $D=0,;a=frac{4}{3}Rightarrow x=-4$ – является решением второго неравенства.

$ax^{2}+2left ( a+1 right )x+a+1geq 0$ – решением является точка, если – не является решением первого неравенства.

Ответ: $a=-frac{3}{4},;a=frac{4}{3}$

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Квадратные уравнения и квадратичные неравенства с параметрами» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
07.05.2023

Источник